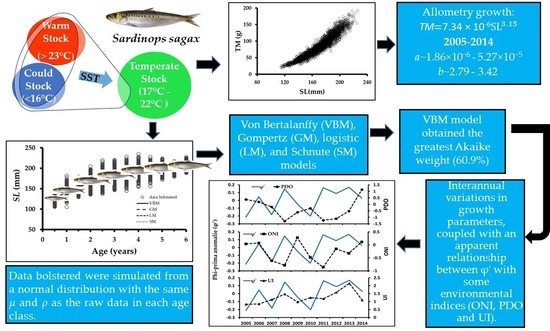
Allometry and Individual Growth of the Temperate Pacific Sardine (Sardinops sagax) Stock in the Southern California Current System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Data Collection
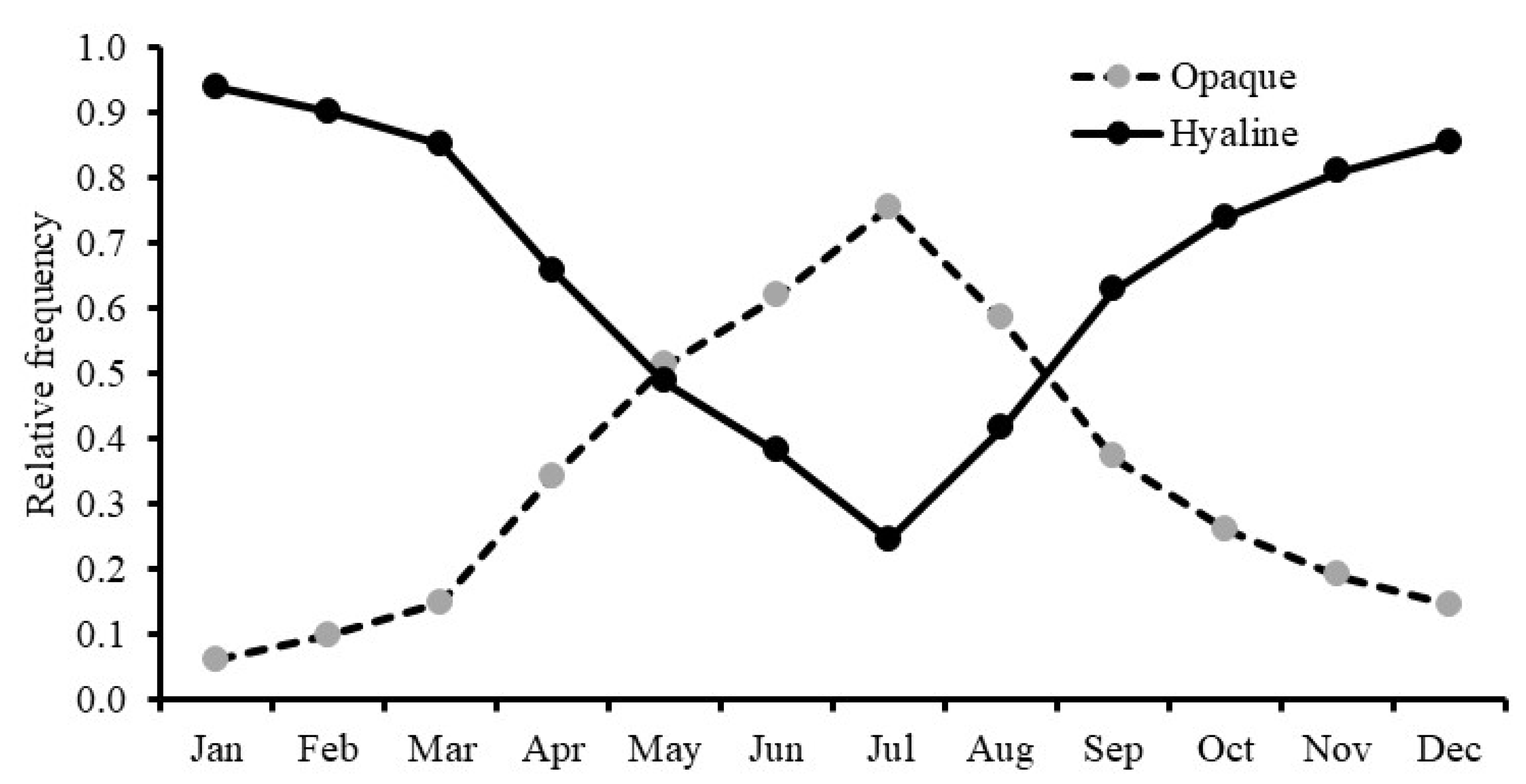
2.3. Age Determination
2.4. Differentiating Sardinops sagax Stock Catches
2.5. Body Mass–Length Relationship
2.6. Selecting the Best Fish Growth Model
2.7. Sensitivity Analysis
2.7.1. Sensitivity in Growth Parameters of VBM
2.7.2. Model VBM—Three Parameters (VBM-3)
2.7.3. Model VBM—Two Parameters (VBM-2)
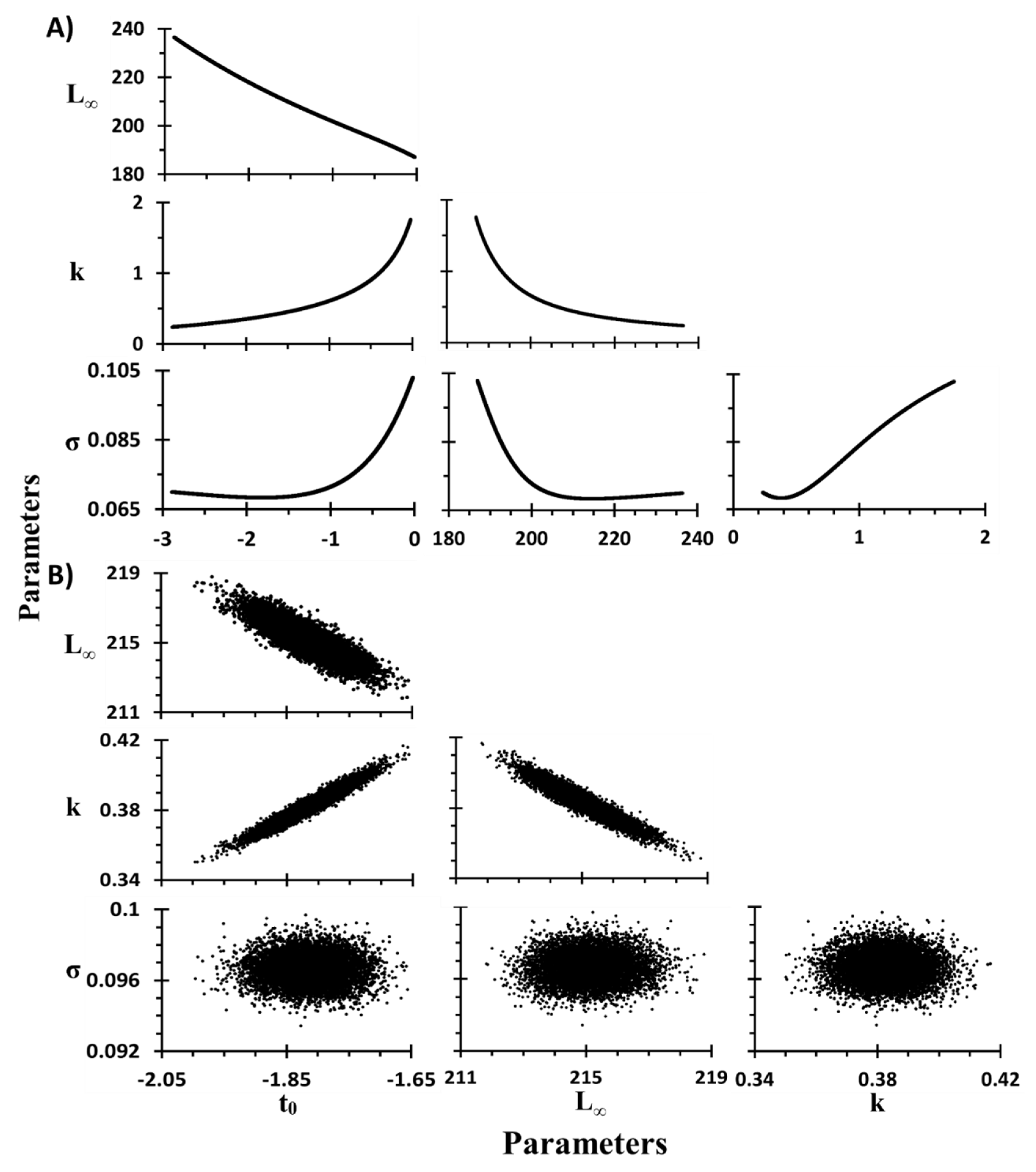
2.7.4. Estimation of Parameters and Confidence Intervals
2.8. Annual Growth (2005–2014)
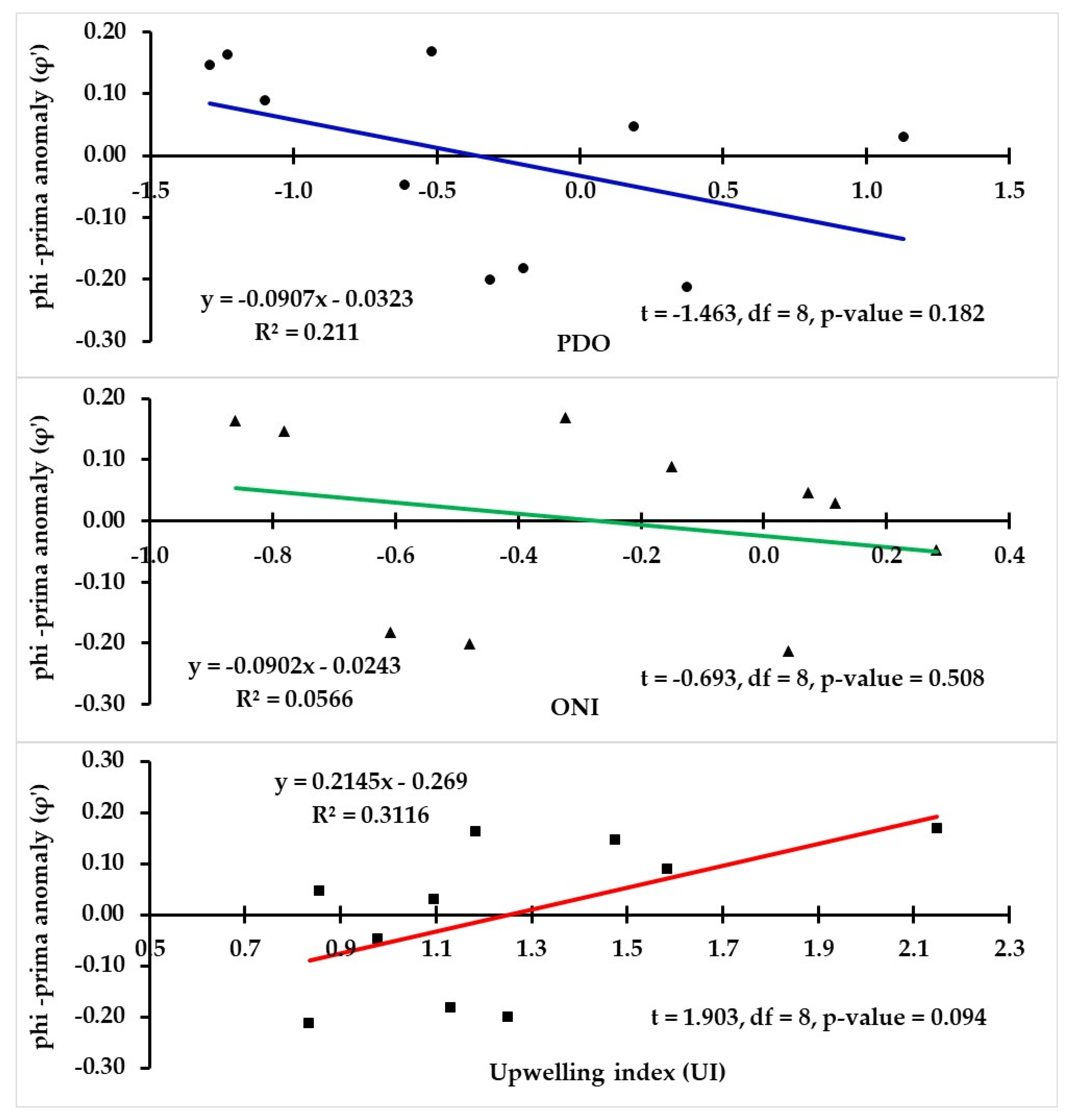
2.9. Relationship between Individual Growth and Environmental Conditions
3. Results
3.1. Differentiating of Sardinops sagax Stock Catches
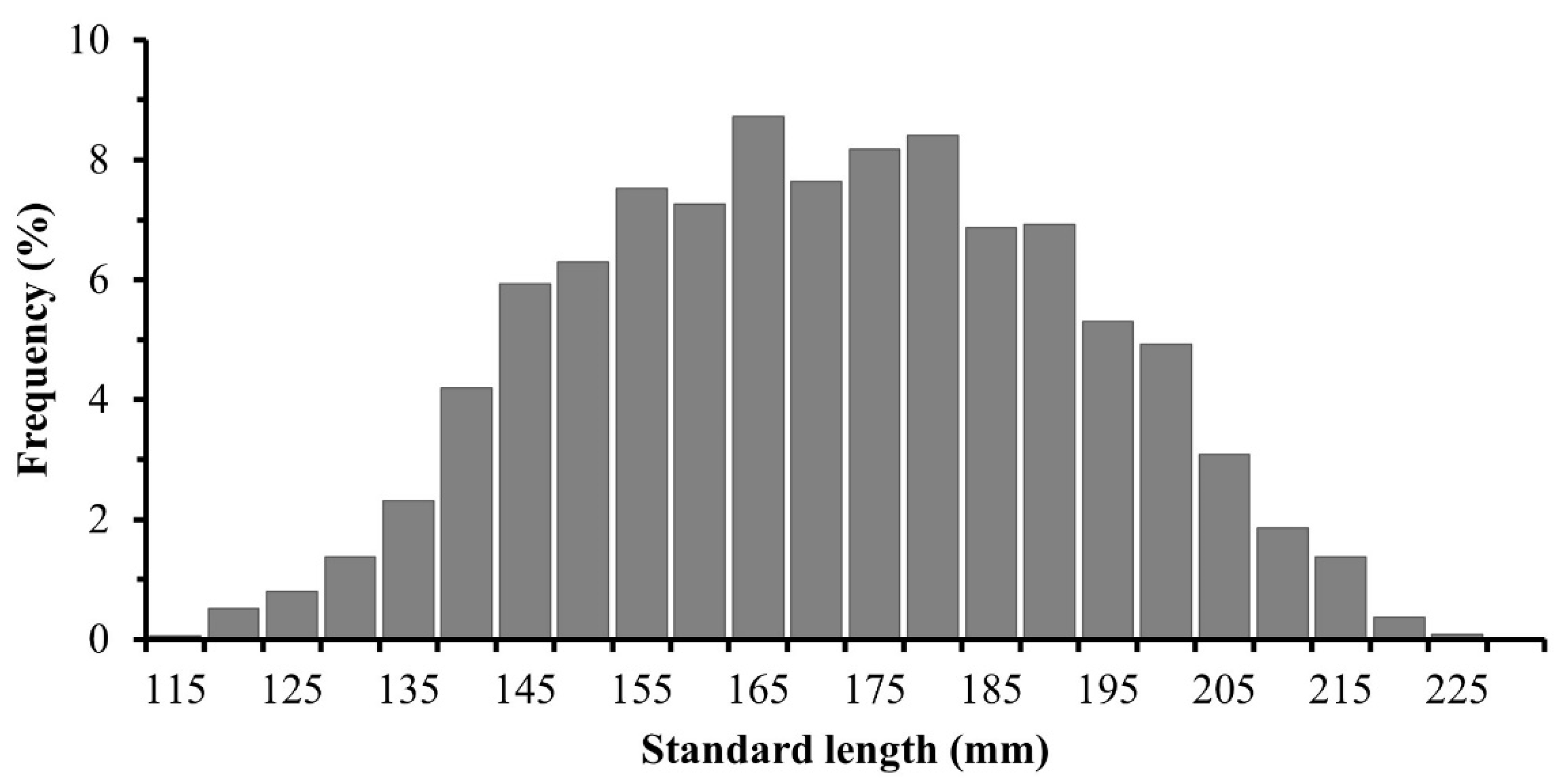
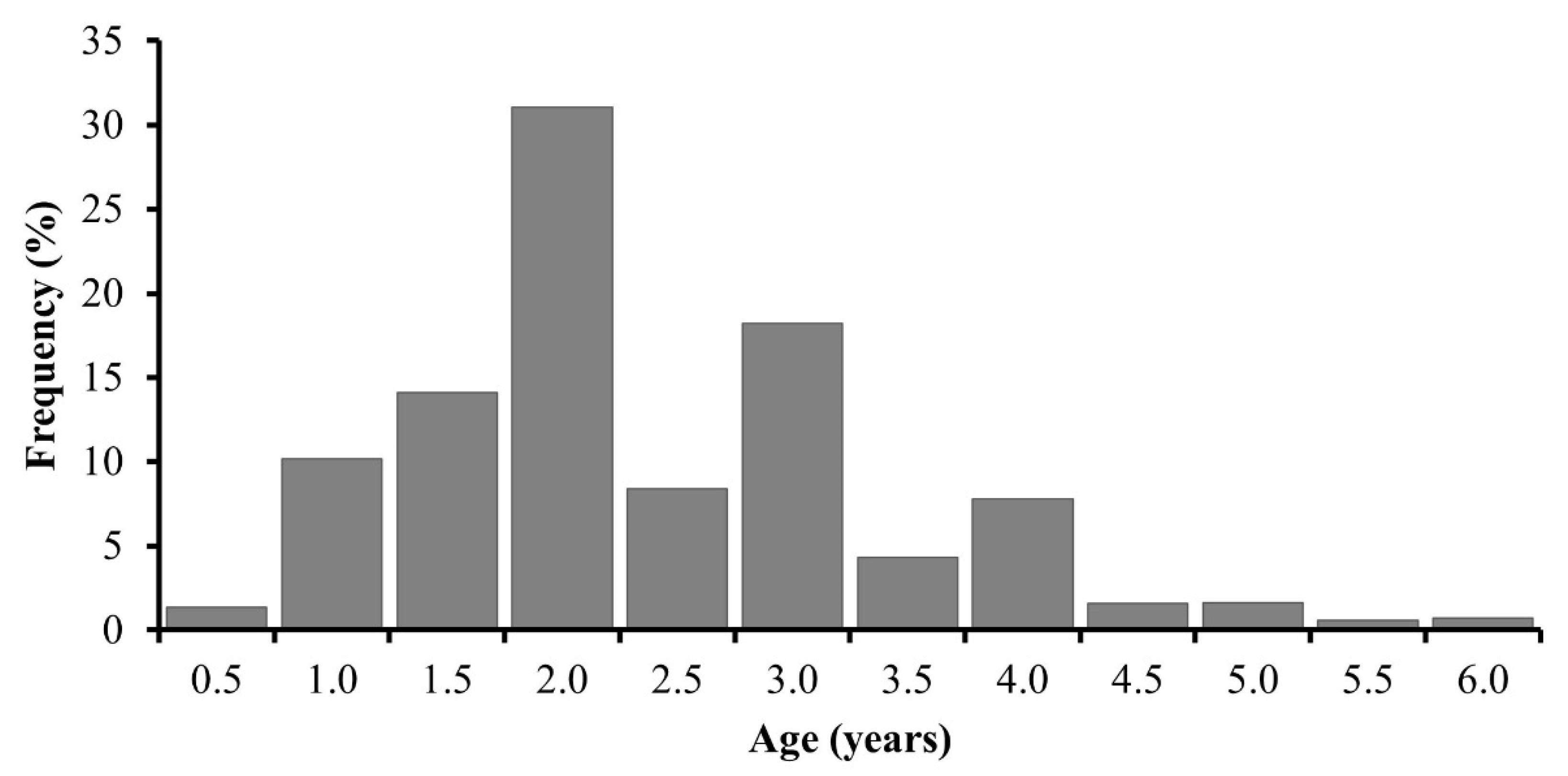
3.2. Structure of Standard Lengths
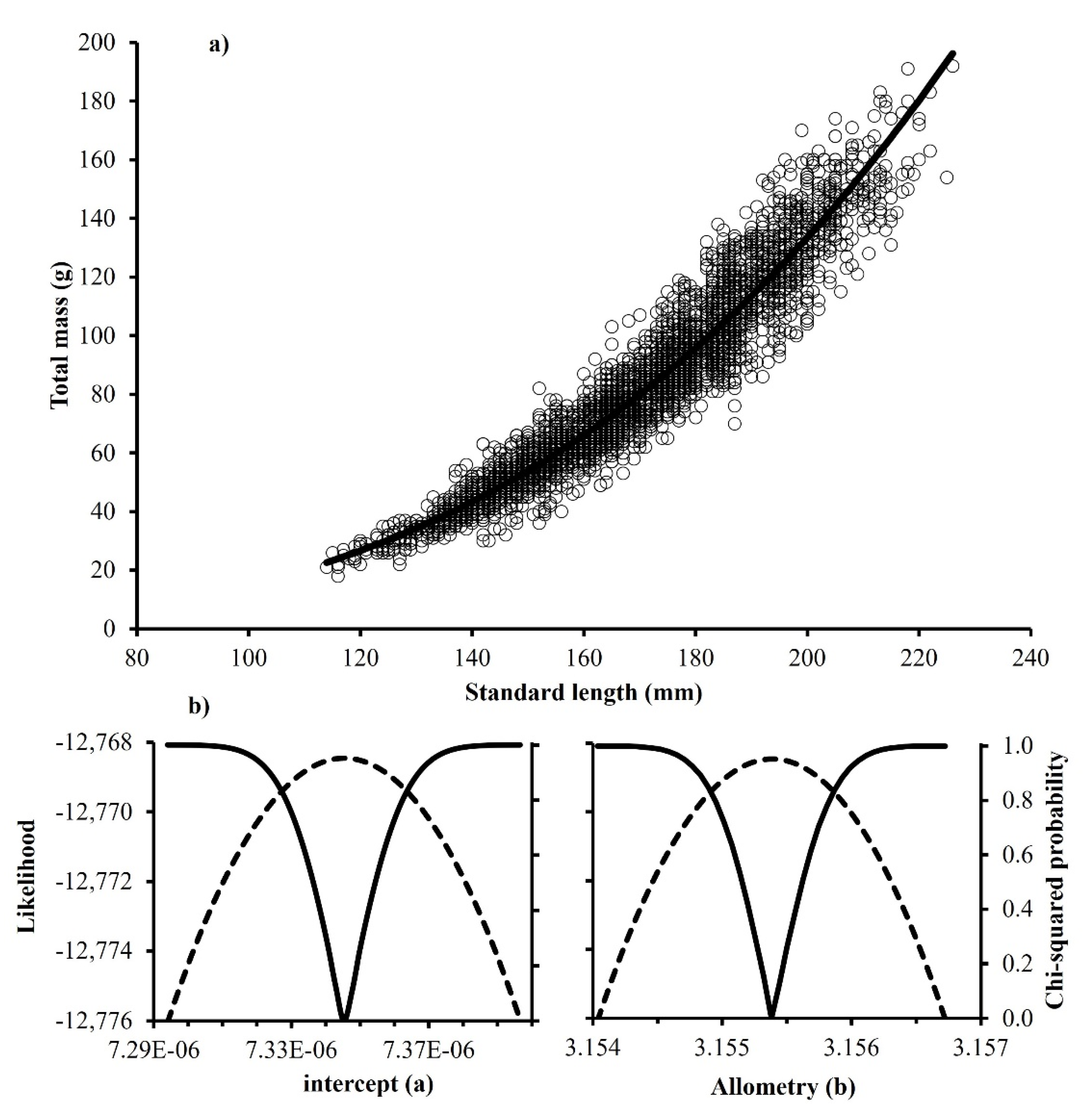
3.3. Body Mass–Length Relationship
3.4. Age Determination
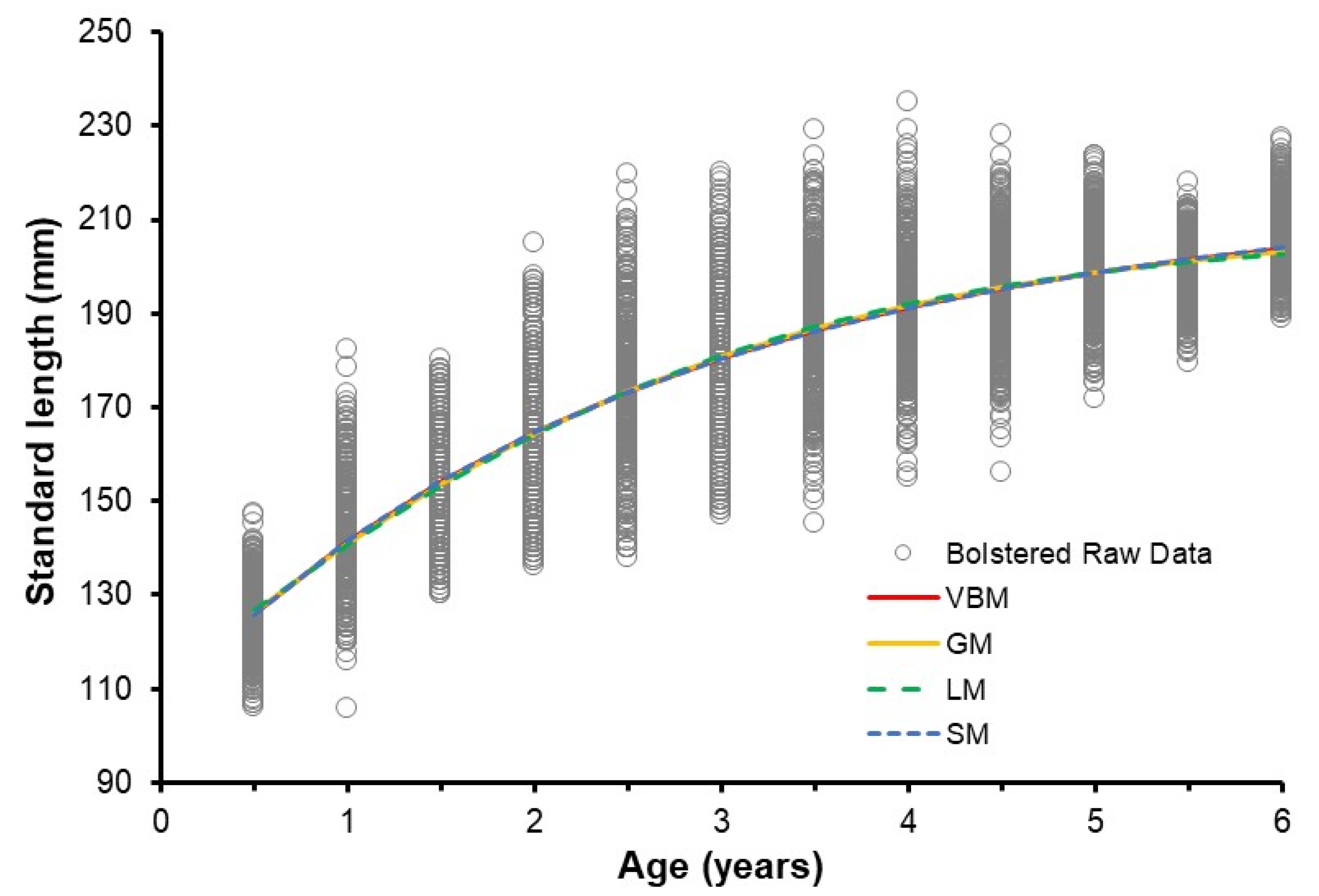
3.5. Selecting the Best Growth Model
3.6. Annual Growth (2005–2014)
3.7. Relationship between Individual Growth and Environmental Conditions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wolf, P. Recovery of the Pacific sardine and the California sardine fishery. Calif. Coop. Ocean. Fish. Investig. Rep. 1992, 33, 76–86. [Google Scholar]
- Deriso, R.B.; Barnes, J.T.; Jacobson, L.D.; Arenas, P.R. Catch-at-age analysis for Pacific sardine (Sardinops sagax), 1983–1995. Calif. Coop. Ocean. Fish. Investig. Rep. 1996, 37, 175–187. [Google Scholar]
- Smith, P.E. Biological effects of ocean variability: Time and space scales of biological response. Rapp. Proces Verbaux Reun. Cons. Int. Explor. Mer 1978, 173, 117–127. [Google Scholar]
- Parrish, R.H.; Serra, R.; Grant, W.S. The monotypic sardines, Sardina and Sardinops: Their taxonomy, distribution, stock structure, and zoogeography. Can. J. Fish. Aquat. Sci. 1989, 46, 2019–2036. [Google Scholar] [CrossRef]
- Emmett, R.L.; Brodeur, R.D.; Miller, T.W.; Pool, S.S.; Bentley, P.J.; Krutzikowsky, G.K.; McCrae, J. Pacific Sardine (Sardinops sagax) Abundance, Distribution, and Ecological Relationships in the Pacific Northwest. Calif. Coop. Ocean. Fish. Investig. Rep. 2005, 46, 122–143. [Google Scholar]
- Kramer, D.; Smith, P.E. Seasonal and geographic characteristics of fishery resources. California current region VII. Pacific Sardine. Commer. Fish. Rev. 1971, 33, 7–11. [Google Scholar]
- Félix-Uraga, R.; Gómez-Muñoz, V.M.; Quiñonez-Velázquez, C.; Melo-Barrera, F.N.; García-Franco, W. On the Existence of Pacific Sardine Groups off the West Coast of Baja California and Southern California. Calif. Coop. Ocean. Fish. Investig. Rep. 2004, 45, 146–151. [Google Scholar]
- Félix-Uraga, R.; Gómez-Muñoz, V.M.; Quiñonez-Velázquez, C.; Melo-Barrera, F.N.; Hill, K.; García-Franco, W. Pacific Sardine (Sardinops sagax) Stock Discrimination off the West Coast of Baja California and Southern California Using Otolith Morphometry. Calif. Coop. Ocean. Fish. Investig. Rep. 2005, 46, 113–121. [Google Scholar]
- Smith, P.E. A History of Proposals for Subpopulation Structure in the Pacific Sardine (Sardinops sagax) Population off Western North America. Calif. Coop. Ocean. Fish. Investig. Rep. 2005, 46, 75–82. [Google Scholar]
- Demer, D.A.; Zwolinski, J.P. Corroboration and refinement of a method for differentiating landings from two stocks of Pacific sardine (Sardinops sagax) in the California Current. ICES J. Mar. Sci. 2014, 71, 328–335. [Google Scholar] [CrossRef]
- Demer, D.A.; Zwolinski, J.P. Optimizing fishing quotas to meet target fishing fractions of an internationally exploited stock of Pacific Sardine. North Am. J. Fish. Manag. 2014, 34, 1119–1130. [Google Scholar] [CrossRef]
- Dorval, E.; McDaniel, J.D.; Macewicz, B.J.; Porzio, D.L. Changes in growth and maturation parameters of Pacific sardine Sardinops sagax collected off California during a period of stock recovery from 1994 to 2010. J. Fish Biol. 2015, 87, 286–310. [Google Scholar] [CrossRef]
- DOF. NORMA Oficial Mexicana NOM-003-SAG/PESC-2018, Para Regular el Aprovechamiento de las Especies de Peces Pelágicos Menores con Embarcaciones de Cerco, en Aguas de Jurisdicción Federal del Océano Pacífico, Incluyendo el Golfo de California, Ciudad de México. Secretaria de Gobernación. 2019. Available online: https://www.dof.gob.mx/normasOficiales/7610/sader11_C/sader11_C.html (accessed on 12 March 2019).
- Checkley, D.M., Jr.; Asch, R.G.; Rykaczewski, R.R. Climate, anchovy, and sardine. Annu. Rev. Mar. Sci. 2017, 9, 469–493. [Google Scholar] [CrossRef]
- De Anda-Montañez, A.; Arreguín-Sánchez, F.; Martínez-Aguilar, S. Length based growth estimates for pacific sardine (Sardinops sagax) in the Gulf of California, Mexico. Calif. Coop. Ocean. Fish. Investig. Rep. 1999, 40, 179–183. [Google Scholar]
- Mercier, L.; Panfili, J.; Paillon, C.; N’diaye, A.; Mouillot, D.; Darnaude, A.M. Otolith reading and multi-model inference for improved estimation of age and growth in the gilthead seabream Sparus aurata (L.). Estuar. Coast. Shelf Sci. 2011, 92, 534–545. [Google Scholar] [CrossRef]
- Lorenzen, K. Toward a new paradigm for growth modeling in fisheries stock assessments: Embracing plasticity and its consequences. Fish. Res. 2016, 180, 4–22. [Google Scholar] [CrossRef]
- Nevárez-Martínez, M.O.; Arzola-Sotelo, E.A.; López-Martínez, J.; Santos-Molina, J.P.; Martínez-Zavala, M.A. Modeling Growth of the Pacific Sardine Sardinops Caeruleus in the Gulf of California, Mexico, Using the Multimodel Inference Approach. Calif. Coop. Ocean. Fish. Investig. Rep. 2019, 60, 1–13. [Google Scholar]
- Beddington, J.R.; Kirkwood, G.P. The estimation of potential yield and stock status using life-history parameters. Philos. Trans. R. Soc. B 2005, 360, 163–170. [Google Scholar] [CrossRef]
- Haddon, M. Modeling and Quantitative Methods in Fisheries, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Alvarado-Castillo, R.M.; Félix-Uraga, R. Edad y crecimiento de la sardina Monterrey Sardinops caeruleus (Pisces: Clupeidae) en Isla de Cedros, Baja California, México, durante 1985 y 1986. Bol. Investig. Mar. Costeras 1996, 25, 77–86. [Google Scholar] [CrossRef]
- Cisneros-Mata, M.A.; Estrada, J.; Montemayor, G. Growth, mortality and recruitment of exploited small pelagic fishes in the Gulf of California. Fishbyte 1990, 8, 15–17. [Google Scholar]
- Quiñonez-Velázquez, C.; Alvarado-Castillo, R.; Félix-Uraga, R. Relación entre el crecimiento individual y la abundancia de la población de la sardina del Pacífico Sardinops Caeruleus (Pisces: Clupeidae) (Girard 1856) en Isla de Cedros, Baja California, México. Rev. Biol. Mar. Oceanogr. 2002, 37, 1–8. [Google Scholar] [CrossRef]
- Félix-Uraga, R. Dinámica Poblacional de la Sardina del Pacífico Sardinops sagax (Jenyns 1842) (Cupleiformes: Clupeidae), en la Costa Oeste de la Península de Baja California y el sur de California. Ph.D. Thesis, CICIMAR, La Paz, México, 2006; 86p. [Google Scholar]
- Katsanevakis, S. Modelling fish growth: Model selection, multi-model inference and model selection uncertainty. Fish. Res. 2006, 81, 229–235. [Google Scholar] [CrossRef]
- Katsanevakis, S.; Maravelias, C.D. Modelling fish growth: Multi-model inference as a better alternative to a priori using von Bertalanffy equation. Fish Fish. 2008, 9, 178–187. [Google Scholar] [CrossRef]
- Ricker, W.E. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 1975, 191, 382. [Google Scholar]
- Schnute, J. A versatile growth model with statistically stable parameters. Can. J. Fish. Aquat. Sci. 1981, 38, 1128–1140. [Google Scholar] [CrossRef]
- Schnute, J.T.; Richards, L.J. A unified approach to the analysis of fish growth, maturity, and survivorship data. Can. J. Fish. Aquat. Sci. 1990, 47, 24–40. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Félix-Uraga, R. Crecimiento de Sardinops caeruleus en Bahía Magdalena, México. Investig. Mar. 1990, 5, 27–31. [Google Scholar]
- Durazo, R.; Baumgartner, T.R. Evolution of oceanographic conditions off Baja California: 1997–1999. Prog. Oceanogr. 2002, 54, 7–31. [Google Scholar] [CrossRef]
- Espinosa-Carreon, T.L.; Strub, P.T.; Beier, E.; Ocampo-Torres, F.; Gaxiola-Castro, G. Seasonal and interannual variability of satellite-derived chlorophyll pigment, surface height, and temperature off Baja California. J. Geophys. Res. 2004, 109, C03039. [Google Scholar] [CrossRef]
- Durazo, R. Climate and upper ocean variability off Baja California, Mexico: 1997–2008. Prog. Oceanogr. 2009, 83, 361–368. [Google Scholar] [CrossRef]
- Cavole, L.M.; Demko, A.M.; Diner, R.E.; Giddings, A.; Koester, I.; Pagniello, C.M.L.S.; Paulsen, M.L.; Ramirez-Valdez, A.; Schwenck, S.M.; Yen, N.K.; et al. Biological impacts of the 2013–2015 warm-water anomaly in the Northeast Pacific: Winners, losers, and the future. Oceanography 2016, 29, 273–285. [Google Scholar] [CrossRef] [Green Version]
- Durazo, R.; Castro, R.; Miranda, L.E.; Delgadillo-Hinojosa, F.; Mejía-Trejo, A. Anomalous hydrographic conditions off the northwestern coast of the Baja California Peninsula during 2013–2016. Cienc. Mar. 2017, 43, 81–92. [Google Scholar] [CrossRef]
- Nevárez-Martínez, M.O.; Cisneros-Mata, M.A.; Montemayor-López, G.; Santos-Molina, P. Estructura por edad, y crecimiento de la sardina monterrey (Sardinops sagax caeruleus) del Golfo de California, México: Temporada de pesca 1990/91. Cienc. Pesq. 1996, 13, 30–36. [Google Scholar]
- Yaremko, M. Age Determination in Pacific Sardine, Sardinops sagax; NOAA Technical Memorandum; NOAA-TM-NMFS-SWFSC-223; Southwest Fisheries Science Center: San Diego, CA, USA, 1996; 33p. [Google Scholar]
- Beamish, R.J.; Fournier, D.A. A method for comparing the precision of a set of age determination. Can. J. Fish. Aquat. Sci. 1981, 38, 982–983. [Google Scholar] [CrossRef]
- Chang, W.Y.B. A statistical method for evaluating the reproducibility of age determination. Can. J. Fish. Aquat. Sci. 1982, 39, 1208–1210. [Google Scholar] [CrossRef]
- Froese, R. Cube law, condition factor and weight-length relationships: History, meta-analysis and recommendations. J. Appl. Ichthyol. 2006, 22, 241–253. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Introduction of Biostatistics, 2nd ed.; Dover Publications, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Maldonado-Amparo, M.A.; Sanchez-Cardenas, R.; Salcido-Guevara, L.A.; Valdez-Pineda, M.C.; Ramirez-Perez, J.S.; Arzola-González, J.F.; Moreno-Sánchez, X.G.; Marin-Enriquez, E. Length-weight relationship and condition factor of butterfish Peprilus medius (Peters, 1869) in the southeast Gulf of California. Calif. Fish Game 2019, 105, 39–47. [Google Scholar]
- Von Bertalanffy, L. A quantitative theory of organic growth (inquiries on growth laws II). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar]
- Neter, J.; Kutner, M.H.; Nachtsheim, J.; Wasserman, W. Applied Linear Statistical Models; McGraw-Hill: New York, NY, USA, 1996; 1408p. [Google Scholar]
- Venzon, D.J.; Moolgavkor, S.H. A Method for computing profile-likelihood based confidence intervals. J. R. Stat. Society. Ser. C Appl. Stat. 1988, 37, 87–94. [Google Scholar] [CrossRef]
- Hilborn, R.; Mangel, M. The Ecological Detective. Confronting Models with Data; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Polacheck, T.; Hilborn, R.; Punt, A.E. Fitting surplus production models: Comparing methods and measuring uncertainty. Can. J. Fish. Aquat. Sci. 1993, 50, 2597–2607. [Google Scholar] [CrossRef]
- Zar, J.H. Biostatistical Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999; 633p. [Google Scholar]
- Pawitan, Y. In All Likelihood: Statistical Modeling and Inference Using Likelihood; Oxford University Press: Oxford, UK, 2001; 528p. [Google Scholar]
- Bolser, D.G.; Grüss, A.; Lopez, M.A.; Reed, E.M.; Mascareño-Osorio, I.; Erisman, B.E. The influence of sample distribution on growth model output for a highly-exploited marine fish, the Gulf Corvina (Cynoscion othonopterus). PeerJ 2018, 6, e5582. [Google Scholar] [CrossRef]
- Scherrer, S.R.; Kobayashi, D.R.; Weng, K.C.; Okamoto, H.Y.; Oishi, F.G.; Franklin, E.C. Estimation of growth parameters integrating tag-recapture, length-frequency, and direct aging data using likelihood and Bayesian methods for the tropical deepwater snapper Pristipomoides filamentosus in Hawaii. Fish. Res. 2021, 233, 105753. [Google Scholar] [CrossRef]
- Goodyear, C.P. Modeling growth: Consequences from selecting samples by size. Trans. Am. Fish. Soc. 2019, 148, 528–551. [Google Scholar] [CrossRef]
- Kapur, M.; Haltuch, M.; Connors, B.; Rogers, L.; Berger, A.; Koontz, E.; Cope, J.; Echave, K.; Fenske, K.; Hanselman, D.; et al. Oceanographic features delineate growth zonation in Northeast Pacific sablefish. Fish. Res. 2020, 222, 105414. [Google Scholar] [CrossRef]
- Pardo, S.A.; Cooper, A.B.; Dulvy, N.K. Avoiding fishy growth curves. Methods Ecol. Evol. 2013, 4, 353–360. [Google Scholar] [CrossRef]
- Neer, J.A.; Thompson, B.A.; Carlson, J.K. Age and growth of Carcharhinus leucas in the northern Gulf of Mexico: Incorporating variability in size at birth. J. Fish Biol. 2005, 67, 370–383. [Google Scholar] [CrossRef]
- Deriso, R.B.; Quinn, B.J., II; Neal, P.R. Catch-age analysis with auxiliary information. Can. J. Fish. Aquat. Sci. 1985, 42, 815–824. [Google Scholar] [CrossRef]
- Jacobson, L.D.; Lo, N.C.H.; Barnes, J.T. A biomass-based assessment model for northern anchovy, Engraulis mordax. Fish. Bull. 1994, 92, 711–724. [Google Scholar]
- Pauly, D.; Munro, L. Once more on growth comparison in fish and invertebrates. Fishbyte 1984, 2, 21. [Google Scholar]
- García-Morales, R.; Shirasago-German, B.; Félix-Uraga, R.; Perez-Lezama, E.L. Conceptual models of Pacific sardine distribution in the California Current System. Curr. Dev. Oceanogr. 2012, 5, 23–47. [Google Scholar]
- Melo-Barrera, F.N.; Félix-Uraga, R.; Quiñonez-Velázquez, C. Análisis de la pesquería de Sardinops sagax en la costa occidental de Baja California Sur, México, durante 2006–2008. Cienc. Pesq. 2010, 18, 33–46. [Google Scholar]
- Hill, K.T.; Lo, N.C.H.; Macewicz, B.J.; Crone, P.R.; Félix-Uraga, R. Assessment of the Pacific Sardine Resource in 2010 for U.S. Management in 2011; NOAA Technical. Memorandum; NMFS-SWFSC-469; U.S. Department of Commerce: La Jolla, CA, USA, 2010; 137p.
- Lo, N.C.H.; Macewicz, B.J.; Griffith, D.A. Migration of Pacific Sardine (Sardinops sagax) off the West Coast of United States in 2003–2005. Bull. Mar. Sci. 2011, 87, 395–412. [Google Scholar] [CrossRef]
- McDaniel, J.; Piner, K.; Lee, H.H.; Hill, K. Evidence that the Migration of the Northern Subpopulation of Pacific Sardine (Sardinops sagax) off the West Coast of the United States Is Age-Based. PLoS ONE 2016, 11, e0166780. [Google Scholar] [CrossRef]
- García-Alberto, G. Reproducción de la Sardina del Pacífico Sardinops Sagax (Jenyns, 1842) en la Región sur de la Corriente de California. Master’s Thesis, CICIMAR, La Paz, México, 2010; 77p. [Google Scholar]
- Costa, M.R.; Araújo, F.G. Length-weight relationship and condition factor of Micropogonias furnieri (Desmarest) (Perciformes, Sciaenidae) in the Sepetiba Bay, Rio de Janeiro, Brazil. Rev. Bras. De Zool. 2003, 20, 685–690. [Google Scholar] [CrossRef]
- Meiri, S. Bergmann’s rule—What’s in a name? Glob. Ecol. Biogeogr. 2011, 20, 203–207. [Google Scholar] [CrossRef]
- Miller, T.J.; O’Brien, L.; Fratantoni, P.S. Temporal and environmental variation in growth and maturity and effects on management reference points of Georges Bank Atlantic cod. Can. J. Fish. Aquat. Sci. 2018, 75, 2159–2171. [Google Scholar] [CrossRef]
- Barnes, J.T.; Foreman, T.J. Recent evidence for the formation of annual growth increments in the otoliths of young Pacific sardines (Sardinops sagax). Calif. Fish Game 1994, 79, 29–35. [Google Scholar]
- Álvarez-Trasviña, E. Variabilidad en el Crecimiento Individual de la Sardina del Pacífico Sardinops Sagax (Jenyns 1842) y su Relación con el Ambiente en Bahía Magdalena, B.C.S. Master’s Thesis, CICIMAR, La Paz, México, 2012; 45p. [Google Scholar]
- Holt, S.J. A preliminary comparative study of the growth, maturity and mortality of sardines. In Proceedings of the World Scientific Meeting on the Biology of Sardines and Related Species, Rome, Italy, 14–21 September 1959; FAO: Rome, Italy, 1960; Volume 2, pp. 553–561. [Google Scholar]
- Beverton, R.J.H. Maturation, growth and mortality of clupeid and engraulid stocks in relation to fishing. Rapp. Procès Verbaux Réunions Cons. Perm. Int. Explor. Mer 1963, 1954, 44–67. [Google Scholar]
- Méndez-Dasilveira, B. Edad y Crecimiento de Sardinops Sagax Caerulea en el Golfo de California. Bachelor’s Thesis, Facultad de Ciencias, Universidad de Guadalajara, Guadalajara, México, 1987; 91p. [Google Scholar]
- Jiménez-Rodríguez, J.G. Análisis Comparativo del Crecimiento y la Estructura Poblacional de Sardina Monterrey Sardinops Caruleus (Girard) en el Golfo de California de las Temporadas 1988/1989 y 1989/1990. Bachelor’s Thesis, Escuela de Biología, Universidad Autónoma de Guadalajara, Guadalajara, México, 1991; 60p. [Google Scholar]
- Cailliet, G.M.; Smith, W.D.; Mollet, H.F.; Goldman, K.J. Age and growth studies of chondrichthyan fishes: The need for consistency in terminology, verification, validation, and growth function fitting. Environ. Biol. Fishes 2006, 77, 211–228. [Google Scholar] [CrossRef]
- McClatchie, S. Oceanography of the Southern California Current System Relevant to Fisheries. In Regional Fisheries Oceanography of the California Current System; Springer: Dordrecht, The Netherlands, 2014; pp. 13–60. [Google Scholar] [CrossRef]
- Helfman, G.S.; Collette, B.B.; Facey, D.E.; Bowen, B.W. The Diversity of Fishes, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Veron, M.; Duhamel, E.; Bertignac, M.; Pawlowski, L.; Huret, M. Major changes in sardine growth and body condition in the Bay of Biscay between 2003 and 2016: Temporal trends and drivers. Prog. Oceanogr. 2020, 182, 102274. [Google Scholar] [CrossRef]
- Félix-Uraga, R.; Melo-Barrera, F.N.; Quiñones-Velázquez, C. Parámetros poblacionales de la sardina del Pacífico Sardinops sagax y su contribución a la pesquería de Bahía Magdalena: Enfoques de stocks. In Estudios Ecológicos en Bahía Magdalena; Funes-Rodríguez, R., Gómez-Gutiérrez, J., Palomares-García, R., Eds.; CICIMAR-IPN: La Paz, México, 2007; pp. 221–230. [Google Scholar]
- Cope, J.M.; Punt, A.E. Admitting Ageing Error When Fitting Growth Curves: An Example Using the Von Bertalanffy Growth Function with Random Effects. Can. J. Fish. Aquat. Sci. 2007, 64, 205–218. [Google Scholar] [CrossRef]
- Thorson, J.T.; Minte-Vera, C.V. Relative magnitude of cohort, age, and year effects on size at age of exploited marine fishes. Fish. Res. 2016, 180, 45–53. [Google Scholar] [CrossRef]
- Morrongiello, J.R.; Thresher, R.E. A statistical framework to explore ontogenetic growth variation among individuals and populations: A marine fish example. Ecol. Monogr. 2015, 85, 93–115. [Google Scholar] [CrossRef]
- Cadigan, N.G.; Campana, S.E. Hierarchical Model-Based Estimation of Population Growth Curves for Redfish (Sebastes mentella and Sebastes fasciatus) off the Eastern Coast of Canada. ICES J. Mar. Sci. 2017, 74, 687–697. [Google Scholar] [CrossRef]
- Lee, Q.; Punt, A. Extracting a time-varying climate-driven growth index from otoliths for use in stock assessment models. Fish. Res. 2018, 200, 93–103. [Google Scholar] [CrossRef]
- Dey, R.; Cadigan, N.; Zheng, N. Estimation of the von Bertalanffy Growth Model When Ages Are Measured with Error. J. R. Stat. Soc. Ser. C Appl. Stat. 2019, 68, 1131–1147. [Google Scholar] [CrossRef]
- Chasco, B.E.; Thorson, J.T.; Heppell, S.S.; Avens, L.; McNeill, J.B.; Bolten, A.B.; Bjorndal, K.A.; Ward, E.J. Integrated mixed-effect growth models for species with incomplete ageing histories: A case study for the loggerhead sea turtle Caretta caretta. Mar. Ecol. Prog. Ser. 2020, 636, 221–234. [Google Scholar] [CrossRef]

| Model | Equation | Description |
|---|---|---|
| VBM | is size (in mm SL) at age t, is asymptotic length (mm SL), is the growth rate coefficient (year−1), in VBM and SM is the theoretical age at which length is zero (years). in GM and LM corresponds to an inflection point on the growth curve is age at size is a relative growth rate (time constant) is an incremental relative growth rate (incremental time constant), is the lowest age in the dataset, is the highest age in the dataset, is the size at age , is the size at age | |
| GM | ||
| LM | ||
| SM |
| Year | a | b | n | GT | ||||
|---|---|---|---|---|---|---|---|---|
| CIinf | Mean | CIsup | CIinf | Mean | CIsup | |||
| 2005 | 3.218 × 10−6 | 3.242 × 10−6 | 3.281 × 10−6 | 3.319 | 3.321 | 3.323 | 463 | +H |
| 2006 | 1.710 × 10−5 | 1.742 × 10−5 | 1.773 × 10−5 | 2.982 | 2.986 | 2.989 | 164 | +H |
| 2007 | 9.194 × 10−6 | 9.209 × 10−6 | 9.302 × 10−6 | 3.103 | 3.104 | 3.106 | 550 | +H |
| 2008 | 2.841 × 10−5 | 2.869 × 10−5 | 2.896 × 10−5 | 2.890 | 2.892 | 2.893 | 392 | −H |
| 2009 | 1.835 × 10−6 | 1.861 × 10−6 | 1.876 × 10−6 | 3.419 | 3.421 | 3.423 | 215 | +H |
| 2010 | 3.755 × 10−5 | 3.800 × 10−5 | 3.845× 10−5 | 2.833 | 2.835 | 2.838 | 214 | −H |
| 2011 | 1.297 × 10−5 | 1.309 × 10−5 | 1.322 × 10−5 | 3.051 | 3.053 | 3.055 | 285 | +H |
| 2012 | 5.230 × 10−5 | 5.274 × 10−5 | 5.319 × 10−5 | 2.788 | 2.790 | 2.791 | 444 | −H |
| 2013 | 4.234 × 10−6 | 4.269 × 10−6 | 4.328 × 10−6 | 3.252 | 3.254 | 3.256 | 358 | +H |
| 2014 | 1.574 × 10−5 | 1.588 × 10−5 | 1.601 × 10−5 | 2.991 | 2.992 | 2.994 | 424 | −H |
| 2005–2014 | 7.32 × 10−6 | 7.34 × 10−6 | 7.37 × 10−6 | 3.154 | 3.155 | 3.156 | 3509 | +H |
| Age | SL | SD | n |
|---|---|---|---|
| 0.5 | 125.7 | 6.9 | 48 |
| 1.0 | 143.8 | 11.8 | 357 |
| 1.5 | 152.3 | 11.4 | 495 |
| 2.0 | 165.2 | 14.2 | 1090 |
| 2.5 | 175.5 | 14.7 | 295 |
| 3.0 | 182.0 | 15.1 | 640 |
| 3.5 | 186.8 | 13.3 | 152 |
| 4.0 | 192.0 | 13.1 | 274 |
| 4.5 | 193.9 | 10.3 | 55 |
| 5.0 | 199.2 | 9.8 | 57 |
| 5.5 | 199.4 | 6.5 | 21 |
| 6.0 | 206.4 | 6.8 | 25 |
| Model | Parameter | Value | Lower CI | Upper CI |
|---|---|---|---|---|
| VBM | (year) | −1.845 | −1.870 | −1.821 |
| (mm) | 216.3 | 215.6 | 217.1 | |
| (year−1) | 0.372 | 0.369 | 0.375 | |
| GM | (year) | −0.906 | −0.934 | −0.880 |
| (mm) | 211.0 | 210.4 | 211.7 | |
| (year−1) | 0.479 | 0.474 | 0.483 | |
| LM | (year) | −0.296 | −0.324 | −0.269 |
| (mm) | 207.4 | 206.7 | 208.1 | |
| (year−1) | 0.586 | 0.578 | 0.593 | |
| SM | 0.536 | 0.523 | 0.344 | |
| −0.538 | −0.685 | 1.574 | ||
| (mm) | 127.1 | 126.3 | 127.9 | |
| (mm) | 202.8 | 201.8 | 204.0 |
| Model | K | LL | AIC | Δi | WAICi% | SE |
|---|---|---|---|---|---|---|
| VBM | 4 | 3864.11 | −7720.23 | 1.290 | 18.15 | 0.08 |
| GL | 4 | 3864.73 | −7721.47 | 0.049 | 33.77 | 0.08 |
| LM | 4 | 3864.76 | −7721.52 | 0.000 | 34.61 | 0.08 |
| SM | 5 | 3864.82 | −7719.63 | 1.886 | 13.47 | 0.08 |
| Model | Parameter | Value | Lower CI | Upper CI |
|---|---|---|---|---|
| VBM | (year) | −1.813 | −1.828 | −1.799 |
| (mm) | 214.6 | 214.2 | 215.0 | |
| (year−1) | 0.383 | 0.381 | 0.384 | |
| GM | (year) | −0.889 | −0.904 | −0.874 |
| (mm) | 210.6 | 210.3 | 211.0 | |
| (year−1) | 0.484 | 0.481 | 0.487 | |
| LM | (year) | −0.262 | −0.278 | −0.247 |
| (mm) | 207.9 | 207.5 | 208.2 | |
| (year−1) | 0.587 | 0.582 | 0.592 | |
| SM | 0.335 | 0.326 | 0.344 | |
| 1.474 | 1.378 | 1.574 | ||
| (mm) | 125.8 | 125.3 | 126.4 | |
| (mm) | 204.1 | 203.6 | 204.5 |
| Model | K | LL | AIC | Δi | WAICi% | SE |
|---|---|---|---|---|---|---|
| VBM | 4 | 7590.59 | −15,173.18 | 0.00 | 60.92 | 0.07 |
| GM | 4 | 7586.12 | −15,164.24 | 8.94 | 0.70 | 0.07 |
| LM | 4 | 7577.67 | −15,147.33 | 25.85 | 0.00 | 0.07 |
| SM | 5 | 7591.13 | −15,172.25 | 0.92 | 38.38 | 0.07 |
| Parameter | Value | Mean | SD | CV | Bias | %Bias | Lower CI | Upper CI | |
|---|---|---|---|---|---|---|---|---|---|
| Two parameters (t0 fixed) | t0 (year) | −1.81 | −1.45 | 0.83 | −0.57 | 0.36 | −19.84 | −2.81 | −0.09 |
| L∞ (mm) | 214.60 | 209.77 | 13.74 | 0.07 | −4.82 | −2.25 | 188.72 | 235.00 | |
| k (year−1) | 0.38 | 0.58 | 0.34 | 0.59 | 0.20 | 52.11 | 0.27 | 1.71 | |
| σ | 0.07 | 0.07 | 0.01 | 0.11 | 0.01 | 7.83 | 0.07 | 0.10 | |
| Three parameters | t0 (year) | −1.81 | −1.81 | 0.05 | −0.03 | 0.00 | 0.02 | −1.91 | −1.73 |
| L∞ (mm) | 214.60 | 215.11 | 0.94 | 0.00 | 0.51 | 0.24 | 213.34 | 217.06 | |
| k (year−1) | 0.38 | 0.38 | 0.01 | 0.02 | 0.00 | 0.02 | 0.37 | 0.40 | |
| σ | 0.07 | 0.10 | 0.00 | 0.01 | 0.03 | 41.50 | 0.10 | 0.10 |
| Year | t0 (year) | L∞ (mm) | k (year−1) | φ′ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lower CI | Mean | Upper CI | Lower CI | Mean | Upper CI | Lower CI | Mean | Upper CI | ||
| 2005 | −2.18 | −2.16 | −2.13 | 198.7 | 199.2 | 199.7 | 0.300 | 0.301 | 0.302 | 2.13 |
| 2006 | −1.17 | −1.15 | −1.13 | 188.7 | 189.2 | 189.6 | 0.681 | 0.687 | 0.693 | 2.39 |
| 2007 | −2.36 | −2.33 | −2.30 | 189.6 | 190.1 | 190.6 | 0.398 | 0.402 | 0.405 | 2.16 |
| 2008 | −0.79 | −0.78 | −0.76 | 189.2 | 189.7 | 190.2 | 0.853 | 0.861 | 0.870 | 2.49 |
| 2009 | −1.53 | −1.51 | −1.49 | 196.6 | 197.0 | 197.5 | 0.507 | 0.511 | 0.514 | 2.30 |
| 2010 | −2.47 | −2.44 | −2.42 | 185.9 | 186.4 | 186.8 | 0.397 | 0.400 | 0.403 | 2.14 |
| 2011 | −0.76 | −0.75 | −0.74 | 189.4 | 189.7 | 190.1 | 0.887 | 0.894 | 0.901 | 2.51 |
| 2012 | −1.01 | −1.00 | −0.99 | 199.2 | 199.6 | 200.0 | 0.676 | 0.680 | 0.685 | 2.43 |
| 2013 | −0.77 | −0.76 | −0.74 | 208.6 | 209.0 | 209.5 | 0.740 | 0.746 | 0.752 | 2.51 |
| 2014 | −1.29 | −1.27 | −1.26 | 210.9 | 211.3 | 211.8 | 0.526 | 0.529 | 0.533 | 2.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enciso-Enciso, C.; Nevárez-Martínez, M.O.; Sánchez-Cárdenas, R.; Marín-Enríquez, E.; Salcido-Guevara, L.A.; Minte-Vera, C. Allometry and Individual Growth of the Temperate Pacific Sardine (Sardinops sagax) Stock in the Southern California Current System. Fishes 2022, 7, 226. https://doi.org/10.3390/fishes7050226
Enciso-Enciso C, Nevárez-Martínez MO, Sánchez-Cárdenas R, Marín-Enríquez E, Salcido-Guevara LA, Minte-Vera C. Allometry and Individual Growth of the Temperate Pacific Sardine (Sardinops sagax) Stock in the Southern California Current System. Fishes. 2022; 7(5):226. https://doi.org/10.3390/fishes7050226
Chicago/Turabian StyleEnciso-Enciso, Concepción, Manuel Otilio Nevárez-Martínez, Rebeca Sánchez-Cárdenas, Emigdio Marín-Enríquez, Luis A. Salcido-Guevara, and Carolina Minte-Vera. 2022. "Allometry and Individual Growth of the Temperate Pacific Sardine (Sardinops sagax) Stock in the Southern California Current System" Fishes 7, no. 5: 226. https://doi.org/10.3390/fishes7050226
APA StyleEnciso-Enciso, C., Nevárez-Martínez, M. O., Sánchez-Cárdenas, R., Marín-Enríquez, E., Salcido-Guevara, L. A., & Minte-Vera, C. (2022). Allometry and Individual Growth of the Temperate Pacific Sardine (Sardinops sagax) Stock in the Southern California Current System. Fishes, 7(5), 226. https://doi.org/10.3390/fishes7050226