The Standard Deviation Structure as a New Approach to Growth Analysis in Weight and Length Data of Farmed Lutjanus guttatus
Abstract
:1. Introduction
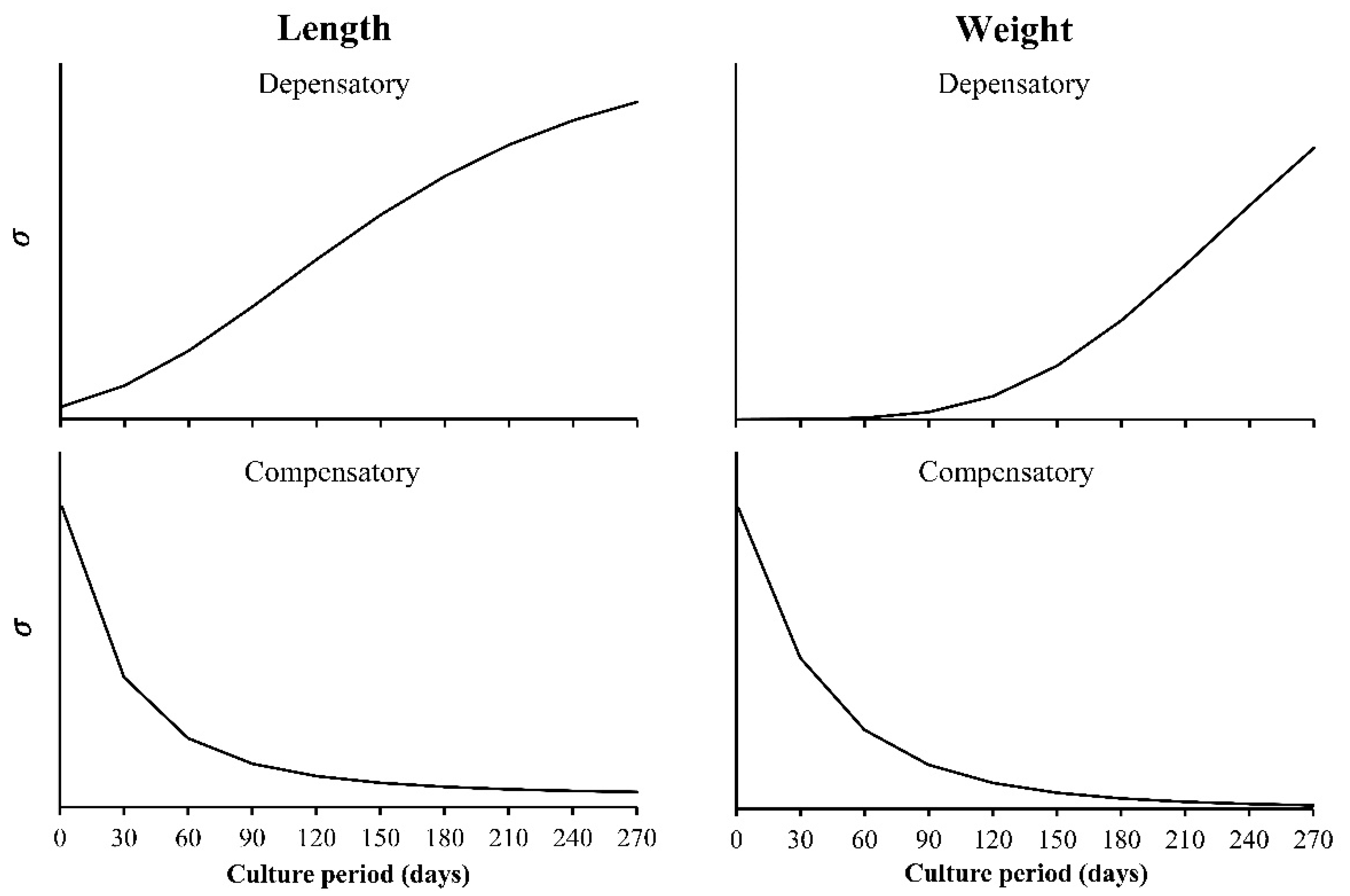
- Constant variance, this is the one that is usually assumed. The variance does not change with the value of x, the independent variable, which is valid when errors are normal.
- Decreasing the variance with x, the independent variable. Here, the included functions are used to simulate the growth compensatory effect [6].
- The observed variance or age-specific variances. Instead of assuming some type of variances (a, b, or c), the variance obtained from the sample is used, which is estimated from the data. The variance of size at any age (Yo for each value of x), has a square root of σ, which is incorporated into the loglikelihood function. In this case, the lognormal distribution of the residuals is assumed. Then, the sample variance is obtained from the ln(Yo) and not from the original Yo, whereas in the normal distribution, it is calculated from the Yo data for each value of x. For this reason, and despite the importance of the multi-model approach (MMA) or information theory to select models, the focus on variability at age becomes a core strategy in growth analysis.
2. Materials and Methods
2.1. Data Source
2.2. Models and Selection Criterion
2.3. Confidence Intervals
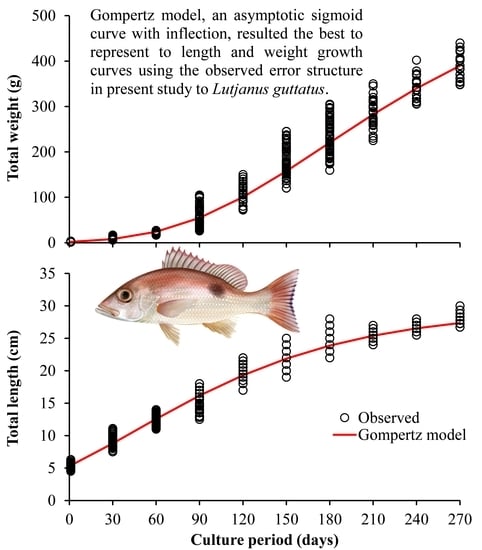
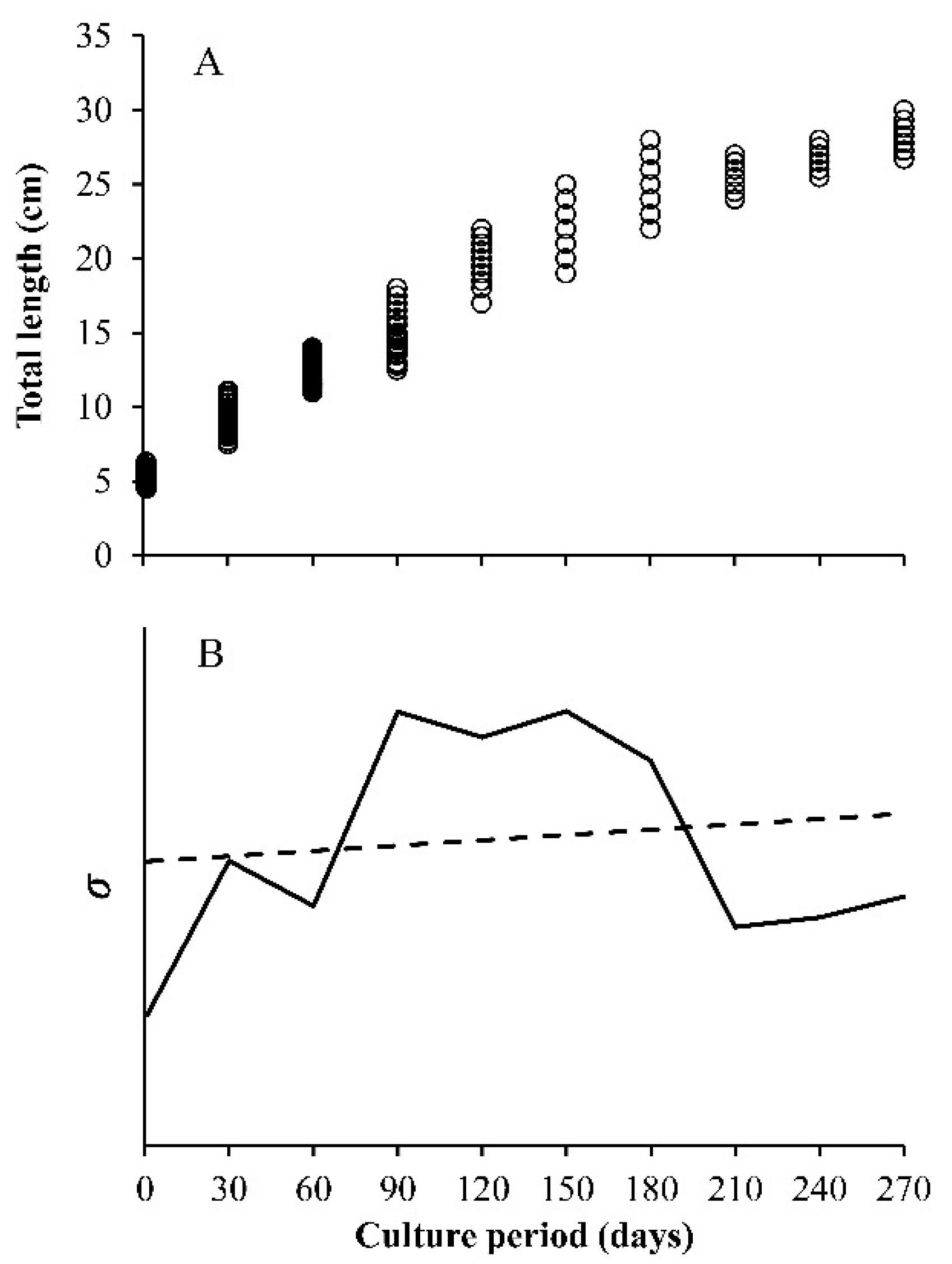
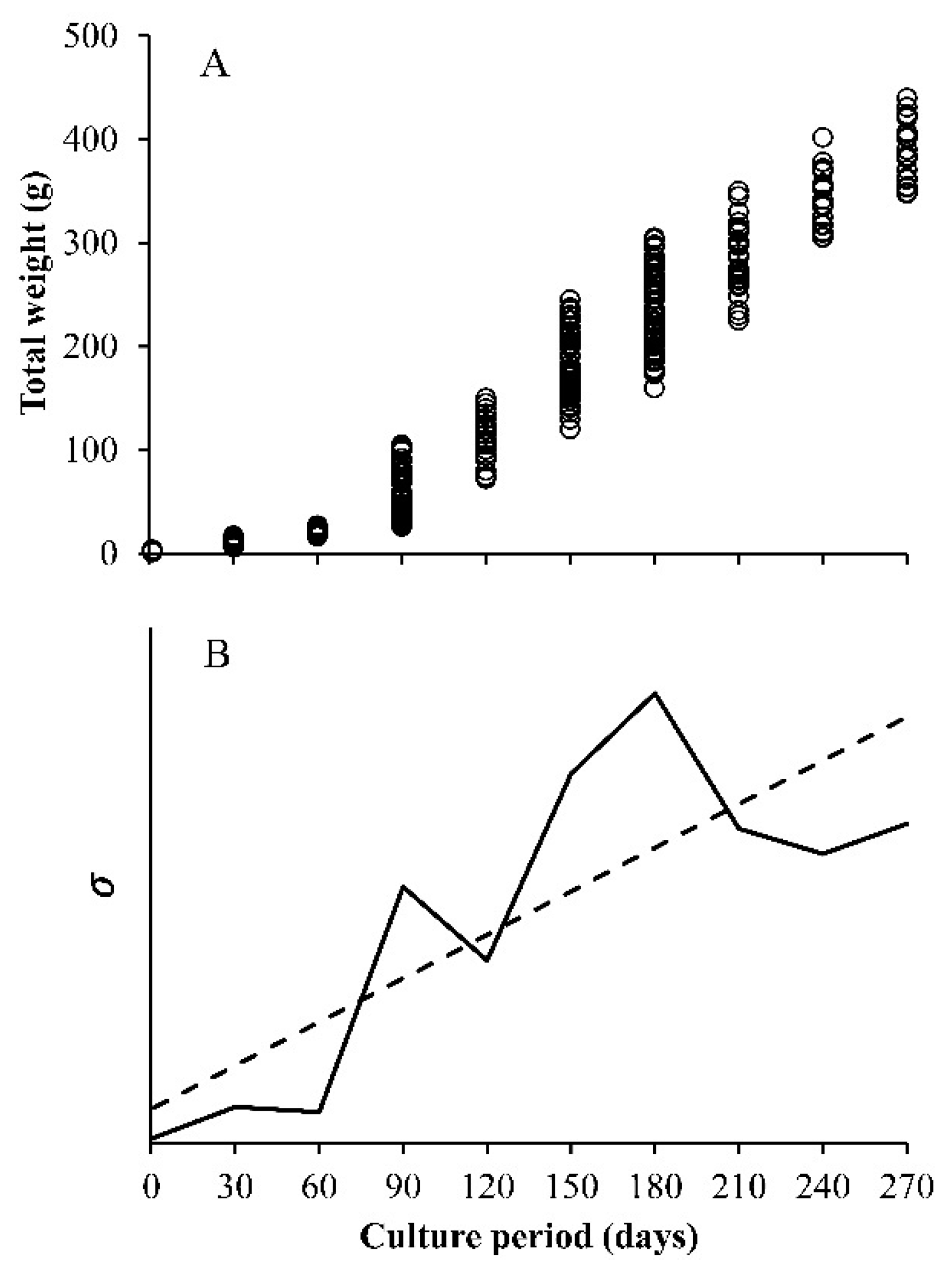
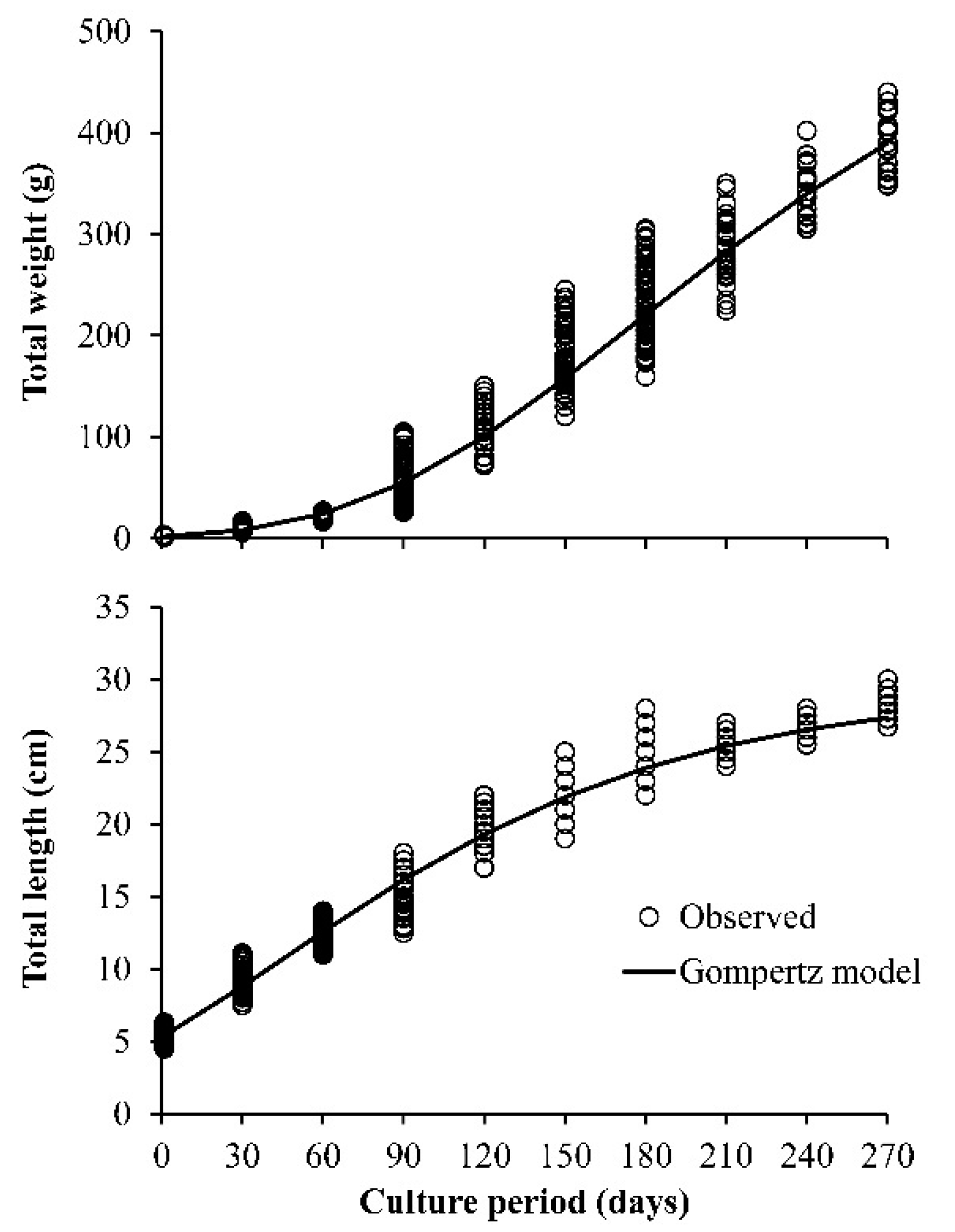
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Beverton, R.J.H.; Holt, S.J. On the Dynamics of Exploited Fish Populations; Ministry of Agriculture, Fisheries and Food; Fisheries Investigations: London, UK, 1957. [Google Scholar]
- Schnute, J.; Fournier, D. A New Approach to Length–Frequency Analysis: Growth Structure. Can. J. Fish. Aquat. Sci. 1980, 37, 1337–1351. [Google Scholar] [CrossRef]
- Sainsbury, K.J. Effect of Individual Variability on the von Bertalanffy Growth Equation. Can. J. Fish. Aquat. Sci. 1980, 37, 241–247. [Google Scholar] [CrossRef]
- Letcher, B.H.; Coombs, J.A.; Nislow, K.H. Maintenance of phenotypic variation: Repeatability, heritability and size-dependent processes in a wild brook trout population. Evol. Appl. 2011, 4, 602–615. [Google Scholar] [CrossRef] [PubMed]
- Luquin-Covarrubias, M.A.; Morales-Bojórquez, E.; González-Peláez, S.S.; Hidalgo-De-La-Toba, J.Á.; Lluch-Cota, D.B. Modeling of Growth Depensation of Geoduck Clam Panopea globosa Based on a Multimodel Inference Approach. J. Shellfish. Res. 2016, 35, 379–387. [Google Scholar] [CrossRef]
- Félix-Ortiz, J.A.; Aragón-Noriega, E.A.; Castañeda-Lomas, N.; Rodríguez-Domínguez, G.; Valenzuela-Quiñónez, W.; Castillo-Vargasmachuca, S. Individual growth analysis of the Pacific yellowlegs shrimp Penaeus californiensis via multi-criteria approach. Lat. Am. J. Aquat. Res. 2020, 48, 768–778. [Google Scholar] [CrossRef]
- Restrepo, V.R.; Diaz, G.A.; Walter, J.F.; Neilson, J.D.; Campana, S.E.; Secor, D.; Wingate, R.L. Updated estimate of the growth curve of Western Atlantic bluefin tuna. Aquat. Living Resour. 2010, 23, 335–342. [Google Scholar] [CrossRef] [Green Version]
- Aragón-Noriega, E.A.; Mendivil-Mendoza, J.E.; Alcántara-Razo, E.; Valenzuela-Quiñónez, W.; Félix-Ortiz, J.A. Multi-criteria approach to estimate the growth curve in the marine shrimp, Penaeus vannamei Boone, 1931 (Decapoda, Penaeidae). Crustaceana 2017, 90, 1517–1531. [Google Scholar] [CrossRef]
- Castillo-Vargasmachuca, S.G.; Ponce-Palafox, J.T.; Muñoz, E.A.; Rodríguez-Domínguez, G.; Aragón-Noriega, E.A. The spotted rose snapper (Lutjanus guttatus Steindachner 1869) farmed in marine cages: Review of growth models. Rev. Aquac. 2016, 10, 376–384. [Google Scholar] [CrossRef]
- Baer, A.; Schulz, C.; Traulsen, I.; Krieter, J. Analysing the growth of turbot (Psetta maxima) in a commercial recirculation system with the use of three different growth models. Aquac. Int. 2010, 19, 497–511. [Google Scholar] [CrossRef]
- Ansah, Y.B.; Frimpong, E.A. Using Model-Based Inference to Select a Predictive Growth Curve for Farmed Tilapia. N. Am. J. Aquac. 2015, 77, 281–288. [Google Scholar] [CrossRef]
- Katsanevakis, S. Modelling fish growth: Model selection, multi-model inference and model selection uncertainty. Fish. Res. 2006, 81, 229–235. [Google Scholar] [CrossRef]
- Katsanevakis, S.; Maravelias, C.D. Modelling fish growth: Multi-model inference as a better alternative to a priori using von Bertalanffy equation. Fish Fish. 2008, 9, 178–187. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. A quantitative theory of organic growth. Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Ricker, W.E. Growth rates and models. In Fish Physiology. Bioenergetics and Growth; Hoar, W.S., Randall, D.J., Brett, J.R., Eds.; Academic Press: London, UK, 1979; pp. 677–744. [Google Scholar]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Venzon, D.J.; Moolgavkar, S.H. A Method for Computing Profile-Likelihood-Based Confidence Intervals. Appl. Stat. 1988, 37, 87. [Google Scholar] [CrossRef]
- Chen, Y.; Fournier, D. Impacts of atypical data on Bayesian inference and robust Bayesian approach in fisheries. Can. J. Fish. Aquat. Sci. 1999, 56, 1525–1533. [Google Scholar] [CrossRef]
- Curiel-Bernal, M.V.; Aragón-Noriega, E.A.; Cisneros-Mata, M.Á.; Sánchez-Velasco, L.; Jiménez-Rosenberg, S.P.A.; Parés-Sierra, A. Using Observed Residual Error Structure Yields the Best Estimates of Individual Growth Parameters. Fishes 2021, 6, 35. [Google Scholar] [CrossRef]
| Variable | Residual Structure | VBGM | Logistic | Gompertz |
|---|---|---|---|---|
| Length | Observed | 1711 | 1771 | 1668 |
| Constant | 1852 | 1829 | 1811 | |
| Depensatory | 2673 | 1947 | 1867 | |
| Compensatory | 3001 | 2011 | 2022 | |
| Weight | Observed | 4411 | 4695 | 4403 |
| Constant | 5127 | 5199 | 5199 | |
| Depensatory | 4674 | 4854 | 4669 | |
| Compensatory | 5953 | 11768 | 5939 |
| Length | Weight | |||
|---|---|---|---|---|
| Criterion | Optimum (CI) | Significance | Optimum (CI) | Significance |
| L∞ (cm) | W∞ (g) | |||
| Observed | 29.44 (29.25–29.64) | a | 578 (570–586) | a |
| Constant | 29.79 (29.44–30.19) | ab | 403 (398–409) | b |
| Depensatory | 29.23 (28.99–29.47) | a | 507 (493–521) | c |
| Compensatory | 30.25 (29.64–30.94) | b | 1738 (1707–1776) | d |
| k (days−1) | k (days−1) | |||
| Observed | 0.01168 (0.01143–0.01194) | a | 0.00993 (0.00988–0.00999) | a |
| Constant | 0.01138 (0.01090–0.01188) | ab | 0.02320 (0.02240–0.02420) | b |
| Depensatory | 0.01179 (0.01154–0.01204) | a | 0.01054 (0.01046–0.01061) | c |
| Compensatory | 0.01056 (0.00980–0.01133) | b | 0.00340 (0.00329–0.00341) | d |
| t* (days) | t* (days) | |||
| Observed | 46.2 (45.5–46.9) | ab | 176.3 (175.8–176.9) | a |
| Constant | 47.3 (46.2–48.3) | a | 165.3 (163.9–166.7) | b |
| Depensatory | 45.0 (44.4–45.7) | ab | 161.6 (161.0–162.2) | c |
| Compensatory | 44.8 (43.4–46.2) | ab | 386.2 (384.7–387.7) | d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Vargasmachuca, S.G.; Aragón-Noriega, E.A.; Rodríguez-Domínguez, G.; Martínez-Cárdenas, L.; Arámbul-Muñoz, E.; Burgos Arcos, Á.J. The Standard Deviation Structure as a New Approach to Growth Analysis in Weight and Length Data of Farmed Lutjanus guttatus. Fishes 2021, 6, 60. https://doi.org/10.3390/fishes6040060
Castillo-Vargasmachuca SG, Aragón-Noriega EA, Rodríguez-Domínguez G, Martínez-Cárdenas L, Arámbul-Muñoz E, Burgos Arcos ÁJ. The Standard Deviation Structure as a New Approach to Growth Analysis in Weight and Length Data of Farmed Lutjanus guttatus. Fishes. 2021; 6(4):60. https://doi.org/10.3390/fishes6040060
Chicago/Turabian StyleCastillo-Vargasmachuca, Sergio G., Eugenio Alberto Aragón-Noriega, Guillermo Rodríguez-Domínguez, Leonardo Martínez-Cárdenas, Eulalio Arámbul-Muñoz, and Álvaro J. Burgos Arcos. 2021. "The Standard Deviation Structure as a New Approach to Growth Analysis in Weight and Length Data of Farmed Lutjanus guttatus" Fishes 6, no. 4: 60. https://doi.org/10.3390/fishes6040060
APA StyleCastillo-Vargasmachuca, S. G., Aragón-Noriega, E. A., Rodríguez-Domínguez, G., Martínez-Cárdenas, L., Arámbul-Muñoz, E., & Burgos Arcos, Á. J. (2021). The Standard Deviation Structure as a New Approach to Growth Analysis in Weight and Length Data of Farmed Lutjanus guttatus. Fishes, 6(4), 60. https://doi.org/10.3390/fishes6040060