Influence of Spatial Scale Selection of Environmental Factors on the Prediction of Distribution of Coilia nasus in Changjiang River Estuary
Abstract
:1. Introduction
2. Materials and Methods
2.1. Time, Area, and Method of Investigation
2.2. Variables Selection
2.3. Model Development
s(pH) + s(Sal) + s(Chla) + s(DO) + s(COD) + ε
s(pH) + s(Sal) + s(Chla) + s(DO) + s(COD) + ε
2.4. Model Validation
2.5. Model Prediction and Mapping
3. Results
3.1. Model Results
3.2. Interpolation Analysis of Environmental Factors
3.3. Prediction of Spatial and Temporal Distribution of C. nasus
4. Discussion
4.1. Predictive Performance of the Two-Stage GAM Model for C. nasus Distribution
4.2. The Relationship between the Interpolation Results between Environmental Factors and Spatial Scale
4.3. The Relationship between Fish Resource Forecasts and Spatial Scale
5. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Legendre, P.; Fortin, M.J. Spatial pattern and ecological analysis. Vegetatio 1989, 80, 107–138. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, S.Y.; Wang, Z.H.; Lin, J.; Zhou, X.J. Fish community diversity distribution and its affecting factors based on GAM model. Chin. J. Ecol. 2013, 32, 3226–3235. [Google Scholar]
- Allen, L.G.; Daniel, I.I.; Shane, M.A. Fisheries independent assessment of a returning fishery: Abundance of juvenile white seabass (Atractoscion nobilis) in the shallow nearshore waters of the Southern California Bight, 1995–2005. Fish. Res. 2007, 88, 24–32. [Google Scholar] [CrossRef]
- Bacha, M.; Jeyid, M.A.; Vantrepotte, V.; Dessailly, D.; Amara, R. Environmental effects on the spatio-temporal patterns of abundance and distribution of Sardina pilchardus and sardinella off the Mauritanian coast (North-West Africa). Fish. Oceanogr. 2017, 26, 282–298. [Google Scholar] [CrossRef]
- Fahrig, L. Relative Importance of Spatial and Temporal Scales in a Patchy Environment. Theor. Popul. Biol. 1992, 41, 300–314. [Google Scholar] [CrossRef]
- Hale, R.; Colton, M.A.; Peng, P.; Swearer, S.E. Do spatial scale and life history affect fish–habitat relationships? J. Anim. Ecol. 2019, 88, 439–449. [Google Scholar] [CrossRef]
- Basher, Z.; Bowden, D.A.; Costello, M.J. Diversity and distribution of deep-sea shrimps in the Ross Sea region of Antarctica. PLoS ONE 2014, 9, e103195. [Google Scholar] [CrossRef] [Green Version]
- Crook, D.A.; Robertson, A.I.; King, A.J.; Humphries, P. The influence of spatial scale and habitat arrangement on diel patterns of habitat use by two lowland river fishes. Oecologia 2001, 129, 525–533. [Google Scholar] [CrossRef]
- Petitgas, P. Allocation of survey effort between small scale and large scale and precision of fisheries survey-based abundance estimates. ICES CM 2001, 17. Available online: https://www.ices.dk/sites/pub/CM%20Doccuments/2001/P/P1701.pdf (accessed on 7 October 2021).
- Rufino, M.M.; Bez, N.; Brind’Amour, A. Influence of data pre-processing on the behavior of spatial indicators. Ecol. Indic. 2019, 99, 108–117. [Google Scholar] [CrossRef]
- Zhang, T.T.; Gao, Y.; Wang, S.K.; Liu, J.Y.; Zhang, T.; Song, C.; Zhao, F.; Zhuang, P. Landscape pattern of estuarine wetland and its multi-scale effects on macrobenthos diversity. Mar. Fish. 2018, 40, 679. [Google Scholar]
- Alam, R.Q.; Benson, B.C.; Visser, J.M.; Gang, D.D. Response of estuarine phytoplankton to nutrient and spatio-temporal pattern of physico-chemical water quality parameters in Little Vermilion Bay, Louisiana. Ecol. Inform. 2016, 32, 79–90. [Google Scholar] [CrossRef]
- Rivoirard, J.; Wieland, K. Correcting for the effect of daylight in abundance estimation of juvenile haddock (Melanogrammus aeglefinus) in the North Sea: An application of kriging with external drift. ICES J. Mar. Sci. 2001, 58, 1272–1285. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, P. Fishes of Yangtze Estuary; China Agriculture Press: Beijing, China, 2018. [Google Scholar]
- Yuan, X.Z.; Liu, H.; Lu, J.J. The ecological and environmental characteristics and conservation of the wetlands in the Changjiang Estuary, China. Environmentalist 2002, 22, 311–318. [Google Scholar] [CrossRef]
- Jing, Y.H. The Characteristics of Estuarine in China. Donghai Mar. Sci. 1988, 3, 5–15. [Google Scholar]
- Dai, L.B.; Hodgdon, C.; Tian, S.Q.; Cheng, J.H.; Gao, C.X.; Han, D.Y.; Kindong, R.; Ma, Q.Y.; Wang, X.F. Comparative performance of modelling approaches for predicting fish species richness in the Yangtze River Estuary. Reg. Stud. Mar. Sci. 2020, 35, 101161. [Google Scholar] [CrossRef]
- Pan, S.Y.; Tian, S.Q.; Wang, X.F.; Dai, L.B.; Gao, C.X.; Tong, J.F. Comparing different spatial interpolation methods to predict the distribution of fishes: A case study from Coilia nasus in the Changjiang River Estuary. Acta Oceanol. Sin. 2021, 40, 119–132. [Google Scholar] [CrossRef]
- Liu, X.X.; Wang, J.; Zhang, Y.L.; Yu, H.; Xu, B.; Zhang, C.L.; Ren, Y.P.; Xue, Y. Comparison between two GAMs in quantifying the spatial distribution of Hexagrammos otakii in Haizhou Bay, China. Fish. Res. 2019, 218, 209–217. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Sagarese, S.R.; Frisk, M.G.; Cerrato, R.M.; Sosebee, K.A.; Musick, J.A.; Rago, P.J. Application of generalized additive models to examine ontogenetic and seasonal distributions of spiny dogfish (Squalus acanthias) in the Northeast (US) shelf large marine ecosystem. Can. J. Fish. Aquat. Sci. 2014, 71, 847–877. [Google Scholar] [CrossRef]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography; Newnes: Oxford, UK, 2014. [Google Scholar]
- Li, B.; Cao, J.; Chang, J.H.; Wilson, C.; Chen, Y. Evaluation of effectiveness of fixed-station sampling for monitoring American lobster settlement. N. Am. J. Fish. Manag. 2015, 35, 942–957. [Google Scholar] [CrossRef]
- Wood, S.N.; Augustin, N.H. GAMs with integrated model selection using penalized regression splines and applications to environmental modelling. Ecol. Model. 2002, 157, 157–177. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.H.; Chen, Y.; Holland, D.; Grabowski, J. Estimating spatial distribution of American lobster Homarus americanus using habitat variables. Mar. Ecol. Prog. Ser. 2010, 420, 145–156. [Google Scholar] [CrossRef]
- Barry, S.C.; Welsh, A.H. Generalized additive modelling and zero inflated count data. Ecol. Model. 2002, 157, 179–188. [Google Scholar] [CrossRef]
- Strawderman, R.L. Model selection and inference: A practical information-theoretic approach. J. Am. Stat. Assoc. 2000, 95, 341. [Google Scholar] [CrossRef]
- Planque, B.; Bellier, E.; Lazure, P. Modelling potential spawning habitat of sardine (Sardina pilchardus) and anchovy (Engraulis encrasicolus) in the Bay of Biscay. Fish. Oceanogr. 2007, 16, 16–30. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Ijcai 1995, 14, 1137–1145. [Google Scholar]
- Appice, A.; Malerba, D. Leveraging the power of local spatial autocorrelation in geophysical interpolative clustering. Data Min. Knowl. Disc. 2014, 28, 1266–1313. [Google Scholar] [CrossRef]
- Mueller, T.G.; Pusuluri, N.B.; Mathias, K.K.; Cornelius, P.L.; Barnhisel, R.I.; Shearer, S.A. Map quality for ordinary kriging and inverse distance weighted interpolation. Soil Sci. Soc. Am. J. 2004, 68, 2042–2047. [Google Scholar] [CrossRef]
- Stow, C.A.; Jolliff, J.; McGillicuddy, D.J., Jr.; Doney, S.C.; Allen, J.I.; Frtendrichs, M.A.M.; Rose, K.A.; Wallhead, P. Skill assessment for coupled biological/physical models of marine systems. J. Marine Syst. 2009, 76, 4–15. [Google Scholar] [CrossRef] [Green Version]
- Ott, R.L.; Longnecker, M.T. An Introduction to Statistical Methods and Data Analysis; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Jensen, O.P.; Seppelt, R.; Miller, T.J.; Bauer, L.J. Winter distribution of blue crab Callinectes sapidus in Chesapeake Bay: Application and cross-validation of a two-stage generalized additive model. Mar. Ecol. Prog. Ser. 2005, 299, 239–255. [Google Scholar] [CrossRef] [Green Version]
- Al-Kharusi, L.H. Predicting the distribution and abundance of emperor fishes (Lethrinus spp.) in the Arabian Sea using two-stage generalized additive models and a geographic information system. J. Agr. Mar. Sci. 2008, 13, 7–22. [Google Scholar] [CrossRef] [Green Version]
- Ciannelli, L.; Fauchald, P.; Chan, K.S.; Agostini, V.N.; Dingsør, G.E. Spatial fisheries ecology: Recent progress and future prospects. J. Mar. Syst. 2008, 71, 223–236. [Google Scholar] [CrossRef]
- Bostrom, B. Relations between chemistry, microbial biomass and activity in sediments of a polluted vs. a nonpolluted eutrophic lake. Verh. Int. Ver. Limnol. 1988, 23, 451–459. [Google Scholar] [CrossRef]
- Andersen, J.M. Nitrogen and phosphorus budgets and the role of sediments in six shallow Danish lakes. Arch. Hyd. 1974, 74, 527–550. [Google Scholar]
- Jackson, H.B.; Fahrig, L. What size is a biologically relevant landscape? Landsc. Ecol. 2012, 27, 929–941. [Google Scholar] [CrossRef]
- Maravelias, C.D. Habitat associations of Atlantic herring in the Shetland area: Influence of spatial scale and geographic segmentation. Fish. Oceanogr. 2001, 10, 259–267. [Google Scholar] [CrossRef]
- Song, W.; Kim, E.; Lee, D.; Lee, M.; Jeon, S. The sensitivity of species distribution modeling to scale differences. Ecol. Model. 2013, 248, 113–118. [Google Scholar] [CrossRef]
- Huang, R.S. Biological characteristics, resource status and protection countermeasures of Coilia nasus. Res. Fish. 2005, 25, 33–37. [Google Scholar]
- Guo, H.Y.; Zhang, X.G.; Tang, W.Q.; Li, H.H.; Shen, L.H.; Zhou, T.S.; Liu, D. Temporal variations of Coilia nasus catches at jingjiang section of the Yangtze river in fishing season in relation to environmental factors. Res. Environ. Yangtze Basin 2016, 25, 1850–1859. [Google Scholar]
- Yuan, C.M. Spawn migration of Coilia nasus. B Biol. 1978, 12, 1–3. [Google Scholar]
- Ma, J.; Li, B.; Zhao, J.; Wang, X.F.; Hodgdon, C.T.; Tian, S.Q. Environmental influences on the spatio-temporal distribution of Coilia nasus in the Yangtze River estuary. J. Appl. Ichthyol. 2020, 36, 315–325. [Google Scholar] [CrossRef]
- Wu, J.H.; Dai, L.B.; Dai, X.J.; Tian, S.Q.; Liu, J.; Chen, J.H.; Wang, X.F.; Wang, J.Q. Comparison of generalized additive model and boosted regression tree in predicting fish community diversity in the Yangtze River Estuary, China. J. Appl. Ecol. 2019, 30, 644–652. [Google Scholar]
- Inui, R.; Onikura, N.; Kawagishi, M.; Makatani, M.; Oikawa, S. Selection of spawning habitat by several gobiid fishes in the subtidal zone of a small temperate estuary. Fish. Sci. 2010, 76, 83–91. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman and Hall: New York, NY, USA, 1990. [Google Scholar]
- Miguet, P.; Jackson, H.B.; Jackson, N.D.; Martin, A.E.M.; Fahrig, L. What determines the spatial extent of landscape effects on species? Landsc. Ecol. 2016, 31, 1177–1194. [Google Scholar] [CrossRef]
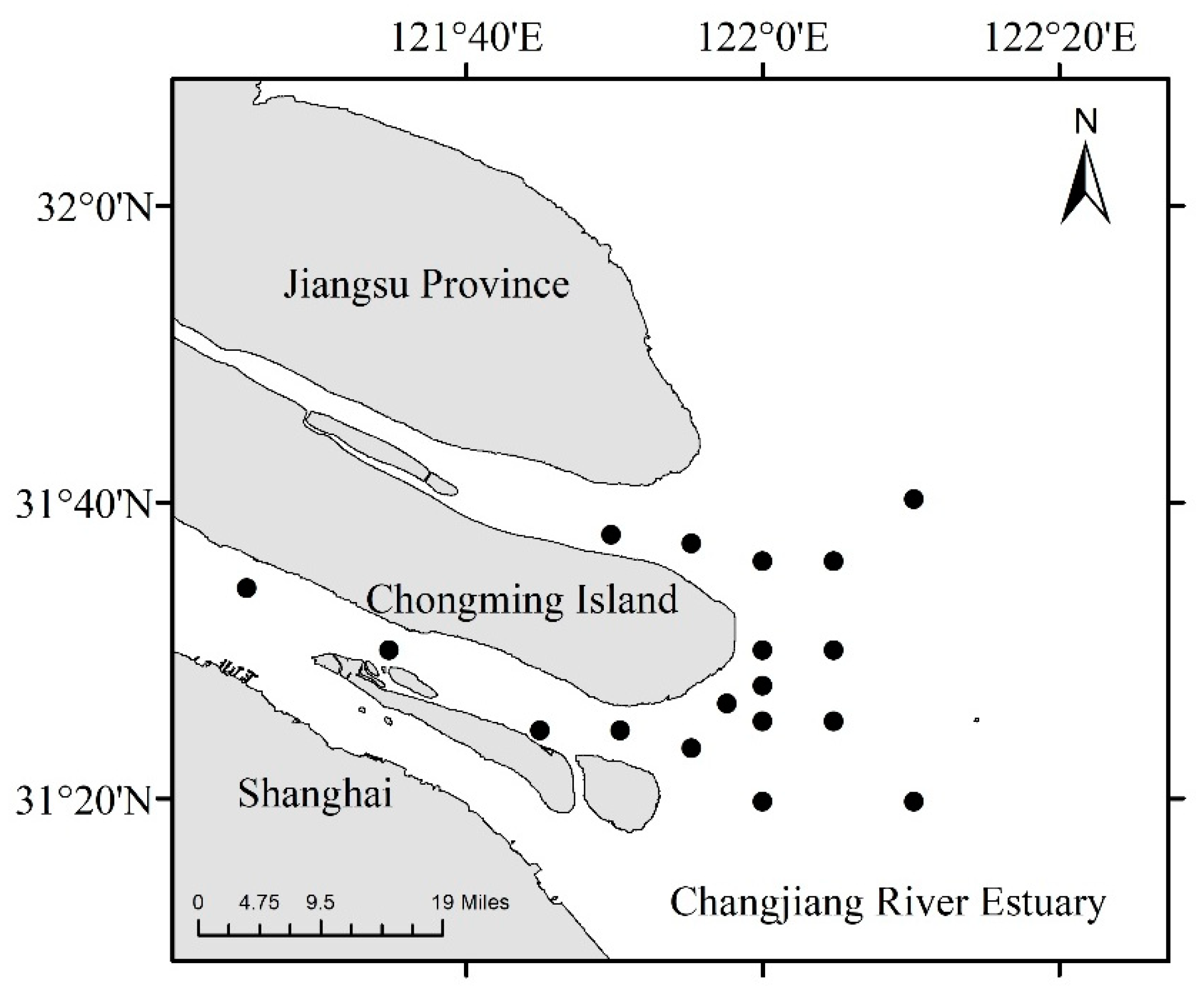
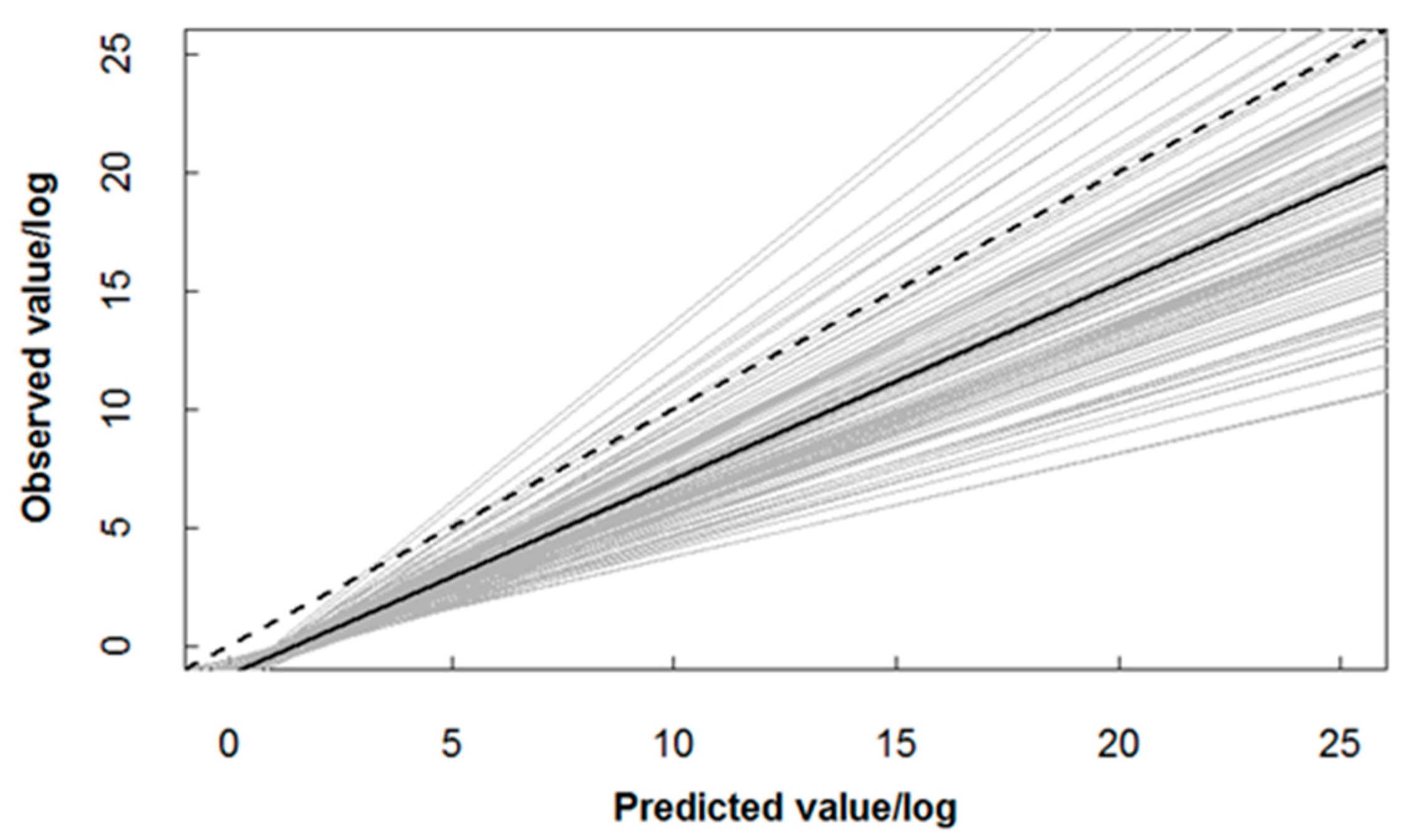

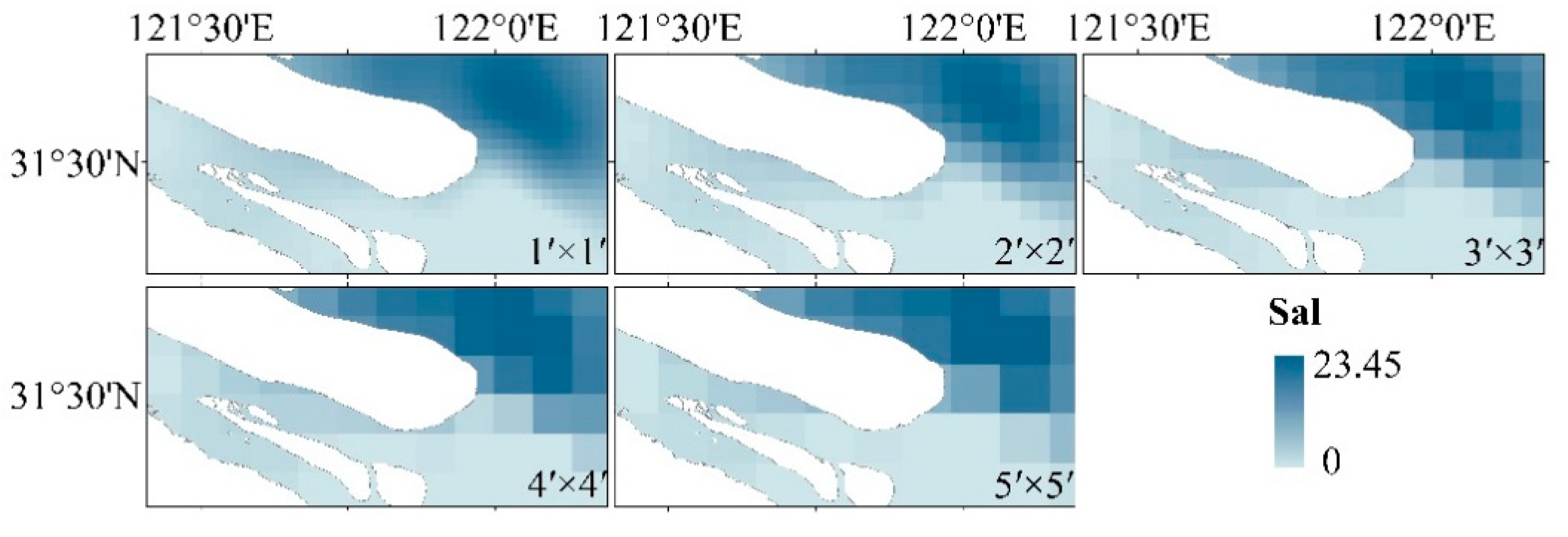
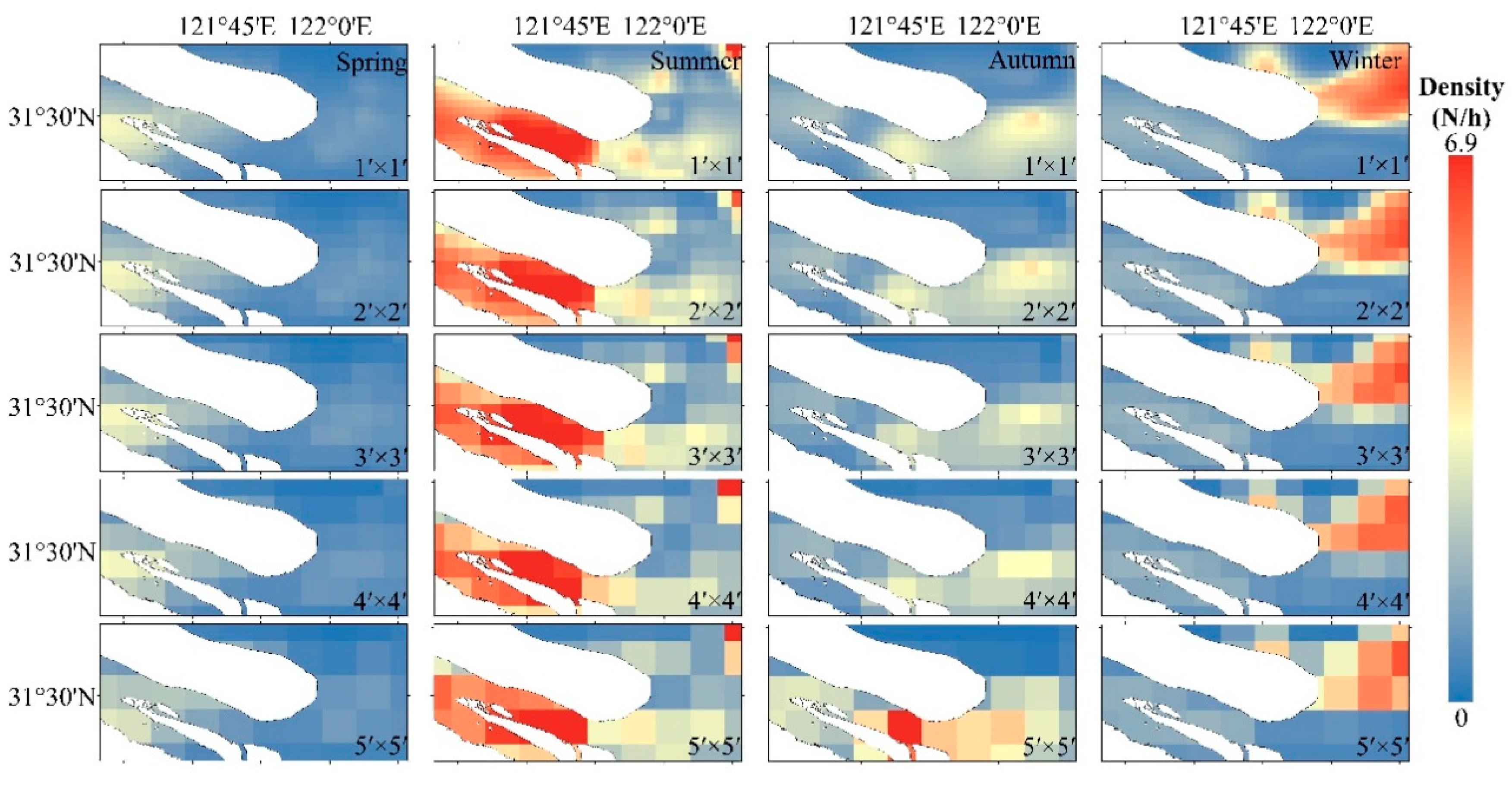


| Year | 2009 | 2012 | 2013 | 2014 | 2016 | 2017 | 2018 | Total |
|---|---|---|---|---|---|---|---|---|
| Total number of sites surveyed throughout the year | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 364 |
| Number of sites used | 52 | 39 | 46 | 51 | 5 | 23 | 36 | 252 |
| Predictive Variables | p Value | AIC | AUC | Deviance Explained | R2 | |
|---|---|---|---|---|---|---|
| GAM1 | Month | 0.016329 | 207.84 | 0.83 | 25.5% | 0.257 |
| COD | 0.030504 | |||||
| Temp | 0.054044 | |||||
| Sal | 0.000681 | |||||
| Year | 0.002734 | |||||
| Lat | 0.004118 | |||||
| GAM2 | Year | 0.005802 | 151.76 | 22.5% | 0.172 | |
| Lat | 0.070189 | |||||
| pH | 0.066935 | |||||
| Chla | 0.000818 |
| Spatial Scale | Chlorophyll a/μg·L−1 | CV | pH | CV | ||
| Mean (Range) | SD | Mean (Range) | SD | |||
| True | 1.781 (0.086–11.250) | 1.975 | 1.109 | 8.013 (6.620–9.032) | 0.368 | 0.0459 |
| 1′ × 1′ | 1.920 (0.104–11.250) | 2.040 | 1.063 | 8.018 (7.142–8.596) | 0.263 | 0.0328 |
| 2′ × 2′ | 1.922 (0.104–11.250) | 2.041 | 1.062 | 8.017 (7.153–8.555) | 0.264 | 0.0329 |
| 3′ × 3′ | 1.872 (0.105–11.250) | 2.072 | 1.107 | 8.001 (7.137–8.549) | 0.264 | 0.0330 |
| 4′ × 4′ | 1.919 (0.111–11.250) | 2.045 | 1.066 | 8.018 (7.213–8.549) | 0.261 | 0.0326 |
| 5′ × 5′ | 1.925 (0.112–11.250) | 2.071 | 1.076 | 8.017 (7.203–8.549) | 0.264 | 0.0329 |
| Spatial Scale | COD/mg·L−1 | CV | Salinity/mg·L−1 | CV | ||
| Mean (Range) | SD | Mean (Range) | SD | |||
| True | 1.034 (0.400–1.600) | 0.470 | 0.455 | 9.112 (0.000–29.800) | 10.077 | 1.106 |
| 1′ × 1′ | 0.962 (0.410–1.618) | 0.281 | 0.292 | 7.754 (0.000–34.687) | 7.700 | 0.993 |
| 2′ × 2′ | 0.963 (0.430–1.614) | 0.281 | 0.292 | 7.771 (0.000–34.777) | 7.703 | 0.991 |
| 3′ × 3′ | 0.964 (0.464–1.608) | 0.284 | 0.294 | 7.853 (0.000–34.272) | 7.719 | 0.983 |
| 4′ × 4′ | 0.963 (0.479–1.603) | 0.290 | 0.301 | 7.893 (0.000–34.314) | 7.748 | 0.982 |
| 5′ × 5′ | 0.948 (0.485–1.616) | 0.285 | 0.301 | 8.135 (0.000–32.396) | 7.790 | 0.958 |
| Spatial Scale | Water Temperature/°C | CV | ||||
| Mean (Range) | SD | |||||
| True | 18.168 (5.600–30.100) | 8.002 | 0.4404 | |||
| 1′ × 1′ | 18.098 (5.442–30.528) | 7.892 | 0.4361 | |||
| 2′ × 2′ | 18.098 (5.446–30.526) | 7.894 | 0.4362 | |||
| 3′ × 3′ | 18.015 (5.468–30.157) | 7.819 | 0.4340 | |||
| 4′ × 4′ | 18.103 (5.475–30.512) | 7.895 | 0.4361 | |||
| 5′ × 5′ | 18.118 (5.448–30.525) | 7.893 | 0.4356 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, W.; Gong, Y.; Wang, X.; Tong, J.; Han, D.; Chen, J.; Wu, J. Influence of Spatial Scale Selection of Environmental Factors on the Prediction of Distribution of Coilia nasus in Changjiang River Estuary. Fishes 2021, 6, 48. https://doi.org/10.3390/fishes6040048
Meng W, Gong Y, Wang X, Tong J, Han D, Chen J, Wu J. Influence of Spatial Scale Selection of Environmental Factors on the Prediction of Distribution of Coilia nasus in Changjiang River Estuary. Fishes. 2021; 6(4):48. https://doi.org/10.3390/fishes6040048
Chicago/Turabian StyleMeng, Weizhao, Yihe Gong, Xuefang Wang, Jianfeng Tong, Dongyan Han, Jinhui Chen, and Jianhui Wu. 2021. "Influence of Spatial Scale Selection of Environmental Factors on the Prediction of Distribution of Coilia nasus in Changjiang River Estuary" Fishes 6, no. 4: 48. https://doi.org/10.3390/fishes6040048
APA StyleMeng, W., Gong, Y., Wang, X., Tong, J., Han, D., Chen, J., & Wu, J. (2021). Influence of Spatial Scale Selection of Environmental Factors on the Prediction of Distribution of Coilia nasus in Changjiang River Estuary. Fishes, 6(4), 48. https://doi.org/10.3390/fishes6040048







