Abstract
Advances in quantum computers may pose a significant threat to existing public-key encryption methods, which are crucial to the current infrastructure of cyber security. Both RSA and ECDSA, the two most widely used security algorithms today, may be (in principle) solved by the Shor algorithm in polynomial time due to its ability to efficiently solve the discrete logarithm problem, potentially making present infrastructures insecure against a quantum attack. The National Institute of Standards and Technology (NIST) reacted with the post-quantum cryptography (PQC) standardization process to develop and optimize a series of post-quantum algorithms (PQAs) based on difficult mathematical problems that are not susceptible to being solved by Shor’s algorithm. Whilst high-powered computers can run these PQAs efficiently, further work is needed to investigate and benchmark the performance of these algorithms on lower-powered (constrained) devices and the ease with which they may be integrated into existing protocols such as TLS. This paper provides quantitative benchmark and handshake performance data for the most recently selected PQAs from NIST, tested on a Raspberry Pi 4 device to simulate today’s IoT (Internet of Things) devices, and provides quantitative comparisons with previous benchmarking data on a range of constrained systems. CRYSTALS-Kyber and CRYSTALS-Dilithium are shown to be the most efficient PQAs in the key encapsulation and signature algorithms, respectively, with Falcon providing the optimal TLS handshake size.
1. Introduction
Modern-day applications need security to protect the confidentiality and integrity of data, particularly during digital communications. Internet users rely on this security for numerous critical services, including online banking, mobile and cloud computing, e-commerce, and home automation. Cryptography is a key tool used to grant digital security, allowing the encryption, transfer, and decryption of data during their transmission between devices. Encryption and decryption occur via the use of cryptographic keys, which can either be private or public depending on whether the encryption is symmetric or asymmetric, respectively.
Devices employing symmetric encryption (private-key encryption) use a single (secret) key for both encryption and decryption; hence, devices using private-key encryption exchange this key, which is subsequently used in the decryption process [1]. Asymmetric encryption (public-key encryption) uses an encryption key (public key) and a separate decryption key (private key) [2].
Whilst current symmetric encryption methods including ChaCha20 and AES offer users confidentiality (attacks based on the quantum Grover algorithm are possible, but their effectiveness is limited and mitigable, redefining the cryptosystem parameters like the key size), it is public-key methods that are fundamental to many digital systems for providing both key negotiation and digital signing. The public-key cryptographic protocol transport layer security (TLS) builds encrypted tunnels between digital entities and is used in over 60% of internet connections in the form of a TLS-based secure HTTPS protocol [3,4]. TLS also provides authentication with the use of digital certificates, issued by trusted certificate authorities. Endpoints can verify a communicating device’s identity and public key as those contained within the certificate. The two most widely used public-key methods within certificates today are the Elliptic Curve Digital Signature Algorithm (ECDSA) and Rivest–Shamir–Adleman method (RSA).
The robustness of these two cryptographical methods relies on strong mathematical calculations that cannot be practically broken by conventional computer systems without the legitimate cryptographical key. ECDSA relies on the difficulty of its elliptic curve discrete logarithm (ECDL), and RSA relies on integer factorization, meaning that it could take a powerful computer system several years to break. However, both ECDL and RSA are no longer quantum-resistant following the discovery, by Peter Shor, of quantum factorization algorithms that could solve both ECDL and integer factorization problems in polynomial time [5]. Today, despite the fact that quantum computers (QCs) able to run the Shor algorithm are still not available to us, recent advances in the implementation of QCs by global companies like IBM, Google, and other players in the quantum computer race make the advent of the quantum era feel closer and more plausible, along with its threat to the security of cryptosystems that are reliant on the hardness of the factorization problem [6] and discrete logarithms, including the Diffie–Hellman key-exchange method [7].
For a cryptographic system to remain secure from quantum attacks, hard mathematical problems that are not susceptible to either Shor’s or any other quantum algorithm are now being developed for both key encapsulation mechanisms (KEMs) and signatures. Research into PQC has become both a significant area of interest in fundamental research and a necessity towards practical application, e.g., to update current cryptographic infrastructures, as recommended by the NIST post-quantum standardization process. Moreover, meeting the need to integrate such algorithms into existing devices, particularly ‘constrained’ IoT devices with limited performance, has become a worthy endeavor amongst researchers.
2. Background and Research Questions
In this section we provide a short description of the background that motivates our research questions, we summarize the existing work carried out on post-quantum cryptographic protocols, and we review the existing literature on the benchmarking of constrained devices.
2.1. Post-Quantum Algorithm Families
To address the issue of current security protocols potentially being broken by QC-equipped attackers, the cryptographic community has been developing problems and subproblems of NP hardness (i.e., at least as hard as a nondeterministic polynomial time problem) that cannot be solved by quantum algorithms in polynomial time. The current PQAs span five key families of mathematical problems that are hard to solve even for a quantum adversary. The distinct family classifications of asymmetric algorithms are described in more detail below. This grounding in PQAs and their respective classifications is essential to help answer all the related research questions, as the performance of each PQA is correlated with its family class.
In lattice-based cryptography, a mathematical structure named a lattice is used to provide an infinite number of grid points. Vectors (tuples) represent the coordinates of a given point in the lattice relative to the origin (a tuple of 0 s), and vectors can be defined as ‘far’ vectors or ‘short’ vectors depending on their proximity to the origin. Any vector in the lattice space originates from a basis, i.e., a smaller set of vectors used to represent the entire lattice space, and can be represented as a linear combination of the basis vectors [8,9]. A basis can be identified as long or short depending on the lattice location, which has given rise to a series of hard lattice problems, including the following:
- Shortest-Vector Problem: Finding the shortest vector in the Euclidean norm [10];
- Closest-Vector Problem: Finding a lattice vector that minimizes the distance from another target lattice [11];
- Short-Integer Solution Problem: finding a non-zero integer vector given a number of uniformly random vectors grouped as the column of a matrix [12];
- Learning with Errors: Recover a secret (s) given a sequence of ‘approximate’ random linear equations on s. For example, the input could be where each equation is correct up to some small additive error and the goal is to recover [13].
The difficulty of each of these problems is increased by the vast dimensions of the lattice and has therefore yielded some promising lattice-based PQAs that have been considered for standardization. Examples include CRYSTALS-Kyber (Kyber) [14], CRYSTALS-Dilithium (Dilithium) [15], NTRU [16], and Falcon [17]. All of these except NTRU (which was excluded in NIST Round 4) are performance-tested in this paper, to represent lattice methods and help answer RQ1, and then integrated with TLS [18] to answer RQ3. Data gleaned from previous studies on the performance of these PQAs will support us in answering RQ2 and will provide input for the advantages/disadvantages for RQ4.
Hash-based cryptography represents an alternative to current digital signature schemes, relying on Merkle trees and one-time signatures or few-time signatures used with secure cryptographic hash functions. The security of these algorithms depends on the properties of the hash function collision and preimage resistance. Assuming that the hash function is good, finding collisions and primages would be difficult if not impossible even for a quantum algorithm, meaning that hash-based approaches represent a good option for post-quantum authentication. The main disadvantage is that the hash-based digital signatures are stateful, meaning that they can only be used once requiring state management. A prime example of a hash-based PQA considered for standardization is SPHINCS+ [19], which is a combination of Merkle hash trees in the Forest of Random Subsets Scheme [20] and Witerniz One-Time Signatures Plus Scheme [21] and is stateless, which alleviates the latter issue of stage-managing but subsequently increases the signature size (approximately 40–60 KB), resulting in slower performance. SPHINCS+ will be performance-tested to obtain primary data to answer RQ1 and RQ3. Secondary data regarding SPHINCS+ performance will be used as input for RQ2 and RQ4.
Code-based cryptography, proposed by Robert McEliece in 1978, has remained unthreatened by cryptanalysis until relatively recently [22]. The concept is based on the use of a cyphertext comprising a word of an appropriate linear error-correcting code, which in this instance is a binary Goppa code, to which random errors are introduced [23]. The generator matrix (i.e., the arbitrary basis of the code) is the public key that allows anyone receiving it to encrypt it. Authentic users who have access to the decoding algorithm for the code (a polynomial time algorithm termed a ‘trapdoor’ or private key) can remove the errors and recover the cleartext. The scheme security relies on two key principles: (i) generic decoding is usually hard, and (ii) the public key used to generate the cyphertext is hard to distinguish from a random matrix.
Examples considered for standardization include the Classic McEliece scheme [24], which has a much larger public key than its classical counterparts such as RSA. BIKE and HQC are also code-based KEMs that are being considered for standardization. BIKE is based on Quasi-Cyclic Moderate-Density Parity-Check (QC-MDPC) codes that take inspiration from the McEliece scheme but have improved bandwidth and a decoder (Black Gray Flip) [25]. Hamming Quasi-Cyclic (HQC) [26] is reliant on the difficulty of decisional quasi-cyclic syndrome decoding with parity problems. HQC is INDCPA-secure and is alleged to also be secure against adaptive chosen-ciphertext attack (CCA2) [27]. It does, however, have significantly larger keys and ciphertexts compared to BIKE, but its key-generation and decapsulation mechanisms are considerably faster. Classic McEliece, BIKE, and HQC are all performance-tested in this paper to represent the code-based methods for RQ1. HQC and BIKE are available for TLS handshake performance testing for RQ3, and secondary data are obtained for all the algorithms to contribute to RQ2 and RQ4.
Isogeny-based cryptography is based on elliptic curves for KEMs. The first elliptic curve key exchange algorithm was the Elliptic Curve Diffie–Hellman, based on the discrete logarithm problem over elliptic curves [28]. It was theoretically solved by Shor’s algorithm, and, therefore, it is no longer considered secure against quantum algorithms. This has prompted the development of isogeny-based schemes, such as the Supersingular Isogeny-based Diffie–Hellman (SIDH). Isogenies are surjective and homomorphic structure-preserving functions that map two groups together. Between two elliptic curves, an isogeny ϕ will map points on the domain curve E1 to points on a co-domain curve E2. These isogenies are calculated using Velu’s formulas [29] as ϕ: E → E/κ, where κ is defined as the kernel. An isogeny is generated from random values and used for private keys in secure communications, and, as yet, no significant attacks against it have been identified. For this reason, SIKE (Supersingular Isogeny-based Key Encapsulation) [30] is an SIDH-based PQA that is being considered for standardization, and it will be assessed further in this paper. Given its close relationship with ECC and Diffie–Hellman protocols, SIKE’s integration into existing systems is considered relatively easy compared to its other PQA counterparts. SIKE also has a very small key size of 750 bytes but is an order of magnitude slower than the alternative PQAs being considered.
Multivariate polynomial cryptography (MPC) involves the hardness of solving problems of multivariate quadratic equations across finite fields, which is an NP-hard problem. MCP often results in excessive signature or key sizes, and many of the developed PQAs considered for standardization have focused on reducing these. MPC candidates include GeMSS [31] and Rainbow [32]. Unfortunately, attacks on these PQAs have significantly reduced their security, and, therefore, they are not being considered for PQC standardization [33,34,35]. Consequently, this class of PQAs will not be investigated in this paper.
Relevant PQA winners of the NIST round 4, and alternatives, are represented in Figure 1.
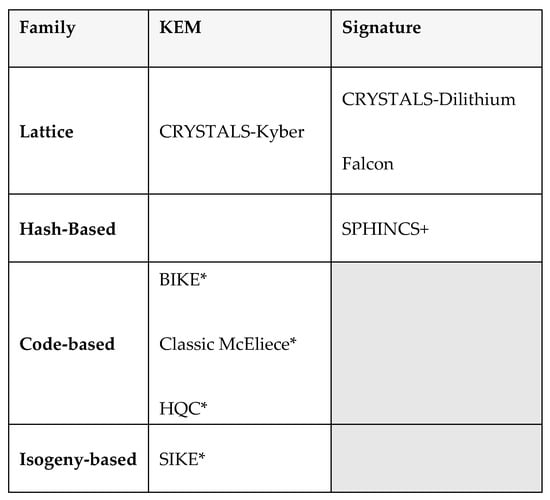
Figure 1.
The four PQA winners [14,15,17,19] and the four PQA alternatives (*) [24,25,26,30] from NIST Round 4. Five of the algorithms are employed for KEM (with CRYSTALS-Kyber as the primary PQA), three are selected for signatures.
2.2. Post-Quantum Cryptography and IoT Devices
The IoT connects embedded sensors and actuators using networking protocols. As such, the IoT has contributed significantly to the creation of novel applications, including smart homes, smart cities, smart farms, healthcare, smart sensors, drones, and many more. The majority of devices involved in such IoT networks are constrained devices with limited CPU, memory, wireless bandwidth, and/or power resources [36]. Given the high asset value of the sectors and environments in which these systems operate, they have become a significant target for cyberattacks [37,38]. Whilst the security protocols for most information technology (IT) devices can be patched in the future, performing this task for today’s billions of embedded IoT devices presents a significant challenge, and the security risks to such devices are further increased in a post-quantum world [39]. There therefore needs to be consideration of how quantum-resistant algorithms perform on these constrained IoT devices, as opposed to focusing on their non-constrained counterparts.
Given the increase in the number of IoT devices transmitting encrypted data, the work developed in ref. [40] discusses the need for ‘lightweight’ PQAs that are quantum-safe but with minimal overheads. Ref. [41] supports the need for PQAs to maintain security against quantum adversaries but emphasizes the ease with which higher-powered computing devices can run such algorithms; therefore, the testing of constrained devices with limited capabilities is necessary to simulate the performance of current IoT devices. Ref. [41] achieves this in an IoT laboratory where the constrained device is a Raspberry Pi 3B+ (1.2 GHz quad core ARMv8 (A53) 64-bit processor, 1 GB RAM and 32 GB storage). This is used for benchmarking the performance of the selected PQAs from Round 2 of the NIST PQC standardization competition. Both KEMs (including Kyber, Saber, NTRU, Classic McEliece, and FrodoKEM) and signatures (including Dilithium, qTESLA, Rainbow, and SPHINCS+) are benchmarked in [41], which is relevant to this study, as it provides a similar justification and methodology for generating the quantitative data-measuring time (ms) to assess the performance of each algorithm on individual constrained devices. This previous work also combines the performance of KEM/signature PQAs during a handshake between two constrained devices, communicating using TLS1.3 over a wired network and also providing secondary data to answer RQ2. The methods used in [41] will aid in generating the benchmarking data to answer RQ1, and the data from [41] can also be a source of secondary quantitative data to assist in answering RQ2 and RQ4. The work in ref. [41] also points to previous studies that used higher-powered CPUs in their constrained devices to obtain similar results [42,43], which could be of use for the control used in this study for the first two research questions.
The interpretation of this quantitative data will provide the basis of an assessment for identifying the advantages and disadvantages of the PQAs being investigated.
2.3. Research Questions
- RQ1: The PQA standardization competition was updated by NIST in July 2022 [44], which highlights how cutting-edge the post-quantum field is and prompts further inquiry into the efficiency and practicality of PQAs. This includes the ease with which they integrate with current security technologies and how they perform in current IoT devices, which have significantly less processing power than their high-powered counterparts and yet are widely distributed within smart systems and are therefore more prone to cyber-attacks. For this reason, there is the need to ask the question: how do the selected PQAs perform relative to each other on constrained devices and compared to higher-powered devices?
- RQ2: There are numerous groups within the cryptographic community that have tested the performance of PQAs on a range of constrained devices and lower power processors [41,45,46,47,48]. Whilst the data may not be directly comparable, it would be useful to have supporting data to either confirm or refute the findings of RQ1, and, therefore, we should ask: how do the data from this study compare to those from similar previous studies?
- RQ3: The integration of PQAs into existing network security protocols such as TLS will be a requirement even for future networks that QCs form part of. For this reason, this question should be posed: how do the PQAs perform on constrained target devices when tested in combination (KEM and Sign) over TLS?
- RQ4: Finally, to summarize the findings, we need to ask what the concluding key advantages and disadvantages of PQAs are, when they are implemented in constrained devices.
2.4. Primary Data Collection and Experimental Methods
The method defined in this section was employed to generate primary quantitative data to help answer RQ1. Quantitative data were collected and analyzed to determine the benchmark performance of each PQA, encompassing the four NIST winners and the four alternate candidates in the fourth round for PQC standardization (see Table 1). Benchmarking measures mean the time (µs) during key exchange and signing for each of the PQA algorithms when tested on both constrained and higher-performance devices. For KEMs, the process timings were subdivided into key generation, encapsulation, and decapsulation, and for signatures, they were subdivided into Keypair, Sign, and Verify.

Table 1.
This table summarizes the performance of PQA KEM, comparing the benchmarking performed in this work with that of other existing works. * SSF = Classic McEliece with semi-systematic form of public-key generation.
Benchmarking was achieved using Open Quantum Safe (OQS), an open source project chosen for this paper due to its correlation in experimenting with NIST-selected algorithms and the ability to evaluate PQC within a testing environment [51]. Liboqs is a library from the OQS platform containing the relevant PQAs that is available through GitHub (https://github.com/open-quantum-safe, accessed on 15 May 2024) and provides benchmarking functionality for both KEM and signing. This library has been used in previous benchmarking studies [41] and allows greater comparability of data, to answer RQ2.
A second component was to performance-test the TLS1.3 handshake between the two constrained devices using a fork in the OQS-OpenSSL 1.1.1 project, which integrates liboqs (version 0.7.1). The TLS handshake size (bytes) and timings (ms) were determined for different combinations of KEM and signing PQAs. The OpenSSL fork’s protocol involves simulated client–server handshake on the same device, but here, it was adapted for client–server handshake measurement between two networked, constrained devices. These data were generated within an IoT laboratory setting, using the equipment and configurations described below:
- Two Raspberry Pi 4 devices with a 1.5 GHz quad core ARMv8 (A72) 64-bit processor, 4GB RAM. Given that a 64-bit operating system is required to run liboqs, Raspberry Pi OS 64-bit Debian version 11 (bullseye) was installed with 64 GB microSD storage. Access to the devices was over SSH (using PuTTY 0.77) from a desktop PC.
- A standalone network generated between the two devices using a home-based switch (Netgear GS308).
Comparative PQA performance testing on non-constrained (control) devices was performed using the following:
- Windows 11 OS Desktop PC with 4.9 GHz 16 core (32 thread) Ryzen 9 5950x processor, 64 GB DDR4 3600 MHz RAM, and 1 TB of M.2 NvMe SSD storage.
- A Windows 11 OS laptop (Razer Blade) with up to 2.6 GHz 6-core (12-thread) i7-9750H processor, 8 GB GDDR6 VRAM, and 1 TB SSD.
- For both control devices, testing was performed on a Linux-based hypervisor using VM Virtual Box version 6.1.36 (Oracle) running Ubuntu 22.04.01 LTS Jammy Jellyfish OS. The hypervisors were set to access all CPU cores within each respective system, and all additional parameters were maximized to optimize performance.
- All PQA benchmarks were run in triplicate on both Raspberry Pi 4 devices and control devices, and the mean values are presented in the Results section.
- All TLS performance tests were run in singlet due to the lack of variance in the data generated. The designated server Raspberry Pi 4 device (RPi4-1) was configured to have a static IP address, as per the configuration shown in Figure 2. The OQS-OpenSSL protocol was adapted to enable testing across both devices using the connect ip address command on the client device (RPi4-2).
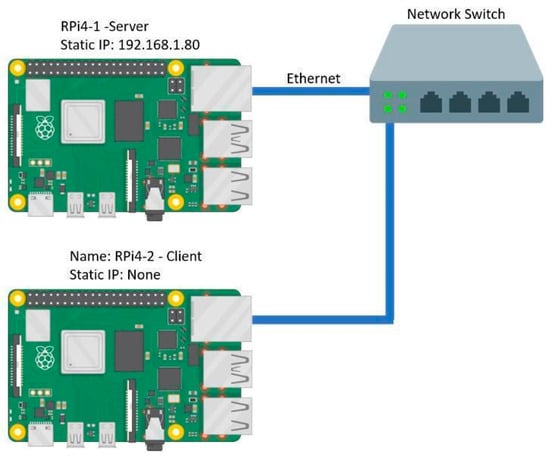 Figure 2. Standalone wired network for measuring PQA handshake sizes and timings over TLS between RPi4-1 (server) and RPi4-2 (client). A static IP address was configured for the server to allow connection from the client.
Figure 2. Standalone wired network for measuring PQA handshake sizes and timings over TLS between RPi4-1 (server) and RPi4-2 (client). A static IP address was configured for the server to allow connection from the client.
3. Results and Analysis
OQS benchmark analysis assessed the performance of the KEM and signature PQA schemes and the TLS handshake (combining KEM and signature mechanisms). Given the number of parameter variations in each PQA, the volume of quantitative data generated needed restricting, as follows:
- The selection of the PQA parameters required to achieve NIST Level 3 security only (equivalent to cracking AES-256 or 128 bits of quantum security, as required for NIST standardization). Where this was not available, NIST Level 5 security was selected. We observed that Falcon-512 and Falcon-1024 had claimed NIST security levels of 1 and 5, respectively; therefore, the latter was selected.
- Only those PQAs with representation in liboqs were used. During benchmarking, SIKE was no longer available in liboqs, having been compromised by a classical computer attack, after having reached NIST Round 4 selection [52]. It was therefore excluded from testing.
- Where significant variations in a PQA existed, specific parameters were selected and taken as representative of the group (as for SPHINCS+).
The summarized results of this paper are represented graphically in the relevant sections and then compared, where possible, with other benchmarks from the literature. In order to allow further understanding of the different PQAs in the context of the results generated in this paper, both public- and private-key sizes are provided. These can be found in Appendix A, Table A1 for each KEM, and in Table A2 for each signature PQA, selected based on the above criteria [50].
3.1. KEM Benchmarking
Benchmark performance testing of the KEM PQAs on the two constrained devices (RPi4-1 and RPi4-2) and two control devices (PC and laptop) provided mean times (µs) for the individual stages of key generation, encapsulation, and decapsulation. The data are represented graphically (bar charts) in Figure 3 for each of the devices on a logarithmic axis due to the broad range of values.
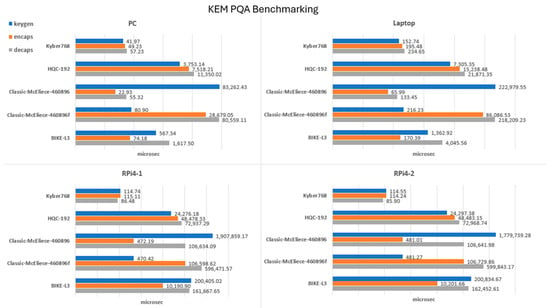
Figure 3.
Logarithmic plot of time (µs) versus KEM PQA processes for key generation (keygen), encapsulation (encaps), and decapsulation (decaps) on constrained (RPi4-1 and RPi4-2) and higher-powered (PC and laptop) devices. Kyber768 processes are fastest for all devices and show the least difference between the two device power classifications.
Across all devices tested, the lattice-based solution Kyber (Kyber768) was the front runner, with a moderate key size and performing encapsulation and decapsulation in approximately 0.05 milliseconds. Of the code-based algorithms—HQC (parameter HQC-192), BIKE (parameter BIKE-L3), and Classic McEliece—HQC demonstrated the best overall performance across all devices. BIKE’s performance was more costly than HQC, with the highest cost being for decapsulation for the higher-powered devices and key generation for the low-powered systems. Classic McEliece parameter 460,896 showed the best performance in the code-based solutions for encapsulation, but the key generation was substantially more costly, given the large public-key size and the fact that the system would reject 3–4 Goppa polynomials on average, thus restarting the key-generation process [24]. Despite having the same large public-key size, the alternatively designed parameter for Classic McEliece 460896f used a semi-systematic form (SSF) of public-key generation, which offered a far better key-generation performance due to its the lower probability of key-generation failure compared to the systematic form [24] and generated a much-improved performance compared to that of HQC. This was, however, hindered by the excessive decapsulation latency noted across all platforms, which requires further investigation via comparison with previous studies.
In addition to this, comparison between the constrained devices and the higher-powered devices revealed a difference in latency of up to an order of magnitude for the constrained platforms, except for Kyber768, which showed only a ~50% improvement
When run on the PC (see Figure 3), interestingly, kyber768 tested on the constrained devices showed a marginally improved performance compared to when it was run on the laptop.
This performance testing has answered RQ1 regarding KEM PQAs, placing the lattice-based Kyber method as the fastest of the KEM PQAs for key generation, encapsulation, and decapsulation on both constrained devices; it demonstrates the least difference in performance between constrained devices and higher-powered platforms. HQC appears to be another promising algorithm, with a uniformly distributed performance across key generation, encapsulation, and decapsulation on constrained platforms; however, the difference in performance between constrained and higher-powered devices is more pronounced. These results are further supported by the NIST competition that marked Kyber as the winning KEM lattice-based PQA due to its security and performance across other constrained devices [44].
3.2. Comparison with Other KEM Works
In Table 1, we compare three relevant publications testing KEM PQAs. In the comparison, the speeds are converted to micro seconds, and, where comparative data are not available on constrained devices, PC benchmarks from this work are also included.
Given that each benchmarking is performed under slightly different conditions and parameters, a summary of these divergencies is explained below in Table 1. The work developed in ref. [41] uses a Raspberry Pi 3 B+, which, while less powerful than the Raspberry Pi 4, provides comparative results for Kyber768, supporting the speed and consistency of Kyber’s performance across key generation, encapsulation, and decapsulation. Ref. [41] also performance-tests BIKE-L3 and provides similar performances on constrained platforms. In contrast, the work developed in ref. [50] delivers a comprehensive study focused on Classic McEliece, including a semi-systematic form (SSF) variant, in comparison with the other code-based PQAs, such as HQC and BIKE. These data are primarily collected on a device with a 3.5 GHz CPU (non-constrained). However, consistency is maintained in the high key-generation latency for Classic McEliece compared to its SFF counterpart.
The performance of HQC on the PC, compared with that described in ref. [49], shows an increase in latency. The work developed in ref. [45] uses a Samsung Galaxy A5, model SM-A500H, which is equipped with an Exynos 7880 Octa-core 1.9 GHz processor, to benchmark a range of PQAs, including Classic McEliece [45], again showing extensive key-generation times compared to the other KEM PQAs, listed with no SSF comparison in this case. No previous studies support the extended SSF decapsulation time that we observed.
3.3. Signature Benchmarking
Benchmark performance testing of the signature PQAs on the two constrained devices and control devices provided mean times (µs) for the individual stages of Keypair, Sign, and Verify processes (see Figure 4).
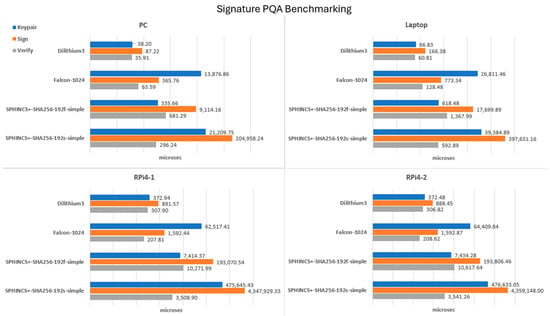
Figure 4.
This figure describes the performance of signature PQA processes Keypair, Sign, and Verify for constrained (RPi4-1 and RPi4-2) and higher-powered (PC and laptop) devices. Dilithium3 is the fastest for all devices and shows a moderate difference in performance between the two power classifications of devices. The performance is measured using a Log of time in µs.
The hash-based method SPHINCS+ can use either Haraka, SHA56, or SHAKE256 hash functions, each of which has a ‘robust’ and ‘simplified’ version, as well as parameters for ‘fast processing’ (denoted ‘f’) and ‘small signatures’ (denoted ‘s’) [18]. This provides 12 combinations for NIST security level 3 alone, and, therefore, this has been limited to two SHPINCS+ variants by taking the SHA256 hash-base to be representative and testing ‘simplified’ versions only, as the ‘robust’ alternatives were no longer available in the OQS benchmark options.
The data in Figure 4 indicate that Dilithium performs the best across all devices for Keypair, Sign, and Verify. Falcon offers faster verification speeds for constrained devices but is slower on Keypair and signature. This comparison may, however, be less direct, given that Falcon’s level 5 security parameter (Falcon-1024) has been used in place of the level 3 parameter (due to the removal of the latter in the second round of the NIST competition [27]).
SPHINCS+ ‘s’ variants denote small signatures and SHPINCS+ ‘f’ denotes fast processing. SPHINCS+ has the smallest of the public keys, which is reflected in the Keypair phase being faster than Falcon’s for the f variants. However, the SPHINCS+ Sign and Verity phases are at least an order of magnitude slower across all devices as a result of its large stateless signatures.
A comparison of the constrained device performance compared to the PC indicates that, overall, the PC’s speed is approximately between 5 and 10 times faster than the Raspberry Pi 4 across the PQAs. The laptop is approximately 50% slower than the PC but is significantly faster than the Raspberry Pi 4 across the board.
Dilithium is the clear front-runner, with consistently low latency across the Keypair, Sign, and Verify processes for all platforms compared to the other PQAs. Dilithium runs approximately one order of magnitude slower on constrained platforms compared to non-constrained devices, but this is moderate when performing the same comparison for the other signature PQAs.
The PQA performance testing in this work has answered RQ1, indicating that the lattice-based PQAs CRYSTALS-Dilithium and CRISTALS-Kyber provide optimal latency as, respectively, signature and KEM PQAs for IoT devices compared to the remaining NIST winners/alternatives tested. Section 3.4 looks to verify these findings by measuring the TLS handshake size for KEM/signature combinations communicated between two constrained platforms.
D. Comparison with other signature works
Two relevant publications related to performance-testing signature PQAs have been identified, and Table 2 compares these works to the results of this work. Timings are listed only for the Sign and Verify processes for most publications selected, with Keypair excluded. Benchmarking is conducted under slightly differing conditions, which are indicated below in Table 2.

Table 2.
This table summarizes the performance of PQA signature in this work and compares it with the results of other existing works.
The work developed in ref. [41] uses a Raspberry Pi 3 B+, providing results for Dilithium IV, but has also included the same SPHINCS+ variants as those selected in this work. The findings of [41] are consistent with Dilithium’s leading performance with the lowest latency. As per this study, ref. [41] also demonstrated that SPHINCS+ had the highest latency for the Sign process, further supporting our results.
Ref. [53] uses a non-constrained device operating a virtual machine with an Intel i5-8350U processor utilizing four cores set at 1.7 GHz each with 8GB of RAM [53]. Dilithium 4 is tested and again is the front-runner for speed overall. Falcon1024 has approximately ten times more latency for signing, but verification is approximately three times faster than Dilithium 4, given its smaller signature size [17]. These supporting data have been helpful in answering RQ2 through verifying these papers’ findings through comparison with these previous works.
3.4. TLS Handshake
For TLS performance, a fork in OpenSSL, which integrates liboqs to measure quantum-safe key exchange and authentication in TLS1.3, is used to determine the size and time of a handshake between the two constrained devices for each combination of the KEM and signature PQAs. NIST Security Level 3 parameters for SHPINCS+ SHA-256-192 variants are not active in the OpenSSL liboqs provided by Open Quantum Safe. For this reason, SPHINCS+-SHA256-128f-robust for NIST security level 1 was used instead.
Despite having a smaller public-key, private-key, and signature size (32 bytes, 64 bytes, and 17,088 bytes, respectively) compared to the level 3 variants, this parameter still provides the smallest of the public-/private-key sizes and the largest signature size compared to the other signature PQAs tested.
These data are presented in Table 3 and indicate that SPHINCS+ uses the greatest number of bytes, independent of the KEM algorithm used. Dilithium provided the second-lowest byte data observed across all KEM combinations, but Kyber768 combinations were shown to be optimal. Falcon was the front-runner, with the smallest handshake size, independent of the combined KEM, but using Kyber768 led to the lowest byte cost. This is attributed to Kyber having the smallest key sizes of the KEMs and Falcon having the smallest signature size of the signature PQAs tested. Handshake timing data for these KEM/signature combinations could not be obtained at the time of testing due to a TLS1.3 specific error caused by a configuration issue with Nginx SSL that prevented connection to the server [54,55,56,57,58,59].

Table 3.
This table shows that SPHINCS+ has the greatest byte cost, independent of the KEM algorithm. Falcon and Dilithium have the lowest and second-lowest byte data, respectively, for all KEM combinations, but Kyber768 was optimal. * NIST Level 1 SPHINCS+ alternative was used due to there being no activation of level 3 (192) in OpenSSL at time of testing.
4. Discussion and Conclusions
A summary of the results obtained in this work is given in Table 4, showing the key advantages and disadvantages of the PQAs tested on IoT devices.
This work contributes to the field of post-quantum cryptography by benchmarking the winning and front-running PQAs on the Raspberry Pi 4. At the time of writing, quad core processors with speeds between 1.2 and 1.5 GHz and at least 4 GB of RAM can typically be found in smart TVs, smart home devices, and mobile phones [55,56,57]. Comparably, the Raspberry Pi 4 has similar specifications and therefore more closely represents the IoT devices of today. Previous studies have either used non-constrained devices [40,42] due to the availability of technology or devices of very limited capability compared to current IoT device standards [58,59,60]. Furthermore, some finalist PQAs, such as BIKE and Classic McEliece, have been modified for performance optimization between the second and third rounds of the NIST competition, and it is therefore prudent to test the most recent iterations of these PQAs [24,25].
The limitations of this work included the lack of TLS handshaking timings due to an OpenSSL configuration issue [54]. It would be prudent to add these timings to support the handshake size data in future work. Furthermore, SPHINCS+ SHA256-192-based parameters were disabled in OpenSSL at the time of testing and were therefore replaced with SHA256-128 parameters. Whilst this is inconsistent with the benchmarking data, SHA256-192 testing for level 3 security is unlikely to add any value, given the large size of the SPHINCS+ handshake, even at security level 1. Finally, this work has only benchmarked PQAs using timings, which has limited the number of comparable prior studies for RQ2. The literature ranges regarding the type of PQA benchmarking data collected and includes timings, CPU cycles, memory usage, and energy consumption. Broadening these measurements in follow-up studies can provide greater insight into PQA performance.
In terms of outlook and future work, the consistent and excessive decapsulation time observed for the Classic McEliece SST parameter across all platforms tested is not supported in the literature, prompting further investigation in order to better understand these findings. The current literature reflects the need to adapt PQAs for the most vulnerable, constrained nodes within a network, and introduce lighter-weight versions with reduced latency and memory costs [61,62,63,64]. The benchmarking of these variants would be prudent in order to build on the findings of this paper.
Aside from timings, PQA fitness for purpose and ‘cryptoagility’ needs to be considered for migration into existing IT infrastructures and real-world use. The work developed in ref. [65] indicates the main open issues that need to be addressed in order for robust PQAs to achieve a quantum secure network that may be shared by both quantum and classical infrastructures.

Table 4.
The Table summarizes the key advantages and disadvantages of the PQAs tested on IoT devices. * Includes reference to this paper. White cells denote KEMS, and gray cells denote signatures.
Table 4.
The Table summarizes the key advantages and disadvantages of the PQAs tested on IoT devices. * Includes reference to this paper. White cells denote KEMS, and gray cells denote signatures.
| Advantages | Disadvantages | |
|---|---|---|
| CRYSTALS-Kyber |
|
|
| HQC |
|
|
| Classic McEliece |
|
|
| BIKE-L3 |
|
|
| CRYSTALS- Dilithium |
|
|
| Falcon |
|
|
| SPHINCS+ |
|
|
Author Contributions
G.F. developed the analysis. C.O. supervised the project. Both authors contributed to the conceptualization of the analysis. Both authors contributed to writing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
Carlo Ottaviani acknowledges support from EPSRC and DSIT TMF-uplift CHEDDAR: Communications Hub For Empowering Distributed ClouD Computing Applications And Research (EP/X040518/l) and (EP/Y037421/l).
Data Availability Statement
All reported data are included in the manuscript.
Acknowledgments
Greg Fitzgibbon would like to acknowledge his son William Fitzgibbon for the motivation to deliver this work.
Conflicts of Interest
Author Gregory Fitzgibbon was employed by the company Quantum and AI Research, Tession Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
Private- and public-key sizes (and signature sizes) for the PQAs selected based on [55]. This provides a frame of reference for the relative performance of each PQA in the benchmarking analyses.

Table A1.
KEM PQA private- and public-key sizes.
Table A1.
KEM PQA private- and public-key sizes.
| Family | Protocol | Parameter Set | Private-Key Size (Bytes) | Public-Key Size (Bytes) |
|---|---|---|---|---|
| Lattice | Crystal-Kyber | Kyber-768 | 2400 | 1184 |
| Kyber-768-90s | 2400 | 1184 | ||
| Code-based | BIKE | BIKE-L3 | 10,105 | 3083 |
| HQC | HQC-192 | 4586 | 4522 | |
| Classic McEliece | Classic-McEliece-460896 | 13,608 | 524,160 | |
| Classic-McEliece-460896f | 13,608 | 524,160 |

Table A2.
Signature PQA public-key, private-key, and signature sizes.
Table A2.
Signature PQA public-key, private-key, and signature sizes.
| Family | Protocol | Parameter Set | Private-Key Size (Bytes) | Public-Key Size (Bytes) | Signature Size (Bytes) |
|---|---|---|---|---|---|
| Lattice | Dilithium | Dilithium3 | 4000 | 1952 | 3293 |
| Falcon | Falcon-1024 | 2305 | 1793 | 1462 | |
| Hash-based | SPHINCS+ | SPHINCS+-SHA256-192f-robust ‡ | 96 | 48 | 35,664 |
| SPHINCS+-SHA256-192f-simple | 96 | 48 | 35,664 | ||
| SPHINCS+-SHA256-192s-robust ‡ | 96 | 48 | 16,224 | ||
| SPHINCS+-SHA256-192s-simple | 96 | 48 | 16,224 |
‡ Public-key, private-key, and signature sizes for SPHINCS+ robust variants were sourced from [26].
References
- Delfs, H.; Knebl, H. Introduction to Cryptography: Principles and Applications. In Information Security and Cryptography: Texts and Monographs, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Li, N. Asymmetric Encryption. In Encyclopedia of Database Systems; Liu, L., OZsu, M.T., Eds.; Springer: Boston, MA, USA, 2009; p. 142. [Google Scholar]
- Chan, C.L.; Fontugne, R.; Cho, K.; Goto, S. Monitoring TLS adoption using backbone and edge traffic. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Honolulu, HI, USA, 15–19 April 2018; pp. 208–213. [Google Scholar] [CrossRef]
- Naylor, D.; Finamore, A.; Leontiadis, I.; Grunenberger, Y.; Mellia, M.; Munafò, M.; Papagiannaki, K.; Steenkiste, P. The Cost of the “S” in HTTPS. In Proceedings of the 10th ACM International on Conference on Emerging Networking Experiments and Technologies, Sydney, Australia, 2–5 December 2014. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th Annual Symposium on Foundation of Computer Science, Washington, DC, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Bernstein, D.J. Introduction to post-quantum cryptography. In PostQuantum Cryptography; Bernstein, D.J., Buchmann, J., Dahmen, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar]
- Buchanan, W.; Woodward, A. Will quantum computers be the end of public key encryption? J. Cyber Secur. Technol. 2017, 1, 1–22. [Google Scholar] [CrossRef]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-Quantum Lattice-Based Cryptography Implementations: A Survey. ACM Comput. Surv. 2019, 51, 129. [Google Scholar] [CrossRef]
- Peikert, C. A Decade of Lattice Cryptography. Found. Trends® Theor. Comput. Sci. 2016, 10, 283–424. [Google Scholar] [CrossRef]
- Micciancio, D. Shortest Vector Problem. In Encyclopedia of Algorithms; Kao, M.-Y., Ed.; Springer: Boston, MA, USA, 2008; pp. 841–843. [Google Scholar]
- Micciancio, D. Closest Vector Problem. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Ed.; Springer: Boston, MA, USA, 2005; pp. 79–80. [Google Scholar]
- Ajtai, M. Generating hard instances of lattice problems (extended abstract). In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2009, 56, 34. [Google Scholar] [CrossRef]
- Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehle, D. CRYSTALS-Kyber: A CCA-Secure Module-Lattice-Based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar] [CrossRef]
- Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Dilithium: A Lattice-Based Digital Signature Scheme. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 2018, 238–268. [Google Scholar] [CrossRef]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Algorithmic Number Theory; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar]
- Fouque, P.-A.; Hoffstein, J.; Kirchner, P.; Lyubashevsky, V.; Pornin, T.; Prest, T.; Ricosset, T.; Seiler, G.; Whyte, W.; Zhang, Z. Falcon: Fast-Fourier Lattice-based Compact Signatures over NTRU. Submiss. NIST’s Post-Quantum Cryptogr. Stand. Process 2019, 36, 1–75. [Google Scholar]
- Crockett, E.; Paquin, C.; Stebila, D. Prototyping Post-Quantum and Hybrid Key Exchange and Authentication in TLS and SSH. 2019. Available online: https://eprint.iacr.org/2019/858 (accessed on 15 May 2024).
- Aumasson, J.-P.; Bernstein, D.J.; Beullens, W.; Dobraunig, C.; Eichlseder, M.; Fluhrer, S.; Gazdag, S.-L.; Hülsing, A.; Kampanakis, P.; Kölbl, S.; et al. SPHINCS+ Submission to the NIST Post Quantum Project, v3. 1 October 2020. Available online: https://sphincs.org/data/sphincs+-round3-specification.pdf (accessed on 15 May 2024).
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Buchmann, J.; Dahmen, E.; Ereth, S.; Hulsing, A.; Ruckert, M. On the Security of the Winternitz One-Time Signature Scheme. In Proceedings of the Progress in Cryptology—AFRICACRYPT 2011, Dakar, Senegal, 5–7 July 2011; pp. 363–378. [Google Scholar]
- Canteaut, A.; Sendrier, N. Cryptanalysis of the Original McEliece Cryptosystem. In Advances in Cryptology—ASIACRYPT’98; Ohta, K., Pei, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 187–199. [Google Scholar]
- McEliece, R.J. A Public-Key Cryptosystem Based on Algebraic Coding Theory. Deep Space Network Progress Report. Volume 44, pp. 114–116, 1 January 1978. Available online: https://ui.adsabs.harvard.edu/abs/1978DSNPR..44..114M (accessed on 15 May 2024).
- Bernstein, D.J. Classic McEliece: Conservative Code-Based Cryptography. 10 October 2020. Available online: https://cryptojedi.org/papers/mceliecenistr3-20201010.pdf (accessed on 15 May 2024).
- Aragon, N.; Barreto, P.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.-C.; Gaborit, P.; Ghosh, S.; Gueron, S.; Güneysu, T.; et al. BIKE: Bit Flipping Key Encapsulation. 29 September 2021. Available online: https://bikesuite.org/files/v4.2/BIKE_Spec.2021.07.26.1.pdf (accessed on 15 May 2024).
- Gaborit, P.; Deneuville, J.-C. Hamming Quasi-Cyclic (HQC) Third Round Version. 1 October 2020. Available online: https://pqc-hqc.org/doc/hqc-specification_2023-04-30.pdf (accessed on 15 May 2024).
- Alagic, G.; Alperin-Sheriff, J.; Apon, D.; Cooper, D.; Dang, Q.; Kelsey, J.; Liu, Y.-K.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process. NIST, July 2020. Available online: https://nvlpubs.nist.gov/nistpubs/ir/2020/NIST.IR.8309.pdf (accessed on 15 May 2024).
- Haakegaard, R.; Lang, J. The Elliptic Curve Diffie-Hellman (ecdh). 2015. Available online: https://koclab.cs.ucsb.edu/teaching/ecc/project/2015Projects/Haakegaard+Lang.pdf (accessed on 15 May 2024).
- Moody, D.; Shumow, D. Analogues of Velu’s Formulas for Isogenies on Alternate Models of Elliptic Curves. Math. Comput. 2011, 85, 1929–1951. Available online: https://eprint.iacr.org/2011/430 (accessed on 15 May 2024). [CrossRef]
- Jao, D. SIKE: Supersingular Isogeny Key Encapsulation. Soumission a l’appel a candidatures “Post-Quantum Cryptography” du NIST. 2017. Available online: https://joostrenes.nl/publications/sike-rd1.pdf (accessed on 15 May 2024).
- Casanova, A.; Faugere, J.-C.; Macario-Rat, G.; Patarin, J.; Perret, L.; Ryckeghem, J. GeMSS: A Great Multivariate Short Signature; Université Pierre-et-Marie-Curie: Paris, France, 2017. [Google Scholar]
- Ding, J.; Schmidt, D. Rainbow, a New Multivariable Polynomial Signature Scheme. In Applied Cryptography and Network Security; Springer: Berlin/Heidelberg, Germany, 2005; pp. 164–175. [Google Scholar]
- Tao, C.; Petzoldt, A.; Ding, J. Improved Key Recovery of the HFEv-Signature Scheme. 2020. Available online: https://eprint.iacr.org/2020/1424 (accessed on 15 May 2024).
- Beullens, W. Improved Cryptanalysis of UOV and Rainbow. In Advances in Cryptology—EUROCRYPT 2021; Springer International Publishing: Cham, Germany, 2021; pp. 348–373. [Google Scholar]
- Beullens, W. Breaking Rainbow Takes a Weekend on a Laptop; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Bormann, C.; Ersue, M.; Keranen, A. Terminology for ConstrainedNode Networks. IETF. Available online: https://datatracker.ietf.org/doc/html/rfc7228#:˜constrained%20nodes%22%20in%20that%20network (accessed on 15 May 2024).
- Hossain, M.; Xie, J. Third Eye: Context-Aware Detection for Hidden Terminal Emulation Attacks in Cognitive Radio-Enabled IoT Networks. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 214–228. [Google Scholar] [CrossRef]
- Alaba, F.A.; Othman, M.; Hashem, I.A.T.; Alotaibi, F. Internet of Things security: A survey. J. Netw. Comput. Appl. 2017, 88, 10–28. [Google Scholar] [CrossRef]
- Kumar, A.; Ottaviani, C.; Gill, S.S.; Buyya, R. Securing the future internet of things with post-quantum cryptography. Secur. Priv. 2022, 5, e200. [Google Scholar] [CrossRef]
- Bavdekar, R.; Chopde, E.J.; Bhatia, A.; Tiwari, K.; Daniel, S.J. Post Quantum Cryptography: Techniques, Challenges, Standardization, and Directions for Future Research. arXiv 2022, arXiv:2202.02826. [Google Scholar]
- Barton, J.; Buchanan, W.; Pitropakis, N.; Sayeed, S.; Abramson, W. Post Quantum Cryptography Analysis of TLS Tunneling on a Constrained Device. In Proceedings of the 8th International Conference on Information Systems Security and Privacy—ICISSP, Online, 9–11 February 2022. [Google Scholar] [CrossRef]
- Bos, J.W.; Costello, C.; Naehrig, M.; Stebila, D. Post-Quantum Key Exchange for the TLS Protocol from the Ring Learning with Errors Problem. In Proceedings of the 2015 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 17–21 May 2015; pp. 553–570. [Google Scholar] [CrossRef]
- Bos, J.; Costello, C.; Ducas, L.; Mironov, I.; Naehrig, M.; Nikolaenko, V.; Raghunathan, A.; Stebila, D. Frodo: Take off the ring! Practical, Quantum-Secure Key Exchange from LWE. In Proceedings of the CCS’16: 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016. [Google Scholar] [CrossRef]
- Alagic, G. Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process. NIST, NIST, July 2022. Available online: https://nvlpubs.nist.gov/nistpubs/ir/2022/NIST.IR.8413.pdf (accessed on 15 May 2024).
- Chikouche, N.; Ghadbane, A. Performance Evaluation of Post-Quantum Public-Key Cryptography in Smart Mobile Devices. In Proceedings of the IFIP International Federation for Information Processing, Kuwait City, Kuwait, 12 October 2018; pp. 67–80. [Google Scholar] [CrossRef]
- Septien-Hernandez, J.-A.; Arellano-Vazquez, M.; Contreras-Cruz, M.A.; Ramirez-Paredes, J.-P. A Comparative Study of Post-Quantum Cryptosystems for Internet-of-Things Applications. Sensors 2022, 22, 489. [Google Scholar] [CrossRef] [PubMed]
- Kannwischer, M.J.; Rijneveld, J.; Schwabe, P.; Stoffelen, K. pqm4: Testing and Benchmarking NIST PQC on ARM Cortex-M4. IACR Cryptol. ePrint Arch. 2019, 2019, 844. Available online: https://eprint.iacr.org/2019/844 (accessed on 15 May 2024).
- Hattenbach, H. Quantum-resistant digital signatures schemes for low power IoT. arXiv 2021, arXiv:2106.11710. [Google Scholar]
- Røneid, P.N. Hardware Implementations of the McEliece Cryptosystem for Post Quantum Cryptography. Master’s Thesis, Department of Informatics Faculty of Mathematics and Natural Sciences, University of Oslo, Oslo, Norway, 2021. Available online: https://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=8878692&fileOId=8878700 (accessed on 15 May 2024).
- Algorithms in Liboqs. Available online: https://openquantumsafe.org/liboqs/algorithms/ (accessed on 15 May 2024).
- Stebila, D.; Mosca, M. Post-quantum Key Exchange for the Internet and the Open Quantum Safe Project. In Selected Areas in Cryptography—SAC 2016; Springer International Publishing: Cham, Germany, 2017; pp. 14–37. [Google Scholar]
- Goodin, D. Post-Quantum Encryption Contender Is Taken out By Singlecore PC and 1 Hour. ARS Technica. Available online: https://arstechnica.com/informationtechnology/2022/08/sike-once-a-post-quantum-encryption-contender-iskoed-in-nist-smackdown/ (accessed on 15 May 2024).
- Sikeridis, D.; Kampanakis, P.; Devetsikiotis, M. Post-Quantum Authentication in TLS 1.3: A Performance Study. IACR Cryptol. ePrint Arch. 2020, 2020, 71. [Google Scholar]
- Nginx SSL Handshake Error (No Suitable Key Share). Available online: https://serverfault.com/questions/932102/nginx-ssl-handshake-errorno-suitable-key-share (accessed on 15 May 2024).
- Ravenscraft, E. How Much RAM Does My Smartphone Really Need? PC Mag UK. Available online: https://uk.pcmag.com/gallery/120531/how-much-ram-doesmy-smartphone-really-need (accessed on 15 May 2024).
- Price, D. Is a Smart TV Worth It in 2017? 6 Things to Check Before You Buy. Make Use of (MUO). Available online: https://www.makeuseof.com/tag/buy-smart-tv-2017/#:˜:text=Today’s%20TVs%20have%20proved.,as%206%20or%208%20GB (accessed on 15 May 2024).
- Alvey, J. Google Home Mini Teardown, Comparison to Echo Dot, and Giving Technology a Voice. Available online: https://justlv.medium.com/google-homemini-teardown-comparison-to-echo-dot-and-giving-technology-a-voicec59a23724a26 (accessed on 15 May 2024).
- Czypek, P.; Heyse, S.; Thomae, E. Efficient Implementations of MQPKS on Constrained Devices. In Cryptographic Hardware and Embedded Systems—CHES 2012; Prouff, E., Schaumont, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 374–389. [Google Scholar]
- Strahl, T.; Johansson, R. Post-Quantum Secure Communication on a Low Performance IoT Platform. 2016. Available online: https://www.duo.uio.no/bitstream/handle/10852/87158/Master.pdf?sequence=1:text=Introduction%20Small%20devices%20with%20limited (accessed on 15 May 2024).
- Suomalainen, J.; Kotelba, A.; Kreku, J.; Lehtonen, S. Evaluating the Efficiency of Physical and Cryptographic Security Solutions for Quantum Immune IoT. Cryptography 2018, 2, 5. [Google Scholar] [CrossRef]
- Botros, L.; Kannwischer, M.J.; Schwabe, P. Memory-Efficient HighSpeed Implementation of Kyber on Cortex-M4. In Progress in Cryptology—AFRICACRYPT 2019; Springer International Publishing: Cham, Germany, 2019; pp. 209–228. [Google Scholar]
- Becker, H.; Hwang, V.; Kannwischer, M.J.; Yang, B.-Y.; Yang, S.-Y. Neon NTT: Faster Dilithium, Kyber, and Saber on Cortex-A72 and Apple M1. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 2022, 221–244. [Google Scholar] [CrossRef]
- Kim, Y.; Song, J.; Youn, T.-Y.; Seo, S.C. Crystals-Dilithium on ARMv8. Secur. Commun. Networks 2022, 2022, 5226390. [Google Scholar] [CrossRef]
- pqm4: Post-Quantum Crypto Library for the ARM Cortex-M4. Available online: https://github.com/mupq/pqm4 (accessed on 15 May 2024).
- Wiesmaier, A.; Alnahawi, N.; Grasmeyer, T.; Geißler, J.; Zeier, A.; Bauspieß, P.; Heinemann, A. On PQC Migration and Crypto-Agility. arXiv 2021, arXiv:2106.09599. [Google Scholar]
- Bischof, M.; Oder, T.; Guneysu, T. Efficient Microcontroller Implementation of BIKE. In Innovative Security Solutions for Information Technology and Communications; Springer International Publishing: Cham, Germany, 2020; pp. 34–49. [Google Scholar]
- Zhao, C.; Zhang, N.; Wang, H.; Yang, B.; Zhu, W.; Li, Z.; Zhu, M.; Yin, S.; Wei, S.; Liu, L. A Compact and High-Performance Hardware Architecture for CRYSTALS-Dilithium. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 2022, 270–295. [Google Scholar] [CrossRef]
- Schöffel, M.; Lauer, F.; Rheinländer, C.C.; Wehn, N. Secure IoT in the Era of Quantum Computers—Where Are the Bottlenecks? Sensors 2022, 22, 2484. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).