Defence against Side-Channel Attacks for Encrypted Network Communication Using Multiple Paths

Abstract

As more network communication is encrypted to provide data privacy for users, attackers are focusing their attention on traffic analysis methods for side-channel attacks on user privacy. These attacks exploit patterns in particular features of communication flows such as interpacket timings and packet sizes. Unsupervised machine learning approaches, such as Hidden Markov Models (HMMs), can be trained on unlabelled data to estimate these flow attributes from an exposed packet flow, even one that is encrypted, so it is highly feasible for an eavesdropper to perform this attack. Traditional defences try to protect specific side channels by modifying the packet transmission for the flow, e.g., by adding redundant information (padding of packets or use of junk packets) and perturbing packet timings (e.g., artificially delaying packet transmission at the sender). Such defences incur significant overhead and impact application-level performance metrics, such as latency, throughput, end-to-end delay, and jitter. Furthermore, these mechanisms can be complex, often ineffective, and are not general solutions—a new profile must be created for every application, which is an infeasible expectation to place on software developers. We show that an approach exploiting multipath communication can be effective against HMM-based traffic analysis. After presenting the core analytical background, we demonstrate the efficacy of this approach with a number of diverse, simulated traffic flows. Based on the results, we define some simple design rules for software developers to adopt in order to exploit the mechanism we describe, including a critical examination of existing communication protocol behavior.

1. Introduction

The use of encryption on data packets can provide data privacy, thus protecting sensitive information from direct inspection if intercepted during transmission. However, it is still possible for an attacker to successfully employ side-channel attacks instead, thereby examining traffic characteristics to attack user privacy even for encrypted traffic. This typically involves the examination of traffic patterns and attributes of a sequence—a flow—of packets that constitute a communication session or dialogue, such as packet sizes and packet delay information [1].

For an attacker—an eavesdropper—to intercept the flow and launch such an attack, they must be on path; that is, they must have access to part of the end-to-end path (from sender to receiver) to read packets and process them. On the Internet, the nature of routing algorithms means that, typically, there is a single end-to-end path used for all packets in a flow between two communicating parties, even though routing protocols might discover multiple paths between those two parties. However, as the design of communication protocols has progressed, a trend towards a new feature has emerged: multipath transmission. While this has mainly been motivated by a need for load distribution and robustness, multipath transmission also has the potential to disrupt eavesdroppers who are present on only one of several paths.

1.1. Contribution

In this paper, we argue that multipath communication can act as a defence against traffic analysis attacks based on side channels. It is not totally intuitive that sending traffic for a single flow across multiple paths would yield such a defence, as one might consider that, for a flow of a long duration, the patterns visible on a single path emerge on each of the multiple paths. However, we examine this issue in depth and show that, indeed, multipath communication can perturb traffic patterns sufficiently to thwart traffic analysis.

The key contributions of this paper are the following:

• A multipath mechanism that prevents analysis by known and unknown side channels due to the underlying behavior being protected, which avoids the overheads associated with other defences, as no artificial delay, junk packets, or padding is added to the packet flow.
• A thorough analysis of protection against privacy attacks based on the use of Hidden Markov Models (HMMs), which are common attacks for (encrypted) traffic based on traffic analysis of a stream of packets—a flow.
• Recommendations that are based on challenges from our analysis for real-world implementation in protocols.

1.2. Paper Structure

We first present some background in to the development of side-channel attacks based on HMMs (Section 2). Then, we give a high-level view of how such attacks could be evaded, thus setting the scene for the defence mechanism presented in this paper (Section 3). We then describe the two key aspects of an effective and realistic defence: (i) having a communication protocol architecture that permits easy, flexible multipath communication (Section 4) and (ii) an analysis of HMM-based attacks on side channels to understand how they work and which key features we wish to perturb in order to foil an attacker (Section 5). We present a simulation-based evaluation of our approach based on models using various datasets and our specific protocol approach (Section 6); we then present a set of challenges and recommendations for application to real protocols (Section 7). We then conclude and provide a summary and pointers to future work (Section 8).

2. Traffic Analysis for Network Communication

Traffic analysis attacks compromise data privacy by exploiting side channels to reveal sensitive information in supposedly private communications. This is possible because the side channels—although potentially not sensitive in and of themselves—are influenced by sensitive patterns of secured communications. Unsupervised machine learning algorithms, such as Hidden Markov Models (HMMs), can be trained on unlabelled data to estimate these sensitive characteristics from the exposed information, thus making this a highly feasible attack for an eavesdropper to perform. In addition to the immediate threat of compromising data privacy, this advanced form of packet inspection can also form the basis of censorship techniques [2].

2.1. Traffic Analysis Techniques

Even when common privacy and data confidentiality protections are in place, such as encryption, some information about a communication is still exposed—such as the size of each packet; interpacket arrival times (IPATs); the date, time, and duration of the communication; and the fact that a communication occurred [3]. While these information leaks are often indirect, they function as side channels that reveal information about potentially sensitive data, which can then be exploited by an eavesdropper using various machine learning-based techniques.

Each approach creates a statistical model of the sensitive communication it targets. Once trained on sufficient data, the model can be used to estimate the likelihood of a particular communication exchange resulting in some set of side-channel observations. This can then be used to find the communication exchange most likely to have produced an observed sequence of side-channel observations. If this communication exchange corresponds to the sensitive part of the communication, that attacker could extract the sensitive data from the estimated exchange, thus bypassing traditional defences like encryption.

HMMs are a machine learning technique that are very effective at solving this problem, so they are widely used in the literature [4,5,6]. While other machine learning algorithms are also used, they all target the same principle: that patterns in the sensitive communication influence the observable side channels [7,8]. This work focuses on HMMs as an example, but as the defence disrupts this principle, it is expected to provide resilience against any machine learning algorithm that makes this assumption.

2.2. Use of the Hidden Markov Model (HMM)

HMMs are a widely used solution for modeling the characteristics of human language [9]. As such, they have also proven effective at modeling (and therefore analyzing) traffic with behavior derived from natural language, such as real-time Voice over IP (VoIP) calls. This section expands on how they can be used for traffic analysis.

VoIP can reduce the throughput capacity required for a communication by using a variable bit rate for lossless compression and by using discontinuous transmission rather than encoding and transmitting periods of silence. During periods of continuous transmission, packets are sent at regular intervals, but the variable bit rate results in different packet sizes depending on the phonemes sent—common phonemes are represented with short codes, thus creating small packets, while uncommon sounds use longer codes, thus resulting in larger packets. The encoded phonemes can be encrypted, so an eavesdropper cannot trivially read them, but the packet size is still exposed. An attacker can construct an HMM with hidden states corresponding to phonemes (and transition probabilities based on natural language). The emitted values are packet sizes, and emission probabilities can be estimated from the variable bit rate codec. Given a set of observed packet sizes, an eavesdropper could then use the Viterbi algorithm to find the set of phonemes most likely to have produced the observed communication [10]. This is sufficient to allow spoken phrases to be recovered from the encrypted packets [5,6].

The same class of attack can be performed against SSH. As with encrypted VoIP, an eavesdropper cannot trivially read the contents of an SSH packet. Unlike VoIP, the character encoding bit rate is constant, but the timings between packets are not—in interactive mode, SSH sends a packet in response to each keystroke so the IPAT depends on the keystroke timings. These timings, in turn, depend on the relative position of the keys on the keyboard—some keys are easier to press in quick succession than others. The emitted values here are IPATs, which depend on the keys pressed for the two packets on either side of the time period, so the hidden states correspond to SSH character pairs, with transition probabilities dependant on the language being typed. Given this model, the Viterbi algorithm can be used to find the sequence of characters most likely to produce a given sequence of IPATs [4].

HMMs are particularly effective, as they can use unsupervised learning. If the transition and emission probabilities are unknown—or even if the set of hidden states is unknown—but unlabelled data are available, an HMM can be trained to search for any pattern that might exist. In this case, the unlabelled data contain emission values, but not the corresponding hidden states. An attacker who is positioned to perform this attack could first use their position to collect training data, then train the model and start performing the attack. Under this approach, the semantics of the hidden states would be unknown until the attacker passed a small amount of labelled data through the model and then matched the hidden states with the corresponding labels.

The efficacy of an HMM depends on its ability to correctly predict the set of hidden states corresponding to a set of observations. The Baum–Welch algorithm provides the mechanism to converge on locally optimal transition and emission probabilities for an HMM via unsupervised learning, and with repeat runs can be used to estimate globally optimal parameters [11]. As training data are available to the attacker, and efficient training algorithms exist, it can be assumed that an attacker knows the optimal parameters for an HMM. So, as an attacker can easily create the best HMM for modeling a given scenario, the efficacy of the HMM depends only on how closely the targeted process resembles a hidden Markov process: if an accurate HMM for the process exists, the attacker will find it, but if even the most accurate HMM does not closely resemble the process, the attacker’s analysis will fail to accurately extract the sensitive information.

2.3. Summary of Existing Countermeasures

Existing defence mechanisms usually do not modify the underlying patterns in the secure communication, as this application behavior is not directly exposed to the protocol and is often closely tied to the real-world behavior that drives the application, such as natural language—so they potentially cannot be changed by any component of the system, including the application. Instead, defences try to protect the side channels: packet sizes might be hidden by the addition of padding, or interpacket arrival times could be modified by artificially adding delay or inserting junk packets.

Tor provides an aggressive form of traffic analysis countermeasures by requiring all packets to be padded or fragmented to a fixed size [12]. As the application behavior no longer influences it, an analysis of the packet sizes cannot reveal sensitive information. However, this defence does nothing to hide packet timings, so timing-based attacks are still possible—preventing them requires additional defences with additional overheads [13]. As it is not possible to use Tor with UDP, this defence is also application-specific, and it cannot be used for many real-time protocols. Even when it is applicable, the resulting traffic is highly distinctive, so an attacker can detect Tor traffic—this is a sufficient degree of traffic analysis for some attacks, such as censorship [14,15].

This approach could be extended to mask packet timings by sending packets at a fixed frequency corresponding to the minimum IPAT. However, as doing so has a prohibitively high bandwidth cost, Wright, Coull, and Monrose instead proposed traffic morphing [16]. Under their scheme, packets produced by one class of traffic (e.g., VoIP) were padded or delayed to reshape the exposed pattern into that of a different class (e.g., web traffic). When such a mapping is possible, this has a lower bandwidth overhead than simply filling the line to maximum capacity. However, as the bandwidth and latency costs are still significant, and the privacy benefits are limited, later work concluded that an efficient solution to this problem does not exist [1].

More recent work has continued to support this hypothesis. Walkie-Talkie, from 2017, reduced information leaks by delaying when a browser requested remote resources, but it incurred bandwidth overheads of 31% and a temporal delay of 34% [17]. FRONT, proposed in 2020, is a zero-delay defence, so it has no temporal cost but incurs a bandwidth cost of around 33% in order to achieve a competitive degree of privacy protection [18]. Other approaches try to achieve an acceptable overhead tradeoff by sending only short bursts of junk data at intelligently selected points to maximize disruption [19,20]. These defences specifically aim to disrupt website fingerprinting attacks by changing application behavior—so even in cases where the overhead tradeoff is acceptable, they do not represent a general purpose solution. Furthermore, many of them exhibit poorer performance in real deployments due to the complexity of packet dependencies and the consequences of congestion and retransmission [21].

BLANKET is a general defence for any packet flow that introduces adversarial features into live communications [22]. These features are designed specifically to disrupt deep neural networks, which have emerged as a recent trend in traffic analysis [23,24]. As such, while it is applicable to any packet flow and can achieve significant disruptions to such attacks with only a 10% bandwidth overhead, the authors acknowledge that it must be integrated with other defences to disrupt other non-neural attacks—this is identified as an area of future work. It is a general defence for all applications, but is not a general defence against all attacks.

As reshaping the profile of a flow of packets has remained costly and offered only limited returns, an alternative defence has been proposed: traffic splitting. The premise of this defence is to spread packets across multiple paths so that an eavesdropper present on only one sees only a portion of the full communication. While various multipath communication protocols exist, they do not typically use such a defence and instead prioritize throughput [25,26]. Existing work on traffic splitting instead operates at the application layer, thus facilitating multipath communication via an overlay, such as a modified version of Tor [27,28,29]. These defences avoid the overheads of padding or delaying packets but face a number of other problems:

• they are application-specific, as they operate at a high level of the stack;
• they require the use of a third party overlay, thus constraining deployability and potentially extending the trust boundary; and
• they are “loud”—that is, an attacker can see that the defence is in use, and may be able to leverage this in further attacks.

While there are a range of existing countermeasures, all of them face limitations. Many incur unacceptable costs to bandwidth and latency. Some prevent only certain methods of analysis and are not general defences. Most are application-specific and do not provide a general purpose solution—this is a particular concern for real-time communication, which is both vulnerable to the analysis of real-time characteristics and cannot be protected by the most defences, as they are designed only to disrupt website fingerprinting.

3. Evading Traffic Analysis

As HMM attacks always work against hidden Markov processes, the defence against them is to ensure that the target system is not a hidden Markov process. There are two approaches to this: ensure the hidden process is not a Markov process; or ensure that emitted values are not dependent on hidden states.

3.1. Limits of Existing Defences

If an application’s behavior is Markovian, this cannot easily be changed. The first obstacle is that the application must be rewritten. Requiring that all potentially vulnerable applications be examined and rewritten in such a way that a fundamental characteristic of their behavior changes is infeasible—while it may be doable for some well-supported applications, smaller and legacy application developers may lack the resources, so this is not a general solution. Furthermore, it may not be possible to change the application’s behavior: if the application is driven by a real Markov process (such as natural language), these characteristics will always remain. Avoiding Markovian behavior in applications is therefore not a feasible general defence against HMM traffic analysis—while traffic splitting defences do try to take this approach, they only work in specific contexts.

As the Markovian aspect of the process cannot generally be changed, existing countermeasures usually target emission behaviors. Emissions can be considered “noisy” channels—they encode the hidden state, but there is some margin for error. By maximizing this error and ensuring that all states have the same emission probabilities, the model’s ability to extract meaningful information is disrupted. However, due to the nature of the side channels (and therefore the nature of the emissions), this is both challenging and disruptive.

Packet size cannot be reduced beyond a certain limit without losing data. Similarly, packets cannot be sent faster than they are produced (unless the protocol inserts “junk” packets to fill the spaces), so the IPAT cannot be reduced indefinitely. Emission patterns for these features could potentially be smoothed to a degree, but due to these inescapable limits passed down by the driving Markov process, some patterns will remain. In the other direction, increasing the packet size either requires the application supplying more data (which may not be possible, particularly in real-time scenarios), or that channel capacity is wasted sending only junk. Additionally, latency and jitter can be artificially increased by adding extra randomized delay to packet transmission. Even if this defence were reliably effective, these extra costs to important performance characteristics make it unappealing.

To hide the different states, a defence must ensure all states have the same emission probabilities. This means that all are subject to the same constraints: if an application has a peak throughput, it must always operate at that throughput, and if there is a peak delay between packets, it must always use that delay. An application cannot intelligently hide these characteristics without inadvertently leaking new information via new emission probabilities.

Hidden Markov Models are a realistic threat to the privacy of systems that can be modelled as hidden Markov processes. This threat cannot be easily disrupted, as the behavioral features that drive it are inherent to the nature of the applications, and the exposed side channels cannot be masked without unmanageable performance and resource costs [1].

3.2. Disrupting Interception

While hiding the vulnerable features of intercepted traffic is impractical, it is possible to decrease the probability of interception. If the attacker cannot see the whole communication—or at least must perform more work to see all of it—they will have less data to analyze, and the difficulty of the attack is increased. If it is sufficiently difficult, the sensitive patterns being targeted by the attack may become infeasibly difficult to detect. In terms of the HMM, the attacker would see only the emissions corresponding to a subset of the hidden states.

This defence is analogous to frequency hopping in radio communications. By switching between frequencies according to some secretly agreed pattern, two parties communicating by radio can decrease the probability of being overheard. An eavesdropper may be listening on one frequency and overhear a portion of the exchange, but will not be able to follow them as they hop frequencies. This principle can also be employed by radar systems that seek to avoid detection. Radar detection techniques can track radar by listening for patterns of radio signals at particular frequencies. To avoid detection, a radar can use a frequency hoping spread spectrum: by rapidly switching frequency, the signal patterns can be hidden in background noise [30].

In the context of Internet Protocol (IP) networks, multipath communication can be used for a spread spectrum-like defence: packets are spread over a number of paths, with the assumption that the attacker will not be present on all of them. As some packets are “lost” to the eavesdropper, they must perform their traffic analysis on only a limited data set. This is multipath evasion.

3.3. Multipath Evasion and Traffic Splitting

Multipath evasion has superficial similarities to traffic splitting solutions. Both work by spreading packets across multiple paths to stop an eavesdropper from observing all of them. However, existing traffic splitting approaches operate at the application layer [27,28,29]. As such, they are unable to take advantage of multipath-aware network or transport protocols, must rely on overlays, and are application-specific. The novel network layer solution in our approach provides both a general, end-to-end defence for all higher-layer protocols, and is able to take advantage of multipath routing directly.

Traffic splitting defences have typically been designed to disrupt web fingerprinting. Different traffic splitting approaches can be directly compared by measuring the accuracy of known state-of-the-art classifiers against the traffic produced when they are in use [23,31,32,33]. These traffic analysis tools specifically perform web fingerprinting, so they do not represent a general form of traffic analysis and are not applicable to real-time communications or other applications. As this work both targets a wider problem (that is, the general case) and operates at a different layer of the network protocol stack, a direct comparison with these solutions is not possible, and a different evaluation method must be employed, as described in Section 6.

4. Multipath Communication

A grossly simplified summary of addressing and routing for IP is as follows:

• Communicating hosts on the Internet have IP addresses, which are included in packets and which serve two key purposes: they provide a global identity for a host and also provide a (topological) location to allow for the correct forwarding of packets. Each packet contains a source address for the sender and a destination address for the receiver.
• Traditionally, routing algorithms for IP could discover multiple paths across the Internet between a given source and destination. However, the usual behavior of routing protocols is to select a single path (based on some metric) for communication between a given source and destination based on the destination IP address.

Both addressing and routing in practice are more complicated, but the two issues listed above are key concepts that are sufficient for our discussion.

4.1. Using Multiple Paths

If the routing algorithms do have knowledge of multiple paths between a given source host, $H_s$, and destination host, $H_d$, then, potentially, it is possible for a communication between $H_s$ and $H_d$ to use those multiple paths with a suitable protocol implementation.

Communication over multiple paths between $H_s$ and $H_d$ has advantages, including the following:

• Spreading load across the network: The traffic load is distributed across the network rather than being concentrated on a single path for a given source/destination. This helps to prevent congestion in the network.
• Resilience for the flow: A communication flow (a sequence of packets) has better resilience to loss and delay in the case of disruption or congestion on a single path.
• Perturbing traffic capture: Having the packets within a (logical) communication flow distributed across multiple (physical) paths makes it harder for an attacker to intercept all of the packets in a flow, as the attacker will need to monitor multiple paths.

Past and current work has focused on the first two of these items, e.g., SCTP [34], MP-TCP [26], and QUIC [25]. The provision of multipath capability for QUIC is a work in progress at the time of writing. Our work focuses on the last of these items while still providing the benefits of the first two at the same time.

4.2. Practicalities of Multiple Paths in Networking

An IP address of 128 bits for IPv6 [35] (the most recent version of the Internet Protocol) consists of two parts: a network prefix (the upper 64 bits), also called a routing prefix (sometimes just referred to as an address prefix); and an interface identifier (IID) (the lower 64 bits). The prefix can be seen as the ‘name’ of a network: it is globally unique, administratively allocated through global registries, and the prefix values are used in routing protocols to find paths between networks. The IID value can be seen as the ‘name’ of an interface and is locally generated and managed: it should be unique within the scope of a given prefix, but it does not need to be globally unique. It transpires that the various mechanisms that are defined for generating IID values use algorithms that are likely to yield values with a high probability of being globally unique, e.g., stateless address autoconfiguration [36].

The current address usage for IPv6 treats a single IP address as a one-to-one binding between a prefix value and an IID value, and it treats each address as an atomic unit. The address is used as an identifier for a communication endpoint as part of the communication protocol state at the transport layer (layer 4), but it is bound to a physical interface (layer 1).

This means, in practice, that multipath communication is enabled through the use of multiple IPv6 addresses, with the assumption that each address represents a different path (even if the paths are not completely disjoint). Additionally, of the protocols listed above—SCTP, MP-TCP, and QUIC—each provides a multipath capability that is specific only to a particular transport protocol above the network layer (layer 3) of the communication protocol stack. However, if a privacy mechanism was provided at the network layer (layer 3), then it could be used by any transport layer (layer 4) protocol. At the time of writing, none of those protocols have support for privacy as described in this work as part of their design.

4.3. The Identifier Locator Network Protocol (ILNP) and Privacy

The Identifier Locator Network Protocol (ILNP) explicitly recognizes that the two different parts of the IPv6 address function as different namespaces, each with its own semantics. For ILNP, the prefix is renamed as a locator (given the symbol (L64), as it is 64 bits in IPv6), as the prefix is effectively a topological locator as far as the routing system is concerned. The IID is given different semantics: it is renamed to a node identifier (NID) and is bound to the communicating node, not a single interface on that node. The binding between L64 and NID is dynamic: a NID value can be bound to more than one L64, and a node can have multiple NID values. Effectively, this means that a node can be located on multiple networks by binding a NID value to multiple L64 values, and changing that binding effectively ‘moves’ the nodes to a new network.

Our experiments with ILNP have shown that (i) this flexibility in the use of multiple L64 values and multiple networks can be implemented over existing IPv6 networks, with ILNP operating effectively as a superset of IPv6, e.g., an experiment on the Linux operating system [37]; and (ii) that the dynamic generation and use of multiple ephemeral NID values is also possible over existing IPv6 networks, e.g., with the FreeBSD operating system [38,39].

Our mechanism based on ILNP works at the network layer, so it will work for standard TCP and UDP architectures, and does not require specialized transport protocols such as MP-TCP or QUIC. This also has the benefit that it will work for existing applications that use TCP and UDP, thus not requiring the applications to be redesigned or re-engineered to work with new transport protocols.

The work presented here is the underlying basis for an implementation using ILNP at the network layer on IPv6 as a general feature rather than at the transport layer for a specific transport protocol. However, in Section 7, we discuss the challenges in protocol design and implementation posed by our work.

5. Analysis of HMMs

From the attacker’s perspective, packets sent on a path they cannot observe are lost. Clearly, this would disrupt a model that assumed no loss; however, an HMM that sensibly models for loss will be more resilient. Evaluating this defence therefore requires examining how loss is handled in an HMM.

A loss event can be considered an observation, like the packet size or IPAT. If transport headers are not encrypted, the packet numbers could be used to explicitly detect lost packets and insert the loss observations into the appropriate point in the sequence of events. If the packet numbers are not exposed, the attacker must estimate when loss occurs, possibly by assuming loss if the IPAT exceeded a threshold or by correctly predicting the path selection algorithm if a multipath evasion defence were in place. If loss observations are only implied, the input data will be less reliable than in the case of explicit loss observations, and the attacker must perform extra work to make these guesses—potentially by running several possible estimated sequences through the HMM. This explicit loss observation scenario is preferable for the attacker, so it is the worst case for the defender. This analysis assumes that this worst case occurs—if loss is not explicitly detectable, this defence will be more effective.

HMMs have only two components—emission and transition probabilities—so they must handle loss with one of these parameters. This gives two possible approaches: an emission model, and a transition model.

5.1. The Emission Model

If loss observations are treated like packet size or IPAT observations, they can be incorporated into the HMM in emission probabilities as a new possible emittable value—referred to as loss emissions. This approach is the emission model, as shown in Figure 1.

As loss is introduced at the network layer (either intentionally by multipath evasion or inadvertently through normal loss conditions), the loss rate is independent of the HMM state—the loss of any packet is equally probable, regardless of the (hidden) transport state. The loss emission probability will therefore be the same for all states. As multipath evasion would introduce a loss rate of 50% even if only two paths were used (and one was observed), this artificial loss will dominate the much lower loss rate introduced by network conditions. The artificial loss rate will remain approximately constant throughout the communication, as it is determined by the number of paths in use. The attacker can therefore estimate the loss rate from the frequency of the loss observations:

$$p_l=\frac{\mathit{loss}\mathit{observations}}{\mathit{total}\mathit{observations}}$$

(1)

Normally, the Viterbi algorithm guesses the most probable state by combining the transition and emission probabilities to find a state that is both (i) likely to occur at this point in the chain, and (ii) is a good candidate to explain the observed emission. However, in the case of loss, the emission probability will be $p_l$ regardless of the state. Based on the emission probabilities, every state is equally likely, so the model must infer the most likely state based on transition probabilities alone. The more packets that are lost, the fewer observations an attacker can use to infer hidden states. In the worst case, where the attacker observes no packets, any attempt to use an HMM will just produce the most likely chain of transitions, and the attacker will be unable to infer anything about the specific communication being observed. Under the emissions model, loss observations will therefore reduce the precision of the attack.

5.2. The Transition Model

The emission model can be transformed to a new model. This is possible because the loss emission probability is constant. The transition model, shown in Figure 2, is created by combining this loss rate into the transition probabilities, thus creating a new set of transition probabilities, which have loss as a side effect. This approach is not practical to implement, but it is helpful for analytical purposes.

Treating loss as a side effect of transitions rather than as the emission from a particular state has two consequences for the way the model is built. First, it requires an infinite set of transitions: where other HMMs require a table of transition probabilities with one row per current state and one column per possible next state, this model requires one table of this size for each possible number of loss events—that is, a table of transition probabilities with no loss and a table with a single loss event as a side effect, as well as a table with two consecutive loss events, and so on. As the maximum number of loss events that may occur as a side effect of a transition (i.e., between two observations) is unlimited, this produces an infinite set of transition probabilities.

A second consequence of treating loss as a side effect is that the chain of states produced by this model will not include states corresponding to loss events—compared to the emission model, these states are effectively “skipped”. However, as the emission model selects states corresponding to loss events based on transition probabilities alone anyway, the same approach (that is, just assuming the most probable set of states occurred) could be used to fill in these gaps with the most probable values. This would produce the same Markov chain as the emission model. Filling in these “pseudo-states” transforms the output of this model into the same output as the emission model.

The transition model does not emit loss events, but the relative probabilities of other emissions are the same. The model’s emission probabilities, $P^{\prime }\left(x_i\right|y_i)$ (when $y_i$ is not a loss), can therefore be derived from those of the emission model (denoted $P\left(x_i\right|y_i)$) by scaling:

$$\begin{array}{cc}\hfill P^{\prime }\left(y_i\right|x_i)& =\frac{P\left(y_i\right|x_i)}{1-p_l}\hfill \end{array}$$

(2)

The transition probabilities for the transition model can also be derived from those in the emission model. Each transition in the new model combines several transitions in the old, as it encompasses a subchain of skipped loss event states—these states are later filled in as the pseudostates. $\dot{X}$ is the set of t intermediate pseudostates ${\dot{x}}_n$ between the states $x_i$ and $x_{i+1}$ (which have nonloss emissions). For ease of notation, ${\dot{x}}_0=x_i$. The probability of the transition from $x_i$ to $x_{i+1}$ with intermediate pseudostates $\dot{X}$ can be found in the same way as any chain. This can be expressed as follows:

$$P^{\prime }(\dot{X},x_{i+1}|x_i)=\left(\prod _{u=0}^{t-1}{p}_l·P\left({\dot{x}}_{u+1}\right|{\dot{x}}_u)\right)·(1-p_l)·P\left(x_{i+1}\right|{\dot{x}}_t)$$

(3)

The Viterbi algorithm [10] constructs a table of the probabilities of the most likely paths to produce certain observations:

$$\begin{array}{cc}\hfill T_P[i,j]& =\underset{k\in S}{max}\left(T_P[k,j-1]·P\left(x_i\right|x_k)·P\left(y_j\right|x_i)\right)\hfill \end{array}$$

(4)

By combining the emission probabilities from Equation (2) and the transition probabilities from Equation (3), the Viterbi algorithm’s probability table for the transition model can be expressed in terms of the parameters of the emission model:

$$\begin{array}{cc}\hfill {T^{\prime }}_P[i,j]& =\underset{k\in S}{max}\left\{{T^{\prime }}_P[k,j-1]·P^{\prime }\left(x_i\right|x_k)·P^{\prime }\left(y_j\right|x_i)\right\}\hfill \\ \hfill & =\underset{k\in S}{max}\left\{{T^{\prime }}_P[k,j-1]·\left(\prod _{u=0}^{t-1}{p}_l·P\left({\dot{x}}_{u+1}\right|{\dot{x}}_u)\right)·(1-p_l)·P\left(x_{i+1}\right|{\dot{x}}_t)·\frac{P\left(y_{i+1}\right|x_{i+1})}{1-p_l}\right\}\hfill \\ \hfill & =\underset{k\in S}{max}\left\{{T^{\prime }}_P[k,j-1]·\left(\prod _{u=0}^{t-1}{p}_l·P\left({\dot{x}}_{u+1}\right|{\dot{x}}_u)\right)·P\left(x_{i+1}\right|{\dot{x}}_t)·P\left(y_{i+1}\right|x_{i+1})\right\}\hfill \end{array}$$

(5)

Under the emission model, the pseudostates in $\dot{X}$ would instead be additional states in $T_P$ (the emission model’s probability table). Each state has a loss event, so $P\left(y_i\right|{\dot{x}}_i)=p_l$. The transition probabilities will be the same as those in the ∏ portion of Equation (5) (as the states are the same). So, the transition model will perform maximization over the whole product, while the emission model will perform it piecewise for each state in $\dot{X}$. As the results are multiplied in both cases, each approach will produce the same result—they are equivalent. As the two models are equivalent, they have the same characteristics, and analysis of one generalizes to the other. As transition and emission probabilities are the only parameters of a Markov model, this covers all mechanisms by which an HMM could handle loss.

Analysis of Loss Models

While the emission model is simpler to implement and does not require an infinite set of transition probabilities to handle unlimited successive loss observations, the transition model is helpful for understanding the impact of loss. As the models are equivalent, the behavior of the emission model will match the behavior of the transition model.

All Markov models are built upon the Markov assumption: that the probability of the next state depends only on the current state and not on past states [40]. This means that transition probabilities are independent of any variable except the current state. If this Markov assumption does not hold for a system, it cannot be modeled with (or attacked by) HMMs.

Assumption 1.

The probability of the next hidden state depends only on the current hidden state.

Under the transition model, state transitions occur between nonloss observations. This results in a new set of transitions, which occur between states for which the attacker observed the emission rather than between all hidden states of the application. This new set of transitions must also exhibit Markovian behavior in order for this method of modeling loss to produce accurate results—if it does not, then the transition model no longer models a Markov process, so using an HMM will not be meaningful. In order for the transition model to correspond to a Markov process, the transitions between observed states (those for which the emission was seen by the attacker) must be Markovian:

Assumption 2.

The probability of the next observed state depends only on the last observed state.

An HMM’s predictions in the event of loss are contingent on these assumptions. If Markov Assumption 1 does not hold, the process is not Markovian, and it cannot be accurately modeled with an HMM, regardless of loss. If Markov Assumption 2 does not hold, the transition model’s (and therefore also the emission model’s) loss handling mechanism will not meaningfully account for loss. So, both assumptions must hold in order for an HMM to correctly model loss.

When no loss occurs (that is, the attacker observes the emission from each hidden state), the hidden states and their transitions will be the same as the observed states and their transitions. So, if the underlying (i.e., hidden) process is Markovian, both assumptions will hold. In regular Internet communication, loss is rare—if it is not, application behavior is disrupted, and the connection may fail. So, in a typical real-world scenario, an attacker can use an HMM for a traffic analysis by assuming that loss does not occur and that these assumptions hold. In the rare event that loss does occur, it may disrupt the model briefly, but it will not have a lasting impact, as the Markov assumption means the system is memoryless: transition probabilities between states not immediately after the loss event will be independent of the earlier history, so they will recover from loss.

When loss observations occur, the transition model accounts for it by making transitions with loss as a side effect and then filling in the skipped pseudostate later. So, if there is a single loss observation, $x_l$, between two nonloss observations, $x_0$ and $x_1$, the transition probabilities $P\left(x_1\right|x_0)$ and $P\left(x_1\right|x_l)$ must both be independent—that is, the probability of $x_1$ occurring must be conditional only on $x_0$ (Markov Assumption 2), and it must also be conditional only on $x_l$ and not the preceding history (Markov Assumption 1).

If Markov Assumption 1 holds, then the probability of $x_1$ is not conditional on any state preceding $x_l$; thus, it is not conditional on $x_0$, so Assumption 2 does not hold. That is, if the underlying (hidden) process is Markovian, then the transition model will not correctly account for loss, so loss observations will result in a loss of accuracy.

If the second assumption holds, then Assumption 1 does not hold: the probability of the next state is conditional on earlier history, so the process is not Markovian. If the process is not Markovian, an HMM will not be able to model it correctly.

In all cases, the transition model is an imperfect solution to accounting for loss. Either it accurately accounts for loss, in which case the underlying process is not Markovian and the rest of the model is invalid, or the underlying process is Markovian, but the measures for accounting for loss will not work. As the models are equivalent, this also applies to the emission model.

As Markov models are memoryless, they can recover from loss, even if they cannot model for it. Should loss occur, the HMM will fail to model the scenario accurately, so the predictor’s accuracy will be disrupted. However, this disruption will be localized to the loss event, and the model will soon forget the loss and return to correctly exploiting Markovian behavior. As loss is typically rare, this self-healing normally provides sufficient resilience for HMMs, and their inability to model for loss does not majorly disrupt their utility. However, if the attacker sees only packets on one of several paths, and packets are sent out in a round-robin fashion, then loss will be much higher (at least 50%), and all transitions will be disrupted by the loss events in their proximity. When all transitions are impacted by loss, the HMM is unable to recover, as there is no period in which it can perform “correct” analysis.

While the two Markov assumptions expressed above can be considered in binary terms for analysis of how a Markov model will perform, in practice, many processes that are modeled with HMMs are not strictly Markovian—the model is just a sufficiently accurate approximation of the system’s behavior. Rather than either assumption being strictly true or false, they exist on a spectrum. The more accurately Assumption 1 holds, the more accurately the process can be modeled by an HMM, but the more vulnerable it is to loss; the more accurately Assumption 2 holds, the more resilient an HMM will be to loss, but the worse it will model the underlying process in general. Therefore, there are cases where loss may not disrupt the attacker so effectively; however, in such situations, the attacker’s ability to analyze traffic is already limited—the viability of this defence scales with the viability of the attack. Regardless, the disruption caused by loss makes such attacks harder than they would be otherwise.

6. Evaluation

The evaluation methodology is based on a simulation of traffic—a single stream of output symbols—from a single source, which was then split into multiple streams. The single stream consisted of data items as they would be transmitted by a single source, i.e., individual messages sent as individual packets as part of a communication flow. The multiple streams represented the multiple paths over which individual packets from the single stream have been transmitted in order to offer the multipath protection proposed.

The effectiveness of multipath evasion as a traffic analysis defence was evaluated by examining the characteristics of the individual streams. The simulated traffic was produced using several generalized models with different packet distributions. Then, as a worst case scenario for a victim, we derived simulated traffic characteristics from a natural language corpus where the initial distribution is well-known.

The data and results presented in this section plus the simulation software used to create the data and the visualizations are all freely available from [41].

6.1. General Markov Model Simulations

To test the effectiveness of this defence in general, traffic was produced using a simulated Markov process (corresponding to the hidden communication state), and the multipath defence was applied. As the base process was Markovian, Assumption 1 from above held. So, the attacker would be able to perform traffic analysis with an HMM only if the second assumption also held: that the observations they made were also governed by a Markov process. As discussed, it was not expected that both assumptions could be true, but the results would reflect the degree to which either assumption held.

Markov processes can be detected by comparing unigram (single symbol) and bigram (2-symbol sequence, a single pair) frequencies. In a Markov process, the probability of the next state depends on the current state, so each transition will have a different probability and resulting observable frequency. In a non-Markov process, the probability of the next state is independent of the current state, so the transition probabilities will instead reflect the unigram probability of the next state—the probability of that state occurring next regardless of the current state. So, to test for Markovian behavior, the unigram and bigram frequencies can be compared: if they differ, the difference is caused by an interstate pattern—this is Markovian behavior.

As this analysis is concerned only with the behavior of the Markov process, the emission probabilities of an HMM were ignored—this corresponds to a special case of an HMM where every state emits a unique value with 100% probability. For an attacker, this is the best case (worst case scenario for a victim)—every emission they observe gives them perfect information about the hidden state. If a state’s emission probabilities can instead produce a range of emissions, the attacker’s certainty in the hidden state responsible for producing a given emission is reduced, as there may now be many possible states that could have caused this behavior. A hidden Markov model can be described as a Markov model exposed over a noisy channel—the hidden information is visible, but imperfectly. Evaluating only a (nonhidden) Markov model therefore shows how this defence will perform in the worst case—in a typical scenario, the emission probabilities will introduce more noise, thus further weakening the attack.

6.2. Methodology

The output symbols (representing packets in a communication flow) were generated by a set of simulated Markov processes with different characteristics, i.e., a single chain of symbols. This single chain of symbols was then protected by a simulated m-way multipath defence by splitting them into m new chains in a round-robin fashion—these new chains correspond to the packet flows that would be seen on each of the m separate paths.

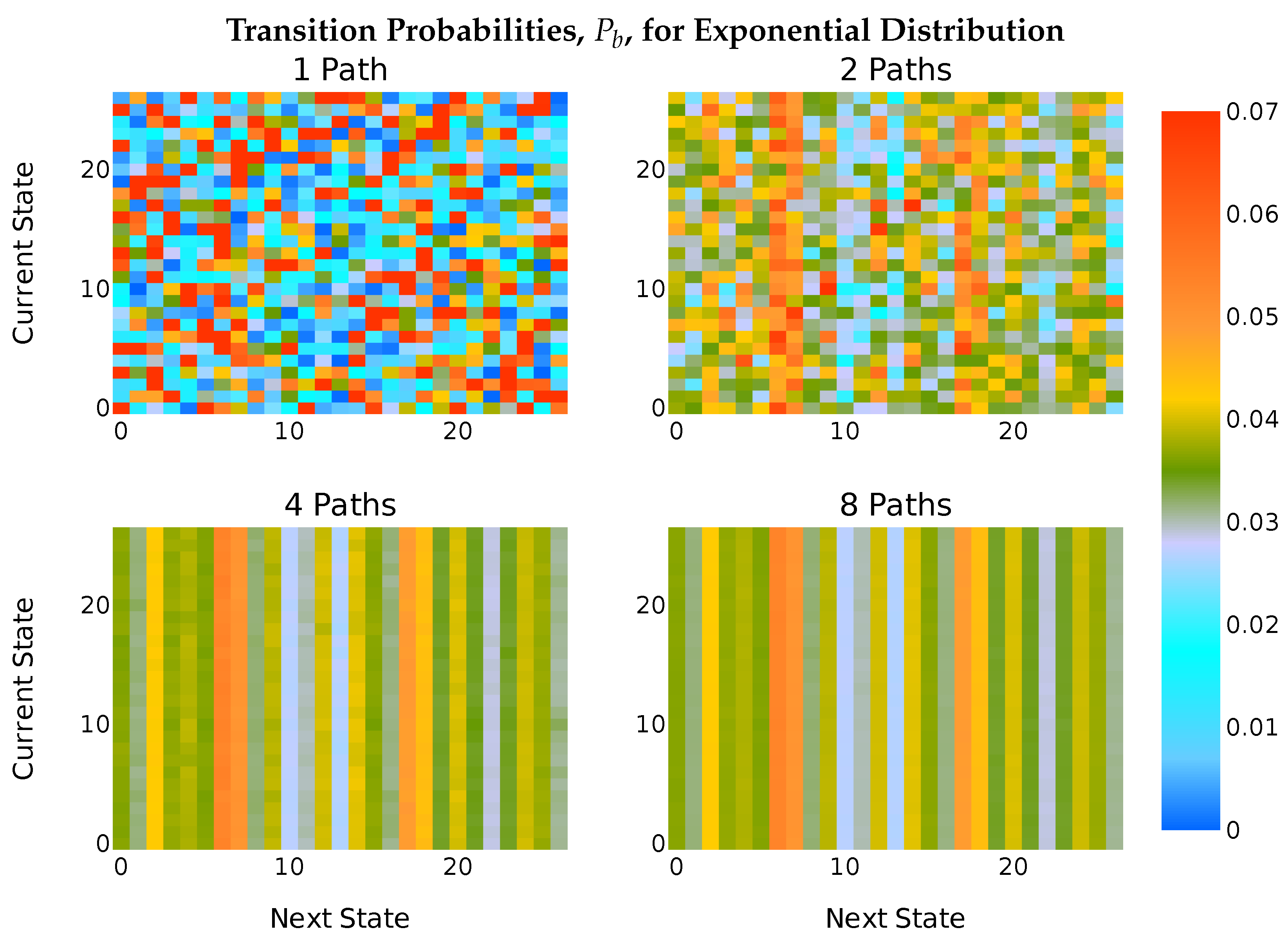
6.2.1. Traffic Distributions and Transition Probabilities

The simulator generated a table of transition probabilities according to a selection of probability distributions. The distributions used were as follows:

• A uniform random distribution from 0 to 1000;
• A normal distribution with a mean of 250 and standard deviation of 150;
• An exponential distribution with a rate parameter of 1.0;
• The same exponential distribution but with 1 added to each frequency sampled so that all transition probabilities were nonzero.

These parameters were selected to yield a large range of frequencies, with some being orders of magnitude more frequent than others and with each being greater than or equal to 0 (negative frequencies from the normal distribution were treated as 0).

6.2.2. Markov Models

Using each of the tables generated from each distribution, the simulation defined a Markov model as a set of Markov chains via a random walk according to the transition probability table—the unigram probabilities. An initial state was included in the table of transition probabilities, but all transitions to it were given a probability of 0.

A total of 28 possible states were used (including the starting state). This resulted in a sufficiently complex Markov process to model the English language, with one state per letter and some punctuation. A more complex model could use more states for more language features, such as one for each of the ∼44 phonemes of spoken English [42]. However, Markov models can also be composed by replacing a state in one model with a new Markov process (or the reverse). Due to this composition, the behavior of a Markov process with N states will be representative of the behavior with more or fewer states, so using 28 states is sufficient to test the behavior of the model.

For each distribution, transition probabilities between each pair of states—bigram probabilities—were selected by sampling frequencies for each transition and then converting those frequencies to relative frequencies (normalization), which were used as the bigram probabilities.

Each generated Markov chain was ${10}^6$ states long. A total of ${10}^3$ chains were generated for each simulated Markov model. As Markov processes are memoryless, the length of each chain is unimportant. In a real-world sceanrio, while a short text message might have only 10s or 100s of characters, they will exhibit the same behavior as subsegments of arbitrarily large messages, so these values were selected for the convenience of parallelizing the simulation.

This gave a total of ${10}^9$ transition observations per simulated Markov model, as indicated in

Table 1. Summary of simulation parameters.

Parameter	Value	Description
Types ($N_t$)	5	Normal, Uniform, Exponential, Nonzero Exponential
		English Corpus (worst case, model known by attacker).
States	28	Letters in English alphabet, plus a space character and a starting state.
Chain size ($S_c$)	${10}^6$	Representing, for example, a document or a long-lived interactive communication.
Chains per model (Nc)	${10}^3$	Representing multiple communications per model use.
		Each chain is different but follows the same model.
Transitions per model	${10}^9$	$S_c\times N_c$, giving a possible attacker a large number of transitions for a successful attack.
Models ($N_m$)	250	Randomized Markov models of each type to reduce random error due to possible outliers.
		(Number of runs to evaluate $U_d$ for each path.)

. As these values were split over fewer than 10 paths by the multipath evasion simulated, this resulted in at least ${10}^8$ transition observations per path. With 28 possible states, there are 784 possible transitions. The smallest changes in relative frequency of any transition would occur when all frequencies yielded by the underlying distribution were high (that is, ${10}^3$ from the uniform model, for example). A change of 1 in the sampled frequency would result in a change of $\frac{1}{\mathrm{784,000}}$ in the relative frequency (that is, $\sim 1\times {10}^{-6}$). Even in this unlikely case, these parameters would reflect this change with a shift of 100 in the final observed frequency counts. So, if a bigram pattern existed, it was expected to have a visible impact on the results.

This process was repeated for 250 different randomized Markov models of each type to reduce random error from atypical distributions that could occur from the random walk. Preliminary experiments showed that this was sufficient, as the different random models showed very similar behavior.

The unigram frequencies of each state and the bigram frequencies of each pair of states were recorded for each simulated chain. Then, a two-path ($m=2$) multipath evasion defence was simulated by splitting the generated chain into two new chains—one with every odd state, and the other with every even state. This is the same transformation as would be seen when splitting a flow of packets across two network paths using a round-robin algorithm. Each of these new chains was similarly evaluated using the unigram and bigram frequencies. These frequencies were then summed to produce an aggregate result that was not biased towards patterns in one path or the other. The final unigram count was necessarily the same as in the base case where the same unigrams were used, but the bigram counts could differ because of the way the symbols were split across the two ($m=2$) paths. The counts from the two paths can be safely summed, as Markov processes are memoryless, so they are not influenced by earlier behavior—the overall behavior in the rest of the chain will be the same regardless of whether it started with the first or second state. This same process was repeated to produce aggregate unigram and bigram counts from $m=1$ to $m=8$ paths.

6.3. Results

The heatmap in Figure 3 shows the transition probabilities calculated from the frequency counts for a particular Markov model generated according to the exponential distribution. The counts for successive runs of the same simulated Markov model were summed to give aggregate counts, and transition probabilities, $P_b$, were calculated as

$$\begin{array}{cc}\hfill P_b\left(s_a{s}_b\right)& =\frac{F_m\left(s_a{s}_b\right)}{N}\hfill \end{array}$$

(6)

where $F_m\left(s_a{s}_b\right)$ is the measured (observed) frequency for bigram $s_a{s}_b$, and N is the total number of observations of all bigrams.

When only a single path was used, the Markovian behavior of the application was exposed to the attacker: each row of the heatmap varied, as the transition probabilities depended on the current state. When two paths were used, the attacker’s view was changed: there was less variation between rows—most probabilities fell between 0.015 and 0.025 rather than between 0.01 and 0.06 like the first heatmap. Some Markovian behavior was still exposed, but it was no longer as distinctive of a characteristic. As the number of paths increased, the proportion of packets seen by the attacker decreased. The banding pattern clearly visible in the final figures was caused by the transition probabilities converging on the unigram probabilities of the second symbol: there was no pattern extending over eight states, so the observations the attacker could make were independent of one another. The attacker’s observations reflect the unigram probabilities of the source they sampled, and they appear independent of the current state. So, an attack based on a Hidden Markov Model approach was no longer possible.

Figure 4 shows the same behavior being exhibited by the simulation when a normal distribution of bigram frequencies was used. The transition probabilities appear to converge on unigram probabilities more rapidly, as there was less variation in the base case in need of “smoothing”.

In both cases, when multiple paths were used, the observed behavior was not Markovian. This violates Assumption 2. So, even if the underlying process may be Markovian, as the observed states were not Markvoian, the model could not account for loss, and the attack is expected to be disrupted.

6.4. Convergence on Unigram Probability

With $F_m\left(s_a{s}_b\right)$ defined as above for Equation (6), the unigram-based estimator for bigram frequencies, $F_u\left(s_a{s}_b\right)$, is calculated as the proportion of the occurrences of $s_a$ that are expected to be followed by $s_b$:

$$\begin{array}{cc}\hfill F_u\left(s_a{s}_b\right)& =\frac{F_m\left(s_a\right)·F_m\left(s_b\right)}{N}\hfill \end{array}$$

(7)

As Markovian behavior is avoided with use of multiple paths, the transition probabilities will converge on the unigram probabilities. This can be seen by measuring the error between the observed bigram frequency and the expected bigram frequency based on the unigrams alone and using the error function:

$$\begin{array}{cc}\hfill e_b\left(s_a{s}_b\right)& =\frac{1}{N}\sum _{n=1}^N|F_u{\left(s_a{s}_b\right)}_n-F_m{\left(s_a{s}_b\right)}_n|\hfill \end{array}$$

(8)

Using the absolute error (the difference between the observed bigram frequencies and unigram-based estimate) is more tolerant of outliers than a squared error estimate. Outliers are likely in this kind of analysis, as the unigrams of the underlying Markov process may have sparse probabilities (e.g, “Q” in English), thus resulting in some very rare bigrams, regardless of the defence used. As Markov processes are memoryless, these sparse events are not a risk: even if an attacker sees occasional distinctive, rare events, they will not be able to leverage this for a longer-term attack unless other bigram patters are still visible. So, a metric that is resilient to outliers gives a better indication of how much the measured bigram frequency differs from what was expected. This was expressed as the proportion of transitions that the two models—bigram and unigram—disagree on.

A high value for $e_b$ indicates that the unigram probabilities are insufficient to accurately model the process, and the bigram frequencies reveal new information—in this case, the sensitive patterns within the communication. A low value for $e_b$ shows the opposite: if a unigram model can accurately predict bigrams, there is no interstate pattern to exploit, so the bigram frequencies reveal no new information, and a Markov model will not provide any greater insights. So, we can define the utility function for the efficacy of the defence, $U_d$, as the complimentary error function:

$$\begin{array}{cc}\hfill U_d& =1-e_b\left(s_a{s}_b\right)\hfill \end{array}$$

(9)

where $0\le U_d\le 1$, with 1 indicating the best utility for defence and 0 indicating the poorest utility for defence.

The values for $U_d$ for each source distribution model are shown in Figure 5. Each subfigure shows the results from a full set of random bigram models created by drawing bigram probabilities from the specified distribution.

When a single path was used, the bigram frequencies in the output chain were directly driven by the Markov process. As the unigram-based estimators cannot account for this, they were highly inaccurate. With two paths, the influence of the Markov process was lessened—alternate values are sent over alternate paths, so the observed bigrams consist of every other symbol. This is still influenced by the Markov process—for example, a highly probable transition followed by another highly probable transition will result in a common bigram. However, as the number of paths increased, this influence faded. This can be seen in the rapid improvement in $U_d$: even at only two paths, the unigram estimator was much more accurate, and by five paths, $U_d$ was very close to 1.

Even when there is no Markovian behavior, some random error still occurs. This was measured by simulating a random walk based on unigram probabilities alone—each symbol in the produced chain was selected independently from the previous values. The first row of

Table 2. $U_d$ when using $m=1\dots 8$ paths (2 s.f.).

Distribution	1	2	3	4	5	6	7	8
Unigram Only	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0
Normal	0.67	0.73	1.0	1.0	1.0	1.0	1.0	1.0
Uniform	0.52	0.95	0.99	1.0	1.0	1.0	1.0	1.0
Exponential	0.29	0.86	0.98	1.0	1.0	1.0	1.0	1.0
Nonzero Exponential	0.65	0.97	1.0	1.0	1.0	1.0	1.0	1.0
English Corpus	0.25	0.45	0.74	0.82	0.88	0.91	0.94	0.96

shows the values of $U_d$ between the expected and measured bigram frequencies for this simulated chain. So, if no Markovian behavior is present, this represents the best value for $U_d$.

Table 2 also shows $U_d$ for each simulated Markov model and for different numbers of paths. The final row is discussed in the following section. For all simulated models, $U_d$ rapidly increased towards 1 with the addition of a single path. For all models other than the English Corpus (final row), it converged at 1.0 (2 s.f.) when four or more paths are used. At 3 s.f., the value of convergence was 0.998 due to the random perturbation introduced by the nature of the stochastic process. This is the same as $U_d$ seen in the first row, where there was no Markovian behavior. So, when four or more paths were used, no more Markovian patterns remained visible in the output, and Assumption 2 did not hold.

6.5. Specific Markov Model Analysis

In addition to tests with simulated Markovian behavior, the defence was tested against real-world Markovian data. The English language was used as the data source, as natural language exhibits Markovian behavior, and large bodies of English text are in the public domain. The texts used were the following:

• Bram Stoker’s Dracula (published in 1897);
• Homer’s The Odyssey (translated in 1897);
• Homer’s The Iliad (translated in 1899).

The texts were combined to give 2,682,565 characters. All texts are from approximately the same time, so spelling and other language features are similar. As different clusters of letters are more common than others in English spelling, this chain of characters will exhibit Markovian behavior: for example, “S” will often be followed by “H”, while “Q” will rarely be followed by anything other than “U”. While a more complex Markov model with sufficient training data could account for character case and uncommon punctuation, a simpler model was used here: all alphabetic characters were converted to uppercase, and all nonalphabetic characters were replaced with the “ ” (space) character. This was sufficient for testing the behavior of a Markov process by the same principle of composition as used above. This also allowed the corpus to be modeled by a Markov process with the same number of states as those used above (27 plus the starting state).

After preprocessing, the 2.5-million state Markov chain with 27 possible states was subjected to the same analysis as the simulated chains above: it was multiplexed over $m=1\dots 8$ paths, one of which was exposed to an attacker. This resembles a scenario like an eavesdropper listening to an SSH session, where each keypress is transmitted in a different packet.

Figure 6 shows the transition probabilities observed by the attacker when different numbers of paths were in use. With a single path, the Markovian behavior was visible: each row was different. Even the very common symbols—“E” and the wildcard “ ”—were not equally probable after every symbol. With two paths, the banding pattern seen in Figure 3 and Figure 4 became visible in some areas, such as for transitions to “R”, “S”, and “T”. However, the convergence onto unigram probabilities did not appear to be so rapid nor so pronounced as in the simulated “Q”.

Figure 7 shows the values for $U_d$ when applied to the English corpus. The value for $U_d$ for a single path was lower than for other models. As the number of paths increased, it increased as expected, but not as sharply as in Figure 5. Table 2 shows that value with eight paths was still 0.96. This is significantly better than the initial value of 0.25, but not as good as the that achieved for simulated models. This suggests that, while the simulated models were truly Markovian, the English Corpus only approximates Markovian behavior, so Assumption 1 perhaps does not apply so strongly. Regardless, the use of multiple paths resulted in a better value for $U_d$, and so an HMM-based attack was made harder.

7. Discussion and Recommendations

7.1. Limitations of the Defence When Applied to the English Corpus

The lower value for $U_d$ for the English corpus is driven by two features: the imperfections of the language model; and the sparsity of the data.

While a Markov process can provide an approximation, the English language is not a purely Markovian process. Trigrams and larger character clusters have frequencies that do not depend only on bigram frequencies. This is particularly clear in the “2 Paths” part of Figure 6: certain rows were highly distinctive because the bigrams they showed corresponded to the first and third symbols of common trigrams. This characteristic of the language means the memoryless assumption of the Markov model does not hold, so an HMM will only function as an approximation. The less Markovian the underlying model is, the less effective this defence will be, but the less effective the attacks will be as well.

Certain characters were extremely rare, such as “J”, “Q”, “X”, and “Z”. As can be seen in the later subfigures in Figure 6, it is the rows corresponding to these characters that did not converge so quickly on the unigram probabilities. The sparsity of data for these rows left them vulnerable to random variation, thus resulting in a higher error value. While they did benefit from the defence, like all characters, they did not occur frequently enough in the corpus to be accurately represented here.

Even against these limits, the defence provides a significant reduction in the power of a Markov model. However, these limits both apply to real-world applications. Extremely rare (i.e., sparse) features of a communication may still be visible, thus giving an attacker brief glimpses of a communication, and applications driven by non-Markovian processes with a state that has a long-term impact may have characteristics that this defence smooths but does not fully hide.

7.2. Implementation Concerns

Multipath evasion could be implemented for any multipath protocol: the necessary change is not the capability to use multiple paths but the manner in which multiple paths are managed. While in theory this is a control plane concern that could be handled transparently by the protocol, without careful consideration, an implementation could introduce unintended consequences for higher level applications. In particular, care must be taken in handling congestion control and retransmission.

Existing multipath protocols do not use this round-robin approach to path selection. Most follow the pattern of MP-TCP, thereby using only one path until a single-path congestion control algorithm prevents more packets from being sent before switching to a new path. This approach minimizes the number of handovers between paths, which is important when the handovers are costly. However, this also results in sporadic bursts of traffic on each path, and link failure or congestion may not be detected until many packets have been sent and lost. Spreading packets across all links simultaneously provides a more even load for the network and better resilience to congestion or link failure. This is particularly advantageous for protocols like ILNP, which have seamless handovers between different paths [37]. In such cases, a round-robin algorithm is desirable for improving a range of metrics, not just privacy.

Existing congestion control methods have been designed for single-path communications. For example, TCP’s fast retransmit mechanism assumes that out-of-order delivery is rare. This is true for single-path communications, where all packets typically take the same route through the network and are delivered in order, but this is not necessarily true when using multiple heterogeneous paths—sending alternate packets by a path with high latency and a path with low latency could result in significant out-of-order delivery. With more paths, this may frequently trigger fast retransmit, even though no loss has occurred.

This could be resolved by using multipath-aware congestion control algorithms that account for these broken assumptions. One approach could be to use the same method but to track congestion for each path independently—for ILNP, this could be achieved by looking at the source and destination L64 tuple of each packet. Better performance may be achieved using more complex approaches that account for the different characteristics of heterogeneous paths. Multipath-aware congestion control algorithms are an area of future research; a contribution of this work is in highlighting that such algorithms have implications for privacy.

7.3. Pathological Topology

A low probability of intercept defence only works if it actually decreases the probability of interception. In the case of using multiple paths, this is not guaranteed. If the paths share common links, an attacker need only be present on the overlapping segment to eavesdrop on all paths. This may be a particularly feasible attack when the attacker is topologically close to the target. For example, if one communicating node is multihomed and the other is not, the single-homed node’s ISP will see all paths between them.

This is a general challenge for multipath communications—not just for privacy. Multihoming only provides fault tolerance if the paths are sufficiently diverse so as not to be taken out by the same fault. Similarly, using multiple paths to avoid congestion will only work if the congestion does not occur on a common segment.

A related problem is the availability of multihoming. Home networks, for example, rarely have multiple upstream links. Without multiple paths, multipath evasion is impossible.

One potential mitigation to these problems is to use locator rewriting [43]. ILNP’s locators are not part of the transport end state, and they are excluded from checksums, thus making them mutable. A locator rewriting relay (LRR) is a forwarding node that takes advantage of this and changes the values of the source or destination L64s of packets it forwards. An ILNP node could forward traffic to an LRR that then forwarded it to the true destination in order to provide relay functionality at the network layer without an encrypted tunnel. As ILNP connections can use multiple L64s, a node could also forward each packet to one of several different LRRs to forcibly and explicitly introduce multiple routes. Unlike physical multihoming, this allows a user to use routes that are known to be geographically and topologically diverse—for example, they could use an LRR in Berlin and an LRR in Madrid to force traffic through two different routes, while allowing a tolerable increase in latency. Selecting disparate LRRs potentially reduces the overlapping segments of the paths, although if the final node is single-homed, this last step will inevitably be shared and therefore vulnerable.

7.4. Coarse Feature Analysis

A multipath evasion defence does not directly prevent the analysis of coarse features, such as a communication’s date, time, and duration; however, it may make it harder.

Analysis based on the amount of data exchanged may be less accurate, as the attacker must estimate how many packets were exchanged based only on what they saw. If they can see packet numbers, they may be able to estimate the proportion of packets they saw and scale their measurements accordingly. However, if they do not have this information, they will not be able to estimate this. Estimating the number of bytes exchanged accurately is also difficult, as the attacker must assume the unseen packets had a similar size to those they saw. This may be a reasonable assumption, but it will not give them byte-level accuracy.

Time-of-day and duration analysis are not disrupted by this defence. An attacker could still see when a user was active and for how long, even if they did not see all the activity the user performed. However, a similar defence is possible: multiple paths could be used in sequence via some dynamic multihoming mechanism. In this case, the attacker would not know the full duration of the flow, as they would see it only for a short period before it moved to a new path. Combining these approaches would create a dynamic multipath evasion defence, which would disrupt attacks on per-packet side channels and hide the flow duration in both real time and the number of packets or bytes exchanged.

7.5. Resilience against Other Attacks

While this work has focused on HMMs, there are other machine learning algorithms that could be used for traffic analysis [7,8]. There are potentially limitless machine learning algorithms that could be used to perform this analysis, so this defence cannot be tested against all of them. However, as it works by removing the targeted pattern from the exposed data, multipath evasion is expected to prevent all attacks targeting this pattern. Traffic analysis against protected traffic must either target coarse features (including the unigram distributions of packet features) or exploit some unknown vulnerable pattern that is not hidden by using this defence. Further analysis of the defence’s utility against other methods of analysis is an area of future research.

8. Conclusions, Summary, and Future Work

We have shown through simulation and analysis that the use of multipath communication can perturb side-channel attacks on traffic (including encrypted traffic) where HMMs are used.

The key findings of this paper are as follows:

• That the emission and transition properties of an HMM can be transformed to a single transition model for an HMM. This is achieved by combining the loss rate into the transition probabilities, because the loss emission probability can be evaluated as a constant for a communication flow. Also, as Markov models are memoryless, loss events have limited impact on the HMM modeling of a communication flow, especially a flow that is a long-lived flow in time.
• As the Markov models only depend on the current state for computing the probability of the next state, we treat a communication flow, even an encrypted flow, as a set of transitions of states represented by the packets in the flow. If the set of probabilities from current state to next state can be perturbed, then an attack based on observation of those state transitions can also be perturbed.
• A communication system that distributes the packets in a communication flow across multiple paths effectively perturbs the observation of correct state transitions. If an observer only has visibility of one of these paths, the full transition model is perturbed, even for long-lived flows, and an HMM-based attack is perturbed. So, a multipath communication can act as a defence against an HMM-based attack. The overall utility of such a defence improves as the number of paths over which flow is distributed increases. Our simulation results show that there is a significant utility to such a defence with three or more paths. However, in our worst case scenario, where an attacker has full knowledge of the nature of the source, five or more paths are required.
• The use of a protocol such as ILNP at the network layer (layer 3) of the communication stack would enable the distribution of packets in the way described in this paper. This would enable any transport protocol (layer 4), and therefore any application protocol, to benefit from this mechanism. This method of distributing packets below the transport layer will require transport layer mechanisms such as congestion control to be redesigned for optimal performance.

We believe these be to fundamental results. The approach could be applicable at multiple points in the communication protocol architecture, anywhere that packet flows could be distributed across multiple paths.

8.1. Summary of This Paper

Although increased desire for data privacy encourages the use of data encryption, it is still possible for an attack to obtain useful information from examining side channels (such as IPATs and packet size distributions) using HMMs (Section 2).

Such exploitation of side channels relies on an attacker gaining access to the victim’s packet flows. So, an effective defence must perturb an attacker’s access to the packet flow. One such defence is to distribute the flow across multiple network paths—to use multipath communication (Section 3).

However, modern communication protocols might not necessarily be able to exploit mutliple network paths, even though they might exist. The current use of addressing within IP is a constraint when enabling efficient, flexible multipath mechanisms, which must typically be implemented for each transport protocol indepedently. These constraints can be overcome by using ILNP, which would offer a common facility to all transport protocols (Section 4).

When confronted with a packet flow suitably distributed across mutliple paths, HMM-based attacks can be effectively perturbed. The overall effectiveness of a multipath defence does depend on (i) the nature of the original traffic and (ii) how much perturbation is evident to side channels based on multiple paths (Section 5).

When evaluated based on the flexibility in multipath communication offered by ILNP, we find that (i) the use of more paths is better, but within our test cases, significant perturbation to HMM-based attacks is possible with four paths; and (ii) transmitting packets round-robin across those paths provides, effectively, a random selection of packets to an attacker that only has access to a single path (Section 6).

8.2. Future Work

This does present some challenges to the design of existing protocols, both in terms of the way they use addressing and multiple network paths, and in the way that they transmit packets on each path of a multipath communication. Both of these issues can be resolved by the use of ILNP (Section 7).

For future work, an implementation and testing of this for real-world systems is currently in progress, which is based on an implementation on the FreeBSD operating system. Our focus in this work is on privacy, but existing protocol designs for multipath communication have focused on performance-related features, such as distributing network load or tolerance to network failure. So, future mechanisms that can cater to all of these performance features, as well as privacy, need to be investigated.

However, if protection against side channels for existing transport protocols and applications is required, then the use of ILNP with the mechanism described in our work presents an effective defence against side-channel attacks based on HMMs.