A Provably Secure Anonymous Authentication Protocol for Consumer and Service Provider Information Transmissions in Smart Grids
Abstract
1. Introduction
1.1. Motivation
1.2. Threat Model
- Modifying and deleting the contents of intercepted messages;
- Generating and forwarding bogus messages to unsuspecting entities;
- Physically capturing and compromising network entities such as smart meters;
- Retrieving sensitive security tokens stored in the smart meter’s memory;
- Deploying extracted smart meter memory content to execute attacks;
- Intercepting derived session keys and other session state parameters.
1.3. Security Requirements
1.4. Contributions
- We deploy shared keys and pseudo-identities to encipher the communication channel so as to enhance security and privacy preservation.
- To protect against MitM and replay attacks, each entity computes the session keys for traffic protection.
- We deploy BAN logic for the revelation of the probably secure nature of the negotiated session key.
2. Related Work
3. The Proposed Protocol
| Algorithm 1 Secure and efficient authentication |
| Begin |
| #*****************System setup phase ********************# |
|
| #*****************Registration phase ********************# |
|
|
|
|
|
|
|
|
|
| #***************** Authentication and key negotiation phase ***************# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| End |
3.1. System Setup
3.2. Registration
3.2.1. Smart Meter Registration
3.2.2. Utility Service Provider Registration
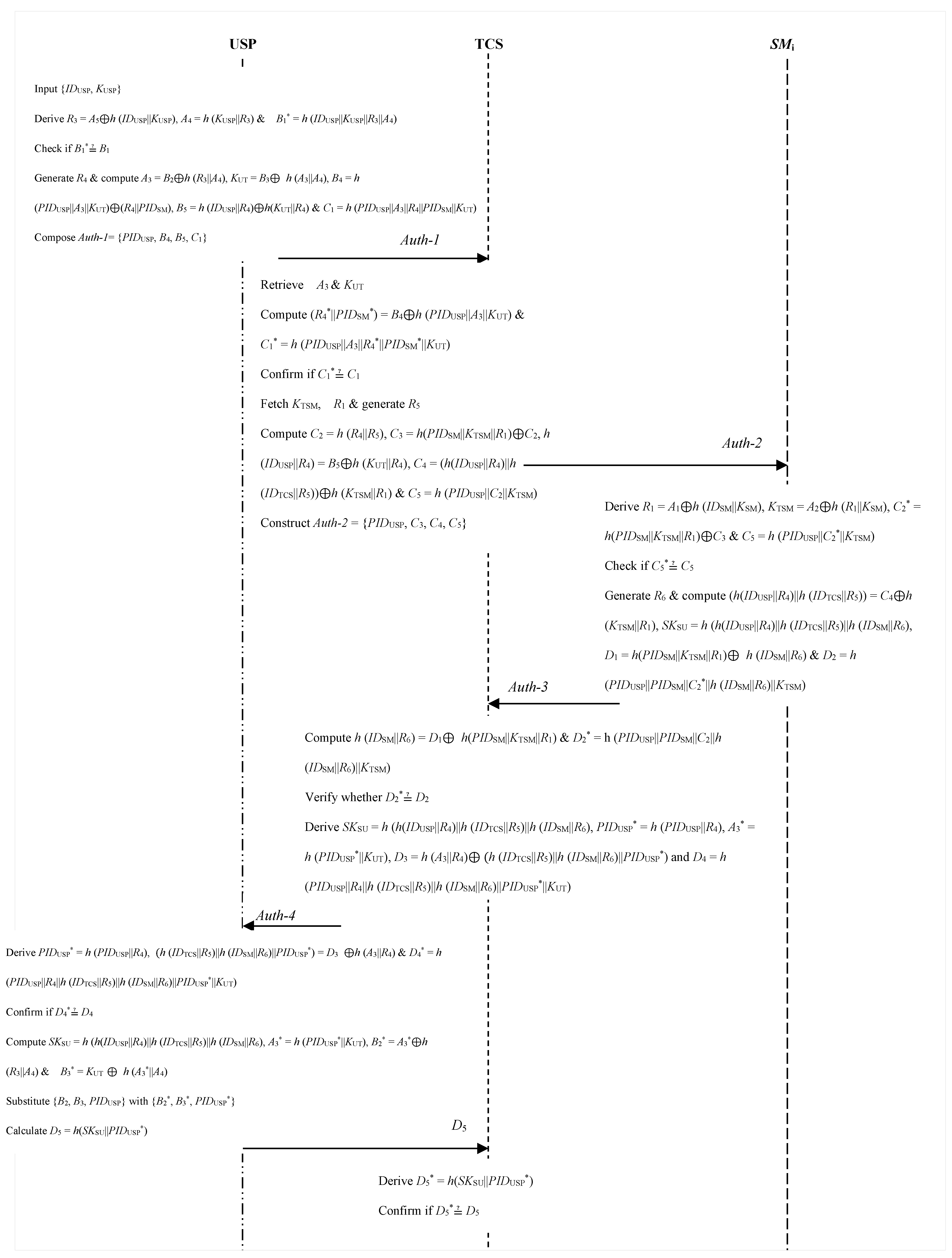
3.3. Authentication and Key Setup
3.4. Parameter Update
4. Security Analysis
4.1. Formal Security Analysis
4.2. Informal Security Analysis
5. Performance Evaluations
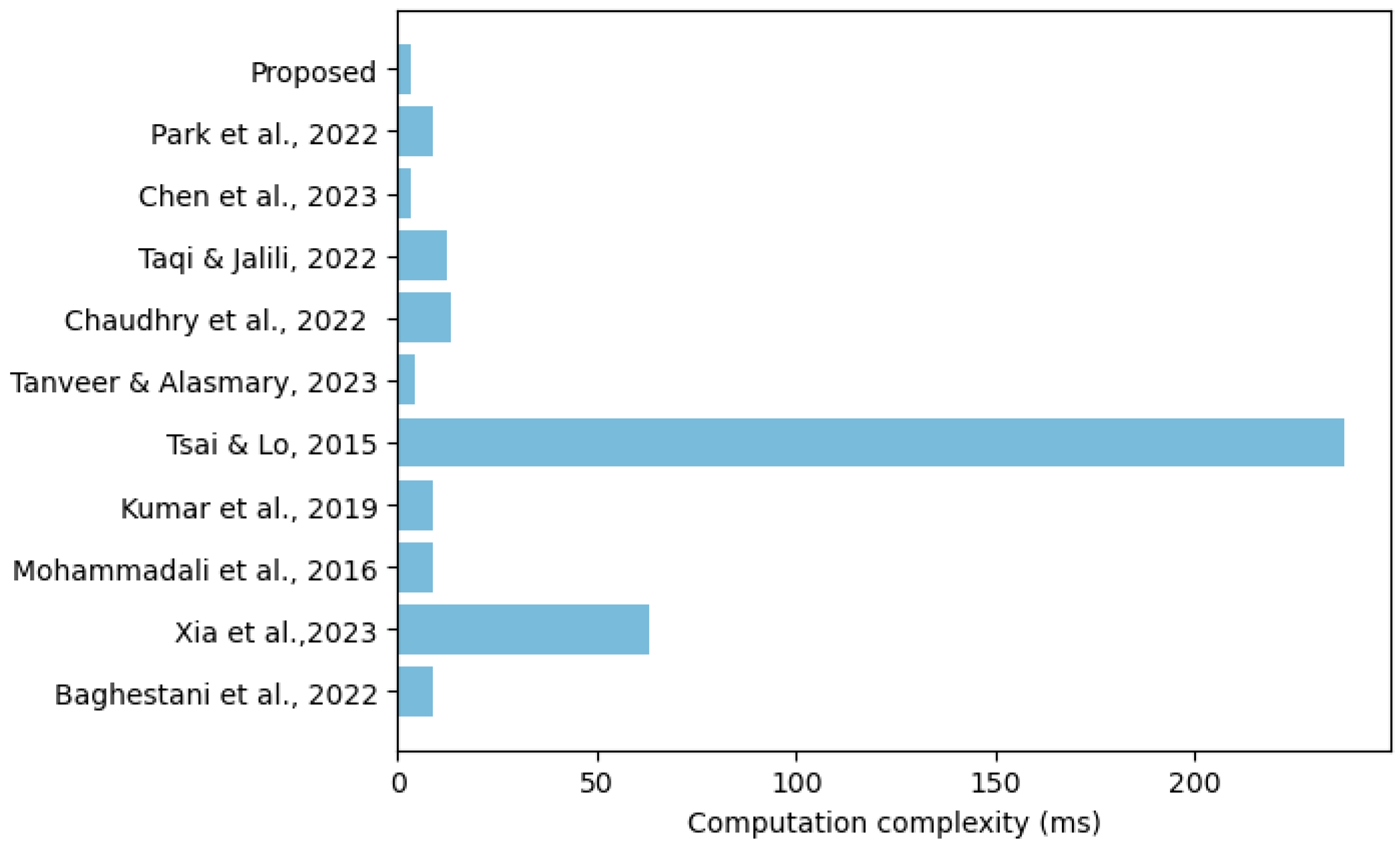
5.1. Computation Overheads
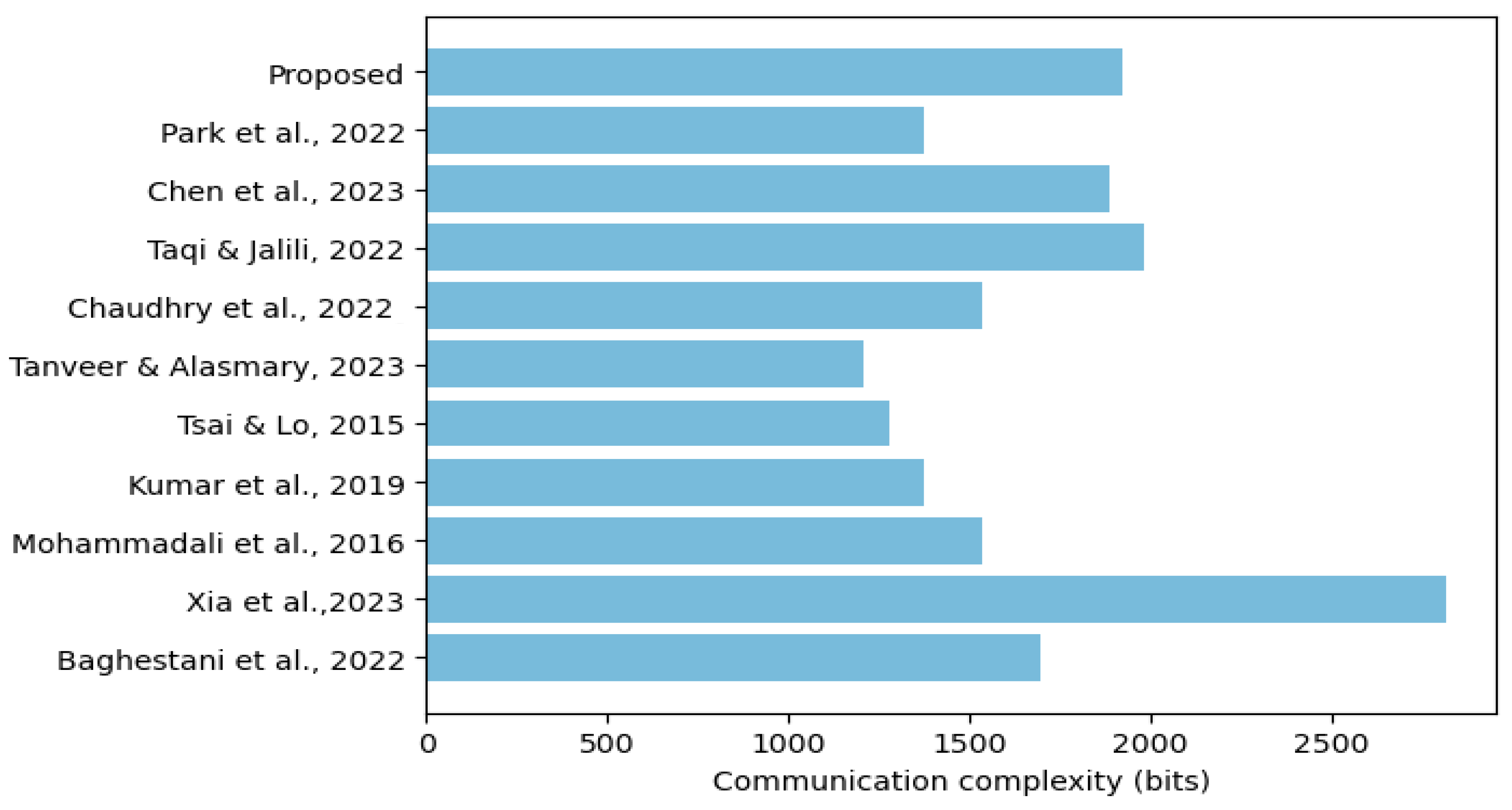
5.2. Communication Overheads
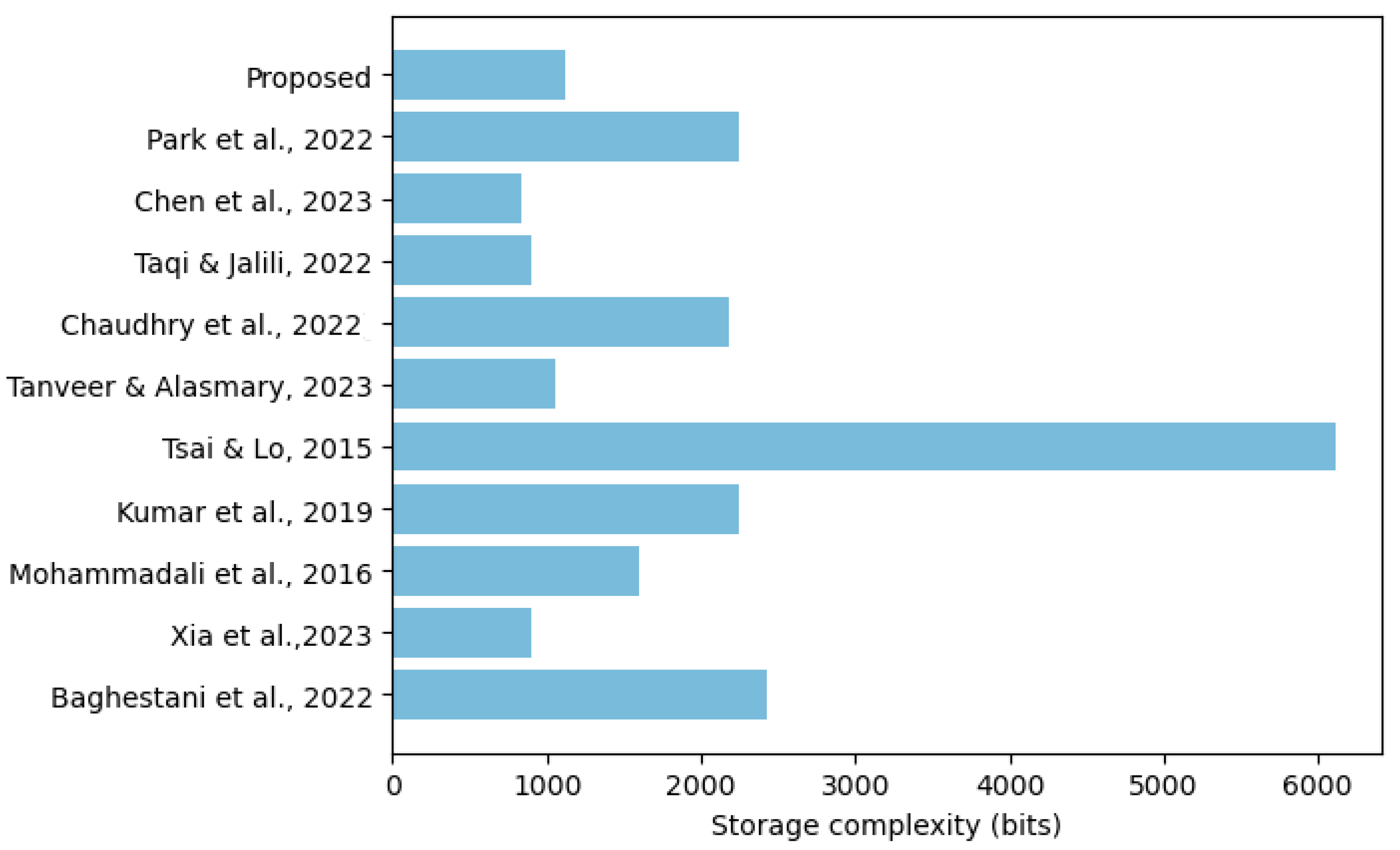
5.3. Storage Overheads
5.4. Supported Functionalities
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baghestani, S.H.; Moazami, F.; Tahavori, M. Lightweight authenticated key agreement for smart metering in smart grid. IEEE Syst. J. 2022, 16, 4983–4991. [Google Scholar] [CrossRef]
- Sun, C.-C.; Hahn, A.; Liu, C.-C. Cyber security of a power grid: State-of-the-art. Int. J. Electr. Power Energy Syst. 2018, 99, 45–56. [Google Scholar] [CrossRef]
- Salem, F.M.; Ibrahim, E.; Elghandour, O. A lightweight authenticated key establishment scheme for secure smart grid communications. Int. J. Saf. Secur. Eng. 2020, 10, 549–558. [Google Scholar] [CrossRef]
- Numan, M.; Baig, M.F.; Yousif, M. Reliability evaluation of energy storage systems combined with other grid flexibility options: A review. J. Energy Storage 2023, 63, 107022. [Google Scholar] [CrossRef]
- Nyangaresi, V.O.; Abduljabbar, Z.A.; Al Sibahee, M.A.; Abood, E.W.; Abduljaleel, I.Q. Dynamic ephemeral and session key generation protocol for next generation smart grids. In Proceedings of the International Conference on Ad Hoc Networks, Virtual Event, 6–7 December 2021; pp. 188–204. [Google Scholar] [CrossRef]
- Xia, Z.; Liu, T.; Wang, J.; Chen, S. A secure and efficient authenticated key exchange scheme for smart grid. Heliyon 2023, 9, e17240. [Google Scholar] [CrossRef]
- Huseinović, A.; Mrdović, S.; Bicakci, K.; Uludag, S. A survey of denial-of-service attacks and solutions in the smart grid. IEEE Access 2020, 8, 177447–177470. [Google Scholar] [CrossRef]
- Zhu, L.; Li, M.; Zhang, Z.; Xu, C.; Zhang, R.; Du, X.; Guizani, N. Privacy-preserving authentication and data aggregation for fog-based smart grid. IEEE Commun. Mag. 2019, 57, 80–85. [Google Scholar] [CrossRef]
- Kumar, P.; Lin, Y.; Bai, G.; Paverd, A.; Dong, J.S.; Martin, A. Smart grid metering networks: A survey on security, privacy and open research issues. IEEE Commun. Surv. Tutor. 2019, 21, 2886–2927. [Google Scholar] [CrossRef]
- Mohammadali, A.; Haghighi, M.S.; Tadayon, M.H.; Mohammadi-Nodooshan, A. A novel identity-based key establishment method for advanced metering infrastructure in smart grid. IEEE Trans. Smart Grid 2016, 9, 2834–2842. [Google Scholar] [CrossRef]
- Tanveer, M.; Ahmad, M.; Khalifa, H.S.; Alkhayyat, A.; Abd El-Latif, A.A. A new anonymous authentication framework for secure smart grids applications. J. Inf. Secur. Appl. 2022, 71, 103336. [Google Scholar] [CrossRef]
- Abbasinezhad-Mood, D.; Nikooghadam, M. An anonymous ECC-based self-certified key distribution scheme for the smart grid. IEEE Trans. Ind. Electron. 2018, 65, 7996–8004. [Google Scholar] [CrossRef]
- Kumar, N.; Aujla, G.S.; Das, A.K.; Conti, M. ECCAuth: A secure authentication protocol for demand response management in a smart grid system. IEEE Trans. Ind. Inform. 2019, 15, 6572–6582. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, Y.; Ren, W.; Wang, Y.; Choo, K.-K.R.; Xiong, N.N. An energy-efficient authentication scheme based on Chebyshev chaotic map for smart grid environments. IEEE Internet Things J. 2021, 8, 17120–17130. [Google Scholar] [CrossRef]
- Gope, P.; Sikdar, B. A privacy-aware reconfigurable authenticated key exchange scheme for secure communication in smart grids. IEEE Trans. Smart Grid 2021, 12, 5335–5348. [Google Scholar] [CrossRef]
- Kaveh, M.; Mosavi, M.R. A lightweight mutual authentication for smart grid neighborhood area network communications based on physically unclonable function. IEEE Syst. J. 2020, 14, 4535–4544. [Google Scholar] [CrossRef]
- Tahavori, M.; Moazami, F. Lightweight and secure PUF-based authenticated key agreement scheme for smart grid. Peer-To-Peer Netw. Appl. 2020, 13, 1616–1628. [Google Scholar] [CrossRef]
- Gope, P.; Sikdar, B. Privacy-aware authenticated key agreement scheme for secure smart grid communication. IEEE Trans. Smart Grid 2018, 10, 3953–3962. [Google Scholar] [CrossRef]
- Nyangaresi, V.O.; Petrovic, N. Efficient PUF based authentication protocol for internet of drones. In Proceedings of the 2021 International Telecommunications Conference (ITC-Egypt), Alexandria, Egypt, 13–15 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Li, X.; Wu, F.; Kumari, S.; Xu, L.; Sangaiah, A.K.; Choo, K.-K.R. A provably secure and anonymous message authentication scheme for smart grids. J. Parallel Distrib. Comput. 2019, 132, 242–249. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.; Zeadally, S.; He, D. Anonymous and efficient message authentication scheme for smart grid. Secur. Commun. Netw. 2019, 2019, 4836016. [Google Scholar] [CrossRef]
- Tsai, J.-L.; Lo, N.-W. Secure anonymous key distribution scheme for smart grid. IEEE Trans. Smart Grid 2015, 7, 906–914. [Google Scholar] [CrossRef]
- Odelu, V.; Das, A.K.; Wazid, M.; Conti, M. Provably secure authenticated key agreement scheme for smart grid. IEEE Trans. Smart Grid 2016, 9, 1900–1910. [Google Scholar] [CrossRef]
- Abduljabbar, Z.A.; Nyangaresi, V.O.; Jasim, H.M.; Ma, J.; Hussain, M.A.; Hussien, Z.A.; Aldarwish, A.J. Elliptic curve cryptography-based scheme for secure signaling and data exchanges in precision agriculture. Sustainability 2023, 15, 10264. [Google Scholar] [CrossRef]
- Deng, L.; Gao, R. Certificateless two-party authenticated key agreement scheme for smart grid. Inf. Sci. 2021, 543, 143–156. [Google Scholar] [CrossRef]
- Mahmood, K.; Chaudhry, S.A.; Naqvi, H.; Kumari, S.; Li, X.; Sangaiah, A.K. An elliptic curve cryptography based lightweight authentication scheme for smart grid communication. Future Gener. Comput. Syst. 2018, 81, 557–565. [Google Scholar] [CrossRef]
- Abbasinezhad-Mood, D.; Nikooghadam, M. Design and hardware implementation of a security-enhanced elliptic curve cryptography based lightweight authentication scheme for smart grid communications. Future Gener. Comput. Syst. 2018, 84, 47–57. [Google Scholar] [CrossRef]
- Banerjee, S.; Odelu, V.; Das, A.K.; Chattopadhyay, S.; Park, Y. An efficient, anonymous and robust authentication scheme for smart home environments. Sensors 2020, 20, 1215. [Google Scholar] [CrossRef] [PubMed]
- Tanveer, M.; Alasmary, H. LACP-SG: Lightweight authentication protocol for smart grids. Sensors 2023, 23, 2309. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, J.; Das, A.K.; Li, X.; Khan, M.K.; Jo, M. Designing anonymous signature-based authenticated key exchange scheme for Internet of Things-enabled smart grid systems. IEEE Trans. Ind. Inform. 2020, 17, 4425–4436. [Google Scholar] [CrossRef]
- Chaudhry, S.A.; Yahya, K.; Garg, S.; Kaddoum, G.; Hassan, M.M.; Zikria, Y.B. LAS-SG: An elliptic curve-based lightweight authentication scheme for smart grid environments. IEEE Trans. Ind. Inform. 2022, 19, 1504–1511. [Google Scholar] [CrossRef]
- Taqi, S.A.M.; Jalili, S. LSPA-SGs: A lightweight and secure protocol for authentication and key agreement based Elliptic Curve Cryptography in smart grids. Energy Rep. 2022, 8, 153–164. [Google Scholar] [CrossRef]
- Chen, C.; Guo, H.; Wu, Y.; Shen, B.; Ding, M.; Liu, J. A Lightweight Authentication and Key Agreement Protocol for IoT-Enabled Smart Grid System. Sensors 2023, 23, 3991. [Google Scholar] [CrossRef] [PubMed]
- Abdi Nasib Far, H.; Bayat, M.; Kumar Das, A.; Fotouhi, M.; Pournaghi, S.M.; Doostari, M.-A. LAPTAS: Lightweight anonymous privacy-preserving three-factor authentication scheme for WSN-based IIoT. Wirel. Netw. 2021, 27, 1389–1412. [Google Scholar] [CrossRef]
- Khan, A.A.; Kumar, V.; Ahmad, M.; Rana, S.; Mishra, D. PALK: Password-based anonymous lightweight key agreement framework for smart grid. Int. J. Electr. Power Energy Syst. 2020, 121, 106121. [Google Scholar] [CrossRef]
- Chaudhry, S.A. Correcting “PALK: Password-based anonymous lightweight key agreement framework for smart grid”. Int. J. Electr. Power Energy Syst. 2021, 125, 106529. [Google Scholar] [CrossRef]
- Wazid, M.; Das, A.K.; Kumar, N.; Alazab, M. Designing Authenticated Key Management Scheme in 6G-Enabled Network in a Box Deployed for Industrial Applications. IEEE Trans. Ind. Inform. 2021, 17, 7174–7184. [Google Scholar] [CrossRef]
- Nyangaresi, V.O.; Abduljabbar, Z.A.; Abduljabbar, Z.A. Authentication and Key Agreement Protocol for Secure Traffic Signaling in 5G Networks. In Proceedings of the IEEE 2nd International Conference on Signal, Control and Communication (SCC), Hammamet, Tunisia, 20–22 December 2021; pp. 188–193. [Google Scholar] [CrossRef]
- Esfahani, A.; Mantas, G.; Matischek, R.; Saghezchi, F.B.; Rodriguez, J.; Bicaku, A.; Maksuti, S.; Tauber, M.G.; Schmittner, C.; Bastos, J. A Lightweight Authentication Mechanism for M2M Communications in Industrial IoT Environment. IEEE Internet Things J. 2019, 6, 288–296. [Google Scholar] [CrossRef]
- Nyangaresi, V.O.; Abood, E.W.; Abduljabbar, Z.A.; Al Sibahe, M.A. Energy Efficient WSN Sink-Cloud Server Authentication Protocol. In Proceedings of the 5th International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 22–23 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, L.; Yin, S.; Chi, C.-H.; Liu, R.; Zhang, Y. A lightweight authentication scheme with privacy protection for smart grid communications. Future Gener. Comput. Syst. 2019, 100, 770–778. [Google Scholar] [CrossRef]
- Ikeda, K. Long-range quantum energy teleportation and distribution on a hyperbolic quantum network. IET Quantum Commun. 2023, 1–8. [Google Scholar] [CrossRef]
- Ikeda, K.; Lowe, A. Quantum protocol for decision making and verifying truthfulness among N-quantum parties: Solution and extension of the quantum coin flipping game. IET Quantum Commun. 2023, 4, 218–227. [Google Scholar] [CrossRef]
- Broadbent, A.; Fitzsimons, J.; Kashefi, E. Universal blind quantum computation. In Proceedings of the 2009 50th Annual IEEE Symposium on Foundations of Computer Science, Atlanta, GA, USA, 25–27 October 2009; pp. 517–526. [Google Scholar] [CrossRef]
- Hiroka, T.; Morimae, T.; Nishimaki, R.; Yamakawa, T. Certified everlasting zero-knowledge proof for QMA. In Annual International Cryptology Conference; Springer Nature: Cham, Switzerland, 2022; pp. 239–268. [Google Scholar] [CrossRef]
- Ikeda, K. Security and privacy of blockchain and quantum computation. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 2018; Volume 111, pp. 199–228. [Google Scholar] [CrossRef]
- Park, K.; Lee, J.; Das, A.K.; Park, Y. BPPS: Blockchain-enabled privacy-preserving scheme for demand-response management in smart grid environments. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1719–1729. [Google Scholar] [CrossRef]
- Zhou, L.; Diro, A.; Saini, A.; Kaisar, S.; Hiep, P.C. Leveraging zero knowledge proofs for blockchain-based identity sharing: A survey of advancements, challenges and opportunities. J. Inf. Secur. Appl. 2024, 80, 103678. [Google Scholar] [CrossRef]
- Crocetti, L.; Di Rienzo, R.; Verani, A.; Baronti, F.; Roncella, R.; Saletti, R. A novel and robust security approach for authentication, integrity, and confidentiality of Lithium-ion Battery Management Systems. In Proceedings of the 2023 IEEE 3rd International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), Shanghai, China, 26–28 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Al Sibahee, M.A.; Nyangaresi, V.O.; Ma, J.; Abduljabbar, Z.A. Stochastic Security Ephemeral Generation Protocol for 5G Enabled Internet of Things. In International Conference on Internet of Things as a Service; Springer: Cham, Switzerland, 2022; pp. 3–18. [Google Scholar] [CrossRef]


| Symbol | Descriptions |
|---|---|
| TCS | Trusted control server |
| SMi | ith smart meter |
| USP | Utility service provider |
| KTCS | Master key of the TCS |
| IDTCS | Unique identifier of the TCS |
| IDSM | Unique identifier of the SMi |
| KSM | SMi’s private key |
| Ri | Random nonce i |
| PIDSM | SM’s pseudo-identity |
| KTSM | Shared key between TCS and SM |
| IDUSP | Unique identity of the USP |
| KUSP | USP’s private key |
| PIDUSP | USP’s pseudo-identity |
| KUT | Shared key between USP and TCS |
| SKSU | Session key between SMi and USP |
| h (.) | Hashing function |
| || | Concatenation operation |
| ⊕ | XOR operation |
| Notation | Details |
|---|---|
| R | Secret key |
| AX | Entity A believes statement X |
| A| ~ X | Entity A once said statement X |
| <X>M | X is combined with M |
| A | Entity A sees statement X |
| Entity A has jurisdiction over X | |
| # (X) | Message X is fresh |
| (X)R | Message X is hashed using key R |
| (X, M) | X or M is part of formula (X, M) |
| Entities A and B share secret key R | |
| {X}R | Message X is enciphered using key R |
| B | R is only known to A and B |
| Rule | Details |
|---|---|
| Message Meaning Rule (MMR) | |
| Nonce Verification Rule (NVR) | |
| Believe Rule (BR) | |
| Jurisdiction Rule (JR) | |
| Freshness rule (FR) |
| Scheme | Costs (ms) | |
|---|---|---|
| SM | USP | |
| Bilinear pairing operations, TBP | 95.72100 | 9.52800 |
| ECC point addition, TECA | 0.13400 | 0.00700 |
| One-way hash function, TH | 0.34500 | 0.03900 |
| ECC point multiplication, TPM | 2.70000 | 0.70500 |
| Symmetric encryption, TSE | 0.41000 | 0.00460 |
| Symmetric decryption, TSD | 0.41000 | 0.00460 |
| Esch256 one-way hash function, THE | 0.33000 | 0.03200 |
| Physically unclonable function, TPUF | 0.00049 | - |
| Counter-mode encryption with authentication tag, TCO | 0.34900 | 0.04100 |
| Bio-metric key generation and reproduction, TREP | 2.70000 | 0.70500 |
| Modular exponential, TE | 30.7920 | 0.31200 |
| Scalar multiplication, TSM | 2.70000 | 0.70500 |
| Scheme | SM | USP | Total (ms) |
|---|---|---|---|
| Baghestani et al. [1] | 5TH + 2TPM | 11TH + 2TPM | 17TH + 4TPM ≈ 8.964 |
| Xia et al. [6] | 19TPM | 17TPM | 10TH + 8TPM ≈ 63.285 |
| Mohammadali et al. [10] | 3TH + 2TPM | 4TH + 3TPM | 7TH + 5TPM ≈ 8.706 |
| Kumar et al. [13] | 5TH + 2TPM | 6TH + 2TPM | 11TH + 4TPM ≈ 8.769 |
| Tsai & Lo [22] | 5TH + 4TPM + TE | 2TBP + 3TPM + TE + 5TH | 2TBP + 7TPM + 2TE + 10TH ≈ 237.381 |
| Tanveer & Alasmary [29] | 2THE + 2TCO + TREP + TPUF | 5THE + 2TCO | 7THE + 4TCO + TREP + TPUF ≈ 4.300 |
| Chaudhry et al. [31] | 4TH + 2TSE + 3TPM | 6TH + 2TSE + 4TPM | 10TH + 4TSE + 7TPM ≈ 13.363 |
| Taqi & Jalili [32] | 4TH + TSE + TSD + 3TPM | 3TH + TSE + TSD + 3TPM | 7TH + 2TSE + 2TSD + 6TPM ≈ 12.5412 |
| Chen et al. [33] | 7TH + TSD | 9TH + 2TSE + TSD | 16TH + 2TSE + 2TSD ≈ 3.1898 |
| Park et al. [47] | 5TH + 2TSM | 6TH + 2TSM | 11TH + 4TSM ≈ 8.769 |
| Proposed | 7TH | 16TH | 16TH + 7TH ≈ 3.0390 |
| Scheme | Messages Exchanged | Total (Bits) |
|---|---|---|
| Baghestani et al. [1] | SM | 1696 |
| Xia et al. [6] | SM | 2816 |
| Mohammadali et al. [10] | USP | 1536 |
| Kumar et al. [13] | USP | 1376 |
| Tsai & Lo [22] | USP | 1280 |
| Tanveer & Alasmary [29] | SM | 1206 |
| Chaudhry et al. [31] | SM | 1536 |
| Taqi & Jalili [32] | USP | 1984 |
| Chen et al. [33] | SM | 1888 |
| Park et al. [47] | USP | 1376 |
| Proposed | USP | 1920 |
| Scheme | Stored Parameters | Total (Bits) |
|---|---|---|
| Baghestani et al. [1] | SM: {H1, H2, n, E, P, FP, SMsj, xj, yj} USP: {SMIDj,Mk} | 2432 |
| Xia et al. [6] | SM: {xS, R2} USP: {xC} | 896 |
| Mohammadali et al. [10] | SM: {SM, RM, yM, rM} USP: {yAHE, rAHE} | 1600 |
| Kumar et al. [13] | SM: {RIDi, TCi, h (·),Ep (a, b),G} USP: {RIDj, TCj, {RIDi |i = 1, 2, …, l}, h (·),Ep (a, b),G} | 2240 |
| Tsai & Lo [22] | SM: {G1, G2, P, e,H, H1, H2, H3, H4, q, Ppub, g} USP: {G1, G2, P, e, H, H1, H2, H3, H4, q, Ppub, g}, Kj, H1 (SIDj)P + Ppub | 6112 |
| Tanveer & Alasmary [29] | SM: {CHSMi, TIDSMi, RNr, HD} USP: {SIDi, Bi, RNr} | 1056 |
| Chaudhry et al. [31] | SM: {E, P, Fp, n, SMprj, σj, idSTj, STj, H (.), SMIDj, Pidstj} USP: {Mk} | 2176 |
| Taqi & Jalili [32] | SM: {ai, Ai} USP: {aj, Aj} | 896 |
| Chen et al. [33] | SM: {IDi, N1, Xi} USP: {Si} | 832 |
| Park et al. [47] | SM: {PIDi, LSSMi, H, E(a, b), G} USP: {PCUIDj, H, E(a,b), G, PIDi=1…l} | 2240 |
| Proposed | SM: {A1, A2, PIDSM} USP: {A5, B1, B2, B3} | 1120 |
| Symbol | Details |
|---|---|
| xS, SMsj, SMprj, SM | SM’s private keys |
| RM, | SM’s public key |
| R2 | Keying parameter based on smart meter’s public key |
| xC, Kj | USP’s private keys |
| H1, H2, H, H (..), h (.), H1, H2, H3, H4 | One-way hash functions |
| n, E, P | Elliptic curve E and a point P of order n |
| FP | Finite field |
| xj, yj, Xi, LSSMi, σj, STj, Ai, Aj, SIDi, Bi, yM, yAHE, g | Derived intermediary parameters |
| SMIDj, IDi, SMIDj | SM’s unique identity |
| idSTj | Unique identifier for SM |
| SIDj | USP’s unique identity |
| Mk | Master key |
| N1, ai, aj, RNr, rM, rAHE | Random numbers |
| Si | SM’s unique identification stored in the table |
| PIDi, Pidstj, TIDSMi, RIDi | Pseudo-identities for SM |
| PCUIDj, RIDj | Pseudo-identities for USP |
| TCi | SM’s temporal credential |
| TCj | USP’s temporal credential |
| E(a, b), G, Ep (a, b) | Elliptic curve with base point G. |
| P, G1, G2 | Generator of G1, cyclic additive group, and cyclic multiplicative group, respectively |
| q | Prime order of G1 and G2 |
| e | Pairing operation |
| Ppub | Public key of the trust anchor |
| CHSMi | Registration authority (RA) challenge parameter |
| HD | Helper data |
| [10] | [13] | [22] | [29] | [6] | [1] | [31] | [32] | [33] | [47] | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Functionality | |||||||||||
| Session key agreement | √ | × | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Anonymity and untraceability | × | √ | √ | √ | × | √ | √ | √ | √ | × | √ |
| Key security | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Mutual authentication | √ | × | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Formal verification | √ | √ | √ | √ | × | √ | √ | √ | √ | √ | √ |
| Resilience against | |||||||||||
| De-synchronization | √ | × | × | √ | × | √ | × | × | √ | × | √ |
| Backdoor-based DoS | × | × | × | √ | × | √ | × | √ | √ | × | √ |
| Privileged insider | × | × | × | √ | × | × | × | × | √ | × | √ |
| Guessing | × | × | × | × | × | × | × | √ | × | × | √ |
| KSSTI | × | × | × | √ | × | × | √ | × | × | √ | √ |
| Eavesdropping | × | × | × | × | × | × | × | × | × | × | √ |
| Ephemeral secret leakage | × | √ | × | √ | × | √ | × | × | × | × | √ |
| Spoofing | × | × | × | × | × | × | × | × | × | × | √ |
| Physical capture | × | √ | × | √ | × | × | √ | √ | × | × | √ |
| Impersonation | √ | √ | √ | √ | √ | √ | √ | × | √ | √ | √ |
| Replay | √ | √ | √ | √ | √ | √ | √ | √ | √ | × | √ |
| MitM | √ | √ | √ | √ | √ | √ | √ | × | √ | √ | √ |
| Forgery | × | × | × | √ | × | × | × | × | × | × | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.A.; Abduljabbar, Z.A.; AL-Asadi, H.A.A.; Nyangaresi, V.O.; Abduljaleel, I.Q.; Aldarwish, A.J.Y. A Provably Secure Anonymous Authentication Protocol for Consumer and Service Provider Information Transmissions in Smart Grids. Cryptography 2024, 8, 20. https://doi.org/10.3390/cryptography8020020
Ali ZA, Abduljabbar ZA, AL-Asadi HAA, Nyangaresi VO, Abduljaleel IQ, Aldarwish AJY. A Provably Secure Anonymous Authentication Protocol for Consumer and Service Provider Information Transmissions in Smart Grids. Cryptography. 2024; 8(2):20. https://doi.org/10.3390/cryptography8020020
Chicago/Turabian StyleAli, Zahraa Abdullah, Zaid Ameen Abduljabbar, Hamid Ali Abed AL-Asadi, Vincent Omollo Nyangaresi, Iman Qays Abduljaleel, and Abdulla J. Y. Aldarwish. 2024. "A Provably Secure Anonymous Authentication Protocol for Consumer and Service Provider Information Transmissions in Smart Grids" Cryptography 8, no. 2: 20. https://doi.org/10.3390/cryptography8020020
APA StyleAli, Z. A., Abduljabbar, Z. A., AL-Asadi, H. A. A., Nyangaresi, V. O., Abduljaleel, I. Q., & Aldarwish, A. J. Y. (2024). A Provably Secure Anonymous Authentication Protocol for Consumer and Service Provider Information Transmissions in Smart Grids. Cryptography, 8(2), 20. https://doi.org/10.3390/cryptography8020020