Abstract
Cross-chain transaction technologies have greatly promoted the scalability of cryptocurrencies, which then facilitates the development of Metaverse applications. However, existing solutions rely heavily on centralized middleware (notary) or smart contracts. These schemes lack privacy considerations, and users’ cross-chain transactions are easy to master by other parties. Some signature-based payment schemes have good privacy but do not support multi-party cross-chain protocols or rely heavily on some time assumptions. The uncertainty of user behavior makes it difficult to design a secure multi-party cross-chain protocol. To solve these problems, we investigate how to design a secure multi-party cross-chain transaction protocol with offline tolerance. We propose a new signature algorithm called the pre-adaptor signature scheme, an extension of the adaptor signature scheme. The pre-adaptor signature scheme combines the multi-signature and adaptor signature schemes, which can realize the secret transmission channel between multiple parties. To provide offline tolerance, we encode our protocol into the P2SH script. Our protocol provides better privacy due to no dependence on smart contracts. The performance evaluation was conducted with ten participants. For each participant of our cross-chain protocol, the initialization and execution process can be performed in 3 milliseconds and with 6 k bytes of communication overhead at most. The cost increases linearly with the increase in the number of participants.
1. Introduction
After the advent of Bitcoin [1], cryptocurrency has become a new payment choice in which users can transact with each other without relying on a trusted third party. However, influenced by the size of the block and the efficiency of the consensus mechanism, the transaction efficiency is not high. Later, new technologies such as the Lightning Network [2] and sharding [3] were presented to reduce management overhead and resource demand. Although the ecosystem of cryptocurrency is developing rapidly, effective interconnection and communication between different blockchains remain a problem. Traditional payment services are supported by national credit and allow almost all transactions and exchange services between currencies in the world. Traditional payment services offer significantly faster and more flexible transaction speeds when compared to the most widely used cryptocurrencies. This is because each cryptocurrency operates independently and possesses its unique encryption and consensus system.
Cross-chain technologies were proposed to improve chain interoperability. In applications like Decentralized Finance and the Metaverse, various blockchains are needed to serve the interconnection with each other [4,5]. However, apart from cross-chain data access, the exchange of assets and funds across different chains is also important in the current Metaverse ecosystems [6,7], which drove us to dive into the research within this scope. A typical cross-chain transaction scenario [8] is that in which Alice, Bob, and Calorie have assets A, B, and C on different chains, respectively. Calorie wants to exchange asset C for asset B, and Alice wants asset C but only owns asset A, so they find Bob as the converter of asset A and asset B. Then, they can exchange assets by running a cross-chain transaction protocol to ensure atomicity. Once the protocol is completed, the ownership of assets on the cryptocurrency ledger will change as originally defined.
Known cross-chain protocols provide practical ways to realize the above-mentioned transactions such as Binance (the largest exchange), Polkadot [9], InterLedger [10], and others. The earliest cross-chain technology is the notary scheme [11]. All the transaction participants transfer their assets to a trusted third party (an individual or a service such as an exchange) and exchange assets fairly. However, the notary scheme requires a strong promise of trust which destroys the decentralization feature of blockchain and is vulnerable to the attack of hackers. To address these problems, the side chain technique [12] was proposed. This technique can be applied to verify inter-chain transactions, implement complex transaction protocols, and achieve a good balance between decentralization and practicability. However, the side chain technique still has some limitations, described as follows:
- Its implementation depends on smart contracts, which makes it incompatible with those chains that do not support smart contracts.
- It lacks privacy considerations such that the information exposed by transactions on different cryptocurrencies is sufficient for cross-chain transaction tracing.
- It requires long-term on-chain state maintenance, which makes attackers capable of destroying the entire network by conquering the weakest side chain.
To correct the above problems, scriptless scripts [13] were proposed to avoid the usage of a smart contract as well as the maintenance of the chain state. A derivative technique of a scriptless script—an adaptor signature—is used to construct a cross-chain protocol, which achieves higher flexibility and privacy as described in [14,15]. However, existing schemes do not consider multi-party transaction scenarios. Therefore, to enhance the interoperability and privacy of cryptocurrencies, a cross-chain protocol that does not rely on smart contracts and supports multi-party transactions is necessary. This prompts us to ask the following question:
Can we build a secure multi-party cross-chain protocol that only relies on the underlying scripts and signatures?
In this work, we give a positive answer to this question. In addition, our protocol also provides offline tolerance to achieve higher robustness. Before describing the details of our approach, we elaborate on the potential challenges.
1.1. The Challenges of Constructing Secure Cross-Chain Protocols
Transaction Topology. Similar to the network communication model, cross-chain transaction methods can be roughly divided into four types, as shown in Figure 1a–d, according to the situation and complexity. The dots represent transaction participants, and the directed lines represent the flow of assets. An atomic swap is the simplest form of cross-chain asset exchange which can be achieved by the hashed time-lock contract (HTLC) [2,16] or an adaptor signature [14,15]. Based on smart contracts, more complex multi-party transaction protocols (Net topology) could be achieved by encoding the principles. A Payment Channel Network (PCN) [2] realized a Linear payment topology, where there is only one sender and receiver and several intermediate nodes. Such schemes can be extended to cross-chain scenarios easily [17,18]. A payment hub [19,20] is another way to achieve cross-chain payments by introducing an intermediary without any trusted settings.

Figure 1.
Transaction topologies of different types of cross-chain transactions.
In particular, a transaction model with a Ring topology exists, as shown in Figure 1e, which can be regarded as a compromise between a Net topology and Linear topology. Compared with constructing a transaction model with a Linear topology, constructing one with a Ring topology will face more significant security challenges. In the previous scenario, the sender hopes that the receiver will eventually receive the token; otherwise, the transaction will fail. So, they will be willing to play a role as a supervisor to monitor the execution process of the entire transaction. Therefore, the existence of a responsible supervisor can lower the difficulty of protocol design and provide other features such as offline tolerance and resistance to wormhole attacks [17,18]. However, in the second scenario, every participant will send and receive tokens. In this circumstance, no participant can be the supervisor, since everyone is likely to deviate from the protocol after receiving the token. The excellent work of Thyagarajan [21] can achieve a secure transaction protocol under a Ring topology by linearly constructing an n-to- atomic swap between adjacent participants. However, their approach has higher complexity, both in protocol rounds (two rounds of operations per path) and computational overhead (Verifiable Timed Dlog [22]).
Without Smart Contracts. At present, most of the multi-party cross-chain transaction protocols are realized by using smart contracts. Alexei et al. [23] presented such a protocol in terms of smart contracts to encourage users to pledge a certain amount of cryptocurrency to become a “warehouse”, and their participation in the protocol can be viewed as an intermediary for cross-chain transactions. Moreover, in [23], chain relays and security logs were used to restrict the behavior of warehouses and users and to eliminate absolute trust in the middleman. Liu et al. [24] proposed a unified cross-chain programmable framework and a universally composable security [25] protocol to restrict the behavior of parties in cross-chain transactions.
Smart contracts provide great programmability in the construction of the cross-chain protocols so that exchange rate fluctuations, offline, and other conditions can be taken into consideration. But it has certain privacy and security defects. Chen [26] showed that the internal and external transaction data of smart contract platforms can be obtained via transaction replay. In addition, once all the transaction details are reconstructed, logically related transactions can be easily associated under specific heuristics settings [27,28]. Although the privacy of smart contracts can be enhanced by introducing cryptographic techniques [29,30] such as Bulletproofs [31], the Pederson Commitment [32], and others, they are not easy to use in practice due to the huge computational overhead. Moreover, there are many cryptocurrencies [33,34] that do not support smart contracts.
Atomicity. The participants of the transaction may behave maliciously. In particular, all the participants may be malicious except one, which will put them at risk of a collusion attack. Therefore, we define the atomicity requirement in our multi-party cross-chain protocol. That is, if a user does not deviate from the protocol, then either the asset swap is successfully carried out, or the user’s assets are refunded. It is worth mentioning that the traditional “all-or-nothing” atomic concept was proven to be inapplicable in multi-party transaction scenarios in [35]. Compared with the protocol in the PCN scenario [18], there is a greater challenge to achieve atomicity under cross-chain situations. Because in the PCN scenario, the transaction graph is a directed acyclic graph, the initiator of the transaction can act as a third party to supervise the operation of the entire capital flow. In the cross-chain transaction scenario, the transaction flow is a directed graph with at least one loop; thus, each participant only cares about the assets flowing to themselves [8], and no one has the incentive to maintain the stable operation of the entire protocol.
Offline Tolerance. Based on the adaptor signature algorithm, a participant can calculate the pre-negotiated secret from the signature signed by the previous participant. Then, they can construct a valid signature as well as sign a transaction to obtain target assets. However, if the participant goes offline, not only will their assets be lost, but also the protocol will be terminated due to their offline behavior because the secret information cannot be delivered to the subsequent participant as expected. As an improvement, our protocol provides offline tolerance.
1.2. Our Contributions
In this paper, we study how to design and construct a privacy-preserving cross-chain transaction protocol with unlinkability and public verifiability. Our protocol only relies on the basic scripting language of Bitcoin to assist the protocol design. Theoretically, any cryptocurrencies with signatures that support an adaptor signature can be compatible with our protocol.
To realize secure multi-party cross-chain transactions, we propose a novel signature algorithm called the pre-adaptor signature scheme, which is an extension of the adaptor signature scheme. To the best of our knowledge, known adaptor signature schemes can only achieve secret transfer channels between two users. Nevertheless, our pre-adaptor signature scheme can achieve a secret transfer channel between several users by combining a multi-signature and Schnorr signature scheme. Informally, our signature scheme can be regarded as the adaptor signature affiliated with the time attribute.
Moreover, our protocol provides offline tolerance. We use P2SH technology to encode our protocol. With the combination of the participant’s public keys, the unlocking conditions of our protocol are strictly coded into the script. Before our work, smart contracts are indispensable to implementing a cross-chain protocol with offline tolerance.
We implemented our cross-chain protocol and showed that each participant takes at most 3 milliseconds to calculate and requires a communication overhead of fewer than 6 bytes in the scenario of ten participants. These two kinds of consumption increase linearly with the increase in participants. The results show that our protocol is practical.
1.3. Related Work
Affected by the development of blockchain techniques, the earliest cross-chain technique is the notary mechanism [10] where the transaction is completed with the help of a trusted third party. Later, the side chain technique was proposed in [12] such that block data of the side chain can be read and verified before publishing the relevant transaction on the main chain. HTLC [2] was first constructed based on the concept of two-party atomic transfer proposed by Nolan [36], in which both parties can set up a contract on different blockchains involved in the transaction and use the pre-image of a certain hash value to trigger the contract. However, these methods have some limitations, as follows:
- Notary: It needs a strong trust system; thus, the decentralized nature of the blockchain is destroyed, and it is easy to become the target of hackers.
- Side chain: Computing power attack is its potential risk. In side chain schemes, the attacker only needs to destroy the weakest chain to attack the entire network because most of these schemes only check whether the coins involved are from the longest known chain and do not trace the historical source of the coins to the genesis block.
- Hashed time-lock contract: It is mainly based on the strong anti-collision characteristic of the hash function. However, using the same hash value on different blockchains will make the associated transactions easy to track.
In addition, by using smart contract technology, complex transaction logic can be coded into programs and executed automatically. Some works [23,24,37,38,39] implemented cross-chain transaction protocols based on smart contracts. However, these protocols do not consider the privacy of transactions and need long-term condition maintenance. In [40], adaptor signatures were used to achieve cross-chain atomic swaps between two parties, but this type of protocol is capable only in specific chains. Apoorvaa [14] used a similar technology to implement the atomic exchange protocol using Schnorr signatures, but the protocol does not provide support for cross-chain transactions between multiple parties. Zhang [41] maps all heterogeneous tokens to a special consortium chain for trading and auditing. However, the introduction of the consortium chain increases the complexity of cross-chain transactions. Chen [42] proposes a three-stage cross-chain protocol based on transaction and verification notary groups, which can address efficiency and centralization issues in cross-chain transactions. But the notary group remains fragile under the circumstances, while the number of malicious opponents exceeds one-third. In conclusion, none of the known results can simultaneously (i) construct a multi-party transaction protocol without the help of smart contracts or high-level scripting languages, (ii) protect the privacy of transaction participants, and (iii) provide offline tolerance.
1.4. Organization
The rest of the paper is organized as follows. Section 2 introduces some preliminaries about the script, transaction of Bitcoin, and signature schemes. Section 3 gives a brief description of our cross-chain transaction protocol. Section 4 presents three core algorithms that will be applied to construct the full cross-chain transaction protocol. Section 5 provides the construction of the full protocol. Section 6 gives the security analysis of our protocol. Section 7 studies the implementation and performance of our protocol.
2. Preliminaries
2.1. Pay to Script Hash
The principle of Pay To Script Hash (P2SH) technology [43] is shown in Figure 2, where the script is essentially a payment condition that describes how to withdraw the funds stored in the P2SH address. The generation of the P2SH address is similar to the generation of the Pay To Public Key Hash (P2PKH) address, which is the most common form of transaction on Bitcoin. Instead of hashing the public key, it hashes the script content into script hash and maps it to an address. This is also the biggest difference between it and P2PKH. The participant who sets the fund withdrawal conditions changes from the sender to the receiver. Due to the introduction of programmability, P2SH technology is capable of constructing complex payment conditions, so it is often used to implement multi-signatures and time locking. In this work, we will use P2SH technology to construct our cross-chain protocols. Specifically, in our protocol, all participants can generate and verify the scripts according to some special rules, and hence, the script can be viewed as a substitute for smart contracts, which play a role as a trusted medium.
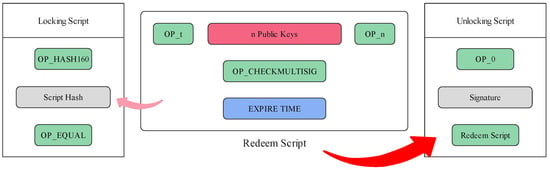
Figure 2.
Overview of P2SH scheme.
2.2. Transaction Generation
A transaction is defined concerning a blockchain , and two kinds of information are needed to generate it, including the source of the funds and where it will be sent. In the Bitcoin system, the two kinds of information can be represented as two scripts. The construction of the transaction data in Bitcoin is shown in Table 1. We focus on the following problems:

Table 1.
The construction of Bitcoin transaction.
- Input: This attribute represents an Unspent Transaction Output (UTXO) in the transaction referred to with the Transaction ID (TXID). “ScriptSig” is a script that meets unlocking conditions.
- Output: A script will be used to lock the output, which makes it a new UTXO. “ScriptPubKey” is a script that locks the output. The locking mechanism has some specific format depending on the transaction type, and its availability can be easily verified.
- TXID: The unique identifier for a transaction, which is obtained by hashing transaction data through the SHA256 function twice. All the signatures in unlocking scripts are essentially the signatures of the current TXID.
In summary, to complete a transfer, users need to construct complete transaction contents, such as input UTXO, output UTXO, and TXID, and then obtain the “ScriptSig” corresponding to TXID.
2.3. Adaptor Signature and Multi-Signature
In this section, we introduce the adaptor signature and multi-signature schemes, both of which are based on the Schnorr signature scheme [44]. The group parameters are , where g is a generator of G and p is a k-bit integer and the prime order of group G. Let be the security parameter and be a strong anti-collision hash function. The algorithm mainly consists of three parts:
- : Randomly select the parameter , and calculate , where x and X denote the private key and the public key, respectively.
- : Randomly select the parameter . Calculate and broadcast , . The signing message is .
- : Receive as input and verify the equation .
2.3.1. Adaptor Signature
The adaptor signature algorithm can be constructed based on the Schnorr signature [45]. It uses signature information to construct a secret transmission channel. Only those who know the adaptor signature and the complete signature can calculate the value of secret t. The algorithm is described as follows:
- : The same as the basic Schnorr algorithm.
- : Randomly select the signing parameter and the secret . Calculate and and broadcast the adaptor signature and the full signature . The signing message is .
- : The adaptor signature is not complete, but it can be verified by calculating .
- : The validity of the complete signature can be verified by calculating . If the verification is passed, the secret t can be obtained by calculating .
2.3.2. Multi-Signature
The traditional multi-signature scheme is implemented by adding (or multiplying) signatures, which makes it vulnerable to rogue public key attacks [46]. Precisely, a malicious user can randomly select public and private key pair and declare that their public key is . In this case, the aggregated public key is “forged” into his real public key, that is, , and thus, the malicious user obtains the ability to generate an illegal multi-signature.
Maxwell [47] proposed a secure multi-signature scheme based on Schnorr signatures which improved the practicability of the signature aggregation technique. Before the signing stage, the user needs to use the aggregated public key list and the hash function to calculate the additional parameter . The improved signature algorithm can be described as follows:
- : For all , calculate and aggregated public key .
- : First, calculate , then, calculate the global challenge , and finally, calculate .
- : Calculate . The signing message is , where s is the multi-signature.
- : With , the aggregated public key and challenge c can be calculated. If the equation holds, the verification is passed.
3. Brief Description of the Cross-Chain Protocol
In this section, we design a multi-party cross-chain protocol under the Ring topology scenario (Figure 1e). Our main observation is that most cross-chain transaction protocols are implemented on top of smart contracts with complicated judging conditions and control flows to support complex application requirements. To better illustrate the possibility of adaptor signatures and the basic scripting language of blockchain in building multi-party cross-chain protocols, we did not use the complex topology of mesh topology to describe our protocol. The transaction scenario is described below.
We assume that n protocol participants are labeled from 0 to . The protocol initiator () owns assets (assuming ) in a cryptocurrency and wants to exchange them for assets (assuming ) in another cryptocurrency. Due to the privacy considerations of the initiator, they do not want to use exchanges to realize the cross-chain transaction. Then, they can find another currency exchange service provider, where the ith participant () has and is willing to change it into with and . Under this circumstance, the initiator themselves will play a role as , so that the services provided by the currency exchange service providers can be linked together and meet the initiator’s asset exchange demand. The asset flow of the transaction will form a ring.
Nevertheless, multi-party cross-chain transactions are hard to be safely realized in this case because there are problems such as participants’ offline behavior or malicious deviation. Therefore, some necessary rules must be designed to prevent malicious participants from doing evil while protecting the rights and interests of honest participants.
3.1. Overview
To briefly explain our cross-chain protocol, we use the HTLC scheme [2]. The brief process is shown in Figure 3. The arrows between users represent the execution direction of the protocol. is the secret value exposed by while obtaining assets from with and .
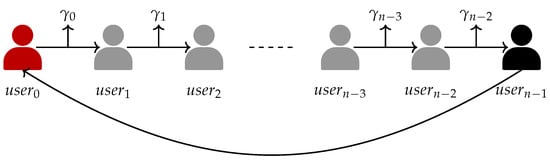
Figure 3.
Workflow of the proposed protocol.
Initialization:
- According to the flow of currency exchange, the participants will play the roles of to in turn. The transaction initiator is . For all , they own the assets and hope to obtain by paying ;
- (who owns the asset and hopes to exchange for ) is the first to execute the protocol. Value s will be selected as the “solution” of the HTLC. then calculates and sends h to all other participants. is a hash function;
- For each adjacent and , they construct an HTLC which locks , and they set the timeout for assets refound. Notice that increases with i. By providing the correct answer x such that , can obtain the assets locked in the contract.
Execution:
- releases the secret s to the HTLC between themselves and and withdraws ;
- For each subsequent , they will obtain the secret s if triggers the smart contract. Then, they can take and pass the secret s to .
If each participant is honest and active, then the whole protocol will be executed normally as expected. After the protocol procedure, each participant can obtain the funds that meet the pre-negotiated conditions. Finally, the currency exchange demand of the transaction initiator can be supplied.
As mentioned above, we describe an ideal protocol to implement the basic multi-party cross-chain transaction functionality, but it is far from fulfilling our requirements for preserving privacy. Specifically, the ideal protocol has the following defects:
- The use of smart contracts does not meet the generality and privacy demands;
- It is vulnerable under the wormhole attack [18]. Any two malicious participants can collude to steal the transaction fees of intermediate participants since the smart contracts can be triggered by the same secret;
- The offline behavior of a single participant will terminate the protocol. When is offline, the secret s cannot be transmitted in the subsequent transaction path.
3.2. Some Improvements
In this section, we propose some necessary principles to attack the defects presented in Section 3.1. We will give three algorithms in Section 4 based on these principles to design a privacy-preserving multi-party cross-chain transaction protocol.
For defect defect1, we will use the adaptor signature and multi-signature schemes to improve it. The function of the smart contract will be implemented using signature schemes. For defect defect2, different secret values will be used to evade the attack. Inspired by the definitions of atomicity and balanced security in [17], we plan to introduce two principles to optimize defect defect3 of the ideal model.
For every , let .
3.2.1. Principle 1
For , if is taken away, then will obtain enough information to trigger the “contract” and obtain .
This principle guarantees the security of the assets of participants. Furthermore, it achieves a kind of weak atomicity. That is, it ensures the consistency of the participant’s payment and collection. This principle will also make the collusion attacks (including wormhole attacks) invalid in our protocol because the attackers cannot steal a participant’s assets without paying them back.
3.2.2. Principle 2
For , if all previous participants have correctly executed the protocol except , then can still gather enough information to trigger the “contract” and obtain .
Principle 2 indicates that the protocol will not be interrupted by a participant’s offline behavior. In addition, this principle is a tradeoff between the realizability and robustness of the protocol. To handle the problem caused by the offline behavior of users, highly programmable smart contracts are usually needed [35,37]. In addition, the transactions that have been packaged into blocks are irreversible, that is, transaction rollback is not supported. This is also one of the significant differences between the signature-based method and the method based on smart contracts in cross-chain transactions.
We assume that (the starting point of the protocol) and are not included in both principles due to the particularity of their order.
3.3. Design Goals
We present the design goals of our cross-chain transaction protocol.
Unlinkability: A adversary which did not participate in the protocol cannot determine whether the two transaction records on different chains belong to the same cross-chain transaction or not, just through information collision.
Public Verifiability:This property requires that all the parts of our cross-chain transaction protocol can be publicly observed and verified. This implies that our protocol will not affect the normal transaction verification process.
Offline Tolerance:Offline tolerance means that the protocol can continue executing if one of the participants has not completed the protocol steps.
Privacy Preservation:Our protocol is designed to protect the membership privacy of the participants. By only analyzing on-chain information, observers cannot distinguish whether there exists a cross-chain transaction. And no one can obtain the membership information of a cross-chain transaction except the participant.
4. Algorithm Definition
In response to the principles proposed in Section 3.2, we propose three algorithms to implement our protocol, which are the script generation algorithm, adaptor signature algorithm with multi-signature, and pre-adaptor signature algorithm. The first one is a theoretical framework that achieves the goals of both principles mentioned in Section 3.2. The second algorithm extends the usage scenario of the adaptor signature by combining it with the multi-signature algorithm. The last algorithm adds a time-sequential attribute to the adaptor signature.
4.1. Script Generation Algorithm
The script plays a role in building a trusted transfer station between adjacent participants. Based on P2SH technology, the script can be used to specify the identity of the participant, payment condition, or other information. Moreover, the script can also be used to generate the corresponding collection address.
The script generation algorithm realizes both principles mentioned in Section 3.2, and its content is shown in Figure 4. The script for will be used to obtain assets from another participant. is a key aggregation function. CLTV, CS, and CMS are abbreviations of BTC opcodes: OP_CHECKLOCKTIMEVERIFY, OP_CHECKSIG, and OP_CHECKMULTISIG. The <> in each script for could be calculated as , while is the initialization time of the protocol and is the operation time for each participant during different stages. and denote the participant’s secret value and its statement.
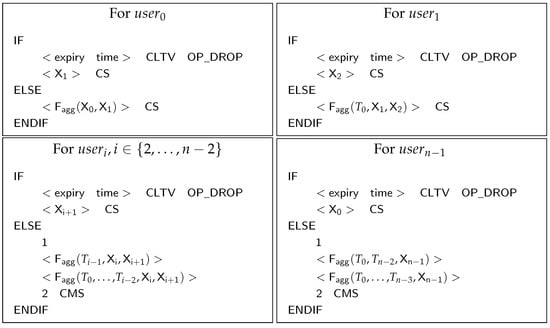
Figure 4.
Script generation algorithm. We mark the redeem condition (expire time) as and the withdraw condition () as .
The algorithm combines the public keys of the participants according to a certain strategy and sets the timeout for each type of script. After the timeout, the participant can sign the transaction and refund the assets. According to the participant sequence, the algorithm divides the participants into four parts, namely, , , , where , and . We will elaborate on the details of the combination of public keys below.
- For , the first one to execute the protocol, the script contains two public keys and . can construct an adaptor signature with to obtain the ability to sign a valid signature. Once the signature is revealed, will obtain as well as reveal its secret value to other participants.
- For , the script contains three public values , , and . can construct an adaptor signature with to obtain the ability to sign a valid signature and reveal later. Since the secret value of is known to all, only needs to negotiate with .
- For , the script contains the combinations of two different types of public values, which are ,, and ,…,,,. Both key combinations correspond to the principles proposed in Section 3.2.
- For , the script contains combinations of two different types of public values, which are , , and ,…,,. The negotiation for an adaptor signature with is not required since the secret value of was leaked early in the protocol.
In summary, the secret value revealed by the participants can be regarded as their pre-vote on subsequent transactions. To achieve this, the secret value will be used as a “special” private key and random number which will be used to construct a multi-signature later.
4.2. Adaptor Signature with Multi-Signature
In Section 2.3, we introduce the adaptor signature algorithm and the multi-signature algorithm. Among them, the adaptor signature algorithm realizes the secret transmission channel by introducing additional addition operations and modifying the parameter in the challenge generation process. The multi-signature algorithm hides the public key list of the participants by submitting an additional multiplication coefficient in the signing and verifying processes and modifying the first parameter in the challenge generation process. The changes of both signature algorithms to the Schnorr signature algorithm are orthogonal, so there is a possibility of combining them.
Here, we give the formal definition of the adaptor signature with multi-signature scheme:
- : It assigns key pairs to every participant which are denoted as (). It randomly selects , with , as the secret value to be revealed. Every participant secretly selects a signature parameter r and publicly shares .
- : It receives all public keys , all signing parameters , the witness of the secret , and a message m as input, and it outputs the public challenge c and the aggregated public key .
- : It receives participant secret key x, a message m, and the public challenge c as input, and it calculates a partial signature as output.
- : It receives the aggregated public key , signer’s public key X, public challenge c, and partial signature , and it outputs 1 if the pre-signature is legitimate and ⊥ otherwise.
- : It receives the partial signatures from all users and aggregates them as .
- : It receives the aggregated partial signature and secret value as input, and it calculates a signature as output.
- : It receives the aggregated partial signature and signature as input, and it calculates the secret value as output.
The execution process of the algorithm is shown in Figure 5. The hash function is used in the commitment phase, is to compute the aggregated key, and is to compute the signature. As mentioned in [47], these hash functions could be constructed from a single one with proper domain separation. In the rest of the paper, we will continue to use these definitions. This algorithm broadens the scope of the application of the adaptor signature scheme. Now, multiple participants can establish a secret transmission channel by only relying on the signature algorithm.

Figure 5.
The combination of adaptor signature and multi-signature schemes.
4.3. Pre-Adaptor Signature Algorithm
In this section, we introduce a novel signature algorithm based on an adaptor signature. Figure 6 shows the detail of the pre-adaptor signature scheme. The public key list L varies according to the situation. It can be regarded as a weaker version of the adaptor signature scheme. The protocol assumes that some secret information, which can turn a pre-adaptor signature into an adaptor signature, will be released with the execution of the protocol.

Figure 6.
Pre-adaptor signature based on multi-signature.
The adaptor signature algorithm has online requirements for participants during the negotiation process. In addition, once the adaptor signature is successfully generated, one participant will be able to construct a valid signature. These features will lead to two contradictions.
Sequential execution of the protocol. Our cross-chain protocol defines a task where a sequence of exchanges takes place at each cryptocurrency. Specifically, the sequence corresponds to the sequential transmission of the secret value. Thus, the adaptor signatures on each payment path cannot be negotiated in the initialization stage of the protocol. Otherwise, any intermediate participant can complete the transaction in advance regardless of the sequence.
The offline tolerance. To ensure the security of assets, participants need to join the negotiation process before letting others take away their assets. However, this requires the intermediate participants to be online during the execution stage of the protocol. If goes offline, the former participant () will face the risk of losing assets whether acts honestly or not.
These two contradictions are also a pair of paradoxes. Therefore, based on the script generation algorithm, we propose the concept of a pre-adaptor signature. It integrates the demand of sequential execution into the adaptor signature algorithm and realizes the dynamic generation of the adaptor signature.
5. Protocol Instantiation
Assume that there are n participants in the protocol. Let the initiator of the protocol be . For each (), they wish to exchange some with the they possess. In addition, j and k refer to the previous and next sequences of i, respectively, where and . In Figure 7, we give an example which shows the interaction steps of when the protocol is running normally. Each time triggers a withdraw condition, the secret value will be leaked due to the feature of adaptor signature. Then, will be able to calculate a full signature to trigger the withdraw condition of the P2SH address where is stored.
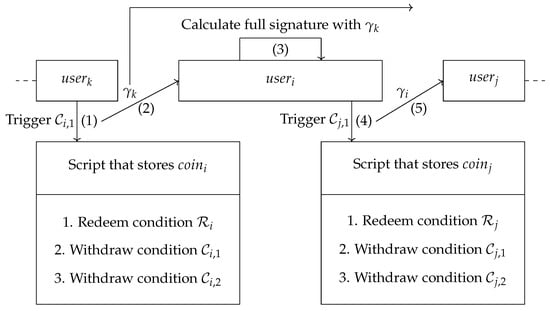
Figure 7.
A running example for during the protocol execution.
Figure 8 shows the detailed protocol workflow. Other parameters are displayed in Table 2. Arrows between the participants represent the execution direction of the protocol. It is worth mentioning that the preparation and construction stages constitute the initialization phase, while the operation stage represents the execution phase.
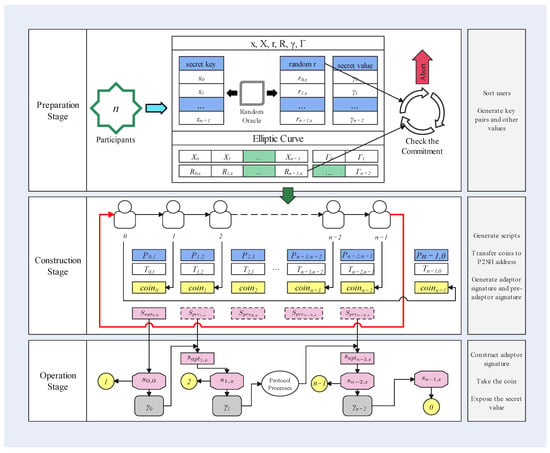
Figure 8.
A detailed workflow of our protocol.

Table 2.
Parameters of our protocol.
Initialization:
For all participants with :
- Randomly select as the private key, and then calculate and broadcast the public key ;
- Generate and according to the script generation algorithm;
- Transfer their assets to the P2SH address which was constructed by and ;
- Create a transaction that transfers the assets from to the private account of , and broadcast it;
- Randomly select the parameter and construct a pre-adaptor signature (and , if necessary) with , and broadcast it.
After the initialization stage, all the participants will obtain the content of , , , and . If all data pass validation, then continue. Otherwise, abort.
Execution:
- 1.
- uses a valid signature to obtain from address corresponding to script ;
- 2.
- Other participants can then calculateNotice that (so as all ) can be publicly calculated as mentioned in Section 2.3.2;
- 3.
- uses a valid signature to obtain from address corresponding to script ;
- 4.
- Other participants can then calculate
- 5.
- For , where :
- (a)
- If no participant has become offline yet:
- i
- If ’s secret value was released, then calculateA valid signature can be used to obtain . Other participants can then calculate
- ii
- If went offline and their secret value was not released, then calculate:A valid signature can be used to obtain . Other users can then calculate:
- (b)
- If a participant has already become offline:
- i
- If ’s secret value was released, then calculate:A valid signature can be used to obtain . Other users can then calculate:
- ii
- If goes offline, the protocol will terminate.
- 6.
- For :
- (a)
- If ’s secret value was released, then calculate a valid signature:to obtain ;
- (b)
- If only went offline and their secret value was not released, then calculate:
- (c)
- If more than one user goes offline, the protocol will terminate.
For different P2SH scripts, it is sometimes necessary for the participants to negotiate and generate two kinds of signatures. For example, while dealing with the script between and (that is, ), both signature and can meet the unlocking conditions of it. It is worth mentioning that does not need to construct an adaptor signature with since they are the last to execute the protocol.
6. Security Analysis
Our schemes are mainly based on adaptor signatures. It is reasonable that the same security bases of adaptor signatures were preserved, including pre-signature correctness, existential unforgeability under chosen message attack for security for adaptor signature (-), pre-signature adaptability, and witness extractability, as illustrated in [48]. In our protocol, we have modified the signature scheme to a certain extent (the so-called pre-adaptor signature scheme). The security definition of the modified signature scheme will be given below.
As mentioned in [48], a valid pre-signature with respect to cannot be completed as a valid signature if and only if the corresponding secret for is unknown and vice versa because it is computationally hard to find a secret under the assumption that the discrete logarithm problem is hard [49]. In addition, if the Schnorr signature scheme is --secure and is a hard relation, then the adaptor signature scheme is secure.
Furthermore, the pre-adaptor signature scheme plays an important role in our protocol. With several additional secret values, it can be composed into a valid adaptor signature and become capable of leaking a secret value via a valid signature. Let be the list of the secret values, which is still unknown, and be the statement of . denotes the pre-adaptor signature scheme.
Lemma 1.
The correctness of a pre-adaptor signature is verifiable under scheme .
Proof.
Assume that , and let , , and . The secret list is and . The public key list is . Let be the secret value that the target adaptor signature aims to release. The public parameters can be calculated:
Then, the goal adaptor signature will be:
For the pre-adaptor signature , it can be completed as , since
The adaptor signature can be constructed with corresponding secret list and valid . Thus, the correctness of can be verified. □
Lemma 2.
The cross-chain protocol we proposed is unlinkable if the multi-signature based on the Schnorr signature is provably secure under the discrete logarithm assumption [47].
Proof.
According to the multi-signature algorithm, the public key needs to be calculated in the form . Without the knowledge of the secret value of a user secret key x, can perfectly hide the public keys that make up the aggregated public key. So, the observers of the cryptocurrencies will not be able to link transactions from different blockchains together. □
Lemma 3.
The cross-chain protocol we proposed achieves public verifiability if the blockchain is publicly verifiable.
Proof.
Due to the decentralized P2P network of blockchain, everyone can join the Bitcoin network freely to verify transactions. In addition, in our protocol, the signatures, as well as the scripts, will be uploaded on Bitcoin, and anyone can easily obtain them and verify that the script can be executed correctly. □
Lemma 4.
The cross-chain protocol we proposed satisfies offline tolerance if participants with adjacent serial numbers will not collude to destroy the protocol and there is no more than one offline participant.
Proof.
In the script generation phase, the rule is set that the locked assets can be redeemed by the owner if timeout occurs. If participants with adjacent serial numbers will not collude, then after every successful execution of the script, the other participants will be able to extract the secret value from the signature. The participant with the corresponding pre-adaptor signature can transfer them by constructing a full signature by collecting the secret value of or . When the second offline participant occurs (the first one was marked as ), the other participants can only collect the secret value of , so the script cannot be executed until the timeout. □
7. Performance Analysis
The implementation of our cross-chain protocol is written in Rustlang, and it relies on the multi-party Schnorr library [50] for signature operations in groups. We implemented the cryptographic operations of the algorithms depicted in Section 4. We instantiated Schnorr over the elliptic curve secp256k1 (the one used in Bitcoin), and the basic adaptor signature algorithm was implemented. Then, we tested the runtimes of these main functionalities without considering the impact of communication. But we gave the size of the communication message. The source code will be available online.
Testbed. We conducted our experiments on a machine with an Intel Xeon Silver, 2.2 GHz, and 32 GB RAM. We consider the Preparation, Construction, and Operation stages as shown in Figure 8. Moreover, key generation and random number selection were executed only once, upon creating a payment link and secret channel, and thus did not affect the other two stages.
Computation and communication. We measured the computation time and communication overhead required by the participants. The experiment was conducted in the scenario of 10 participants. Table 3 shows the consumption of the basic operations in each stage, including the computation time spent generating some necessary objects (e.g., the aggregate public key) and the communication overhead cost from transferring some important information (e.g., the statement of random numbers). The most time-consuming part of the protocol was completed before the operation stage. Figure 9 shows the time cost of different participants. When the protocol runs smoothly (Figure 9a), the time cost increases approximately linearly from to because the participants at the back of the sequence need to calculate the secret information corresponding to all the previous users. If a participant goes offline (as shown in Figure 9b, where goes offline), then a longer public key list is required for to generate a valid adaptor signature. Correspondingly, the latter participants who want to obtain the secret of also need to compute more calculations. Figure 10 shows the communication cost of different participants. Similar to the computation time cost, communication overhead increases approximately linearly as the protocol runs, since later participants need to collect more information broadcast by the earlier participants to calculate the secrets hidden in the signatures.

Table 3.
Computation time and communication costs.
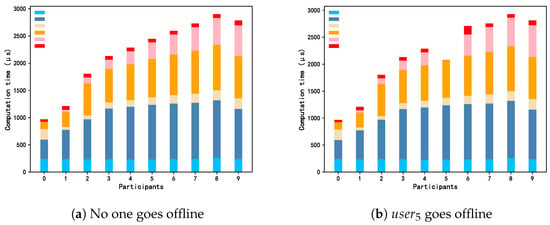
Figure 9.
Computation times of different participants under different situations. The color blocks in the upper left corner of the figures (from blue to red) represent Gen KeyPair, Gen Random Nums, Gen Script, Gen Pre-adaptor Signature, Extract Secret, and Gen Signature respectively.
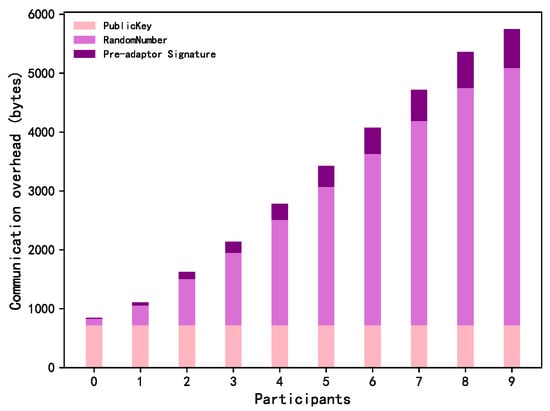
Figure 10.
Communication costs of different users.
8. Conclusions
In this paper, we proposed a privacy-preserving multi-party cross-chain transaction protocol based on adaptor signatures and P2SH scripts. We leveraged the capability of digital signature and the basic scripting language of blockchain to construct a protocol with properties such as unlinkability, public verifiability, offline tolerance, and privacy preservation. We introduced novel cryptographic primitives like pre-adaptor signatures and pre-adaptor signatures to support the protocol design. Furthermore, we provided security analysis to ensure that our proposals satisfied the essential security requirements. The performance analysis shows that the computational and communication overhead of our protocol are acceptable. For future work, supporting more complex transaction topologies is an interesting direction. And the tradeoff between privacy and efficiency can also be further optimized.
Author Contributions
Conceptualization, C.C.; methodology, C.C. and G.Y.; validation, C.C.; formal analysis, Q.C.; investigation, Z.L.; data curation, C.C. and G.Y.; writing—original draft preparation, C.C. and G.Y.; writing—review and editing, C.C. and F.X.; visualization, G.Y.; supervision, Q.C. and J.L.; project administration, Q.C. and J.L.; funding acquisition, Q.C. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key Project of China (Grant No. 2020YFB1005700), the National Natural Science Foundation of China (Grant No. 62261160651, 62172117, 62272118, 62132018).
Data Availability Statement
No data were used to support this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://assets.pubpub.org/d8wct41f/31611263538139.pdf (accessed on 30 October 2023).
- Poon, J.; Dryja, T. The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments. 2016. Available online: https://static1.squarespace.com/static/6148a75532281820459770d1/t/61af971f7ee2b432f1733aee/1638897446181/lightning-network-paper.pdf (accessed on 23 October 2023).
- Corbett, J.C.; Dean, J.; Epstein, M.; Fikes, A.; Frost, C.; Furman, J.J.; Ghemawat, S.; Gubarev, A.; Heiser, C.; Hochschild, P.; et al. Spanner: Google’s globally distributed database. ACM Trans. Comput. Syst. TOCS 2013, 31, 3. [Google Scholar]
- Werner, S.; Perez, D.; Gudgeon, L.; Klages-Mundt, A.; Harz, D.; Knottenbelt, W. Sok: Decentralized finance (defi). In Proceedings of the 4th ACM Conference on Advances in Financial Technologies, Cambridge, MA, USA, 19–21 September 2022; pp. 30–46. [Google Scholar]
- Ren, Y.; Lv, Z.; Xiong, N.N.; Wang, J. HCNCT: A Cross-chain Interaction Scheme for the Blockchain-based Metaverse. ACM Trans. Multimed. Comput. Commun. Appl. 2023. [Google Scholar] [CrossRef]
- Jiang, Z.; Zha, C.; Li, X.; Xu, Z.; Zhang, X.; Yin, H. A Cross-Chain framework for Industry Collaboration and Transaction. In Proceedings of the 2022 IEEE Smartworld, Ubiquitous Intelligence & Computing, Scalable Computing & Communications, Digital Twin, Privacy Computing, Metaverse, Autonomous & Trusted Vehicles (SmartWorld/UIC/ScalCom/DigitalTwin/PriComp/Meta), Haikou, China, 15–18 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2436–2443. [Google Scholar]
- Wang, Y.; Su, Z.; Zhang, N.; Xing, R.; Liu, D.; Luan, T.H.; Shen, X. A survey on metaverse: Fundamentals, security, and privacy. IEEE Commun. Surv. Tutor. 2022, 25, 319–352. [Google Scholar] [CrossRef]
- Herlihy, M. Atomic cross-chain swaps. In Proceedings of the 2018 ACM Symposium on Principles of Distributed Computing, Egham, UK, 23–27 July 2018; pp. 245–254. [Google Scholar]
- Wood, G. Polkadot: Vision for a heterogeneous multi-chain framework. White Pap. 2016, 21, 4662. [Google Scholar]
- Thomas, S.; Schwartz, E. A Protocol for Interledger Payments. 2015. Available online: https://interledger.org/interledger.pdf (accessed on 15 August 2023).
- Buterin, V. Chain Interoperability. 2016. Available online: https://allquantor.at/blockchainbib/pdf/buterin2016chain.pdf (accessed on 16 August 2023).
- Back, A.; Corallo, M.; Dashjr, L.; Friedenbach, M.; Maxwell, G.; Miller, A.; Poelstra, A.; Timón, J.; Wuille, P. Enabling Blockchain Innovations with Pegged Sidechains. 2014. Available online: http://kevinriggen.com/files/sidechains.pdf (accessed on 15 August 2023).
- Jedusor, T.E. Mimblewimble. 2016. Available online: https://docs.beam.mw/Mimblewimble.pdf (accessed on 7 March 2023).
- Deshpande, A.; Herlihy, M. Privacy-preserving cross-chain atomic swaps. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kota Kinabalu, Sabah, Malaysia, 10–14 February 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 540–549. [Google Scholar]
- Hoenisch, P.; del Pino, L.S. Atomic Swaps between Bitcoin and Monero. arXiv 2021, arXiv:2101.12332. [Google Scholar]
- Koutsos, V.; Papadopoulos, D.; Chatzopoulos, D.; Tarkoma, S.; Hui, P. Agora: A privacy-aware data marketplace. In Proceedings of the 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS), Singapore, 29 November–1 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1211–1212. [Google Scholar]
- Thyagarajan, S.A.K.; Malavolta, G. Lockable Signatures for Blockchains: Scriptless Scripts for All Signatures. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021. [Google Scholar]
- Malavolta, G.; Moreno-Sanchez, P.; Schneidewind, C.; Kate, A.; Maffei, M. Anonymous multi-hop locks for blockchain scalability and interoperability. In Proceedings of the 26th Annual Network and Distributed System Security Symposium, NDSS 2019, San Diego, CA, USA, 24–27 February 2019; pp. 1–15. [Google Scholar]
- Tairi, E.; Moreno-Sanchez, P.; Maffei, M. A2l: Anonymous atomic locks for scalability in payment channel hubs. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), Francisco, CA, USA, 24–27 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1834–1851. [Google Scholar]
- Heilman, E.; Alshenibr, L.; Baldimtsi, F.; Scafuro, A.; Goldberg, S. Tumblebit: An untrusted bitcoin-compatible anonymous payment hub. In Proceedings of the Network and Distributed System Security Symposium (NDSS 2017), San Diego, CA, USA, 26 February–1 March 2017; pp. 1–15. [Google Scholar]
- Thyagarajan, S.A.; Malavolta, G.; Moreno-Sanchez, P. Universal atomic swaps: Secure exchange of coins across all blockchains. In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP), Francisco, CA, USA, 22–26 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1299–1316. [Google Scholar]
- Thyagarajan, S.A.K.; Bhat, A.; Malavolta, G.; Döttling, N.; Kate, A.; Schröder, D. Verifiable timed signatures made practical. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 9–13 November 2020; pp. 1733–1750. [Google Scholar]
- Zamyatin, A.; Harz, D.; Lind, J.; Panayiotou, P.; Gervais, A.; Knottenbelt, W. Xclaim: Trustless, interoperable, cryptocurrency-backed assets. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–22 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 193–210. [Google Scholar]
- Liu, Z.; Xiang, Y.; Shi, J.; Gao, P.; Wang, H.; Xiao, X.; Wen, B.; Hu, Y.C. Hyperservice: Interoperability and programmability across heterogeneous blockchains. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 549–566. [Google Scholar]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Newport Beach, CA, USA, 8–11 October 2001; pp. 136–145. [Google Scholar]
- Chen, T.; Li, Z.; Zhu, Y.; Chen, J.; Luo, X.; Lui, J.C.S.; Lin, X.; Zhang, X. Understanding ethereum via graph analysis. ACM Trans. Internet Technol. TOIT 2020, 20, 1–32. [Google Scholar] [CrossRef]
- Yousaf, H.; Kappos, G.; Meiklejohn, S. Tracing transactions across cryptocurrency ledgers. In Proceedings of the 28th {USENIX} Security Symposium ({USENIX} Security 19), Santa Clara, CA, USA, 14–16 August 2019; pp. 837–850. [Google Scholar]
- Kalodner, H.; Möser, M.; Lee, K.; Goldfeder, S.; Plattner, M.; Chator, A.; Narayanan, A. Blocksci: Design and applications of a blockchain analysis platform. In Proceedings of the 29th {USENIX} Security Symposium ({USENIX} Security 20), Berkeley, CA, USA, 12–14 August 2020; pp. 2721–2738. [Google Scholar]
- Bünz, B.; Agrawal, S.; Zamani, M.; Boneh, D. Zether: Towards privacy in a smart contract world. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kota Kinabalu, Sabah, Malaysia, 10–14 February 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 423–443. [Google Scholar]
- Kosba, A.; Miller, A.; Shi, E.; Wen, Z.; Papamanthou, C. Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 839–858. [Google Scholar]
- Bünz, B.; Bootle, J.; Boneh, D.; Poelstra, A.; Wuille, P.; Maxwell, G. Bulletproofs: Short proofs for confidential transactions and more. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–24 May 2018; pp. 315–334. [Google Scholar]
- Pedersen, T.P. Non-interactive and information-theoretic secure verifiable secret sharing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; Springer: Berlin/Heidelberg, Germany, 1991; pp. 129–140. [Google Scholar]
- Kumar, A.; Fischer, C.; Tople, S.; Saxena, P. A traceability analysis of monero’s blockchain. In Proceedings of the European Symposium on Research in Computer Security, Oslo, Norway, 11–15 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 153–173. [Google Scholar]
- Möser, M.; Böhme, R. Anonymous alone? measuring Bitcoin’s second-generation anonymization techniques. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW), Paris, France, 29–30 April 2017; pp. 32–41. [Google Scholar]
- Herlihy, M.; Liskov, B.; Shrira, L. Cross-chain deals and adversarial commerce. VLDB J. 2021, 31, 1291–1309. [Google Scholar] [CrossRef]
- Nolan, T. Alt Chains and Atomic Transfers. 2013. Available online: https://bitcointalk.org/index.php?topic=193281.0 (accessed on 8 September 2023).
- Dziembowski, S.; Eckey, L.; Faust, S. Fairswap: How to fairly exchange digital goods. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 967–984. [Google Scholar]
- Zakhary, V.; Agrawal, D.; El Abbadi, A. Atomic Commitment Across Blockchains. Proc. VLDB Endow. 2020, 13, 1807–2800. [Google Scholar] [CrossRef]
- Xiong, A.; Liu, G.; Zhu, Q.; Jing, A.; Loke, S.W. A notary group-based cross-chain mechanism. Digit. Commun. Netw. 2022, 8, 1059–1067. [Google Scholar] [CrossRef]
- Gugger, J. Bitcoin-Monero Cross-chain Atomic Swap. Cryptol. ePrint Arch. 2020, 2020, 1126. [Google Scholar]
- Zhang, Y.; Hu, S.; Wang, Q.; Qin, B.; Wu, Q.; Shi, W. PXCrypto: A Regulated Privacy-Preserving Cross-Chain Transaction Scheme. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, Copenhagen, Denmark, 10–12 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 170–191. [Google Scholar]
- Chen, L.; Yao, Z.; Si, X.; Zhang, Q. Three-Stage Cross-Chain Protocol Based on Notary Group. Electronics 2023, 12, 2804. [Google Scholar] [CrossRef]
- Okupski, K. Bitcoin developer reference. In Working Paper; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2016; pp. 1–43. [Google Scholar]
- Schnorr, C.P. Efficient signature generation by smart cards. J. Cryptol. 1991, 4, 161–174. [Google Scholar] [CrossRef]
- Aumayr, L.; Ersoy, O.; Erwig, A.; Faust, S.; Hostáková, K.; Maffei, M.; Moreno-Sanchez, P.; Riahi, S. Generalized channels from limited blockchain scripts and adaptor signatures. In Proceedings of the Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 6–10 December 2021; Proceedings, Part II 27. Springer: Berlin/Heidelberg, Germany, 2021; pp. 635–664. [Google Scholar]
- Bellare, M.; Neven, G. Multi-signatures in the plain public-key model and a general forking lemma. In Proceedings of the 13th ACM conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 390–399. [Google Scholar]
- Maxwell, G.; Poelstra, A.; Seurin, Y.; Wuille, P. Simple schnorr multi-signatures with applications to bitcoin. Des. Codes Cryptogr. 2019, 87, 2139–2164. [Google Scholar] [CrossRef]
- Aumayr, L.; Ersoy, O.; Erwig, A.; Faust, S.; Hostáková, K.; Maffei, M.; Moreno-Sanchez, P.; Riahi, S. Generalized Bitcoin-Compatible Channels. IACR Cryptol. ePrint Arch. 2020, 2020, 476. [Google Scholar]
- Kiltz, E.; Masny, D.; Pan, J. Optimal security proofs for signatures from identification schemes. In Proceedings of the Advances in Cryptology–CRYPTO 2016, Santa Barbara, CA, USA, 14–18 August 2016; pp. 33–61. [Google Scholar]
- ZenGo-X. Multi-Party-Schnorr. 2018. Available online: https://github.com/ZenGo-X/multi-party-schnorr (accessed on 2 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
