Abstract
Information security is a fundamental and urgent issue in the digital transformation era. Cryptographic techniques and digital signatures have been applied to protect and authenticate relevant information. However, with the advent of quantum computers and quantum algorithms, classical cryptographic techniques have been in danger of collapsing because quantum computers can solve complex problems in polynomial time. Stemming from that risk, researchers worldwide have stepped up research on post-quantum algorithms to resist attack by quantum computers. In this review paper, we survey studies in recent years on post-quantum cryptography (PQC) and provide statistics on the number and content of publications, including a literature overview, detailed explanations of the most common methods so far, current implementation status, implementation comparisons, and discussion on future work. These studies focused on essential public cryptography techniques and digital signature schemes, and the US National Institute of Standards and Technology (NIST) launched a competition to select the best candidate for the expected standard. Recent studies have practically implemented the public key encryption/key encapsulation mechanism (PKE/KEM) and digital signature schemes on different hardware platforms and applied various optimization measures based on other criteria. Along with the increasing number of scientific publications, the recent trend of PQC research is increasingly evident and is the general trend in the cryptography industry. The movement opens up a promising avenue for researchers in public key cryptography and digital signatures, especially on algorithms selected by NIST.
1. Introduction
The first communication requirement is to ensure transmission quality, evaluated by the bit error rate. In addition, the need for information security for users, ensuring the integrity of information, or the ability to resist attacks to falsify or steal information is also a highly demanding essential requirement. Moreover, the advent of the concept of quantum computers and quantum algorithms, such as Shor’s algorithm [1], threatens to collapse cryptography based on mathematical difficulties. Therefore, researchers have embarked on research and testing of cryptographic algorithms to resist attacks by quantum computers in the future.
A quantum computer is a type of computer that uses the principles of quantum mechanics to perform calculations. Unlike classical computers, which use bits that can be either 0 or 1, quantum computers use quantum bits or qubits, which can be in multiple states simultaneously. This property of qubits allows quantum computers to perform certain types of calculations much faster. For instance, quantum computers can solve specific mathematical problems that are computationally infeasible for classical computers, such as factoring large integers. Quantum computers are still at an experimental stage and are not yet widely available. However, significant progress in recent years has been made in building prototypes and demonstrating their potential capabilities. They can revolutionize many fields, from cryptography to optimization and machine learning. However, there are also significant technical and practical challenges to address before quantum computers perform useful computations at scale.
PQC refers to cryptographic algorithms designed to be secure against attacks by quantum computers. Quantum computers have the potential to break many of the cryptographic protocols that are currently in use, including those that are widely used to secure Internet communications. PQC aims to develop new cryptographic protocols that can resist such attacks. The threat posed by quantum computers arises from their ability to perform specific calculations much faster than classical computers. Specifically, quantum computers can solve specific mathematical problems that are computationally infeasible for classical computers. One example is factoring large integers, the basis for many current cryptographic protocols. Post-quantum cryptography is an active area of research and development, with many different proposals for new cryptographic algorithms evaluated for their security and practicality. The goal is to develop algorithms that can replace existing cryptographic protocols, ensuring the long-term safety of sensitive information. Actually, people need to pay attention to PQC while the large-scale quantum computer is still far from reality. A few reasons can be listed here. (1) Preparation: Developing PQC algorithms allows us to prepare for the future threat of quantum computers. Cryptographic systems are often used to protect data for long periods, so it is essential to start planning for the possibility of quantum-based attacks now. (2) Longevity: PQC algorithms are designed to secure against classical and quantum-based attacks. This means they will remain secure even if classical computing power continues to increase. (3) Adoption: it takes time for cryptographic systems to be developed, tested, and adopted. By starting work on PQC algorithms now, we can ensure that there will be suitable replacements for current cryptographic systems when needed.
The first significant work on PQC started in the late 1990s. At that time, mathematicians and computer scientists realized that quantum computers could break widely used cryptographic systems such as Rivest–Shamir–Adleman (RSA) and elliptic curve cryptography (ECC), which rely on mathematical problems that can be solved efficiently by a quantum computer. The discovery of this threat led to a renewed interest in developing cryptographic algorithms that would resist quantum-based attacks. One of the earliest PQC algorithms proposed was the McEliece cryptosystem. It was introduced in 1978 by Robert McEliece and is based on the theory of error-correcting codes. The McEliece cryptosystem is known for its resistance to quantum-based attacks, but it has yet to see widespread adoption due to its large key sizes. Another approach to PQC is lattice-based cryptography. This involves using lattices, which are mathematical structures that can be used to generate encryption keys. Lattice-based cryptography is believed to be secure against both classical and quantum-based attacks, and it has been the subject of extensive research in recent years. Code-based cryptography is another approach to PQC that relies on the security of error-correcting codes. It has been shown to be resistant to quantum-based attacks, but, like the McEliece cryptosystem, it requires large key sizes.
Hash-based cryptography [1] is a type of PQC based on hash functions, which are mathematical functions that take input data of arbitrary length and produce a fixed-length output. Hash-based cryptography has the advantage of being relatively easy to implement, and it does not require large key sizes. However, there are concerns about the efficiency of hash-based schemes. Multivariate cryptography is another approach to PQC, based on the difficulty of solving systems of multivariate polynomial equations. Multivariate cryptography is known for its small key sizes but it is vulnerable to certain types of attacks. In recent years, there has been significant research and development in PQC. NIST started a public competition in 2016 to develop new PQC standards. The competition attracted more than 80 submissions from researchers worldwide, and the first round of finalists was announced in 2019. The goal of the competition is to identify new cryptographic algorithms that will resist attacks by quantum computers and can be used to secure sensitive information in the future.
Thus, the main algorithms in the PQC family are code-based with fast encryption and decryption capabilities, a low decryption fault rate, but often a very large key size to ensure security, used for the PKE/KEM. Lattice-based algorithms have the advantages of short key and ciphertext sizes, simple implementation, and good performance, although signature sizes are often huge. Hash-based algorithms are well suited to digital signature schemes.
This article conducts an investigation of PQC in the period from its inception to the present time. This article does not focus only on a particular algorithm or a specific application of PQC, like [2,3] or previous surveys. This article summarizes the entire process of selecting the PKE/KEM from the candidates through each round. We re-counted the number of publications in this field over the past 20 years, and found that the research trend on PQC has been increasing very strongly in recent years, which has yet to be reported in any survey mentioned. Then, while the other investigations all focused on a particular scheme or an area of application, we analyzed and reviewed the research results on the selected schemes that are in the competition, as these schemes will be the PQC standards of the future. This survey will help researchers have an overview of PQC up to the present time and see potential research directions in the future. The structure of the article is arranged as follows. Section 2 presents the standardization process of NIST. An overview of PQC algorithms and the theoretical basis of PQC are presented in Section 3. In Section 4, we discuss the actual implementation situation of the schemes. The results are discussed and future research directions are presented in Section 5, and the conclusion is in Section 6.
2. NIST Standardization
2.1. Overview
The study of cryptography began to be carried out very early, starting from ancient times, thousands of years BC. After cryptography had gone through many different stages of development, NIST came up with the idea in the 1970s of choosing a cipher to become a common standard for the country, from which the data encryption standard (DES) algorithm was introduced, with a relatively small key size. After being broken in 1997 because of that drawback, NIST again asked for proposals for new block codes and received 50 submissions. By 2000, the AES algorithm was chosen and is widely used today as a standard for symmetric encryption. However, the advent of quantum computers and quantum cryptographic algorithms has threatened the existence of ciphers based on mathematical difficulty. Therefore, in 2016, NIST continued to call for proposals on post-quantum algorithms to find algorithms that resist the power of quantum computing. Currently, the NIST standardization process is in its fourth round.
2.2. First Round
The first round of NIST’s PQC standardization process began in December 2016 and ended in July 2019. During this period, NIST invited cryptographers and researchers worldwide to submit post-quantum cryptographic algorithms capable of replacing current public-key cryptosystems. NIST received 82 submissions, which were judged on their security, performance, and implementation characteristics. The first round consists of two phases. The first phase includes an initial screening of all submissions to identify those that do not meet the minimum security or functionality requirements. The second stage involves a more detailed evaluation of the remaining proposals. In the second phase, NIST established criteria for evaluating algorithms, including security for classical and quantum computers, flexibility, and ease of implementation. NIST also conducted several rounds of testing and analysis to ensure the algorithms met these criteria. At the end of the first round, NIST selected 26 candidate algorithms for further research and evaluation in the second round [4].
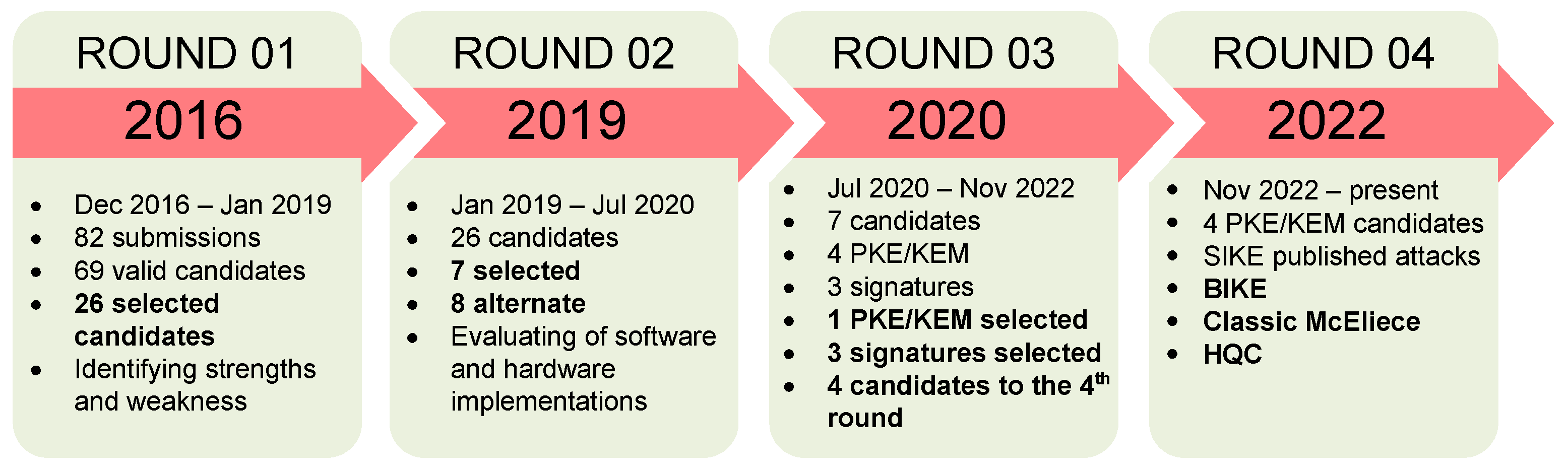
These candidate algorithms included many key encryption, signature, and agreement schemes. Overall, the first round of the NIST PQC standardization process is essential in identifying and assessing the strengths and weaknesses of various post-quantum encryption algorithms. It builds the foundation for further research and development in the field. It paves the way for the eventual selection of standardized PQC algorithms that can resist attacks from classical and conventional quantum computers. The PQC standardization process can be summarized in Figure 1.

Figure 1.
PQC the standardization process of NIST.
2.3. Second Round
The second round of the PQC standardization process began in January 2019 and ended in July 2020. During this period, the focus was on evaluating and analyzing the 26 candidate algorithms selected from the first round. The goal was to determine their security, effectiveness, and suitability for different use cases. The second round involved extensive testing and evaluation of candidate algorithms, including software and hardware implementations. Submissions were evaluated based on their security against different types of attacks, their speed and memory consumption performance, and flexibility in terms of key size and security level. In addition to the technical assessments, the second round included two virtual workshops where applicants presented their algorithms and answered questions from the NIST team and other participants. Based on the second round assessment results, NIST selected seven finalists and eight alternate candidates who advanced to the third round of the standardized process [5]. The algorithms will be further analyzed and tested before NIST selects the final set of standardized PQC algorithms.
2.4. Third Round
The third round started in July 2020 and ran for 18 months, with 15 candidates selected after the end of the second round. In this round, NIST asked the candidates to analyze the proposals and prove they achieved adequate security in experiments and theory. In addition, the candidates also evaluated the performance of the algorithm on a variety of software and hardware platforms. In June 2021, NIST hosted the third PQC Standardization Conference. Candidates and researchers presented their updates and related results at this conference. After 18 months of selection, 7 out of 15 candidate algorithms were selected for the final of the third round, including four PKE/KEM encryption algorithms and three digital signature schemes; eight candidate algorithms were alternatives [6], where necessary, including five PKE/KEM algorithms and three digital signature schemes. Selected candidate algorithms are suitable for most applications and are ready for standardization, and alternative candidate algorithms are potential candidates for the future. Candidate algorithms were updated with minor modifications up until October 2020, before being posted on the NIST website and evaluated publicly.
Finalists include:
- PKE/KEM algorithms: Classic McEliece, CRYSTALS-Kyber, NTRU, Saber;
- Digital signature schemes: CRYSTALS-Dilithium, Falcon, Rainbow.
Alternative candidate algorithms include:
- PKE/KEM algorithms: BIKE, FrodoKEM, HQC, NTRU Prime, SIKE;
- Digital signature schemes: GeMSS, Picnic, .
During the evaluation, the Rainbow digital signature algorithm was broken by Ward Beullens using a classical computer. After the selection process, NIST selected four algorithms to standardize right after the third round, including:
- The PKE/KEM algorithm is CRYSTALS-Kyber;
- Digital signatures are CRYSTALS-Dilithium, Falcon, and , in which Dilithium is the main algorithm.
NIST also selected four PKE/KEM candidate algorithms to continue the selection in the fourth round, including BIKE, Classic McEliece, HQC, and SIKE. These were selected for standardization after the end of the fourth round.
2.5. Fourth Round
In the fourth round, the four candidates selected for the standardization implementation for PKE/KEM had passed the third round. During the selection process, the SIKE candidate algorithm was broken by Wouter Castryck and Thomas Decru using a classical computer. Thus, only three candidates were left for this code-based PKE/KEM round. From 29 November 2022 to 1 December 2022, NIST held its fourth online conference on PQC. At this conference, NIST and researchers discussed candidate algorithms and valuable responses to reach conclusions, and candidates were also able to present their updates to the algorithm. After seven sections, the reports suggested the updates and hardware implementations of the nomination algorithms and their applications. From the positive results of the conference, NIST has the basis for choosing the appropriate algorithm for standardization shortly. To evaluate each scheme, the levels of security are defined by NIST as described in Table 1.

Table 1.
The security levels of NIST.
2.6. Summary
Thus, after four rounds of selection, three rounds have been completed, and the final round is underway; three candidate algorithms are left for PKE/KEM standardization. Only four PKE/KEM algorithms and three digital signature schemes have been selected out of 69 valid candidates in the first round. Out of seven selected candidate algorithms, a PKE/KEM and three digital signature schemes will be standardized, while the remaining three PKE/KEM algorithms will be further selected when choosing a standard algorithm for PKE. The selection process is expected to close in 2023, and NIST have announced that the first standard will be published in 2024.
3. Literature Overview
3.1. Research Status on PQC
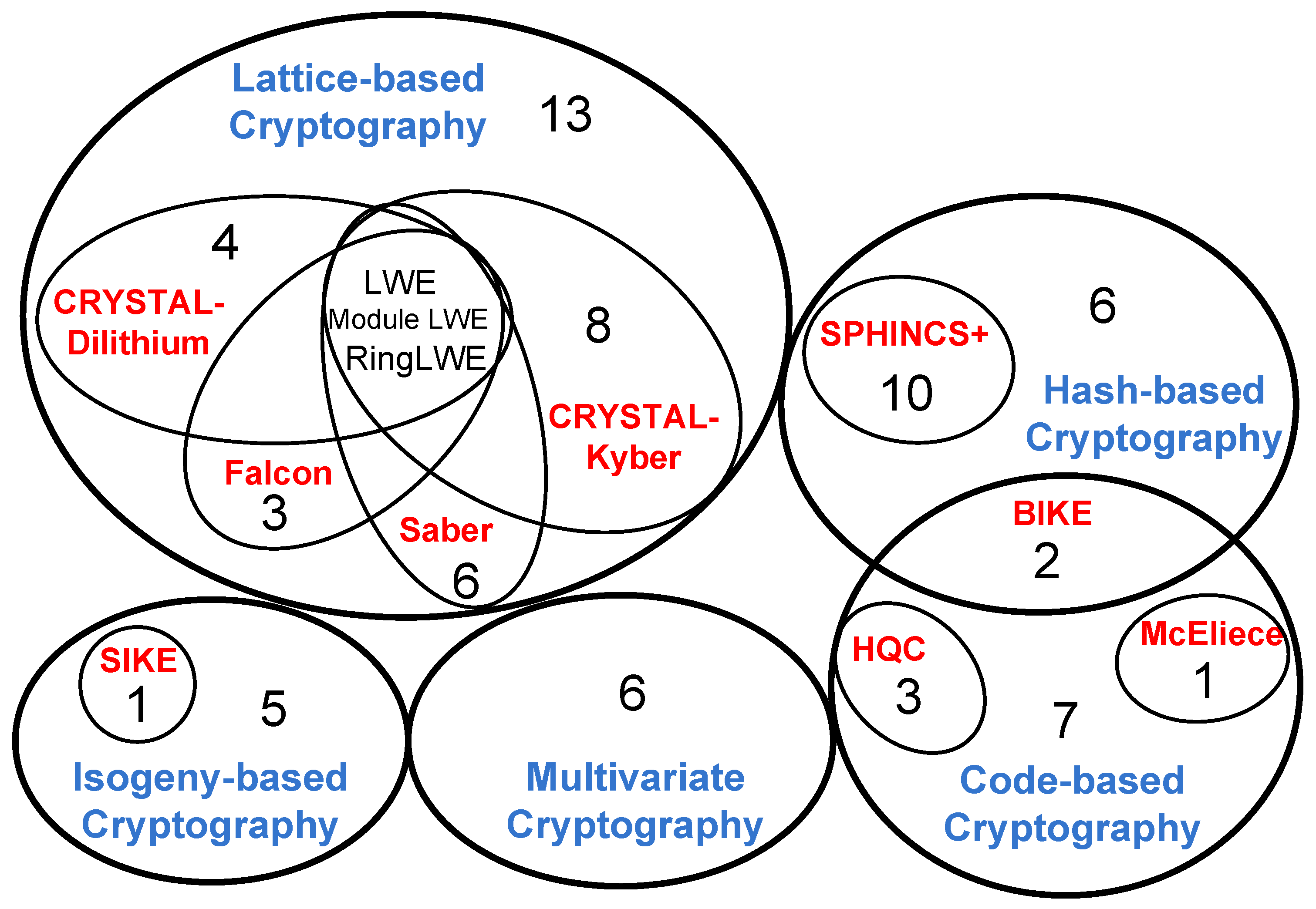
Research on PQC has been increasing in quantity and quality in recent years. Studies focus on candidate algorithms that have been selected through the stages. The Venn diagram in Figure 2 briefly describes the current state of research on PQC, in which the circles with blue words are the basis of encryption, the red words are the names of the algorithms that are candidates, and the numbers in the circles point to the quantity of corresponding references.

Figure 2.
The Venn diagram describes the fields of PQC research related to the references.
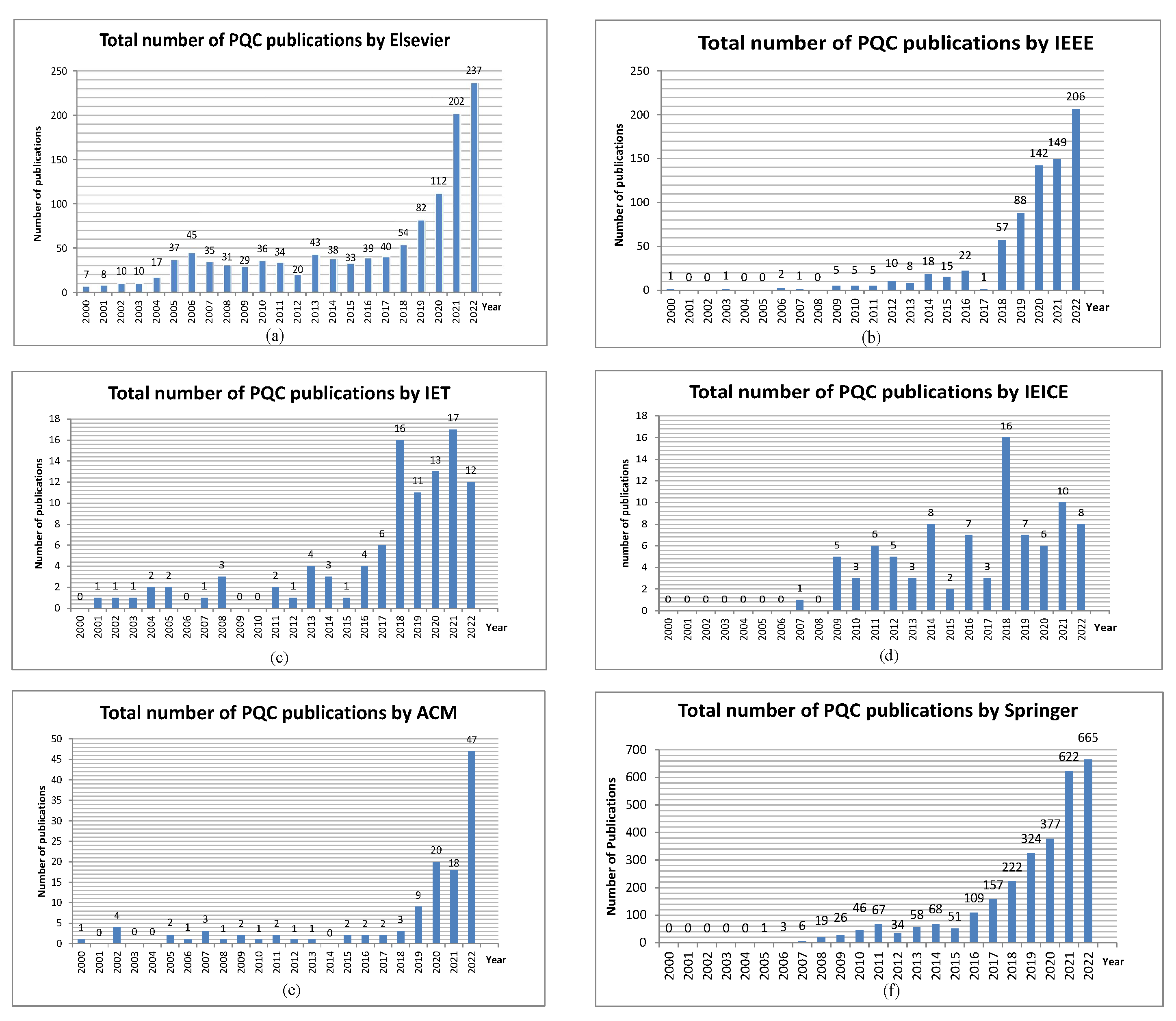
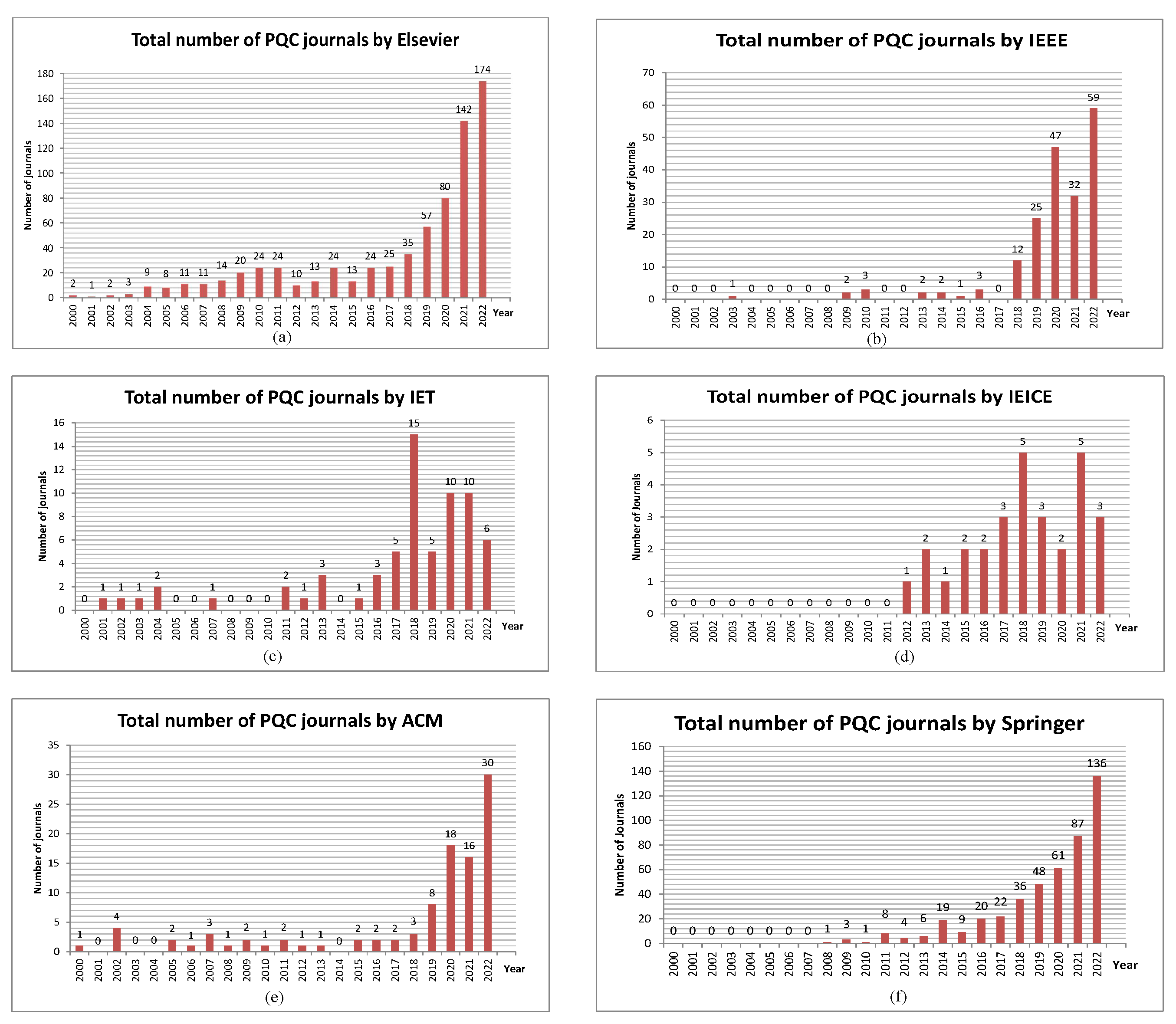
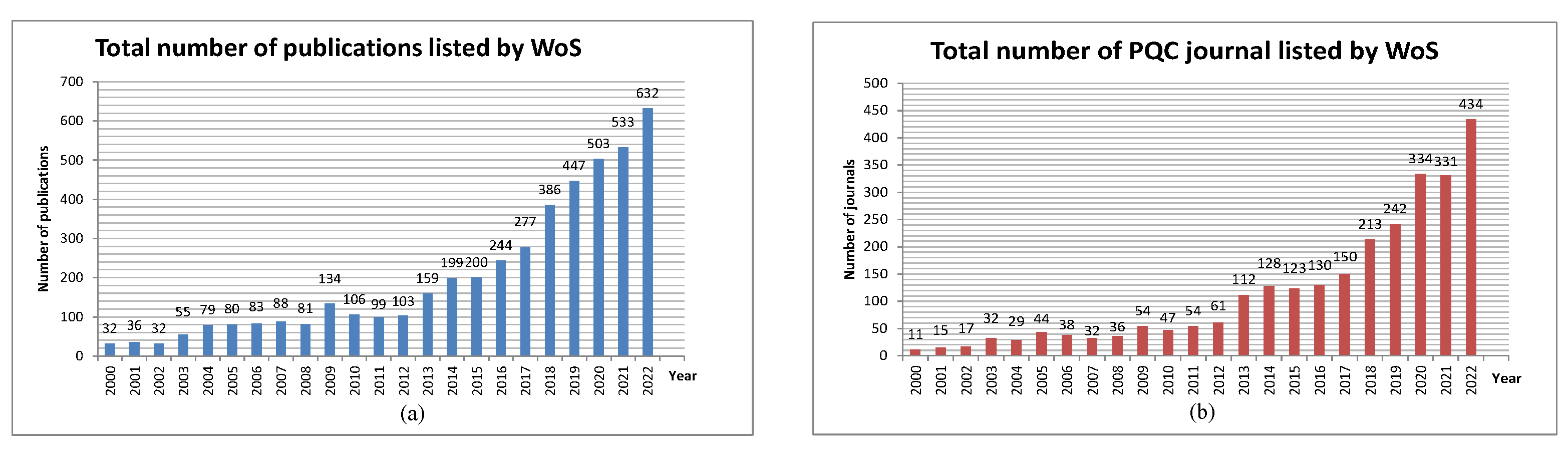
From the above figures, it can be seen that the research on PQC in recent years has increased in level and scope. Studies in other areas related to PQC are also carried out continuously and widely and yield promising results. However, a number of studies still focus on groups of PKE/KEMs, such as BIKE and CRYSTALS-Kyber, or digital signature schemes, such as and Falcon, because these are the candidates selected by NIST to be used as standardized schemes or are candidates in the fourth round. The activities show that the research on PQC, especially the candidates selected by NIST, is the current trend in secure encryption against quantum attacks. This trend is pointed out in Figure 3 and Figure 4. In Figure 3, the vertical axis represents the number of publications published on the subject of PQC, including scientific journals, conferences, books, symposiums, or technical reports. In Figure 4, the vertical axis represents the number of scientific journals on the topic taken into account, and it is easy to understand that these journals are among the publications listed in Figure 3. The horizontal axes for both figures represent the time of the survey in years. We can see how the rapidly increasing number of publications and articles in recent years shows a clear trend in research on PQC. Figure 5 shows statistics for the database from the Web of Science (WoS), which is a very reliable source of statistics for scientific publications, with the figure on the left showing the number of publications by each year. The figure on the right shows the number of journal articles as of the end of 2022. The results show the same general trend as other statistics by publishers.

Figure 3.
The number of scientific publications published from 2000 to 2022, listed in order from (a) Elsevier Library, (b) IEEE Xplore, (c) IET Digital Library, (d) The Institute of Electronic, Information and Communication Engineers (IEICE), (e) ACM Digital Library, and (f) Springer.

Figure 4.
Number of journals published from 2000 to 2022, listed in order from (a–f), as mentioned in Figure 3.

Figure 5.
Number of publications published from 2000 to 2022, listed by Web of Science.
Table 2 demonstrates the number of publications in the last 5 years since 2019 and its proportion compared with the total number of scientific papers in 2000–2023. Similar to the bar chart above, statistics show that the number of publications on PQC in the last 5 years accounts for half of the articles in the nearly 25 years in this field. This further shows that research on PQC is currently trending in cryptography.

Table 2.
Number of scientific publications in last 5 years compared with the total number of papers on PQC.
3.2. The Theoretical Basis of Post-Quantum Cryptography
3.2.1. Lattice-Based Cryptography
Lattice-based encryption is the most popular algorithm for public key generation researched for PQC. A lattice is a network of infinitely many points; each vector is a point, and the set of vectors representing any point in the lattice is called a basis. In lattice-based encryption, messages are presented under vectors, and the public key is a matrix in which the messages are multiplied to generate the ciphertext. There are three lattice-based schemes, including lattice-based encryption (Learning With Errors—LWE, Ring-LWE, NTRU), lattice-based signature schemes (Falcon, Rainbow, Dilithium), and lattice-based key exchanges (Kyber, Frodo). Lattice-based schemes have been studied extensively, and many of them have been proposed and implemented in hardware [7]. Notably, up to three out of the four selected candidates for standardization are lattice-based. The basis of the other candidate algorithms is shown in Table 3.

Table 3.
The theoretical basis of the selected candidate algorithms after the third round.
3.2.2. Hash-Based Cryptography
Hash-based cryptography is a cryptographic algorithm based on the security of a hash function, and some popular algorithms using hash functions, such as MD5 and SHA. In the late 1970s, Merkle invented hash-based digital signatures as Merkle signatures schemes, and then the architecture called Merkle tree was proposed [8]. The essence of the hash function is to convert a variable-length message into a fixed-length block. Hence, the major disadvantage of public keys using hash functions is that the limited number of signatures with a corresponding set of private keys reduces the interest of the public key researchers. However, hash-based digital signatures received more research interest as quantum computers emerged with new attack threats [9].
Hash-based signature schemes combine a one-time signature scheme with a Merkle tree structure. Since a one-time signature scheme key can only securely sign a single message, combining multiple such keys in a larger structure and Merkle tree structure is carried out for this purpose. In this hierarchical data structure, hash functions are used repeatedly to compute the nodes of the tree. Some hash-based signature schemes use multiple layers of the tree, providing faster signing at the cost of larger signatures. In such schemes, only the lowest tree layer is used to sign the messages, while all other trees sign the root values of the lower trees. Some digital signatures, such as XMSS, WOTS, and LMS, are currently being studied, and is a hash-based digital signature that NIST selected for standardization at the end of third round.
3.2.3. Code-Based Cryptography
Code-based cryptography is a secure encryption algorithm based on error-correcting codes, such as McEliece and Niederreiter and related schemes. In the McEliece algorithm, security is based on randomizing the message by adding random errors. Where the private key is a Goppa random binary code [10], the public key is a random generator matrix generated from a random permutation of that code, and the ciphertext is an error-added codeword. Only the recipient who knows the private key can remove those errors. Although this algorithm was proposed very early, security is still guaranteed, even with quantum attacks. Therefore, NIST selected this algorithm as a candidate for the fourth round.
3.2.4. Multivariate Cryptography
Multivariable cryptography is asymmetric encryption based on multivariable polynomials over a finite field. Solving the multivariable polynomial problem is proven to be non-deterministic polynomial-time (NP)-complete, which is why it is suitable for PQC. This algorithm is known to be very efficient when designing cryptanalysis. Multivariable cryptography is used in digital signature generation and is considered to produce the shortest digital signature of the PQC algorithms. Several digital signature schemes, such as Rainbow, TTS, QUARTZ, and QUAD, are based on this method.
3.2.5. Isogeny of Elliptic Curves
Cryptosystems of this type rely on the property of congruent graphs of elliptic curves over finite fields, or super anomalous congruence graphs, to create a secure system. Several specific schemes are based on this, such as the CSIDH key exchange scheme, an alternative quantum attack candidate to the Diffie–Hellman key exchange scheme, and the current Diffie–Hellman elliptic curve is being used, or the SQISign digital signature scheme. In addition, an isogeny-based public key encryption, SIKE, is a PKE/KEM selected after the third round of NIST, and there are some studies on this scheme [11]; however, this PKE/KEM was attacked and removed from the list of fourth-round candidate algorithms.
4. Current Implementation Status
4.1. Public Key Encryption/Key Encapsulation Mechanism
4.1.1. CRYSTALS-Kyber
Kyber is a lattice-based key encapsulation mechanism that achieves chosen ciphertext (IND-CCA) resistance based on the difficulty of the Module Learning with Errors (MLWE) problem. Kyber includes a PKE scheme that achieves CPA security in a standard LWE style, with algebraic objects in the power of TWO cyclotomic rings. During the nomination and editing process, Kyber reached a CCA confidentiality level, making Kyber a potential candidate for key exchange. Kyber uses SHAKE256 for key generation. Up to this point, Kyber had been selected by NIST to implement standardization for PKE/KEM.
In one study [12], the author performed on a TSMC 40nm LP CMOS process chip, and evaluated the results for the CRYSTALS-Kyber algorithm with three parameter sets, Kyber-512, Kyber-768, and Kyber-1024, corresponding to security levels of 1, 3, and 5, respectively. The evaluation of the results is based on the criteria of the number of clock cycles, power consumption, and power, assessing three steps in the protocol, including key generation, encryption, and decryption. The results of this study are compared with previous research carried out on Cortex-M4. The results show that the on-chip execution cycle is reduced by 3 to 16 times, and the energy is reduced by 10 to 20 times, compared with previous studies, depending on the step in the protocol. In two studies [13,14], the authors evaluated and analyzed the functions of Kyber on RISC-V. The parameter sets included three sets with security levels 1, 3, and 5 and evaluation on keypair, encrypt, and decrypt steps. One article [13] proposed the structure of the post-quantum ALU (PQ ALU) set to execute mathematical functions based on the extensions of the instruction set. After that, research was carried out on implementing a basic SoC on a Xilinx ZCU106 board and conducting assessments on resources, power consumption, and performance. The results show that using the PQ ALU structure with an extended instruction set is more efficient in speed and energy efficiency. Ref. [14] proposed a domain-specific processor based on matrix extension. Then, this structure was implemented on TSMC 28 nm technology. The evaluation results show that it is up to 3.5 times more efficient in cycle count than the Cortex-M4, Sapphire, or VPQ implementation. One study [15] also proposed a PQC coprocessor with an RISC-V instruction set architecture (ISA) extension that supports Kyber, Dilithium, and upcoming algorithms. In this research, a RISC-V core and a PQC coprocessor are attached through an interface module inside the PQC coprocessor. The results show that the architect not only accelerates the operation of cryptographic primitives but also supports third-round PQC candidate algorithms of NIST.
Research in [16] introduces a masked hardware implementation of Kyber that is secure against side-channel power analysis. The design uses hiding-only and hiding-plus masking techniques to resist SCA. The method is loop unrolling and pipelining, where unrolled modules process a maximum of eight operations parallelly, and these modules are repeated in pipelining. Test vector leakage assessment (TVLA) is used to evaluate the security of the countermeasure. Ref. [17] designed a high-speed and low-power consumption ASIC that performs encryption for Kyber, and then some measurements in power consumption were taken. The SOTB 65 nm CMOS process implemented the design to produce a 3 mm × 3 mm die. Then, the result was compared with previous works, and was executed on an Intel Core i5-8400 at 2.80 GHz. The comparison shows faster performance and lower energy consumption. One study [18] addressed the importance of security in vehicle-to-vehicle communication to achieve cooperative intelligent transportation systems (C-ITS). Given the difficulties encountered with the elliptic curve cryptography (ECC) standard for constraints, the article surveyed and selected a new encryption standard to replace the old one, and then Kyber and Falcon were researched, based on the advantages of these candidates.
4.1.2. BIKE
The bit-flipping key encapsulation mechanism (BIKE) is a code-based KEM consisting of three similar structures with a decoding algorithm using bit-flipping decoders for QC-MDPC codes . These constructs are intended to disallow key reuse for an IND-CPA level of security. The secret key is a parity check matrix, , for a QC-MDPC code, where r is prime. Each row of has weight , where . The secret key is and the public key is . To encrypt, a message is considered as an error vector, e, of weight t, and then the ciphertext is calculated as . Decryption is performed by multiplying the ciphertext by to produce the syndrome , which is then decoded by a Black-Grey-Flip (BGF) decoder to recover e or message. The security of this scheme lies in designing a bit-flipping decoder with a low enough decoding error rate for adequate protection. With low-security requirements, BIKE can compete with lattice-based mechanisms in key and cipher text size. Structurally, BIKE I and BIKE II are similar to NTRU, and BIKE III is similar to RLWE, followed by similarities in Hamming and Euclidean metrics. The use of BIKE will aim to balance performance for general purposes. The decoder architectures may differ when the security requirements are different. BIKE resists side-channel attacks (SCAs) and achieves CCA security by reducing the failure rate to very low. However, there are few studies evaluating the effectiveness of BIKE.
Research [19] reviewed and analyzed BIKE-related attack techniques, primarily focusing on the challenges for BIKE and McEliece to achieve IND-CCA security. The BIKE algorithm is based on QC-MDPC code, and it uses Fujisaki–Okamoto (FO) CCA transform and a BGF decoder to achieve IND-CCA security. There are three schemes for BIKE, namely BIKE-1, BIKE-2, and BIKE-3, but, according to NIST, it is mainly based on BIKE-2. The study analyzed two solutions to combat reaction attacks. The solutions are: (1) generating a new public–private key pair for each session to protect against key regeneration attack, thus requiring only IND-CPA, but this alternative leads to a large latency; and (2) reuse of the public-private key pair in asynchronous communication, thus requiring tight decryption, and this solution can be resistant to key regeneration attack if used enough times small. As for the SCA attack, BIKE uses a fixed-time solution or a fixed number of iterations for different code segments so that a third person cannot determine the decryption process when it is attacked. The failure rate of decryption determines the security of BIKE, and many studies have shown that some codes have a negative effect on the decryption failure rate (DFR), which is called a weak key. One paper [20] shows a deep investigation into the negative effect of a weak key on the DFR, which the security of BIKE is based on. A private key is considered weak if decryption using the corresponding public key results in a greater failure rate of decryption than is allowed. The author demonstrated that weak keys have a negative impact on the security of BIKE and identified three types of weak keys. To evaluate the effect of the issue on performance, BIKE simulated a specific BIKE scheme using MatLab and evaluated type 1 weak keys. Then, the author proposed a key-check algorithm to generate non-weak private keys towards the IND-CCA security level.
4.1.3. Classic McEliece
Classic McEliece is a code-based KEM with an IND-CAA2 security level. McEliece has been upgraded for greater efficiency and better security by applying several improvements. Classic Eliece has a substantial public key size, making it challenging to apply to typical applications, but the ciphertext is the smallest of the KEMs. Goopa code McEliece is a structure that has been published for many years and still ensures high security. The encryption process is performed simply as the result of multiplication between the private key, a random string, and the public key, the generation matrix G, a random permutation of the codeword. McEliece’s security is based on the difficulty of decoding the codeword of a linear cipher subjected to random errors.
Since the encryption and decryption algorithms used in code-based cryptography, including McEliece, are based on arithmetic algorithms, one [10] study suggested changes in the ISA of RISC-V to make the execution of mathematical expressions during encryption and decryption faster and more efficient. The K extension has cryptographic support but only supports specific hardware or algorithms, and it does not keep performing PQC encryption on non-binary fields. With an extension called Zbc, a hardware implementation was carried out on the RISC-V SweRV-EL2 v1.3 core using Verilator v4.032. Evaluations were then performed to evaluate the computational efficiency based on the clock cycles used for encoding and decoding and the number of resources required by deploying on the Nexys A7 FPGA board. The results show that improving ISA in the direction of optimizing the computation process effectively reduces the number of clock cycles required and the requirements on hardware resources. The improvement of hardware for arithmetic calculations can bring significant effects when applied to code-based cryptography because this method is mainly based on arithmetic calculations.
One study [19] also deals with the analysis of variants of McEliece cryptosystems, which emphasizes that McEliece’s disadvantage is the key size, because the key size of McEliece is often very large. One proposal for a simple variant of the McEliece scheme is to use a low-density parity-check (LDPC) encryption algorithm that allows iterative decoding, and the study proposes the quasi-cyclic moderate-density parity-check (QC-MDPC) algorithm and the decoding using the bit-flipping algorithm. The article evaluates the effectiveness of the decoding algorithm through the DFR for the IND-CCA2 security goal. The authors proposed three solutions to improve DFR and evaluated the effectiveness of those solutions according to different types of attacks. These studies show that enhancing the capabilities of code-based cryptosystems should focus on improving the hardware’s computing power and paying attention to the kinds of attacks that can affect the algorithm’s security, for example, the DFR.
4.1.4. HQC
Hamming quasi-cyclic (HQC) is a code-based PKE. The difficulty of the algorithm is based on the decision problem in quasi-cyclic decoding. This algorithm is geared towards the IND-CCA2 security level by using FO transformation. In the current phase, the proposed team has upgraded the code to improve its security further. The HQC PKE scheme consists of the same three steps as other schemes, including: (1) key generation using a random vector, h, and a codeword vector that combines from a random error vector, thereby generating a public key; (2) encryption using a combination of Reed–Muller and Reed–Solomon codes, and then combined with the recipient’s public key to create a ciphertext; and (3) decrypt execution using its private key to decrypt, and decrypt in reverse order. Elements in vectors can be considered as polynomials in . The secret key is a randomly sampled pair , the public key is the pair , where h is randomly sampled, and h is used to construct the generator matrix, . To encrypt a message, m, the sender samples the polynomials randomly of appropriate weights, and then the ciphertext is calculated by . Then, the receiver decrypts the ciphertext using the decoding algorithm to decode . The HQC KEM scheme is also implemented through three steps: (1) generate the same key as PKE; (2) encapsulation of the secret value encrypted with the public key is then sent; and (3) decapsulation to regenerate the secret value after one or several decryptions.
In one study, Ref. [21] conducted HQC PKE/KEM implementation on the Artix 7 board and then evaluated the results of the schema. The hash algorithm in this implementation uses SHAKE256. The results of the evaluation are two variants of HQC, including balanced and high-speed with a single clock (SC) domain and balanced and high-speed with a dual clock (DC) domain. The results show that the time for the phases in the schema is reduced, or the execution time is faster than the previously published results. In addition, the paper also compares with other candidate algorithms in the fourth round, focusing on hardware design for the lowest level of security, giving equivalent or better results in terms of the execution time of phases in the process diagram. Research [22] introduced optimized high-level synthesis (HLS) and software (SW) implementation of HQC-128, which target level 1 security. The authors detailed the design flow methodology and HLS implementation, then compared and synthesized. After the results were available, the article, in turn, compared the results achieved with the implementation results on the software, with the RTL implementation, and compared the results with other state-of-art implementations. Thus, the article has come up with a feasible plan for determining and evaluating the bottleneck of the algorithm to serve the hardware optimization process in the future, which is a fairly simple and quick method when working with this algorithm.
In one study [23], an HW/SW co-design implementation of HQC in FPGA and ASIC was proposed. The software and hardware were optimized for designs and solutions for the application of HQC for IoT devices. The design architecture’s main idea was to include a RISC-V core that supports the RV32IC instruction set and an HQC accelerator. This design was then implemented on 22 nm FD-SOI technology and achieved an IP core 0.12 mm2 ASIC with a maximum frequency of 700 MHz, and then the study used specialized tools to measure and verify the results. This design was also implemented on the Artix 7 FPGA and compared with previous results. The results show that this design performs similarly to the state-of-art hardware implementation but requires fewer resources, consumes less energy, and shortens the computation time, proving this design has great potential for IoT applications.
4.2. Digital Signatures Schemes
4.2.1. CRYSTALS-Dilithium
CRYSTALS-Dilithium is a lattice-based digital signature scheme built using the Fiat–Shamir heuristic [24]. The confidentiality of this scheme is based on the difficulty of the MLWE problem and the module short integer solution problem (MSIS). In terms of key and signature size, and efficiency in generation, signing, and authentication, Dilithium offers a very balanced performance. In the second round of NIST, Dilithium added features and implemented the AES algorithm. New research on security on the quantum random oracle model (QROM) was also performed to demonstrate the effectiveness of hardware deployment. This scheme uses the ring , where q is the prime number . With as a matrix, are error vectors over , is the secret key, and the public key is . The scheme starts with the prover computing a vector, W, from and sending it to a verifier. The verifier responds with a random polynomial, , and, after that, the prover responds with a vector . Finally, the verifier accepts if . Several works have implemented the Dilithium digital signature scheme on FPGA, ASIC, and RISC-V platforms. In [12], Dilithium is implemented on an ASIC platform, and the results are compared with previous studies. In addition to other schemes, the paper has implemented Dilithium digital signatures schemes with incremental security levels: Dilithium-I, Dilithium-II, Dilithium-III, and Dilithium-IV, respectively. The evaluation parameters are the number of cycles, power, and energy. Measurement results show that, in all three phases of digital signature schemes, namely keyGen, sign, and verify, this design gives many times better results than the performance on the Cortex-M4 core.
In [13], the authors also implemented this digital signature scheme on RISC-V by changing the ISA and then implementing it on the Xilinx ZCU106 board. The results of synthesis and evaluation on complexity, computation time, and energy show that the proposed solution accelerates 65% of the computational functions of Dilithium, compared with the implementation of FPGA. This acceleration is carried out directly on the RISC-V core through new instructions. The Dilithium scheme is implemented in [14] with dual-core architecture (Rocket core and crypto core) on TSMC 28nm technology, and gives better results than 3.3× in cycles. In addition, the authors also deployed the NTT core on the Artix 7 platform to evaluate previous results. In comparison, this design takes up more resources on the FPGA but reduces the number of cycles many times. Moreover, this design includes Kyber and Dilithium, while previous studies only have one or two, either a PKE/KEM or digital signature. If compared based on the area × cycle ratio, this design proved quite effective because it achieved a lower ratio than the previous designs.
4.2.2.
is a hash-based stateless digital signature scheme. The security of this scheme is based on the safety of the hash function. has a rather large design, is relatively slow, and has the most significant signature size of all the NIST candidates. With security level 1, the shortest signature of [6] is also four times the size of Dilithium and requires a thousand times more computation. In return, the public key of is the shortest. Implementing on hardware requires a lot of different parameter sets; judging the quality of based on attaching it to existing systems using RSA or ECDSA signatures does not give good results, so newer assessments are needed. was selected for standardization after the third round of NIST. Research [25] proposes an accelerated solution for digital signature schemes, including , using the TLS Crypto-processor architecture. This architecture includes a RISC-V core and an encryption accelerator. This acceleration is performed based on parallel ALUs, and then schemes are implemented in software on the RISC-V and the accelerator. The cycles and power consumption results show that the hardware accelerator provides a seven-fold improvement over the software on RISC-V, and a one-order improvement in power consumption, compared with Cortex-M4 implementation. Thus, this structure will help to improve speed and energy efficiency, not only with but also with other PQC schemes.
One study [26] introduces a parallelization architecture for ( is the pre-upgrade version of ). With this architecture, we can deploy different multi-core platforms. The design has been implemented on Intel Xeon CPUs and NVIDIA GPUs, and evaluates the results based on two criteria: throughput and latency. The results show that this parallelized design is efficient in both throughput and latency and is scalable across multiple CPUs and GPUs. Research [27] proposed four scheme architectures for the Haraka algorithm for , from Case I to Case IV. The architectures were then synthesized on TSMC 28nm CMOS technology. Several optimization measures were applied to balance throughput and hardware efficiency during design. Combined results show that Case IV is up to 7.79 times faster than the Cortex-A72 implementation, and gives the best performance efficiency. This result can be used as the state-of-art implementation of Haraka.
One study [28] implemented a – digital signature scheme on Xilinx Artix-7 and Kintex-7 FPGA. The analysis results were analyzed on many schemes corresponding to different levels of security, giving us data for future studies. Then, the design was examined for fault attack resistance, which was very vulnerable to this type of attack. The countermeasure to protect the schemes against fault attacks is to duplicate the core and compare the output, which can effectively resist this type of attack. For the supply-voltage glitch attack, just delaying one core in a dual-core architecture can be countered because the probability of the same bit being flipped at different times is very low. The analysis in the [29] study also presented a risk for hardware implementations, with the case study ChaCha on . Similarly, another study [30] introduces an area-efficient design architecture on simulation and implementation on Xilinx XZU3EG FPGA. The analysis results are compared with a software implementation on a high-performance computer CPU, and the comparison results show that the design of the FPGA is slower but uses fewer resources and very little memory. This result shows the potential for deployments that do not require speed and are constrained by design resources, such as IoT applications.
4.2.3. Falcon
Falcon is a lattice-based digital signature scheme that follows a “hash and sign” model, with security based on the difficulty of the short integer solution problem on number theory research unit (NTRU) lattices. Falcon has more hardware implementation complexity than Dilithium because it requires a data tree structure and other maths. However, Falcon requires the smallest bandwidth among the participating candidates. Although key generation is slower than Dilithium, Falcon is more efficient in signing and verifying. This scheme is also easy to incorporate into existing protocols and performs well. One study [31] introduced a cryptographic processor architecture with scheduling functions, hybrid processing element arrays (HPEAs), and parallel processing flows. This architecture is implemented on a 28nm processor, allowing operation at 500 MHz, 0.9 V, achieving 232× in throughput and 3.9× in power efficiency, compared with published results. Other research [18] tried to find suitable post-quantum schemes, and, through the survey results, it was found that the Falcon schema achieves many of the set criteria, such as the number of operations per second threshold (required 2000) and the key size. Therefore, Falcon is a potential digital signature scheme standardization research object, especially for C-ITS applications.
5. Discussion and Future Work
Up to now, theoretical studies of PQC are still being upgraded. The candidates selected in the fourth round of NIST continue to update their works through the results of the conference and the public comments of scientists worldwide. Through the survey results, many theoretical and practical studies focus on lattice-based and code-based schemes because most selected candidate algorithms belong to these two groups. Regarding hash-based cryptography, most of the research focuses on the digital signature scheme, as it is the only candidate in the group that uses the selected hash function. For hardware implementation studies, many schemes have been applied to PQC research. Algorithms with key size, security, or other configuration parameters are applied in each scheme. Because multiplication is performed in many algorithms, many studies focus on improving and optimizing the structure of multipliers on different platforms [32,33,34]. Along with research on accelerators for algorithms, this direction is also interesting, and deployed by many researchers. ASIC is also a potential platform for PQC research [35], but the difficulty with this platform is that achieving results requires actual circuits and modern measuring facilities. However, the results will be clear and convincing if this method succeeds.
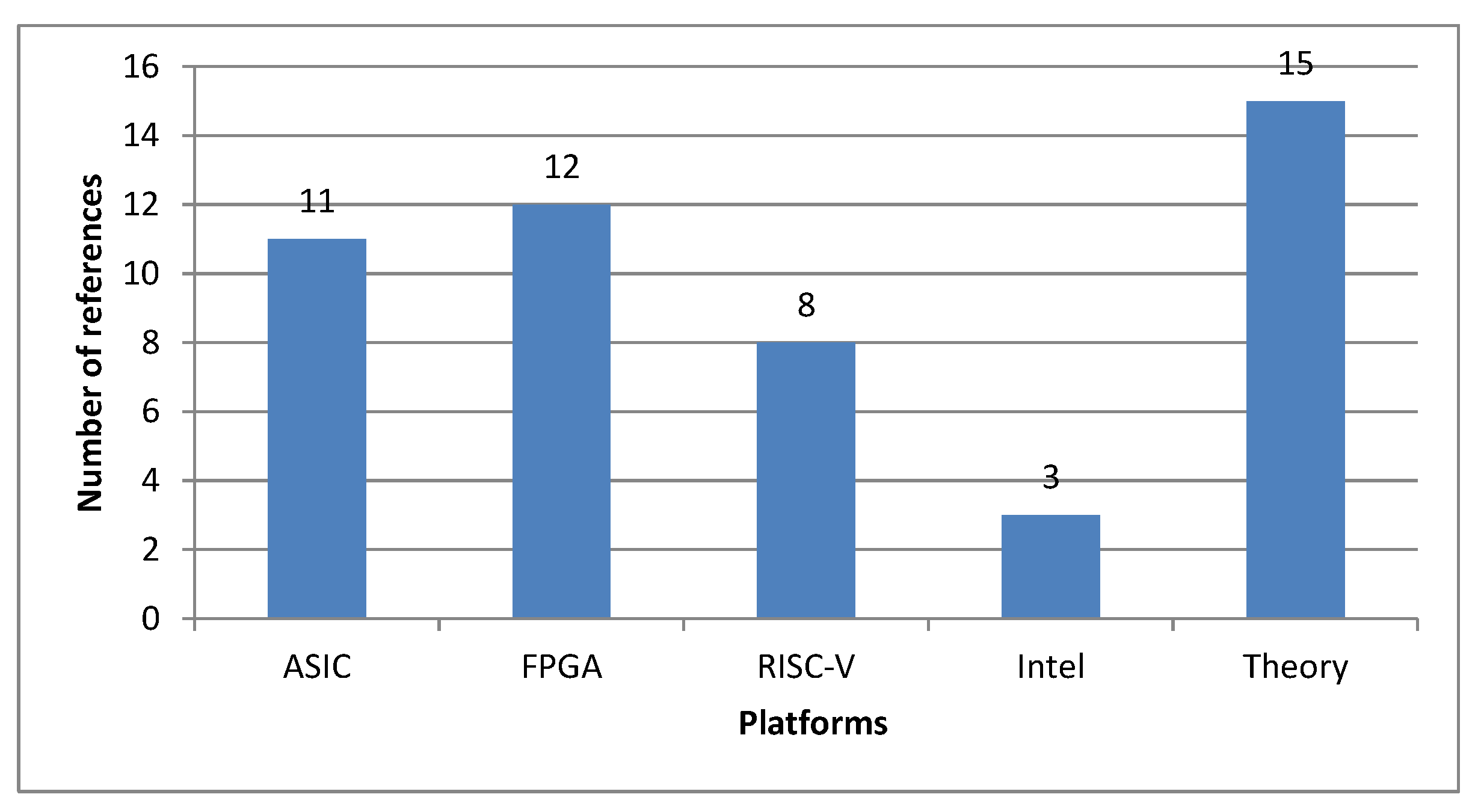
From there, evaluation and comparison with published studies are made. Some candidate algorithms are highly implemented, like Kyber, Dilithium, and . Other algorithms are also studied and executed, but in more modest numbers. Therefore, these are also areas that need further investigation and research. Execution platforms are also very diverse but mainly focus on two platforms, RISC-V and FPGA. The reason is that, for RISC-V, which has a flexible structure, the instruction set architecture can be customized and directed toward solving specific problems, especially complex mathematical operations. For FPGAs, the architecture is open and accessible, and the tools are diverse, and they can execute many different schemes, and achieve results at the synthesis level quickly, thereby efficiently evaluating the algorithm’s effectiveness [36]. It is easy to verify the effectiveness of the improved solutions. In addition, FPGA is also a very convenient means for testing RISC-V configurations in PQC research. Figure 6 shows the platforms used for the design, with the number of references representing the number of publications used in this survey. In addition, some constraints in resources [37], computation time, and memory or energy efficiency, such as IoT devices, show that optimizing cryptoprocessors [38,39,40], specialized applications, drones, for instance [41], or communication systems [42,43] are also possible research directions. Another method to improve the hardware structure to be more suitable for the PQC algorithm is to modify the instruction set architecture to suit each algorithm [44,45].

Figure 6.
Number of references implemented on different platforms.
6. Conclusions
The article has surveyed the number of studies on PQC over the past 20 years and focused on publications in the last five years. Statistical results on the number of publications from reputable sources and the percentage of articles in recent years show that PQC is increasingly becoming a research trend in security encryption. The report also summarizes the process of selecting PQC candidate algorithms for the standardization of PKE/KEM and digital signature schemes in the fourth round. From the fact that these candidates have been selected, the article summarizes recent studies on PQC, drawing out the aspects that cybersecurity developers and hardware developers focus on. From the statistics, the paper has suggested several research directions that can be focused on, thereby showing that the field of PQC still has much potential as a promising avenue for the research process of cryptographic encryption, especially when the end of the NIST’s competition is expected later this year.
Author Contributions
Conceptualization, T.-H.T.; methodology, V.-P.H.; investigation, D.-T.D.; original draft preparation, D.-T.D.; review and editing, D.-T.D. and T.-T.H.; visualization, T.-T.H.; supervision, C.-K.P. and T.-T.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Institute of Information and Communications Technology (NICT), Japan.
Data Availability Statement
The data is collected from the sources: Elsevier’s Library, IEEE Xplore, IET Digital Library, The Institute of Electronic, Information and Communication Engineers (IEICE), ACM Digital Library, Springer and Web of Science (WoS).
Acknowledgments
The ASEAN IVO (http://www.nict.go.jp/en/asean_ivo/index.html (accessed on 1 August 2023)) project, “Artificial Intelligence Powered Comprehensive Cyber-Security for Smart Healthcare Systems (AIPOSH)”, was involved in the production of the contents of this publication and financially supported by NICT (http://www.nict.go.jp/en/index.html (accessed on 1 August 2023)).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. J. ACM 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Karakaya, A.; Ulu, A. A Review on Latest Developments in Post-quantum Based Secure Blockchain Systems. In Proceedings of the 2023 11th International Symposium on Digital Forensics and Security (ISDFS), Chattanooga, TN, USA, 11–12 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Iqbal, S.S.; Zafar, A. A Survey on Post Quantum Cryptosystems: Concept, Attacks, and Challenges in IoT Devices. In Proceedings of the 2023 10th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 15–17 March 2023; pp. 460–465. [Google Scholar]
- Alagic, G.; Alperin-Sheriff, J.; Apon, D.; Cooper, D.; Dang, Q.; Liu, Y.-K.; Miller, C.; Moody, D.; Peralta, R.; Perlner, R.; et al. Status Report on the First Round of the NIST Post-Quantum Cryptography Standardization Process; Technical Report; National Institute of Standards and Technolog: Gaithersburg, MD, USA, 2019. [Google Scholar] [CrossRef]
- Moody, D.; Alagic, G.; Apon, D.C.; Cooper, D.A.; Dang, Q.H.; Kelsey, J.M.; Liu, Y.-K.; Miller, C.A.; Peralta, R.C.; Perlner, R.A.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process; Technical Report; National Institute of Standards and Technolog: Gaithersburg, MD, USA, 2020. [Google Scholar] [CrossRef]
- Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Liu, Y.-K.; Miller, C.; Moody, D.; et al. Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process; Technical Report; National Institute of Standards and Technolog: Gaithersburg, MD, USA, 2022. [Google Scholar] [CrossRef]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-quantum Lattice-based Cryptography Implementations. ACM Comput. Surv. 2019, 51, 1–41. [Google Scholar] [CrossRef]
- Merkle, R.C. Secrecy, Authentication, and Public Key Systems; Technical Report; Stanford University: Stanford, CA, USA, 1979. [Google Scholar]
- Potii, O.; Gorbenko, Y.; Isirova, K. Post Quantum Hash-based Digital Signatures Comparative Analysis. Features of Their Implementation and Using in Public Key Infrastructure. In Proceedings of the 2017 4th International Scientific-Practical Conference Problems of Infocommunications. Science and Technology (PIC S&T), Kharkov, Ukraine, 10–13 October 2017; pp. 105–109. [Google Scholar] [CrossRef]
- Kuo, Y.-M.; -Herrero, F.G.; Ruano, O.; Maestro, J.A. RISC-V Galois Field ISA Extension for Non-binary Error-correction Codes and Classical and Post-quantum Cryptography. IEEE Trans. Comput. 2022, 72, 682–692. [Google Scholar] [CrossRef]
- Elkhatib, R.; Koziel, B.; Azarderakhsh, R.; Kermani, M.M. Accelerated RISC-V for Post-quantum SIKE. IEEE Trans. Circ. Syst. I Regul. Pap. (TCAS-I) 2022, 69, 2490–2501. [Google Scholar] [CrossRef]
- Banerjee, U.; Ukyab, T.S.; Chandrakasan, A.P. Sapphire: A Configurable Crypto-processor for Post-quantum Lattice-based Protocols. IACR Trans. Crypto. Hardw. Embed. Syst. 2019, 2019, 17–61. [Google Scholar] [CrossRef]
- Nannipieri, P.; Matteo, S.D.; Zulberti, L.; Albicocchi, F.; Saponara, S.; Fanucci, L. A RISC-V Post Quantum Cryptography Instruction Set Extension for Number Theoretic Transform to Speed-Up CRYSTALS Algorithms. IEEE Access 2021, 9, 150798–150808. [Google Scholar] [CrossRef]
- Zhao, Y.; Xie, R.; Xin, G.; Han, J. A High-performance Domain-specific Processor with Matrix Extension of RISC-V for Module-LWE Applications. IEEE Trans. Circ. Syst. I Regul. Pap. (TCAS-I) 2022, 69, 2871–2884. [Google Scholar] [CrossRef]
- Lee, J.; Kim, W.; Kim, S.; Kim, J.-H. Post-quantum Cryptography Coprocessor for RISC-V CPU Core. In Proceedings of the 2022 International Conference on Electronics, Information, and Communication (ICEIC), Jeju, Republic of Korea, 6–9 February 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Kamucheka, T.; Nelson, A.; Andrews, D.; Huang, M. A Masked Pure-hardware Implementation of Kyber Cryptographic Algorithm. In Proceedings of the 2022 International Conference on Field-Programmable Technology (ICFPT), Hong Kong, China, 5–9 December 2022. [Google Scholar] [CrossRef]
- Shimada, T.; Ikeda, M. High-speed and Energy-efficient Crypto-processor for Post-quantum Cryptography CRYSTALS-Kyber. In Proceedings of the 2022 IEEE Asian Solid-State Circuits Conference (A-SSCC), Taipei, Taiwan, 6–9 November 2022; pp. 12–14. [Google Scholar] [CrossRef]
- Lonc, B.; Aubry, A.; Bakhti, H.; Christofi, M.; Mehrez, H.A. Feasibility and Benchmarking of Post-quantum Cryptography in the Cooperative ITS Ecosystem. In Proceedings of the 2023 IEEE Vehicular Networking Conference (VNC), Istanbul, Turkiye, 26–28 April 2023; pp. 215–222. [Google Scholar] [CrossRef]
- Nosouhi, M.R.; Shah, S.W.A.; Pan, L.; Doss, R. Bit Flipping Key Encapsulation for the Post-quantum Era. IEEE Access 2023, 11, 56181–56195. [Google Scholar] [CrossRef]
- Nosouhi, M.R.; Shah, S.W.; Pan, L.; Zolotavkin, Y.; Nanda, A.; Gauravaram, P.; Doss, R. Weak-key Analysis for BIKE Post-quantum Key Encapsulation Mechanism. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2160–2174. [Google Scholar] [CrossRef]
- Deshpande, S.; Xu, C.; Nawan, M.; Nawaz, K.; Szefer, J. Fast and Efficient Hardware Implementation of HQC; Cryptology ePrint Archive, Paper 2022/1183; 2022; Available online: https://eprint.iacr.org/2022/1183 (accessed on 1 August 2023).
- Melchor, C.A.; Deneuville, J.-C.; Dion, A.; Howe, J.; Malmain, R.; Migliore, V.; Nawan, M.; Nawaz, K. Towards Automating Cryptographic Hardware Implementations: A Case Study of HQC; Cryptology ePrint Archive, Paper 2022/1425; 2022; Available online: https://eprint.iacr.org/2022/1425 (accessed on 1 August 2023).
- Schöffel, M.; Feldmann, J.; Wehn, N. Code-Based Cryptography in IoT: A HW/SW Co-Design of HQC. arXiv 2023, arXiv:2301.04888. [Google Scholar]
- Xu, G.; Mao, J.; Sakk, E.; Wang, S.P. An Overview of Quantum-safe Approaches: Quantum Key Distribution and Post-quantum Cryptography. In Proceedings of the 2023 57th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Banerjee, U.; Das, S.; Chandrakasan, A.P. Accelerating Post-quantum Cryptography Using an Energy-efficient TLS Crypto-processor. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, R.; Ma, H. Efficient Parallelism of Post-quantum Signature Scheme SPHINCS. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2542–2555. [Google Scholar] [CrossRef]
- Dai, Y.; Song, Y.; Tian, J.; Wang, Z. High-throughput Hardware Implementation for Haraka in SPHINCS. In Proceedings of the International Symposium on Quality Electronic Design (ISQED), San Francisco, CA, USA, 5–7 April 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Amiet, D.; Leuenberger, L.; Curiger, A.; Zbinden, P. FPGA-based SPHINCS Implementations: Mind the Glitch. In Proceedings of the 2020 23rd Euromicro Conference on Digital System Design (DSD), Kranj, Slovenia, 26–28 August 2020; pp. 229–237. [Google Scholar] [CrossRef]
- Satheesh, V.; Shanmugam, D. Implementation Vulnerability Analysis: A Case Study on ChaCha of SPHINCS. In Proceedings of the 2020 IEEE International Symposium on Smart Electronic Systems (iSES) (Formerly iNiS), Chennai, India, 14–16 December 2020; pp. 97–102. [Google Scholar] [CrossRef]
- Berthet, Q.; Upegui, A.; Gantel, L.; Duc, A.; Traverso, G. An Area-efficient SPHINCS Post-quantum Signature Coprocessor. In Proceedings of the 2021 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Portland, OR, USA, 17–21 June 2021; pp. 180–187. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, W.; Zhu, M.; Li, C.; Deng, C.; Chen, C.; Yin, S.; Yin, S.; Wei, S.; Liu, L. A 28nm 48KOPS 3.4uJ/Op Agile Crypto-processor for Post-quantum Cryptography on Multi-mathematical Problems. In Proceedings of the 2022 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; Volume 65, pp. 514–516. [Google Scholar] [CrossRef]
- Imran, M.; Aikata, A.; Roy, S.S.; Pagliarini, S. High-speed Design of Post Quantum Cryptography with Optimized Hashing and Multiplication. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Tan, W.; Wang, A.; Zhang, X.; Lao, Y.; Parhi, K.K. High-speed VLSI Architectures for Modular Polynomial Multiplication via Fast Filtering and Applications to Lattice-based Cryptography. IEEE Trans. Comput. 2023, 72, 2454–2466. [Google Scholar] [CrossRef]
- Putranto, D.S.C.; Wardhani, R.W.; Larasati, H.T.; Kim, H. Space and Time-efficient Quantum Multiplier in Post Quantum Cryptography Era. IEEE Access 2023, 11, 21848–21862. [Google Scholar] [CrossRef]
- Ghosh, A.; Mera, J.M.B.; Karmakar, A.; Das, D.; Ghosh, S.; Verbauwhede, I.; Sen, S. A 334uW 0.158mm2 ASIC for Post-quantum Key-encapsulation Mechanism Saber with Low-latency Striding Toom-cook Multiplication. arXiv 2023, arXiv:2305.10368. [Google Scholar] [CrossRef]
- Guerrieri, A.; Marques, G.D.S.; Regazzoni, F.; Upegui, A. H-Saber: An FPGA-optimized Version for Designing Fast and Efficient Post-quantum Cryptography Hardware Accelerators. In Proceedings of the 2023 24th International Symposium on Quality Electronic Design (ISQED), San Francisco, CA, USA, 5–7 April 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, J.; Liu, Z.; Roy, S.S. Time-memory Trade-offs for Saber on Memory-constrained RISC-V Platform. IEEE Trans. Comput. 2022, 71, 2996–3007. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Sarmadi, S.B.; Boorani, H.M. Post-quantum Cryptoprocessors Optimized for Edge and Resource-constrained Devices in IoT. IEEE Internet Things J. 2019, 6, 5500–5507. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Sarmadi, S.B. Lightweight and DPA-resistant Post-quantum Cryptoprocessor Based on Binary Ring-LWE. In Proceedings of the 2020 20th International Symposium on Computer Architecture and Digital Systems (CADS), Rasht, Iran, 19–20 August 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Hadayeghparast, S.; Sarmadi, S.B.; Ebrahimi, S. High-speed Post-quantum Cryptoprocessor Based on RISC-V Architecture for IoT. IEEE Internet Things J. 2022, 9, 15839–15846. [Google Scholar] [CrossRef]
- Bagchi, P.; Maheshwari, R.; Bera, B.; Das, A.K.; Park, Y.; Lorenz, P.; Yau, D.K.Y. Public Blockchain-envisioned Security Scheme Using Post Quantum Lattice-based Aggregate Signature for Internet of Drones Applications. IEEE Trans. Veh. Technol. 2023, 1–16. [Google Scholar] [CrossRef]
- Qassim, Y.; Magana, M.E.; Yavuz, A. Post-quantum Hybrid Security Mechanism for MIMO Systems. In Proceedings of the 2017 International Conference on Computing, Networking and Communications (ICNC), Silicon Valley, CA, USA, 26–29 January 2017; pp. 684–689. [Google Scholar] [CrossRef]
- Volya, D.; Zhang, T.; Alam, N.; Tehranipoor, M.; Mishra, P. Towards Secure Classical-quantum Systems. In Proceedings of the 2023 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), San Jose, CA, USA, 1–4 May 2023; pp. 283–292. [Google Scholar] [CrossRef]
- Fritzmann, T.; Sigl, G.; Sepulveda, J. Extending the RISC-V Instruction Set for Hardware Acceleration of the Post-quantum Scheme LAC. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 1420–1425. [Google Scholar] [CrossRef]
- Koleci, K.; Mazzetti, P.; Martina, M.; Masera, G. A Flexible NTT-based Multiplier for Post-quantum Cryptography. IEEE Access 2023, 11, 3338–3351. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).