1. Introduction
In 1991, Rivest [
1] presented a talk about relationships between machine learning and cryptography. Surprisingly, while artificial intelligence (AI) is being extensively developed in a number of applications, a very limited number of research studies have been done in the area of using AI in cryptography.
AI is the set of tools, methodologies, and implementations deployed to enable a digital computer or a robot to perform tasks that are usually associated with human intelligence [
2,
3]. In the last few decades, AI has exponentially developed in many sectors, such as big data, Internet of Things, robotics, banking, finance, healthcare, e-commerce, meteorology, education, facial recognition, information systems, autonomous driving, data security, etc. Machine learning (ML) is a subset of AI that enables smart machines and computers to learn without human intervention and gives them the ability to imitate human behavior. The goal of ML is to design algorithms that extract information from data in order to build models capable of deriving predictions and patterns. ML covers a range of methodologies and applications, such as facial recognition, natural language, online chatbots, medical imaging, diagnostics, self-driving of vehicles, etc.
On the other hand, cybersecurity is the set of various methods and tools deployed to protect electronic devices, such as information systems, servers, computers, networks, and data centers, from all kind of threats, vulnerabilities, and attacks. Often, an attack on an electronic device has severe impacts on the regular operations, or even worse, can completely destroy the stored data. Therefore, the goal of cybersecurity is to detect any attack, handle it, and recover the system after the accident. Cybersecurity includes the use of cryptography and cryptographic protocols for protecting data in transit and in storage.
The aim of this paper is to present an overview of the applications of AI and ML in cryptography with a focus on four prominent cryptosystems, namely, AES, RSA, LWE, and Ascon. For this, we start by providing an overview of AI and ML techniques before embarking on presenting the above-referenced cryptosystems and explaining how AI and ML can be applied to improve their security for the benefit of cybersecurity.
Cryptography is concerned with protecting information and communications transferred over public communication channels in the presence of adversaries. It allows only the recipient of a message to view its contents and is used in all domains where the security is a concern. To transmit a message or electronic data, two families of cryptography can be used:
symmetric and
asymmetric cryptography. In symmetric cryptography, also called secret key cryptography, the same key is used for both encryption and decryption. Typically, a message is encrypted using a secret key, and both the encrypted message and the secret key are sent to the recipient for decryption. In asymmetric cryptography, invented by Diffie and Hellman [
4] in 1976, and mostly known as public key cryptography, two keys are involved: one is public, and one is private. In general, the two keys are related by a mathematical process with the idea that it is computationally infeasible to determine one key given the other one. To encrypt and send a message, the sender uses the public key of the recipient. To decrypt, the recipient uses his or her private key.
Cryptanalysis is the study of cryptographic schemes for vulnerabilities. Specifically, there are mainly two methods of deploying cryptanalysis: mathematical and side-channel. Mathematical cryptanalysis, or algebraic cryptanalysis, consists of breaking cryptographic schemes by scrutinizing their mathematical properties, while side-channel cryptanalysis consists of studying and manipulating the implementations in order to collect information on the keys or on the plaintext itself.
In symmetric cryptography, the security of any scheme is based on the robustness of its S-box, a nonlinear operator that is often related to a vectorial Boolean function with very good cryptographic properties, such as resistance to differential cryptanalysis; linear cryptanalysis; boomerang cryptanalysis; and a variety of other cryptographic criteria [
5]. Artificial intelligence can be used to design S-boxes from vectorial Boolean functions and to study their cryptographic properties in order to select the most efficient and the most secure schemes.
In asymmetric cryptography, security is often based on a hard mathematical problem such as the integer factorization problem, the discrete logarithm problem, the Shortest Vector Problem (SVP), and the Closest Vector Problem (CVP) in a lattice.
Currently, the most widely used asymmetric cryptosystem is RSA, invented in 1978 by Rivest, Shamir, and Adleman [
6]. RSA is used for encryption, signatures, and key distribution, and is a powerful tool to provide privacy and to ensure authenticity of emails, digital data, and payment systems. The mathematics behind RSA are based on the ring
, where
is the product of two large prime numbers. In RSA, the public key is an integer
e satisfying
, and the private key is the integer
d satisfying
. To encrypt a message
, one computes
, and to decrypt it, one computes
. Since its invention, RSA has been intensively analyzed for vulnerabilities [
7,
8,
9,
10].
A promising family of asymmetric cryptography has appeared with the Learning With Error (LWE) problem and its variants. LWE was proposed by Regev [
11] in 2005. Several homomorphic encryption libraries, public key encryptions, and digital signature systems are based on LWE or on one of its variants [
12]. In 2016, NIST initiated a process to select and standardize post-quantum cryptography standardization [
13], and in 2022, it selected CRYSTALS–Kyber [
14] for public-key encryption and CRYSTALS–Dilithium [
15], Falcon [
16], and SPHINCS+ [
17] for digital signatures. Among the four selected algorithms for standardization, three are based on hard problems in lattices, namely CRYSTALS–Kyber, CRYSTALS–Dilithium, and Falcon. There are several variants of LWE, such as Polynomial-LWE [
18], Ring-LWE [
19], Module-LWE [
20], and Continuous LWE [
21]. The goal in LWE is to find a secret vector
given
samples of the form
, where
is uniformly generated,
is a small vector chosen according to a probability density, and
is the inner product of
and
s. The security of LWE is based on several hard problems in lattices, specifically the Gap Shortest Vector Problem (GapSVP) and the Shortest Independent Vectors Problem (SIVP).
The explosion of the Internet of Things (IoT), characterized by low-energy and low-computation power devices, has prompted the need for efficient and strong lightweight ciphers for protecting the privacy and authenticity of data transmitted by these devices. The U.S. government’s National Institute of Standards and Technology (NIST) recently selected the Ascon family of lightweight symmetric ciphers for authenticated encryption [
22,
23] to be used by IoT devices. The Ascon family ensures 128-bit security and uses a 320-bit permutation internally.
Common attacks on both symmetric and asymmetric cryptography are side-channel attacks, introduced by Kocher [
24] in 1996. Side-channel attacks are used to retrieve private keys from electronic devices. There are various types of possible side-channel attacks depending on the cryptosystem and the device. This includes timing execution [
24], power consumption [
25], electromagnetic radiation [
26], fault injection [
27], and acoustic attack [
28].
In symmetric and asymmetric cryptography, a plaintext M is encrypted by a nonlinear trapdoor function F together with a secret or a private key K so that . An algebraic attack consists of finding the plaintext M or the key K using publicly accessible and, eventually, finding their known corresponding . Moreover, for symmetric ciphers, an algebraic attack can be used to approximate the hole or a partial (reduced-round) encryption process by a linear function, which makes the cipher vulnerable.
The rest of this paper is organized as follows. In
Section 2, we review the main facts of artificial intelligence (AI) and machine learning (ML). In
Section 3, we discuss the differences between AI and ML. In
Section 4, we provide a list of possible applications of AI in cryptography. In
Section 5,
Section 6,
Section 7 and
Section 8, we review the four prominent cryptosystems, namely AES, RSA, LWE, and Ascon, and present possible applications of AI to test and enhance their security. We conclude the paper in
Section 9.
2. Artificial Intelligence and Machine Learning
Artificial intelligence (AI) is a subarea of computer science that concerns itself with building rational agents, i.e., agents that sense the world (i.e., read a percept), map the percept to some internal representation, and identify the best action to take among a set of possible actions given the percept. The selected action is the one that minimizes the agent’s objective function, then enacts the action and updates the internal representation of the world as a consequence of the action. There exist various types of agents: search agents, adversarial search agents, planning agents, logical agents, probabilistic agents, and learning agents. The latter are data-driven and use machine learning algorithms to predict the action to take as a function of the input percept from a collection of tuples (percept, action) [
29].
Machine learning (ML) is a subarea of AI that concerns itself with learning agents and algorithms. There exist three (3) major classes of learning agents/algorithms:
Supervised learning algorithms. These use tuples (input vector; output vector, also called Label) to learn/approximate the output vector for an unseen given input vector.
Unsupervised learning algorithms. These do not make use of the label and use the input vector only to learn/infer/approximate the output vector for an unseen given input vector.
Reinforcement learning algorithms. This class progressively learns/infers/approximates the output vector for an unseen given input vector from the positive or negative feedback returned from the external world.
Recently, two more subclasses have come to light. These are:
Self-supervised learning algorithms. These algorithms mask parts of the input and try to learn it. In essence, these algorithms transform an unsupervised problem (i.e., a problem for which no labels exist) into a supervised problem by auto-generating the labels.
Imitation learning algorithms. These are very recent. In essence, imitation learning algorithms reproduce others’ actions from observing the actions performed by other agents/machine learning algorithms [
30].
A comprehensive review and taxonomy of artificial intelligence and machine learning techniques together with their disadvantages and challenges can be found in [
31].
Artificial neural networks (ANNs) in particular have proven to be more powerful than others in many applications, including computer vision (CV), natural language processing (NLP), and autonomous driving (AD).
Artificial Neural Networks (ANNs) as a Non-Linear Approximation Function
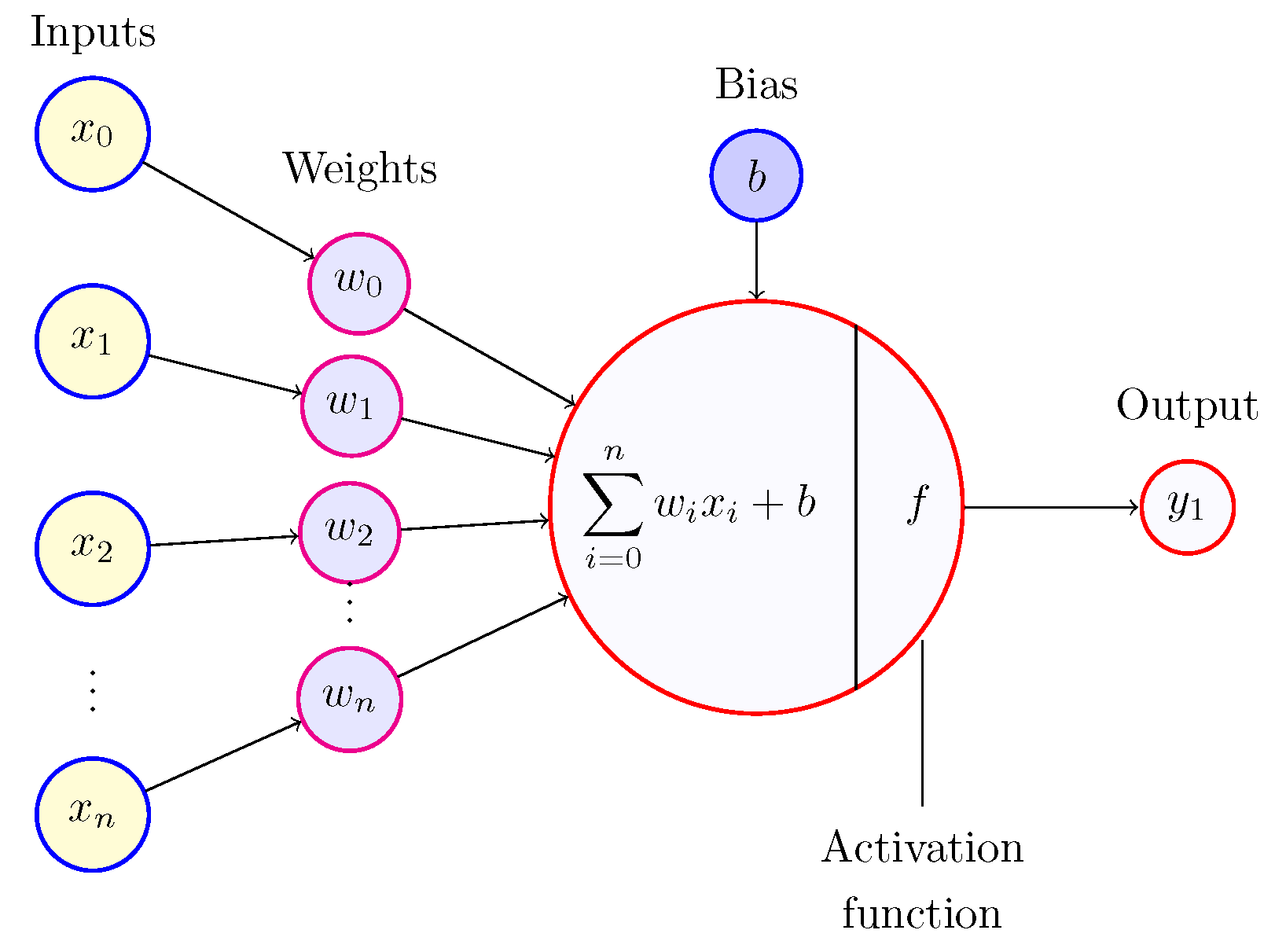
Artificial neural network models are mainly characterized by their architecture, the number of densely connected hidden layers, the number of cells/perceptrons (see
Figure 1) per layer, activation functions used in the neurons for firing, and the cost function used to train the network (or, similarly, to find the weights of the interconnections between layers) using gradient descent and back propagation for computing the gradient of the cost function in the weight space [
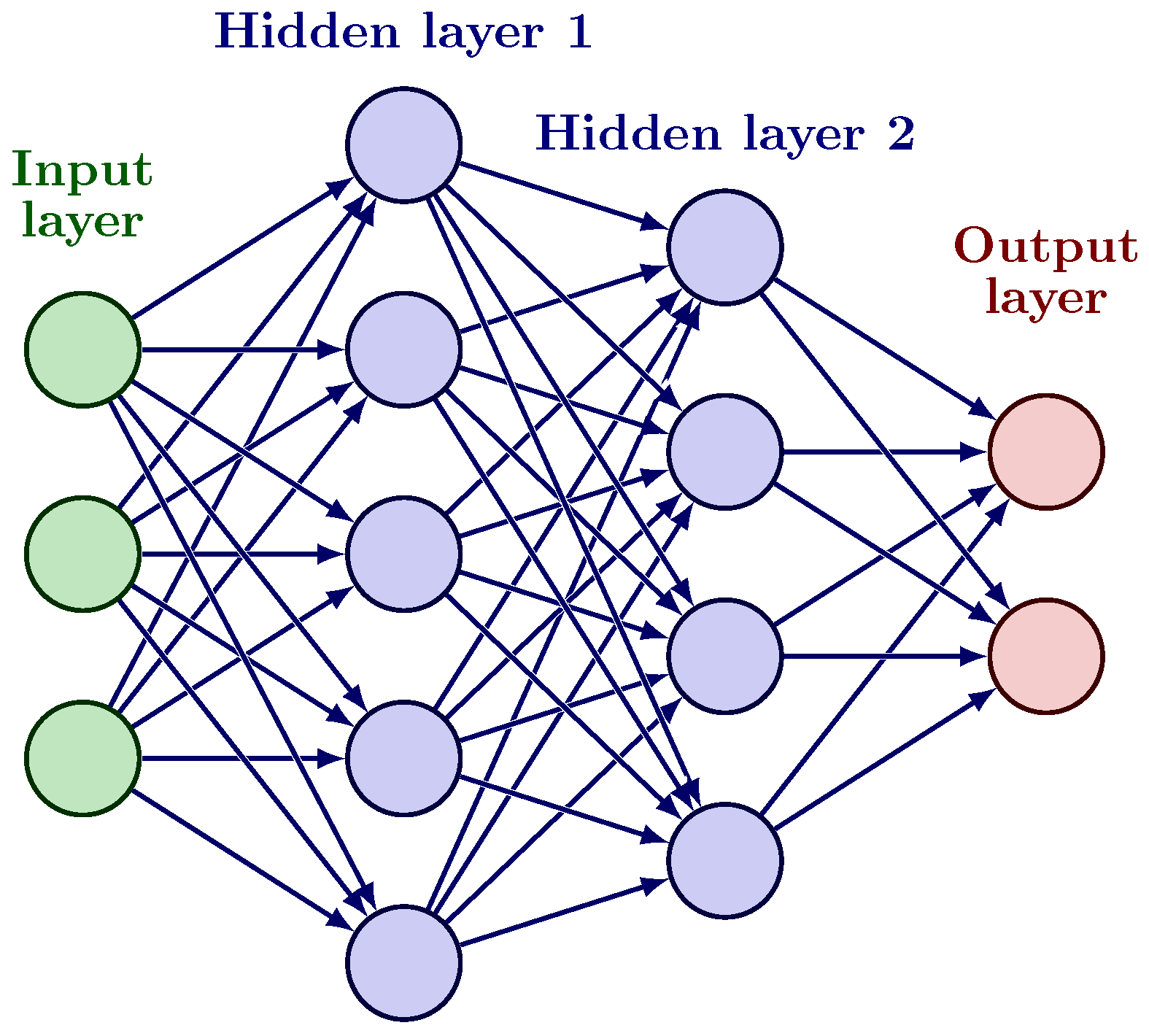
32] (see
Figure 2). ANNs can be divided into three major categories: those that perform input classification, sequence learning, or function approximation.
Thanks to nonlinear activation functions such as the Sigmoid, Tanh or RELU functions, ANNs are great at approximating arbitrary nonlinear functions (often as piece-wise linear approximations).
In fact, an ANN with at least one hidden layer is a universal approximator, i.e., it can represent any function [
33]. However, one hidden layer might need an exponential number of neurons, so often an architecture with many fully connected hidden layers (deep neural network) is preferred, as it is more compact. Arguably, the performance of the network increases with more hidden units and more hidden layers (see
Figure 3).
Although there is no universal method to approximate any arbitrary given function, there are development procedures that consistently lead to successful approximations of nonlinear functions within a specific field. There is wealth of literature for such applications in all fields, including bioengineering, mechanics, agriculture, digital design, and, last but not least, intrusion detection and cybersecurity.
As arbitrary function approximators, ANNs lend themselves naturally to cryptanalysis techniques, such as known and chosen plaintext attacks, linear, nonlinear, and differential attacks. Furthermore, the feed-forward of the data process through multiple layers of the neural networks has functional resemblance to multiple-round operations in a symmetric cipher, i.e., linear permutations, followed by nonlinear transformations. This also invites the attempt to leverage ANNs for the design of ciphers.
3. ANN Types and Their Domains of Application
Due to numerous advantages over other ML techniques, such as the ability to learn hierarchical features, the ability to handle multiple output, and the ability to deal with nonlinear data, which is clearly highlighted by the rapid development of foundation models (FMs) [
35], ANN-based learning agents have overshadowed other types of intelligent agents, including the ones that use other machine learning techniques. They have become a synonym for AI. This said, and despite the aforementioned advantages, it is not guaranteed that, because deep ANNs demonstrate excellent performance for domain problems dealing with language, images, and videos, they will necessarily outperform other ML techniques in cryptography [
36,
37]. Unless otherwise specified, we will use the term AI to designate agents that use ANNs.
There are many types of neural networks, such as auto-encoders, convolutional neural networks (CNNs), long short-term memory networks (LSTMs), recurrent neural networks (RNNs), generative adversarial networks (GANs), and transformers. They stand apart from one other through the type of processing attached to individual layers and the architecture used to connect the hidden layers, among other things, as well as whether a cell uses its own output from previous excitation or not.
3.1. Convolutional Neural Networks (CNNs)
In addition to hidden layers, a CNN contains multiple convolution layers, which are responsible for the extraction of important features, such as images, from spatial data. The earlier layers are responsible for low-level details, and the later layers are responsible for more high-level features. As such, CNNs are well-suited for applications such as facial recognition, medical analysis, and image classification.
3.2. Recurrent Neural Networks (RNNs)
RNNs are used to predict the next item in sequential data, which can be videos or text. In RNNs, a neuron in a layer also receives a time-delayed input from its own previous instance prediction. This instance prediction is stored in the RNN cell, which is a second input for every prediction. RNNs are typically used in tasks such as text or speech generation, text translation, and sentiment analysis.
3.3. Autoencoders
An autoencoder is a type of artificial neural network used to learn efficient coding of unlabeled data (unsupervised learning). An autoencoder learns two functions: an encoding function that transforms the input data into a low-dimension latent space representation, and a decoding function that recreates the input data from the latent space representation. Autoencoders are used in dimensionality reduction, image compression, image denoising, feature extraction, image generation using generative adversarial networks (GANs), sequence-to-sequence predictions, and recommendation systems.
3.4. Long Short-Term Memory Networks (LSTMs)
LSTMs use gates to control which output should be used or forgotten, including: input gate, output gate, and forget gate. LSTMs are best applied in speech recognition and text prediction.
3.5. Generative Adversarial Networks (GANs)
GANs learn to create new data instances that resemble the training data. For example, GANs can create images that look like photographs of human faces, even though the faces do not belong to any real person [
38].
3.6. Transformers
The transformer model architecture drops recurrence and convolutions and uses an attention mechanism to connect an encoder network with a decoder network. Applications of this model include machine translation [
39].
All of these variants of ANNs are mainly characterized by their architecture, the number of parameters/weights that make up the model and that have to be learned, and the training corpora used (Common Crawl, The Pile, MassiveText, Wikipedia, GitHub, books, articles, logs, etc.). As this paper is being written, the Megatron-Turing Natural Language Generation (MT-NLG), a transformer-based language generation model, uses 530 billion parameters, more than 7 times the average number of neurons in the adult human brain. These are also called foundation/base models since they can be adapted/fine-tuned for different tasks/contexts. Head-to-head comparison of existing (commercial and open source) large models (LMs) can be found in [
40]. It is worth noting that the size of a model depends largely on the nature of the problem at hand. In many engineering domains, the models used are not as big as foundation models.
5. The Advanced Encryption Standard (AES)
The Advanced Encryption Standard [
58], also known as the Rijndael algorithm, is a symmetric block cipher that was designed by Daemen and Rijmen [
59] in 1999. It was adopted by the U.S. National Institute of Standards and Technology (NIST) in 2001 to supersede the Data Encryption Standard (DES) [
60]. AES allows key lengths of size 128, 192, or 256 bits, with a block length of 128 bits. In AES, the encryption performs 10 rounds for a 128-bit key, 12 rounds for a 192-bit key, and 14 rounds for a 256-bit key.
The encryption and the decryption in the AES algorithm start with two parameters: a block
B of length 128 bits, and a key
K of length 128, 192, or 256 bits (see
Table 1). In all steps of the encryption and decryption in AES, the blocks
are represented by
square matrices of bytes called state arrays.
5.1. The Encryption Process of AES
At the beginning of the encryption, each key
K is expanded into
subkeys by an algorithm called
key expansion, where
is the number of rounds. The encryption phase starts with the initial round by XORing the plaintext with the first subkey. Then, the rounds are composed of four algorithms, namely AddRoundKey, SubBytes, ShiftRows, and MixColumns, so that a round
with
is in the form:
The four algorithms can be summarized as follows:
5.2. The Decryption Process in AES
The decryption process in AES is performed by applying the inverse of the algorithms used in the encryption process. If
n is the number of rounds in the encryption process, then there are
rounds in the decryption process. The decryption starts by XORing the ciphertext with the last subkey of the key expansion. For
, the the inverse round
is composed of four algorithms as follows:
The algorithms can be summarized as follows.
InvAddRoundKey: As in the AddRoundKey algorithm, the subkey for the round is bitwise XORed, with the state array computed in the previous step. In the first round, the state array is the ciphertext block, and in the last round, the resultant state array is the plaintext.
InvSubBytes: In this operation, the inverse S-box replaces each byte of the state with another byte by a substitution method. Specifically, each byte
y is transformed into a list of 8 bits,
and is transformed via the rule
,
where
The inverses are computed in the finite field modulo the polynomial .
InvShiftRows: In this transformation, the bytes of the first row in the state array remain unchanged, and the bytes of rows 2, 3, and 4 are cyclically shifted right by 1, 2, and 3 cases, respectively (see
Table 6).
InvMixColumns: In this transformation, each column is multiplied by a fixed matrix, as in
Table 7.
In InvMixColumns, the operations are performed in modulo the polynomial .
5.3. Main Attacks on AES
The goal of the attacks on an asymmetric cryptosystem is to find good properties inside the cipher that allow for retrieval of partial or total information on the secret key. In addition to the exhaustive attack, the two prominent attacks are the linear cryptanalysis and the differential cryptanalysis.
Exhaustive search attack. Brute force attacks, or exhaustive attacks, consist of trying all possible keys to a ciphertext and checking whether the plaintext is recognizable. It is easy to prevent such attacks by using large keys. In AES, the key lengths are 128, 192, and 256 bits. This makes the total key combination of each key length
,
, and
, respectively, which is infeasible even for the fastest supercomputers today. On the other hand, with a computer with quantum technology, due to Grover’s algorithm [
61], it is possible to perform an exhaustive search in the square root of the classical time, and the key lengths should be
.
Linear attack. In 1993, Matsui [
62] invented one of the most practical attacks on DES, known as linear cryptanalysis. It can be applicable to AES by approximating the nonlinear parts in the rounds by linear expressions. This makes the round a linear function where the input or the output is easy to compute.
In the situation where the S-box of the system is constructed following a vectorial boolean function
, the linear cryptanalysis is constructed on the value of its nonlinearity, which is defined by:
where
is the inner product in
, defined as
. The nonlinearity of the function
F represents the minimum Hamming distance between
F and all possible affine functions. It is well-known that
is upper bounded by
. Vectorial Boolean functions that achieve
are called
bent. Bent functions exist only when
n is even and are important for building balanced S-boxes.
In practice, the nonlinearity of the vectorial Boolean function
F is studied via the linear probability table (LPT) defined for the entry
by:
For AES, except for the first row and first column, all rows and columns of the LPT have the same distribution of values as given in
Table 8.
Differential attack. In 1991, Biham and Shamir [
63] proposed differential cryptanalysis and applied it to DES. Differential cryptanalysis is a chosen-plaintext attack and works with two pairs of plaintext
with a fixed difference
and their corresponding ciphertext
. The goal of the differential cryptanalysis is to study the behavior of the difference
.
For a vectorial Boolean function
, the differential cryptanalysis is studied via the difference distribution table (DDT), which is defined for
by:
The differential uniformity of
F is defined by:
The differential cryptanalysis exploits the differential probability
, specifically:
For a randomly chosen permutation and for any , the value is expected to be uniformly distributed with equiprobability. This makes a reliable and practical distinguisher if is sufficiently small.
For the AES S-box,
Table 9 shows the distribution of the
values and their frequencies.
If
is a solution to the equation
, then
is also a solution. This implies that
for all
and, consequently,
. Vectorial Boolean functions satisfying
are called almost perfect nonlinear (APN) functions. As shown in
Table 9, the differential uniformity of the AES S-box is 4. Hence, AES does not belong to the APN family; nevertheless, its differential uniformity is too small. This makes AES resistant to differential cryptanalysis.
5.4. Applications of AI to Block Ciphers
There are plenty of attacks on AES that can be performed by AI. The goal of using AI with AES is to test the resistance of its secret keys and its S-boxes to such attacks. AI can be used for the following tasks.
Resistance to side-channel attacks [
64]: Side-channel attacks exploit the operations performed by a cryptographic system during encryption or decryption to gain information about the private key. The most used channel attacks are timing attacks, simple power attacks, differential power attacks, electromagnetic radiation attacks, correlation power attacks, etc. These attacks rely on collecting and interpreting observations in order to infer information about key size and bits. These inferences lend themselves naturally to ML and ANNs in general and to advanced ANNs/models in particular. As described earlier, some work has already been initiated in this direction [
52].
Resistance to fault attacks [
65]: Fault attacks are deployed to disturb the normal functioning of a cryptosystem. They are injected by various techniques such as laser, light pulses, electromagnetic perturbations, tampering with the clock, etc. This enables the attacker to collect the erroneous result and to gain information about the private key. As with side-channel attacks, fault attacks can be overcome by testing implementations against an advanced ANN that tries to leverage the erroneous results to infer information about the key. AES cipher implementations need to be tested against an advanced ANN model that tries to leverage collected output to infer the key before deployment.
Resistance to linear attacks [
62]: This task can be processed by computing the linear probability table of the S-box. ANNs as excellent function approximators can be used to model nonlinearity of S-boxes, similarly to the work of [
53] on DES.
Resistance to differential attacks [
63]: This task can be performed by computing the difference distribution table of the S-box. As with linear attacks, ANNs as excellent function approximators can be used to model the differential properties of S-boxes, similarly to what has been done by [
55] on the round-reduced Speck cipher and by [
47] on the round function of GIFT.
Resistance to truncated differentials [
66]: This variant of the differential attack was presented by Knudson in 1994. This task can be processed by adapting the difference distribution table of the S-box under the truncated differentials criteria. As with differential attacks, ANNs as excellent function approximators can be used to model the truncated differential properties of S-boxes.
Resistance to boomerang attacks [
67]: The task of testing the boomerang cryptanalysis can be accomplished by studying the boomerang connectivity table (BCT) as defined by Cid et al. in 2018 [
68]. The BCT of an invertible vectorial function
is defined at the entry
by:
Algebraic immunity [
69,
70]: The algebraic immunity of a vectorial Boolean function
F defined on
is the lowest degree of all functions
satisfying
or
, where
is the inner product of the vectors
a and
b. The underlying vectorial Boolean function of AES can be modeled and tested using advanced ANNs.
Balancedness [
71]: A vectorial Boolean function
is balanced if every value of
is the image of exactly
values from
. The task of verifying balancedness can be processed by studying the vectorial Boolean function that defines the S-box of AES.
Resistance to other attacks: There are plenty of attacks and criteria that can be implemented with AI to test the security of block ciphers. This includes correlation immunity [
72], strict avalanche criterion (SAC) [
73], fixed points and opposite fixed points [
59], algebraic degree [
72], impossible differential [
74], etc. A complete list of such attacks can be found in [
5,
75].
In sum, AI can be used to test AES SubBytes() and MixColumns() functions, and the AES cipher with its modes of operations and their implementations can be used to test against all former attacks and to propose useful and efficient solutions, such as the choice of the key space, MixColumns() matrix polynomials, etc., that nullify/undermine the attacks.
9. Conclusions
Artificial intelligence (AI) and, in particular, deep learning using sophisticated artificial neural network (ANN) architecture, is exponentially developing and gaining practical use in all sectors of daily life. In this paper, we presented areas where the use of AI can help enhance the security of cryptographic systems. We particularly focused on four prominent systems in modern cryptography, namely, the Advanced Encryption Standard (AES), the Rivest–Shamir–Adleman (RSA) scheme, the Learning With Errors (LWE) scheme, and the lightweight Ascon cipher family. We reviewed their security and pinpointed layers, functions, and areas that could potentially benefit from cryptanalysis that uses advanced ANN architectures. This said, depending on the function to approximate S-box and vectorial Boolean functions for AES, S-box and permutations for Ascon, Diophantine equations and factorization for RSA, lattice problems for LWE), ANNs may not necessarily outperform other machine learning (ML) techniques. For instance, LWE introduces vectors of errors similar to noise in the encryption process, which may hinder the performance of ANNs, since it is a well-known fact that ANNs suffer from noisy training data. Experimentation is needed to confirm this hypothesis. Furthermore, sophisticated ANN architectures can have the tendency to overfit the presented training data, which may lead to errors for unseen encrypted data or plaintext.
Finally, beyond prediction, ANNs do not provide any insights into the structure of the function being approximated, which may not help in fine-tuning the function/layer being approximated (see [
110] for Explainable AI). For further research, we envisage experimenting with different ANN architectures and building an ANN generator that automatically generates an adversary ANN from the specification of the S-box or the vectorial Boolean function to help cryptosystem designers quickly test the strength of the cryptographic functions and substitution layers.