3.2.1. The BBS Generator
The BBS generator, proposed by L. Blum, M. Blum and M. Shub in [
26], is one of the most often deployed
cryptographically strong PRNGs. Its security (unpredictability) is founded on the difficulty of the
quadratic residue problem.
For every integer N, is its length in bits, and , its length in base . If , is the set of finite sequences with elements from , and , the set of sequences with an infinite number of elements from . Also, we define , i.e., the set of finite sequences of length k. For all sequences , we denote by the initial part of sequence x of length k (i.e., its first k elements), and we denote by the k-th element of x (its first element is ).
We denote by the smallest non-negative integer remainder from dividing x by integer N. A quadratic residue is any number x for which there exists an integer u such that . Recall that integers and , i.e., the set of integers that are smaller than N and relatively prime with N. Set has order, i.e., number of elements, equal to . The set of quadratic residues modulo N is denoted by . This is a subset of and has order . Additionally, we denote by the subset of consisting of its elements that have a Jacobi symbol equal to 1 and by the subset of its elements that have Jacobi symbol . All quadratic residues belong in subset .
Each quadratic remainder has four different roots in , which are and . If, however, we assume that , then every quadratic residue has exactly one square root, which is also a quadratic residue. In other words, the function is a and onto mapping (i.e., bijection) from to itself.
Finally, we state the definition of
Carmichael’s function, which will also be needed for the concept of special primes. Carmichael’s
-function [
27] is closely related to
Euler’s totient function. However, while Euler’s totient function
provides the
order of unit group
, Carmichael’s function
provides its
exponent. In other words,
is the
smallest positive integer for which it holds that
for any
a that is coprime to
n. Carmichael’s
function is not multiplicative but has a related property, which can be called
lcm-multiplicative, as follows:
Some special values include
, for
an odd prime power,
,
, as well as
for
. Based on these special values and Equation (
5),
can be computed for any positive integer
n.
A prime number P is called special if and , where are primes greater than 2. A composite number is special if and only if P, Q are two distinct special primes and .
Set of the generator parameters consists of all positive integers , where P, Q are distinct prime numbers of equal length (i.e., ) and . For any integer N, set is the set consisting of the quadratic residues . The domain of the generator seeds is . The seeds should be selected from X according to the uniform distribution for increased generator security.
Given as input a pair
, the BBS pseudorandom number generator outputs a pseudorandom sequence of bits
, where
and
.
is the least significant bit of integer
x. The construction of the pseudorandom sequence obviously takes place in polynomial time. As it is shown in [
26], the period (
) of the pseudorandom sequence divides or is equal to (under some condition)
. Given
and
, we can efficiently calculate
for
. To calculate
for
, we use the equality
. As we will see below, if
and
N are known, but not the values of
P and
Q, we can construct the pseudorandom sequence forward (i.e., for
) but not backwards (for
). thus, it appears that the prediction of the sequence is as hard as factoring a large integer
. Alexi et al. [
28] proved that the BBS generator remains cryptographically secure even if it outputs up to
low-order bits instead of only one. With this result, the generator’s efficiency is greatly improved. Practically, a BBS generator can be realized as follows:
Find primes p and q such that mod 4.
Set .
Start with = seed (a truly random value), .
Set mod N.
Output the least significant bit of .
Set , go to step 3.
Now, regarding the security of this generator, as mentioned above in the introduction, all cryptographically secure generators base their security on the difficulty of solving number theory problems. This problem, in the case of the BBS generator, is the quadratic residuosity problem. The problem is defined as follows: Given N and , decide whether x is a quadratic residue . Recall that exactly half the elements of are quadratic residues.
The quadratic residuosity assumption states that any efficient algorithm for solving the quadratic residuosity problem would give wrong results for at least a percentage of the inputs to the algorithm. More formally, the assumption is as follows: Let be a polynomial and be a polynomial algorithm that, when given as input N and x, with , returns 0 if x is not a quadratic residue and 1 otherwise. Also, let be a constant and t be a positive integer. Then, for n very large and for a fraction d of numbers N, with , the probability that process gives the wrong answer for integer x (given that x is chosen according to the uniform distribution from ) exceeds , that is, . The quantity can be replaced with .
The details of the discussion that follows can be found in [
26]. We also recall that in what follows,
, with P, Q prime numbers and
, and that the function
is a
mapping from QRN to QRN.
According to the definition of the BBS generator, knowledge of N is sufficient for the efficient generation of the sequence starting from a seed value . However, knowing only N and not its two factors P and Q does not suffice for the generation of the sequence in reverse direction, i.e., the sequence starting from . For this purpose, factors P and Q are needed. This necessity follows from the following argument: Suppose that we can efficiently calculate without knowing the factors of N. Then, in order to factor N, we choose an , and we set and calculate . We then compute or Q. Therefore, the ability to compute for at least a percentage of the values of x would allow us to factor N efficiently with a high probability of success.
On the other hand, if we could factor N, we could generate the pseudorandom sequence backwards. This fact follows from the following theorem: There exists an efficient deterministic algorithm A that, when given as inputs N, factors P and Q, and any quadratic residue , computes the unique quadratic residue for which . In other words, .
Moreover, the factors of
N are necessary to have an
-advantage in finding the parity bit of
in polynomial time, given
. A probabilistic process
P that returns 0 or 1 is said to have an
-advantage, with
, in guessing the parity bit of
if and only if
. Similarly, we can define a probabilistic procedure that would have an
-advantage in deciding whether some
is a quadratic residue (which is the quadratic residuosity problem). More simply, we would say (according to a lemma of [
26]) that an
-advantage in finding the parity bit of
can be converted into an
-advantage for the quadratic residuosity problem.
In [
26], a theorem that proves the unpredictability of the BBS generator is given. By this theorem, for any constant
and any positive integer
t, any probabilistic polynomial process
P has at most a
advantage in predicting the sequences generated by BBS backwards (for sufficiently large
and for all but a fraction
of
N). In short, if the BBS generator were predictable, the quadratic residuosity assumption described previously would not hold. For this reason, the generator can be safely assumed to also pass every probabilistic, polynomial, statistical test on its long-term output.
Having shown that the output of the generator cannot be efficiently predicted, its period remains to be calculated. The fact that the sequence
cannot be predicted shows that the period of
should be very large. According to a theorem proved in [
26], period
divides
. However, it would be best for the period to be as long as possible, i.e., equal to
. The equality
can indeed hold under two conditions. The first is that integer
N is
special as defined earlier, and the second is to choose a seed
so that its order is equal to
.
Finally, we define the
linear complexity of a sequence of pseudorandom numbers
as the
smallest number
L for which the linear relationship
holds for
The linear complexity of any pseudorandom sequence does not exceed the period of the sequence. Obviously, the higher the linear complexity of a sequence is, the more cryptographically secure it is with respect to the prediction of its output. As demonstrated in [
29], the BBS generator does not exhibit any particular form of linear structure, a property that excludes the possibility of applying attacks such as the
Lattice Reduction attack on its outputs.
3.2.3. Generators Based on Block Ciphers
The other two generators that are deployed in the lottery are based on the encryption algorithms
DES (Data Encryption Standard) and
AES (Advanced Encryption Standard). The implementations provided by version 2.5.3 of the mcrypt library (available at [
30]) were used with key sizes of 64 bits for DES and 192 bits for AES.
DES and AES are used in their CFB (cipher-text feed-back) mode, and they are operated as follows: An initial random seed is constructed from the combined output of the true random generators; then, DES and AES are invoked, using the seed as the Initial Vector (IV), as many times as the values we need to generate. In particular, every time the encryption function is called, a byte with all zeros is encrypted (always in CFB mode), and the encryption result is the output of the corresponding generator.
The cryptographic strength of these two generators is based on the security of the corresponding encryption algorithms and not on a presumed computationally hard mathematical problem, like RSA and BBS. However, both generators have passed, separately, all the Diehard tests; thus, their output is considered secure.
Bruce Schneier et al., in [
31], present the design and analysis of the Yarrow cryptographically secure PRNG. Yarrow relies on a one-way hash function
with an
m-bit digest and a block cipher
with a
k-bit key and an
n-bit block size. The designer should select a one-way hash function that is collision-intractable (e.g., one from the SHA-2 family of hash functions) and a block cipher (e.g., AES) that is highly resistant to known-plaintext and chosen-plaintext attacks.
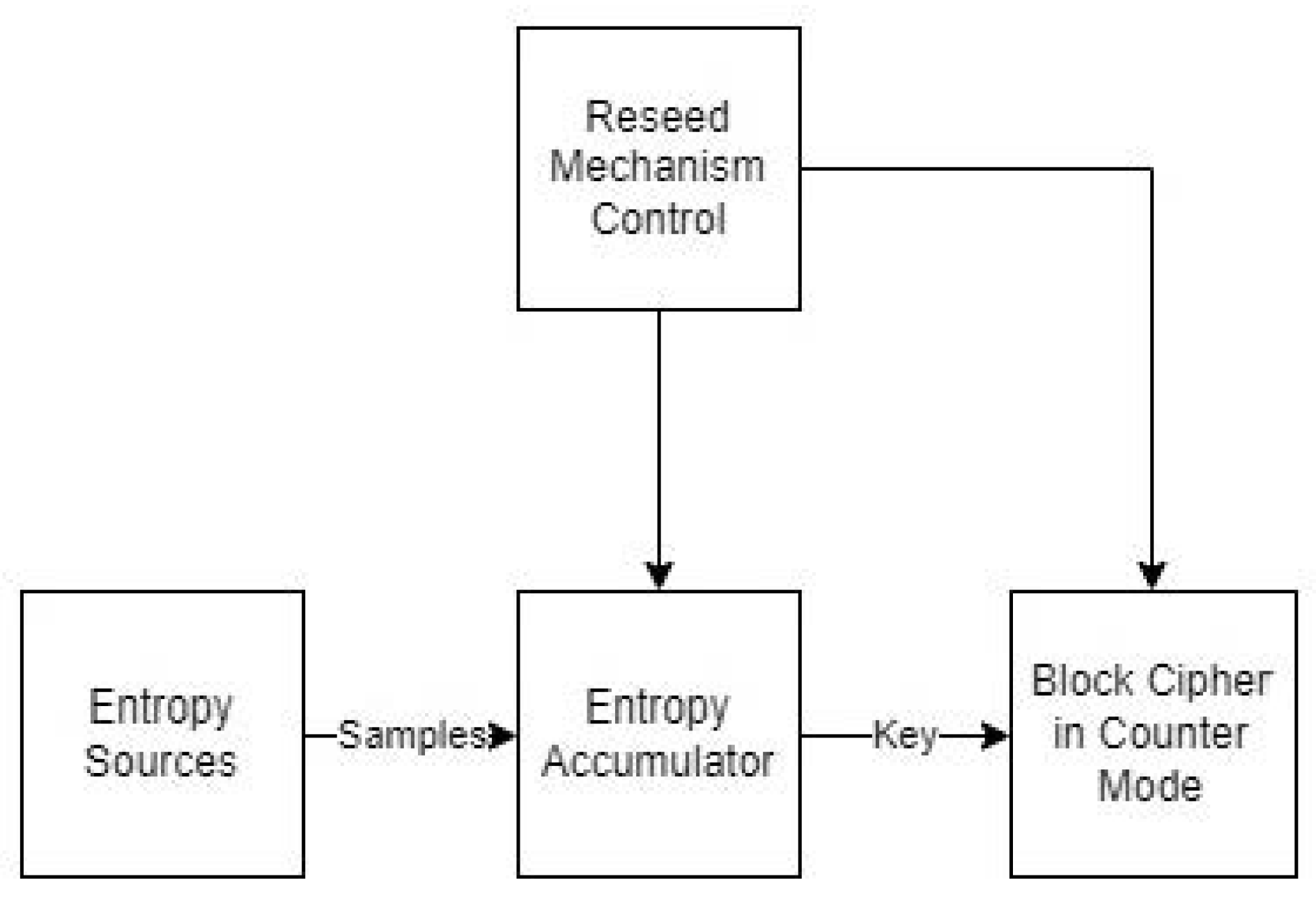
The major components of Yarrow are an
entropy accumulator, which collects samples from entropy sources in two pools; a
reseeding mechanism, which periodically reseeds the key with new entropy from the pools; and a
block-cipher-based generation mechanism, which generates random numbers (
Figure 1). The basic idea behind the generation mechanism is that if an attacker does not know the block-cipher key, they cannot distinguish the generated outputs from a truly random sequence of bits.
The entropy accumulator determines the next unguessable internal state of the PRNG. Each source of entropy sends samples to the entropy accumulator, and their hashed values are stored to either a fast pool or a slow pool. The fast pool is used for frequent key reseeding, while the slow one, for rare reseeding. It is obvious that the collected entropy is no more than the size of the hash digest, i.e.,
m-bit entropy. Initially, the entropy accumulator collects samples until the collected estimated entropy is high enough for reseeding the block cipher with a new key. Recommendations for entropy estimation can be found in [
4].
3.2.4. Algorithms M and B
Given two sequences of pseudorandom numbers X and Y, algorithm M produces a sequence significantly “more random”. Essentially, the numbers in are the same as those that make up X, except that they are in different positions (i.e., they form a permutation of the original sequence, X) in the new sequence. These positions are dictated by sequence Y.
More specifically, an array
N with
k elements is formed, where
k is an integer depending on the application, often close to 100. The elements in array
N are the first
k elements of sequence
X. The steps of algorithm
M (applied iteratively) appear in Algorithm 2.
| Algorithm 2 Description of the algorithm M |
- 1:
The next elements of the sequences X and Y are placed in the variables x and y. Initially and where , are the k-th elements of the sequences X and Y respectively. - 2:
if m is the modulus of the sequence Y then - 3:
, i.e., j is a random integer between 0 and specified by y. - 4:
end if - 5:
The next element in the sequence is set equal to . - 6:
.
|
It turns out that in most cases, the period of the sequence produced by algorithm M is the least common multiple of the periods of sequences X and Y.
However, there is a more effective way to transpose the elements of a sequence X. The corresponding algorithm is called Algorithm B. It is similar to M, but it achieves better results in practice. At the same time, it has the advantage that only one sequence of pseudorandom numbers is needed, and not two as in the case of M.
Initially (as in M), the first k elements of sequence X are placed in array N. Then, variable y takes the value , and the following steps are applied iteratively:
, where m is the modulus of sequence X.
is the next new element of sequence .
We set , and is set to the next element of sequence X.
Although algorithm M can produce satisfactory pseudorandom number sequences, given as input even non-random sequences (e.g., the Fibonacci numbers sequence, for example), it is still likely to produce a less random sequence than the original sequences if they are strongly
correlated. Such issues do not arise with algorithm B. Algorithm B does not, in any way, reduce the “randomness” of the given sequence of pseudorandom numbers. On the contrary, it increases it with a small computational cost. For these reasons, it is recommended to use algorithm B with any PRNG. Both algorithms are described in detail in Knuth’s book [
22].
A notable disadvantage of algorithms M and B is that they only modify the order of the numbers in a sequence and not the numbers of the sequences themselves. Although, for most applications, the ordering of the numbers is important, if the initial generators we choose do not pass some basic statistical tests, permuting their elements with the M and B algorithms does not render them stronger. For this reason, in applications that require pseudorandom number sequences with strong randomness properties with theoretical guarantees that imply unpredictability, it is better to deploy cryptographically secure PRNGs, such as BBS and RSA, optionally using algorithms M and B.