Improvements on Making BKW Practical for Solving LWE †
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
- A generalized reduction step that we refer to as smooth-LMS, allowing us to use non-integer step sizes. These steps allow us to use the same time, space, and sample complexity in each reduction step of the algorithm, which improves performance compared to previous work.
- A binary-oriented method for the guessing phase, transforming the LWE problem into an LPN problem. While the previous FFT method guesses a few positions of the secret vector and finds the correct one, this approach instead finds the least significant bits of a large amount of positions using the FWHT. This method allows us to correctly distinguish the secret with a larger noise level, generally leading to an improved performance compared to the FFT-based method. In addition, the FWHT is much faster in implementation.
- Concrete complexity calculations for the proposed algorithm showing the lowest known complexity for some parameter choices selected as in the Darmstadt LWE Challenge instances, but with unrestricted number of samples.
- Two implementations of the algorithm that follow two different strategies in memory-management. One is fast, light, and uses solely RAM-memory. The latter follows a file-based strategy to overcome the memory limitations imposed by using only RAM. The file read/write is minimized by implementing the algorithm in a clever way. Simulation results on solving larger instances are presented and verifies the previous theoretical arguments.
1.3. Organization
2. Background
2.1. Notation
- We write for the base 2 logarithm.
- In the n-dimensional Euclidean space , by the norm of a vector , we consider its -norm, defined asThe Euclidean distance between vectors and in is defined as .
- Elements in are represented by the set of integers in .
- For an linear code, N denotes the code length, and k denotes the dimension.
2.2. The LWE and LPN Problems
2.3. Discrete Gaussian Distributions
3. A Review of BKW-Style Algorithms
3.1. The LWE Problem Reformulated
3.2. Transforming the Secret Distribution
3.3. Sample Amplification
3.4. Iterating and Guessing
3.5. Plain BKW
3.6. Coded-BKW and LMS
3.7. LF1, LF2, Unnatural Selection
3.8. Coded-BKW with Sieving
4. BKW-Style Reduction Using Smooth-LMS
4.1. A New BKW-Style Step
4.1.1. First Step
- the absolute value of each position is ,
- the absolute value of position is .
4.1.2. Next Steps
4.2. Smooth-Plain BKW
4.3. How to Choose the Interval Sizes
4.4. Unnatural Selection
4.5. On Optimizing Values
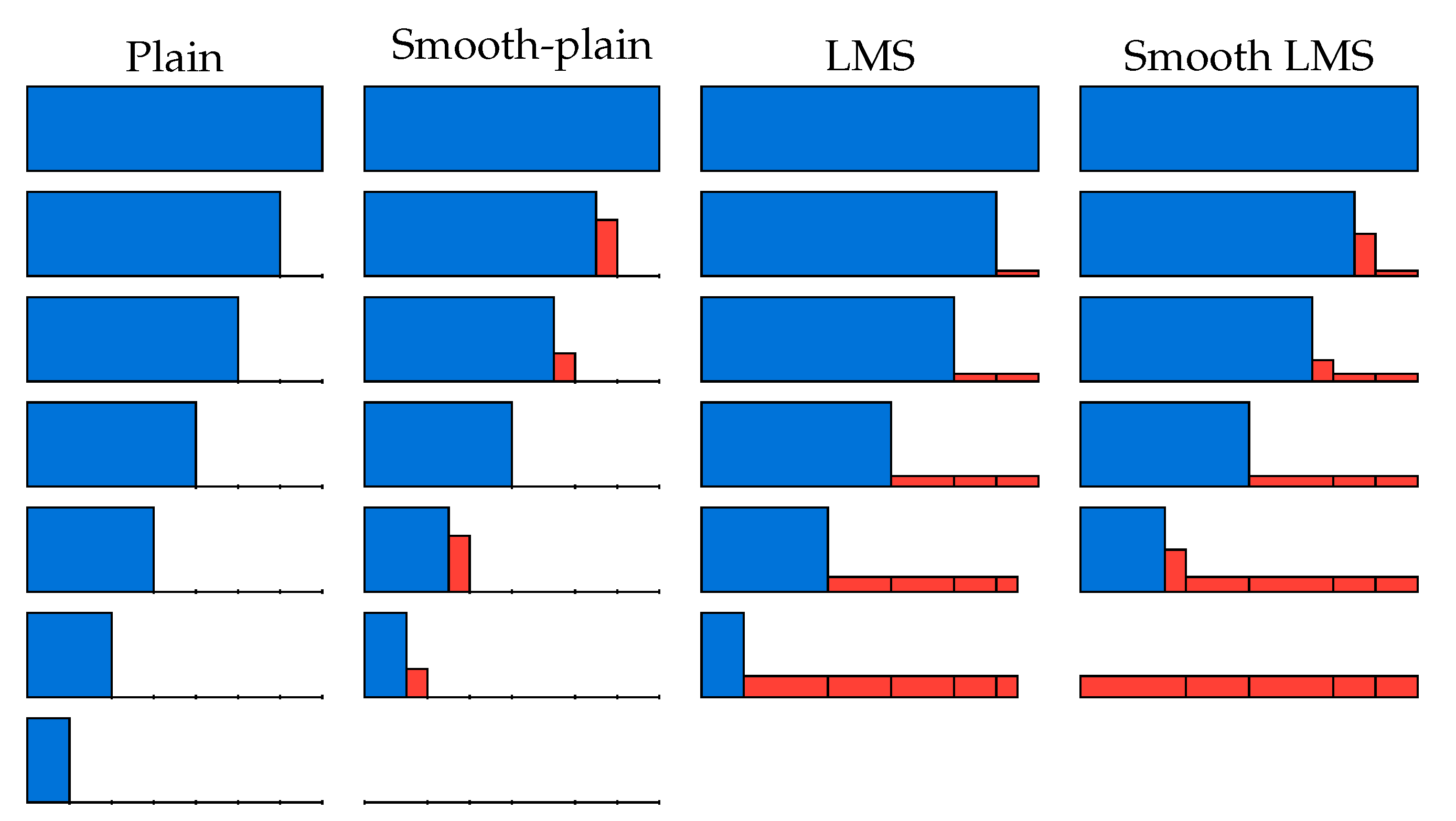
4.6. An Illustration of Smooth Reduction Steps
5. A Binary Partial Guessing Approach
5.1. From LWE to LPN
- there are no errors (or almost no errors), corresponding to . Then, one can solve for directly using Gaussian elimination (or possibly some information set decoding algorithm in the case of a few possible errors).
5.2. Guessing Using the FWHT
5.2.1. Soft Received Information
5.2.2. Hybrid Guessing
5.2.3. Even Selection
5.3. Retrieving the Original Secret
| s0: | ( | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | ) |
| s1: | ( | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | ) |
| s2: | ( | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ) |
| s3: | ( | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | ) |
| s: | ( | −3 | 0 | 2 | 0 | 1 | −1 | 4 | 3 | −2 | −4 | ) |
6. Analysis of the Algorithm and Its Complexity
6.1. The Algorithm
| Algorithm 1 BKW-FWHT with smooth reduction (main framework). |
Input: Matrix with n rows and m columns, received vector of length m and algorithm parameters
|
6.2. The Complexity of Each Step
6.2.1. Smooth-Plain BKW Steps
6.2.2. Smooth-LMS Steps before the Multiplication of 2
6.2.3. Smooth-LMS Steps after the Multiplication of 2
6.2.4. FWHT Distinguisher and Partial Guessing
6.3. The Data Complexity
6.4. In Summary
6.5. Numerical Estimation
7. Implementations
7.1. RAM-Based Implementation
7.1.1. Memory and Sample Organization
7.1.2. Parallelization
7.2. File-Based Implementation
7.2.1. File-Based Sample Storage
7.2.2. Optional Sample Amplification
7.2.3. Employing Meta-Categories
7.2.4. Parallelization
7.3. A Novel Idea for Fast Storage Writing
7.3.1. Intuition
7.3.2. Technical Description
7.4. Other Implementation Aspects
7.4.1. Strict Unnatural Selection
7.4.2. Skipping the All 0 s Guess When Using the FWHT Distinguisher
7.4.3. FWHT Distinguisher When the RAM Is a Limitation
7.4.4. On the Minimum Population Size
- By design, a small fraction of the categories will get fewer samples on average.
- Even ignoring the first point, the spread will, due to randomness, not be perfectly even.
8. Experimental Results
8.1. Target Machine
8.2. Unlimited Number of Samples
8.3. Limited Number of Samples
9. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- NIST Post-Quantum Cryptography Standardization. Available online: https://csrc.nist.gov/Projects/Post-Quantum-Cryptography/Post-Quantum-Cryptography-Standardization (accessed on 24 September 2018).
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. In Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; Gabow, H.N., Fagin, R., Eds.; ACM Press: Baltimore, MA, USA, 2005; pp. 84–93. [Google Scholar] [CrossRef]
- Blum, A.; Furst, M.L.; Kearns, M.J.; Lipton, R.J. Cryptographic Primitives Based on Hard Learning Problems. In Advances in Cryptology—CRYPTO’93; Stinson, D.R., Ed.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 1994; Volume 773, pp. 278–291. [Google Scholar] [CrossRef] [Green Version]
- Arora, S.; Ge, R. New Algorithms for Learning in Presence of Errors. In Proceedings of the ICALP 2011: 38th International Colloquium on Automata, Languages and Programming, Part I, Zurich, Switzerland, 4–8 July 2011; Aceto, L., Henzinger, M., Sgall, J., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Zurich, Switzerland, 2011; Volume 6755, pp. 403–415. [Google Scholar] [CrossRef]
- Albrecht, M.; Cid, C.; Faugere, J.C.; Fitzpatrick, R.; Perret, L. On the complexity of the Arora-Ge algorithm against LWE. In Proceedings of the SCC 2012–Third international conference on Symbolic Computation and Cryptography, Castro Urdiales, Spain, 11–13 July 2012. [Google Scholar]
- Albrecht, M.R.; Player, R.; Scott, S. On the concrete hardness of Learning with Errors. J. Math. Cryptol. 2015, 9, 169–203. [Google Scholar] [CrossRef] [Green Version]
- Herold, G.; Kirshanova, E.; May, A. On the asymptotic complexity of solving LWE. Des. Codes Cryptogr. 2018, 86, 55–83. [Google Scholar] [CrossRef]
- Guo, Q.; Johansson, T.; Mårtensson, E.; Stankovski Wagner, P. On the Asymptotics of Solving the LWE Problem Using Coded-BKW With Sieving. IEEE Trans. Inf. Theory 2019, 65, 5243–5259. [Google Scholar] [CrossRef]
- Katsumata, S.; Kwiatkowski, K.; Pintore, F.; Prest, T. Scalable Ciphertext Compression Techniques for Post-quantum KEMs and Their Applications. In Advances in Cryptology—ASIACRYPT 2020; Moriai, S., Wang, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 289–320. [Google Scholar]
- Blum, A.; Kalai, A.; Wasserman, H. Noise-tolerant learning, the parity problem, and the statistical query model. In Proceedings of the 32nd Annual ACM Symposium on Theory of Computing; Portland, OR, USA, 21–23 May 2000, ACM Press: Portland, OR, USA, 2000; pp. 435–440. [Google Scholar] [CrossRef]
- Levieil, É.; Fouque, P.A. An Improved LPN Algorithm. In Proceedings of the SCN 06: 5th International Conference on Security in Communication Networks, Maiori, Italy, 6–8 September 2006; Prisco, R.D., Yung, M., Eds.; Lecture Notes in Computer Science. Springer: Heidelberg, Germany; Maiori, Italy, 2006; Volume 4116, pp. 348–359. [Google Scholar] [CrossRef]
- Guo, Q.; Johansson, T.; Löndahl, C. Solving LPN Using Covering Codes. In Advances in Cryptology—ASIACRYPT 2014, Part I; Sarkar, P., Iwata, T., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Kaoshiung, Taiwan, 2014; Volume 8873, pp. 1–20. [Google Scholar] [CrossRef]
- Guo, Q.; Johansson, T.; Löndahl, C. Solving LPN Using Covering Codes. J. Cryptol. 2020, 33, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, M.R.; Cid, C.; Faugère, J.; Fitzpatrick, R.; Perret, L. On the complexity of the BKW algorithm on LWE. Des. Codes Cryptogr. 2015, 74, 325–354. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, M.R.; Faugère, J.C.; Fitzpatrick, R.; Perret, L. Lazy Modulus Switching for the BKW Algorithm on LWE. In Proceedings of the PKC 2014: 17th International Conference on Theory and Practice of Public Key Cryptography, Buenos Aires, Argentina, 26–28 March 2014; Krawczyk, H., Ed.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Buenos Aires, Argentina, 2014; Volume 8383, pp. 429–445. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Johansson, T.; Stankovski, P. Coded-BKW: Solving LWE Using Lattice Codes. In Advances in Cryptology—CRYPTO 2015, Part I; Gennaro, R., Robshaw, M.J.B., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 2015; Volume 9215, pp. 23–42. [Google Scholar] [CrossRef]
- Kirchner, P.; Fouque, P.A. An Improved BKW Algorithm for LWE with Applications to Cryptography and Lattices. In Advances in Cryptology—CRYPTO 2015, Part I; Gennaro, R., Robshaw, M.J.B., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 2015; Volume 9215, pp. 43–62. [Google Scholar] [CrossRef] [Green Version]
- Becker, A.; Ducas, L.; Gama, N.; Laarhoven, T. New directions in nearest neighbor searching with applications to lattice sieving. In Proceedings of the 27th Annual ACM-SIAM Symposium on Discrete Algorithms, Arlington, VA, USA, 10–12 January 2016; Krauthgamer, R., Ed.; ACM-SIAM: Arlington, VA, USA, 2016; pp. 10–24. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Johansson, T.; Mårtensson, E.; Stankovski, P. Coded-BKW with Sieving. In Advances in Cryptology—ASIACRYPT 2017, Part I; Takagi, T., Peyrin, T., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Hong Kong, China, 2017; Volume 10624, pp. 323–346. [Google Scholar] [CrossRef]
- Mårtensson, E. The Asymptotic Complexity of Coded-BKW with Sieving Using Increasing Reduction Factors. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 2579–2583. [Google Scholar]
- Duc, A.; Tramèr, F.; Vaudenay, S. Better Algorithms for LWE and LWR. In Advances in Cryptology—EUROCRYPT 2015, Part I; Oswald, E., Fischlin, M., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Sofia, Bulgaria, 2015; Volume 9056, pp. 173–202. [Google Scholar] [CrossRef] [Green Version]
- Esser, A.; Kübler, R.; May, A. LPN Decoded. In Advances in Cryptology—CRYPTO 2017, Part II; Katz, J., Shacham, H., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 2017; Volume 10402, pp. 486–514. [Google Scholar] [CrossRef]
- Esser, A.; Heuer, F.; Kübler, R.; May, A.; Sohler, C. Dissection-BKW. In Advances in Cryptology—CRYPTO 2018, Part II; Shacham, H., Boldyreva, A., Eds.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 2018; Volume 10992, pp. 638–666. [Google Scholar] [CrossRef]
- Delaplace, C.; Esser, A.; May, A. Improved Low-Memory Subset Sum and LPN Algorithms via Multiple Collisions. In Lecture Notes in Computer Science, Proceedings of the 17th IMA International Conference on Cryptography and Coding, Oxford, UK, 16–18 December 2019; Springer: Heidelberg, Germany; Oxford, UK, 2019; pp. 178–199. [Google Scholar] [CrossRef]
- Wiggers, T.; Samardjiska, S. Practically Solving LPN. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021. [Google Scholar]
- Applebaum, B.; Cash, D.; Peikert, C.; Sahai, A. Fast Cryptographic Primitives and Circular-Secure Encryption Based on Hard Learning Problems. In Advances in Cryptology—CRYPTO 2009; Halevi, S., Ed.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 2009; Volume 5677, pp. 595–618. [Google Scholar] [CrossRef] [Green Version]
- Kirchner, P. Improved Generalized Birthday Attack. Cryptology ePrint Archive, Report 2011/377. 2011. Available online: http://eprint.iacr.org/2011/377 (accessed on 25 October 2021).
- TU Darmstadt Learning with Errors Challenge. Available online: https://www.latticechallenge.org/lwe_challenge/challenge.php (accessed on 1 May 2021).
- Lindner, R.; Peikert, C. Better Key Sizes (and Attacks) for LWE-Based Encryption. In Topics in Cryptology—CT-RSA 2011; Kiayias, A., Ed.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; San Francisco, CA, USA, 2011; Volume 6558, pp. 319–339. [Google Scholar] [CrossRef]
- Mulder, E.D.; Hutter, M.; Marson, M.E.; Pearson, P. Using Bleichenbacher’s solution to the hidden number problem to attack nonce leaks in 384-bit ECDSA: Extended version. J. Cryptogr. Eng. 2014, 4, 33–45. [Google Scholar] [CrossRef]
- Guo, Q.; Mårtensson, E.; Stankovski Wagner, P. On the Sample Complexity of solving LWE using BKW-Style Algorithms. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021. [Google Scholar]
- Baignères, T.; Junod, P.; Vaudenay, S. How Far Can We Go Beyond Linear Cryptanalysis? In Advances in Cryptology—ASIACRYPT 2004; Lee, P.J., Ed.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Jeju Island, Korea, 2004; Volume 3329, pp. 432–450. [Google Scholar] [CrossRef] [Green Version]
- Mårtensson, E. Some Notes on Post-Quantum Cryptanalysis. Ph.D. Thesis, Lund University, Lund, Sweden, 2020. [Google Scholar]
- Meier, W.; Staffelbach, O. Fast Correlation Attacks on Certain Stream Ciphers. J. Cryptol. 1989, 1, 159–176. [Google Scholar] [CrossRef]
- Chose, P.; Joux, A.; Mitton, M. Fast Correlation Attacks: An Algorithmic Point of View. In Advances in Cryptology—EUROCRYPT 2002; Knudsen, L.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 209–221. [Google Scholar]
- Lu, Y.; Meier, W.; Vaudenay, S. The Conditional Correlation Attack: A Practical Attack on Bluetooth Encryption. In Advances in Cryptology—CRYPTO 2005; Shoup, V., Ed.; Lecture Notes in Computer Science; Springer: Heidelberg, Germany; Santa Barbara, CA, USA, 2005; Volume 3621, pp. 97–117. [Google Scholar] [CrossRef] [Green Version]
- Budroni, A.; Guo, Q.; Johansson, T.; Mårtensson, E.; Stankovski Wagner, P. Making the BKW Algorithm Practical for LWE. In Progress in Cryptology—INDOCRYPT 2020, Proceedings of the International Conference on Cryptology in India (INDOCRYPT 2020), Bangalore, India,13–16 December 2020; Lecture Notes in Computer Science; Springer: Cham, Germany, 2020; pp. 417–439. [Google Scholar]
| q | |||
|---|---|---|---|
| 1601 | |||
| 1601 | |||
| 1601 | |||
| 1601 |
| n | q | LWE Estimator [7] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BKW- FWHT-SR | Coded- BKW | usvp | dec | dual | ||||||
| ENU | Sieve | ENU | Sieve | ENU | Sieve | |||||
| 40 | 1601 | 0.005 | 34.4 | 42.6 | 31.4 | 41.5 | 34.7 | 44.6 | 39.1 | 47.5 |
| 0.010 | 39.3 | 43.7 | 34.0 | 44.8 | 36.3 | 44.9 | 51.1 | 57.9 | ||
| 0.015 | 42.4 | 52.6 | 42.5 | 54.2 | 43.1 | 50.6 | 61.5 | 64.4 | ||
| 0.020 | 46.2 | 52.6 | - | - | 51.9 | 58.2 | 73.1 | 75.9 | ||
| 0.025 | 48.3 | 52.7 | - | - | 59.2 | 66.1 | 84.7 | 85.4 | ||
| 0.030 | 50.0 | 52.7 | - | - | 67.1 | 68.9 | 96.3 | 92.5 | ||
| 45 | 2027 | 0.005 | 37.7 | 55.2 | 31.8 | 41.9 | 35.0 | 44.8 | 41.5 | 51.6 |
| 0.010 | 43.5 | 55.2 | 39.5 | 51.2 | 41.2 | 48.2 | 57.0 | 64.6 | ||
| 0.015 | 48.3 | 55.2 | 50.4 | 61.3 | 51.2 | 58.3 | 74.3 | 74.9 | ||
| 0.020 | 51.2 | 55.2 | - | - | 61.1 | 65.0 | 86.8 | 86.1 | ||
| 0.025 | 54.1 | 55.3 | - | - | 71.0 | 71.4 | 100.7 | 95.0 | ||
| 0.030 | 56.3 | 64.1 | - | - | 80.2 | 78.7 | 116.2 | 104.1 | ||
| 50 | 2503 | 0.005 | 41.8 | 46.4 | 32.4 | 42.6 | 35.5 | 45.1 | 46.7 | 58.0 |
| 0.010 | 48.7 | 56.0 | 46.0 | 57.5 | 47.6 | 54.1 | 66.8 | 65.4 | ||
| 0.015 | 52.5 | 56.8 | - | - | 60.8 | 63.6 | 84.9 | 83.5 | ||
| 0.020 | 56.4 | 61.9 | - | - | 72.1 | 72.1 | 101.9 | 96.5 | ||
| 0.025 | 59.3 | 66.1 | - | - | 83.5 | 80.8 | 120.0 | 105.7 | ||
| 0.030 | 63.3 | 66.3 | - | - | 94.2 | 89.1 | 134.0 | 115.6 | ||
| 70 | 4903 | 0.005 | 58.3 | 62.3 | 52.3 | 54.2 | 55.2 | 63.3 | 76.2 | 75.9 |
| 0.010 | 67.1 | 73.7 | - | - | 80.4 | 77.1 | 111.3 | 98.9 | ||
| 0.015 | 73.3 | 75.6 | - | - | 102.5 | 93.2 | 146.0 | 118.0 | ||
| 120 | 14,401 | 0.005 | 100.1 | 110.5 | 133.0 | 93.2 | 135.5 | 111.4 | 181.9 | 133.2 |
| 0.010 | 115.1 | 124.0 | - | - | 195.0 | 150.4 | 266.2 | 165.7 | ||
| 0.015 | 127.0 | 136.8 | - | - | 246.4 | 183.2 | 334.0 | 209.8 | ||
| n | q | n. of Initial Samples | Running Time | Library | Machine | Cores | |
|---|---|---|---|---|---|---|---|
| 40 | 1601 | 0.005 | 16 M | 19 s | RBBL | B | 15 |
| 40 | 1601 | 0.005 | 16 M | 5 min 53 s | FBBL | B | 15 |
| 40 | 1601 | 0.005 | 16 M | 3 min 57 s | FBBL | A | 15 |
| 40 | 1601 | 0.010 | 570 M | 1 h 41 min | FBBL | A | 15 |
| 40 | 1601 | 0.015 | 4.2 B | 1 d 14 h | FBBL | A | 15 |
| 45 | 2027 | 0.005 | 250 M | 1 h 0 min | FBBL | A | 15 |
| 45 | 2027 | 0.010 | 8.3 B | 4 d 21.5 h | FBBL | A | 15 |
| 50 | 2503 | 0.005 | 2.7 B | 1 d 1.5 h | FBBL | A | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Budroni, A.; Guo, Q.; Johansson, T.; Mårtensson, E.; Wagner, P.S. Improvements on Making BKW Practical for Solving LWE. Cryptography 2021, 5, 31. https://doi.org/10.3390/cryptography5040031
Budroni A, Guo Q, Johansson T, Mårtensson E, Wagner PS. Improvements on Making BKW Practical for Solving LWE. Cryptography. 2021; 5(4):31. https://doi.org/10.3390/cryptography5040031
Chicago/Turabian StyleBudroni, Alessandro, Qian Guo, Thomas Johansson, Erik Mårtensson, and Paul Stankovski Wagner. 2021. "Improvements on Making BKW Practical for Solving LWE" Cryptography 5, no. 4: 31. https://doi.org/10.3390/cryptography5040031
APA StyleBudroni, A., Guo, Q., Johansson, T., Mårtensson, E., & Wagner, P. S. (2021). Improvements on Making BKW Practical for Solving LWE. Cryptography, 5(4), 31. https://doi.org/10.3390/cryptography5040031






