A New Class of Q-Ary Codes for the McEliece Cryptosystem
Abstract
1. Introduction
2. Preliminaries and Problem Statement
2.1. The McEliece Cryptosystem
2.2. Information-Set Decoding
2.3. Gaussian Integers
2.4. One Mannheim Error Correcting (OMEC) Codes
3. Product Codes Based on OMEC Codes
4. Erasure Only Decoding of RS Codes
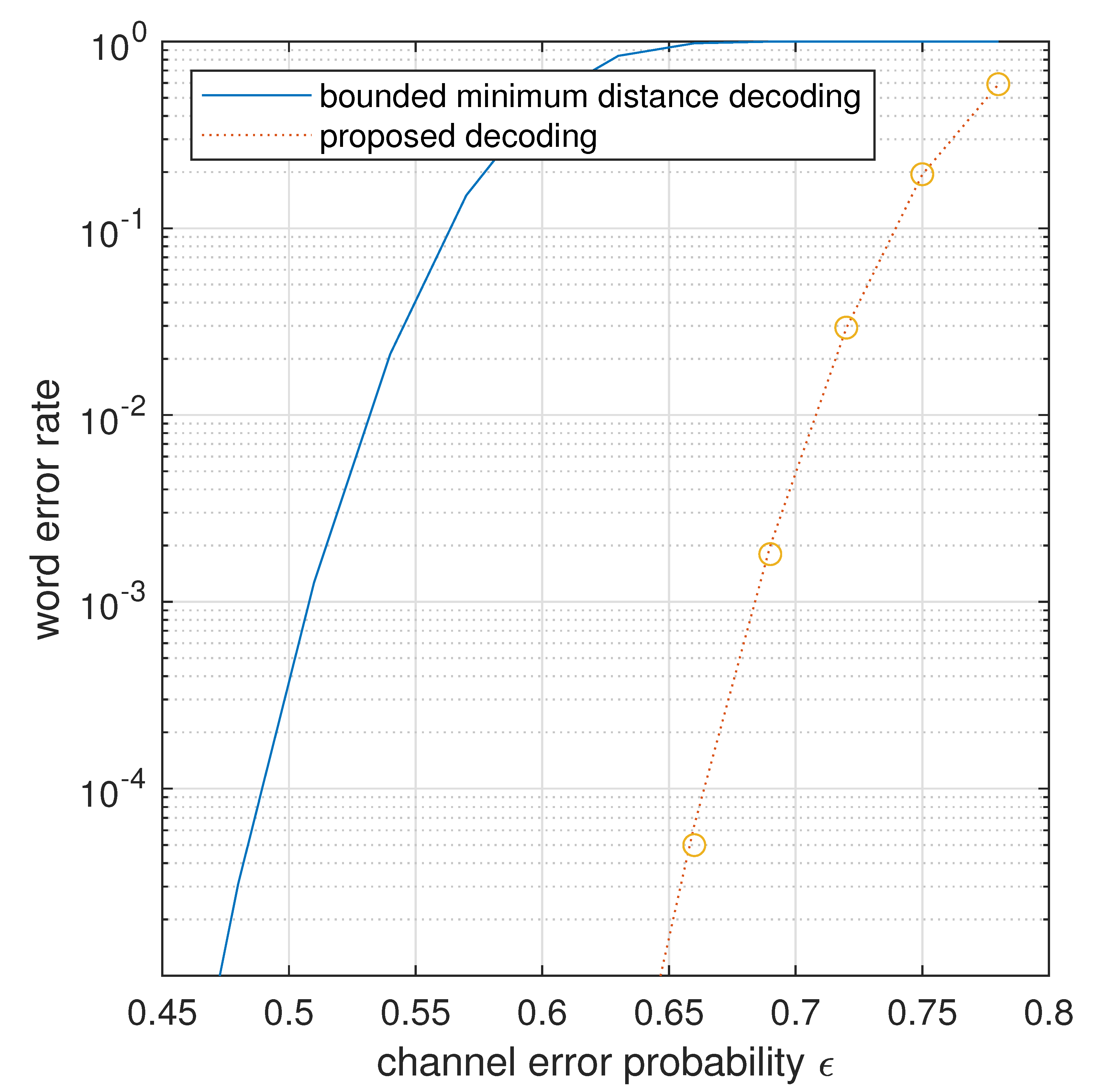
5. Decoding beyond Half the Minimum Distance
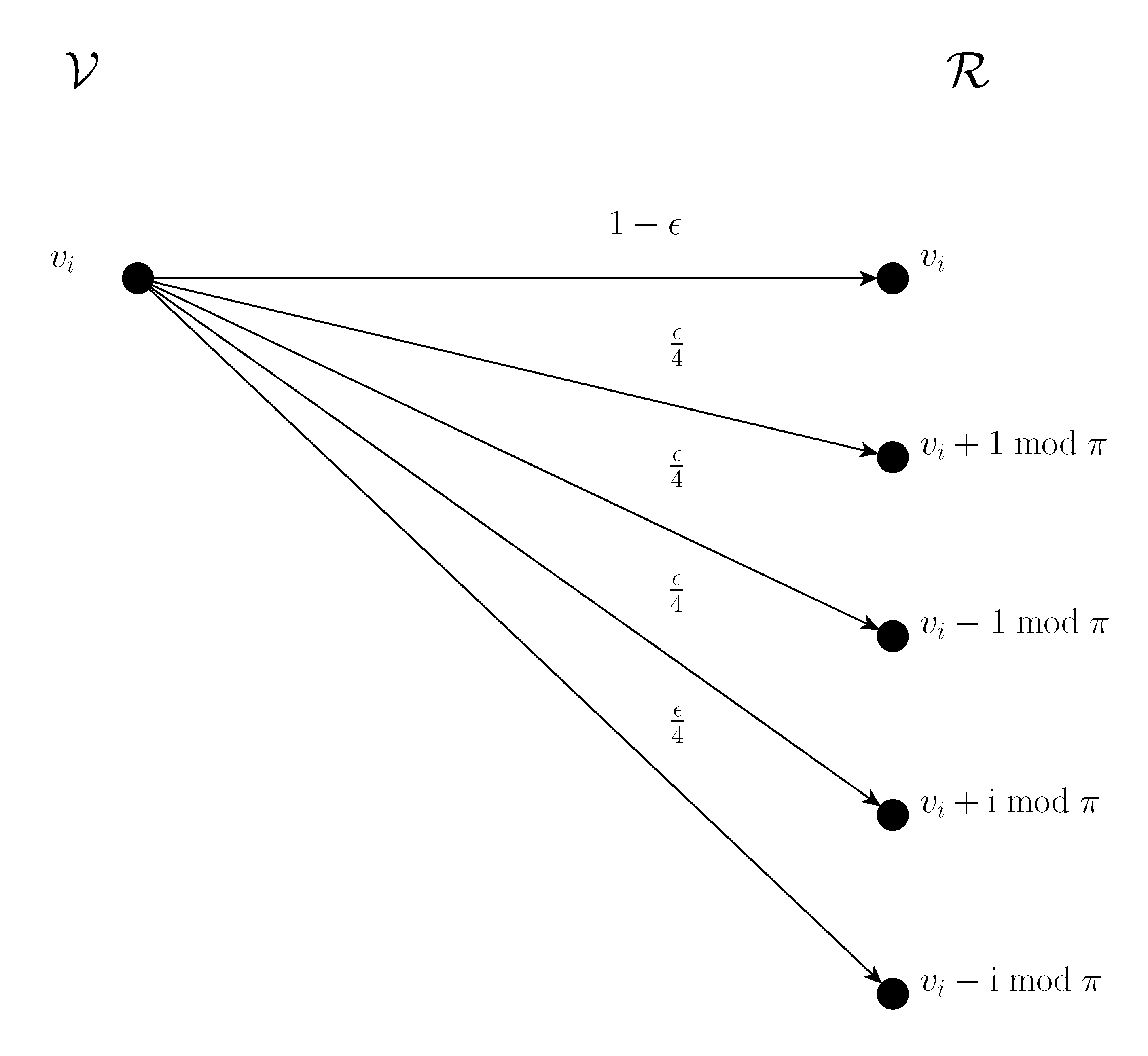
6. Capacity of the One Mannheim Error Channel
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- McEliece, R. A public-key cryptosystem based on algebraic coding theory. DSN Prog. Rep. 1978, 42–44, 114–116. [Google Scholar]
- Alagic, G.; Alperin-Sheriff, J.; Apon, D.; Cooper, D.; Dang, Q.; Kelsey, J.; Liu, Y.K.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process; Nistir 8309; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020.
- Berlekamp, E.; McEliece, R.; Van Tilborg, H. On the inherent intractability of certain coding problems. IEEE Trans. Inf. Theory 1978, 24, 384–386. [Google Scholar] [CrossRef]
- Wieschebrink, C. Two NP-complete problems in coding theory with an application in code based cryptography. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 1733–1737. [Google Scholar] [CrossRef]
- Berger, T.P.; Cayrel, P.L.; Gaborit, P.; Otmani, A. Reducing key length of the McEliece cryptosystem. In Progress in Cryptology—AFRICACRYPT; Preneel, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 77–97. [Google Scholar]
- Le Van, T.; Hoan, P.K. McEliece cryptosystem based identification and signature scheme using chained BCH codes. In Proceedings of the International Conference on Communications, Management and Telecommunications (ComManTel), DaNang, Vietnam, 28–30 December 2015; pp. 122–127. [Google Scholar] [CrossRef]
- Monico, C.; Rosenthal, J.; Shokrollahi, A. Using low density parity check codes in the McEliece cryptosystem. In Proceedings of the 2000 IEEE International Symposium on Information Theory, Sorrento, Italy, 25–30 June 2000; p. 215. [Google Scholar] [CrossRef]
- Shooshtari, M.K.; Ahmadian, M.; Payandeh, A. Improving the security of McEliece-like public key cryptosystem based on LDPC codes. In Proceedings of the 11th International Conference on Advanced Communication Technology, Gangwon-Do, Korea, 15–18 February 2009; Volume 2, pp. 1050–1053. [Google Scholar]
- Baldi, M.; Bianchi, M.; Maturo, N.; Chiaraluce, F. Improving the efficiency of the LDPC code-based McEliece cryptosystem through irregular codes. In Proceedings of the IEEE Symposium on Computers and Communications (ISCC), Split, Croatia, 7–10 July 2013; pp. 000197–000202. [Google Scholar] [CrossRef]
- Moufek, H.; Guenda, K.; Gulliver, T.A. A New Variant of the McEliece Cryptosystem Based on QC-LDPC and QC-MDPC Codes. IEEE Commun. Lett. 2017, 21, 714–717. [Google Scholar] [CrossRef]
- Hooshmand, R.; Shooshtari, M.K.; Eghlidos, T.; Aref, M.R. Reducing the key length of McEliece cryptosystem using polar codes. In Proceedings of the 11th International ISC Conference on Information Security and Cryptology, Tehran, Iran, 3–4 September 2014; pp. 104–108. [Google Scholar] [CrossRef]
- Lee, P.J.; Brickell, E.F. An observation on the security of McEliece’s public-key cryptosystem. In Advances in Cryptology—EUROCRYPT’88; Barstow, D., Brauer, W., Brinch Hansen, P., Gries, D., Luckham, D., Moler, C., Pnueli, A., Seegmüller, G., Stoer, J., Wirth, N., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 275–280. [Google Scholar]
- Stern, J. A method for finding codewords of small weight. In Coding Theory and Applications; Cohen, G., Wolfmann, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 106–113. [Google Scholar]
- May, A.; Meurer, A.; Thomae, E. Decoding random linear codes in (20.054n). In Advances in Cryptology—ASIACRYPT 2011; Lee, D.H., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 107–124. [Google Scholar]
- Bernstein, D.J.; Lange, T.; Peters, C. Attacking and defending the McEliece cryptosystem. In Post-Quantum Cryptography; Buchmann, J., Ding, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 31–46. [Google Scholar]
- Huber, K. Codes over Gaussian integers. IEEE Trans. Inf. Theory 1994, 40, 207–216. [Google Scholar] [CrossRef]
- Rifa, J. Groups of complex integers used as QAM signals. IEEE Trans. Inf. Theory 1995, 41, 1512–1517. [Google Scholar] [CrossRef]
- Dong, X.; Soh, C.B.; Gunawan, E.; Tang, L. Groups of algebraic integers used for coding QAM signals. IEEE Trans. Inf. Theory 1998, 44, 1848–1860. [Google Scholar] [CrossRef]
- Freudenberger, J.; Ghaboussi, F.; Shavgulidze, S. New Coding Techniques for Codes over Gaussian Integers. IEEE Trans. Commun. 2013, 61, 3114–3124. [Google Scholar] [CrossRef]
- Juraphanthong, W.; Jitprapaikulsarn, S. An asymmetric cryptography using Gaussian integers. Eng. Appl. Sci. Res. 2020, 47, 153–160. [Google Scholar]
- Freudenberger, J.; Shavgulidze, S. New Four-Dimensional Signal Constellations From Lipschitz Integers for Transmission Over the Gaussian Channel. IEEE Trans. Commun. 2015, 63, 2420–2427. [Google Scholar] [CrossRef]
- Rohweder, D.; Freudenberger, J.; Shavgulidze, S. Low-density parity-check codes over finite Gaussian integer fields. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 481–485. [Google Scholar] [CrossRef]
- Neubauer, A.; Freudenberger, J.; Kühn, V. Coding Theory: Algorithms, Architectures and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ivanov, F.; Kabatiansky, G.; Krouk, E.; Rumenko, N. A new code-based cryptosystem. In Proceedings of the 8th International Workshop on Code-Based Cryptography, CBCrypto, Zagreb, Croatia, 9–10 May 2020; pp. 41–49. [Google Scholar]
- Martinez, C.; Beivide, R.; Gabidulin, E. Perfect Codes for Metrics Induced by Circulant Graphs. IEEE Trans. Inf. Theory 2007, 53, 3042–3052. [Google Scholar] [CrossRef]
- Safieh, M.; Freudenberger, J. Montgomery Reduction for Gaussian Integers. Cryptography 2021, 5, 6. [Google Scholar] [CrossRef]
- Bossert, M. Channel Coding for Telecommunications; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Jiang, Y. A Practical Guide to Error-Control Coding Using Matlab; Artech House: Boston, MA, USA, 2010. [Google Scholar]
- Spinner, J.; Freudenberger, J. Decoder Architecture for Generalized Concatenated Codes. IET Circuits Devices Syst. 2015, 9, 328–335. [Google Scholar] [CrossRef]
- Spinner, J.; Rohweder, D.; Freudenberger, J. Soft input decoder for high-rate generalised concatenated codes. IET Circuits Devices Syst. 2018, 12, 432–438. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; John Wiley & Sons, Inc.: New York, NY, USA, 1968. [Google Scholar]
- Sidelnikov, V.M.; Shestakov, S.O. On insecurity of cryptosystems based on generalized Reed-Solomon codes. Discret. Math. Appl. 1992, 2, 439–444. [Google Scholar] [CrossRef]
- Fabsic, T.; Hromada, V.; Stankovski, P.; Zajac, P.; Guo, Q.; Johansson, T. A reaction attack on the QC-LDPC McEliece cryptosystem. In Proceedings of the Post-Quantum Cryptography—8th International Workshop (PQCrypto), Utrecht, The Netherlands, 26–28 June 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 51–68. [Google Scholar] [CrossRef]
- Huber, K. Codes over Eisenstein-Jacobi Integers. Contemp. Math. 1994, 165–179. [Google Scholar] [CrossRef]


| Proposed Codes Over Gaussian Integers | MDS Codes | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| p | n | k | t | p | n | k | t | ||
| 137 | 272 | 55 | 163 | 277 | 272 | 55 | 109 | ||
| 157 | 312 | 63 | 187 | 313 | 312 | 63 | 124 | ||
| 173 | 344 | 69 | 207 | 347 | 344 | 69 | 137 | ||
| 193 | 384 | 77 | 231 | 389 | 384 | 77 | 153 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freudenberger, J.; Thiers, J.-P. A New Class of Q-Ary Codes for the McEliece Cryptosystem. Cryptography 2021, 5, 11. https://doi.org/10.3390/cryptography5010011
Freudenberger J, Thiers J-P. A New Class of Q-Ary Codes for the McEliece Cryptosystem. Cryptography. 2021; 5(1):11. https://doi.org/10.3390/cryptography5010011
Chicago/Turabian StyleFreudenberger, Jürgen, and Johann-Philipp Thiers. 2021. "A New Class of Q-Ary Codes for the McEliece Cryptosystem" Cryptography 5, no. 1: 11. https://doi.org/10.3390/cryptography5010011
APA StyleFreudenberger, J., & Thiers, J.-P. (2021). A New Class of Q-Ary Codes for the McEliece Cryptosystem. Cryptography, 5(1), 11. https://doi.org/10.3390/cryptography5010011






