Abstract
Herder et al. (IEEE Transactions on Dependable and Secure Computing, 2017) designed a new computational fuzzy extractor and physical unclonable function (PUF) challenge-response protocol based on the Learning Parity with Noise (LPN) problem. The protocol requires no irreversible state updates on the PUFs for security, like burning irreversible fuses, and can correct for significant measurement noise when compared to PUFs using a conventional (information theoretical secure) fuzzy extractor. However, Herder et al. did not implement their protocol. In this paper, we give the first implementation of a challenge response protocol based on computational fuzzy extractors. Our main insight is that “confidence information” does not need to be kept private, if the noise vector is independent of the confidence information, e.g., the bits generated by ring oscillator pairs which are physically placed close to each other. This leads to a construction which is a simplified version of the design of Herder et al. (also building on a ring oscillator PUF). Our simplifications allow for a dramatic reduction in area by making a mild security assumption on ring oscillator physical obfuscated key output bits.
1. Introduction
Physical unclonable functions or PUFs [,] utilize inherent manufacturing variations to produce hardware tokens that can be used as building blocks for authentication protocols. Many different physical phenomena have been proposed to provide PUF behavior including Ring Oscillators (ROs) [,,], cross-coupled latches or flip-flops [], capacitive particles in a coating [], and beads in an optical card []. PUFs can be categorized by the type of functionality they provide: Weak PUFs, also called Physically Obfuscated Keys (POKs), are used for secure key storage. Strong PUFs implement (pseudo) random functions based on exploiting manufacturing variations that vary from PUF instance to PUF instance; strong PUFs are used for device identification and authentication. The primary advantage of using a strong PUF is that the communication between the authenticator and the physical device need not be protected. This is because each authentication uses a distinct input to the “pseudorandom function”.
In this work, we deal with the design and implementation of strong PUFs. A strong PUF is a physical token that implements a function that translates challenges into responses. The reliability property of a strong PUF says that if the same challenge is provided multiple times, the responses should be close (according to some distance metric) but not necessarily the same. The security property is that an adversary with access to the PUF (and the ability to see responses for chosen queries) should not be able to predict the response for an unqueried challenge. Recently, attacks in this model allow creation of accurate models for many proposed strong PUFs [,,,,]. We only consider attacks using the input and output behavior. An additional required security property is that the adversary should not be able to physically clone the device to create a device with similar behavior (see [] for more on required properties).
These attacks can be mitigated by designing new PUFs or adding protections to the PUF challenge-response protocol. Our focus is on improving the challenge-response protocol. A natural way to prevent learning attacks is to apply a one-way hash to the output. However, the PUF reliability property only says that responses are noisy: they are close, not identical. Fuzzy extractors [] can remove noise at the cost of leaking information about the response. This information leakage prevents fuzzy extractors from being reused across multiple challenges [,,,]. Computational fuzzy extractors do not necessarily leak information [] and some constructions may be reusable []. Herder et al. have designed a new computational fuzzy extractor and PUF challenge-response protocol designed to defeat modeling attacks []. Their construction is based on the learning parity with noise (LPN) problem [], a well-studied cryptographic problem. Essentially, the LPN problem states that a product of a secret vector and a random matrix plus noise is very hard to invert. However, their work did not implement the protocol, leaving its viability unclear.
Our Contribution: We provide the first implementation of a challenge-response protocol based on computational fuzzy extractors. Our implementation allows for arbitrary interleaving of challenge creation, called , and the challenge response protocol, called , and is stateless. Our implementation builds on a Ring Oscillator (RO) PUF on a Xilinx Zynq All Programmable SoC (System on Chip) [], which has an FPGA (Field Programmable Gate Array) and a co-processor communicating with each other.
Our approach is based on the LPN problem, like the construction of Herder et al. [], with the following fundamental differences:
- In order to minimize area overhead so that all control logic and other components fit well inside the FPGA, we reduce storage (by not storing the whole multiplication matrix of the LPN problem, but only storing its hash) and, most importantly, we outsource Gaussian elimination to the co-processor.
- We keep the same adversarial model: we only trust the hardware implementation of and in FPGA, i.e., we do not trust the co-processor. In fact, we assume that the adversary controls the co-processor and its interactions with the trusted FPGA logic; in particular, the adversary observes exactly what the co-processor receives from the trusted FPGA logic and the adversary may experiment with the trusted FPGA logic through the communication interface. As in Herder et al. [], we assume that an adversary can not be successful by physically attacking the trusted FPGA logic with its underlying RO PUF. We notice that in order to resist side channel attacks on the FPGA logic itself, the logic needs to be implemented with side channel counter measures in mind. This paper gives a first proof-of-concept without such counter measures added to its implementation.
- In order to outsource Gaussian elimination to the co-processor, the trusted FPGA logic reveals so-called “confidence information” about the RO PUF to the co-processor, which is controlled by the adversary. This fundamentally differs from Herder et al. [] where confidence information is kept private.
- To prove security of our proposal, we introduce a mild assumption on the RO PUF output bits: we need to assume that the RO PUF output bits are represented by an “LPN-admissible” distribution for which the LPN problem is still conjectured to be hard. We argue that the RO PUF output distribution is LPN-admissible for two reasons (see Definition 1 and discussion after Theorem 1):
- Since we reveal the “confidence information”, we can implement a masking trick which, as a result, only reveals a small number of equations, making the corresponding LPN problem very short; we know that very short LPN problems are harder to solve than long ones.
- Studies have shown that the RO pairs which define the RO PUF on FPGA can be implemented in such a way that correlation among RO pairs can be made extremely small; this means that the RO PUF creates almost identical independent distributed (i.i.d.) noise bits in the LPN problem and we know that, for i.i.d. noise bits, the LPN problem has been well-studied and conjectured to be hard for decades.
Our main insight is that “confidence information” does not have to be kept private—this is opposed to what has been suggested in Herder et al. []. As a result of our design decisions:
- The area of our implementation on FPGA is 49.1 K LUTs (Look-up Tables) and 58.0 K registers in total. This improves over the estimated area overhead of 65.7 K LUT and 107.3 K registers for the original construction of Herder et al. [].
- The throughput of our implementation is 1.52 K executions per second and 73.9 executions per second.
- According to our experiments on real devices, even though the underlying RO PUF has a measured maximum error rate (i.e., the fraction of RO pairs producing a wrong response bit) of 8% for temperatures from 0 to 70 degree Celsius, correctly reconstructed responses for 1000 measurements.
- The source code of our complete implementation is available at github.com/scluconn/LPNbased_PUF.
Organization: This paper is organized as follows: In Section 2, we introduce the necessary background and the original LPN-based PUF design of []. Our simplified and implementation friendly LPN-based PUF construction is described in Section 3. The implementation details and security analysis with discussion on admissible LPN distributions are provided in Section 4 and Section 5, respectively. We compare our work with related work in Section 6. The paper concludes in Section 7.
2. Background
2.1. Adversarial Model
In this paper, we use the same adversarial model as that in []:
- We assume that the hardware implementation of and in FPGA cannot be tampered with by the adversaries.
- The software running on the processor does not need to be trusted. This implies that its computation and interactions with FPGA hardware logic can be observed, tampered, and controlled by the adversaries.
- The adversaries are able to read all the digital secrets stored in the non-volatile memory on the device by imaging attacks, so no digital secret is allowed in the hardware device.
- The adversaries can also experiment with the trusted FPGA logic through the communication interface and get a polynomial number of valid challenge response pairs. However, notice that side channel analysis is not considered in our proof-of-concept implementation. In order to resist side channel attacks on the FPGA logic itself, the logic needs to be implemented in a side channel resilient way.
2.2. Learning Parity with Noise
We recall the definition of the LPN problem. Informally, this is the problem of decoding random linear codes under independently and identically distributed (i.i.d.) bit errors, which is widely conjectured to be hard for large enough error []. Based on LPN, many cryptographic primitives are proposed [,,,]. Formally, the LPN problem is defined as follows []:
Conjecture 1.
Let and be chosen uniformly at random, . Let be a vector that has all its entries chosen from a distribution χ, which implies that each is independently and identically distributed (i.i.d). We define as
Given the pair and knowledge of distribution χ, the (computational) LPN problem is to determine . The LPN conjecture states that there is no algorithm that solves an LPN problem instance in time with non-negligible probability in n where χ is a Bernoulli distribution with bias τ.
As shown in [,,,,], the current best known algorithm is slightly sub-exponential with running time . Note that this algorithm requires samples. The construction in this paper only provides samples in which case the best known algorithm is []. Typically, for RO POK outputs, [,] (this is also verified by the experiments in this paper). This means that, for practical parameters, constant factors in are the same size as the term making the algorithm take time of approximately .
Related to Conjecture 1, we define, besides Bernoulli distributions with bias , the larger set of LPN-admissible distributions:
Definition 1.
For arbitrary distributions (here, outputs a binary vector of length m), we define LPN-admissible if there is no algorithm that solves an LPN problem instance with knowledge of the distribution in time with non-negligible probability in n.
We will use this definition of an LPN-admissible distribution in the security analysis of our construction. Please note that does not require that each dimension is i.i.d.
2.3. Original Construction
Herder et al. [] proposed the first computationally secure PUF design, called the LPN-based PUF, which self-corrects measurement noise even when measurement noise is large. The PUF has two main procedures: (see Figure 1) and (see Figure 2), which are used to generate challenge-response pairs (CRPs) and regenerate a response for a given challenge , respectively.
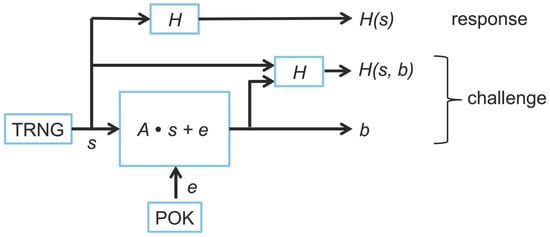
Figure 1.
Redrawn from []: : produces a challenge response pairs , where and
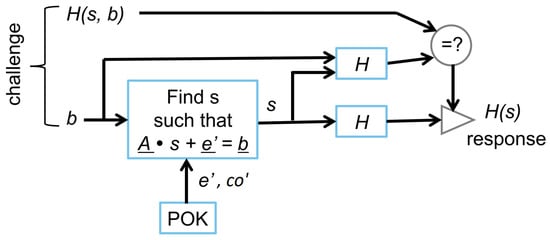
Figure 2.
Redrawn from []: : reproduces the response corresponding to challenge .
In (Figure 1), a Physical Obfuscated Key (POK) generates a noise vector . The proposed POK is implemented as a sequence of independent RO pairs (i.e., an RO PUF), which together produce . We assume this implements an LPN-admissible distribution; implicitly, this means that we assume that RO pairs that are close together in the concrete circuit implementation of the POK still produce sufficiently (admissible) independent output bits. Notice that the response vector of the POK is vector and this should not be confused with the response of the larger LPN-based PUF construction. We notice that the POK ideally creates ‘close to’ unbiased response bits—in practice, the worst-case bias per response bit we have seen in the literature and our experiments is [,] (in our implementation, we measured ).
As a final step in , vector together with the hash of concatenated with are outputted as challenge, and the hash of is outputted as the corresponding response.
In (Figure 2), the POK generates vector together with a confidence information vector , where each bit measures the reliability of . In the context of using ring oscillator pairs as the POK, the confidence information is the absolute value of the frequency difference between two ring oscillators, and the generated bit encodes the sign of this difference. If the confidence information value is larger, it is less likely that generated by this ring oscillator pair will be flipped under environmental condition variations. Notice that this implies that the confidence information is correlated with the reliability of , but it does not imply correlation between and the value of .
Vector is used to locate the reliable bits in , and it is kept secret inside the device. The subset of equations in that correspond to these reliable positions has a very high likelihood of containing a completely noise free subset of equations. Let indicate the n indices of a set of noise free bits, and let be vector truncated to the positions indexed by , and, similarly, let indicate the submatrix corresponding to the rows in indexed by . For , , hence, can be computed from , , and . With high likelihood, is invertible and Gaussian elimination allows us to regenerate the secret . Thus, the LPN problem becomes easy if confidence information can be used. That is, the measurement noise should be small enough in order to be able to find a proper set in time—in practice, an exhaustive search over to most likely candidates . The reader is referred to [] for further details and security proof of this construction.
The above technique creates a noise-free PUF in that the exact same previously generated response is reconstructed by . This implies that responses can serve as keys in cryptographic primitives.
3. Our Construction
It costs significant area overhead to perform Gaussian elimination in hardware. For this reason, we propose a hardware software co-design of LPN-based PUFs where Gaussian elimination is pushed to the untrusted software, i.e., only the hardware components are assumed to be trusted in that they are not tampered with and an adversary can only observe the interactions between hardware and software.
As in the original construction, our LPN-based PUF has a Physical Obfuscated Key (POK), which always measures the same response, at its core. It also has two modes of operation: (Figure 3) and (Figure 4). Each instance of creates a challenge-response pair. If a correctly created challenge is given to the LPN-based PUF operating in mode, then the corresponding response is regenerated. In Figure 3 and Figure 4, the functions in white boxes are implemented in hardware and are trusted. The processor (in the grey box) and the software running on it are considered to be untrusted; therefore, all of the computation executed by the software should be verified by the trusted hardware in the diamond shaped boxes.
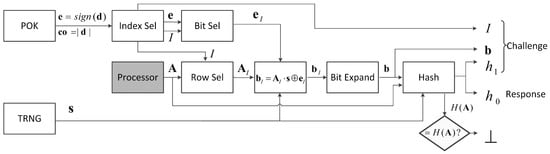
Figure 3.
: produces a challenge response pair , where with and with , and where with .
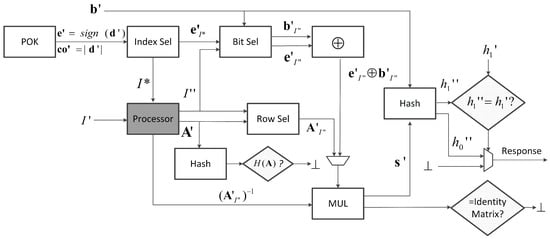
Figure 4.
: takes input , and either outputs an exception symbol ⊥, or outputs the response . Notice that is continuously fed into the multiplier with a small amount of bit flips (less than t bits). The regenerated index set of reliable bits is denoted as .
Generation : Matrix is selected at random by the manufacturer, and it can be the same for all the devices. Therefore, its hash value can be completely hard coded into the circuit to prevent adversaries from manipulating matrix . In our construction, a POK is implemented by m Ring Oscillator pairs (RO pairs), where m is the number of rows in matrix . Note that we use a POK, but our protocol supports a large number of challenge-response pairs yielding a strong PUF overall.
The POK generates a vector with count differences coming from the RO pairs. The sign of each entry in gives a binary vector , and the absolute value of the entries in represents confidence information . selects a set of bits from where the corresponding confidence information is at least some predefined threshold .
The processor feeds the rows of one by one into the hardware. By using a bit select module based on set , the hardware extracts and feeds the rows of to a hardware matrix-vector multiplier. The hardware matrix-vector multiplier takes input matrix , an input vector generated by a True Random Number Generator (TRNG), and , and computes . We set all bits for to generate the complete vector of m bits. This masking trick has the advantage that no unnecessary information is given to the adversary (and will allow us to have a reduction to a very short LPN-problem). After is constructed, hash values and are computed. The challenge is with response .
Since any software computation is considered untrusted, the hardware needs to verify the hash of . This circuitry (with hash embedded) is used in mode to verify that the (untrusted) processor provides the correct specified by the manufacturer, instead of an adversarially designed matrix. This is needed because the underlying LPN problem is only hard if is a randomly chosen matrix; an adversarially designed could leak the POK behavior. Similarly, matrix also needs to be verified in for the same reason.
Verification : In mode, the adversary inputs a possibly corrupted or maliciously generated challenge ( in , we denote all the variables, which should have the same values as the corresponding variables used in , as the original variable followed with a single quotation mark (). e.g., in should be equal to in , if it is not maliciously manipulated by adversaries). Before a corresponding response will be reconstructed, the hardware in mode needs to check whether was previously generated in mode.
The POK measures again count differences from its RO pairs and obtains and . There are some errors in , so . For indices i corresponding to high confidence, we expect with (very) small probability. We use this fact to remove (almost all of) the noise from the linear system.
The POK observes which i corresponds to a bit that has high confidence value; we call the set of reliable bit positions , which should have a similar size as that of . The POK then sends to the processor. The processor takes input challenge and picks a subset with such that matrix has full-rank. We notice that, by using a subset of both and the probability for is much smaller than for or .
The processor computes and transmits to the hardware matrix-vector multiplier the inverse matrix of matrix . Next, the rows of matrix are fed one by one into the hardware and its hash is computed and verified against . The rows corresponding to submatrix are extracted (using a bit select functionality based on ) and the columns of are fed into the hardware matrix-vector multiplier one by one. This verifies that and are inverses of one another (the equal identity matrix box in Figure 4 verifies that the columns of the identity matrix are being produced one after another). The correctness of matrix is guaranteed by checking whether the hash of matrix matches the hash value (as was done in ). The correctness of implies the correctness of (since was fed as part of into the hardware). Therefore, if all checks pass, then is indeed the inverse of a properly corresponding submatrix of the matrix used in . (The reason why this conclusion is important is explained in Section 5.).
Next, the hardware computes the vector and multiplies this vector with matrix using the hardware matrix-vector multiplier:
The (non-malleable) hash value is compared with the input value from the challenge.
Suppose that input was generated as for some and . If , we conclude that is correct in that it is equal to input which was hashed into when was generated, and is correct in that it is equal to input which was hashed into when was generated.
Since the adversary is not able to solve the LPN problem, the check together with the conclusion that led to a proper solution of the LPN problem by using the bits in the POK-generated vector implies that only the LPN-based PUF itself could have generated and, hence, the challenge. This means that the LPN-based PUF must have selected and produced the inputted challenge with during an execution of . We notice that vector can only be recovered if in the execution of equals in (1). We conclude that is now able to generate the correct response (since must have been the response that was generated by the LPN-based PUF when it computed the challenge with ).
If , then likely and only differ in a few positions (if there is no adversary). By flipping up to t bits in (in a fixed pattern, first all single bit flips, next all double bit flips, etc.), new candidate vectors can be computed. When the hash verifies, the above reasoning applies and with the correct response . Essentially, since the bits we are using for verification are known to be reliable, if the system is not under physical attacks, then very likely there are no more than t bit errors in . Internally, we can try all the possible error patterns on with at most t bit flips, and check the resulted against to tell whether the current was used in or not.
If none of the t bit flip combinations yields the correct hash value , then the exception ⊥ is output. This decoding failure can be caused by attackers who feed invalid CRPs, or a very large environmental change that results in more than t bit errors in , which can also be considered as a physical attack. We notice that allowing t-bit error reduces the security parameter with ≈t bits since an adversary only needs to find within t bit errors from . In order to speed up the process of searching for the correct , we use a pipelined structure which keeps on injecting possible (with at most t bit flips) to the hardware matrix-vector multiplier.
Being able to recover is only possible if in the execution of and in Equation (1) are equal up to t bit flips. This is true with high probability if is large enough and was properly selected as a subset of . As explained by Herder et al. [], m should be large enough so that an appropriate can be selected with the property that, when the RO pairs are measured again, there will be a set of n reliable bits: in particular, according to the theorical analysis in [], for , this corresponds to m at most 450 RO pairs for operating temperature from 0 to 70 degrees Celsius and error probability (of not being able to reconstruct ) less than . Readers are referred to Equation (2) in [] for an estimation of given the distribution of RO outputs and the desired error rate.
Comparison with previous work: Our approach differs from the construction of Herder et al. in [] in the following ways:
- We output the indices of reliable bits to the untrusted processor, instead of keeping the positions of these reliable bits private inside the hardware. In Section 5, we argue that the distribution of and, in general, are still LPN-admissible.
- By masking (i.e., making all-zero outside ), we can reduce the security to a very short LPN problem with equations (corresponding to set ).
- By revealing and to the processor, the processor can select a submatrix with which is a full rank matrix. This would consume more area if done in hardware.
- Since the processor knows the selected submatrix , the processor can compute the inverse matrix. Hence, we do not need a complex Gaussian eliminator in hardware and we reuse the matrix-vector multiplier used in mode.
- Because the processor with executing software is considered to be untrusted, we add mechanisms to check manipulation of and .
- Matrix does not need to be hard-coded in circuitry. Instead, a hash-of--checking circuitry is hard coded in hardware giving less area overhead.
4. Implementation
We implemented our construction on Xilinx Zynq All programmable SoC []. The Zynq platform contains an ARM-based programming system with some programmable logic around it. Having a hard core embedded, this platform makes our software hardware co-design implementation easier and more efficient in software execution. We implemented the software units on the ARM core and the hardware units in the programmable logic. The communication between these two parts is over an AXI Stream Interface in order to maximize the communication throughput. The FPGA layout of the implemented LPN-based PUF is shown in Figure 5.
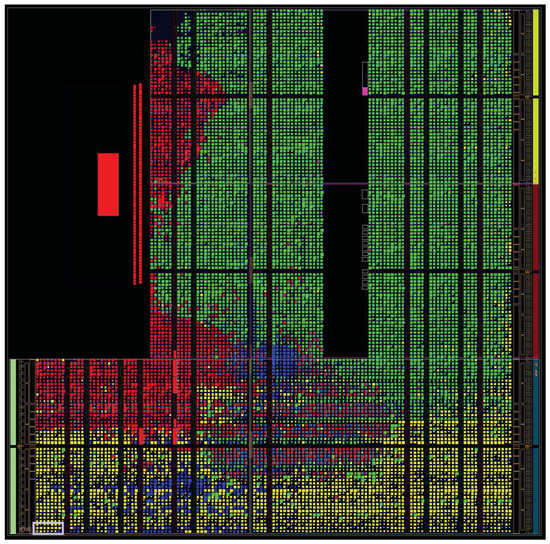
Figure 5.
FPGA layout of the entire LPN-based PUF implementation. Four main components are highlighted: LPN core (Green), RO pairs (Yellow), communication (Red), hash function SHA-256 (Blue). The ARM core is positioned at the large black rectangle top left; the thick black column in the middle is block RAM. We magnify the left bottom corner in this figure (highlighted by a purple box) to be Figure 6.
We have 450 RO pairs for generating with confidence information as depicted in Figure 3 and Figure 4. Each RO has five stages, and the two ROs in each RO pair are manually placed at adjacent columns on the FPGA to minimize the systematic effects [] (see Figure 6). We measure the toggles at the output of each RO for 24 clock cycles to generate and . In mode, module Index Selection compares vector with a threshold to produce an index vector, which indicates the positions of all the reliable bits. This is used in module Bit Selection to condense the 450-bit vector to a 256-bit vector by selecting 256 bits out of all the reliable bits. Set restricted to these 256 bits is sent to the processor as part of the generated challenge.
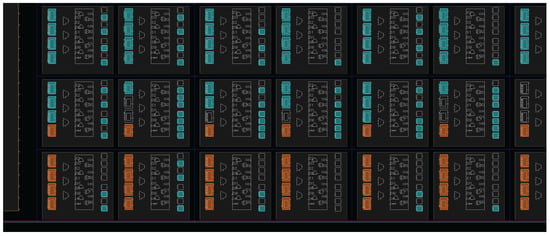
Figure 6.
In this figure, we magnify the area at the left bottom corner in Figure 5. We only highlighted the LUTs implementing RO arrays as orange blocks. Each LUT is implemented as one inverter. Therefore, they are 5-stage ROs, and they are placed manually in adjacent columns on the FPGA.
Next, the processor sends matrix (450 rows times 128 columns) to the hardware row by row. All the rows will be fed into the hash function to compute to verify the correctness of . Only the rows in , which will be used later in a matrix multiplication, are selected and stored by the Row Selection module. Since we implemented a pipelined matrix-vector multiplier for multiplying a matrix with a 128-bit vector, multiplies the submatrix of with a randomly generated vector by loading this submatrix in two parts. After XORing , we obtain a 256-bit vector . Module Bit Expand adds zeroes to create the full 450-bit vector . After Bit Expand, we feed the 450 bits of and the 128 bits of to the hash module to compute and . We implemented a multiple ring oscillator based true random number generator [] to generate the 128-bit vector , and SHA-256 [] is implemented as the hash function.
In mode, 450 RO pairs are evaluated in the same way as in . Now, the module Index Selection generates index set , which is sent to the processor. A correctly and non-maliciously functioning processor should take the intersection of and the correct set , which was produced by . From this intersection, the processor selects an index set such that the submatrix is invertible. Since a randomly selected 128 × 128 submatrix may not be invertible, it may require the processor to try a couple of times until finding an invertible matrix. Matrix is streamed to the hardware row by row and is stored in registers, which will be the matrix input for the matrix-vector multiplier.
Next, the processor streams into the hardware row by row. All the rows will be fed into the hash function to compute to verify the correctness of . At the same time, the rows of are fed into the Row Selection module for selecting the 128 × 128 submatrix . All the rows in are temporarily saved in an array of shift registers. After all the rows of are streamed in, the array of shift registers can shift out column by column and reuse the pipelined matrix-vector multiplier in to check whether the product of and each column of is a column of the identity matrix or not.
If the above two checks pass, then the inverse matrix will be multiplied with to recover . Here, the processor should have given to the hardware so that the Bit Selection module can be used to obtain (with ). The recovered is further verified by computing . If ; then, the hardware computes and outputs . According to the calculation in [], we set . This means that we need to exhaustively try all the one bit flips. This means that there are 129 possible possible in total (these can be fed one by one into the pipelined matrix-vector multiplier). If none of these yields a correct , then the hardware will output an all-zero vector to indicate a ⊥ response. Similarly, if any of the above checks (of the hash of and of the inverse matrix) fails, then the hardware will output the all-zero vector as well.
Our implementation results. The area of our full design on FPGA is 49.1 K LUTs and 58.0 K registers in total. The area utilization of each part is shown in Table 1. The three most costly components are two 128 × 128 register arrays and the 450 RO pairs, which form together the underlying RO PUF. The dynamic power consumption of the complete implementation is 1.753 W, and its static power consumption is 0.163 W.

Table 1.
Area utilization of the implemented LPN-based PUF.
The throughput of our implementation is measured as 1.52 K executions per second and 73.9 executions per second. The execution time of is dominated by the matrix transmission, which takes 91% of the overall execution time. However, is dominated by the software Gaussian elimination, where each Gaussian elimination takes about 3880 s to finish, and each requires 3.47 Gaussian eliminations on average.
Comparison. The original construction in [] would need a hardware Gaussian eliminator in an implementation. The most efficient implementation of a pipelined Gaussian eliminator takes 16.6 K LUT and 32.9 K registers on FPGA for a 128 row matrix []. In our design, we save this area by pushing the computation to the software.
One may argue that, in order to push Gaussian elimination to untrusted software, we have to add extra hardware to check for the correctness of the inverse matrix. Notice, however, for checking this inverse matrix, we reuse the matrix-vector multiplier in . Therefore, the only additional hardware overhead is one 128 × 128 register array. If we do Gaussian elimination in hardware, then we need registers to store the whole matrix of size 128 × 256 and the output matrix of the Gaussian elimination, which is another 128 × 128 bits: this is because a random matrix constructed by 128 rows in may not have full rank. As a result, the hardware may need to try a couple of times in order to find an invertible submatrix of . For these reasons, compared to our implementation in this paper, Gaussian elimination in hardware will cost an additional 128 × 128 register utilization together with the control logic for randomly selecting 128 rows out of a 256-row matrix.
If we would implement the original construction in hardware, then its area overhead without additional control logic is estimated at 65.7 K LUT (49.1 K + 16.6 K) and 107.3 K register (58.0 K + 32.9 K + 16.4 K). This resource utilization would be larger than the available resources on our FPGA (53.2 K LUT and 106.4 K registers).
Experimental Results. We characterized the error rate of RO pairs defined as the percentage of error bits generated in one 450 bit vector . The error rate of the implemented 450 RO pairs at room temperature is , which is in the range (2∼) that has been reported in a large scale characterization of ring oscillators []. We measured the error rate of 450 RO pairs under different temperatures from 0 to 70 degrees Celsius where the output of the 450 RO pairs is compared to a reference output vector generated at 25 degrees Celsius. We observed a maximum error rate of 8% (36 out of 450) over 1000 repeated measurements. This error rate is within the range of the error correction bound (9%) estimated in []. We also characterized the bias of all the RO pair outputs, for our implementation.
We experimented with the whole system under different temperatures (at C, C and C). This showed that was always able to reconstruct the proper response. No failure was observed over 1000 measurements under different tempratures. We did not perform testing on voltage variation and aging because the overall error rate is only affected by the error rate of the RO pair output bits. As long as the error rate of RO outputs is lower than 9% [], given the current implementation, we can have a large probability to regenerate the correct response. The overall error rate will not be affected by how we introduce the errors in RO pairs.
If a TRNG has already been implemented in the system, then the TRNG can be reused for the LPN-based PUF as well. As a part of a proof-of-concept implementation of the LPN-based PUF, we did not perform a comprehensive evaluation of our implemented TRNG.
Future Direction. In our implementation, the area of LPN core mainly consists of two 128 × 128 bit register arrays for storing two matrices. It is possible to eliminate storage of these two matrices in order to significantly reduce the area at the cost of paying a performance penalty.
The proposed alternative implementation works as follows: instead of storing two matrices for checking (in ) whether and are indeed inverse matrices of one another, we only store at most one row or one column in the hardware at the same time. In , we will need to first feed in matrix , and let the hardware check its hash. At the same time, the rows in are selected and fed into another hash engine to compute which is separately stored. However, the hardware does not store any of the rows of (and this avoids the need for a 128 × 128 bit register array). Notice that after this process the authenticity of matrix has been verified, and, as a result, we know that the rows of are equal to the rows of , hence, the stored hash which can now be used to verify the submatrix whenever it is loaded again into the hardware.
Next, matrix is fed into the hardware column by column. When a column is fed into the hardware, e.g., the i-th column, we store it in the hardware temporarily. Then, the processor sends the whole matrix to the hardware row by row. Its hash is computed on the fly and in the end compared with the stored hash . At the same time, each received row of is multiplied (inner product) with the current stored i-th column of . This is used to check if the product is indeed equal to the corresponding bit in the i-th column of the identity matrix. If this check passes for all rows of and the hash verifies as well, then this column will be added to the intermediate value register of , based on whether i-th bit of equals 1 or not.
In the above protocol, we also hash all received columns of and store the hash in a separate register. If the above checks pass for all columns, then we know that this hash must correspond to . This will facilitate the process of trying other possible versions of in the future (where the processor again feeds matrix column by column so that its hash and at the same time can be computed).
The first trial/computation of requires the processor to feed in matrix (450 × 128 bits) once, matrix (128 × 128 bits) 128 times (since it needs to be fed in once after each column of is fed in), and (128 × 128 bits) once. If the first trial on fails, we will need to feed in a few more times until it recovers the correct ; now, only needs to be checked, hence, does not need to be sent again and again. Therefore, we can estimate the throughput upper bound of this new implementation by our time measurement in our current implementation. Since the hardware computation time in our implementation does not dominate the overall computation time, we can estimate the performance of the new alternative implementation by only counting software computation time and data transmission time. In , this alternative implementation will have a similar execution time because the matrix can be multiplied with vector row by row and output bit by bit. in this alternative implementation will require transmitting 2,171,136 bits for the first trial/computation of . Knowing that it takes about 600 s to send 57,600 bits in our implementation, transmitting 2,171,136 will require about 22,626 s, and on average we will need to try Gaussian elimination 3.472 times to find an invertible matrix, which will take about 13,471s. The throughput upper bound of this alternative implementation would be 27.0 per second.
To implement this alternative solution, we can reuse some of the current components: Bit Select, Index Select, Bit Expand, ROs, TRNG and Communication (technically, Row Select can be reused as well, but in our current implementation, Row Select is highly integrated with matrix registers. Therefore, we cannot get a separate area utilization number of Row Select without matrix registers). We will need to double the size of the hash circuitry because we will always need two hash engines to run at the same time. The area of LPN core can be reduced significantly, the lower bound (without the state machine for controlling all the components) of the area utilization would be 2 K LUTs and 4.8 K registers. Adding to this the utilization of the other components, the total size would be at least 23.4 K LUTs and 24.8 K registers.
If area size needs to be further reduced, we recommend implementing the alternative solution at the cost of a 1/3 lower throughput of .
The comparison between our implementation and the estimation of the previous construction and an alternative implementation is summarized in Table 2.

Table 2.
Comparison between three implementations.
5. Security Analysis
We adopt the following security definition from Herder et al. []:
Definition 2.
A PUF defined by two modes and is ϵ-secure with error δ if
and for all probabilistic polynomial time (PPT) adversaries , , which is defined in terms of the following experiment [].
| Algorithm 1 Stateless PUF Strong Security |
|
The advantage of is defined as
For our construction (reusing the proof in []), the security game in Definition 2 is equivalent to that where the adversary does not make any queries to .
The adversary in control of the processor can repeatedly execute and and receive various instances of sets and . This information can be used to estimate confidence information and this gives information about to the adversary. Therefore, we assume the strongest adversary, who has full knowledge about in the following theorem.
Theorem 1.
Let be the conditional distribution of given and given index set with and . If the distribution is LPN-admissible, then the proposed PUF construction has negligible in n under the random oracle model.
The proof uses similar arguments to those found in sections VIII.A and VII.C.2 of [], with three differences: (1) the adversary who wants to break LPN problems takes an LPN instance , where and . Thus, the related LPN problem is restricted to only equations, instead of m equations (m > 2n) in []; (2) the distribution of is from which is conditioned on , instead of in []; (3) in our construction, the querries to the random oracle are and , which are different from and used in the original construction. But this does not affect the capability of recovering from the look up table constructed in the original proof in [].
The above theorem talks about LPN-admissible distributions for very short LPN problems (i.e., the number of linear equations is , twice the length of ). Short LPN problems are harder to solve than longer LPN problems []. Thus, we expect a larger class of LPN-admissible distributions in this setting.
In our implementation, is generated by RO pairs on the FPGA. It has been shown in [] that, across FPGAs, the behavior of ROs correlate, i.e., if one depicts the oscillating frequency as a function of the spatial location of the RO, then this mapping looks the same across FPGAs. This means that different RO pairs among different FPGAs with the same spatial location behave in a unique way: an adversary may still program its own FPGAs from the same vendor and measure how the output of RO pairs depend on spatial locality its on its own FPGAs (which is expected to be similar across FPGAs).
The spatial locality of one RO pair does not influence the behavior of another RO pair on the same FPGA. However, if the output of one RO pair is known, the adversary is able to refine its knowledge about spatial locality dependence. In this sense, RO pairs with different spatial locations on the same FPGA become correlated. However, since the two neighboring ROs are affected almost the same by systematic variations, the correlation (even with knowledge of confidence information) between the RO pair outputs generated by physically adjacent ROs is conjectured to be very small. This claim is also verified experimentally in []. We can conclude that different RO pairs will show almost i.i.d. behavior, if all the bits are generated by comparing neighboring ROs. However, even though the larger part of spatial locality is canceled out, conditioned on the adversary’s knowledge of how spatial locality influences RO pairs, an RO pair’s output does not look completely unbiased with . In general, however, (this corresponds to the inter Hamming distance between RO PUFs) [,]. Hence, the 450 RO pairs seem to output random independent bits, i.e., Bernoulli distributed with a bias . Since we conjecture the hardness of LPN stating that Bernoulli distributions (with much smaller bias) are LPN-admissible, this makes it very likely that in our implementation an LPN-admissible distribution is generated.
As a final warning, we stress that replacing the 450 RO pairs by, e.g., a much smaller (in area) ring oscillating arbiter PUF introduces correlation, which is induced by how such a smaller PUF algorithmically combines a small pool of manufacturing variations into a larger set of challenge response pairs. This type of correlation will likely not give rise to a LPN-admissible distribution (the confidence information may be used by the attacker to derive an accurate software model of the smaller PUF which makes —as perceived by the adversary—a low entropy source distribution).
Including and in the hash computation. We analyze the reasons why and must be included in :
Parameter . is the only dynamic variable in the design so it ensures that challenge-response pairs are unpredictable. (We cannot directly use as a part of the challenge or response itself as this would provide information about to the adversary.)
Parameter . This inclusion is because of a technicality regarding Definition 2 (one bit flip in likely gives a new valid challenge-response pair).
Checking the hash of . We note that checks if the adversary provides the correct matrix as input by verifying the hash of . If this check is not done, then the adversary can manipulate matrix , and, in particular, submatrix and its inverse in . This leads to the following attack: suppose the inverse of the manipulated matrix is close to the original inverse with only one bit flipped in column j. Let be an all-zero matrix with only the one bit flipped in the j-th column. Then, computes
Since repeats this computation by flipping at most t bits in , we may assume that the term will be equal to zero for one of these computations. This means that outputs the correct response based on only if . Due to the specific choice for this happens if and only if the j-th row of has inner product zero with . By observing whether outputs a valid response or ⊥, the adversary is able to find out whether this inner product is equal to 0 or 1 and this leaks information about .
Machine Learning Resistance. Current strong PUF designs are delay-based and vulnerable to Machine Learning (ML) attacks. In order to obtain a strong PUF design with provable security, we bootstrap a strong PUF from a weak PUF (also called POK) by including a digital interface within the trusted computing base. This makes the new LPN-based strong PUF from [] provably secure as its security is reduced to the hardness of the LPN problem (at the price of not being lightweight due to the larger digital interface). In other words, no ML attack can ever attack the LPN-based PUF unless an ML approach can solve LPN.
6. Related Work
6.1. Attacks on PUFs
We classify all the attacks on PUFs based on what kind of information the attacks require.
Pure Machine Learning Attacks and Cryptanalysis. Strong PUF designs are vulnerable to pure machine learning attacks and cryptanalsis, which only require a sufficient amount of challenge response pairs to build a software model of a PUF. Many existing machine learning algorithms can be used to model a strong PUF, e.g., Support Vector Machine, Logistic Regression [,], Probably Approximately Correct Learning [,], Evolution Strategy [], and Linear Programming []. Moreover, cryptanalysis attacks exploit the mathematical model of PUFs and builds a model of a specific PUF without using any machine learning algorithms [].
Hybrid Attacks. Hybrid attacks refer to the attacks that run machine learning algorithms on the CRPs collected with some extra side channel information [], or the CRPs collected when some faults are introduced in the PUF evaluation intentionally [,].
Side Channel Attacks. By photonic emission analysis, the adversaries are able to extract the delay information of delay-based PUFs without invasive attacks [,]. This advanced attack allows the adversaries to characterize a delay-based PUF easily.
Notice that, as the first proof-of-concept implementation of the LPN-based PUF, we did not add countermeasures against side channel attacks in our implementation. However, some generic countermeasures against side channel attacks can be easily added on top of our implementation [].
6.2. Secure PUF-Based Authentication Protocols
In recent work, new ideas are proposed to secure a potentially vulnerable PUF at protocol level. As an example of a PUF-based authentication protocol, the Slender PUF protocol requires a strong PUF with strict avalanche property to be wrapped around by a digital interface for obfuscating its challenges and responses []. In this way, the full challenge response pairs will not be exposed to the adversaries, and thus it is heuristically secure against the current attacking methods.
Another method, called Lockdown technique, adds a digital interface around the PUF for limiting the number of used challenge response pairs []. By not revealing too many CRPs, it is very hard for adversaries to successfully build a model.
The PUF primitives themselves in the authentication protocols referred to above are vulnerable to attacks. However, if, as in this paper, their digital interfaces are considered to be part of the full PUF design, then these PUF+Interface designs can be shown to be heuristically secure against all the known machine learning attacks.
6.3. Secure Lightweight PUF Designs
Given the recent development in attacking techniques, to the best of our knowledge, there is only one lightweight (meaning without digital interface) secure PUF that is resistant against all known attacks. MXPUF is inspired by a deep understanding of state-of-the-art attacks, and the authors show heuristic security by performing all known attacks on their design [].
6.4. Comparison with Related Work
There are three main differences between our work and the existing machine learning resilient designs: (1) the security of the LPN-based PUF can be reduced to a well-established computational hardness assumption; however, the security of the existing machine learning resilient designs is heuristic; (2) the LPN-based PUF does not require e-fuses, which implies no non-volatile storage as a possible attack point and allows arbitrary interleaving of generation and verification processes; (3) the LPN-based PUF can generate an error-free response that can be used for key generation; however, the PUFs enhanced as described in Section 6.2 can only be used for authentication because the challenge applied to the PUFs cannot be fully controlled by the user/verifier. The MXPUF of Section 6.3 is likely to be more sensitive to noise leading to error-prone responses than other constructions due to its concatenated XOR-PUF structure; this will require it to use a fuzzy extractor with several coding layers. Given these advantages, the LPN-based PUF is a good candidate for secure key management.
7. Conclusions
In this work, we present the first implementation of a PUF challenge response protocol based on computational fuzzy extractors. Specifically, our approach is built on the LPN problem that is related to the hardness of decoding a random binary code with errors. The LPN problem allows us to transform a weak PUF into a strong PUF that supports an exponential number of challenges and responses. In fact, our system retains security when and are arbitrarily interleaved. Even with these security advantages, our implementation retains the efficiency benefits of traditional challenge response protocols, requiring (essentially) one matrix multiplication and two hash computations. Our implementation is secure if the LPN problem is hard for RO outputs in the presence of confidence information.
As one of the future research directions, one can build a compact LPN-based PUF by reducing trusted internal registers and having more interactions and input validations. According to our estimation, this will lead to a significant area reduction with at least three times more performance overhead.
Acknowledgments
This project was supported in part by the AFOSR MURI under award number FA9550-14-1-0351, and in part funded by an NSF grant CNS-1617774 “Self-Recovering Certificate Authorities using Backward and Forward Secure Key Management.”, and in part funded by NSF grant CNS-1523572.
Author Contributions
Chenglu Jin implemented the whole design, and performed the experiments. Chenglu Jin, Phuong Ha Nguyen and Marten van Dijk collectively contributed to the simplified construction and the compact implementation as a future direction. Ling Ren contributed the idea of pushing Gaussian elimination to untrusted software. Benjamin Fuller and Marten van Dijk provided the idea of LPN admissible distributions. All the authors collectively provided the security analysis. Srinivas Devadas provided contributions to all sections by giving fruitful feedback that significantly improved the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Pappu, R.S.; Recht, B.; Taylor, J.; Gershenfeld, N. Physical one-way functions. Science 2002, 297, 2026–2030. [Google Scholar] [CrossRef] [PubMed]
- Gassend, B.; Clarke, D.; van Dijk, M.; Devadas, S. Silicon physical random functions. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, 18–22 November 2002; pp. 148–160. [Google Scholar]
- Yin, C.E.D.; Qu, G. LISA: Maximizing RO PUF’s secret extraction. In Proceedings of the 2010 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Anaheim, CA, USA, 13–14 June 2010; pp. 100–105. [Google Scholar]
- Maiti, A.; Casarona, J.; McHale, L.; Schaumont, P. A large scale characterization of RO-PUF. In Proceedings of the 2010 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Anaheim, CA, USA, 13–14 June 2010; pp. 94–99. [Google Scholar]
- Kumar, S.; Guajardo, J.; Maes, R.; Schrijen, G.J.; Tuyls, P. The butterfly PUF protecting IP on every FPGA. In Proceedings of the IEEE International Workshop on Hardware-Oriented Security and Trust, Anaheim, CA, USA, 9 June 2008; pp. 67–70. [Google Scholar]
- Tuyls, P.; Schrijen, G.J.; Škorić, B.; van Geloven, J.; Verhaegh, N.; Wolters, R. Read-proof hardware from protective coatings. In Proceedings of the 8th International Conference on Cryptographic Hardware and Embedded Systems, Yokohama, Japan, 10–13 October 2006; pp. 369–383. [Google Scholar]
- Rührmair, U.; Sehnke, F.; Sölter, J.; Dror, G.; Devadas, S.; Schmidhuber, J. Modeling attacks on physical unclonable functions. In Proceedings of the 17th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 4–8 October 2010; pp. 237–249. [Google Scholar]
- Rührmair, U.; Sölter, J.; Sehnke, F.; Xu, X.; Mahmoud, A.; Stoyanova, V.; Dror, G.; Schmidhuber, J.; Burleson, W.; Devadas, S. PUF modeling attacks on simulated and silicon data. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1876–1891. [Google Scholar] [CrossRef]
- Rührmair, U.; Xu, X.; Sölter, J.; Mahmoud, A.; Majzoobi, M.; Koushanfar, F.; Burleson, W.P. Efficient Power and Timing Side Channels for Physical Unclonable Functions. In Proceedings of the 16th International Workshop on Cryptographic Hardware and Embedded Systems, Busan, South Korea, 23–26 September 2014; pp. 476–492. [Google Scholar]
- Delvaux, J.; Verbauwhede, I. Fault Injection Modeling Attacks on 65 nm Arbiter and RO Sum PUFs via Environmental Changes. IEEE Trans. Circuits Syst. 2014, 61-I, 1701–1713. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Sahoo, D.P.; Chakraborty, R.S.; Mukhopadhyay, D. Efficient Attacks on Robust Ring Oscillator PUF with Enhanced Challenge-Response Set. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2015. [Google Scholar]
- Armknecht, F.; Maes, R.; Sadeghi, A.R.; Standaert, F.X.; Wachsmann, C. A Formal Foundation for the Security Features of Physical Functions. In Proceedings of the 2011 IEEE Symposium on Security and Privacy (SP), Berkeley, CA, USA, 22–25 May 2011. [Google Scholar]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; pp. 523–540. [Google Scholar]
- Simoens, K.; Tuyls, P.; Preneel, B. Privacy Weaknesses in Biometric Sketches. In Proceedings of the 2009 30th IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 17–20 May 2009; pp. 188–203. [Google Scholar]
- Boyen, X. Reusable Cryptographic Fuzzy Extractors. In Proceedings of the 11th ACM Conference on Computer and Communications Security, Washington, DC, USA, 25–29 October 2004; pp. 82–91. [Google Scholar]
- Blanton, M.; Aliasgari, M. On the (non-)reusability of fuzzy sketches and extractors and security in the computational setting. In Proceedings of the International Conference on Security and Cryptography (SECRYPT), Seville, Spain, 18–21 July 2011; pp. 68–77. [Google Scholar]
- Blanton, M.; Aliasgari, M. Analysis of reusability of secure sketches and fuzzy extractors. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1433–1445. [Google Scholar] [CrossRef]
- Fuller, B.; Meng, X.; Reyzin, L. Computational Fuzzy Extractors. In Proceedings of the 19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 1–5 December 2013; pp. 174–193. [Google Scholar]
- Canetti, R.; Fuller, B.; Paneth, O.; Reyzin, L.; Smith, A. Reusable Fuzzy Extractors for Low-entropy Distributions. In Proceedings of the 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016; pp. 117–146. [Google Scholar]
- Herder, C.; Ren, L.; van Dijk, M.; Yu, M.M.; Devadas, S. Trapdoor Computational Fuzzy Extractors and Stateless Cryptographically-Secure Physical Unclonable Functions. IEEE Trans. Dependable Secur. Comput. 2017, 14, 65–82. [Google Scholar] [CrossRef]
- Blum, A.; Kalai, A.; Wasserman, H. Noise-tolerant learning, the parity problem, and the statistical query model. J. ACM 2003, 50, 506–519. [Google Scholar] [CrossRef]
- Xilinx. Zynq-7000 All Programmable SoC Overview. Available online: https://www.xilinx.com/support/documentation/data_sheets/ds190-Zynq-7000-Overview.pdf (accessed on 1 May 2017).
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2009, 56, 34. [Google Scholar] [CrossRef]
- Blum, A.; Furst, M.L.; Kearns, M.J.; Lipton, R.J. Cryptographic Primitives Based on Hard Learning Problems. In Proceedings of the 13th Annual International Cryptology Conference, Santa Barbara, CA, USA, 22–26 August 1993; pp. 278–291. [Google Scholar]
- Hopper, N.J.; Blum, M. Secure Human Identification Protocols. In Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 9–13 December 2001; pp. 52–66. [Google Scholar]
- Applebaum, B.; Cash, D.; Peikert, C.; Sahai, A. Fast Cryptographic Primitives and Circular-Secure Encryption Based on Hard Learning Problems. In Proceedings of the 29th Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2009; pp. 595–618. [Google Scholar]
- Applebaum, B.; Barak, B.; Wigderson, A. Public-key cryptography from different assumptions. In Proceedings of the Forty-Second ACM Symposium on Theory of Computing, Cambridge, MA, USA, 5–8 June 2010; pp. 171–180. [Google Scholar]
- Levieil, É.; Fouque, P. An Improved LPN Algorithm. In Proceedings of the 5th International Conference, Maiori, Italy, 6–8 September 2006; pp. 348–359. [Google Scholar]
- Arora, S.; Ge, R. New Algorithms for Learning in Presence of Errors. In Proceedings of the 38th International Colloquium, Zurich, Switzerland, 4–8 July 2011; pp. 403–415. [Google Scholar]
- Bernstein, D.J.; Lange, T. Never Trust a Bunny. In Proceedings of the 8th International Workshop, RFIDSec 2012, Nijmegen, The Netherlands, 2–3 July 2012; pp. 137–148. [Google Scholar]
- Guo, Q.; Johansson, T.; Löndahl, C. Solving LPN Using Covering Codes. In Proceedings of the 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, Taiwan, 7–11 December 2014; pp. 1–20. [Google Scholar]
- Lyubashevsky, V. The parity problem in the presence of noise, decoding random linear codes, and the subset sum problem. In Proceedings of the 8th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems, APPROX 2005 and 9th International Workshop on Randomization and Computation, RANDOM 2005, Berkeley, CA, USA, 22–24 August 2005; pp. 378–389. [Google Scholar]
- Maiti, A.; Schaumont, P. Improved Ring Oscillator PUF: An FPGA-friendly Secure Primitive. J. Cryptol. 2011, 24, 375–397. [Google Scholar] [CrossRef]
- Sunar, B.; Martin, W.J.; Stinson, D.R. A provably secure true random number generator with built-in tolerance to active attacks. IEEE Trans. Comput. 2007, 56. [Google Scholar] [CrossRef]
- Standard, S.H. Federal Information Processing Standard Publication 180-2. US Department of Commerce, National Institute of Standards and Technology (NIST), 2002. Available online: https://csrc.nist.gov/publications/fips/fips180-2/fips180-2withchangenotice.pdf (accessed on 1 May 2017).
- Scholl, S.; Stumm, C.; Wehn, N. Hardware implementations of Gaussian elimination over GF (2) for channel decoding algorithms. In Proceedings of the Africon 2013, Pointe-Aux-Piments, Mauritius, 9–12 September 2013; pp. 1–5. [Google Scholar]
- Ganji, F.; Tajik, S.; Fäßler, F.; Seifert, J.P. Strong machine learning attack against PUFs with no mathematical model. In Cryptographic Hardware and Embedded Systems—CHES 2016, Proceedings of the 18th International Conference, Santa Barbara, CA, USA, 17–19 August 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 391–411. [Google Scholar]
- Ganji, F.; Tajik, S.; Seifert, J. Why Attackers Win: On the Learnability of XOR Arbiter PUFs. In Proceedings of the 8th International Conference, TRUST 2015, Heraklion, Greece, 24–26 August 2015; pp. 22–39. [Google Scholar]
- Becker, G.T. The Gap Between Promise and Reality: On the Insecurity of XOR Arbiter PUFs. In Proceedings of the 8th International Conference, TRUST 2015, Heraklion, Greece, 24–26 August 2015. [Google Scholar]
- Liu, Y.; Xie, Y.; Bao, C.; Srivastava, A. A Combined Optimization-Theoretic and Side-Channel Approach for Attacking Strong Physical Unclonable Functions. IEEE Trans. Very Large Scale Integr. Syst. 2017, PP, 1–9. [Google Scholar] [CrossRef]
- Tajik, S.; Lohrke, H.; Ganji, F.; Seifert, J.P.; Boit, C. Laser Fault Attack on Physically Unclonable Functions. In Proceedings of the 12th Workshop on Fault Diagnosis and Tolerance in Cryptography, St. Malo, France, 13 September 2015. [Google Scholar]
- Tajik, S.; Dietz, E.; Frohmann, S.; Seifert, J.; Nedospasov, D.; Helfmeier, C.; Boit, C.; Dittrich, H. Physical Characterization of Arbiter PUFs. In Proceedings of the 16th International Workshop on Cryptographic Hardware and Embedded Systems, Busan, Korea, 23–26 September 2014; pp. 493–509. [Google Scholar]
- Ganji, F.; Krämer, J.; Seifert, J.; Tajik, S. Lattice Basis Reduction Attack against Physically Unclonable Functions. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 1070–1080. [Google Scholar]
- Gross, H.; Mangard, S.; Korak, T. An efficient side-channel protected aes implementation with arbitrary protection order. In Proceedings of the Cryptographers’ Track at the RSA Conference 2017, San Francisco, CA, USA, 14–17 February 2017; pp. 95–112. [Google Scholar]
- Majzoobi, M.; Rostami, M.; Koushanfar, F.; Wallach, D.S.; Devadas, S. Slender PUF Protocol: A Lightweight, Robust, and Secure Authentication by Substring Matching. In Proceedings of the 2012 IEEE Symposium on Security and Privacy Workshops (SPW), San Francisco, CA, USA, 24–25 May 2012; pp. 33–44. [Google Scholar]
- Yu, M.D.M.; Hiller, M.; Delvaux, J.; Sowell, R.; Devadas, S.; Verbauwhede, I. A lockdown technique to prevent machine learning on PUFs for lightweight authentication. IEEE Trans. Multi-Scale Comput. Syst. 2016, 2, 146–159. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Sahoo, D.P.; Jin, C.; Mahmood, K.; van Dijk, M. MXPUF: Secure PUF Design against State-of-the-art Modeling Attacks. IACR Cryptol. ePrint Arch. 2017, 2017, 572. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).