Induction, Experimentation and Causation in the Social Sciences

Abstract

Inductive thinking is a universal human habit; we generalise from our experiences the best we can. The induction problem is to identify which observed regularities provide reasonable justification for inductive conclusions. In the natural sciences, we can often use strict laws in making successful inferences about unobserved states of affairs. In the social sciences, by contrast, we have no strict laws, only regularities which most often are conditioned on ceteris paribus clauses. This makes it much more difficult to make reliable inferences in the social sciences. In particular, we want knowledge about general causal relations in order to be able to determine what to do in order to achieve a certain state of affairs. Knowledge about causal relations that are also valid in the future requires experiments or so called ‘natural experiments’. Only knowledge derived from such experiences enable us to draw reasonably reliable inferences about how to act in order to achieve our goals.

1. Introduction

Social science is usually regarded as inferior to natural science. Natural science is often described as a steady progress towards better and better theories as more and more scientific problems are solved. By contrast, the advances in social science are not impressive, and some would say they are totally absent. Not even economics, which by some is regarded as the social science most akin to natural science, is a clear success story. Several economic policy makers repeatedly expressed their bewilderment, just before the outbreak of the COVID-19 pandemic, with almost no inflation, zero interest rates and meagre growth in the majority of OECD countries: ‘We are in a new territory’ a spokesperson for the FED reportedly said. Why this profound difference between natural and social science?

One may reasonably object to this comparison as being unfair on two counts. The first is that natural science has been practiced for a much longer time than social science. Natural science began with the pre-Socratic philosophers (Thales, Anaximander, Anaximenes, Democritus and some others) practicing natural philosophy, and Aristotle’s book Physics, published circa 350 BC, was the first systematic attempt to study change and motion. It took a very long time, more than 2000 years, before the first real breakthrough in this inquiry came with Galilei’s and Newton’s analysis of motion. In medicine, it took an even longer time, until circa 1860, when it was discovered that the cell is the functional unit in living bodies, before doctors had any real and useful knowledge of how to cure diseases. Virtually no treatment recommended by doctors before Pasteur had any positive effect. Worst of all, bloodletting, which was widely used as a cure for many diseases until the end of the 19th century, often made the patient more ill, without the medical profession really understanding that.

The social sciences are, in comparison with physics and medicine, new disciplines. Psychology, economics, sociology and political science all began as organised scientific inquiries during the 19th century. Even though many more people nowadays are engaged in scientific research, thus speeding up the pace, one may hold that the social sciences are still in their infancy. (The same is true of some natural sciences, e.g., plate tectonics, so it is not the case that all natural sciences are older and more advanced than the social sciences.) In this perspective, it is perhaps understandable that the results so far are meagre in comparison with some natural science disciplines.

Another aspect to consider when we complain about the limits of our understanding and ability to make predictions in the social world is that we often think of macroeconomics and politics and the subject matter in these fields as systems comprising of huge numbers of interacting individuals. If we consider something analogous in the natural world such as the weather, the climate or a human body in constant interaction with its environment, we realise that such systems likewise consist of a very great number of individual items, i.e., molecules and cells. In these fields, one cannot say that the predictive capacity is overwhelming: It is, for example, said that weather forecasting for a longer period than circa 10 days is virtually meaningless. One may compare with our knowledge of, e.g., exchange rates between currencies: In the short term, one can make reasonable predictions, but it is notoriously difficult, not to say impossible, to make long term predictions about such matters. In short, our knowledge about long-term tendencies in the social world is very limited, and the same holds about many complex systems in the natural world.

A fairer comparison between natural and social science is to compare the reliability of predictions of the dynamics of small isolated physical systems, bodies and molecules with the actions of individual agents; the latter may be conceived as the atoms in the social world. In both cases, we can, sometimes, make predictions with reasonable success, provided their respective environments are sufficiently stable.

Bringing these two aspects into the picture, the difference between natural and social science appears to be not so big. We have, for sure, better knowledge of fundamental physics than of human agency, but one could defend the view that it is a matter of degree, not a difference in kind. In addition, there are disciplines in natural science, plate tectonics and meteorology, for example, which appear to not be in any better shape than sociology or political science. Our ability to make long-term forecasts in these disciplines is equally weak.

When we aggregate individual humans to collective entities such as organisations, institutions, societies or states, we have no laws for the dynamics of these things. Therefore, the predictive capacity in social science is weak. Economics, political science and sociology can often explain what has happened, but forecasting is difficult, often impossible. Since we want to make better decisions and avoid catastrophes such as wars or economic depressions, we look for guidance from the social sciences; we want to know what to do in order to improve our conditions. In other words, we want knowledge about causal relations in the social world; which causes determine our future, and which of these are such that we can intervene and change things in desired directions? This is, to a great extent, the induction problem in social science.

However, not all agree that the main task of social science is to provide guidance for future action or finding general causal relations; some hold that the prime goal of social science is understanding, following Weber. Inspired by Windelbrand [1] and Richert [2], he distinguished sharply between natural and social science: Natural science aims at explanations (by which he meant causal explanations using natural laws) while social science aims at understanding (german ‘Verstehen’).1

It is clear that Weber thought of causal explanations in the natural sciences, but what he more exactly meant by ‘Verstehen’ is a topic of debate. It seems to me that a crucial element of his notion ‘Verstehen’ was empathy (german ‘Einfühlung’). According to Weber, the aim of an inquiry into a particular social phenomenon or historical event is achieved when we understand why the agents acted as they did, and this requires knowledge of the individual agents’ beliefs and desires; we understand when we know their thoughts in the concrete settings they live. Understanding is knowing the meaning of concrete individual or collective actions in specific contexts, and this requires empathy. (This notion of understanding the meaning differs from the common one in philosophy of science and philosophical semantics, where understanding the meaning is to know the truth conditions of sentences, i.e., it is propositions, not actions, that are attributed meaning).

In Weber’s conception, there is no real use for the distinction between data and theory in the process towards understanding. It is implicitly held that there are no such things as data, understood as observed and uninterpreted facts. When we observe someone doing something or hear someone saying something, we immediately perceive the person’s behaviour as a purposeful action driven by a desire and a belief. When we observe a person doing something, the content of our perception is not that of a body moving from one place to another but of an agent purposely acting, even if we do not recognise which action it is. Additionally, we do not hear mere sounds when we listen to someone talking, we hear sentences with meaning. In cases the speaker talks a language unknown to the listener, the latter still takes for granted that the speaker utters meaningful sentences; this is the default option. There is an irreducible intentional component in our perceptions of social phenomena.

I grant these points, but if we stop here, we will never be able to arrive at any useful general knowledge in the social sciences. This is so because a core feature of such interpretative processes is that they are about individual cases, and no general laws about such things are available. Weber expressed this clearly: Natural science aims at the discovery of general laws, social science aims at understanding individual phenomena.

However, what scientific use is there for understanding an individual phenomenon? One might claim that in history it is interesting to know the desires and beliefs of (in)famous historical agents, but that interest is also motivated by the desire to learn from history, to obtain guidance for social and political action. Social science in general and to a great extent aims at knowledge useful for solving societal problems.

Many social scientists nowadays dismiss the Weberian view about the purpose of social science, and so do I; knowledge about general features are eagerly sought for also in the social sciences. Interpretation of individual agents, their motives for actions, is seldom of little interest in itself. We want to be able to generalise, we want to know what we can learn from past events. This is the induction problem in the social sciences.

Malcolm Williams [4] has argued that (i) interpretivists deny the possibility of generalisations but nevertheless do generalise and that this is inevitable and (ii) that generalisations in interpretative research is possible. His arguments for the first claim are convincing, in particular his observation that interpretivists address questions of generalisation in terms of ‘transferability’, ‘external validity’ or ‘confirmability’. He likens interpretivists’ attitude to generalisation to Victorian middle class people’s attitude to sex: They do it and they know it is going on, but they rarely talk about it.

Williams’ second claim, that generalisations are possible in interpretivism and qualitative research in general, is based on his distinction between three forms (or grades) of generalisations: (i) total generalisations, (ii) statistical generalisations and (iii) moderatum generalisations. The first category comprises generalisations based on laws, which function as axioms in the respective theory. Williams mentions the second law of thermodynamics as an example. The second category is common in disciplines where inferences from samples to populations are made. The third category, moderatum generalisations, is described as ‘where aspects of S can be seen to be instances of a broader recognisable set of features. This is the form of generalisation made in interpretative research, either knowingly or unknowingly.’ ([4], p. 215) This form of generalisation is, Williams claims, based on shared culture, ‘cultural consistency’ or ‘prior existence of a shared world of meaning’: ‘The “order” or social human life needs some form of communicative cement, a stock of phrases, expressions or languages themselves, and it is these that the interpretivist needs to understand to be able to “say something.”’ ([4], p. 220).

It is not altogether clear to me what moderatum generalisations are. My preliminary understanding is that it is a kind of theory building. As an example, Williams quotes from Clifford Geertz’s famous ’Notes on the Balinese Cockfight’ [5]: ‘Every people loves its own form of violence.’ ([5], p. 219) This is by Williams understood as Geertz’s generalisation of Balinese peoples interest in cockfights. A particular social phenomenon, as described by a researcher, is classified as falling under a broader category; this is the attempted generalisation. To me, however, it appears more as the converse; Geertz, already in advance of observing cockfights, thinks that all humans are interested in violence in some form or another and finds cockfights to be instances of this previously assumed general trait of humans.

In any case, Williams’ perspective invites the question how such generalisations are justified. Clearly, it is much riskier than statistical generalisations, which are based on observations of samples drawn, ideally at random, from a population. Williams’ answer is that moderatum generalisations need to be justified by statistical generalisations. I agree on that, but statistical inferences from samples to populations are seldom made in qualitative research. In other words, moderatum generalisations, as described by Williams, are normally not any form of generalisation given some sort of explicit justification; they may at best function as a way of formulating statistically testable hypotheses. A moderatum generalisation by itself does not give us any knowledge about general features of the social world.

However, even if we have made justifiable generalisation based on statistics, this is not enough; the question is whether the result, a trustworthy correlation, reflects a causal connection between the observed variables or whether it is the effect of a common cause?

In order to have any knowledge useful for policy decisions, we need knowledge about causes at the general level. Two steps are needed: first to establish, using inductions from observations, laws or at least regularities with as little unknown ceteris paribus conditions as possible, and second, to determine whether these connections are causal or not. The second step require experiments or observations of natural experiments, to be discussed in Section 4 and Section 5.

2. Induction in the Social Sciences

A main reason why we are interested in disciplines such as psychology, sociology, economics and political science is that we want to know what to do to avoid unpleasant events such as a great depression or a civil war or to promote desirable states of affairs such as freedom, good governance and happiness. We hope that the social sciences may guide us in this endeavour. A necessary condition for such guidance is that we have made successful inductive generalisations from observed phenomena.

It is, however, a sad fact that we often draw wrong conclusions from past events in economics, political science and history. This has to do with the fact that any set of social phenomena has a great number of common characteristics and the question is which to use as basis for generalisations. This question was called by Goodman [6] ‘The new riddle of induction’. The induction problem is, according to Goodman, not the question of how to justify any general principle of inductive inference; that cannot be done, as Hume [7] showed long ago. The problem is rather which inductive inferences to draw. Hájek [8], expressed the point succinctly:

Goodman taught us: That the future will resemble the past in some respect is trivial; that it will resemble the past in all respects is contradictory.

Thus, the problem is to tell which properties of a number of historical and social events can be expected to also occur in the future.

Many in the debate about methodology in the social sciences, e.g., Rosenberg [9]2 and Mesjasz [10]3, have argued that social phenomena are much more complex than physical ones, hence it is in practice impossible to make successful inductions in these disciplines. This argument immediately triggers the question: How do we measure the degree of complexity?

Any reasonably convincing argument to the effect that something is more complex than something else must provide a measure of complexity that applies to descriptions of the compared entities; talking about the complexity of a phenomenon or situation in itself is senseless, a point made by Allen et al. [11]:

Much discussion of complexity is confused because complexity is mistaken as a material issue. Complexity arises from the way the situation is addressed, and is not material in itself. (p. 39)

Those who have argued that social phenomena are more complex than natural phenomena seem to compare social and natural systems in themselves, independently of any models or descriptions we have of those things. This is, in my view, impossible. We cannot directly see, or grasp, anything in such a direct way. What we can compare are models or descriptions of things.

In order for such a comparison to be relevant for the question of the possibility of successful inductions into future states of affairs, we need a measure of complexity, which is relevant to computability: for making an inductive inference from a number of observed situations is to use a description of these as input in a computation of how a future situation will look like.

I know of one such measure, algorithmic complexity, first formulated in Solomonoff [12,13], Kolmogorov [14] and developed by Chaitin [15]. It goes under several names: Kolmogorov complexity, Kolmogorov–Chaitin complexity or algorithmic complexity.

Any object, situation or state of affairs under consideration can be described in some language, and the description is a text, a finite string of characters. One can always write a programme in some programming language that produces that text as output. This can often be accomplished by several different programmes of different length. The complexity of the object may now be defined as the length of the shortest programme that as output gives that description of the object. If L(s) is the length of a programme that as output produces the description s, $K\left(s\right)=min\left(L\right(s\left)\right)$ is the minimal length of a programme producing s. Chaitin [15] showed that the function $K\left(s\right)$ is not computable. That means that, using algorithmic complexity, one cannot in general decide which of two descriptions is the more complex one.

For a particular comparison between two systems described in a certain way, one may be able to determine which is more complex using algorithmic complexity as a measure, but the statement that the social sciences in general are more complex than the natural sciences cannot be supported using this concept.

There might be some other measure of complexity which can be used as basis for such a general claim. However, to my knowledge, no such measure has ever been mentioned.

My guess is that descriptions of social phenomena appear so complex just because we have not yet succeeded in finding sufficiently useful models, i.e., models that allow good predictions about future states, except in rather short time spans. The task of the model builder is to distinguish between more and less relevant aspects, factors and variables for the desired goal; any model is a simplification of the thing modelled. Why has that often been achieved in physics but rarely so in social science? I believe it has to do with the fact that we know several strict laws in natural science, particularly in physics, whereas no such laws are known in social science.

3. Laws in Physics and in the Social Sciences

We know no laws, in the strict sense, in the social sciences, but we observe some regularities. Why this difference between physics and social science? I think the crucial difference is that when formulating a regularity, we need to condition it on ceteris paribus clauses, mostly unspecified, and this is not the case with fundamental laws in physics and therefore neither in any laws derivable from the fundamental ones. This dependence on ceteris paribus clauses makes it difficult to make any strong predictions about the future because one almost never knows whether all relevant aspects will be the same in the future. So what are, then, more precisely, the conditions for something being elevated to the status of being a law, expressing a strict regularity without ceteris paribus conditions?

The concept of natural law is much disputed among philosophers; in my [16] I recorded 11 different suggested definitions. Despite the lack of consensus on the meaning of ‘natural law’, there is, in physics, reasonable consensus that quite a number of general statements are to be classified as fundamental laws, for example, the principle of energy conservation, the law of gravitation, Maxwell’s equations, Dirac’s equation and Einstein’s equation. These are fundamental laws since they satisfy four conditions: (i) they are generalisations from observations, (ii) they are exception-less, (iii) they relate quantities by way of equations to each other and (iv) they function as implicit definitions of scientific general terms, viz., quantitative predicates used in these statements. I guess the last clause will astonish most readers, but in [16] I argued the point briefly as follows.

How could we know that a law is valid without exception if we have never observed all its instances? The answer is that fundamental laws function as implicit definitions of new theoretical predicates introduced in the theory construction; this is one of the four characteristics of a fundamental law. That means that when we are faced with a conflict between observations and a fundamental physical law, the latter is never taken to be falsified; instead, the aberrant observation is taken care of either by adjusting the criteria for the predicates used in the law or by dismissing the observation as erroneous. An example illustrating the first option is the discussions about dark energy and dark matter in astrophysics. Observations of the motions of distant galaxies tell us that their gravitational energy must be much bigger than what can be derived from their observed radiation. However, no physicist thinks that this disproves the fundamental equations of motion (Maxwell’s equations, Einstein’s equation and the law of gravitation). Instead, it is postulated that there is non-observed ‘dark matter’ and ‘dark energy’.

The other option, to assume there might be a mistake in the measurements, is nicely illustrated by the 2011 report from thee OPERA collaboration. The group reported [17] that they had observed neutrinos travelling faster than light, in outright conflict with a fundamental law of physics. The OPERA group was careful, reporting their measurements in a preprint, and invited the physics community to scrutinise the experiment in order to see if any mistake had been made. Within a year, it was generally agreed that the time measurement had not been accurate, there had been a bad connection in the time measurement device, see e.g., [18]. There was no conflict with any fundamental law.

The fundamental laws are not doubted since they function as implicit definitions of core physical concepts such as mass, electric charge and magnetic field. The fundamental laws build up the conceptual structure of physical theories. Furthermore, laws that are derivable from the fundamental ones are obviously also strict, having no ceteris paribus clauses.

Thus, a general statement satisfying the four criteria mentioned above is recognised as being a fundamental law from which other laws can be derived.4 The discovery of momentum conservation is a good illustration of how it works.

The law of momentum conservation, which is the foundation of dynamics, was the first discovered fundamental law. (See the first scholium in Newton’s Principia [19]). Newton begins Principia with his three laws, but it is clear from his comments in the first scholium that the empirical basis for these laws is momentum conservation, although Newton never uses that very term. Momentum conservation is the principle that when bodies interact, they exchange momentum (=velocity times mass) so that the total momentum in the system of the interacting bodies is conserved. The first experiments indicating this previously unknown law was made by John Wallis, Christopher Wren and Christian Huygens around 1660, and Newton refers to and discusses their findings. In their time, the concept of mass was unknown, so how could they discover a law whose formulation requires this concept?

Wallis, Wren and Huygens performed, independently of each other, experiments with colliding bodies. They found that the velocity changes of two colliding bodies always are proportional and oppositely directed:

$$\frac{\Delta v_1}{\Delta v_2}=constant$$

(1)

in other words

$$k_1\Delta v_1=-k_2\Delta v_2$$

(2)

(The minus sign is introduced in order to have both constants positive.)

These constants are unobservable attributes of the bodies, later by Newton called their quantity of matter and renamed as mass in the very first sentence of Principia: ‘Mass is the quantity of matter.’ This is, obviously, merely a verbal definition. The concept quantity of matter is thoroughly discussed in Newton’s discussion of the experiments performed by Wallis, Wren and Huygens. The law of momentum conservation may, after the introduction of a mass unit, thus be formulated as:

Momentum Conservation: For any two pairs of bodies with masses $m_1$ and $m_2$, the velocity changes upon collision satisfies:

$$m_1\Delta v_1=-m_2\Delta v_2$$

(3)

The crucial point is that no matter the shape, colour, volume or any other directly observable attribute of the colliding bodies, the velocity change of one of the colliding bodies can be calculated, given the velocity change of the other body and their relative masses.

The introduction of this new quantity, mass, implicitly defined by the law of momentum conservation, is the crucial step needed to develop the dynamical part of classical mechanics. (Descartes had, some decades before Newton, made an attempt to construct a dynamics, a theory describing how bodies interact, based on speed and volume, i.e., directly observable properties of matter. However, Descartes failed, neither volume nor speed could be used for formulating a valid dynamical law.5

By introducing the predicate force as short for mass·acceleration, which is Newton’s second law, we immediately obtain his third law as a consequence of momentum conservation. The first law is merely a special case of the second one. Adding the law of gravitation as another fundamental law, we can then derive all of classical mechanics.

Thus, the lesson to learn from this example (and there are several similar ones in the history of physics) is that fundamental laws are simultaneously generalisations of observations and implicit definitions of new quantities; the decision to accept a generalisation of a series of observations is ipso facto the acceptance of this generalisation as an implicit definition of a new general term used to express this generalisation. Discoveries of such laws and inventions of new concepts are inseparable and crucial in the development of new successful theories. In what follows, the terms ‘law of nature’ and ‘law of physics’ will be restricted to denote (i) fundamental laws, (ii) the laws derived from these and (iii) explicit definitions of quantities as described above.

Laws of physics, thus characterised, are true of course; a definition, explicit or implicit, is by its very nature a true statement and so are all their logical consequences. Nancy Cartwright has argued for the opposite view, i.e., that laws of physics are not true:

‘What is important to realise is that if the theory is to have considerable explanatory power, most of its fundamental claims will not state truths, and that will in general include the bulk of our most highly prized laws and equations.’ ([20], p. 78)

Her point is that when we apply a strict law to a real phenomenon, we must in practice take many circumstances into account, more precisely, the causes of the phenomenon. A focus on causes and capacities has been a central theme in her work [21,22,23,24].

Cartwright’s view is that laws have no central role in science, contrary to a common perception among scientists and philosophers alike. Cartwright claims that this role is taken over by capacities and causes. Regarding causes, she writes as if they comprise an ontological category, although she never express herself in such a committing way. Anyway, it is clear that ‘cause’ is a relational term; we are interested in cause–effect relations when explaining what happens and suggesting what to do in order to make something to happen, or not to happen. So the question is not how we obtain knowledge about causes in isolation, but about causal relations. How do we know that a certain event, or state of affairs A preceding another event or state of affairs B is a cause of B?

Well, in science it must be based on inductive generalisations expressed as strict or probabilistic laws. It is true that we ask for causes in science, but that does not mean that laws are false or lack applications; quite the opposite, causal knowledge require knowledge about laws. However, as will be explained in the next section, laws do not in themselves state causal relations; most state numerical relations between quantities. So I disagree with Cartwright’s thesis that laws in physics do not tell the truth. They do.

Moreover, how could we motivate using laws when we make calculations if they were false or lack truth values? The point of using a valid rule or a true statement as a stepping stone when making an inference is that it preserves truth. If we are lucky enough to start with true statements (e.g., describing some observations) and we use laws to calculate unobserved values of some interesting quantity, our degree of confidence in the result is the same as that of the observation. However, if the law is false, or meaningless, it could not fulfill this function.6

Are there any strict laws, i.e., laws that implicitly or explicitly define theoretical quantities, or laws derived from such definitions, in the social sciences? What first comes to ones mind is to look at economics, where some fundamental equations have the character of strict identities. One simple example may be the fact that export minus import summed over all countries must be zero. However, it is well known that the statistical figures of actual export and import when summed over all countries give a net positive result! We seem to export goods and services to extra-terrestrial civilisations! Since this is not the case, we infer that empirical data are flawed; by definition, export from A to B is import to B from A.

However, this example is no real analogy to the law of momentum conservation. The concepts export and import are not new theoretical ones invented in order to describe observed regularities; they belong to our vernacular and the equation ‘export from A to B = import to B from A’ is a conceptual truth in ordinary parlance; no observations are needed to establish this as a general truth.

Perhaps there are some true analogies between physics and economics, i.e., laws in economics that are discovered in empirical research and which utilise new theoretical predicates implicitly defined by the particular law in which it primarily occurs, but I do not know of any.

Other social sciences than economics sometimes collect qualitative data and use qualitative methods. Qualitative data concern individual agents’ beliefs, desires, hopes, fears, etc., i.e., mental states of humans. This is fine if we want to understand individual agents or singular events in history. However, if we desire general knowledge and guidance for future actions, it is inadequate; we need knowledge about how people’s beliefs and desires are formed and how their actions are caused. However, there are no laws which tell us the conditions under which a particular belief or desire will be formed. Donald Davidson [25] and Brian Fay [26] have, in my view convincingly, argued this point.

A substantial portion of social science consists of studies of the desires and beliefs of important actors, since it is commonly assumed that desires and beliefs are the causes of our actions. One is then naturally led to ask: What are the causes of our beliefs, desires and therefore of our actions? What are the conditions for something being a cause? It is profitable to begin by looking at our way of using the causal idiom in physics, more precisely, how causation and laws are connected.

4. Laws and Causation

Most laws in physics relate quantities to each other, see the examples in the previous section. There are also some laws of physics that do not relate quantities, for example, the constancy of velocity of light. However, no physical law tells us about causes, a point Russell once made:

The law of causality, I believe, like much that passes muster among philosophers, is a relic of a bygone age, surviving, like the monarchy, only because it is erroneously supposed to do no harm. ([27], p. 1).

I hold that Russell fundamentally was right. However, there is a connection between laws and our concept of causation, and it goes as follows. A crucial feature of our concept of cause is manipulability.7 Not always, but quite often, we look for causes of states of affairs or events because we want to do something. After a car crash, we ask for the cause (or the causes) in order to prohibit similar events, if possible, or in order to prosecute the driver in case he/she drove drunk, for example.

The cause of an event or state of affairs is in many cases a change that someone or something has brought about, an intervention by an agent acting for a purpose or by some external change of state of affairs affecting the event or state of affairs being in focus. This is a basic idea in Pearl [28], also thoroughly discussed in Woodward [29]. An example of experimental manipulation in psychology is discussed by Byrd [30].

The connection between a certain change of state of affairs and a later change may be given by a law that relates the quantitative attributes of these states of affairs. Quite often, it is possible to manipulate one such quantity, i.e., deliberately change its value in a particular situation, and then observe the change of some other quantity. Consider, for example, the general law of gases:

$$pV=nRT$$

(4)

where p is pressure, V volume, n number of moles, R the general gas constant and T absolute temperature. This law thus relates four quantities that can be attributed to definite portions of gases. (The law is an idealisation since it omits quantum effects, but that is irrelevant for this argument.) In some situations, we can manipulate the pressure and observe the changes in volume and/or temperature. In those cases, we treat the change in pressure as the cause of the changes in volume and/or temperature. In another situation, we may be able to change the temperature and then observe the changes in pressure and/or volume. In such cases, the temperature change is treated as the cause and the changes of the other variables as effects.

It is clear that in this case, as in many others, what we call ‘the cause’ depends on the experimental context, not on the features of the law. Hence, a condition for something to be called ‘a cause’ of something else is often it being manipulable in the specific situation at hand. However, we need a law to connect the variable we directly manipulate and the changes of the other variables that follow.

What if there are no such laws in social science? In such cases, one has to rely on something weaker, which might be called ‘restricted regularities’, i.e., statements about observed regularities conditioned on unspecified ceteris paribus clauses.

Restricted Regularities and Causes

An example of a restricted regularity may be that democratic states so far have never gone to war with each other. (I am not completely certain that this is correct, but it is a common claim.) If we belief that this generality may be valid also in the future, one way to reduce the risk of future wars is to promote democracy.

I do not think that it is a social law that democratic countries never go to war with each other; for if it were a law, there would never be any exceptions and it seems to me possible that democratic countries could go to war; we would not reclassify a democratic country as undemocratic if it would go to war with another democratic country. However, we may call the relation between democratic governance and the disposition not to go to war with other democracies an observed regularity. It seems rational to use it for predictions, although we know that it may be true only under some circumstances, so far not specified. Maybe there are other regularities that are more trustworthy as a basis for future actions. However, lacking laws, we have no other way than to look for regularities with limited and unclear scopes.

One may thus conceive of a restricted regularity as a universally generalised conditional with an antecedent containing a non-specific conjunction of conditions, often called ceteris paribus clauses. The regularity that democratic states never go to war with each other may more fully be expressed as:

Ceteris paribus, For all pairs (X, Y) of states, if X and Y are democratic, X and Y will never go to war with each other.8

Despite the problem with using limited regularities for predictions about the future, one has no choice but trying to find such things. However, merely observing regular connections between kinds of events or variables is not sufficient as guidance for action, even if one has good reason to also generalise to future states of affairs. For it is well known that a regular connection, a correlation or a regression, in itself does not entail a causal connection, and we need knowledge about causal connections when planning what to do. An observed regularity may be due to a common cause for the observed variables, and the crucial problem is to discern cases where a correlation between two variables is the result of a causal connection between them and where the correlation is the result of a common cause; only in former cases is it possible to do something about one variable by manipulating the other.

An example from social science may be the so called education production function, which relates input in schooling and output, i.e., the pupil’s achievements. One might assume that one can improve pupils’ results by reducing the class size, but observational data do not confirm this: (Angrist & Pischke [31], p. 8) writes:

This literature (surveyed in [32]) is concerned with the causal effect of school inputs, such as class size or per-pupil expenditure, on student achievement. The systematic quantitative study of school inputs was born with the report by Coleman [33], which (among other things) used regression techniques to look at the proportion of variation in student outputs that can be accounted for in an $R^2$ sense by variation in school inputs. Surprisingly to many at the time, the Coleman report found only a weak association between school inputs and achievement. Many subsequent regression-based studies replicated this finding. ……The problem with the Coleman report and many of the studies in this mold that followed is that they failed to separate variation in inputs from confounding variation in student, school, or community characteristics. For example, a common finding in the literature on education production is that children in smaller classes tend to do worse on standardized tests, even after controlling for demographic variables. This apparently perverse finding seems likely to be at least partly due to the fact that struggling children are often grouped into smaller classes.

The authors concluded that regression analysis (and thus merely observed correlations) is not useful for answering questions about causal relations between input and output. Instead, one must perform experiments in order to establish whether the correlation is due to a causal connection or to a common cause; ruling out common causes by only considering data from passive observations is impossible. This was also an important message of Pearl [28].

(Angrist & Pischke [31], p. 23) further pointed out the difficulties of generalising from knowledge about a singular causal relation:

Perhaps it’s worth restating an obvious point. Empirical evidence on any given causal effect is always local, derived from a particular time, place and research design. Invocation of a superficially general structural framework does not make the underlying variation or setting more representative. Economic theory often suggests general principles, but extrapolation of causal effects to new settings is always speculative. Nevertheless, anyone who makes a living out of data analysis probably believes that heterogeneity is limited enough that the well-understood past can be informative about the future.

The difficulties of generalising causal relations from studied samples to other populations when no general laws are known are also discussed by (Khosrowi [34], p. 46):

Successful extrapolation hinges on similarities and differences between populations at different levels; and if differences at any of these levels obtain, we will need to learn about them and take them into account. This is not an easy task, however, as learning what the relevant similarities and differences are can be extremely challenging.

Moreover, even if we could be successful in identifying them, there is a second challenge to be addressed: the extrapolator’s circle [35,36]. Specifically, the knowledge about the target required for extrapolation must not be so extensive that we can identify the causal effect in the target based on information from the target alone. This would render the act of extrapolating from the experiment redundant. For instance, suppose X causes Y in A and our aim is to determine whether this also holds true in B. Suppose the mechanism in A is $X\to Z\to Y$. In order to decide whether X causes Y in B it seems important to learn whether a similar mechanism is instantiated there. However, learning that $X\to Z\to Y$ in B makes the extrapolation from A redundant, as one can already answer whether X causes Y in B from information about B alone. This poses a challenge for any persuasive account of extrapolation: any such account should help us extrapolate given only partial information about the target, i.e., information that does not, by itself, permit identification of the effect of interest ([36], p. 87).

The conclusion to draw is once more: In order to have good reason to believe in a causal relation in an untested case, one needs more than regularities with unspecified ceteris paribus clauses, i.e., we need laws. However, lacking laws, we can only make informed guesses. Our certainty is proportional to our certainty about having correctly identified all components of the ceteris paribus clause. The best way to obtain the necessary information is to perform experiments.

5. Experimental Methods in the Social Sciences

To perform a well-conducted experiment with full control of all conditions is often impossible in the social sciences. However, in order to obtain causal information at the general level, one must perform some kind of experiment, and one has to do the best one can.

In the flow of events, it may occur something that can be called a natural experiment, a variation of one variable, not being under deliberate control, while other factors with some justification can be assumed to be stable. Angrist and Pischke found such a natural experiment conducted in Israel that could inform us about the effect of class size on student score, see ([37], p. 13).

In Israel, the class size is capped at 40, so if there is 41 students, these are divided into two classes each with circa 20 students. (Similarly, if there are 81 students, one divides the group into three classes, and so on.) One can then compare rather small classes with classes of 40 and slightly less. Since the enrollment numbers to a particular school can be thought of as random, one has a situation sufficiently similar to one in which one performs a real experiment by randomly dividing schools in those with small classes and those with much bigger classes. In such circumstances, one may assume that schools with different numbers of students per class are quite similar in other characteristics, hence if there is any difference in average scores, one may conclude that it is caused by differences in class size. This situation is in relevant aspects similar to an experiment where one deliberately manipulates one variable. The authors concluded: ‘Regression discontinuity estimates using Israeli data show a marked increase in achievement when class size falls.’ (op. cit. p. 14)9.

Jackson & Cox [38] somewhat astonishingly does not mention natural experiments in their list of experimental methods: The laboratory experiment, the field experiment and the survey experiments.

Laboratory experiments are held to be optimal in experimental design; in the laboratory, one can manipulate one variable at a time and observe how the target parameter changes, while keeping all other variables fixed. However, critics have argued that the external validity, i.e., generalisability to natural settings, is doubtful; the laboratory differs too much from natural settings.

Field experiments are viewed more positively by critics of laboratory experiments. However, the drawback is that in a field study one cannot control, or even know, all relevant factors. So when manipulating one variable, one cannot be certain that an observed variation in the target parameter is due to the manipulated variable. The causal relation is a bit uncertain.

About the third purported type of experimental design, survey experiments, one is prone to ask, what is experimental in such a method? A survey is no intervention at all, one merely observes how people respond to a number of questions.

The results of surveys are basically correlations and regressions between variables. This may be of interest, but, as already pointed out, such information is insufficient for drawing conclusions about causal relations.

If the purpose of social science is to provide causal knowledge that can be used when deciding what intervention one ought to perform in order to achieve a certain goal, then an experimental research design is called for. However, most papers in the social sciences do not report an experimental approach, see next section. Many reasons for this state of affairs have been given. Here is a list of the most cited:

(1) There are so many variables ‘out there’ in the real world that it is impossible to control and measure them all.

(2) Most social groups are too large to study scientifically, you cannot put a city into a laboratory to control all its variables, and you could not even do this in a field experiment.

(3) Human beings have their own personal, emotionally charged reasons for acting, which they often do not know themselves, so they are impossible to measure in any objective way.

(4) Human beings have consciousness and so do not always react in a predictable way to external stimuli: They think about things, make judgments and act accordingly, so it is sometimes impossible to predict human behaviour. We have no general laws in the realm of the mental.

(5) There are also ethical concerns with treating humans as ‘research subjects’ rather than equal partners in the research process.

Reason number 1 in this list is, as already pointed out, nothing specific for social science; the same is true of systems in the natural world. Nevertheless, it is, in natural science, possible to construct models where one can justify omitting most factors as being too small to be of any relevance. So, the problem is to have ways of estimating the relative strengths of different contributing factors in a specific situation. This is often lacking in social science.

Reason number 2 is basically the same as number 1.

Reasons 3 and 4 assume that human minds are somehow independent of the physical and social world and that mind states arise without anything determining them. This is basically mind–body dualism in the vein of Descartes, which I do not believe is true. Mind states supervene on brain states, and brain states are states in the physical world, following the physical laws, so there is in principle no additional difficulty in studying human agents.10

Number 5, ethical concerns, are indeed relevant. Some experiments, such as Milgram’s study of obedience [39] we now judge as unethical, and it would not be allowed to be repeated.

To summarise, it is somewhat more difficult to do experimental research in social sciences than in natural science. However, is that difficulty sufficient to account for the rather small portion of experimental research in social science? In the following subsection I touch on that topic.

Experimentation in Economics, Sociology and Political Science

In an overview of research in econometrics, the last 40 years Angrist & Pischke [31] observed a credibility revolution in this discipline. Some 40 years ago, econometrics was in bad shape. The authors referred to Leamer [40], who urged empirical researchers to ‘take the con out of econometrics’ and memorably observed: ‘Hardly anyone takes data analysis seriously. Or perhaps more accurately, hardly anyone takes anyone else’s data analysis seriously.’ (p. 37).

The target of Leamer’s critique was regression analysis, the default method in econometrics in those days. According to Leamer, the results depended heavily on key assumptions and these seemed ’whimsical’, with no good reason for choosing one over any of a number of alternatives were given.

Empirical researchers in economics have gradually accepted Leamer’s critique, thus more and more trying to apply randomised experiments to justify causal inference. In applied micro-fields such as development, education, environmental economics, health, labour and public finance, researchers seek real experiments where feasible and useful natural experiments in situations where real experiments seem infeasible.

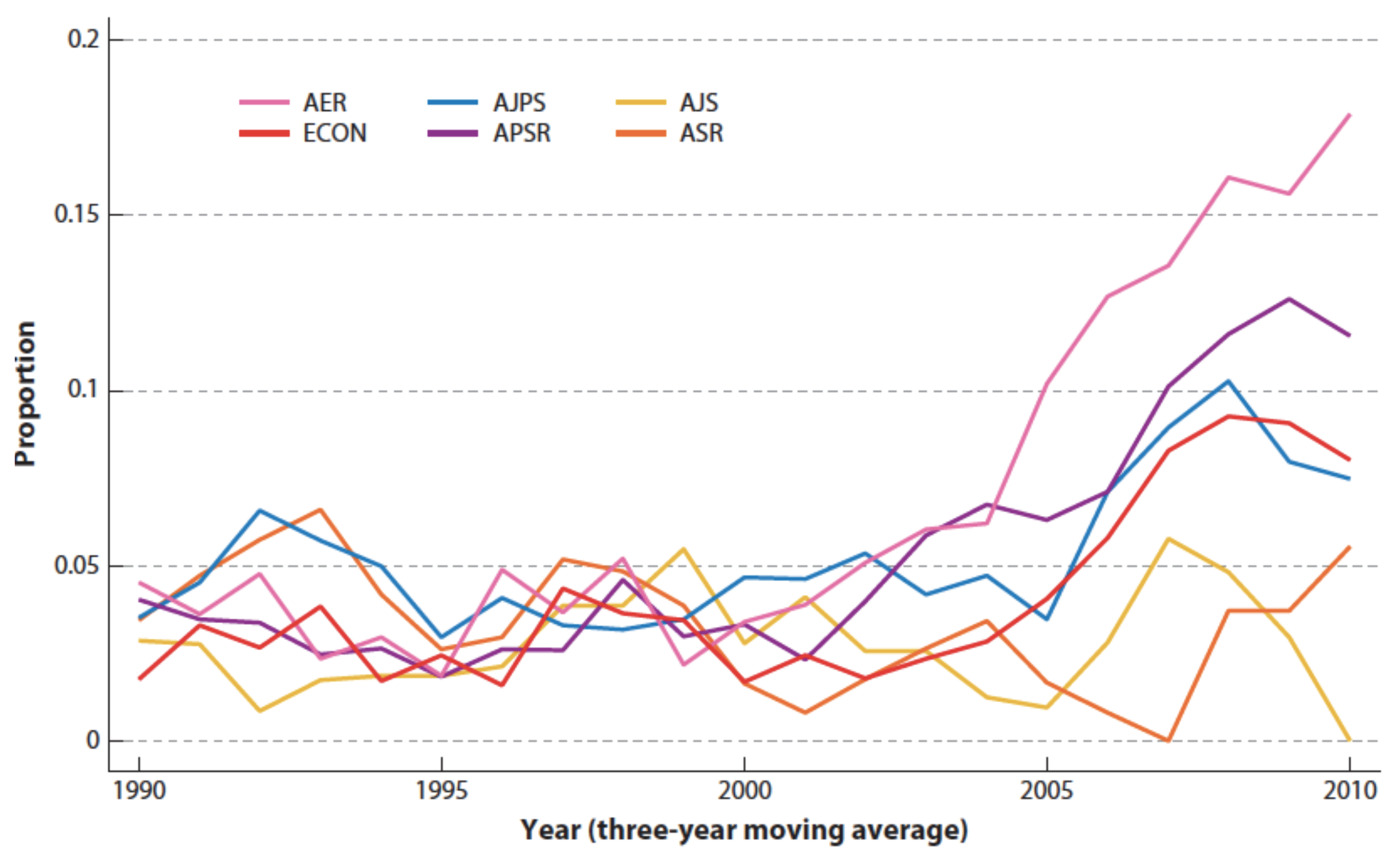
In Jackson & Cox [38], the authors discuss experimental design in sociology. Comparing with economics, they see a substantial increase in the use of experimental research in economy but none in sociology. They compared papers in six leading journals, two in economics, two in political science and two in sociology. The proportion of papers applying experimental methods started to increase after 2000 in economy and political science, whereas no such increase could be observed in the sociological journals, see Figure 1 below. The difference between, on the one hand, economics and political science and, on the other hand, sociology is substantial. Is that because researchers in sociology do not think generalisations to unobserved phenomena and prediction are a goal of their discipline, or is it because it is much more difficult to perform experiments in sociology, or what? I do not know.

6. Summary

In order to deliberate and make rational decisions about future actions, we need causal knowledge; we need knowledge of the form ‘if we do X, Y will probably happen’. However, inductive conclusions from merely passive observations are not sufficient for obtaining such knowledge.

The best way to obtain such knowledge is to perform experiments and then trying to formulate inductive generalisations from these experiments. If we succeed, we have established regularities, more or less stable. A regularity can then be promoted to a law when a predicate used in formulating this regularity is treated as a theoretical one implicitly defined by this very formulation and hence more or less divorced from its original meaning in ordinary language. The change in the meaning of the term ‘force’ when it became part of classical mechanics is a clear illustration.

Laws, properly so called, do not say anything about causes. This is so because there is a contextual element in the concept of cause; a cause is usually a state change which in a particular case can be manipulated by us humans, or else is changed in a random process. If we can manipulate the natural or social environment in such a way that a certain variable achieves a certain value, and we know that this variable correlates with another variable, we know we have caused a change in the second variable.

In physics and closely related disciplines, we have found a great number of such laws, while in the social sciences the lack of success in this respect is obvious. Not few researchers and philosophers of science have claimed that there are no laws to be found in the social sciences. This is, obviously, an inductive inference. I think the conclusion is too pessimistic.

A lack of success in finding laws in social science is no proof that no laws can be found. It could just as well be that scientists apply wrong methods, or that insufficient time and research has been devoted to finding laws. One may recall that physics started with Aristotle, and 2000 years had elapsed when Newton discovered the first laws for the dynamics of bodies in motion.

Lacking laws, one must rely on regularities, conditioned on ceteris paribus clauses and based on experimental data, when inferring from observed to unobserved events. Using a regularity is always more uncertain as a basis for inferences to future events than cases in which we have a law at our disposal; it is difficult to know whether the ceteris paribus conditions needed for formulating a regularity will continue to be satisfied.

The social sciences differ in their use of experiments. If the observations of Jackson & Cox [38] can be generalised, one may infer that economics more than political science and sociology have in the last decades improved in this respect. Since experiments are often impossible, the way to move forward is to look for natural experiments, in so far as one wants causal knowledge useful for future actions.