Abstract
We provide a critical assessment of the account of causal emergence presented in Erik Hoel’s 2017 article “When the map is better than the territory”. The account integrates causal and information theoretic concepts to explain under what circumstances there can be causal descriptions of a system at multiple scales of analysis. We show that the causal macro variables implied by this account result in interventions with significant ambiguity, and that the operations of marginalization and abstraction do not commute. Both of these are desiderata that, we argue, any account of multi-scale causal analysis should be sensitive to. The problems we highlight in Hoel’s definition of causal emergence derive from the use of various averaging steps and the introduction of a maximum entropy distribution that is extraneous to the system under investigation.
1. Introduction
In “When the Map Is Better Than the Territory”, Erik Hoel provides a formal theory of how a system can give rise to causal descriptions at multiple levels of analysis [1]. The proposal has its origins in the formal definition of the measure for consciousness in the Integrated Information Theory of Consciousness [2]. The question of how to describe the causal relations of a system at different scales is closely related to the debates in mental causation in philosophy, where the focus has been on whether mental states (thoughts, beliefs, desires, etc.) can be causes of behavior in their own right, distinct from the physical quantities (neurons, brain chemistry, etc.) that realize the mental states. Of course, multi-scale causal analyses are not restricted to the relation between the brain and the mind. Similar concerns arise in micro- vs. macro-economic theory, or quite generally in understanding how the life sciences relate to the fundamental natural sciences. In many domains there is an accepted level of analysis at which the causal processes are described, while it is understood that these macro-causal quantities supervene on more fine-grained micro-level causal connections. Hoel provides a precise formal account of this supervenience and explains under what circumstances macro-causal descriptions of a system can emerge. By integrating causal concepts with information theoretic ones, Hoel argues that a macro-causal account of a system emerges from micro-causal connections when the coarser, more abstract causal description (the map) is more informative (in a sense that he makes formally precise) than the micro-causal relations (the territory).
Hoel’s account is one of the very few attempts to provide an explicit formalism of causal emergence, which one could apply to a (model of a) real system. While we will be critical of some of the core features of the account, we highly commend Hoel for developing this theory in precise terms. Unlike many other attempts to explain multi-scale causal descriptions, this theory is precise enough for us to pinpoint where we disagree. Our disagreements are not flaws or errors in the account that would refute the theory, but highlight consequences of the theory that we think violate important desiderata of what an account of causal emergence should satisfy. Specifically, our examples show that Hoel’s theory permits so-called “ambiguous manipulations” with rather significant ambiguity (Section 3), and that the operations of abstraction and marginalization do not commute in his theory (Section 4). The latter is a particularly unusual feature for a theory that aims to describe a system at multiple scales of analysis.
Like many formal accounts, Hoel is silent on the metaphysical commitments of his theory. That is, it remains open whether the causal emergence he identifies has an independent objective reality, carving nature at its joints, or whether it is merely a convenient way for an investigator to model the system. None of our concerns hinge on this issue and so we will similarly remain agnostic with respect to the metaphysical commitments. However, depending on the view one takes, the implications of our formal results are different: To the extent that one reads Hoel’s account as a description of objective reality, our results show that the description is not objective, but contains significant modeling artifacts. If instead one interprets Hoel’s account as merely epistemic, then the results point to an arbitrariness in the investigator’s model that is not well justified and that has misleading consequences.
We start by describing Hoel’s theory in Section 2. We have adapted Hoel’s notation to improve clarity. Where we use different notation, we note the mapping to Hoel’s notation in the footnotes. We then provide our main counter-intuitive examples in Section 3 and Section 4 and discuss the implications of our examples for the desiderata of a theory of causal emergence. In Section 5, we cover a few of further curiosities of Hoel’s account before closing in Section 6.
2. Hoel’s Theory of Causal Emergence
Similar to other theories of emergence (see, for example, Shalizi and Moore [3]), Hoel describes his theory in terms of a discrete state space with a finite number of states that characterize the micro-level states of the system under investigation. Micro states are connected to one another by state transitions that are fully specified in a transition probability matrix , whose entry specifies the probability of the system being in state at time given that it was in state at time t. Given that there are no unobserved variables and all state transitions are from one time point to the subsequent one, the transition probabilities correspond to the interventional probabilities that characterize the micro-level causal effect of the system at time t on the system at time . We thus have a simple model of the micro-causal relations.
There are various ways of interpreting this model. Hoel’s notation suggests an interpretation of the model in terms of a fully-observed one-step Markov process evolving over time with one variable that has n states. However, Hoel’s model makes no commitments about further features that a time series may or may not exhibit, such as stationarity. So, one can also read the transition probability matrix as simply specifying an input–output relation of a mechanism (where the input and output have the same state space). For those more familiar with causal Bayes nets, one could also just think of two variables X and Y (with the same state spaces) and use to specify the transition probability matrix. However, no marginal distribution is specified.
To simplify subsequent notation, we let the state transition probability matrix specify the transition probabilities from states of input variable X to states of output variable Y, with the understanding that the state spaces of X and Y are identical.1
Now, given a micro-causal system described by the finite state space and a transition probability matrix , under what circumstances does a macro-level causal description with state space and macro-level transition probability matrix emerge?
Every coarser description of the system has to combine states of into a smaller set of macro states . While any partition that is a coarsening of is in a trivial sense a macro-level description of the original system, Hoel’s theory aims at identifying particular coarsenings that amount to, what he calls, causal emergence. These are coarsenings of the original state space with distinguishing features that make them intuitively more appropriate as (macro-)causal descriptions in their own right. Hoel maintains that effective information is the relevant measure to identify macro-causal descriptions. Effective information has a variety of appealing characteristics that permit a connection between causal and information theoretic concepts. In particular, it specifies the average divergence that a specific intervention on the system achieves, compared to a reference distribution of interventions. The underlying idea is that effective information tracks in a precise sense how causally informative the current state of the system is for its future state. As with many information theoretic notions, effective information is defined not only in terms of the transition probabilities, but also in terms of the input distribution for the “sender”, i.e., in this case, the cause. While Hoel does not discuss his choice of input distribution extensively, we believe that the selection of a maximum entropy intervention distribution over the state space of the cause is motivated by a desire to (a) uniquely determine the value of the measure, and (b) to use a distribution that explores the full causal efficacy of the cause without being affected by its states’ observed or marginal probabilities. Given the finite discrete state space , the maximum entropy intervention distribution is just the uniform intervention distribution over the set of micro states:
Intervening with this distribution on X results in the effect distribution over Y:
In other words, simply computes the uniform average over all rows in the transition probability matrix. To see the effect of each specific intervention , we want to compare with , the specific row of the transition probability matrix. Hoel uses the Kullback–Leibler divergence to compare how different these two distributions are. The effective information () of a (micro-level) system then takes the average of these divergences:
where is the Kullback–Leibler divergence. As the form of Equation (5) already indicates, is the mutual information between the uniform intervention distribution over the cause and the resulting effect distribution :
One way of thinking about effective information is that it provides a measure of how distinct the causal effects of X are on Y, using the maximum entropy distribution as a reference distribution. Consequently, when we now consider a macro-level description of , where the state space of U is a coarsening of the state space of X (recall that the effect always has the same state space as the cause here), then combining states with similar transition probabilities can lead to an improvement of how distinct the causal effects of the remaining aggregated states are, i.e., the mutual information between cause and effect can be increased by abstracting to a macro-level description.
However, in order to fully determine the effective information of a coarsening of the micro space , one has to specify what it means to intervene on a non-trivial macro state u. That is, one has to specify what is when , for two distinct micro states and . Without much explanation or motivation, Hoel defines the intervention on a macro state to correspond to a uniform average of interventions on the micro states that map to the macro state: By slightly overloading notation, let u stand both for a macro state and for the set of micro states that correspond to it (similarly for v and in the effect). Then the intervention on macro state u is given by:
In words: The intervention on macro state u results in a probability of macro state v that is given by intervening on all micro states that correspond to macro state u, averaging the resulting distributions over Y uniformly, and then summing over those micro states that correspond to macro state v.2
With this definition in hand, the effective information of any coarsening of the micro state space of the system can be determined. According to Hoel then, causal emergence occurs when a macro state space that is a strict coarsening of the micro state space maximizes effective information. That is, the brute force3 version of the abstraction operation from micro to macro level is that one searches over all possible coarsenings of the micro space. The coarsened state space applies to both U and V. For each such coarsening , one determines the effective information of by considering a uniform intervention distribution over , the coarsened state space. This uniform intervention distribution over the coarsened state space will in general map to a non-uniform distribution over the micro state space (since the intervention probability on one macro state is divided up evenly among all the micro states that map to it, and different macro states may have different numbers of such micro states). There will be at least one partition that maximizes effective information. Whenever such a partition is coarser than the micro-level partition, Hoel speaks of causal emergence. See Figure 1.
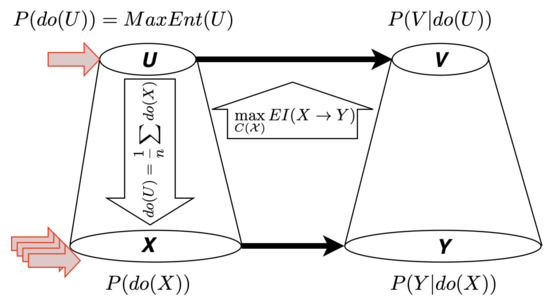
Figure 1.
Hoel’s theory: Causal emergence occurs whenever effective information is maximized for a strict coarsening of the state space of the underlying system. Note that X and Y are required to have the same state spaces (similarly, for U and V). Setting macro variable U to state u by intervention maps to a uniform average over the interventions for those values x that correspond to the value u.
This approach has many attractive features. In particular, it builds a close connection between macro-causal descriptions and channel capacity in information theory. Channel capacity is defined in terms of the input distribution that maximizes the mutual information between sender and receiver across a noisy channel:
Hoel’s search for causal emergence is similar: It is a search over intervention distributions over the micro states in for the intervention distribution that maximizes the mutual information between the intervened macro cause U and the resulting effect V. However, as the differing notation already suggests, the maximization of effective information is a maximization of mutual information subject to two constraints: First, only a subset of possible distributions over X is considered—namely those that correspond to maximum entropy distributions (i.e., uniform distributions in this case) over some coarsening of the micro space . And second, rather than just maximizing mutual information between the sender and receiver, the maximization of effective information requires identical state spaces for the cause and effect.4
Hoel refers to the maximization of effective information as achieving the causal capacity:5
Thus, a macro-level causal description emerges from a micro-level causal system whenever the effective information matches the causal capacity. This is when the map is better than the territory.
Despite the suggestive connection to information theory, several aspects of the definitions give reason for pause: Maximum entropy distributions are theoretically useful distributions, but they are an artificial addition to the analysis of a natural system. It remains an empirical question of whether such distributions have any relevance to the actual system one is investigating. Moreover, averages can obscure significant discrepancies, and in Hoel’s account of causal emergence there are at least two averaging steps: A macro-intervention is a uniform(!) average over the micro interventions that map to it, and effective information is a maximum entropy mixture (so, here again, a uniform average) over a set of KL divergences. Our examples in the following highlight what features of the territory are obscured by a map that uses maximum entropy and averaging of this kind.
3. Ambiguity: Merging States with Different Causal Effects
When two different micro states have the same transition probabilities, it is generally uncontroversial that they should (or at least, can) be combined to form a coarser macro state. The micro states do the same thing, so there is little point in distinguishing them. Indeed, effective information generally6 does just that, as is illustrated by Hoel’s first example of causal emergence where he considers a micro state space with possible states and a transition probability matrix given by
The first seven states have identical effects, so the EI is only 0.55. Unsurprisingly, the EI is maximized when the first seven states are collapsed, such that the macro state space consists only of two states and the corresponding is given by
This two-state macro representation has effective information of 1. More interestingly, as Hoel points out with his second example, the micro states need not have identical transition probabilities in order for a causal macro description to emerge. The following transition probability matrix over 8 states has effective information of 0.81, but collapsing the first seven states as above still maximizes effective information at 1.
Obviously, combining states 1–7 into a single state aggregates micro states with quite different causal effects. For example, state has zero causal effect on states and , while state loads 1/7 and 2/7 of its probability on states and , respectively. Defining macro variables, whose micro-level instantiations have different causal effects, results in macro variables that have so-called ambiguous manipulations [5]. Spirtes and Scheines illustrate ambiguous manipulations with the toy example of the effect of total cholesterol on heart disease. If total cholesterol is constituted of high-density lipids (HDL) and low-density lipids (LDP), and HDL and LDL have different (say, for the sake of argument, opposing) effects on heart disease, then an intervention on total cholesterol is ambiguous, because its effect on heart disease depends on the ratio of HDL to LDL in the intervention on total cholesterol. Unless HDL and LDL have the quantitatively identical effect on heart disease, total cholesterol appears to be an over-aggregated variable. Indeed, there is reason to think that it was this sort of ambiguity that historically led to a revision of total cholesterol as a relevant causal factor of heart disease. Instead, the causal relation was re-described in terms of its components, namely, HDL and LDL. The effect of total cholesterol is just a mixture of two distinct finer-grained causal effects.
On Hoel’s account, the proportion of each of the micro state interventions is fixed by the uniform distribution over micro interventions described in (8), which ensures a well-defined intervention effect, despite it being a mixture of different causal effects. It is as if an intervention on total cholesterol always corresponded to a 50/50 intervention on HDL and LDL. Defining the macro intervention as the average over the micro interventions is, of course, possible, but entirely ad hoc. Why does an intervention on a macro state correspond to many different, presumably simultaneous, interventions on the corresponding micro states? Moreover, why should these micro-state interventions all be weighted equally? For example, when we set a thermostat to F (macro state), then Hoel’s theory claims that the resulting effect is the uniform average over all ways that one could have set the gas particles’ kinetic energies such that their mean is F. This includes micro states with highly uneven distributions over the kinetic energies of the particles, which can have causal consequences that are very different from those we typically associate with F. It seems more realistic to instantiate such a macro intervention in terms of one specific micro state that corresponds to F at the macro level—for example, it could be the micro state corresponding to F that is closest to the actual state of the system at the time of intervention. Moreover, Hoel’s definition implies that one may have to average over completely contradictory micro-level effects: If we have two micro states that map to the same macro state, but one has the effect that the animal in a cage remains alive, whereas the other has the effect that it is killed, then the intervention on the macro state implies that the animal is half-dead, not that it is either dead or alive.
There are various ways one might respond. Some of the responses depend on whether one thinks of Hoel’s theory as describing what is actually happening in a given system or whether one thinks of it as a model of the investigator’s knowledge of the particular system. In the latter case the average over possible micro interventions can be construed as a strategy to handling the epistemic uncertainty about which micro state it might be that instantiated the macro intervention. We will not pursue these routes given that Hoel does not indicate whether the theory should be understood epistemically or metaphysically, but they are discussed in greater detail in Dewhurst [6]. We only note that if one indeed views Hoel’s account as a model of the epistemic state of the investigator, then the investigator might deserve some freedom of thought: Maybe they prefer distributions other than the uniform one over the micro interventions because they have domain knowledge. Maybe they would update their distributions as more evidence comes in? Maybe they are aware of the critiques of objective Bayesianism and its use of uninformative priors. If one allowed for any such epistemic freedom, then the entire story would need to change because there would not be one causally emergent system, but a whole set of admissible macro descriptions.
One can try to avoid philosophical debates, by holding out hope that such dramatic cases as the above examples suggest, do not arise in the first place: If indeed the transition probabilities of the micro states are very different from one another (such as states 1–7 vs. state 8 above), then they would not be collapsed into one macro state, because that may not maximize the effective information. Indeed, in extreme cases, this is true—after all, the remaining two states in the matrix in (12) are kept distinct.
So, how different can the causal effects of two micro states be such that they still end up being collapsed on Hoel’s theory?
Of course, any answer to this question has to specify a distance metric between causal effects (represented here by the rows in the transition probability matrix) and then has to maximize the distance between the two causal effects while ensuring that maximizing effective information of the system still collapses them into the same macro state. Even for systems with three micro states, we are not aware of any analytical solution to this problem for any non-trivial distance-measure. Given a transition matrix, there would be six unknowns:
Each possible macro description of the system leads to combining these unknowns in different ways to determine the macro transition probabilities. Setting the effective information of one of these macro descriptions to be the maximum determines which macro description is chosen. Due to the definition of effective information (and the chosen distance metric), this gives inequality constraints in which the involved fractions and logarithms have different arguments depending on how many micro states are being collapsed. Even for these simple systems, we only have numerical results.
Consider a micro-level state space with three states and a transition probability matrix given by
The effective information for this matrix is , but effective information is maximized when the first two states are collapsed, resulting in a macro state space and a corresponding transition probability matrix
Its effective information is , slightly higher than for the micro level. In this case, the absolute distance between the two rows of the collapsed states and in the transition probability matrix is 0.8. The maximum difference one can achieve using this distance measure is slightly higher, since one can still adjust the transition probabilities by tweaking further digits after the decimal point. Moreover, this matrix is not unique in having an absolute distance of 0.8 between the causal effects of two states and yet collapsing them. In Appendix A, we give additional examples. We also consider what happens when one uses other distance metrics, such as the standard Euclidean distance, the maximum difference between any single transition probability from one state, the maximum of the minimum difference between any transition probability from any state, or—if one instead thinks of these causal effects as distributions—one could use the KL divergence as distance metric.
We give examples for all these cases (and one could pursue many more), but the upshot is the same: The examples have two states with rather different transition probabilities that are collapsed according to Hoel’s account. In what sense can we speak in these cases of causal emergence? At what point are micro-causal effects so different that grouping them together as a macro-effect does not amount to describing the system causally at the macro level, but instead amounts to describing mixtures of lower-level effects? In the example in (14) above an intervention on state has a small chance in resulting in state and a roughly even chance in resulting in state or . In contrast, an intervention on state results with probability 0.7 in state , and roughly equal small probability in state and . Given the distinct causal effects of states and , it makes the choice of collapsing them very counter-intuitive despite the information theoretic result. Yet, on Hoel’s account, which intervenes on all states with equal probability, these two states are grouped together and the example would constitute a case of the emergence of a macro-causal description.
Of course, there is no contradiction in Hoel’s claims, and indeed state provides a starker contrast to both and than they do to each other. But note that if we changed the first row of the transition probability matrix in (14) to , i.e., shifting just of probability from the to , then the transition probabilities of states and would still look more similar to each other than either does to those of , and yet states and would not be collapsed by maximizing effective information. So, it is not as if the causal emergence as defined here tracks any sort of intuitive clustering of close states. Maximizing effective information results in a very specific mixture of states and it remains quite unclear why the resulting clustering is privileged over any other intermediate (or additional) clustering.
The goal, we think, of identifying causally emergent macro descriptions is that we do not just have mixtures of underlying causal effects, but that the identified macro variable can be described as a cause in its own right, and that its micro instantiations are distinguished by differences that are in some sense negligible or irrelevant. This requirement will come as no surprise to those familiar with the literature on mental causation in philosophy, since it is closely related to the demand that macro causes be proportional to their effect (see, e.g., Yablo [7]). Although Yablo uses somewhat different terminology, a proportional cause is the coarsest description of the cause that screens off any finer-grained description of the cause from the effect. That is, it is the coarsest description of the cause for which all interventions are unambiguous.
However, from the formal perspective the absence of ambiguous interventions is a more delicate desideratum. We expect that few would disagree that maximally coarsening while maintaining unambiguity indeed results in a macro-level model with all the features one would expect of a causal model. But the concern is whether the requirement is too strong: If one can only have macro states with unambiguous manipulations, then, for example, the system described by the transition probability matrix in Hoel’s second example (see (13)) could not be coarsened at all.
There are two responses to this: First, indeed the perfect lack of ambiguity is too demanding, so one should permit the collapsing of states that have very similar causal effects, as defined by some distance metric between causal effects. This is exactly what is done for the identification of macro-causal effects in the Causal Feature Learning method of [8,9]. But second, beyond the slight distinctions in causal effect, one might want to bite the bullet on this concern: If the effect granularity is very fine, then indeed it seems appropriate that one should not coarsen the cause, since small changes in the cause may result in fine changes in the effect. But if the effect granularity is coarse, then automatically, it will be possible to also coarsen the cause while preserving unambiguity. For example, in order to predict where exactly the soccer ball will hit the goal, one might need the very precise description of the cause and, consequently, no coarsening (without violating ambiguity) is possible. But if one only wants to know whether the ball is going left or right (like a goalie during a penalty kick), then even a very coarse description of the cause can remain unambiguous.
This suggests a different modeling approach to Hoel’s: While Hoel described the system in terms of one state space that causally influences itself over time, the present considerations suggest that one should disentangle the coarsening of the cause from that of the effect. There can be cases where one can be coarsened while the other cannot. This is in contrast to Hoel’s case where the cause and effect always get coarsened together, because they are described by the same state space.
4. Commutativity: Abstraction and Marginalization
A macro description of a system is an abstraction of the underlying system [10]. Hoel’s account focuses on coarsenings of the state space, but he explicitly notes at the beginning of his Section 3 that such an abstraction can also occur over time and space [1]: “Macro causal models are defined as a mapping , which can be a mapping in space, time, or both”. The discrete time steps , etc., used to define the Markov process are of arbitrary, but fixed, length. As in any time series, these are features of the model reflecting the rate of measurement. Of course, we would expect different causal processes to emerge if we consider longer or shorter time scales, just as we expect different causal descriptions for coarser or finer state spaces. But the marginalization of time steps and the abstraction over the state space should commute: Aggregating to coarser state spaces and then looking at the system at different time scales should result in the same macro-level description as looking at the system at different time scales, and then aggregating.7 Similarly, if we view Hoel’s model only as specifying the input–output relations of a mechanism, then the concatenation of mechanisms (even of identical mechanisms) and abstraction should commute: Aggregating each mechanism by its own lights and then concatenating the aggregated mechanisms vs. concatenating the mechanisms and then aggregating the joint mechanism should result in the same macro-level description.
This is not the case for Hoel’s account: Let denote the abstraction operation, i.e., the transition probability matrix of the corresponding macro state space which maximizes the EI. If abstraction and marginalization commute, then the following equation has to be satisfied:
That is, finding the macro description of the effect over two time steps should be the same as evolving the macro description for two time steps.
Consider the following transition probability matrix for a micro state space with three states:
The left hand side of Equation (16) becomes
None of the states are collapsed, and the EI is If we now consider the right hand side of Equation (16), then
This resulting transition probability matrix collapses states 1 and 2 and has EI . Not only does the EI not match, but the resulting systems have different state spaces depending on whether one marginalizes first and then abstracts, or abstracts first and then marginalizes.
Unlike in Section 3, where we give specific transition probability matrices that maximize the distance between two states that get collapsed, this sort of failure of commutativity occurs in general for Hoel’s account. Only very specific transition probability matrices satisfy commutativity of abstraction and marginalization, most violate it. We note that in this case we have used a Markov process over the same variable X with transition probabilities given in (17). If one considered a causal system with three micro variables X, Y and Z, each with their own state spaces, connected in a causal chain , then marginalizing Y could result in even more extreme discrepancies, because the transition probability matrices and would not have to be the same.
Thus, in Hoel’s account, whether causal emergence occurs at all and what the resulting macro description looks like depend on the order in which state space and time evolution are considered. Ultimately, this should not come as a surprise. Hoel’s account of causal emergence depends not only on the causal relations from one time step to another (which are described by the conditional distribution ), but also on the injection of the input distribution . Since Hoel’s input distribution has nothing to do with the system in question, but is an exogenous maximum entropy distribution, a discrepancy arises when one marginalizes time points whose marginal distribution does not correspond to the maximum entropy distribution naturally.
If abstraction and marginalization do not commute, then the macro-causal account does not actually describe features of the underlying system in question, but features that crucially depend on the rate of measurement (if we think in terms of time series) or on the input–output points (if we think of as a mechanism) chosen by the investigator. A macro-level description of the system would be, so to speak, “bespoke” for the specific start and endpoint, but would not be generalizable or extendable. It would confirm the view of those who hold little regard for causal models in economics or psychology because (they think) their macro-level causes lack a degree of objectivity. This sort of reasoning quickly risks implying the impossibility of causal modeling quite generally in all but the most fundamental sciences. Consequently, for those who are more optimistic about causal models in the special and life sciences, it should come as no surprise that the demand for commutability of abstraction and marginalization is explicit in [11] (in fact, their consistency demands are even stronger) and [10]. The account of natural kinds in Jantzen [12] pursues a somewhat different goal, but the core feature of the natural kinds is also the commutability of intervention and evolution of a system.
Even if one does not require that abstraction and marginalization commute at all time points, at the very least, they should commute at some suitably large intervals to ensure that the macro level description does not completely diverge from the micro level one. Given the sensitivity of Hoel’s account to the intervention distributions, even “occasional commutativity” (however one might reasonably define that) is generally not possible.
5. Further Comments
One of the attractive features of Hoel’s account of causal emergence is the integration of causal with information theoretic concepts. We noted in Section 2 the theoretical similarities between Hoel’s causal capacity and the information theoretic channel capacity. Indeed, Hoel shows with several examples that as the number of possible micro states increases, that the causal capacity can approximate the channel capacity, because the uniform intervention distribution at the macro level generally results in a “warped” distribution over the micro states.8 We are not aware of any formal characterization or proof of this convergence claim.9 But even if we grant that suitably general conditions can be found to support the claim that reaching causal capacity closely corresponds to exploiting channel capacity, then this is still a peculiar macro description of a natural system: Channel capacity in information theory is a normative concept. It describes the input distribution the sender ought to be using in order to optimize information transmission. But a sender who does not use the optimal input distribution obviously does not exploit the channel capacity. The situation applies analogously to causal capacity: If we describe the micro state space of a system and its transition probabilities, then we can determine the causal capacity analytically. If there is causal emergence, then there is a coarsening of the micro state space that maximizes effective information. But whether or not the system actually exploits that causal capacity is an empirical question: It may not employ a maximum entropy distribution over the coarsened state space to maximize its causal effectiveness, just like an inexperienced sender may not use the optimal distribution for the noisy channel they are communicating over. Hoel seems to recognize this concern in the following passage from his paper:
“Another possible objection to causal emergence is that it is not natural but rather enforced upon a system via an experimenter’s application of an intervention distribution, that is, from using macro-interventions. For formalization purposes, it is the experimenter who is the source of the intervention distribution, which reveals a causal structure that already exists. Additionally, nature itself may intervene upon a system with statistical regularities, just like an intervention distribution. Some of these naturally occurring input distributions may have a viable interpretation as a macroscale causal model (such as being equal to at some particular macroscale). In this sense, some systems may function over their inputs and outputs at a microscale or macroscale, depending on their own causal capacity and the probability distribution of some natural source of driving input.” (emphasis added) [1]
Thus, Hoel’s account is about potential causal emergence of a system, but not about actual causal emergence.10 So, even if we otherwise accept the account as a correct formalization of causal emergence, it remains an empirical question of whether a system actually exhibits its potential causal emergence of the form Hoel describes or not. Just like channel capacity in information theory, causal capacity is a normative concept.
A second consideration is that while the maximum effective information (EI) of a system is always unique, it is far from clear whether the corresponding partition that maximizes EI is unique. That is, there may be multiple equally appropriate macro-level descriptions of the same system. Sometimes cases like this are inevitable given the definition of causal emergence: Given a partition with three states, one can generally make the transition probabilities of two states more and more similar such that at some point the two-state partition maximizes the EI. Along the way, there will be a point where the two-state and the three-state partition will both maximize EI. Such cases are expected as there has to be a transition point from micro-level description to causal emergence, and the two partitions with equal maximum EI are hierarchical (one is a coarsening of the other). However, we postulate that it is also possible that two different-sized partitions of the same micro space, neither of which is a coarsening of the other, may both maximize EI. That is, we postulate that there exist state transition probabilities for, say, a 5 state micro system such that its 3 state coarsening, the partition , and its 2-state coarsening, the partition , both maximize EI. In this case, two macro descriptions emerge that both describe the system macroscopically, but in entirely different ways. If such cases indeed exist as we suggest11, then one can, of course, still dismiss them as inevitable edge cases. However, with an increasing number of states, one may want to make sure that such cases are not common. Moreover, even if there is no exact equality in the maximized EI of two very different partitions, or if such cases are rare, a near-match would already appear to make the causal emergence highly unstable. It would be interesting to have examples of real cases where such “incommensurate” macro descriptions seem plausible or appropriate.
Finally, science studies systems at many different scales: Economic theory supervenes on the interactions of the individual economic agents, those agents’ behavior supervenes on the underlying biology, which in turn supervenes on chemical and physical processes. We describe the causal interactions of this system at all of these scales, and at several in between. Yet, causal emergence, as Hoel has defined it, picks out one scale beyond the microscopic one (and perhaps other closely related macro scales that happen to result in the same effective information; see previous point). But it does not explain causal descriptions at multiple (>2) significantly different scales: How should we think about these intermediate scales? Do they not constitute a form of causal emergence? Are there any restrictions of which meso-scale descriptions of a system actually describe genuine causal relations?
These questions interact with the concern about causal capacity mentioned before: Given that causal capacity is not optimal from an information theoretic point of view (but at best approximates channel capacity) and that the system may not actually be exploiting the causal capacity in the first place, then what distinguishes the particular coarsening that Hoel identifies? Why is such a coarsening then still privileged over all the other intermediate coarsenings, or even those that constitute an over-aggregation according to Hoel’s account?
6. Conclusions
We have been critical of Hoel’s theory of causal emergence. While we indeed disagree with the proposal for the reasons stated, the precision and the detail of the account, with its many very attractive features, have advanced the discussion and allowed us to articulate more clearly what we deem to be important desiderata of a macro-level causal description and causal emergence. We agree with Hoel that a macro-level description needs to be sensitive to the causal relations at play, and that interventional probabilities are crucial to getting the abstraction right. But, as we have argued, the introduction of the extraneous maximum entropy intervention distribution can obscure significant distinctions in the causal effects and introduce artifacts that a real system may never exhibit. Moreover, it unnecessarily destroys the possibility for the operations of abstraction and marginalization to commute. These problems can be avoided if the account of causal emergence builds only on the conditional interventional probabilities and does not also use the marginal distribution over the intervened variable X. These ideas have been developed further in Chalupka et al. [8]. Their approach, we believe, also addresses the question of why there can be causal analyses at many different scales: If the effect phenomena are of different granularity, then aggregations in the cause emerge naturally [16].
And finally, of course it can be of interest to explore what a system could achieve and what sort of causes could emerge if only the system were fully optimized. But we need to clearly separate possibility from actuality.
Author Contributions
The ideas for Section 3 and Section 4 originated with F.E. and were refined and implemented numerically by L.L.L. The ideas discussed in Section 5 evolved out of the collaboration. The manuscript was written and revised together. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by NSF grant 1564330. Part of this work was done while FE was visiting the Simons Institute for the Theory of Computing.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Examples of Ambiguous Macro States for Different Distance Metrics
We focus on micro systems with three states and report examples where the transition probabilities for the first two states are very different to one another according to a variety of metrics, and yet the effective information is maximized if the first two states are collapsed. The examples were obtained by a grid search on a grid of probabilities with step size 0.1 in each of the six free dimensions. So, they do not represent the absolute maximal differences that can be obtained between states that collapse, but instead give a sense for each distance metric of how different the states can be that are still collapsed.
In Section 3, we gave the example of a matrix that maximized the absolute distance between two causal effects (on the 0.1 grid). Other matrices that also achieve a distance of 0.8 between states on this measure are the following (and their rotations):
If instead one uses squared Euclidean distance, then the following two matrices (and their rotations) maximize the distance between states and at 0.32 (on the 0.1 grid):
If we instead want to maximize the minimum difference between the transition probabilities from two states, we can choose our distance metric to be the minimum of the absolute value difference between components. That is, let . If we maximize this distance, then two states will not be close together on any one component. Below, the maximum distance (on the 0.1 grid) that each pair of components can be kept apart is .
Alternatively, we may just want to know how different any one transition probability (rather than the whole set) between two states that are collapsed can be. Maximizing this maximum difference between any transition probability is (on the 0.1 grid), and is achieved for:
To maximize the KL divergence, we maximize since the KL divergence is not symmetric. Moreover, we have to decide how to handle zeroes in this measure. Usually, for distributions p and q, if is 0 then it contributes 0 to the KL divergence because we take the limit of as . Since we take the sum of KL divergences in both directions, we assumed that if is also 0, then it contributes 0, too, to avoid a divide-by-0 error. With these adjustments, the KL divergence between the first two states is maximized (over the 0.1 grid) for
and its rotations.
For all the above matrices, effective information is maximized when state and are collapsed.
Of course, the maxima that can be achieved also depend on the number of micro states one starts off with. We have not explored this extensively, since Hoel’s 8-state example repeated above in (13) already indicates how difficult it is to judge intuitively whether these causal effects are very different.
Notes
| 1 | So, X in our notation corresponds to the micro-level variable at time t in Hoel’s notation. There it is referred to as S or at t. Y describes the micro-level system at time , which Hoel denotes by . |
| 2 | But this notation is not precise, since the -operator cannot actually be the object of a summation. |
| 3 | Note that in Griebenow et al. [4], various more efficient algorithms are explored. |
| 4 | See also footnote 6 and the end of Section 3 for comments on this peculiar requirement that the state spaces match. We consider it to be an undesirable, but largely artificial constraint in the account resulting from the specific set-up of a system influencing itself. The constraint could easily be abandoned. |
| 5 | Recall that the state space of X and Y is , that the state space of U and V is and that is a coarsening of the state space . |
| 6 | For the specific way that Hoel has set up the determination of causal emergence, it is not always the case that two states that have identical transition probabilities are collapsed into one macro state through abstraction. For example, consider the following system with three micro states and a transition probability matrix of , where states and have identical transition probabilities. In this case, the effective information is maximized by keeping all three states distinct, rather than collapsing states and into one macro state, despite their identical transition probabilities. This is purely an artifact of Hoel’s set-up: Rather than having a separate cause and effect variable, each with its own state space that one can coarsen independently of the other, the cause and effect variable are the same system at different time points. Consequently, a collapse of the cause state space necessitates a collapse of the effect state space. Given that the transition probabilities from state to states and in the effect are sufficiently different, these two states are kept distinct in the cause as well. But cases like this could easily be avoided in Hoel’s account by separating the coarsening of the cause state space from that of the effect state space. One could then still have the abstraction operation be a search for the maximum effective information. |
| 7 | We do not consider continuous time, since that would require a completely different model in the first place. |
| 8 | Note the discussion in Aaronson [13] that views this sort of inconsistency between a maxEnt distribution at the macro level that corresponds to a non-maxEnt distribution at the micro level rather critically. |
| 9 | We thank an anonymous reviewer for drawing our attention this point. |
| 10 | See Rosas et al. [14], who raise similar concerns about this account, and Janzing et al. [15], p. 6, for an analogous argument in the context of the use of channel capacity to quantify causal influences. |
| 11 | We have not (yet?) been able to solve this system, even numerically, due to the complex nature of EI and the number of inequality constraints required by the postulated example. A proof one way or the other would provide an interesting insight on the nature of EI. |
References
- Hoel, E.P. When the map is better than the territory. Entropy 2017, 19, 188. [Google Scholar] [CrossRef] [Green Version]
- Tononi, G.; Sporns, O. Measuring information integration. BMC Neurosci. 2003, 4, 1–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shalizi, C.R.; Moore, C. What is a macrostate? Subjective observations and objective dynamics. arXiv 2003, arXiv:cond-mat/0303625. [Google Scholar]
- Griebenow, R.; Klein, B.; Hoel, E. Finding the right scale of a network: Efficient identification of causal emergence through spectral clustering. arXiv 2019, arXiv:1908.07565. [Google Scholar]
- Spirtes, P.; Scheines, R. Causal inference of ambiguous manipulations. Philos. Sci. 2004, 71, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Dewhurst, J. Causal emergence from effective information: Neither causal nor emergent? Thought J. Philos. 2021, 10, 158–168. [Google Scholar] [CrossRef]
- Yablo, S. Wide causation. Philos. Perspect. 1997, 11, 251–281. [Google Scholar] [CrossRef]
- Chalupka, K.; Perona, P.; Eberhardt, F. Visual causal feature learning. In Proceedings of the Thirty-First Conference on Uncertainty in Artificial Intelligence, Amsterdam, The Netherlands, 12–16 July 2015; pp. 181–190. [Google Scholar]
- Chalupka, K.; Eberhardt, F.; Perona, P. Causal feature learning: An overview. Behaviormetrika 2017, 44, 137–164. [Google Scholar] [CrossRef]
- Beckers, S.; Halpern, J.Y. Abstracting causal models. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 2678–2685. [Google Scholar]
- Rubenstein, P.K.; Weichwald, S.; Bongers, S.; Mooij, J.M.; Janzing, D.; Grosse-Wentrup, M.; Schölkopf, B. Causal Consistency of Structural Equation Models. In Proceedings of the 33rd Conference on Uncertainty in Artificial Intelligence (UAI 2017), Sydney, Australia, 11–15 August 2017; pp. 808–817. [Google Scholar]
- Jantzen, B.C. Dynamical kinds and their discovery. arXiv 2016, arXiv:1612.04933. [Google Scholar]
- Aaronson, S. Higher-Level Causation Exists (but I Wish It Didn’t). 2017. Available online: https://www.scottaaronson.com/blog/?p=3294 (accessed on 10 February 2022).
- Rosas, F.E.; Mediano, P.A.; Jensen, H.J.; Seth, A.K.; Barrett, A.B.; Carhart-Harris, R.L.; Bor, D. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data. PLoS Comput. Biol. 2020, 16, e1008289. [Google Scholar] [CrossRef] [PubMed]
- Janzing, D.; Balduzzi, D.; Grosse-Wentrup, M.; Schölkopf, B. Quantifying causal influences. Ann. Stat. 2013, 41, 2324–2358. [Google Scholar] [CrossRef]
- Chalupka, K.; Eberhardt, F.; Perona, P. Multi-level cause-effect systems. In Artificial Intelligence and Statistics; PMLR: Cadiz, Spain, 2016; pp. 361–369. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).