MES: A Mathematical Model for the Revival of Natural Philosophy

Abstract

The different kinds of knowledge which were connected in Natural Philosophy (NP) have been later separated. The real separation came when Physics took its individuality and developed specific mathematical models, such as dynamic systems. These models are not adapted to an integral study of living systems, by which we mean evolutionary multi-level, multi-agent, and multi-temporality self-organized systems, such as biological, social, or cognitive systems. For them, the physical models can only be applied to the local dynamic of each co-regulator agent, but not to the global dynamic intertwining these partial dynamics. To ‘revive’ NP, we present the Memory Evolutive Systems (MES) methodology which is based on a ‘dynamic’ Category Theory; it proposes an info-computational model for living systems. Among the main results: (i) a mathematical translation of the part–whole problem (using the categorical operation colimit) which shows how the different interpretations of the problem support diverging philosophical positions, from reductionism to emergentism and holism; (ii) an explanation of the emergence, over time, of structures and processes of increasing complexity order, through successive ‘complexification processes’. We conclude that MES provides an emergentist-reductionism model and we discuss the different meanings of the concept of emergence depending on the context and the observer, as well as its relations with anticipation and creativity.

1. Introduction

For Aristotle, “Natural Philosophy” (NP) is a branch of Philosophy which examines the phenomena of the natural world; it includes fields that are now classified as physics, biology, and other ‘natural’ sciences. This division of Science into specific disciplines came later. In particular Physics only took its more restrictive modern sense around 1690, with Galileo, Descartes, and Newton.

Today, the aim is to search for connected knowledge able to re-unify sciences and revive NP, for instance in Complexity Theory and Network Science. For Truesdell [1]: “The first aim of modern natural philosophy is to describe and study natural phenomena by the most fit mathematical concepts. The most fit need not be the most modern, but <…> we neither seek nor avoid the most abstract mathematics”.

1.1. Mathematical Models in Physics

Among the usual mathematical models in Physics figure dynamic systems (generally employing differential or difference equations), nonlinearity and chaotic dynamics. They are based on the concept of phase space which was developed in the late 19th century by Ludwig Boltzman, Henri Poincaré, and Willard Gibbs. In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. In quantum physics, it is a little more difficult to describe this space, but there exists an analog.

The phase space model cannot lead to an integral model for complex dynamic living systems. By living system, we always mean evolutionary multi-level, multi-agent and multi-temporality self-organized systems, such as biological, social, or cognitive systems. The reason is that these systems are submitted to frequent environmental constraints which would necessitate incessant changes of phase space; thus we cannot find a unique phase space in which to proceed (cf. Longo et al. [2]). In these cases, the phase space model can only be applied locally and on a short duration; for instance, in multi-agent systems, the dynamic of a co-regulator agent is computable on its specific landscape, during one of its steps (Section 3.2); the global dynamic, which results from complex interactions between these local dynamics, is generally non-computable and unpredictable on the long term.

The problem is to develop new methods for studying the system in its integrality, for instance Plamen Simeonov [3] has proposed an Integral Biomathics for studying biological systems. In complexity theory, a complex system is represented as a network (or directed graph) having for objects the components of the system and for arrows the links between them through which they can interact.

1.2. Composed Objects: The Part–Whole Problem

Reductionism dates back to the 1600s when Aristotle’s Laws of Thought were used by Descartes and Newton to explain their theories. The general idea is to deduce the properties of a ‘whole’ complex system from those of (some of) its better known ‘parts’, for instance some of its subsystems justifiable of computational methods. It is related to the philosophical part–whole problem: to determine the new set of integrative properties that acquires the single ‘composed’ object obtained by aggregation of a pattern of interacting objects when these objects are joined together. The problem was already raised by Aristotle in his Metaphysics [4]: “What is composed of something so that the whole be one is similar not to a pure juxtaposition, but to the syllabus. The syllabus is not the same as its component letters: ba is not identical to b and to a, it is still something else”. This sentence has led to different non-equivalent interpretations:

• “The whole is nothing more than the sum of its parts”;
• “The whole is something else than the sum of its parts”;
• “The whole is more than the sum of its parts”.

These interpretations lead to different philosophical positions, from ‘pure’ reductionism, to emergentism (and even holism when conjugated with “the whole must of necessity be prior to the parts”).

In Section 2, we will show how the categorical concept of colimit of a diagram (or pattern) gives a precise mathematical translation of the part–whole correspondence that makes clear the above distinctions. In fact, it allows for a formal definition of a composed object as an aggregate of a pattern of interacting objects, which is at the basis of the concept of a multi-level system.

1.3. Compositional Hierarchy

A multi-level system, such as a living system, can be modeled by a compositional hierarchy (in the sense of Salthe [5], that is a system, in which the components are distributed in different complexity levels (from 0 to m), with the following property: a component C of a higher complexity level is a composed object acting as a ‘whole’ aggregating a pattern of interacting components of lower levels.

This part-whole correspondence can be one-to-one or not, in which case C is the aggregate of several structurally non-isomorphic lower-level patterns P_i. In this case, we say that C is multifaceted and that the P_i’s represent its lower-level multiple realization (compare with Kim [6]). Over time, new multifaceted components of increasing complexity may ‘emerge’, generally due to non-linear phenomena or chaotic dynamics.

A compositional hierarchy is a holarchy, meaning that a component of level other than 0 acts as a holon (Koestler [7]): it is a ‘whole’ with respect to (each of) its lower-level decompositions, and a ‘part’ for a higher component to which it is connected. The different levels are intertwined, with intra-level interactions from lower to higher levels, and vice-versa. A component can simultaneously receive information from objects of any level, and in response send messages to any level, as long as the necessary material (e.g., energy) constraints are satisfied. For instance, an enterprise has such a hierarchical organization with several levels: individuals, departments, from small producing units to higher directorial levels. The links between different components represent channels through which they exchange information and can collaborate to achieve a common goal.

A pure methodological reductionism to the lowest level 0 (e.g., molecular level for biological systems) would mean that each object of a higher level is the simple aggregate of a pattern of interacting objects of level 0. A main result (Section 2.4) asserts that such ‘pure’ reductionism is not possible if there are multifaceted objects, in which case we have an “emergentist reductionism” (in the sense of Mario Bunge [8]). This result is obtained in the frame of the following methodology.

1.4. The MES Methodology for Reviving NP

Reviving NP requires to design pervasive models adjustable to different kinds of systems, from physical systems to multi-level living systems, able to adapt to changing conditions through learning and to account for the development of emergent properties over time. At this end, in the sequel, we propose the mathematical methodology named Memory Evolutive Systems (MES), introduced by Ehresmann and Vanbremeersch [9,10], to study evolutionary multi-level, self-organized complex systems such as living systems, with the following properties:

• they have a tangled hierarchy of components which vary over time, with possible loss of components as well as emergence of more and more complex components and processes;
• through learning, they develop a robust but flexible memory allowing for better adaptation;
• the global dynamic is modulated by the interplay between the local dynamics of a net of specialized agents, called co-regulators, each operating stepwise with the help of the memory.

MES is a kind of info-computational model (in the sense of G. Dodig-Crnkovic [11]) which interweaves two mathematical domains: a Category Theory incorporating time to model the organization of the system and its changes over time; and hybrid Dynamic Systems to study the local dynamics of its co-regulators. While the local dynamics of the co-regulators might be computable via usual physical models, the global dynamic is generally not computable and even unpredictable on the long term (cf. Section 3).

MES have developed applications in different domains: (i) Biology (Integral Biomathics [12], Immune system, Aging theory [10]); (ii) Cognition (integrative model MENS of the neuro-cognitive system, up to the emergence of higher cognitive processes [13], and even neuro-phenomenology [14]); (iii) Collective Intelligence and Design Studies (D-MES [15]); (iv) Anticipation and Future Studies (FL-MES [16]).

For a complete theory of MES, we refer to the book [10] and, for more recent applications, to papers on the site [17].

1.5. Outline of the Article

In Section 2, we briefly recall the categorical notions of a colimit (Kan [18]) and of a hierarchical category [9] and discuss their philosophical implications with respect to the part–whole problem and to the categorical modeling of a compositional hierarchy. Defining the notion of a multifaceted object in a hierarchical category, we prove that the existence of such components is at the basis of emergent properties. The Reduction Theorem asserts that the absence of multifaceted objects is necessary for pure reductionism. A main construction is the Complexification Process (CP) that explains how complex links are at the basis of the emergence of objects of higher complexity orders (Emergence Theorem).

In Section 3, we recall the local and global dynamics of a MES. In particular, we explain how iterated CPs may lead to unpredictable emergent behaviors. We deduce from these results that MES propose an ‘emergentist reductionism’ [8] model for living systems, and so could be a valid candidate to ‘revive’ Natural Philosophy. Section 4 discusses how the meaning of emergence depends on the observer and the context, and studies the relations of emergence with anticipation and creativity.

2. Categories for Modeling Multi-Level Systems

Category theory is a domain of Mathematics introduced by Eilenberg and Mac Lane [19] in 1945. It is a ‘relational’ theory, in which the structure of objects is deduced from the morphisms which connect them. It has a foundational role in mathematics by analyzing the main operations of the “working mathematician” [20], thus reflecting some of the prototypical operations that man does for making sense of his world: distinguishing objects and their interrelations; synthesis of complex objects from more elementary ones (colimit operation) leading to the emergence of more complex objects and processes (complexification process); optimization processes (as solutions of ‘universal problems’ [20]); classification of objects into invariance classes (formation of concepts).

2.1. Categories for Modeling Complex Systems

Networks of any nature are often represented by (oriented multi-)graphs. Such a graph is a set of objects and a set of directed arrows between them. A category is a graph on which there is given an associative and unitary composition law which associates to each path (=sequel of adjacent arrows) of the graph a unique arrow, called its composite, connecting its extremities; an arrow of the category is also called a morphism.

Examples of categories:

• Small categories: A monoid is a category with a unique object. A group is a category with a unique object and in which each morphism has an inverse. A category K with at most one morphism between two objects ‘is’ (associated to) a p(artially)o(rdered)set (K₀, <), where K₀ is the set of objects of K and where the order < on it is defined by: k < k’ if and only if there is a morphism from k to k’ in K.
• Categories of paths: To a graph G is associated the category of paths of G, denoted by L(G): the objects are the vertices of G, a morphism from x to x’ is a path from x to x’ and the composition of paths is given by concatenation.
• Large categories: Sets denotes the category having for objects the (small) sets and for morphisms from A to B the maps from A to B; the composition is the usual composition of maps. Similarly we define categories of structured sets, for instance the category of groups, with homomorphisms of groups as morphisms; the category Top of topological spaces, with continuous maps as morphisms. Cat denotes the category having for objects the (small) categories H and for morphisms the functors between them, where a functor F from H to H’ is a map which associates to an object A of H an object F(A) of H’ and to a morphism f: A → B of H a morphism F(f): F(A) → F’(B) of H’, and which preserves the identities and the composition.

In applications to evolutionary systems whose components vary over time (for instance in MES), the configuration of the system at a given time t will be modeled by a category H. Its objects model the (state at t of the) components of the system which exist at t; its morphisms model their interactions, via channels through which they can exchange information of any nature. More precisely, if C is an object, the morphisms arriving at C transmit information, constraints, or commands sent to C, those issued from C transmit information allowing for actions of C toward other objects. Thus if f: A → C is a morphism (or arrow) from A to C, we think of A as an active transmitter of information and C as a receiver.

The composition law defines an equivalence relation on the set of paths of the category H: two paths are equivalent if they have the same composite; then the category H is the quotient category of the category L(H) of paths of H by this equivalence. In concrete applications, objects and morphisms can represent elements which have specific ‘physical’ properties (measured by real observables, e.g., activity at t, strength, propagation delay,…); and paths which have the same composite correspond to paths which are functionally equivalent. A diagram (or pattern) P in the category H defines a sub-graph of H. The diagram is commutative if, for each pair of objects P_i and P_j, the paths in P from P_i to P_j have the same composite. In category theory, commutative diagrams lead to a kind of calculus in which they play the same role as equations in algebra.

2.2. Interpreting the Part–Whole Problem via the Categorical Notion of Colimit

To interpret a sentence such as: “the whole is nothing more than the sum of its parts”, we need to specify what we mean by ‘parts’, by ‘sum’ and by ‘whole’. In a general network, there is no natural way to do this because we cannot compare parallel paths. The situation is different in a category where the composition law allows distinguishing paths which have the same composite, meaning, in concrete applications, that they are ‘functionally equivalent’.

2.2.1. The Categorical Notion of Sum

The sum of a family of objects can be modeled using an important categorical operation, namely the coproduct operation, which is a particular case of the colimit operation introduced by Kan in 1958 [18]). Formally:

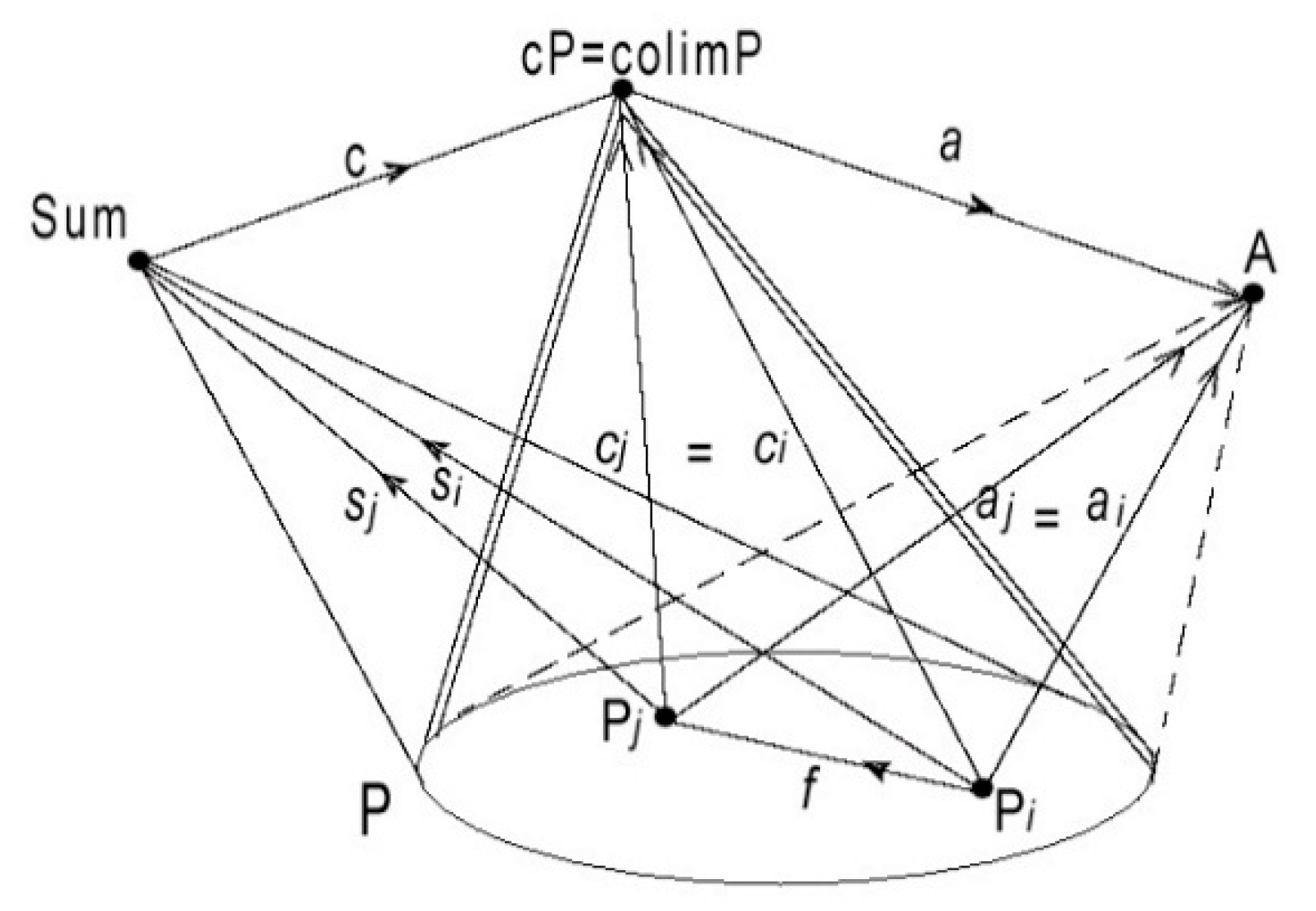
Definition 1.

In a category H, the coproduct (or sum) of a family of objects P_i, if it exists, is an object S of H such that there exists a family of morphisms s_i: P_i → S satisfying the ‘universal’ condition:

if (a_i) is a family of morphisms a_i: P_i → A toward any object A, then there is a unique morphism a from S to A ‘binding’ this family, meaning that a: S → A satisfies the equations a_i = s_ia for each i (cf. Figure 1).

(Let us note that these equations, which mean that for each i the composite s_ia is equal to a, would have no meaning in a network where composites are not defined).

With this notion, the sentence “the whole is nothing more than the sum of its parts” becomes: “The whole is modeled by the coproduct S of the family of objects P_i modeling its parts”. It corresponds to a ‘structural’ reductionism (in a non-relational context).

2.2.2. The Categorical Notion of colimit

Let us consider the sentence: “the whole is something other than the sum of its parts” which corresponds to the Aristotle’s example of the syllabus ([4], cf. Section 1.2): In this case, the data are not only the family of parts P_i but also ‘something else’, namely some given relations between them.

In a category H, these data are represented by a diagram (also called pattern) P whose objects represent the objects P_i and whose morphisms represent the given relations between them, so that the entire P models the parts and their organization.

To characterize the ‘whole’ associated to a pattern P, the idea is to represent it by the colimit of P in H (if it exists). For that, let us first define what is a collective link from P to an object A; in concrete applications, it corresponds to an ‘action’ (emission of a message, constraint, command,…) performed by the pattern acting collectively (whence the name) in the respect of its organization, and which could not be realized by its objects acting separately Translated in categorical terms, a collective link from P to A in H is modeled by a cone with basis P and vertex A, that is a family (a_i) of morphisms a_i from P_i to A such that, for each morphism f: P_i → P_j in P we have a_j = a_if (cf. Figure 1).

Definition 2.

Let P be a diagram in the category H. The colimit of P, if it exists, is an object cP such that there exists a cone (c_i) from P to cP (called a colimit-cone) satisfying the ‘universal’ condition:

For each cone (a_i) from P to any object A there is a unique morphism a from cP to A such that we have: a_i = c_ia for each i; this a is called the binding of the cone (a_i).

For instance, if H models a chemical system, a molecule is the colimit of the pattern formed by its atoms with the chemical bonds which determine its spatial configuration. A pattern P in H may have at most one colimit cP (up to an isomorphism of H). Conversely, different non-structurally isomorphic patterns of H may have the same object C as their colimit; in this case we say that C is multifaceted; we come back to this case in Section 2.3.

By modeling the ‘whole’ as the colimit cP of the pattern P modeling its ‘parts’ and their organization, the sentence “the whole is something other than the sum of its parts” becomes: “the colimit of P is different from the sum of the objects of P”. In a category where there exist both a colimit cP of a pattern P and a sum S of the family of its objects, this sentence takes a precise meaning, allowing to ‘measure’ the difference between S and cP by a well-defined morphism c (Cf. Figure 1).

Proposition 1.

Let P be a pattern in a category H; if there exist both the colimit cP of P and the sum S of its family of objects, then there exists a ‘comparison’ morphism c from S to cP.

Proof. 

By the universal property of the sum, the family (c_i) of morphisms forming the colimit-cone from P to cP binds into the comparison morphism c from S to cP. □

Thus in the relational context H, we have a reduction of the ‘whole’ cP to the pattern P representing its parts and their organization, but not to (the sum S of) its parts. In the other way, to model the ‘whole’ as the colimit of P imparts to it an emergent property in H, namely that any cone with basis P uniquely factors through the colimit cone; we come back to this in Section 4.1.

2.3. Categorification of A Compositional Hierarchy

Using the preceding representation of a ‘whole’ as the colimit of the pattern of its ‘interacting parts’, and thinking of the whole as something more complex than its parts, we can model the notion of a ‘compositional hierarchy given in Section 1.3 as follows.

Definition 3

[9]. A hierarchical category is the data of a category H and a partition of the set of its objects into a finite number of levels of complexity, numbered from 0 to m, verifying the condition: Each object C of the level n+1 is the colimit of at least one pattern P of interacting objects P_i of levels less or equal to n. Then we call P a lower-level decomposition of C. A morphism of level n is a morphism between objects of level n.

By definition of the colimit, it means that C admits at least one lower-level decomposition in a pattern P verifying: for any object A of H there is a one-to-one correspondence between the cones from P to A and the morphisms from C to A. Roughly, each object C of a level > 0 ‘aggregates’ at least one lower-level decomposition P, so that C alone has the same operational role that the pattern P acting collectively. It follows that, in a hierarchical category, an object C of level > 0 acts as a holon playing as a Janus (Koestler [7]): It is a ‘whole’ more complex than the objects of one of its lower-level decompositions P, while accounting for the constraints imposed by their interactions in P. At the same time C acts as a ‘part’ of a more complex object C’ if C is an object of a pattern admitting C’ for colimit. For instance, in the hierarchical category representing a society, a group of interacting people is ‘more complex’ than its members, but ‘less complex’ than a society to which it belongs.

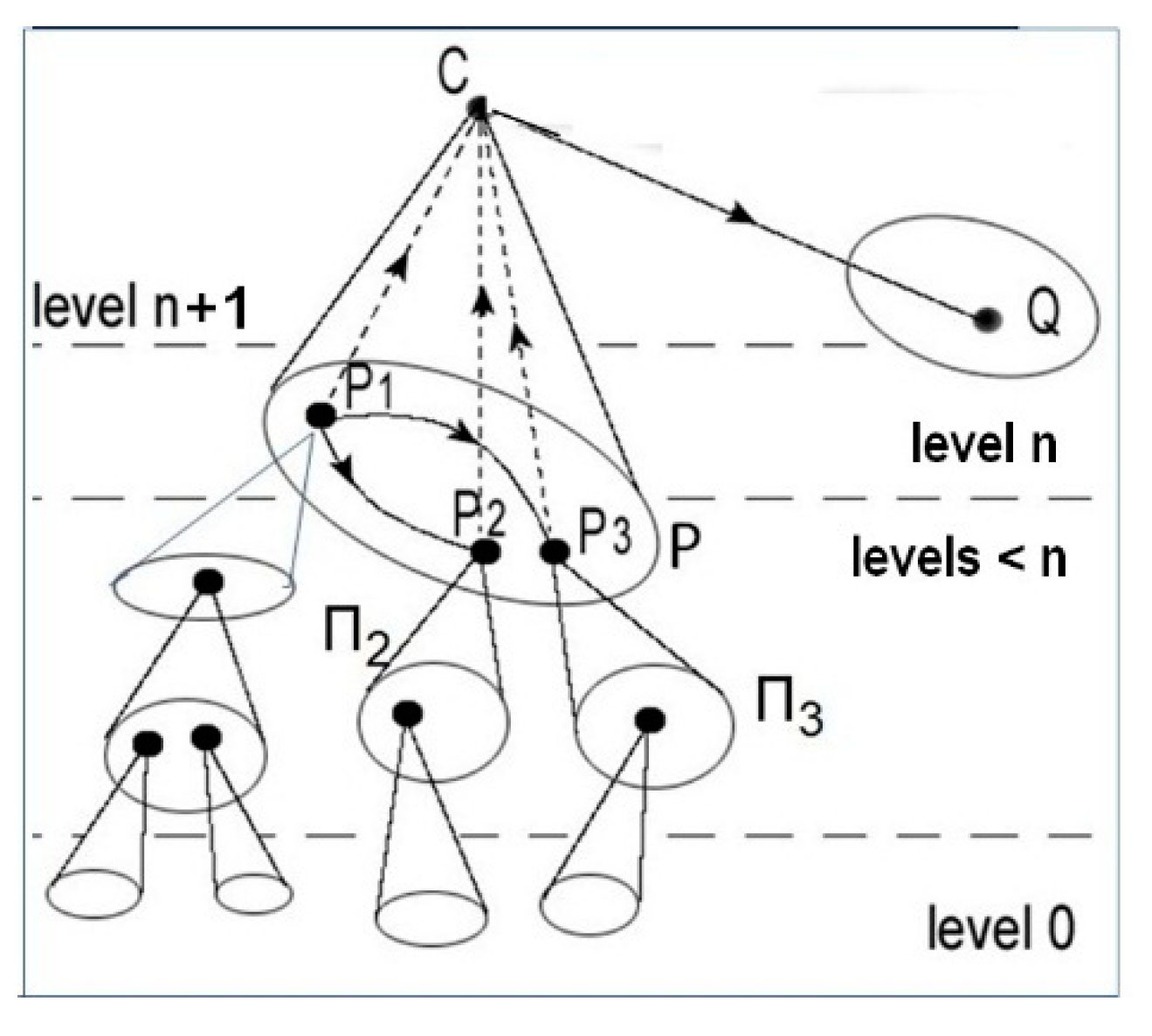
Going down the levels, we can construct at least one ramification of C down to level 0 (cf. Figure 2), obtained by taking a lower-level decomposition P of C, then a lower-level decomposition Π_i of each object P_i of P, and so on, down, till we reach a set of patterns of level 0 which form the base of the ramification.

Definition 4.

In a hierarchical category H, the complexity order of an object C of H is the smallest length of a ramification of C down to level 0. This order is less than or equal to the level of C.

While the complexity level of an object is specified in the definition of the hierarchical category H, its order of complexity (to be compared to the Kolmogorov–Chaitin complexity of a string of bits) is the result of a computation accounting for the whole structure of the category. For instance, if C is an object of complexity order 2, there is no pattern of level 0 of which C is the colimit (otherwise C would be of order 1), but C has a ramification (P, (Π_i)) where P is a pattern of level < 2 having C as its colimit, and Π_i for each object P_i of P is a pattern of level 0 with P_i as its colimit. The patterns Π_i (some of which can possibly be reduced to an object of level 0) form the base of the ramification. This base is not sufficient to re-construct C from level 0 up since we need supplementary data expressing the constraints imposed by the morphisms of P.

2.4. Simple and Complex Morphisms: The Reduction Theorem

The (methodological) reductionism problem in a compositional hierarchy consists in a ‘reduction’ of the system to one of its levels (say the lowest one): can we deduce the properties of the whole system from the properties of its objects of level 0 and their relations? This problem will be analyzed in the categorical setting. Let H be a hierarchical category. We know that all its objects are connected to patterns of level 0 through the unfolding (possibly in several steps) of a ramification of C. Is there something analog for the morphisms? This problem necessitates to characterize different kinds of morphisms.

2.4.1. Morphisms between Complex Objects Deducible from Lower Levels

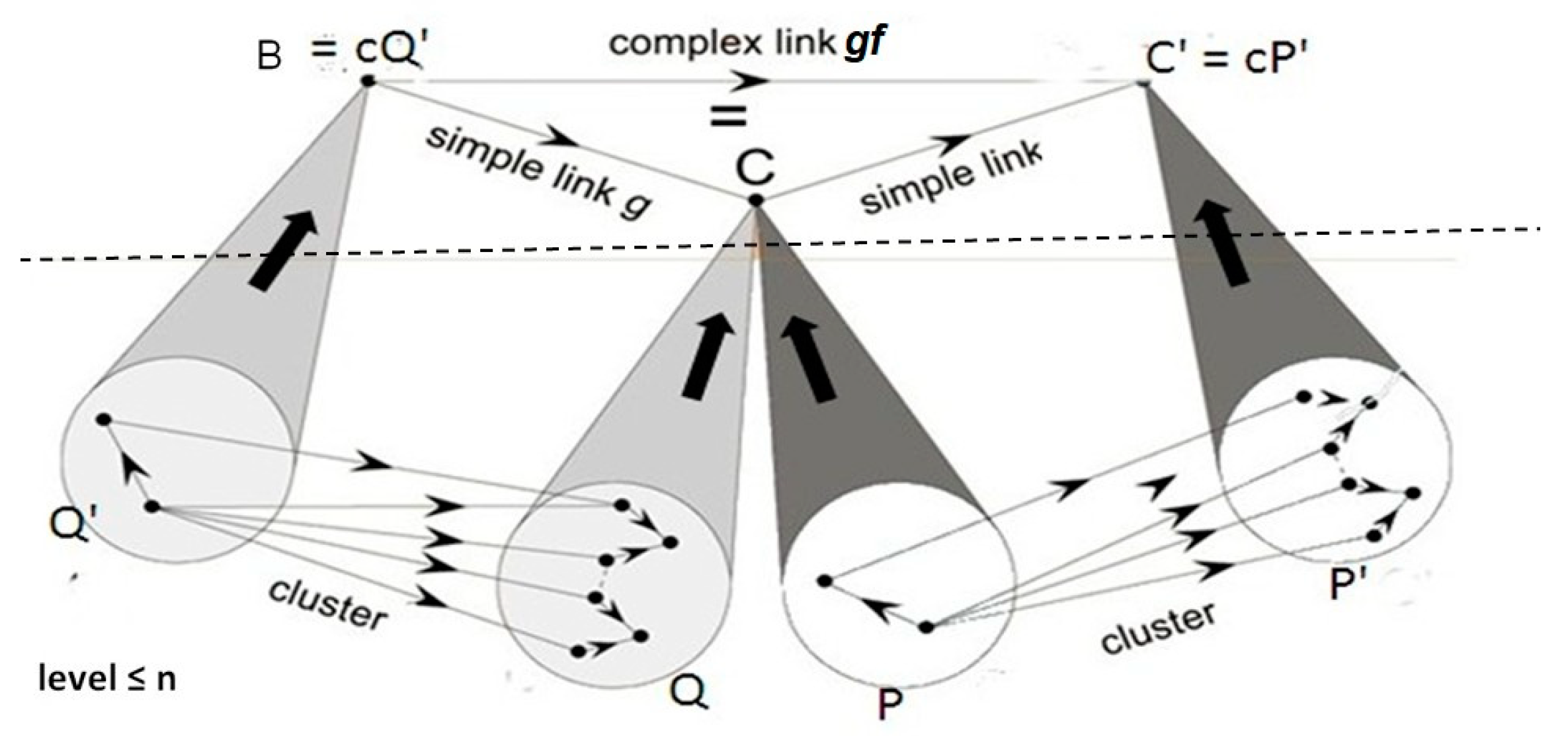
Let C be an object which is the colimit of a pattern P and C’ an object which is the colimit of a pattern P’. A cluster from P to P’ is generated by a family of ‘individual’ morphisms connecting each object P_i of P to objects P’_j of P’, well correlated by a zig-zag of morphisms of P’ (Cf. Figure 3).

From the universal property of the colimit, it follows that such a cluster binds into a unique morphism f from C to C’, called a (P, P’)-simple morphism or just an n-simple morphism if the objects of P and P’ are of levels ≤ n. If C and C’ are of level > n, such an n-simple morphism represents a morphism of level > n which transmits only information mediated through individual objects of the patterns, hence entirely accessible at level ≤ n; we can say that g is reducible to (the cluster) of level ≤ n. Let us note that any morphism f of level ≤ n is n-simple, as well as a morphism connecting an object of level n+1 to an object of a level ≤ n. An n-simple morphism is also n’-simple for n’ > n, A composite of n-simple morphisms binding adjacent clusters is still an n- simple morphism.

2.4.2. Multifaceted Objects

Multifaceted objects [21]. Let C be a complex object of level n+1. Two decompositions P and Q of C are said to be structurally isomorphic if the identity of C is both a (P, Q)-simple morphism and a (Q, P)-simple morphism, meaning that there exista cluster G connecting P and Q whose binding is the identity of C and a cluster from Q to P whose binding is the identity of C. [Formally it means that G defines an isomorphism in the category Ind(H) having for objects the patterns in H and for morphisms the clusters between them.] However C may also have structurally non-isomorphic decompositions.

Definition 5.

Let C be an object of level > n of the hierarchical category H. We say that C is n-multifaceted if C admits at least two structurally non-isomorphic decompositions P and Q of levels ≤ n; the passage from P to Q is called a switch. The category H is said to satisfy the Multiplicity Principle (MP) if, for each n > 0 it has n-multifaceted objects.

If C is multifaceted, it also implies that C has several structurally non-isomorphic ramifications down to level 0.

The notion of multifaceted objects (initially called multiform objects in Ehresmann and Vanbremeersch [21]) and the MP have been introduced to formalize the concept of degeneracy of the neural code introduced by Edelman [22], that he later generalized to all biological systems “Degeneracy, the ability of elements that are structurally different to perform the same function or yield the same output, is a ubiquitous biological property <….> a feature of complexity.” (Edelman and Gally [23]). For instance, different codons of the same amino acid remain unrelated at the atomic level, though they give rise to the same molecule at the molecular level. Or the two possible images in an ambiguous figure gain their ‘symmetry’ only when they are interpreted in relation to the complete figure, not when they are apprehended separately. The word degeneracy reflects a flexible redundancy of function (from bottom to top). We prefer to look from top to bottom and call this property the Multiplicity Principle (MP) to insist on the fact that C admits multiple realization [6] in structurally non-isomorphic lower-level patterns. It follows that C has also multiple structurally non-isomorphic ramifications down to level 0.

2.4.3. Complex Morphisms

Let H be a hierarchical category which satisfies the Multiplicity Principle. In a category each path of morphisms must have a composite; it follows that the composite of a path of two (or more) n-simple morphisms binding non-adjacent clusters must exist; however, it is not always n-simple; in this case it is called an n-complex morphism (Ehresmann and Vanbremeersch [21]).

Definition 6.

An n-complex morphism is a composite of n-simple morphisms which is not n-simple, so that its factors bind non-adjacent clusters. (cf. Figure 3)

More precisely, let C be an n-multifaceted object. The composite of an n-simple morphism g from B to C with an n-simple morphism f from C to C’ must exist by definition of a category. However, since C is n-multifaceted, it admits structurally non-isomorphic decompositions P and Q of levels ≤ n, so that g may bind a cluster from a decomposition Q’ of B to the decomposition Q of C, while f binds a cluster from the structurally non-isomorphic decomposition P of C to a decomposition P’ of C’. In this case, the composite gf of f and g is generally an n-complex morphism (though in some cases it can be n-simple). For instance, the morphism from the group of authors of a Journal to the group of its subscribers is a complex morphism, mediated by the journal as such, considered as a multifaceted object representing both its editorial staff and its administration.

An n-complex morphism gf of level n+1 has properties which ‘emerge’ at this level. Indeed, its properties depend on the lower-level properties of the clusters that f and g bind, but also on the existence of a switch between P and Q which stands for a global property of the lower-levels, not locally recognizable at these levels, namely that P and Q have the same operational role with respect to all objects A. Thus there is no ‘reduction’ of the complex morphism to lower levels.

A composite of n-complex morphisms is generally an n-complex morphism (though it might be an n-simple morphism). In the dynamic case (Section 3), we’ll see that complex morphisms are at the basis of the emergence of new properties corresponding to “change in the conditions of change” (Popper [24]) which make the systems unpredictable.

2.4.4. The Reduction Problem

For a natural system, the reduction problem (under different kinds) searches to ‘reduce’ its higher-level properties to lower-level properties so that methods already developed for these lower levels could be extended; for instance reduction of a biological system to its molecular level to apply and extend methods used in physics or chemistry. As explained above, in a hierarchical category, such a reduction is only possible for a simple morphism whose properties depend on those of the cluster which it binds; but the situation is different for a complex morphism which has emergent properties at its level.

From the following theorem we deduce that a pure reductionism necessitates that the system has only simple morphisms.

Theorem 1 (Reduction Theorem [10,21]).

Let H be a hierarchical category. Let C be an object of level n+1 and P a pattern of level n of which C is the colimit. If all the morphisms of P are (n−1)-simple morphisms, then there exists a pattern V of levels n−1 of which C is also the colimit. Whence the complexity order of C is strictly less than n. The result is generally not true if P has a complex morphism.

Proof. 

Let us explain this in the case of an object C of level 2, with a ramification (P, (Π_i)). If all the morphisms f_ij: P_i → P_j of P are simple morphisms, they bind clusters F_ij of morphisms of level 0 from Π_i to Π_j. We can define a pattern V of level 0 as follows: it contains the Π_i as sub-patterns and has also for morphisms the union of the clusters F_ij. It is proved [10] that the pattern V has also C for its colimit. Since C is colimit of such a pattern of level 0, its complexity order is 1. □

Corollary 1 [pure (methodological) reductionism].

In a hierarchical category in which there are no complex morphisms, all the objects are of complexity order 0 or 1.

In the more general case where the category H admits multifaceted objects of complexity order strictly more than 1. we have no pure reduction to the level 0. Each object can still be related to the level 0, but the reduction cannot be done directly in one step: it necessitates the unfolding of a ramification in several steps, with emergent properties at each different step (through complex morphisms). In Section 4.1, we describe this situation as an ‘emergentist reductionism’ [8].

2.5. The Complexification Process. Main Theorems

The configuration of a natural system such as a living system varies over time. Its structural changes correspond to the four “standard transformations: Birth, Death, Scission, Confluence” characterized by R. Thom [25].

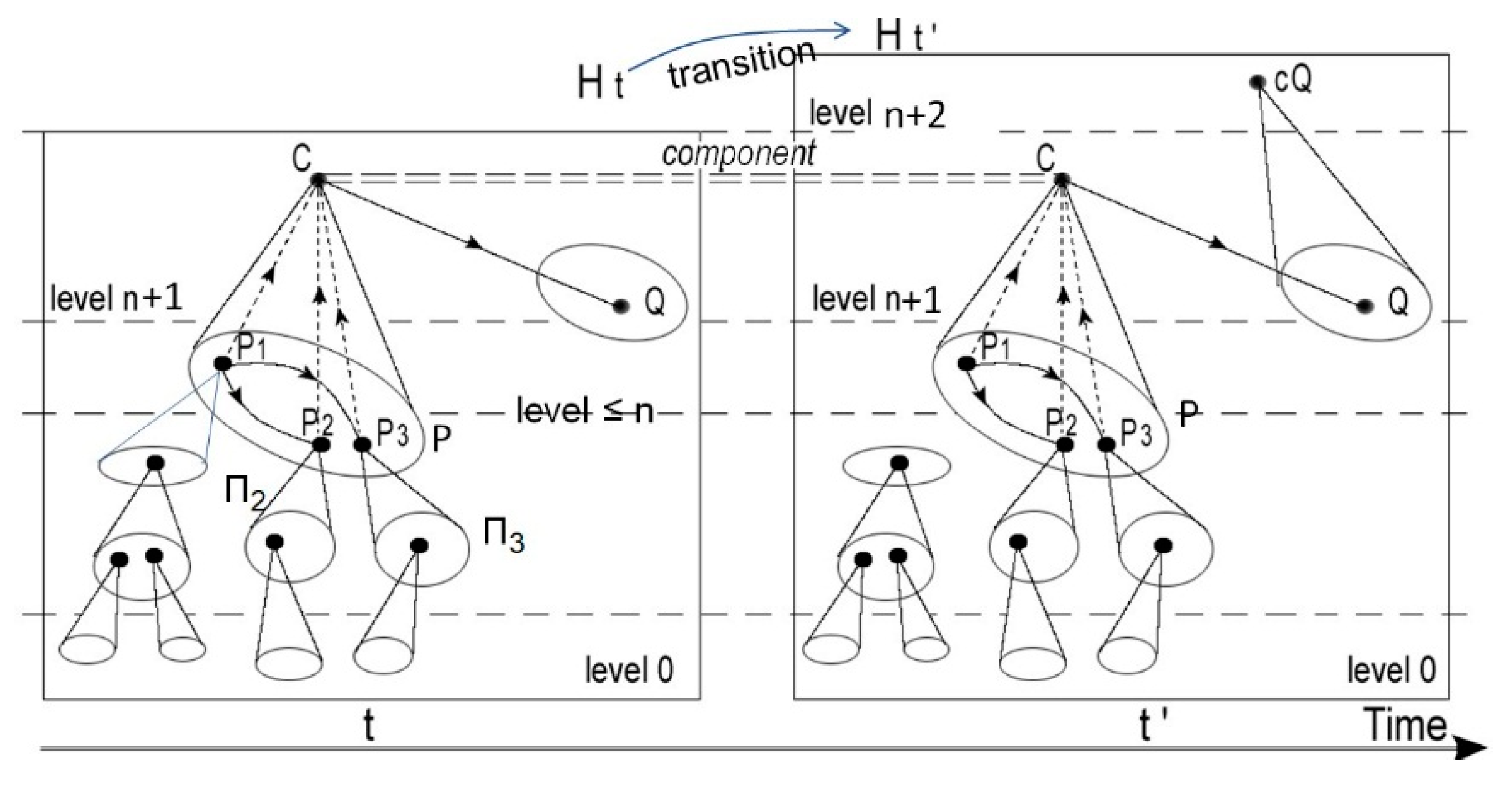
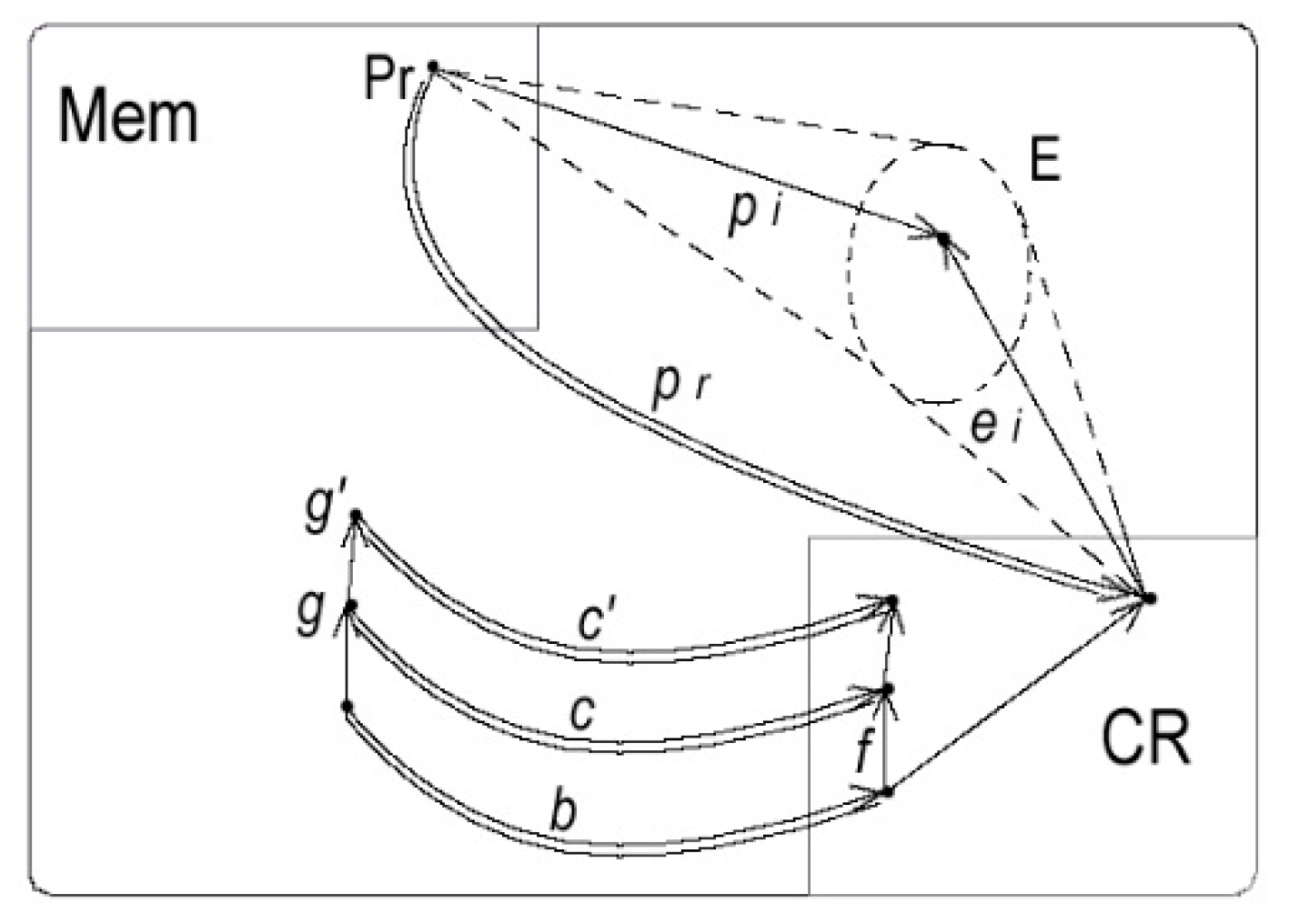
If the system is modeled by a hierarchical category H, these structural changes will correspond to the realization of a procedure Pr = (A, E, U) with objectives (O) of the following kinds:

• ‘adding’ to H a given external graph A,
• ‘suppressing’ a set E of objects and morphisms of H, eventually thus dissociating a complex object by suppressing its colimit;
• ‘binding’ patterns P of a set U of finite patterns in H so that each P acquires a colimit cP or, if P has a colimit in H, preserves this colimit.

The realization of such a procedure Pr imposes a number of other operations. For instance to ‘bind’ a pattern P which has no colimit in H necessitates to add to the system a cone from P to a new object cP and to ‘force’ this cone to satisfy the universal condition of a colimit-cone; and this will eventually lead to the emergence of complex morphisms in the category H’ modeling the system after these modifications.

The interest of the categorical approach is that it gives an explicit construction (by recurrence) of the category H’obtained after application of the procedure Pr to H (including the above-mentioned operations). This category H’, called the complexification of H for Pr, provides a ‘conceptual’ anticipation of the result of Pr, and so allows a ‘virtual’ evaluation of this procedure. However, when H models a natural system, the complexification H’ might not respect some material or temporal constraints (cf. Section 3.1.2), and anticipation raises other problems (cf. Section 4.2).

2.5.1. The Complexification Process

The Complexification Process [9,10]. Given a (hierarchical) category H and a procedure Pr = (A, E, U) on H with objectives of the above kinds (O), the complexification process (CP) for Pr consists in constructing a ‘universal solution’ to the problem:

To construct a (hierarchical) category H’ and a partial functor F from H to H’ satisfying the objectives (O); in particular, it means that, for each P in U, the image of P by F will have a colimit cP in H’.

To say that F is a ‘universal solution’ to the problem means that, if there is another partial functor F’ from H to a category H” in which the objectives of Pr are realized, this F’ factors through F via a comparison functor from H’ to H”.

Remark 1.

In recent publications (e.g., [16], Chapter 3) we use the term de/complexification of H for Pr instead of ‘complexification’ to emphasize that the construction can lead both to a kind of ‘de-complexification’ by loss or dissociation of some complex objects in E, and to a real ‘complexification’ by formation of more complex objects cP becoming the colimit in H’ of patterns P which have no colimit in H.

Theorem 2 (Complexification Theorem [9,10]).

Let Pr = (A, E, U) be a procedure on a hierarchical category H satisfying MP. The complexification process for Pr has a universal solution F: H → H’ where H’ is a hierarchical category which is explicitly constructed (by recurrence).

2.5.2. Construction of the Complexification

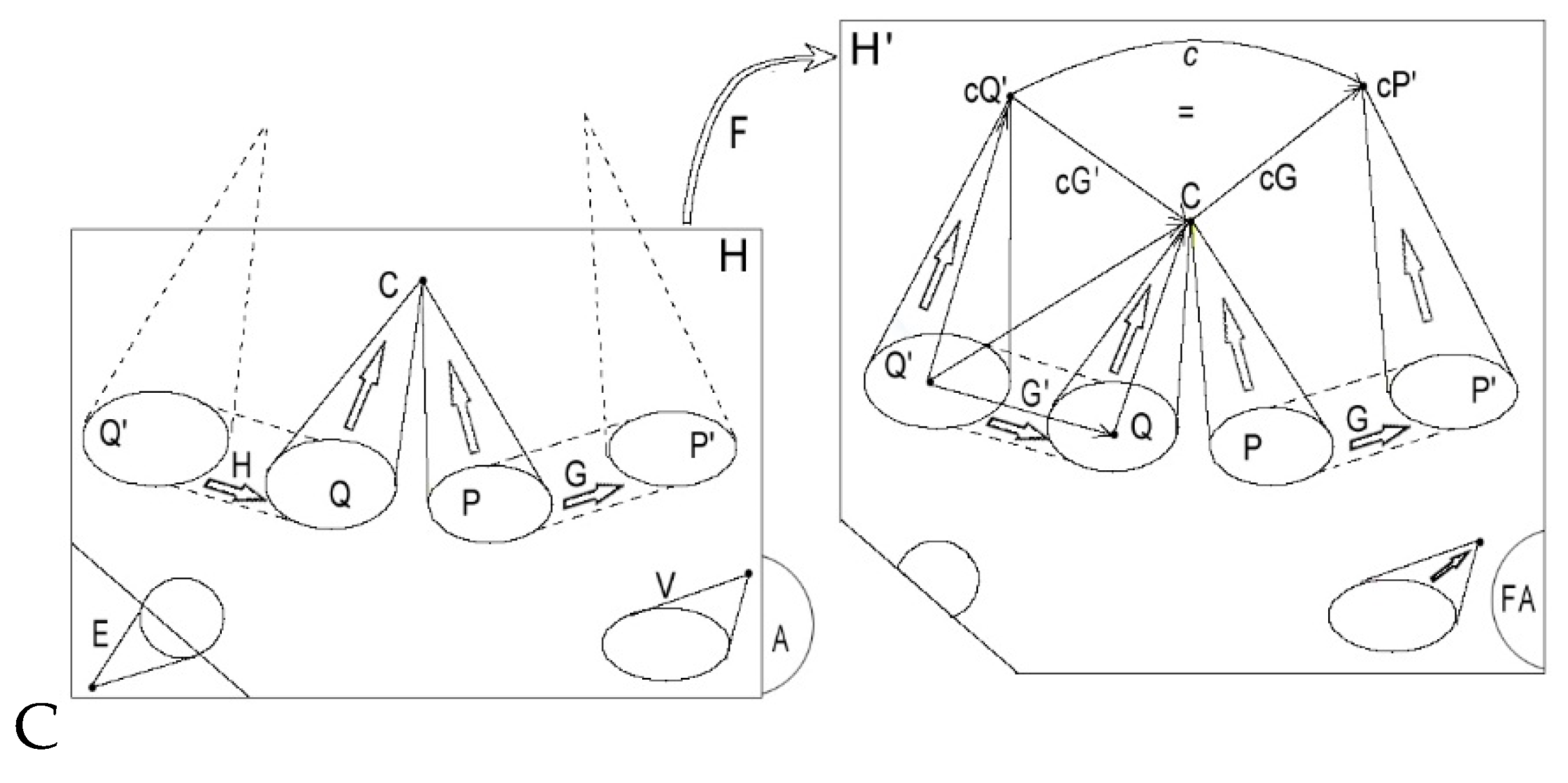
Construction of the Complexification (cf. Figure 4). For an explicit construction of the complexification H’, we refer to ([10], Chapter 4). Let us just indicate the following points:

• The partial functor F from H to H’ is defined on the greatest sub-category of H not meeting E.
• The objects of H’ are: the vertices of A, the (image by F of the) objects of H not in E and, for each pattern P in U, a new object cP which becomes the colimit of F(P) in H’. This cP is selected as follows: (i) if P in U has already a colimit C in H, we take for cP the image of C by F; (ii) If two patterns P and Q in U have the same functional role in H, we take cP = cQ, so that, if P and Q are structurally non-isomorphic, cP will be a multifaceted object in H’.
• The morphisms of H’ are the arrows of A, the (images by F of the) morphisms not in E and new morphisms which are constructed by recurrence to ‘force’ cP to become the colimit of F(P) in H’ for each P in U: At each step of the recurrence, for each P in U we add morphisms from cP to B to bind cones from P to an object B, then we add composites of all the so obtained morphisms; this operation can lead to the emergence of complex morphisms. Then, repetition of such a step on the category so obtained, and so on.

If H is hierarchical, H’ is also hierarchical: the level of a ‘preserved’ object is the same as in H; the level of an emerging object cP is n+1 if P is in levels ≤ n; if P has a complex morphism, the complexity order of cP is more than that of the objects of P (Reduction Theorem, Section 2.4). In particular the complexification process may add a new highest-level m+1 to the hierarchy. It can also add new morphisms between objects in the image of F, and even complex morphisms (the image of F is not a full subcategory of H’).

2.5.3. Main Theorems

From the construction of the complexification, we deduce the theorems.

Theorem 3 (Emergence Theorem [10]).

Let Pr = (A, E, U) be a procedure on a hierarchical category H satisfying MP. The CP for Pr may lead to the emergence of complex morphisms; in particular, if some pattern P in U has a complex morphism, the emerging object cP is of a higher complexity order than (the objects of) P. A sequence of CPs may lead to the emergence of multifaceted objects of increasing complexity orders.

Theorem 4 (Iterated complexification Theorem [10]).

Let Pr = (A, E, U) be a procedure on a hierarchical category H and let Pr’ = (A’, E’, U’) be a procedure on the complexification H’ of H for Pr. If some patterns in U’ have a complex morphism, then there is no procedure Pr” on H such that the complexification H” of H’ for Pr’ be the complexification of H for Pr’.

In Section 4, we will draw the consequences of these theorems in terms of emergence, creativity, anticipation, and unpredictability. Roughly, the formation of a complex morphism can be interpreted as a “change in the conditions of change” (in Popper’s sense [24]), that makes the long term result unpredictable.

3. The MES Methodology

In the preceding Section 2, we have considered the ‘static’ structure of a living system at a time t of its life, modeled by a hierarchical category, and its structural changes over time, generated by successive complexification processes. Here we propose the Memory Evolutive Systems (MES) methodology as a model, not of the invariant structure of the system (as for instance in Rosen’s (M-R)- systems [26]), but as an integral dynamic model sizing up the system ‘in its becoming’ during its life.

A MES consists of:

• a Hierarchical Evolutive System (HES) which describes the components of the system and their variation over time through structural changes, leading to
• a developing flexible long-term memory with emergent properties;
• a network of agents, called co-regulators, which self-organize the system through their cooperation/competition; each co-regulator operating at its own rhythm on its own landscape.

3.1. The Hierarchical Evolutive System underlying a MES

As we have already said the configuration of an evolutionary system at a time t is modeled by a category, say H_t having for objects the states C_t of its components C existing at t and for morphisms the state at t of the links (or communication channels) between these components. The state at t reflects the static and dynamical properties at t, measured by observables depending of the specific system. Among the observables (represented by real functions), we suppose that, at each time, a component has an activity, and a link between components has a propagation delay, a strength and a coefficient of activity. Over time, the components and the links between them vary, with possible addition or suppression, due to structural changes of the kinds indicated in Section 2.5.

3.1.1. Evolutive Systems (ES)

To account for time and the changes it so produces, an evolutionary system cannot be modeled by a unique category: it is modeled by an Evolutive System H which consists of:

• the timeline of the system, modeled by an interval T of the real line R;
• for each t in T, a category H_t called the configuration of H at t which represents the state of the system at t;
• for t’ > t in T, a partial functor from H_t to H_t’ called ‘transition’ from t to t’, which models the changes of configuration; it is defined on the sub-category of H_t consisting of the (states of the) objects and morphisms which exist at t and will still exist at t’. These transitions satisfy a transitivity condition.

The transitivity condition implies that a component C of the system, identified to the ‘dynamic’ trajectory consisting of its successive states C_t from its initial apparition in the system to its ‘death’, is modeled by a maximal family of objects C_t of successive configurations connected by transitions. Similarly, a link f from a component C to a component C’ is modeled by a maximal family of morphisms f_t: C_t → C’_t of successive configurations, connected by transitions, namely the family of its successive states for each t at which both C and C’ exist. At each time t of its existence, a link has a coefficient of activity 1 or 0, to model if it is active (information transfer at t) or not. To sum up more formally:

Definition 7.

An Evolutive System (ES) is defined by a functor H from the category associated to the order on an interval T of R to the category of partial functors between categories; it maps t in T to the configuration category H_t, and the morphism from t to t’ to the transition from t to t’.

3.1.2. Hierarchical Evolutive Systems

In the sequel the aim is to study multi-level ES in which the successive configurations have a compositional hierarchy (for instance, in a biological organism: atoms, molecules, cells, tissues, ….). For that, we suppose that the successive configuration categories of the ES are hierarchical categories (cf. Section 2.3), and we define:

Definition 8.

A Hierarchical Evolutive System (HES) is an ES in which the configuration categories are hierarchical and the transitions preserve the complexity levels (Cf. Figure 5).

Over time in a living system, there are both dynamic changes affecting the observables and structural changes of configurations of the forms indicated in Section 2.5, and both kinds of changes must be compatible. From the results of Section 2.5 we know that the structural changes can be modeled by sequences of complexification processes (CP); however, these CPs must also be compatible with the dynamic changes. In the HES frame, it means that the transitions are generated by CPs for procedures Pr which must be compatible with the dynamic constraints.

Now if we give a procedure Pr = (A, E, U) on the configuration H_t of the HES at a time t, we can always ‘categorically’ construct the complexification H’ of H_t for Pr. However, H’ might become a configuration of the system at a later time t’ (dependent on the material change duration) only if the observables defining the states of components and links (e.g., propagation delays for the links) are extendable to H’ through the partial functor from H_t to H’. This is not always possible because these observables might impose some dynamic constraints which cannot be extended to H’. For instance, if one constraint is that the propagation delay of a composite morphism be the sum of the propagation delays of its factors, we have proved [27] that this constraint can only be extended to H’ if the patterns P in U are polychronous in the sense of Izhikevich [28].

By definition, the complexification H’ for Pr is the universal solution to the problem of realizing Pr. If it is not compatible with some dynamic constraints, there can exist another solution H” of the problem which is compatible with them; in this case, the weight of these constraints can be measured by the comparison functor from H’ to H” (cf. Section 2.5.1).

The HES theory does not propose methods for the selection of adequate procedures. We come back to this selection problem in Section 3.2 in the more specific frame of a MES which is a HES with a multi-agent self-organization modulating the dynamic of the system.

3.1.3. Complex Identity of a Component

Let C be a component of the HES. At each time t of its life, C (or more precisely its state C_t in H_t) is the colimit of a lower-level pattern P in H_t. We say that C is activated by P at t if all the morphisms of the colimit-cone from P to C_t are active at t; roughly, it means that C receives collective information from P itself at t. For instance, the information can be a constraint, or a command imposed on C by lower levels; it can also be an energy supply allowing C to perform a specific action.

At a later time t’, the component C has a new state C_t’ in the configuration at t’_’ and the pattern P is transformed in a pattern P_t’ via the transition from t to t’. However, this pattern P_t’ may not admit C as its colimit in the configuration at t’. Indeed, some objects or morphisms of P may have been suppressed from t to t’ (we recall that the transitions are only partial functors) and it is not supposed that they preserve all colimits. For instance, at a time t a cell is the colimit of the pattern of its molecules existing at that time, but there is a progressive renewal of these molecules and, after some time, the initial molecules will all have disappeared while the cell as such persists

We call the stability span of P at t the largest period (from t to t+d) such that, for each t’ between t and t+d. the image P_t’ of P still admits C_t’ as its colimit, while this is no more the case at t+d. However, if C persists at t+d, it admits at least one other lower-level decomposition Q in the configuration at t+d; this Q can have been progressively deduced from P, or not. In this way, C takes its own complex identity independent from its lower-level constituents; this situation corresponds to the Class-Identity of Matsuno [29].

The complex identity of a component C can be multiple, making it more flexible. It is the case for multifaceted components. We say that a component C is multifaceted on an interval J if its state at each instant t of J is a multifaceted object in the configuration at t. Let us recall that it means that, for each t of J, the state at t of C is the colimit of at least two lower-level patterns which are structurally non-isomorphic; thus at that time C can be activated by either of them, or by both concurrently, and even switch between them. In this way, C takes its own individuation (in the sense of Simondon [30]) allowing for a kind of ‘flexible redundancy’.

From now on, we suppose that the HES satisfies the Multiplicity Principle (MP), meaning that it has such multifaceted components. It follows that there are two kinds of links between components:

Definition 9.

In a HES, a link between components C and C’ on an interval J is called an n-simple link if its state at t is an n-simple morphism in the configuration at t for each t in J. Similarly, we define an n-complex link on J as a link whose successive states on J are n-complex morphisms.

3.1.4. Development of a Memory

Multifaceted components and complex links between them play an important role in the development of a memory of the system. A living system (such as a biological, social, or cognitive system) develops a robust though flexible long-term memory, able to adapt it to changing conditions. This memory consists in interconnected internal representations of knowledge of any kind, such as items (external objects, signals, past events), internal states (conscious or non-conscious and non-volutional, affects, emotions) that the system can recognize, and different procedures that the system can activate. A component of the memory takes its own complex identity in time and can later be ‘recalled’ under its different lower-level decompositions, providing plasticity in time to adapt to environmental changes. For instance, we recognize a person independently from the way (s)he is clothed, and even, on the longer term, independently from his (her) age.

In the HES modeling the system, this memory is modeled by a hierarchical evolutive subsystem Mem, whose components (called ‘records’) and links are obtained through successive complexification processes for adequate procedures. It follows from the Emergence Theorem (Section 2.5), that the number of complexity levels of this memory will increase over time, with formation of more and more complex multifaceted records C, connected by complex links. Such a C can be later ‘recalled’ by activating any of its multiple ramifications to recognize the item it memorizes under different forms and it adapts to changing situations by acquiring new decompositions and suppressing those which are no more valid. The system can also develop ‘resilience’: in an adverse situation or a crisis, some decompositions of multifaceted records can be temporally disactivated (but not suppressed), making it possible to quickly reactivate them after the crisis and so return to pre-crisis status.

3.2. A Memory Evolutive System and Its Multi-Agent, Multi-Temporality Organization

Formally a MES is a HES equipped with:

• a sub-HES which models a flexible long-term memory Mem, still called ‘memory’, developing through the emergence of multifaceted components connected by complex links;
• a multi-agent organization consisting of a network of evolutive subsystems, called co-regulators, each operating stepwise at its own rhythm, which self-organize the system through their interactions.

3.2.1. The Coregulators and Their Landscapes

Living systems have an internal modular organization, with modules of different sizes; for instance, in the neural system we have a variety of such modules, from more or less large specialized areas of the brain to a hierarchy of smaller treatment units (in the sense of Crick [31]). At a given time, each module has only access to a part of the system (its ‘landscape’) on which it operates at its own rhythm, with the help of the memory. The global dynamic results from an ‘interplay’ among the local dynamics of the different modules.

A MES has such a modular organization, in which a module is modeled by an evolutive subsystem CR called a co-regulator. A co-regulator has its own function, complexity, rhythm and differential access to the memory. It acts as a hybrid system, meaning that it has both a discrete timeline delineating its successive steps in the continuous timeline of the system, and, during a step, it follows the continuous dynamic of the system.

At each step, CR only receives partial information from the system via the active links b, c,… arriving to it during the step. This information is processed in the landscape of CR at t which is an Evolutive System L_t having those links for components; in particular the CR is itself included in the landscape. Using the differential access of CR to the memory Mem, an adapted procedure Pr is selected on this landscape (via pr), and the corresponding commands are sent to effectors E of Pr (Cf. Figure 6).

The effectuation of these commands starts a dynamic process whose result will be evaluated at the beginning t’ of the next step; this process can often be studied with usual physical models (e.g., ODE on its specific phase space) making it computable.

If the objectives are not attained at t’, we have a fracture for CR. An important cause of fractures is the non-respect of the dynamic temporal constraints of CR expressed by the synchronicity equations:

p(t) << d(t) << z(t),

where

• p(t)= mean propagation delay of the links in the landscape,
• d(t) = period of CR at t = mean length of its preceding steps,
• z(t) = least remaining life of the effectors of Pr.

3.2.2. The Global Dynamic

In a modular system, there is an “ability of agents to autonomously plan and pursue their actions and goals, to cooperate, to coordinate, and negotiate with others” (Wooldridge & Jennings [32]). Similarly, in a MES, the cooperation and/or competition between the co-regulators modulates the global dynamic which weaves the different internal local dynamics of the co-regulators.

At a given time, the various co-regulators may send conflicting commands to effectors. The global dynamic results from an interplay among them, and it may cause a fracture to some of them. While the local dynamics can be computable, the interplay between co-regulators renders the global dynamic generally non-computable, partly because of the flexibility of multifaceted components (e.g., in the memory) which can be activated through anyone of their lower-level ramifications. The various periods of the co-regulators lead to a dialectic between co-regulators with different rhythms, with a risk of a cascade of fractures and re-synchronizations at increasing levels. It leads to ubiquitous complex events processing, as in the Aging Theory for an organism developed by the authors [10].

MES give a model for a kind of ‘competing local reductionisms’. The whole system cannot be ‘reduced’ to a given subsystem of it, but some ‘parts’, namely the dynamics of the co-regulators during one of their steps, can be modeled by usual Physics’ models (related to different phase-spaces). However, these partial models are incompatible and there is need of an ‘interplay’ among co-regulators to select which ones will be finally retained in the overall dynamic.

4. Discussion

Applied to a living system S, the MES methodology does not lead to a methodological reductionism to a given level; in fact it characterizes the obstacle to such a reductionism, namely the existence of multifaceted components (MP). It is only the local dynamics of the co-regulators which are susceptible of reduction to computable models (eventually nonlinear or chaotic). The global dynamic is not so reducible, and it allows for the emergence of more and more complex phenomena through successive complexification processes.

4.1. Emergentist Reductionism

In philosophy, the concept of emergence is itself multifaceted: it is given different meanings depending on the authors. For the Standard Encyclopedia of Philosophy [33]: “Emergent properties are systemic features of complex systems which could not be predicted (practically speaking; or for any finite knower; or for even an ideal knower) from the standpoint of a pre-emergent stage, despite a thorough knowledge of the features of, and laws governing, their parts”. There is a distinction between what is called ‘synchronic’ and ‘diachronic’ emergence. As we are not philosophers, we are not qualified for a general study of emergence. Hereafter, we successively study these two kinds of emergence in living systems, in connection with the categorical notion of a colimit and its applications to the MES methodology.

4.1.1. Emergence in Terms of Levels

In Section 2.2.2, the part–whole relation has been modeled in a category H by using the notion of a colimit: the whole is represented as the colimit cP of the pattern P of interacting objects in H representing its parts and their organization. To say that a pattern P in a category H admits a colimit if, and only if, there exists a cone from P to cP, called colimit-cone, satisfying the ‘universal property’:

(E) any cone with basis P uniquely factors through the colimit cone from P to cP.

If H is a hierarchical category modeling a complex system S and if we think of a ‘whole’ as an object of a higher complexity level than its ‘parts’, we can say that (E) is an emergent property in H in terms of levels. The word ‘emergent’ is justified for an ‘external’ observer of the system S (be it a human or even a computer) who ‘retrospectively’ has a global vision of H, including the cone from P to cP, independently from the time and circumstances in which cP has appeared (e.g., ‘birth’ of a new object, addition of a new cone or complexification process). Indeed, while (E) is conceptually a well-defined categorical property, its practical verification by the observer would raise a ‘physical’ problem, due to the number of cones to consider: this number can be very large and to observe the behavior of each of them would require too much time.

For similar reasons, the property for an object C of level n+1 to be a multifaceted object (Section 2.4), exemplified by a ‘switch’ between two of its structurally non-isomorphic lower-level decompositions P and Q, is also a well-defined categorical property which is only an emergent property for an observer retrospectively looking at the system. As a consequence, a complex morphism (Section 2.4) also represents such an emergent property in terms of levels.

Let us note that, in all these cases, the physical problem relates to the time necessary to handle large numbers, though we can quickly conceptualize them.

4.1.2. A Hierarchical Category Resorts to An Emergentist-Reductionism

From the Reduction Theorem (Section 2.4) it follows that a hierarchical category H without multifaceted objects is reducible to its level 0. Now let us suppose that H has n-multifaceted objects for each n. An object C of level n+1 has at least one ramification down to level 0, consisting of a lower-level decomposition P of C, then a lower-level decomposition Π_i of each object P_i of P, and so on down to level 0 patterns forming the basis of the ramification (cf. Figure 2). In this way, C is reducible to P, each object P_i of P is reducible to Π_i, and so on top-down through to level 0. This defines a kind of step-by-step reductionism for the objects, with emergent properties related to the bottom to top formation of the different colimits at each step. This situation corresponds to what M. Bunge [8] has called an ‘emergentist-reductionism’.

4.2. Diachronic Emergence in a MES

In the preceding section we have not explicitly considered the dynamic of the system, so that ‘emergence’ relates to a retrospective comparison between complexity levels rather than to a temporal change. Here we consider the dynamic of a living system S modeled by a MES. Its hierarchical configuration categories have emergent properties in terms of levels of the kind considered above, and the transitions are generated by complexification processes for adapted procedures (Section 3.2).

4.2.1. Emergent Properties of Complex Links between Components

As we have already said, the MES methodology aims to model a living system S in its ‘becoming’: knowing the system up to a time t, we study the change of configuration from t to a later time t’. Here we consider a transition from t to t’ consisting in a unique complexification process for an adapted procedure Pr. The categorical construction of the complexification (by recurrence, cf. Section 2.5) gives a ‘conceptual’ anticipation of the resulting category_’, but it does not account for its ‘physical’ implementation nor for the duration of the process because of physical temporal constraints similar to those studied above.

In particular, let us suppose that the construction leads to the formation of a complex link c from B to C’ obtained as the composite of an n-simple link g from B to C and an n-simple link f from C to C’ which bind non adjacent clusters separated by a switch between lower-level decompositions P and Q of C (cf. Figure 3). The successive states of c are complex morphisms which represent emergent properties in their respective configuration categories. Can an external observer of S ‘physically’ anticipate the emergent properties of the link c when it is activated?

For c to become active at t, the link g must be active at t and the information it transfers will arrive at C at t+p(t), where p(t) is the propagation delay of g at t. The activation of C at t+p(t) then activates the morphism f from C to C’, thus imposing a switch between (the states of) P and Q in the configuration category. As said above, this ‘instantaneous’ switch, which plays the role of ‘change in the conditions of change’, is at the root of diachronic emergent properties of the complex link c for an external observer, since it would require the simultaneous treatment of a large number of operations, and this is not ‘physically’ possible for the observer.

This situation agrees with Brian Johnson’s explanation of emergence [34]: “Given that emergence is often the result of many interactions occurring simultaneously in time and space, an ability to intuitively grasp it would require the ability to consciously think in parallel”; and he proposes a “simple exercise <…> used to demonstrate that we do not possess this ability”.

4.2.2. Emergence at the Basis of Unpredictability, Creativity, and Anticipation

The Emergence Theorem (Section 2.5) shows that the formation of complex morphisms in a complexification process is at the basis of the emergence of objects of increasing complexity orders, themselves connected by complex morphisms. The “changes in the conditions of changes” due to these complex morphisms are responsible for the unpredictability of the result of iterated complexifications (Section 2.5). As the long-term evolution of a MES depends on iterated complexification processes, it follows that the long-term evolution of the living system modeled by the MES is also unpredictable.

Emergence has consequences for creativity. Boden [35] has distinguished three forms of creativity: combinatory, exploratory, and transformational. In a living system modeled by a MES, these three forms can exist and be distinguished:

• the complexification process combines the specified patterns into more complex objects;
• the selection of procedures via the co-regulators leads to an exploration of different possibilities;
• transformational creativity is characterized by iterated complexification processes leading to successive changes in the conditions of change which make the result unpredictable, allowing for surprising results.

The role of emergence is also important for anticipation and futures thinking. While the complexification process allows to ‘virtually’ evaluate different procedures in the purely categorical setting, the situation is different when applied to natural systems. Indeed, because of emergent properties, the construction of the complexification for an adequate procedure Pr is not physically implementable. However, a step by step analysis of this construction may suggest new anticipatory assumptions (AA). This is helpful in the Futures Literacy Framework where the aim is to identify and deploy AAs “to ‘use-the-future’ for specific ends in particular contexts” (Miller [16], Chapter 1).

5. Conclusion

Let us mention that the MES methodology can be enriched in a variety of ways, by adding more structures on their configurations, for example by defining:

• K-MES, where K is a category of structures (for instance, topological MES if K =Top, multifold MES if K = Cat) in which the configuration categories are internal categories in K and the transitions partial functors in K [36];
• relational MES in which the transitions are replaced by relations, so that a given object at t is related to different objects at t’, the repartition being assigned a specific probability (not yet published).

To conclude, we propose that the MES methodology could help for a revival of Natural Philosophy, by itself and through some of its possible variants.