Abstract
This paper presents a theoretical study of the binary oppositions underlying the mechanisms of natural computation understood as dynamical processes on natural information morphologies. Of special interest are the oppositions of discrete vs. continuous, structure vs. process, and differentiation vs. integration. The framework used is that of computing nature, where all natural processes at different levels of organisation are computations over informational structures. The interactions at different levels of granularity/organisation in nature, and the character of the phenomena that unfold through those interactions, are modeled from the perspective of an observing agent. This brings us to the movement from binary oppositions to dynamic networks built upon mutually related binary oppositions, where each node has several properties.
1. Introduction
Our understanding of nature, including ourselves as natural beings, is increasingly based on computational models, with simulations and visualizations of the domains inaccessible to our everyday experience. Epistemologically, this requires connecting the domains directly accessible to our cognition with those we reach via tools—instruments and theories. It is therefore instructive to examine the conceptual basis of our contemporary understanding of nature, with an emphasis on the view of computing nature known as info-computation [1], where cognizing agents construct their reality (their view of the world) as information (structured data), with information dynamics understood as computation [2]. The process of reality construction starts with the most fundamental idea of a difference (distinction) and its opposite; similarity, via processes of differentiation and integration.
2. Dichotomy—The Simplest Kind of Classification
Dichotomy is deeply rooted in human cognition. Jakobson and Halle [3] argue that “the binary opposition is a child's first logical operation.” The neurophysiological roots of dichotomy might be found in the oldest parts of visual recognition, where the basic distinction is made between light and dark (input signal: yes/no). The simplest form of observation is thus of the same binary kind.
In the sciences, the empirical method relies on observations and experiments, which lead to the collection of data describing phenomena. In order to establish a pattern or regularity of behavior, we must analyze (compare) the data, searching for similarities (repetitions) and differences. All repetitions are approximate: the repetition B of an event A is not identical with A, or indistinguishable from A, but only similar to A. As repetition is based upon similarity, it must be relative. Two things that are similar are always similar in certain respects. We find that some objects are similar with respect to color, others are similar with respect to shape and some are similar with respect to size. Generally, establishing similarities and, consequently, repetition, always presupposes the adoption of a point of view: some similarities or repetitions will appear if we are interested in one problem and others if we are interested in another problem.
Searching for similarities and differences leads to classifications based on the division of objects or events into different groups/classes. The basic tool for classification is the binary opposition or dichotomy. When we use dichotomy, we only decide if an object is of a kind A or of a kind A (non-A). As an illustration, examples of dichotomies are given in the following list:
yes/no; true/false; positive/negative; affirmation/negation; accept/reject; good/evil; good/bad; right/wrong; being/nothingness; being/becoming; presence/absence; alive/dead; active/passive; on/off; open/closed; particle/wave; position/momentum; angle/angular momentum; energy/time duration; entanglement/coherence; phase/particle number; body/mind; matter/energy; particle/wave; medium/message; discrete/continuous; form/meaning; static/dynamic; structure/process; information/computation; passive/active; permanence/change; in/out; up/down; front/back; left/right; forwards/backwards; before/after; sooner/later; high/low; here/there; figure/ground; text/context, light/dark, one/many; different/similar; part/whole; less/more; unity/diversity; few/many; simple/complex; continuous/discrete; quantity/quality; analysis/synthesis; differentiate/integrate; particular/general; special/common; thought/feeling; reason/emotion; fact/fiction; practice/theory; objective/subjective; thought/feeling; subject/object; self/other; order/chaos; concrete/abstract; token/type; local/global; natural/artificial; form/content; syntax/semantics; means/ends; cause/effect; finite/infinite; force/matter; identity/difference; positive/negative; form/content; chance/necessity; cause/effect; freedom/necessity; subjectivity/objectivity; means/ends; subject/object; abstract/concrete; absolute/relative; positivist/critical; analytic/synthetic; induction/deduction; evolution/involution; complexification/simplification; abstraction/concretization; top/down; excitation/inhibition/; increase/decrease; anticipation/hindsight; future/past; objects/events; extent/duration; simplicity/diversity; data science (world as its own model)/TOE (world in an equation); snapshot/time development; teleology/(blind) mechanics; identity/change; “god’s-eye view” (sees everything at the same time)/observer’s view; reduction/generation; growth/recession; (mechanical) assembly/(biological) growth.
3. Leibniz’s Binary Notation
In messages sent and received, such as in Shannon information (communicated information) [4], the information content of a message is measured by the reduction of receiver’s uncertainty or ignorance. Shannon’s unit of information is the bit—binary digit—defined as the amount of information needed to halve the receiver’s prior uncertainty. From this perspective, information is about the selection between alternatives, which in the simplest case is a sequence of binary choices, each of them equally probable. A close connection between binary choices and information is illustrated by Gell Mann’s example of the Twenty Questions Game [5], in which one person in the group thinks of an object and the other people ask yes/no questions about it, until they determine what it is.
An early attempt to derive physics from empirical binary alternatives was made by Carl Friedrich von Weizsäcker, who developed a theory of ur-alternatives in the book The Unity of Nature [6], starting from the premisses that substance is form. Matter, as well as movement, are forms, while mass and energy are information (for an observer). Later on, John Archibald Wheeler developed a similar approach named “it from bit” [7], asserting that information is fundamental for physics, and every fact about physics (“it”) is derived from observations; that is, bits of information obtained empirically.
Even before ur-alternatives and “it from bit”, Leibniz (1697) proposed the idea of deriving the description of the world from binary alternatives, and he was the first to introduce binary notation [8]. In his book On the Method of Distinguishing Real from Imaginary Phenomena, Leibniz pointed out that the numbers zero (nothing) and one (God), are all that is needed to construct the [description of the] universe. He illustrated this by a figure with the title “In order to make everything from nothing the One suffices”. Beginning with the numbers 0 and 1, he showed how to represent all natural numbers in terms of the two basic digits (1 = 1, 2 = 10, 3 = 11, etc.). Debrock comments:
“To his contemporaries, the picture must have seemed like a somewhat outrageous joke. To us it looks both prophetic and frightening, because it appears as a confirmation of the trend to think the world in terms of digital information. But Leibniz’s picture suggests that we must even go beyond thinking world in terms of digital information, for he presents the world as being the set of all digital information ([8], p. 160).”
4. Dualism in Physics: Discrete vs. Continuous
Binary logic, which is a result of the systematization of simple common-sense reasoning, allows for only two values of the truth variable—one or zero (true or false). These two opposite values may be considered as exhausting the whole space of possibilities. This is expressed as “Tertium non Datur”, (“The third is not given”), also known as the Law of the excluded middle. In connection with dual-aspect characterization, the analysis of a number of binary concepts in physics, such as wave/particle, potential/actual, real/virtual, and positive/negative, which may be used to describe physical phenomena, is of interest. The most discussed binary concept is wave-particle dualism that Einstein commented in the following:
“There are therefore now two theories of light, both indispensable, and—as one must admit today in spite of twenty years of tremendous effort on the part of theoretical physicists—without any logical connections.”Albert Einstein [9]
Bohr [10] formulated his Complementarity principle, stating that particle theory and wave theory are both necessary. Scientists should simply choose whichever theory works better for solving their specific problem.
The currently accepted solution of the wave-particle “problem” is given in quantum electrodynamics (QED), which combines particle and wave properties into a unified whole.
Wave-particle dualism can be seen as a special case of continuum-discrete dichotomy. In terms of computational applications, the question of discrete-continuum opposition may be found in the difference between symbol-based and connectionist (neural network) approaches. However, it is sometimes stated that there is no dichotomy, because most neural networks are modeled in (discrete) software. Similarly, in a transistor, which is a physical device implementing binary 0/1 logic in terms of electric current, the current itself is not discrete, but basically a continuous phenomenon—so it is a matter of convention to assign “zero current” to a sufficiently low current in a transistor. On the same grounds, one can argue that discrete (countable) and continuous (measurable) phenomena are intertwined in digital technology that can represent continuous phenomena, such as sound and speech, photographs, and movements based on discrete phenomena.
Chalmers [11] claims that continuous systems would need to exploit infinite precision to exceed the powers of discrete systems (pp. 330–331). This is contradicted by Siegelman and Sontag in [12] by an analog system that computes a superset of the Turing-computable functions in polynomial time, and with finite linear precision.
5. The Finite (Discrete) Nature Hypothesis
“A fundamental question about time, space and the inhabitants thereof is "Are things smooth or grainy?" Some things are obviously grainy (matter, charge, angular momentum); for other things (space, time, momentum, energy) the answers are not clear. Finite Nature is the assumption that, at some scale, space and time are discrete and that the number of possible states of every finite volume of space-time is finite. In other words Finite Nature assumes that there is no thing that is smooth or continuous and that there are no infinitesimals.”(Fredkin, Finite Nature) [13] (Emphasis added)
One obvious question we may ask is: Why would we need this hypothesis about the discrete nature of the physical world? The computing nature framework (pancomputationalism) is not critically dependent on computations being discrete (or digital). They can equally be continuous and analog. How did this idea arise in the first place? The reason may be that, by analogy with the digital computer, the universe was conceived as digital, in the same way as the Newton-Laplace universe was regarded, by analogy with the machines of the mechanistic era, as a purely mechanical mechanism.
If we see the physical universe as a computer, it is empirically both discrete and continuous, as we can observe both discrete and continuous processes in nature at different levels of scale. Peter Denning argues that computing based on physical computation is a natural science [14]. However, not all approaches to natural computing start from the quantum computers in the physical universe via increasingly more complex computational systems such as evolving living organisms. Some, like Dana Ballard [15,16], focus on the human brain as the most advanced natural computer, connecting results from neuroscience, information theory, and optimization to describe programs of the brain. Seth Lloyd describes the universe as a quantum computer [17], so natural computation in his case is quantum computation.
In the most general formulation of computing nature/pancomputationalism, where all of nature computes on different levels of organisation [1], there is no special reason to consider only discrete aspects—we may instead wish to learn from nature how to compute [18,19].
6. The True Nature of the Universe: Discretely Continuous?
The question of whether the universe, on a fundamental level, is discrete or continuous brings us back to questions of epistemology and cognition—questions of our conceptualization of the universe and its (physical) phenomena. The universe might be fundamentally (a) discrete; (b) continuous; (c) both continuous and discrete, or (d) neither continuous nor discrete [20]. I will argue for (c), referring to the use of dichotomies in epistemological analysis.
Even though, as already mentioned, the idea of computing nature is not crucially dependent on any of the above, different options might have different interpretations, and also different practical consequences.
In The Age of Intelligent Machines [21], Kurzweil discusses “the question of whether the ultimate nature of reality is analog or digital”, and points out that
“(A)s we delve deeper and deeper into both natural and artificial processes, we find the nature of the process often alternates between analog and digital representations of information. As an illustration, I noted how the phenomenon of sound flips back and forth between digital and analog representations. In our brains, music is represented as the digital firing of neurons in the cochlear representing different frequency bands. In the air and in the wires leading to loudspeakers, it is an analog phenomenon. The representation of sound on a music compact disk is digital, which is interpreted by digital circuits. But the digital circuits consist of thresholded transistors, which are analog amplifiers. As amplifiers, the transistors manipulate individual electrons, which can be counted and are, therefore, digital, but at a deeper level are subject to analog quantum field equations. At a yet deeper level, Fredkin, and now Wolfram, are theorizing a digital (i.e., computational) basis to these continuous equations. It should be further noted that if someone actually does succeed in establishing such a digital theory of physics, we would then be tempted to examine what sorts of deeper mechanisms are actually implementing the computations and links of the cellular automata. Perhaps, underlying the cellular automata that run the Universe are yet more basic analog phenomena, which, like transistors, are subject to thresholds that enable them to perform digital transactions.”[21]
Lloyd makes a similar claim in the case of quantum mechanics:
“In a quantum computer, there is no distinction between analog and digital computation. Quanta are by definition discrete, and their states can be mapped directly onto the states of qubits without approximation. But qubits are also continuous, because of their wave nature; their states can be continuous superpositions. Analog quantum computers and digital quantum computers are both made up of qubits, and analog quantum computations and digital quantum computations both proceed by arranging logic operations between those qubits. Our classical intuition tells us that analog computation is intrinsically continuous and digital computation is intrinsically discrete. As with many other classical intuitions, this one is incorrect when applied to quantum computation. Analog quantum computers and digital quantum computers are one and the same device.”[17]
Moreover, even if, in some representations, it may be discrete (and thus conform to the Pythagorean ideal of number as a principle of the world), processes in the universe (and thus computations in computing nature) unfold at many different levels of organization, including quantum computing, bio-computing, spatial computing, membrane computing, etc.; some of which are discrete, others continuous. Computing nature seems to have a use for both discrete and continuous computation. The idea that “discrete and continuous features coexist in any natural phenomenon, depending on the scales of observation” as argued by Lesne [22], who discusses the discrete-versus-continuous controversy in physics, summarized this as follows: “Physics in all instances is an interplay between discrete and continuous features, mainly because any such feature actually characterizes a representation, from a given observer, of the real system and its evolution.” [22].
Wolfram [23] and Fredkin [13], in the tradition of Zuse [24], assume that the universe is, on a fundamental level, a discrete system, and is thus suitably modeled as an all-encompassing digital computer. Given the discussion above, one might say that it is a possible choice of a level of description.
Computing universe hypothesis (computing nature, natural computationalism), as already mentioned, does not depend on the discreteness of the physical world, and there are digital as well as analog computers. On a quantum-mechanical level, the universe performs computation [17] on characteristically dual wave-particle objects, i.e., it performs both continuous and discrete computing. Even though they are often used interchangeably, Maley [25] argues that it is necessary to distinguish between analog and continuous, and between digital and discrete representations. Although typical examples of analog representations use continuous media, this is not what makes them analog. Rather, it is the relationship that they maintain with what they represent. Similar holds for digital representations. The lack of proper distinctions in this respect is a source of much confusion.
From a different perspective, Floridi argues that digital ontology cannot be all that exists:
“Digital vs. analogue is a Boolean dichotomy typical of our computational paradigm, but digital and analogue are only “modes of presentation” of being (to paraphrase Kant), that is, ways in which reality is experienced and/or conceptualized by an epistemic agent at a given level of abstraction. A preferable alternative is provided by an informational approach to structural realism, according to which knowledge of the world is knowledge of its structures.”[20]
7. Continuum as a Result of Interaction
From the cognitive point of view, most of the usual dichotomies are coarse approximations. They are useful, and they speed up our perception and reasoning, but on closer inspection, one would find shades of gray between black and white dichotomies. Following Kant, we can say that the “Ding an Sich” (thing-in-itself) is nothing we have knowledge of. This is also the case for the question of discrete-continuous nature.
Our cognitive categories are the result of our natural evolutionary adaptation to the environment. Given the bodily “hardware” that we have, they are strongly related to the nature of our experiences with the concrete physical world in which we live, and are by no means general tools for understanding the universe at all levels of granularity and for all types of phenomena that exist inaccessibly to our experiences.
If we adopt the dichotomy as our own epistemological necessity (at least for the use in everyday life experiences), how could the general case of continuum vs. discrete universe be understood?
In what follows I will argue that discrete and continuous are dependent upon each other—that logically, there is no way to define the one without the other. So, let us begin by assuming that basic physical phenomena are discrete. Let us also assume that they appear in finite discrete quanta, packages, amounts or extents. If the quanta are infinitely small then they already form a continuum. However, the idea of quantities that can be made arbitrarily small—such as Newton’s fluxions—is logically problematic, although very useful for practical applications where “arbitrarily small” is some finite value, as pointed out by Bishop Berkeley in The Analyst: A Discourse Addressed to an Infidel Mathematician (1734): “And what are these fluxions? The velocities of evanescent increments. And what are these same evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities…?” See also Chaitin’s argument against real numbers along similar lines [26].
Nevertheless, even if we start with finite quanta, a continuum can be constructed as a result of their interaction or aggregation and the processes of communication between different systems (Figure 1) [27]:

Figure 1.
Constructing continuum from finite discrete signals.
Even if the time interval between two signals that one system produces always has some definite value different from zero (i.e., they are discrete signals), two communicating phenomena can in principle appear arbitrarily in time, so that the overlap is achieved, which means that a continuum is realized in a communicative (interactive) process such as computation.
8. Analog/Digital—Continuous/Discrete—Differentiation/Integration
Cognitive theories of intelligent behavior have been the basis for designing and implementing intelligent artificial systems. Although it is commonly agreed that an autonomous intelligent action implies intentionality, meaning, representation, and information processing; various theories of information assume different interrelations. The necessity of representation of information is tacitly assumed, either in the form of a hard, explicit and static representation, or a more implicit and dynamic one.
While we are far from having a consensus on the concept of information, the most general view is that information is a structure consisting of data that is the difference that makes a difference for an agent (a system capable of acting on its own behalf—a molecule, a cell, an animal, a human, or an artifact). Floridi [28] has the following definition of a datum: “In its simplest form, a datum can be reduced to just a lack of uniformity, that is, a binary difference”. Bateson’s “the difference that makes the difference” [29] is a datum in that sense. Information is both the result of observed differences (differentiation of data) and the result of synthesis of those data into a common informational structure (integration of data), as argued by Schroeder:
“Information can be defined in terms of categorical opposition of one and many, leading to two manifestations of information, selective and structural. These manifestations of information are dual in the sense that one always is associated with the other. The dualism can be used to model and explain dynamics of information processes.”(Schroeder [30])
Tymieniecka [31] (p. 173) contemplates the source of the differentiating/integrating opposites “What subtends their differentiative-unifying core? What maintains their intergenerative continuity in which they constantly transform each other and themselves? This dianoia [discursive thinking] thread running through all the contraries, opposites, parallels, etc. is the greatest mystery and the greatest issue in our inquiry into the creative transaction.” According to Ikere [32], Tymieniecka identifies the principles of unity and differentiation as leading to the self-individualization as a continuous of “the constructive vehicle of order within the flux”.
In the process of knowledge generation, the agent moves between those two processes—differentiation and integration of data, see [27] p. 38. For potential information of the world to become actual, there must exist an agent from the perspective of which the relational structure between the world as potential information and its actualization in an agent is established. Thus, (actual) information is a network of data points observed from an agent’s perspective.
Different concepts of representation result in different frameworks for analyzing and modeling the process of cognition in an agent, in which meaning and information are given different functional and explanatory roles. The dominant frameworks of cognition are all characterized by inherent limitations, such as the inability to account for both low- and high-level cognition, or to scale between them (the symbol’s grounding problem—how symbols get their meanings, and of what meanings they are comprised). Neither symbolic nor connectionist frameworks are able to account for the emergence of representation in a purely naturalistic manner (see [33]).
Arnellos et al. [34] propose a system-theoretic framework that seems to suggest a way out of the above difficulties. The proposed framework uses elements from cybersemiotics and tries to model the basic cognitive concepts (representation, meaning and information) by incorporating them in an anticipative and interactive context of information dynamics. Second-order cybernetics and self-organization properties are used to account for a complex and emergent relational structure of representation. The Arnellos et al. approach is not a dynamic/symbolic hybrid, but involves interplay between analog and digital information spaces, in which they model the representational behavior of a system. The focus on the explicitly referential correlation of information between system and environment is shifted towards the interactive modulation of implicit internal content and, therefore, the resulting pragmatic adaptation of the system via its interaction with the environment. This approach shows, not unlike Whitehead’s explanation of how ‘symbolic reference’ may arise as interplay between two modes of perception—‘causal efficacy’ and ‘presentational immediacy’, Whitehead [35]—that computational cognition does not necessarily need to be (only) digital.
Even though dichotomies are very powerful and economical methods of systematization and categorization, they are like black-and-white photographs. Real life is full of colors and gradations, and instead of looking at it in the coarse rendering of dichotomies, we can look at concepts as being parts of dynamic networks of related meanings. In order to understand the meaning of the concept information we look into its relation to other concepts (such as Wittgenstein’s “family resemblance”) [36], and find an infinite network of concepts related in a variety of ways in which each node is the center of a new network. Visual dictionaries, such as Visuwords http://www.visuwords.com, have concepts connected through several kinds of relationships (“kind of”, “instance of”, “member of”, “a part of”, “substance of”, “similar to”, “pertains to”, “participates”, “attributes”, “opposes”, “entails”, “causes”, etc.). If we would pick any two concepts from the network, such as “good” and “bad”, the following picture (Figure 2) would emerge:
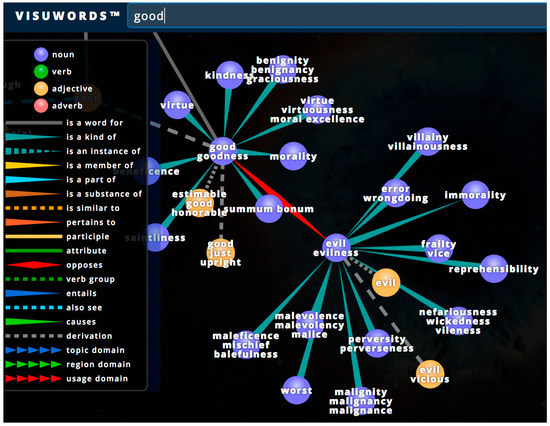
Figure 2.
Visuwords part of the semantic network of “good” vs. “evil”.
Visual dictionaries also relate verbs with nouns, indicating their close semantic connectedness. The noun parallels form or structure while verb corresponds to process or change. Drack [37] makes an interesting observation regarding Ludwig von Bertalanffy’s organismic view of the evolution of life, which connects structures with processes on different time scales: “Structures which seem to be stable on one time scale appear as slow processes and functions as fast processes. This view also entails what Bertalanffy calls a dynamic morphology: it goes beyond a static description and connects the change of form with physiological processes”. Bertalanffy’s dynamic view was meant for biological processes, but has a more general validity. The dynamics provide the unifying mechanism for the motion between the opposites: potential and actual, positive and negative, structure and process. Our cognitive habits rely on dichotomies, but they present only a very first, simplistic and coarse view that, on a deeper level, reveals a richness of structure, which is again possible to look into in greater detail from a closer distance, both spatial and temporal.
9. Conclusions
Computing nature, as an explanatory framework, is a layered architecture of morphological computations over informational structures based on the fundamental layer of physical computations [1]. Sometimes, it is claimed that computational nature essentially depends on the universe being discrete at some fundamental level. This article shows how dichotomies from physics such as discrete vs. continuous dissolve after careful study. Lesne [22] argues: “Rather than motivating a debate about the reality of exclusively discrete or continuous pictures, observations of physical phenomena lead us to elaborate more complex categories, bridging discreteness and continuity: fractal structures, discrete features punctuating a continuum, or continuous behaviour smoothing out an accumulation of discrete events.” Physical theories are based on representations of systems, while the reality is, in practice, inexhaustible, and can never be captured in its entirety in a representation. Different classes of cognitive agents have different representations of reality based on their morphologies (structures), which constrain possible interactions (morphological computations) at different levels of organization, such as physical, chemical, and biological to cognitive computation [1,2,38].
As Bertalanffy discovered, structures are related to processes on different time scales; seemingly stable structures on one time scale turn out to be processes on a finer time scale.
In summary, this article studies the computational dynamics of natural information morphology within the framework of computing nature with respect to the underlying dichotomies discrete/continuous, differentiation/integration, and structure/process. It is argued that dichotomies present useful simplifications, which under closer examination unfold into networks of dynamical relationships.
Acknowledgments
The author would like to thank the anonymous reviewers for their very helpful and constructive comments. The author would like to acknowledge the funding support provided by Swedish Research Council under a grant MORCOM@COG. Parts of this article are based on the book Investigations into Information Semantics and Ethics of Computing [27].
Conflicts of Interest
The author declares no conflict of interest.
References
- Dodig-Crnkovic, G. Nature as a Network of Morphological Infocomputational Processes for Cognitive Agents. Eur. Phys. J. 2017, 226, 181–195. [Google Scholar] [CrossRef]
- Dodig-Crnkovic, G.; von Haugwitz, R. Reality Construction in Cognitive Agents through Processes of Info-Computation. In Representation and Reality in Humans, Other Living Organisms and Intelligent Machines; Dodig-Crnkovic, G., Giovagnoli, R., Eds.; Springer: Basel, Switzerland, 2017; pp. 211–235. [Google Scholar]
- Jakobson, R.; Halle, M. Fundamentals of Language; Mouton & Co.: The Hague, The Netherlands, 1956. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gell-Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; Freeman/Owl Book: New York, NY, USA, 1994. [Google Scholar]
- Von Weizsäcker, C.F. The Unity of Nature; Translation; Farrar Straus Giroux: New York, NY, USA, 1980. [Google Scholar]
- Wheeler, J.A. It from Bit, at Home in the Universe; American Institute of Physics: College Park, MA, USA, 1994. [Google Scholar]
- Debrock, G. Process Pragmatism. Essays on a Quiet Philosophical Revolution; Debrock, G., Ed.; Rodopi: Amsterdam, The Netherlands; New York, NY, USA, 2003. [Google Scholar]
- Einstein, A. The Compton Experiment. In Scientific Papers of Arthur Holly Compton, X-ray and Other Studies, Appendix 3; Shankland, R.S., Ed.; University of Chicago Press: Chicago, IL, USA, 1975. [Google Scholar]
- Bohr, N. The Quantum Postulate and the Recent Development of Atomic Theory. Nature 1928, 121, 580–590. [Google Scholar] [CrossRef]
- Chalmers, A. What Is This Thing Called Science? 4th ed.; University of Queensland Press: Brisbane, Australia, 2013. [Google Scholar]
- Siegelmann, H.T.; Sontag, E.D. Analog computation via neural networks. Theor. Comput. Sci. 1994, 131, 331–360. [Google Scholar] [CrossRef]
- Fredkin, E. Finite Nature. In Progress in Atomic Physics, Neutrinos and Gravitation, Proceedings of the Xxviith Rencontre de Moriond, Les Arcs, Savoie, France, 25 January–1 February 1992; Chardin, G., Fackler, O., Van Thanh, J., Eds.; Editions Frontieres: Gif-sur-Yvette, France, 1992; pp. 345–352. [Google Scholar]
- Denning, P. Computing is a natural science. Commun. ACM 2007, 50, 13–18. [Google Scholar] [CrossRef]
- Ballard, D. An Introduction to Natural Computation; The MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Ballard, D. Brain Computation as Hierarchical Abstraction, (Computational Neuroscience); The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Lloyd, S. Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos; Knopf: New York, NY, USA, 2006. [Google Scholar]
- Rozenberg, G.; Kari, L. The many facets of natural computing. Commun. ACM 2008, 51, 72–83. [Google Scholar]
- Horsman, D.; Kendon, V.; Stepney, S. The Natural Science of Computing. Commun. ACM 2017, 60, 31–34. [Google Scholar] [CrossRef]
- Floridi, L. Against digital ontology. Synthese 2009, 168, 151–178. [Google Scholar] [CrossRef]
- Kurzweil, R. The Age of Spiritual Machines, When Computers Exceed Human Intelligence; Viking Press: New York, NY, USA, 1999. [Google Scholar]
- Lesne, A. The discrete versus continuous controversy in physics. Math. Struct. Comput. Sci. 2007, 17, 185–223. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Zuse, K. Calculating Space; Translation of “Rechnender Raum”; MIT Technical Translation: Cambridge, MA, USA, 1970. [Google Scholar]
- Maley, C.J. Analog and digital, continuous and discrete. Philos. Stud. 2011, 155, 117–131. [Google Scholar] [CrossRef]
- Dodig-Crnkovic, G.; Stuart, S.A.J. Computation, Information, Cognition: The Nexus and the Liminal; Cambridge Scholars Publishing: Newcastle, UK, 2007. [Google Scholar]
- Dodig-Crnkovic, G. Investigations into Information Semantics and Ethics of Computing; Mälardalen University Press: Västerås, Sweden, 2006. [Google Scholar]
- Floridi, L. A defense of informational structural realism. Synthese 2008, 161, 219–253. [Google Scholar] [CrossRef]
- Bateson, G. Steps to an Ecology of Mind: Collected Essays in Anthropology, Psychiatry, Evolution, and Epistemology; Adriaans, P., van Benthem, J., Eds.; University of Chicago Press: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Schroeder, M.J. Dualism of Selective and Structural Manifestations of Information in Modelling of Information Dynamics. In Computing Nature; Dodig-Crnkovic, G., Giovagnoli, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 125–137. [Google Scholar]
- Tymieniecka, A.-T. Logos and Life: Creative Experience and the Critique of Reason: Introduction to the Phenomenology of Life and the Human Condition; Kluwer Academic: Dodrecht, The Netherlands, 1988. [Google Scholar]
- Ikere, Z. The Law of Opposites in the Ontopoiesis of Life and in Language. In Phenomenology of Space and Time, Volume 116 of the Series Analecta Husserliana pp; Springer: Cham, Switzerland, 2013; pp. 71–78. [Google Scholar]
- Taddeo, M.; Floridi, L. A Praxical Solution of the Symbol Grounding Problem. Minds Mach. 2007, 17, 369–389. [Google Scholar] [CrossRef]
- Arnellos, A.; Spyrou, T.; Darzentas, J. The Emergence of Interactive Meaning Processes in Autonomous Systems. In Proceedings of the FIS 2005: Third International Conference on the Foundations of Information Science, Paris, France, 4–7 July 2005. [Google Scholar]
- Whitehead, A.N. Process and Reality: An Essay in Cosmology; The Free Press: New York, NY, USA, 1978. [Google Scholar]
- Dodig-Crnkovic, G.; Cicchetti, A. Computational Aspects of Model-Based Reasoning. In Springer Handbook of Model-Based Science; Magnani, L., Bertolotti, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Drack, M. Ludwig von Bertalanffy’s organismic view on the theory of evolution. J. Exp. Zool. (Mol. Dev. Evol.) 2015, 324B, 77–90. [Google Scholar] [CrossRef] [PubMed]
- Dodig-Crnkovic, G. Physical Computation as Dynamics of Form that Glues Everything Together. Information 2012, 3, 204–218. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).