Abstract
Solution searching that accompanies combinatorial explosion is one of the most important issues in the age of artificial intelligence. Natural intelligence, which exploits natural processes for intelligent functions, is expected to help resolve or alleviate the difficulties of conventional computing paradigms and technologies. In fact, we have shown that a single-celled organism such as an amoeba can solve constraint satisfaction problems and related optimization problems as well as demonstrate experimental systems based on non-organic systems such as optical energy transfer involving near-field interactions. However, the fundamental mechanisms and limitations behind solution searching based on natural processes have not yet been understood. Herein, we present a theoretical background of solution searching based on optical excitation transfer from a category-theoretic standpoint. One important indication inspired by the category theory is that the satisfaction of short exact sequences is critical for an adequate computational operation that determines the flow of time for the system and is termed as “short-exact-sequence-based time.” In addition, the octahedral and braid structures known in triangulated categories provide a clear understanding of the underlying mechanisms, including a quantitative indication of the difficulties of obtaining solutions based on homology dimension. This study contributes to providing a fundamental background of natural intelligence.
1. Introduction
Solution searching that accompanies combinatorial explosion, such as non-deterministic polynomial time (NP)-complete problems, is one of the most important challenges in the age of artificial intelligence [1,2]. While massive digital computing power nowadays can overcome even the conventional difficulties of von Neumann computing architecture, including those in the game of Go [3], natural computing or natural intelligence is an important and exciting branch of research that seeks deeper understandings of computing abilities in nature and exploits them for intelligent functions. The insights into intelligence stemming from nature that have been investigated in the literature range from amoebas [4] to the human brain [5], DNA [6], and even an iron bar [7]; in addition, general frameworks such as noise-based logic [8] and spatiotemporal dynamics [9,10] have been investigated.
Among such research, a plasmodium of the true slime mold Physarum polycephalum, a single-celled amoeba-like organism, is known to exhibit sophisticated information-processing abilities. An early work includes the demonstration of obtaining the shortest-distance solutions between two food sources [11]. Furthermore, Aono et al. demonstrated solution searching of a logical constraint satisfaction problem (CSP) [4] and the traveling salesman problem [12] by utilizing the spatiotemporal oscillatory dynamics of the photoavoidance behavior of the amoeboid organism combined with an external optical stimulus. Moreover, Kim et al. formulated an algorithm that abstracted the photoavoidance dynamics of the organism to solve the multi-armed bandit problem (MAB), which underlay important decision-making problems in dynamically changing uncertain environments in the real world [13].
Moreover, architecture that combines Physarum with an external optical stimulus system implies non-organic realizations of the principles reported in the literature on amoeba-based computing. In fact, Naruse et al. theoretically and experimentally demonstrated that the versatile spatiotemporal dynamics induced in multiple-quantum-dot systems by optical near-field interactions can be used to solve CSP [9,14] and MAB [15,16]. Furthermore, Aono et al. showed that the satisfiability problem (SAT), which is known to be one of the most important NP-complete problems, can be solved [14]. Naruse et al. also demonstrated solving MAB by using single photons emitted from a nanodiamond [17]. Meanwhile, Kasai et al. succeeded experimentally in solving CSP based on solid-state electrical circuits on the basis of spatiotemporal dynamics involving noise sources [18]. Recently, Aono et al. examined nanoarchitecture for an SAT solver based on Gallium arsenide (GaAs) nanowires [19].
However, the fundamental mechanisms of amoeba-based solution searching and its artificial equivalents are not yet completely understood. Furthermore, certain physical and logical constraints and limitations should exist for properly solving given problems, whereas successful demonstrations to date have been based mainly on empirically designed architecture and parameter choices. This study aims to provide a solid foundation for amoeba-inspired solution searching inspired by the category theory.
Category theory is an abstract branch of mathematics that formulates given problems with the notions of objects and arrows [20,21]. By applying category theoretic notions to solution searching problems, we can obtain insights into the underlying mechanisms and operating conditions of the solution searching in a precise manner. In addition to providing qualitative understanding, which we discussed in our previous study on single-photon-based decision making [22], the category theoretic representation in the present study also demonstrates novel quantitative perspectives, such as in the discussion of the operating speed or definition of time, and the perception of obtaining correct solutions as the homology dimension decreases.
This paper is organized as follows. Section 2 reviews solution-searching principles based on optical energy transfer mediated by near-field interactions. As a particular problem, we define a CSP and demonstrate the solution searching behavior to be examined in detail. In Section 3, we present a category theoretic picture of solution searching in a stepwise manner. Beginning with adapting the notions of product, coproduct, complex, and short exact sequence into the solution searching problem, we end by showing that the octahedral and braid structures known in triangulated categories reveal the underlying architecture of solution searching based on stochastic spatiotemporal dynamics. We also propose the notion of short-exact-sequence-based time implied by category theory to describe a properly operating system. Regarding the braid architecture, we demonstrate theoretically and numerically that solution searching can be viewed as unfolding the knots of braids or decreasing the homology dimensions inherent in the system. As described above, the principal aim of this study is not to conduct exact discussions about mathematics itself but to obtain deeper insight into stochastic spatiotemporal solution searching from original perspectives inspired by the category theory, including the development of numerically quantifiable metrics. Section 4 concludes the paper.
2. Solution Searching Based on Bounceback Principles
2.1. Spatiotemporal Amoeba Dynamics
Preserving essential and general properties of the solution searching principle while providing easy comprehension and quantitative discussions, we consider the following CSP, referred to as the NOR problem hereinafter, regarding an array of N binary-valued variables [4,9]. The constraint is that each variable should be the logical NOR of its neighbors, that is, should be satisfied for all i; the constraints regarding and N are given by and , respectively. When , which is the case, we numerically investigate in detail below, the correct solutions are the following five combinations: , , , , and .
The architecture of solution searching based on the amoeba-plus-optical-stimulus system is shown schematically in Figure 1a, in which multiple branches (branches 1 to 6 in the case of Figure 1a) are formed in the substrate. An amoeba, located initially in the center of the substrate, tries to elongate its body into the branches. Because of the photoavoidance nature of the amoeba, it does not like to elongate its body into branches upon which external light shines. Note, however, that body elongation into light-irradiated branches does occur occasionally, which is an important property in exploring correct solutions, as discussed later.
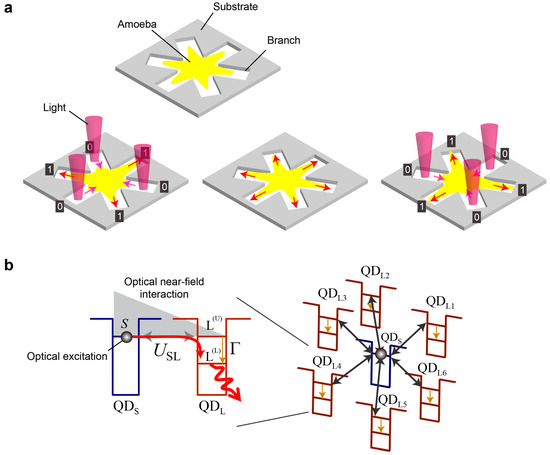
Figure 1.
Solution searching based on stochastic spatiotemporal dynamics. (a) amoeba-plus-optical-stimulus system; (b) optical excitation transfer dynamics in a multiple quantum-dot system.
Here, we define the relation between the shape of the amoeba and the binary variables such that the existence of the amoeba’s body in branch i corresponds to , whereas non-existence corresponds to . Considering the logical NOR operation, if , then both of its neighbors should be zero: . Therefore, the feedback mechanism for deriving correct solutions is given by Equation (1):
Aono et al., called this mechanism the bounceback principle rather than a conventional feedback rule to emphasize that the rule is given in the form of inhibiting certain conditions [10]. Although the particular bounceback rule in the case of the NOR problem (Equation (1)) looks extremely simple, the following important remark should be made.
Suppose that the amoeba were to elongate its body into all branches simultaneously (hence, ). Consequently, all branches would suffer from external light irradiation based on Equation (1). If elongation inhibition were to be applied perfectly, the amoeba would shrink its body out from all branches simultaneously (hence, ). In this manner, the system would fall into a deadlock and never reach a solution, which is analogous to Dijkstra’s dining philosophers problem as pointed out by Aono et al. [4]. Namely, in addition to bounceback rules, fluctuations of oscillatory behavior involving spontaneous symmetry breaking in the amoeboid organism play a vital role in preventing the system from entering a deadlock [9].
2.2. Photoexcitation Transfer Modeling
The amoeba-based solution searching described above utilizes spatiotemporal and probabilistic dynamics, indicating the possibility of realizing equivalent dynamics in solid-state materials [9,18]. In this study, we deal with optical energy transfer among multiple quantum dots as a concrete, quantitatively describable platform [9,10,16,23,24,25]. In accordance with the six-branch amoeba system, Figure 1b represents a quantum-dot system composed of one smaller quantum dot denoted by QDS, located in the center, surrounded by six larger quantum dots denoted by QDLi . The optical excitation generated at QDS, or more precisely the energy level (denoted by S) of QDS in Figure 1b, is transferred to the energy level marked in QDLi via optical near-field interaction . The subsequent energy dissipation induced in QDL transfers the excitation to lower energy level , prohibiting the excitation from being transferred back to the original QDS. The dynamics are described by a density matrix formalism in the Lindbrad form, given by
where represents the Hamiltonian involving the inter-dot near-field interaction network, is concerned with energy dissipation including sublevel relaxation in the quantum dots and radiation, and denotes the density matrix of the system. A detailed treatment of the modeling can be found in [14]. Essentially, the same formulation is found in the research on environment-assisted quantum walks [26,27].
The energy flow from QDS to each QDLi differs depending on the state filling effects induced in the destination QDLi [9]. Figure 2a(0–3) shows evolutions of populations with respect to the lower energy levels of the six larger dots (QDL1,…,QDL6), where zero, one, two, or three QDLi quantum dots experience state fillings. In the numerical calculations, we assume inter-dot near-field interactions ps, sublevel energy dissipation ps, optical radiation from a larger dot ns, and that from a smaller dot ns as a typical parameter set. When there is no state filling, an optical excitation sitting initially at QDS can be transferred to any one of QDL1 to QDL6 with the same probability (Figure 2a(0)). If one of the QDLi quantum dots, for example QDL1, suffers from state filling, the initial exciton in QDS is more likely to be transferred to the non-state-filled QDLi quantum dots (QDL2 QDL6), as shown in Figure 2a(1). Likewise, the energy transfer probability differs depending on the occupation of the destination QDLi quantum dots, as shown in Figure 2a(2,3), where two and three QDLi quantum dots, respectively, are subjected to state filling. The insets of Figure 2a show the energy transfer probabilities to QDLi () derived on the basis of the numerical integral of the calculated populations. There are 26 inherently different energy transfer patterns in total.
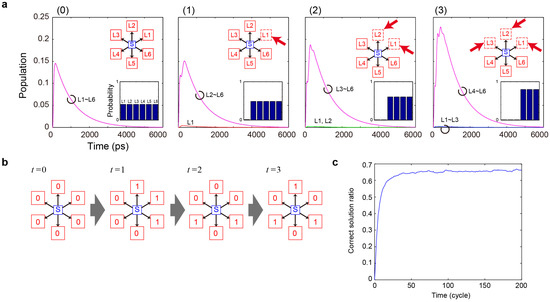
Figure 2.
Solution searching based on photoexcitation transfer. (a) evolutions of populations that differ from each other depending on state fillings induced in the larger quantum dots; (b) example of evolution of the excitation transfer based on the given bounceback rule; (c) correct-solution rate increases with time.
It has been demonstrated that, by applying the bounceback rule given in Equation (1) and using the energy transfer dynamics depicted in Figure 2a, CSP and SAT can be solved successively [9,10]. As an example, Figure 2b shows an example evolution of energy transfer patterns with initial (t = 0) values of . In this initial state, no state filling is induced in the system. Based on the energy transfer dynamics shown in Figure 1a(0), the system evolves to at . Based on the bounceback rules, QDL1, QDL2, QDL3, QDL5, and QDL6 experience state fillings because . The system is transferred to at . Based on the updated state fillings, the system evolves to , which is one of the correct solutions of the given CSP. Figure 2c shows the evolution of the correct-selection rate from the initial state of for 10,000 trials, in which the correct selection rate stabilized at approximately 0.65 after the cycle.
3. Category Theoretic Picture and Analysis
The bounceback rule, which is determined by the given problem, nicely marries with the spatiotemporal and probabilistic attributes of optical excitation transfer and leads to the solution searching as reviewed in the previous section. In this section, we analyze the fundamental mechanism through the notions of category theory.
Category theory is a branch of mathematics that formalizes mathematical structure into collections of objects (denoted by ) and morphisms or arrows (). Category theory extracts the essence of all mathematical subjects to reveal and formalize extremely simple and yet extremely powerful patterns of thinking, which has revolutionized the field of mathematics [28]. For each morphism f, there are given objects and called the domain and codomain of f, respectively. We write to show that and . The complete definition of a category involves the existence of a composition of, for example, morphisms, identity morphisms, and associativities [20,21]. In this study, we apply basic notions in category theory to the solution-searching problem in a stepwise manner. In Section 3.1, we introduce basic notions of the product, coproduct, and short exact sequence. In Section 3.2, followed by the introduction of complex and homology (cohomology), we propose a notion of short-exact-sequence-based time as an important figure for proper operation of systems for intended functionality. Indeed, incorrect operations are demonstrated in the solution searching system in Section 2 when the short-exact-sequence-based time is not stalled properly. Finally, in Section 3.3, the braid structure known in triangulated categories is introduced by which we can grasp an in-depth understanding of the solution searching demonstrated in Section 2.
3.1. Product, Coproduct, and Short Exact Sequence
Let the light emission from the surrounding larger dots be denoted by an object P. In other words, the combination of the variables is represented by P. Based on P, corresponding bounceback rules are activated, which is denoted by another object Q. We can have a rudimentary picture of a feedback-type diagram, as shown in Figure 3a, where P affects Q , that is, the combination of the variables determines the bounceback rule, while Q affects P , meaning that the bounceback rule changes the variables . This picture, however, does not imply any notions associated with energy transfer dynamics, including the fluctuation that is necessary to avoid deadlock.
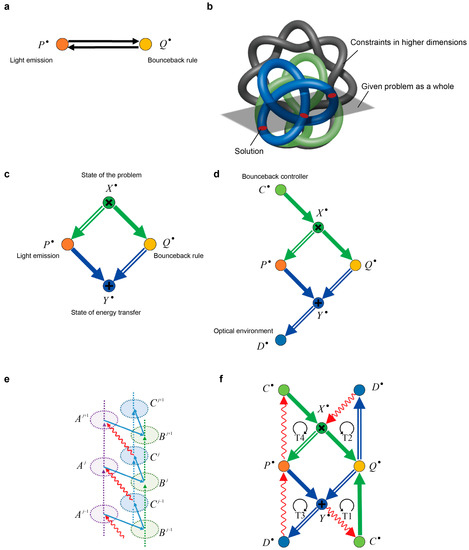
Figure 3.
Category theoretic picture of solution searching. (a) rudimentary picture of solution searching; (b) hyper-dimensional view of constraint satisfaction problem; (c) introducing product and coproduct for the light emission (P) and bounceback rule (Q); (d) introducing bounceback controller (C) and optical environment (D) as the kernel and cokernel of the morphisms and , respectively; (e) schematic diagram of chain-wise short exact sequences and exact long sequences of homology; and (f) derivation of four triangulated sequences known in triangulated categories.
To give a generic understanding from a concrete example, we consider an NOR problem of the case introduced in Section 2. This NOR problem is equivalent to solving the following satisfiability problem instance given in a conjunctive normal form:
From this Equation, the given problem is to satisfy all clauses of the right side of Equation (3), each of which behaves as a constraint of the given problem and spans a high-dimensional space. The given problem as a whole is a cross-sectional profile of this higher-dimensional space, and the solutions are marked by the intersections of constraints, as shown schematically in Figure 3b. In order to formalize such a hyper-dimensional space behind the system, we first introduce the notions of product and coproduct in category theory.
Definition (product and coproduct)
In any category, a product diagram for the objects A and B consists of an object S and morphisms satisfying the following. Given any diagram of the form , there exists a unique , making the diagram
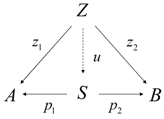 commute, i.e., and . S is written as .
commute, i.e., and . S is written as .

A diagram is a coproduct of A and B, represented by , if for any Z and , there is a unique with and as indicated in
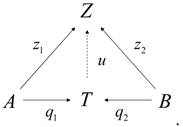

We employ the notions of product and coproduct in the original diagram shown in Figure 3a and obtain the diagram shown in Figure 3c. Here, represents the state of the problem, which is decomposed into the optical emission from the system (P) and the bounceback rule (Q) to be applied to the system, where all the environmental processes are taken into account. In other words, the total system (X) is a composite system comprising P and Q. Therefore, we assume that the total system that is under study forms a monoidal category. Hence, the theorems, lemmas, and axioms of the Abelian category apply to the system.
The morphism from the state of the problem (X) to the selected bounceback rule (Q) indicates that some of the rules may not be concerned, depending on the state of the problem. In other words, all the unnecessary rules are injected into “0” in Q, i.e., the equivalence class in X. Therefore, all conditions with respect to the bounceback rules are included in the kernel of the morphism.. According to the category theory, the kernel can be regarded as a set comprising the preceding object of the morphism u: [29]. Hence, an object denoted by C is placed as shown in Figure 3d, which corresponds physically to the bounceback controller. Here, the sequence is a short exact sequence.
Definition (short exact sequence)
A sequence in the form of
is called a short exact sequence if (image of i corresponds to the kernel of j). In other words, i is a monomorphism and j is an epimorphism, that is, . The zero objects at the left and the right of Equation (6) indicate the reference.
Indeed, diverse possible states of the problem (X) are transferred to certain equivalent rules of the bounceback rule (Q): . For example, although and are different states, they lead to the same bounceback control rules that try to inhibit energy transfer to QDi (where ) according to Equation (1).
The coproduct , denoted by Y in Figure 3c, is introduced on the basis of the representative descriptions combined with the light emission of the system (P) and the bounceback rule (Q) to extract the knowledge for better solutions in subsequent sequences. In other words, the coproduct Y is the object with respect to the state of energy transfer. Here, we pay attention to the morphism . We can naturally introduce the cokernel of v, which is defined as the quotient . According to category theory, the cokernel can also be regarded as a set comprising the subsequent object and morphism [29]. Thus, an object D is placed after as shown in Figure 3d. Physically, the object D corresponds to an optical environmental condition in which all the unobservable environmental conditions for the light emission are included implicitly. For example, suppose that no bounceback rules are active in Q. Hence, no control lights are supplied to inhibit energy transfer. Therefore, the optical environmental conditions allow a variety of energy transfer patterns that could potentially be induced in the QD system. In this manner, we can comprehend the cokernel as implying the potential for growth.
The category theoretic picture shown in Figure 3c indicates that the solution-searching process is to transfer the state of the problem () to the state of energy transfer (). As introduced earlier, we assume a monoidal category; hence, and are isomorphic.
3.2. Short-Exact-Sequence-Based Time
We can naturally assume that the category theoretic diagram shown in Figure 3c indicates the relationships between objects when they have established certain stationary states, i.e., a single process of solution searching is completed. We can then proceed to the next step of solution searching based on the prepared state-filling environment. In order to construct the category theoretic picture, we need to introduce the notion of complex in category theory.
Definition (complex):
A complex is a sequence of objects and morphisms such that for all j, i.e., the nature of the boundary operator or differential operator.
Because of this nature, the object in the complex is injected as the image of the morphism into the kernel of the morphism . Note that the quotient of the kernel of divided by the equivalent class of the image of is referred to as the j-th order homology (or cohomology) of the complex . Namely, .
The remarkable feature is that the homology is irrelevant to the preceding object and is transferred to the subsequent object as the equivalent class of 0 object; that is, the homology represents the local feature added only to the object in the complex . Therefore, a complex describes a sequential evolution of objects with a history of sequential addition of homology. It is useful to introduce the shift or translation of a complex: consisting of with [29]. A physical correspondence of the complex in the quantum-dot-based solution searching is, for example, the evolution of light emission of the system (P): .
A morphism of a complex, , is a set of morphisms that satisfies for all .
Here, one of the most remarkable features known in category theory concerns the chain-wise exact sequence of a complex given by , which comprises short exact sequences, namely, the following sequence holds for all j:
Lemma
(long exact sequence of cohomology: snake lemma)
The chain-wise exact sequence of complexes induces the long exact sequence of cohomology [29,30]:
Figure 4a schematically describes the notion of a long exact sequence of cohomology. Moreover, the existence of the morphism from to is emphasized.
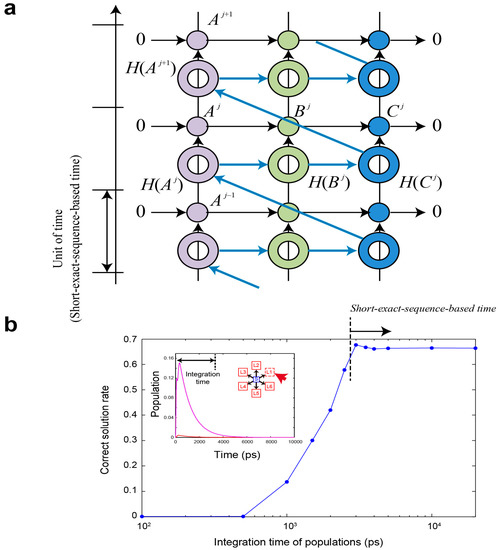
Figure 4.
Short-exact-sequence-based time. (a) schematic diagram of the unit of time based on the satisfaction of short exact sequence; (b) correct-selection rate exhibits poor performances when the integration time of the populations is below approximately 3000 ps; that is, the unit of the short-exact-sequence-based time should be larger than 3000 ps for the particular system under study.
Furthermore, category theory tells us that, within a certain equivalence class of homotopy, one can find a characteristic arrow, also called the translation morphism and lift, , which maintains the long exact sequence of cohomology. That is, the evolution of a chain-wise exact sequence of complexes is described by a triangular structure, [29], as shown schematically in Figure 3e. In other words, we can equate with the history of containing the cohomology of the past. The detailed mathematics behind this can be consulted elsewhere [29,30].
Using the notion of the complex discussed above, we can naturally transform the diagram described in Figure 3d into the diagram of complexes evolving under the bounceback rule updating strategy, as shown in Figure 3f. In this diagram, the updating processes of the bounceback rule controller C and the optical energy transfer environment D have been introduced with the characteristic arrows indicated by wiggly lines. The positions of C, D, and the characteristic arrows are determined on the basis of the commutative relation between and .
Since the step-wise short exact sequences and fulfill certain equilibrium conditions for each solution-searching process, we can derive the composite morphisms and . Accordingly, the category theoretic picture in Figure 3f includes triangular structures given by (marked by T1) and (T2). This diagram coincides naturally with a physical interpretation of the subsequent solution-searching process that is fabricated on the basis of the revised bounceback rule and optical energy transfer status. In addition, by adding composite morphisms and as characteristic arrows, we can find another two triangular structures given by (denoted by T3) and (T4).
The diagrams in Figure 3f give a compact picture of octahedral structure by directly connecting the same complexes at the top and bottom of the diagram with each other, leading to the three-dimensional diagram shown in Figure 5a. This structure corresponds to one of the most important consequences of triangulated category or derived category, called the octahedron axiom [29]. The octahedron consists of four short exact sequences corresponding to the triangulated category and four triangular diagrams as indicated in Figure 3f.
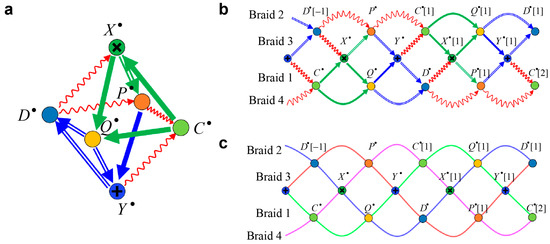
Figure 5.
(a) octahedral structure of solution searching; (b,c) braid structures of the solution searching.
It should be emphasized that all of these triangulated structures require the satisfaction of the chain-wise exact sequence of complexes, as described earlier in Equations (6) and (7). This fact implies that solution searching does not work if the objects are not short exact sequences. In other words, the time for solution searching is defined by way of short exact sequences; here, we would like to propose a new philosophical perception of time, referred to as short-exact-sequence-based time. In the diagram in Figure 4a, the short-exact-sequence-based time is shown by the unit to satisfy a short exact sequence. In other words, it corresponds to the period in which the sequence of a short exact sequence is shifted to the next sequence in the triangular structure.
In fact, the spatiotemporal probability used in the earlier demonstration of CSP uses the time integral of the populations during 20 ns, which is sufficiently long to ensure evident differences depending on induced state-filling effects. Figure 4b represents the correct-solution rate as a function of the integration time of the populations; the system exhibits poor performances if the integration time is smaller than approximately 3000 ps, that is, the short exact sequence does not hold if the operating speed is too high. In other words, the short-exact-sequence-based time should be larger than approximately 3000 ps for this particular problem.
In the case of experimental demonstrations using amoebas conducted by Aono et al. [4], a single step of solution searching was on the scale of minutes, which was sufficiently long to ensure that the amoeba under study responded to the light stimulations. Further discussion on the applications and implications of short-exact-sequence-based time would be an interesting future study.
3.3. Braid Structure of Solution Searching
Here, an important remark concerns the interpretation of the induced long exact sequence of cohomology or the triangular structure of the complex in solution searching. First, it is natural to associate the homology induced in each complex with the local environment. For example, the light emission from each of the quantum dots is determined on the basis of a spontaneous symmetry breaking occurring in each of the quantum dots, which is included in the homology of the optical excitation transfer environment (). In general, descriptions of the intention or preference of the solution searching are represented in homology. This is one of the most important starting points for avoiding deadlocks. In contrast, the short exact sequences, which involve no homology, tightly restrict the evolution of complexes in the triangulated category. Hence, the sequence of cohomology indicates the history of evolution experienced by each object via the triangulated structure; this is one of the most important starting points for the system to arrive at a correct solution.
In the category theoretical context, the octahedral structure is known to be resolvable into two Mayer–Vietoris sequences [29]:
These sequences imply that the structure of the given problem () is decomposed into the light emission () and the bounceback rule () and then transferred to the state of the optical excitation (); namely, solution searching is realized. In terms of the long exact sequence of cohomology, the Mayer–Vietoris sequences decrease the cohomology dimension as the sequence elapses, which will be demonstrated numerically in the solution searching below.
In order to deepen the understanding of the physical and mathematical implications of the solution searching, we have simulated the evolution processes based on the braid structure of the octahedron shown in Figure 5b,c. As a series of solution searching processes, the diagram shown in Figure 5a can be extended by appending shifted diagrams of the octahedral structure as shown in Figure 5b. In particular, the extended diagram in Figure 5b is derived by repeating the diagram in Figure 3f while swapping the positions of and ; consequently, the four short exact sequences are arranged sequentially. Following the category theoretic context, this diagram produces a braid structure [29,31] of the octahedron shown in Figure 5c, which consists of the following four exact sequences as braids:
This braid structure reveals the geometrical structure or interdependence underlying the solution searching based on stochastic spatiotemporal dynamics in a totally simplified manner. The solution searching is regarded as unfolding these braids at the complex by repeating the spatiotemporal dynamic updating processes. Braids 3 and 4 intersect at . To demonstrate this picture numerically, we suppose that these braids have a knot at if the light transmission pattern () is not a correct solution at the cycle j, whereas these braids are unfolded or have no knot if the light transmission pattern is a correct solution at cycle j. As the time elapses, consecutive s are likely to be in the correct solutions, namely the knots are unfolded.
We quantify the length of consecutive unfolded knots (CUKs), which is shown schematically in Figure 6a. Figure 6b summarizes the histogram of the CUKs at the cycles from to every 25 cycles. By definition, the maximum number of CUK cannot be greater than the number of elapsed cycles. Beyond , the histogram characteristics become almost the same, where the maximum CUK is approximately 150. What is particularly noteworthy is the increased occurrence of CUKs near CUK = T when the cycle is in T, which is marked by red rings in Figure 6b. For example, when , the CUK value around 75 occurs more frequently than the shorter CUK value of 64. Similar behavior is observed in , 50, 100, and 125. In other words, the system autonomously seeks longer CUKs as the time elapses. Figure 6c characterizes this tendency from another angle as the time evolutions of the occurrence of some specified length of CUK (25, 50, 75, 100, and 125) are evaluated, where the decrease of shorter CUKs could be viewed as coinciding with the appearance of longer CUKs. This is the verification of the decreasing cohomology dimension in the chain of long exact sequence of cohomology (Equation (8)) owing to Mayer–Vietoris sequences (Equations (9) and (10)) known in category theory.
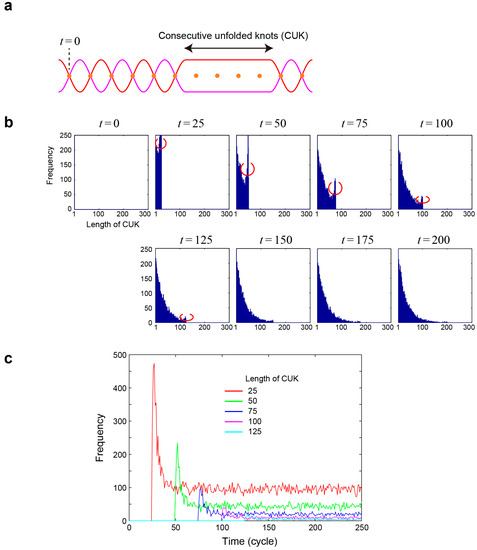
Figure 6.
Solution searching as unfolding of knots of the braids. (a) introduction of the consecutive unfolded knots (CUKs) of the braids; (b,c) evolution of the CUK statistics. Longer-length CUKs emerge as time elapses, which is the manifestation of the decreased homology dimension known in triangulated categories.
4. Conclusions
In conclusion, we presented a category theoretic picture of solution searching based on the stochastic spatiotemporal dynamics of optical excitation transfer, which was originally inspired by amoeba-based computing principles. By introducing category theoretic notions, the underlying mechanism of the solution searching was exactly understood, in which conventional empirical entities were clearly resolved. The short exact sequence gave a solid foundation for the proper operational condition of the solution searching, whereby we introduced a new concept of time called short-exact-sequence-based time. By introducing environmental entities behind the system, we derived octahedral structures known in triangulated categories, in which the four braids interacting with each other. The solution-searching process was viewed as the unfolding of knots of the braids or the decrease of homology dimension. By numerically evaluating the consecutive unfolded knots, the emergence of autonomous solution searching behavior was clearly observed. As described in Section 3.1, the total system has been assumed to form a monoidal category. Owing to this postulate, the category theoretic approach as summarized above is seen to provide significant benefits and critical insights for solution searching based on natural processes or natural intelligence. In our future study, we will try to prove that the entities of the system are indeed monoidal categories.
Acknowledgments
This work was supported in part by the Grant-in-Aid for Challenging Exploratory Research (15K13387), Scientific Research (A) (17H01277), and the Core-to-Core Program, A. Advanced Research Networks from the Japan Society for the Promotion of Science.
Author Contributions
Makoto Naruese, Masashi Aono and Hirokazu Hori directed the project; Makoto Naruese and Masashi Aono designed the system architecture; Makoto Naruese, Masashi Aono and Song-Ju Kim conducted the simulations; Makoto Naruese, Masashi Aono, Song-Ju Kim and Hirokazu Hori designed the physical and mathematical models; Makoto Naruese, Hayato Saigo, Izumi Ojima, Kazuya Okamura and Hirokazu Hori conducted the category theoretic analysis; and Makoto Naruese, Masashi Aono, Izumi Ojima and Hirokazu Hori wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman and Co.: New York, NY, USA, 1979. [Google Scholar]
- Aaronson, S. NP-complete problems and physical reality. SIGACT News 2005, 36, 30–52. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guze, A.; Sifre, L.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; Dieleman, S.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Aono, M.; Hara, M.; Aihara, K. Amoeba-based neurocomputing with chaotic dynamics. Commun. ACM 2007, 50, 69–72. [Google Scholar] [CrossRef]
- Amari, S.; Kasabov, N. Brain-like Computing and Intelligent Information Systems; Springer: Berlin, Germany, 1998. [Google Scholar]
- Pei, R.; Matamoros, E.; Liu, M.; Stefanovic, D.; Stojanovic, M.N. Training a molecular automaton to play a game. Nat. Nanotechnol. 2010, 5, 773–777. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Aono, M.; Nameda, E. Efficient decision-making by volume-conserving physical object. New J. Phys. 2015, 17, 083023. [Google Scholar] [CrossRef]
- Kish, L.B. Noise-based logic: Binary, multi-valued, or fuzzy, with optional superposition of logic states. Phys. Lett. A 2009, 373, 911–918. [Google Scholar] [CrossRef]
- Naruse, M.; Aono, M.; Kim, S.-J.; Kawazoe, T.; Nomura, W.; Hori, H.; Hara, M.; Ohtsu, M. Spatiotemporal dynamics in optical energy transfer on the nanoscale and its application to constraint satisfaction problems. Phys. Rev. B 2012, 86, 125407. [Google Scholar] [CrossRef]
- Aono, M.; Naruse, M.; Kim, S.-J.; Wakabayashi, M.; Hori, H.; Ohtsu, M.; Hara, M. Amoeba-inspired nanoarchitectonic computing: Solving intractable computational problems using nanoscale photoexcitation transfer dynamics. Langmuir 2013, 29, 7557–7564. [Google Scholar] [CrossRef] [PubMed]
- Nakagaki, T.; Yamada, H.; Toth, A. Maze-solving by an amoeboid organism. Nature 2000, 407, 470. [Google Scholar] [CrossRef] [PubMed]
- Aono, M.; Zhu, L.; Hara, M. Amoeba-based neurocomputing for 8-city traveling salesman problem. Int. J. Unconv. Comput. 2011, 7, 463–480. [Google Scholar]
- Kim, S.-J.; Aono, M.; Hara, M. Tug-of-war model for the two-bandit problem: Nonlocally-correlated parallel exploration via resource conservation. BioSystems 2010, 101, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Naruse, M.; Tate, N.; Aono, M.; Ohtsu, M. Information physics fundamentals of nanophotonics. Rep. Prog. Phys. 2013, 76, 056401. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Naruse, M.; Aono, M.; Ohtsu, M.; Hara, M. Decision Maker based on Nanoscale Photo-excitation Transfer. Sci. Rep. 2013, 3, 2370. [Google Scholar] [CrossRef] [PubMed]
- Naruse, M.; Nomura, W.; Aono, M.; Ohtsu, M.; Sonnefraud, Y.; Drezet, A.; Huant, S.; Kim, S.J. Decision making based on optical excitation transfer via near-field interactions between quantum dots. J. Appl. Phys. 2014, 116, 839–862. [Google Scholar] [CrossRef]
- Naruse, M.; Berthel, M.; Drezet, A.; Huant, S.; Aono, M.; Hori, H.; Kim, S.J. Single-photon decision maker. Sci. Rep. 2015, 5, 13253. [Google Scholar] [CrossRef] [PubMed]
- Kasai, S.; Aono, M.; Naruse, M. Amoeba-inspired Computing Architecture Implemented using Charge Dynamics in Parallel Capacitance Network. Appl. Phys. Lett. 2013, 103, 163703. [Google Scholar] [CrossRef]
- Aono, M.; Kasai, S.; Kim, S.-J.; Wakabayashi, M.; Miwa, H.; Naruse, M. Amoeba-inspired nanoarchitectonic computing implemented using electrical Brownian ratchets. Nanotechnology 2015, 26, 234001. [Google Scholar] [CrossRef] [PubMed]
- Mac Lane, S. Categories for the Working Mathematician; Springer: Berlin, Germany, 1971. [Google Scholar]
- Awodey, S. Category Theory; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Naruse, M.; Kim, S.-J.; Aono, M.; Berthel, M.; Drezet, A.; Huant, S.; Hori, H. Category theoretic analysis of single-photon decision maker. arXiv:1602.08199.
- Pistol, C.; Dwyer, C.; Lebeck, A.R. Nanoscale optical computing using resonance energy transfer logic. IEEE Micro 2008, 28, 7–18. [Google Scholar] [CrossRef]
- Algar, W.R.; Kim, H.; Medintz, I.L.; Hildebrandt, N. Emerging non-traditional Förster resonance energy transfer configurations with semiconductor quantum dots: Investigations and applications. Coord. Chem. Rev. 2014, 263, 65–85. [Google Scholar] [CrossRef]
- Ji, J.; He, L.; Shen, Y.; Hu, P.; Li, X.; Jiang, L.P.; Zhang, J.-R.; Li, L.; Zhu, J.J. High-efficient energy funneling based on electrochemiluminescence resonance energy transfer in graded-gap quantum dots bilayers for immunoassay. Anal. Chem. 2014, 86, 3284–3290. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Olaya-Castro, A.; Scholes, G.D. Energy transfer from Förster–Dexter theory to quantum coherent light-harvesting. Int. Rev. Phys. Chem. 2011, 30, 49–77. [Google Scholar] [CrossRef]
- Spivak, D.I. Category Theories for the Sciences; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Iversen, B. Cohomology of Sheaves; Springer: Berlin, Germany, 1986. [Google Scholar]
- Kashiwara, M.; Schapira, P. Categories and Sheaves; Springer: Berlin, Germany, 2006. [Google Scholar]
- Iversen, B. Octahedra and braids. Bull. Soc. Math. Fr. 1986, 114, 197–213. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).