The bounceback rule, which is determined by the given problem, nicely marries with the spatiotemporal and probabilistic attributes of optical excitation transfer and leads to the solution searching as reviewed in the previous section. In this section, we analyze the fundamental mechanism through the notions of category theory.
Category theory is a branch of mathematics that formalizes mathematical structure into collections of objects (denoted by
) and morphisms or arrows (
). Category theory extracts the essence of all mathematical subjects to reveal and formalize extremely simple and yet extremely powerful patterns of thinking, which has revolutionized the field of mathematics [
28]. For each morphism
f, there are given objects
and
called the domain and codomain of
f, respectively. We write
to show that
and
. The complete definition of a category involves the existence of a composition of, for example, morphisms, identity morphisms, and associativities [
20,
21]. In this study, we apply basic notions in category theory to the solution-searching problem in a stepwise manner. In
Section 3.1, we introduce basic notions of the product, coproduct, and short exact sequence. In
Section 3.2, followed by the introduction of complex and homology (cohomology), we propose a notion of
short-exact-sequence-based time as an important figure for proper operation of systems for intended functionality. Indeed, incorrect operations are demonstrated in the solution searching system in
Section 2 when the short-exact-sequence-based time is not stalled properly. Finally, in
Section 3.3, the braid structure known in triangulated categories is introduced by which we can grasp an in-depth understanding of the solution searching demonstrated in
Section 2.
3.1. Product, Coproduct, and Short Exact Sequence
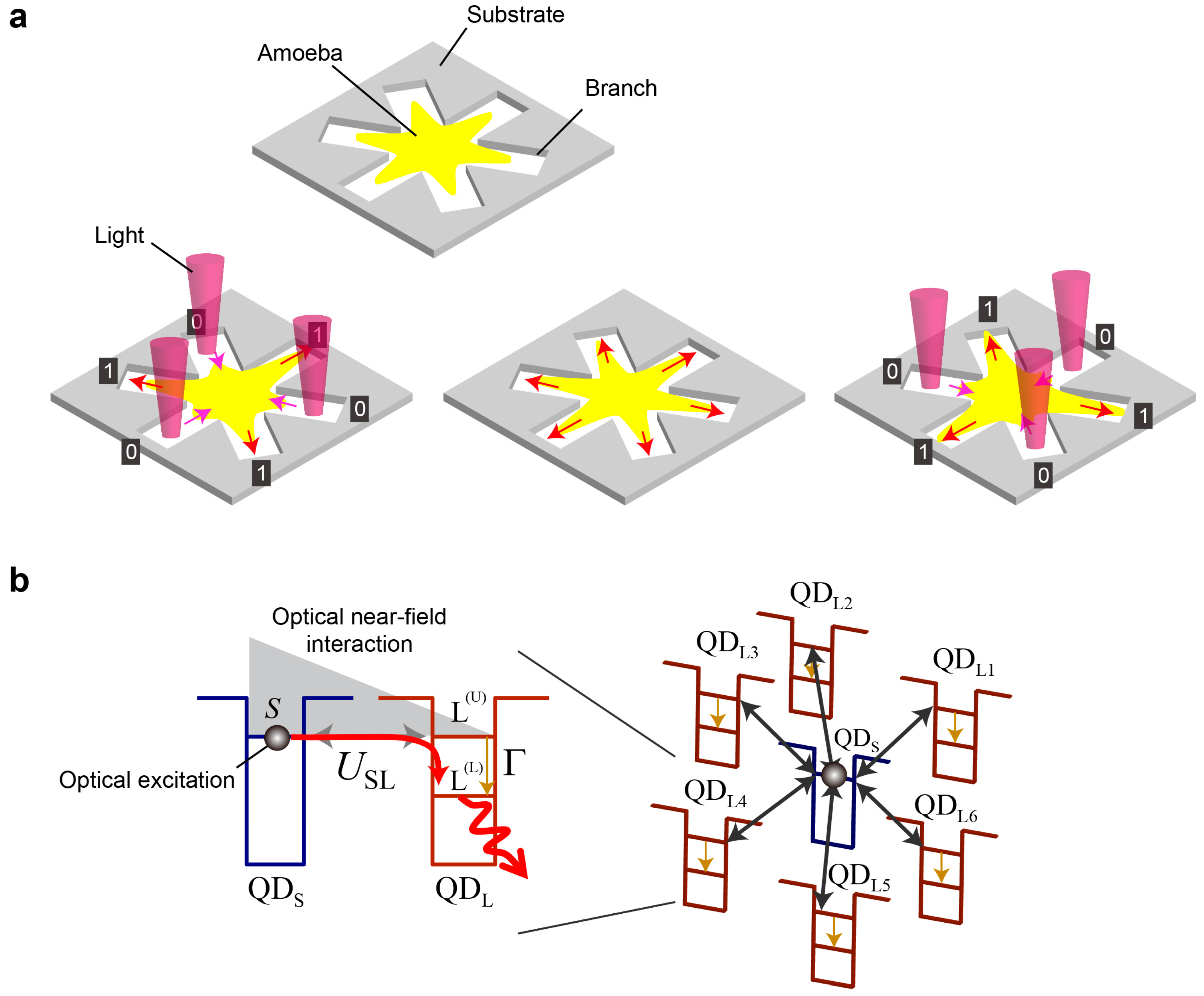
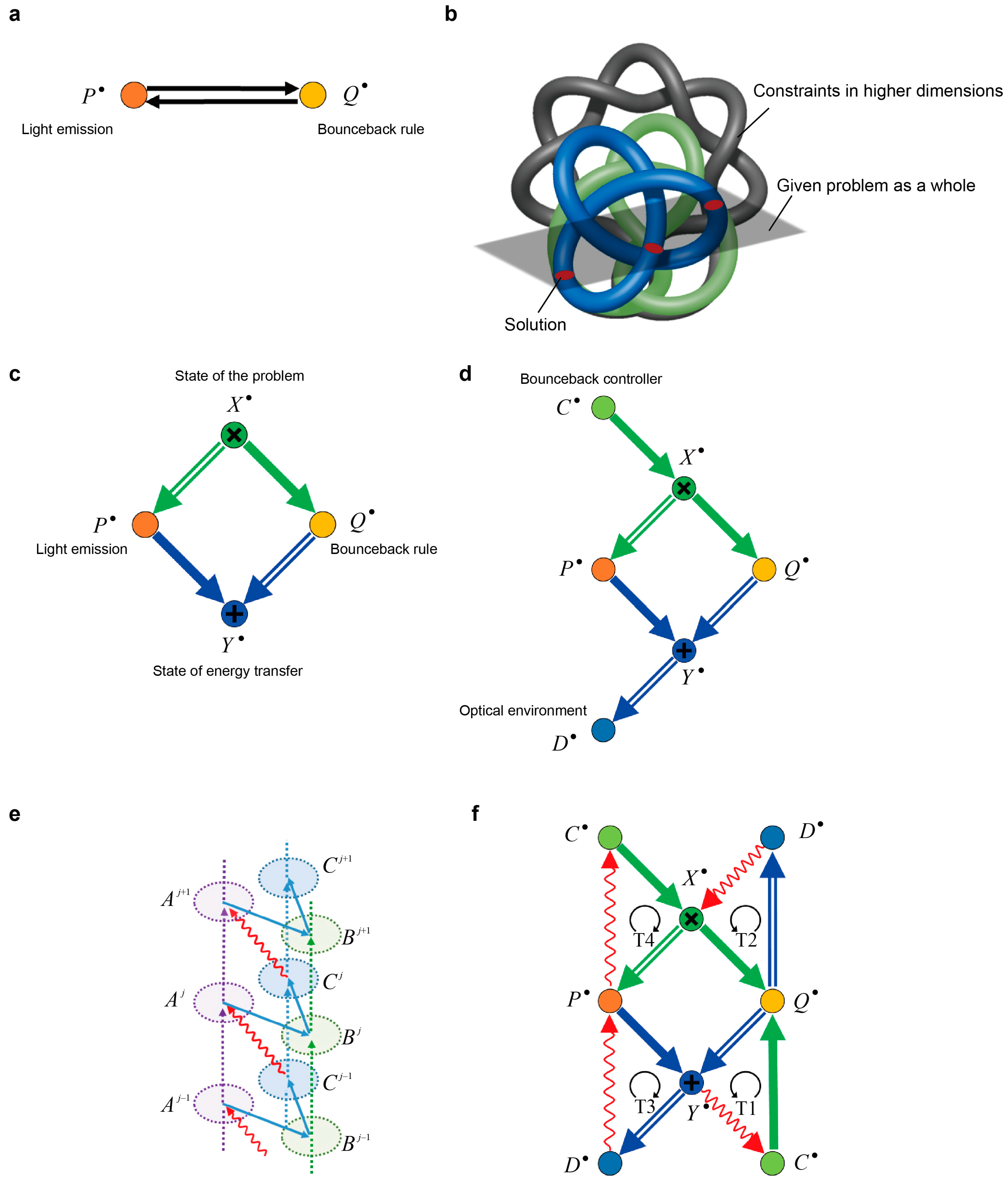
Let the light emission from the surrounding larger dots be denoted by an object
P. In other words, the combination of the variables
is represented by
P. Based on
P, corresponding bounceback rules are activated, which is denoted by another object
Q. We can have a rudimentary picture of a
feedback-type diagram, as shown in
Figure 3a, where
P affects
Q , that is, the combination of the variables
determines the bounceback rule, while
Q affects
P , meaning that the bounceback rule changes the variables
. This picture, however, does not imply any notions associated with energy transfer dynamics, including the fluctuation that is necessary to avoid deadlock.
To give a generic understanding from a concrete example, we consider an
NOR problem of the case
introduced in
Section 2. This
NOR problem is equivalent to solving the following satisfiability problem instance given in a conjunctive normal form:
From this Equation, the given problem is to satisfy all clauses of the right side of Equation (3), each of which behaves as a
constraint of the given problem and spans a high-dimensional space. The given problem as a whole is a cross-sectional profile of this higher-dimensional space, and the solutions are marked by the intersections of constraints, as shown schematically in
Figure 3b. In order to formalize such a hyper-dimensional space behind the system, we first introduce the notions of
product and
coproduct in category theory.
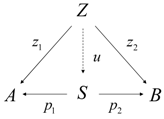
Definition (product and coproduct) In any category, a product diagram for the objects A and B consists of an object S and morphisms satisfying the following. Given any diagram of the form , there exists a unique
, making the diagram
commute, i.e., and . S is written as .
A diagram is a coproduct of A and B, represented by , if for any Z and , there is a unique with and as indicated in We employ the notions of product and coproduct in the original diagram shown in
Figure 3a and obtain the diagram shown in
Figure 3c. Here,
represents the
state of the problem, which is decomposed into the
optical emission from the system (
P) and the
bounceback rule (
Q) to be applied to the system, where all the environmental processes are taken into account. In other words, the total system (
X) is a
composite system comprising
P and
Q. Therefore, we assume that the total system that is under study forms a
monoidal category. Hence, the theorems, lemmas, and axioms of the Abelian category apply to the system.
The morphism from the state of the problem (
X) to the selected bounceback rule (
Q) indicates that some of the rules may
not be concerned, depending on the state of the problem. In other words, all the
unnecessary rules are injected into “0” in
Q, i.e., the equivalence class in
X. Therefore,
all conditions with respect to the bounceback rules are included in the
kernel of the morphism.
. According to the category theory, the kernel can be regarded as a set comprising the preceding object of the morphism
u:
[
29]. Hence, an object denoted by
C is placed as shown in
Figure 3d, which corresponds physically to the
bounceback controller. Here, the sequence
is a short exact sequence.
Definition (short exact sequence) A sequence in the form ofis called a short exact sequence if (image of i corresponds to the kernel of j). In other words, i is a monomorphism and j is an epimorphism, that is, . The zero objects at the left and the right of Equation (6) indicate the reference. Indeed, diverse possible states of the problem (X) are transferred to certain equivalent rules of the bounceback rule (Q): . For example, although and are different states, they lead to the same bounceback control rules that try to inhibit energy transfer to QDi (where ) according to Equation (1).
The coproduct
, denoted by
Y in
Figure 3c, is introduced on the basis of the representative descriptions combined with the light emission of the system (
P) and the bounceback rule (
Q) to extract the knowledge for better solutions in subsequent sequences. In other words, the coproduct
Y is the object with respect to the
state of energy transfer. Here, we pay attention to the morphism
. We can naturally introduce the cokernel of
v, which is defined as the quotient
. According to category theory, the cokernel can also be regarded as a set comprising the subsequent object and morphism [
29]. Thus, an object
D is placed after
as shown in
Figure 3d. Physically, the object
D corresponds to an
optical environmental condition in which all the unobservable environmental conditions for the light emission are included implicitly. For example, suppose that no bounceback rules are active in
Q. Hence, no control lights are supplied to inhibit energy transfer. Therefore, the optical environmental conditions allow a variety of energy transfer patterns that could potentially be induced in the QD system. In this manner, we can comprehend the cokernel as implying the
potential for growth.
The category theoretic picture shown in
Figure 3c indicates that the solution-searching process is to
transfer the state of the problem (
) to the state of energy transfer (
). As introduced earlier, we assume a monoidal category; hence,
and
are isomorphic.
3.2. Short-Exact-Sequence-Based Time
We can naturally assume that the category theoretic diagram shown in
Figure 3c indicates the relationships between objects when they have established certain
stationary states, i.e., a single process of solution searching is completed. We can then proceed to the next step of solution searching based on the prepared state-filling environment. In order to construct the category theoretic picture, we need to introduce the notion of
complex in category theory.
Definition (complex): A complex is a sequence of objects and morphisms such that for all j, i.e., the nature of the boundary operator or differential operator.
Because of this nature, the object in the complex is injected as the image of the morphism into the kernel of the morphism . Note that the quotient of the kernel of divided by the equivalent class of the image of is referred to as the j-th order homology (or cohomology) of the complex . Namely, .
The remarkable feature is that the homology is irrelevant to the preceding object and is transferred to the subsequent object as the equivalent class of 0 object; that is, the homology
represents the
local feature added only to the object
in the complex
. Therefore, a complex describes a sequential evolution of objects with a history of sequential addition of homology. It is useful to introduce the
shift or
translation of a complex:
consisting of
with
[
29]. A physical correspondence of the complex in the quantum-dot-based solution searching is, for example, the evolution of light emission of the system (
P):
.
A morphism of a complex, , is a set of morphisms that satisfies for all .
Here, one of the most remarkable features known in category theory concerns the chain-wise exact sequence of a complex given by
, which comprises short exact sequences, namely, the following sequence holds for all
j:
Lemma (long exact sequence of cohomology: snake lemma)
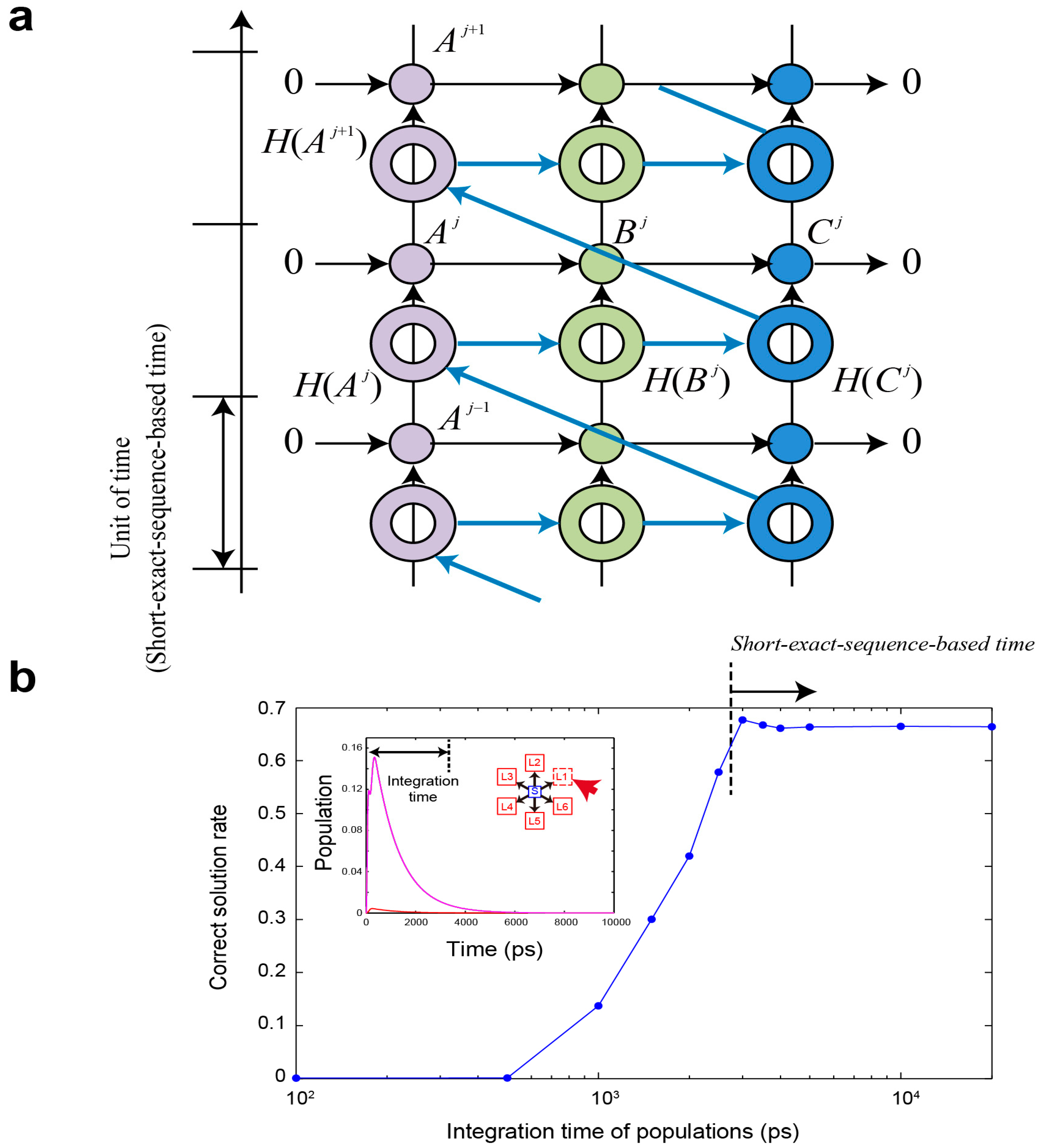
The chain-wise exact sequence of complexes induces the long exact sequence of cohomology [29,30]: Figure 4a schematically describes the notion of a long exact sequence of cohomology. Moreover, the existence of the morphism from
to
is emphasized.
Furthermore, category theory tells us that, within a certain equivalence class of homotopy, one can find a
characteristic arrow, also called the
translation morphism and
lift,
, which maintains the long exact sequence of cohomology. That is, the evolution of a chain-wise exact sequence of complexes is described by a
triangular structure,
[
29], as shown schematically in
Figure 3e. In other words, we can equate
with the history of
containing the cohomology of the past. The detailed mathematics behind this can be consulted elsewhere [
29,
30].
Using the notion of the complex discussed above, we can naturally transform the diagram described in
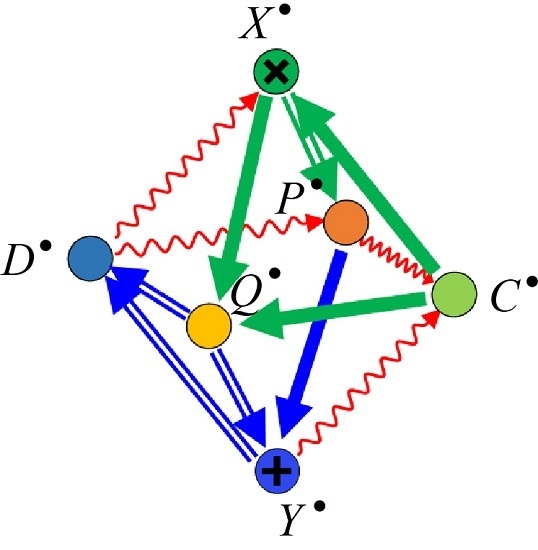
Figure 3d into the diagram of complexes evolving under the bounceback rule updating strategy, as shown in
Figure 3f. In this diagram, the updating processes of the bounceback rule controller
C and the optical energy transfer environment
D have been introduced with the characteristic arrows indicated by wiggly lines. The positions of
C,
D, and the characteristic arrows are determined on the basis of the commutative relation between
and
.
Since the step-wise short exact sequences
and
fulfill certain equilibrium conditions for each solution-searching process, we can derive the composite morphisms
and
. Accordingly, the category theoretic picture in
Figure 3f includes triangular structures given by
(marked by T1) and
(T2). This diagram coincides naturally with a physical interpretation of the subsequent solution-searching process that is fabricated on the basis of the revised bounceback rule and optical energy transfer status. In addition, by adding composite morphisms
and
as characteristic arrows, we can find another two triangular structures given by
(denoted by T3) and
(T4).
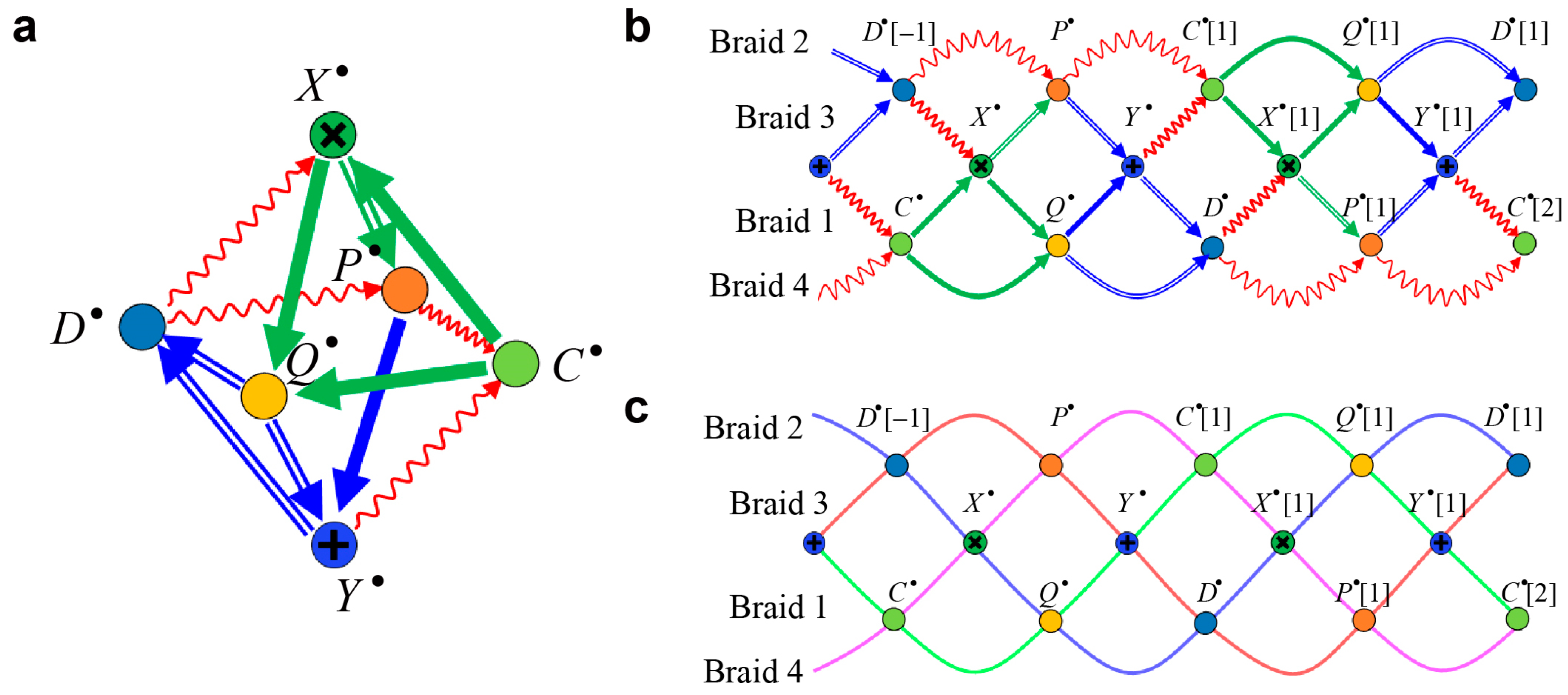
The diagrams in
Figure 3f give a compact picture of
octahedral structure by directly connecting the same complexes at the top and bottom of the diagram with each other, leading to the three-dimensional diagram shown in
Figure 5a. This structure corresponds to one of the most important consequences of
triangulated category or
derived category, called the
octahedron axiom [
29]. The octahedron consists of four short exact sequences corresponding to the triangulated category and four triangular diagrams as indicated in
Figure 3f.
It should be emphasized that all of these triangulated structures require the satisfaction of the chain-wise exact sequence of complexes, as described earlier in Equations (6) and (7). This fact implies that solution searching does
not work if the objects are
not short exact sequences. In other words, the
time for solution searching is defined by way of short exact sequences; here, we would like to propose a new
philosophical perception of time, referred to as
short-exact-sequence-based time. In the diagram in
Figure 4a, the short-exact-sequence-based time is shown by the unit to satisfy a short exact sequence. In other words, it corresponds to the period in which the sequence of a short exact sequence is shifted to the
next sequence in the triangular structure.
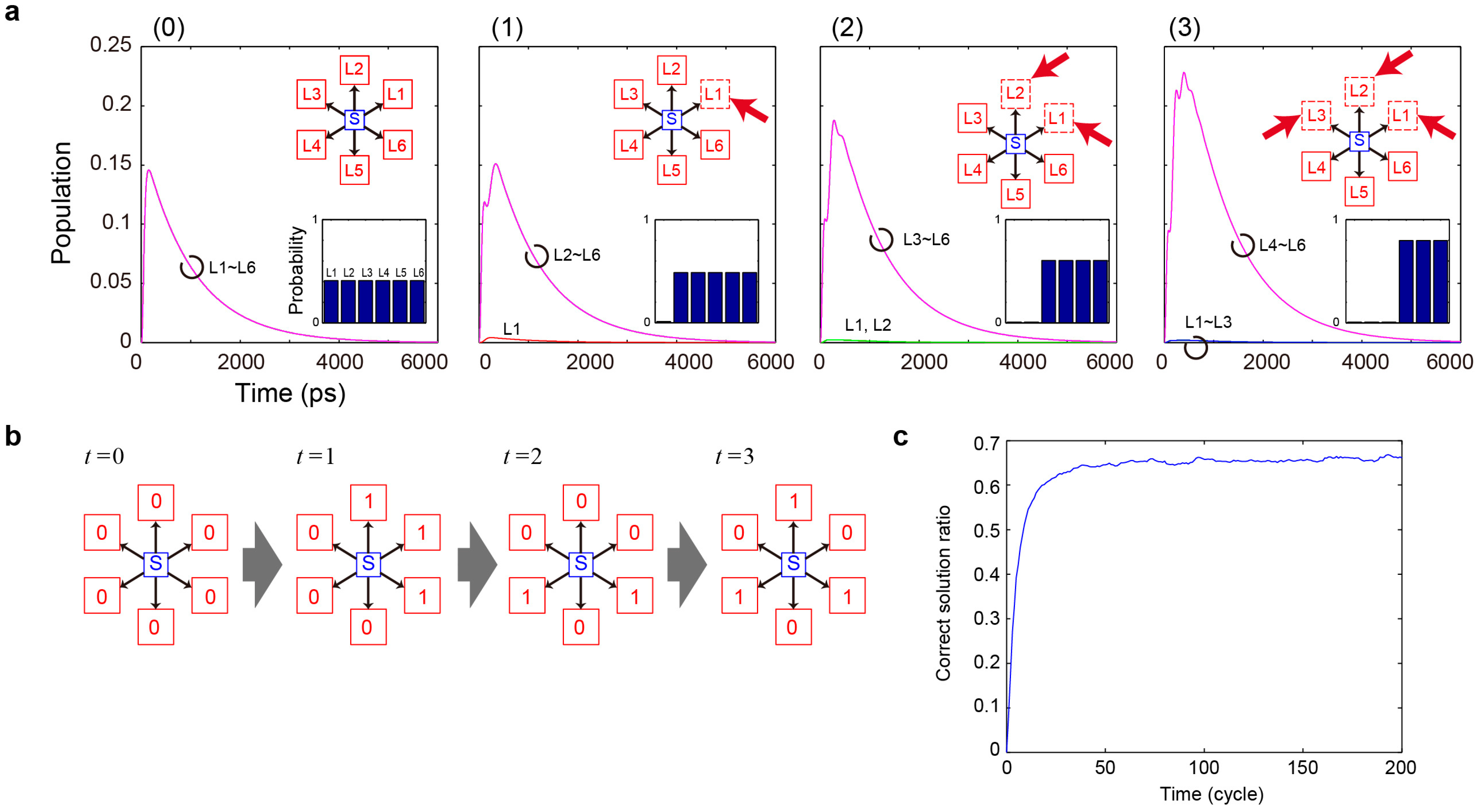
In fact, the spatiotemporal probability used in the earlier demonstration of CSP uses the time integral of the populations during 20 ns, which is
sufficiently long to ensure evident differences depending on induced state-filling effects.
Figure 4b represents the correct-solution rate as a function of the integration time of the populations; the system exhibits poor performances if the integration time is smaller than approximately 3000 ps, that is, the short exact sequence does
not hold if the operating speed is too high. In other words, the short-exact-sequence-based time should be larger than approximately 3000 ps for this particular problem.
In the case of experimental demonstrations using amoebas conducted by Aono et al. [
4], a single step of solution searching was on the scale of minutes, which was sufficiently long to ensure that the amoeba under study responded to the light stimulations. Further discussion on the applications and implications of short-exact-sequence-based time would be an interesting future study.
3.3. Braid Structure of Solution Searching
Here, an important remark concerns the interpretation of the induced long exact sequence of cohomology or the triangular structure of the complex in solution searching. First, it is natural to associate the homology induced in each complex with the local environment. For example, the light emission from each of the quantum dots is determined on the basis of a spontaneous symmetry breaking occurring in each of the quantum dots, which is included in the homology of the optical excitation transfer environment (). In general, descriptions of the intention or preference of the solution searching are represented in homology. This is one of the most important starting points for avoiding deadlocks. In contrast, the short exact sequences, which involve no homology, tightly restrict the evolution of complexes in the triangulated category. Hence, the sequence of cohomology indicates the history of evolution experienced by each object via the triangulated structure; this is one of the most important starting points for the system to arrive at a correct solution.
In the category theoretical context, the octahedral structure is known to be resolvable into two Mayer–Vietoris sequences [
29]:
These sequences imply that the structure of the given problem () is decomposed into the light emission () and the bounceback rule () and then transferred to the state of the optical excitation (); namely, solution searching is realized. In terms of the long exact sequence of cohomology, the Mayer–Vietoris sequences decrease the cohomology dimension as the sequence elapses, which will be demonstrated numerically in the solution searching below.
In order to deepen the understanding of the physical and mathematical implications of the solution searching, we have simulated the evolution processes based on the
braid structure of the octahedron shown in
Figure 5b,c. As a
series of solution searching processes, the diagram shown in
Figure 5a can be extended by appending
shifted diagrams of the octahedral structure as shown in
Figure 5b. In particular, the extended diagram in
Figure 5b is derived by repeating the diagram in
Figure 3f while swapping the positions of
and
; consequently, the four short exact sequences are arranged sequentially. Following the category theoretic context, this diagram produces a
braid structure [
29,
31] of the octahedron shown in
Figure 5c, which consists of the following four exact sequences as braids:
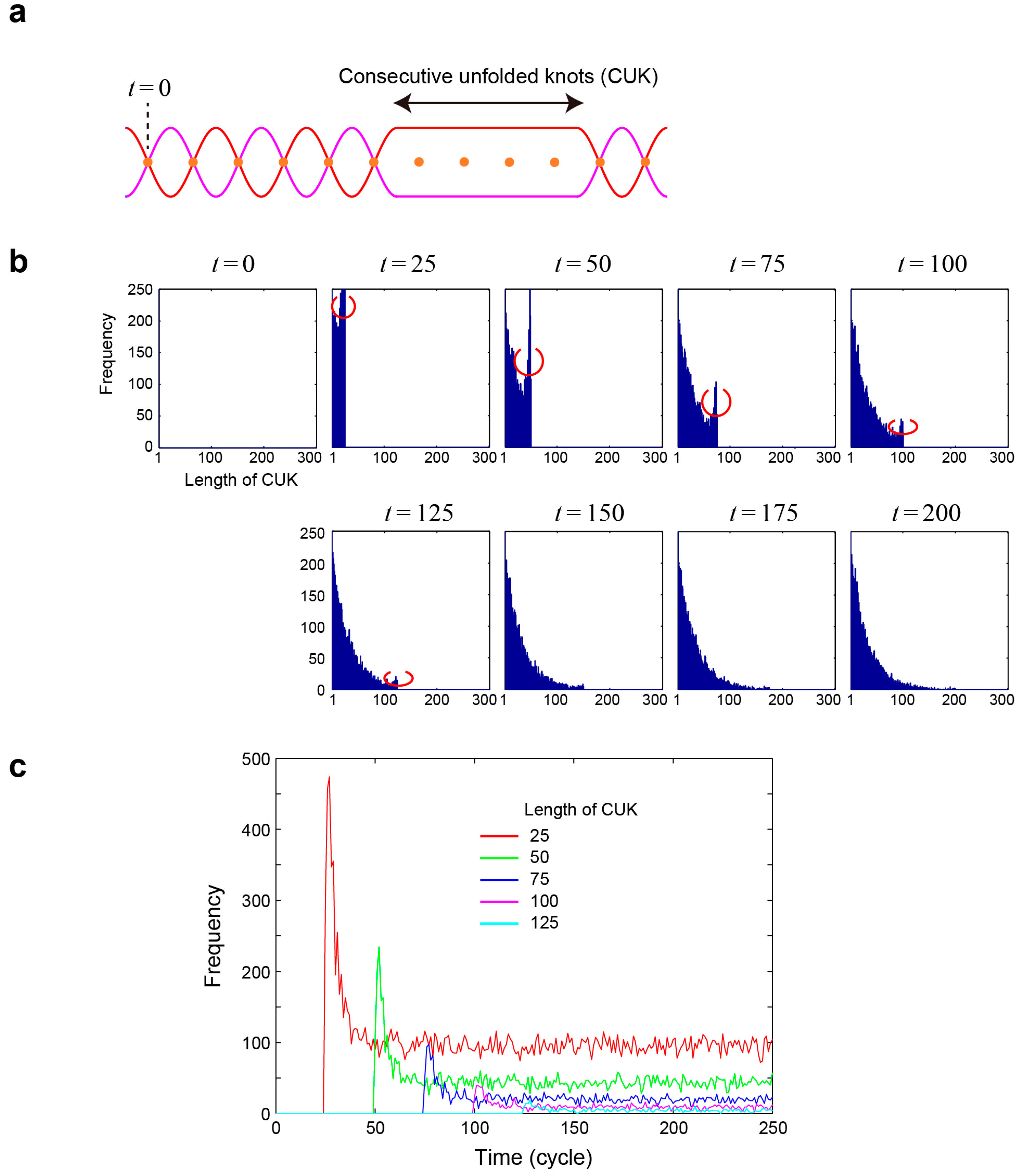
This braid structure reveals the geometrical structure or interdependence underlying the solution searching based on stochastic spatiotemporal dynamics in a totally simplified manner. The solution searching is regarded as unfolding these braids at the complex by repeating the spatiotemporal dynamic updating processes. Braids 3 and 4 intersect at . To demonstrate this picture numerically, we suppose that these braids have a knot at if the light transmission pattern () is not a correct solution at the cycle j, whereas these braids are unfolded or have no knot if the light transmission pattern is a correct solution at cycle j. As the time elapses, consecutive s are likely to be in the correct solutions, namely the knots are unfolded.
We quantify the length of
consecutive unfolded knots (CUKs), which is shown schematically in
Figure 6a.
Figure 6b summarizes the histogram of the CUKs at the cycles from
to
every 25 cycles. By definition, the maximum number of CUK cannot be greater than the number of elapsed cycles. Beyond
, the histogram characteristics become almost the same, where the maximum CUK is approximately 150. What is particularly noteworthy is the increased occurrence of CUKs near CUK =
T when the cycle is in
T, which is marked by red rings in
Figure 6b. For example, when
, the CUK value around 75 occurs more frequently than the shorter CUK value of 64. Similar behavior is observed in
, 50, 100, and 125. In other words, the system
autonomously seeks longer CUKs as the time elapses.
Figure 6c characterizes this tendency from another angle as the time evolutions of the occurrence of some specified length of CUK (25, 50, 75, 100, and 125) are evaluated, where the decrease of shorter CUKs could be viewed as coinciding with the appearance of longer CUKs. This is the verification of the decreasing cohomology dimension in the chain of long exact sequence of cohomology (Equation (8)) owing to Mayer–Vietoris sequences (Equations (9) and (10)) known in category theory.