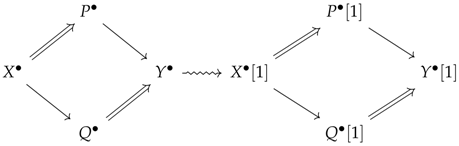1. Introduction
This paper focuses on a new kind of aesthetics, which is made possible by defining the mathematical structure of the aesthetic. By aesthetics, here, we mean various academic approaches to contemplation about the question of how to define the aesthetic, a question about the essence and criteria of what defines the aesthetic sense evoked by nature and the fine arts, as well as aesthetic value [
1].
The term “aesthetics”—originally derived from the Greek “aisthesis” meaning “sensory perception” —took on a new meaning when it was appropriated by the German philosopher Alexander Gottlieb Baumgarten, who redefined the concept to refer to the “lower perception” of senses or sensibility rather than the “high perception” of reason or rationality, and coined the term “aesthetica/Aesthetik”: the science of perception through one’s senses (as opposed to one’s intellect) [
2]. “Aesthetics” prior to that, regardless of whether it was “the science of sensitivity” or “the philosophy of beauty” was studied exclusively based on the correlation between subject and object, and scholars were attempting to describe the aesthetic experience that comprises the aesthetic objectively, as a universal phenomenon. However, such subject = object relations are too simplistic. For example, this approach does not evidently include the aesthetic context (such as history or environment) necessary to recognize or contemplate the aesthetic. As Van Maanen [
3] points out, a great effort has been made to incorporate the background of aesthetic value both within the academic study of aesthetics and outside of it. Therefore, it has become common sense to think about aesthetic value from the perspective of its production and consumption, or the marketplace/group called the “art world” [
4]. However, so far, it has almost always been the case that such a contextualistic background has only been studied from the humanistic approach of semiotics and linguistics (for instance, Alfred Gell’s “Art and Agency: An Anthropological Theory” [
5], or the sociology of fine art, such as T. J. Clark’s “The Conditions of Artistic Creation” [
6]).
Our approach in this research differs from the post-Baumgarten one’s “science of sense”, which mostly focuses on “how humans sense and perceive the aesthetic”, as well as from the approach of analytical aesthetics [
7] formed in the 20th century, which employs the methodology of analytical philosophy. First and foremost, we focus on the structure of how the aesthetic is formed (the ontology of the aesthetic, or what makes the aesthetic aesthetic). With that notion as a fundamental principle, we suggest a new kind of aesthetics established upon mathematics and different from the traditional aesthetics that has been approached as a certain kind of typology that analyses a set of examples in an inductive, and not a deductive, way. By creating a distinct model of aesthetics’ structure through the use of mathematical axioms, we inclusively describe not only the subjects and the objects necessary to provide for the phenomenon of the aesthetic and not only the relation between these subjects and objects, but also the world with their dynamics including human beings and the temporal developments resulting from interactions between various factors. If we could demonstrate that the structure of the aesthetic conforms to the mathematical structure that reflects the context of the aesthetic and the evolution of time, we could describe how it is disclosed and develop structurally from the world including the driving force of aesthetic activities and give birth to a new kind of aesthetics, which is the main objective of this research.
2. Method of Research
In our research, we use mathematics as a language to describe the structure of the aesthetic. There are various fields of mathematics, and to be specific, we are using the contemporary mathematics that has rapidly developed since the beginning of the 20th century, namely topology, homology theory, and category theory. All of these are characterized by mutually connecting algebra and geometry, and because of that, enabling us to operate in an abstract way with objects of interest and their interrelations. In other words, when making an inquiry into a particular object, category theory addresses not the concrete content of that object, but the structure transferred from the nature of its container. By doing that, we make it possible to operate with abstract matters while preserving their structure and with the relationships between these matters. This point is rooted in the mathematical concepts of “homomorphism”, a morphism that retains its structure, and a “quotient group”
1, a quotient set consisting of equivalent classes. The elucidation of functional structures through physical interpretation of category theory has further progressed through the contributions of this paper’s co-authors, Hori and Naruse. By “function”, here, we mean “the emergence of various selectable physical aspects resulting from certain non-trivial processes”, a phenomenon stemming from its relation to the environment system. With this definition in mind, we argue that “intelligence” can be defined as “finding the value in having alternative options and choosing the consequence of function” [
8,
9,
10]. Following these academic works, our research suggests that the aesthetic is a type of function that emerges when the function’s conditions are fulfilled [
11]. In other words, we presume that the aesthetic arises by way of “the emergence of various selectable aesthetic conditions resulting from certain non-trivial processes” and through “the act of finding the value in having these alternative options and the act of aesthetic judgement”, and we further elaborate about the structure of the aesthetic. For this purpose, we consider that the unique world which is a composite of subjects and objects embedded in an environment is undergoing a certain kind of dynamics related to aesthetics.
3. Elementary Process of the Aesthetic
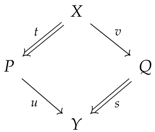
First of all, in addition to the relation Equation (1) between the viewer in traditional aesthetics as the subject
P and the work of art as the object
Q, we introduce the following elements: the “hidden state”
X that enabled such a relation and the image of hidden state
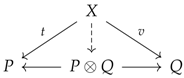
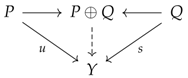
Y. Using the concept of a multiplicative system in category theory, we describe this relation as shown in Equation (2).
The relations of
X to
and of
Y to
correspond to the product Equation (3) and the coproduct Equation (4), respectively. The square-shaped diagram formed by
shown in Equation (2) is called a “commutative diagram” [
12].
There is a variety of options regarding observer P, who possesses an aesthetic mindset, and the aesthetic object or artwork Q, which possesses an aesthetic element(s). Similarly, the choice between representative morphisms t and s (double-lined arrow) is arbitrary and belongs to the multiplicative system of morphisms; i.e., one can describe the process in a different, but equivalent manner based on any set of representative morphisms belonging to the multiplicative system. The morphisms v and u are referred to, respectively, as the right and left quotient morphisms of based on the representatives t and s.
This relationship is ruled by the hidden state X. In other words, X is the overall state of non-trivial aesthetics co-created by the observer and the aesthetic object, which can be understood as an aesthetic concept. Under such circumstances, the relation between observer P and the artwork Q can be inferred from the aesthetic state Y as an image of X.
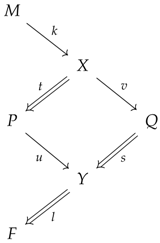
4. Introduction of the Environmental Condition
One of the special characteristics of the aesthetic model proposed in our paper is that in addition to the factors forming the elementary process of the aesthetic, we also introduce the environmental condition surrounding these factors. Here, by “environment”, we mean the diverse social, political, cultural, and technological context of consciously recognizing the aesthetic and sharing aesthetic experience.
First, we introduce as the kernel of , and M here is defined by morphism mapped to zero (equivalent class) by u. M is the generation factor of the aesthetic object Q, and because M in Q is injected into zero and not tangible, we can call M the environment of Q (of the next step). This means that the multifarious works of art Q (e.g., paintings, sculptures, music, and poetry) and their observers P emerge through the aesthetic concept X as an extension of M generating an aesthetic object.
Additionally, we introduce , the cokernel of . The cokernel F here is defined as the quotient space derived from the image of s as seen from the Y codomain of s. In other words, F is the result of the analysis of the aesthetic state and also the result of categorizing the aesthetic state Y created by the elements of the aesthetic object Q where elements Q are employed for such categorization based on s. Since the elements Q with s become the criteria for categorization, they become intangible, and therefore, we can also call this the environment result from Q and s. That is, F is the result of analyzing the aesthetic state Y evoked by aesthetic objects like works of art and nature with each quality and characteristic of the objects Q.
The introduction of these two environmental conditions into diagram Equation (2) can be depicted as Equation (5).
| P | observer |
| Q | aesthetic object |
| X | aesthetic concept |
| Y | aesthetic state |
| M | generation factor of aesthetic object |
| F | analysis results of aesthetic state |
Such sequences of
and
are called short exact sequences. The short exact sequence Equation (6) is the exact sequence where
(image of
i corresponds with the kernel of
j),
i is a monomorphism and
j is an epimorphism
2. In such circumstances,
, or in other words,
C is a cokernel of
B.
A is determined by zero at the left end, which is not
A. The zero at the right end indicates that
A is the reference to categorize
C.
The short exact sequence means that the diverse content of the aesthetic concept X is transferred to the aesthetic (real) object as the “equivalent” and is divided into “equivalence classes” that are included in M (generation factors of the aesthetic object). The factors M, which cannot be categorized directly, are identified based on classification of Q. The identical relation binds Y (an aesthetic state created as a diverse expansion of an aesthetic object) and F (analysis results of aesthetic state categorized by Q).
Moreover, if you interpret the morphism as the appreciation of the aesthetic, the set of morphisms decides how to disclose the relationship between the observer P and the aesthetic object Q (i.e., the “nature of aesthetics”), thereby obtaining an understanding of the dynamics of the aesthetics. At the same time, since the set of morphisms is conformal with the set of morphisms (“commutative diagram”), the relationship between the observer and the aesthetic object in the composite system is disclosed from X based on the “nature of aesthetics”.
5. Introduction of Time
Aesthetics changes and develops not only in the context of the environment conditions, but also dynamically along the time axis (or in other words, as time passes). This is why it is essential that following the introduction of the environment condition, we also introduce time into our model. For that, we use the concept of the complex in homological algebra. Consequently, when you line up the objects one after another, such a chain of objects results in a complex
consisting of objects
mutually connected with a zero homomorphism (
), which in turn can be expressed as an indefinite diagram Equation (7).
Then, “time” is generated from the duration necessary for the short exact sequences Equation (6) to reach equilibrium. The stepwise “histories” of time evolution are recorded in an cohomology of , , where a complex is a container of local features. The diagram of the category that includes this cohomology evidently receives a non-trivial influence from such environmental conditions as society or technology, conditions not limited to the observer and the artwork directly connected to the aesthetic.
In category theory, a complex is also an object, for morphism () is defined by . It is possible to construct a short exact sequence structure in a complex, as well. Therefore, a chain-wise exact sequence of the complex retains the short exact sequence at all degrees, and each of the complexes contains histories and provides the basic diagram that includes generative time structure.
Using the snake lemma in homological algebra, we derive a long exact sequence of cohomology Equation (8) from the chain-wise exact sequence of the complex that is constructed exclusively by homomorphisms [
13].
This allows us to conclude that backed up by diagrams of clear complexes for each chain, the environmental condition (cohomology), a shared fundament supporting the chain of objects, preserves the spatiotemporal chain that includes the invisible non-trivial matters and events. Here, we call the morphism a translation morphism or a characteristic arrow.
6. Triangulated Category and Octahedron Structure
When the arbitrary morphism of category has the image and coimage, and both the image and coimage become isomorphic, we call it the “exact category”. The function of the morphism f of the exact category is—after the relation of the coimage and image have become isomorphic, —to totally annihilate all of the matters prior to that and form the matters that will continue from that point on.
Thus, we make it possible to discuss a chain of matters from the homeomorphic perspective, and if such a chain is a split exact sequence, we can represent a diagram of a long exact sequence of cohomology as a direct conjunction of complexes (Equation (9)) using the homotopy equivalence of category.
When a triangular diagram is constructed in the sense of the derived category, it is called the “triangulated category” [
13]. At this time, by ignoring the future homology of the environment, it is possible to equate
with the history of
containing the cohomology of the past.
The “morphism raising a complex one level higher”:
![Philosophies 02 00014 i015]()
incorporating a wave-shaped arrow is a characteristic morphism (arrow) of the long exact sequence depicted in the diagram Equation (8). The formation of a triangular scheme of complexes is called a triangulated category, and while it changes the “histories”, it is a simple and clear way to represent the evolving, but structure-preserving object(s).
We then replace the object of the commutative diagram Equation (5) with the complex, and expand it using this triangulated category. First, if we add the result of the analysis of the aesthetic state
from the previous step interconnected with translation morphisms and
, the generation factor of the aesthetic object from the later step, we get the relation expressed in the diagram Equation (10).
Moreover, by supplementing the model with morphism
,
, which leads to nature, and characteristic arrow
,
, we get the diagrams Equations (11) and (12).
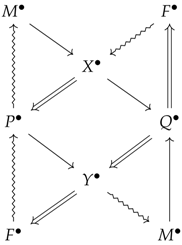
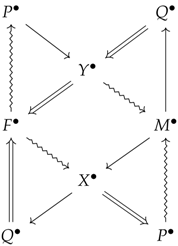
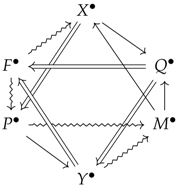
If you overlay
and
, which belong to different strata with different environments, as a result, you get an octahedron consisting of one commutative diagram and four triangulated categories Equation (13).
| observer |
| aesthetic object |
| aesthetic concept |
| aesthetic state |
| generation factor of aesthetic object |
| analysis result of aesthetic state |
7. Aesthetic Activity and Time Evolution
This octahedron corresponds to one of the important consequences of the derived category called an “octahedron axiom”. If we look more closely at these four triangulated categories, they correspond, respectively, to “aesthetic contemplation”, “artwork criticism”, “artwork production”, and “aesthetic experience”, with each of these being part of aesthetic activity as elements of the formation aesthetics, which are mutually connected and shape a mathematical model that progresses over time.
Aesthetic contemplation
generation factor of aesthetic object → aesthetic concept → observer → generation factor of aesthetic object [1]
Artwork criticism
aesthetic concept → aesthetic object → analysis result of aesthetic state → aesthetic concept [1]
Artwork production
generation factor of aesthetic object → aesthetic object → aesthetic state → generation factor of aesthetic object [1]
Aesthetic experience
observer → aesthetic state → analysis result of aesthetic state → observer [1]
By describing relations of aesthetic activities through these four exact sequences shown in
Table 1, the mutual connection of the objects (complexes) through the braid structure of the octahedron [
13,
14] becomes evident.
Finally, we go back to the elementary process of the aesthetic Equation (2) at the beginning again. Assuming that
is a simple sum of two objects,
has the meaning of factor
X, various phenomena
expanded from
X and
Y that categorized by
X, just like a short exact sequence. Furthermore, referring to
introduced as the environmental condition Equation (5), the set
of the environmental conditions—which is all except for those surrounded by the commutative diagram—supports the structure of time evolution of the elementary process of the aesthetic. In that process,
captures the singularity as the aesthetic of the environmental condition step by step, and acquires its non-trivial history. Each time, it acquires the singularity, the dimension of cohomology increases (the dimension of homology decreases), then its structure becomes simpler. This is one expression of Mayer–Vietoris sequences [
15]. It shows that an unknown aesthetic concept
X is gradually elucidated by specifying its nature according to the aesthetic state
Y generated by the aesthetic object
Q and observer
P (Equation (14)).
8. Conclusions
Mathematician Saunders MacLane has stated in his work “Categories for the Working Mathematician” (a textbook in category theory that is regarded as the premier and classic authority on the subject) [
12]: “A category (distinguished from a metacategory) will mean any interpretation of the category axioms within set theory”. This paper extends this statement and attempts the interpretation of category axioms into aesthetics.
Mathematician Andr Weil analyzed the data about kinship relations in primitive society collected and organized by anthropologist Claude L vi-Strauss and concluded that there is a mathematical structure of “group” evidently present in those relations [
16]. This achievement points at the possibility and usefulness of applying a mathematical approach to humanities studies such as anthropology. Our research takes such prior works into account and points out that the derived category in category theory and octahedron category (which is the mathematical structure that describes the way “it has to be”) might be the base of the structure of the aesthetic—an essential activity for human beings.
There has been a number of attempts to apply mathematics or science to aesthetics from various perspectives. Older works and topics include “aesthetics measure” by George David Birkhoff [
17], “information aesthetics” by Abraham Moles [
18] Frieder Nake [
19], Max Bense [
20] and Hiroshi Kawano [
21] and the “algorithmic theory of beauty” by J rgen Schmidhubern [
22]. Among more recent developments, we can name, for instance, “neuroaesthetics”, which discusses the process of beauty representation inside the human brain [
23,
24].
What remains different between prior works and our research is the core purpose. The former attempts to apply methods and knowledge of mathematics and other sciences, such as information theory or semiotics to “measuring” beauty and materializing this process, while our approach focuses on describing the structure (function) of the aesthetic with axioms; in other words, on expressing the structure of the aesthetic with mathematical structure itself. As mentioned in the beginning of this paper, the purpose of our research is to describe generative aesthetics, which dynamically changes as the result of interaction with the environment by employing mathematical axioms that express the structure of the aesthetic, and to execute an interdisciplinary investigation based on this notion. As Arthur Danto points out in his research [
4,
25], the value and meaning of the aesthetic is not the universal and unchanging “nature” of the phenomenon, but something relative to and depending on the context of its environment: certain time periods, ethnic groups, society, or culture. Therefore, it seems essential to describe the structure of the aesthetic axiomatically, in its true state of being generated together with its environment, and express through axioms this mechanism generated by the dynamism of aesthetic contemplation, artwork criticism, artwork production, and aesthetic experience, all of these forming “the aesthetics”, which is exactly what our model aims to achieve. As a result, we offer a new model of aesthetics called axiomatic functionalism.

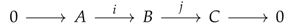
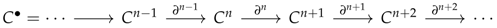
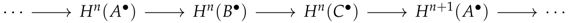
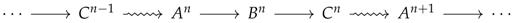
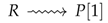 incorporating a wave-shaped arrow is a characteristic morphism (arrow) of the long exact sequence depicted in the diagram Equation (8). The formation of a triangular scheme of complexes is called a triangulated category, and while it changes the “histories”, it is a simple and clear way to represent the evolving, but structure-preserving object(s).
incorporating a wave-shaped arrow is a characteristic morphism (arrow) of the long exact sequence depicted in the diagram Equation (8). The formation of a triangular scheme of complexes is called a triangulated category, and while it changes the “histories”, it is a simple and clear way to represent the evolving, but structure-preserving object(s).