Harnessing the Computational Power of Fluids for Optimization of Collective Decision Making
Abstract
:1. Introduction
1.1. Competitive Multi-Armed Bandit Problem (CBP)
1.2. TOW Dynamics
1.3. The TOW Bombe
2. Results for CBP
3. Results for the Extended Prisoner’s Dilemma Game
- A: keep silent;
- B: confess (implicate him- or herself);
- C: implicate the next person (circulative as 1,2,3,1,2,3,⋯);
- D: implicate the third person (circulative as 1,2,3,1,2,3,⋯);
- E: implicate both of the others.
- the set of reward probabilities for the charges is (, , );
- the → (, , );
- the or or → (R, R, R): the social maximum;
- the → (P,P,P): the Nash equilibrium.
4. Conclusions
5. Discussion
Methods
The Weighting Parameter ω
TOW Dynamics for General BP
Generating Methods of Fluctuations
Internal Fixed Fluctuations
Internal Random Fluctuations
- r is a random value from . We call this “seed”.
- There are () possibilities for a seed position. Choose the seed position (, ) randomly from = and = and place the seed r at the point,
- All elements of the th column other than (, ) are substituted with .
- All elements of the -th row other than (, ) are substituted with .
- All remaining elements are substituted with .
- The matrix sheet is summed up in a summation matrix .
- Repeat from two to six for D times. Here, D is a parameter.
Internal M-Random Fluctuations (Exponential)
- For each player i, independent random value is generated from . We call these “seeds”.
- There are () possibilities for a seed position pattern. For each player i, choose the seed position (i, ) randomly from = and place the seed at the pointHowever, we choose s to be distinct. Therefore, there are really (=60) possibilities.
- For each i, all elements of the -th column other than (i, ) are substituted with .
- All remaining elements of the 1th row are substituted with .
- All remaining elements of the 2th row are substituted with .
- All remaining elements of the 3th row are substituted with .
- The matrix sheet is summed up in a summation matrix .
- Repeat from two to seven for D times. Here, D is a parameter.
External Oscillations
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mesquita BBDe. The Predictioneer’s Game; Random House Inc.: New York, NY, USA, 2009. [Google Scholar]
- Narendra, K.S.; Member, S.; Thathachar, M.A.L. Learning automata—A survey. IEEE Trans. Syst. Man Cybern. 1974, SMC-4, 323–334. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K. The Theory of Learning in Games; The MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Marden, J.R.; Young, H.P.; Arslan, G.; Shamma, J. Payoff based dynamics for multiplayer weakly acyclic games. SIAM J. Control Optim. 2009, 48, 373–396. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1936, 42, 230–265. [Google Scholar]
- Turing, A.M. Computability and λ-definability. J. Symb. Log. 1937, 2, 153–163. [Google Scholar] [CrossRef]
- Moore, C. A complex legacy. Nat. Phys. 2011, 7, 828–830. [Google Scholar] [CrossRef]
- Feynman, R.P. Feynman Lectures on Computation; Perseus Books: New York, NY, USA, 1996. [Google Scholar]
- Roughgarden, T. Selfish Routing and the Price of Anarchy; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V.V. Algorithmic Game Theory; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Kim, S.-J.; Aono, M.; Hara, M. Tug-of-war model for multi-armed bandit problem. In Unconventional Computation; LNCS 6079; Calude, C.S., Hagiya, M., Morita, K., Rozenberg, G., Timmis, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 69–80. [Google Scholar]
- Kim, S.-J.; Aono, M.; Hara, M. Tug-of-war model for two-bandit problem: Nonlocally correlated parallel exploration via resource conservation. BioSystems 2010, 101, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Aono, M. Amoeba-inspired algorithm for cognitive medium access. NOLTA 2014, 5, 198–209. [Google Scholar] [CrossRef]
- Kim, S.-J.; Aono, M.; Nameda, E. Efficient decision-making by volume-conserving physical object. New J. Phys. 2015, 17, 083023. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Kocsis, L.; Szepesvári, C. Bandit based monte-carlo planning. In Proceedings of the 17th European Conference on Machine Learning, Berlin, Germany, 18–22 September 2006; LNAI 4212. Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–293. [Google Scholar]
- Gelly, S.; Wang, Y.; Munos, R.; Teytaud, O. Modification of UCT with Patterns in Monte-Carlo Go. (Research Report) RR-6062. 2006, pp. 1–19. Available online: https://hal.inria.fr/inria-00117266/document (accessed on 6 December 2016).
- Lai, L.; Jiang, H.; Poor, H.V. Medium access in cognitive radio networks: A competitive multi-armed bandit framework. In Proceedings of the IEEE 42nd Asilomar Conference on Signals, System and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 98–102.
- Lai, L.; Gamal, H.E.; Jiang, H.; Poor, H.V. Cognitive medium access: Exploration, exploitation, and competition. IEEE Trans. Mob. Comput. 2011, 10, 239–253. [Google Scholar]
- Agarwal, D.; Chen, B.-C.; Elango, P. Explore/exploit schemes for web content optimization. In Proceedings of the Ninth IEEE International Conference on Data Mining, Miami, FL, USA, 6–9 December 2009.
- Davies, D. The Bombe—A remarkable logic machine. Cryptologia 1999, 23, 108–138. [Google Scholar] [CrossRef]
- Kim, S.-J.; Aono, M. Decision maker using coupled incompressible-fluid cylinders. Adv. Sci. Technol. Environmentol. 2015, B11, 41–45. [Google Scholar]
- Helbing, D.; Yu, W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc. Natl. Acad. Sci. USA 2009, 106, 3680–3685. [Google Scholar] [CrossRef] [PubMed]
- Arrow, K.J. A difficulty in the concept of social welfare. J. Political Econ. 1950, 58, 328–346. [Google Scholar] [CrossRef]
- Kim, S.-J.; Naruse, M.; Aono, M.; Ohtsu, M.; Hara, M. Decision maker based on nanoscale photo-excitation transfer. Sci. Rep. 2013, 3, 2370. [Google Scholar] [CrossRef] [PubMed]
- Naruse, M.; Nomura, W.; Aono, M.; Ohtsu, M.; Sonnefraud, Y.; Drezet, A.; Huant, S.; Kim, S.-J. Decision making based on optical excitation transfer via near-field interactions between quantum dots. J. Appl. Phys. 2014, 116, 154303. [Google Scholar] [CrossRef]
- Naruse, M.; Berthel, M.; Drezet, A.; Huant, S.; Aono, M.; Hori, H.; Kim, S.-J. Single photon decision maker. Sci. Rep. 2015, 5, 13253. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Tsuruoka, T.; Hasegawa, T.; Aono, M.; Terabe, K.; Aono, M. Decision maker based on atomic switches. AIMS Mater. Sci. 2016, 3, 245–259. [Google Scholar] [CrossRef]
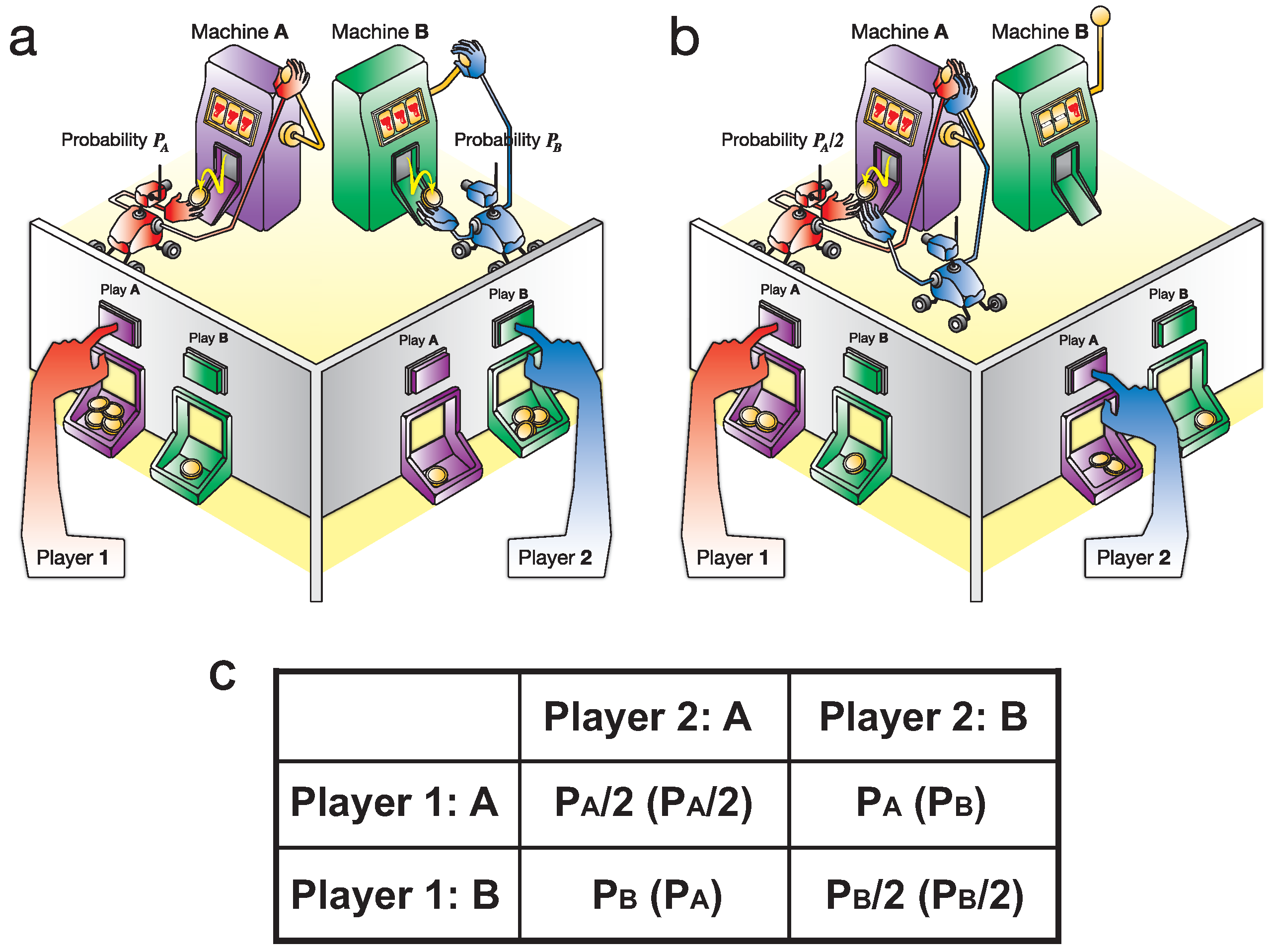
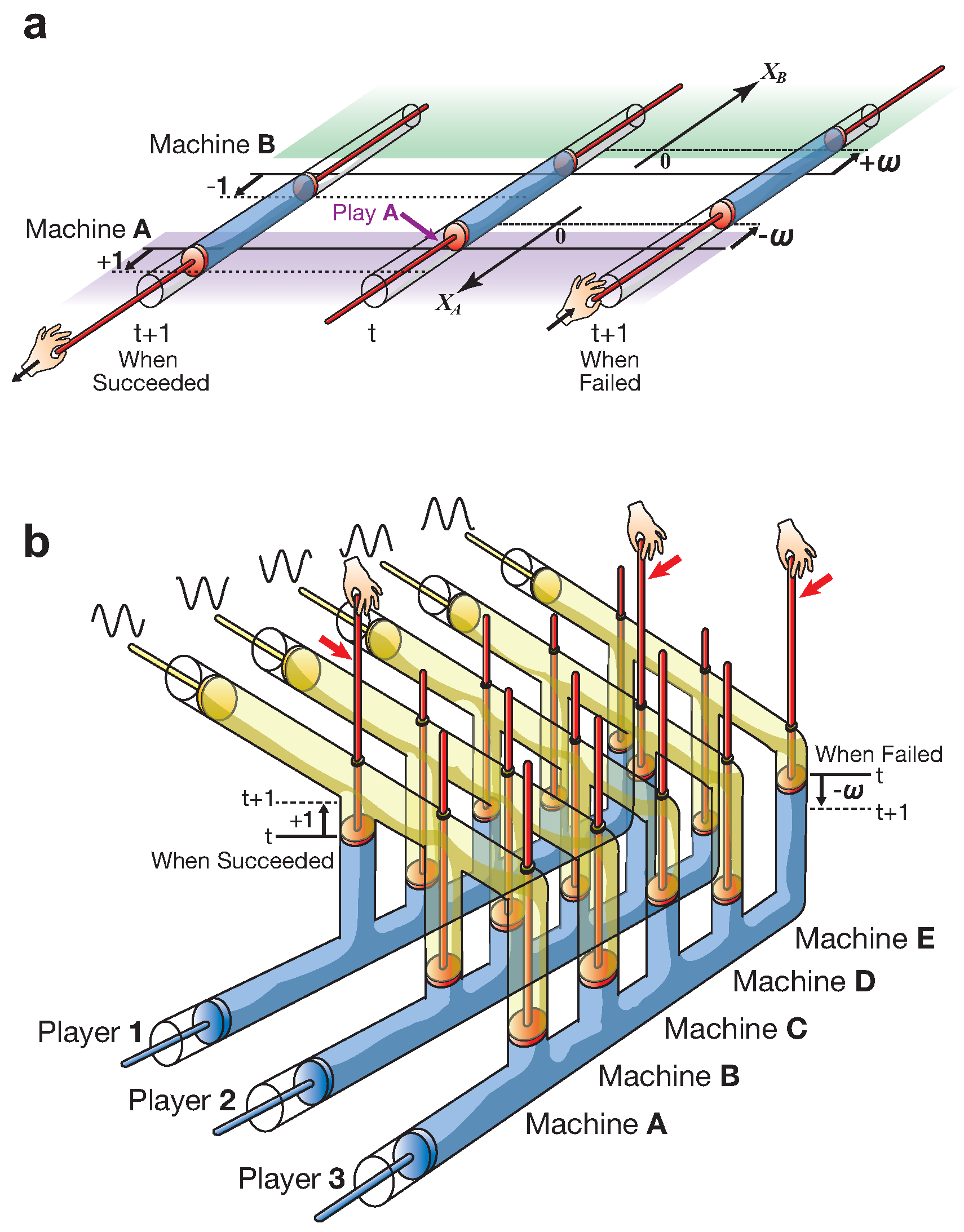
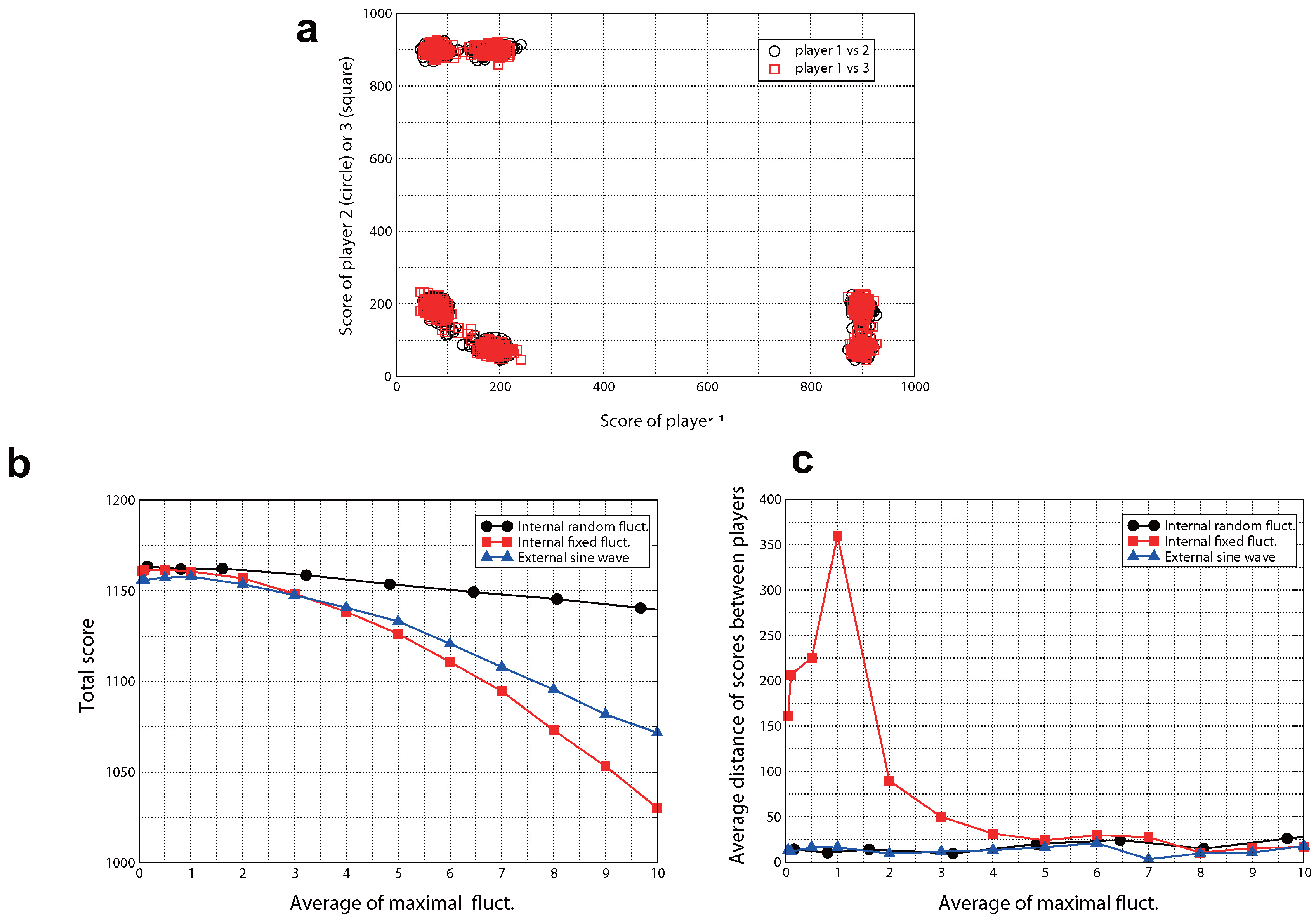
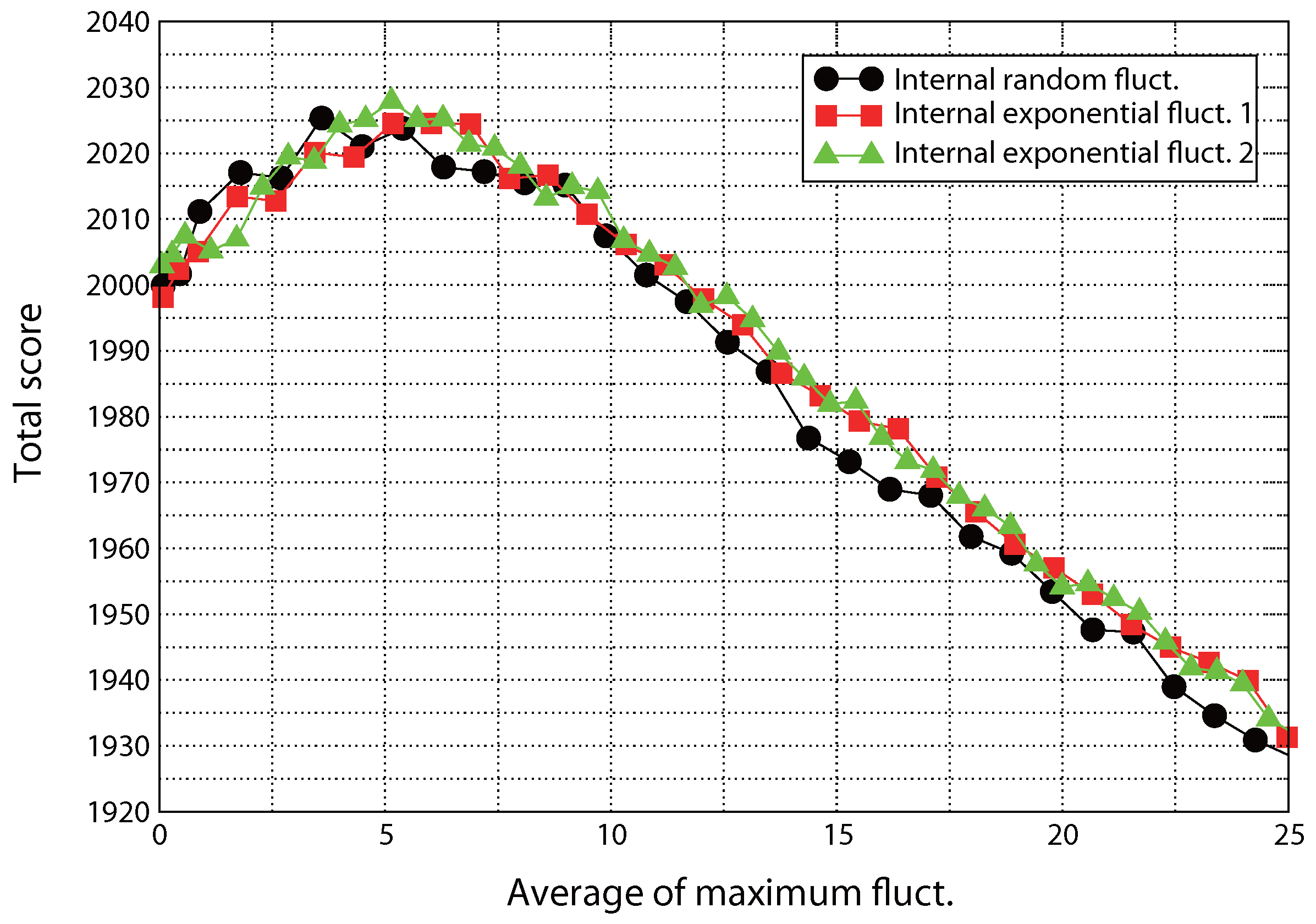
| Player 2: C | Player 2: D | Player 2: E | |
|---|---|---|---|
| player 1: C | , , | , , | , , |
| player 1: D | , , | , , | , , SM |
| player 1: E | , , | , , SM | , , |
| Player 2: C | Player 2: D | Player 2: E | |
|---|---|---|---|
| player 1: C | , , | , , | , , SM |
| player 1: D | , , | , , | , , |
| player 1: E | , , SM | , , | , , |
| Player 2: C | Player 2: D | Player 2: E | |
|---|---|---|---|
| player 1: C | , , | , , SM | , , |
| player 1: D | , , SM | , , | , , |
| player 1: E | , , | , , | , , NE |
| Selection Pattern | Degree of Charges | Probability |
|---|---|---|
| ( A, A, A ) | ( 0, 0, 0 ) | 0.55 0.55 0.55 |
| ( A, A, B ) | ( 0, 0, 1 ) | 0.73 0.73 0.40 |
| ( A, A, C ) | ( 1, 0, 0 ) | 0.40 0.73 0.73 |
| ( A, A, D ) | ( 0, 1, 0 ) | 0.73 0.40 0.73 |
| ( A, A, E ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( A, B, A ) | ( 0, 1, 0 ) | 0.73 0.40 0.73 |
| ( A, B, B ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( A, B, C ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( A, B, D ) | ( 0, 2, 0 ) | 0.76 0.30 0.76 |
| ( A, B, E ) | ( 1, 2, 0 ) | 0.73 0.30 0.76 |
| ( A, C, A ) | ( 0, 0, 1 ) | 0.73 0.73 0.40 |
| ( A, C, B ) | ( 0, 0, 2 ) | 0.76 0.76 0.30 |
| ( A, C, C ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( A, C, D ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( A, C, E ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( A, D, A ) | ( 1, 0, 0 ) | 0.40 0.73 0.73 |
| ( A, D, B ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( A, D, C ) | ( 2, 0, 0 ) | 0.30 0.76 0.76 |
| ( A, D, D ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( A, D, E ) | ( 2, 1, 0 ) | 0.30 0.73 0.76 |
| ( A, E, A ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( A, E, B ) | ( 1, 0, 2 ) | 0.73 0.76 0.30 |
| ( A, E, C ) | ( 2, 0, 1 ) | 0.30 0.76 0.73 |
| ( A, E, D ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( A, E, E ) | ( 2, 1, 1 ) | 0.70 0.70 0.70 |
| ( B, A, A ) | ( 1, 0, 0 ) | 0.40 0.73 0.73 |
| ( B, A, B ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( B, A, C ) | ( 2, 0, 0 ) | 0.30 0.76 0.76 |
| ( B, A, D ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( B, A, E ) | ( 2, 1, 0 ) | 0.30 0.73 0.76 |
| ( B, B, A ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( B, B, B ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( B, B, C ) | ( 2, 1, 0 ) | 0.30 0.73 0.76 |
| ( B, B, D ) | ( 1, 2, 0 ) | 0.73 0.30 0.76 |
| ( B, B, E ) | ( 2, 2, 0 ) | 0.30 0.30 0.76 |
| ( B, C, A ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( B, C, B ) | ( 1, 0, 2 ) | 0.73 0.76 0.30 |
| ( B, C, C ) | ( 2, 0, 1 ) | 0.30 0.76 0.73 |
| ( B, C, D ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( B, C, E ) | ( 2, 1, 1 ) | 0.70 0.70 0.70 |
| ( B, D, A ) | ( 2, 0, 0 ) | 0.30 0.76 0.76 |
| ( B, D, B ) | ( 2, 0, 1 ) | 0.30 0.76 0.73 |
| ( B, D, C ) | ( 3, 0, 0 ) | 0.20 0.79 0.79 |
| ( B, D, D ) | ( 2, 1, 0 ) | 0.30 0.73 0.76 |
| ( B, D, E ) | ( 3, 1, 0 ) | 0.20 0.76 0.79 |
| ( B, E, A ) | ( 2, 0, 1 ) | 0.30 0.76 0.73 |
| ( B, E, B ) | ( 2, 0, 2 ) | 0.30 0.76 0.30 |
| ( B, E, C ) | ( 3, 0, 1 ) | 0.20 0.79 0.76 |
| ( B, E, D ) | ( 2, 1, 1 ) | 0.70 0.70 0.70 |
| ( B, E, E ) | ( 3, 1, 1 ) | 0.30 0.76 0.76 |
| ( C, A, A ) | ( 0, 1, 0 ) | 0.73 0.40 0.73 |
| ( C, A, B ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( C, A, C ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( C, A, D ) | ( 0, 2, 0 ) | 0.76 0.30 0.76 |
| ( C, A, E ) | ( 1, 2, 0 ) | 0.73 0.30 0.76 |
| ( C, B, A ) | ( 0, 2, 0 ) | 0.76 0.30 0.76 |
| ( C, B, B ) | ( 0, 2, 1 ) | 0.76 0.30 0.73 |
| ( C, B, C ) | ( 1, 2, 0 ) | 0.73 0.30 0.76 |
| ( C, B, D ) | ( 0, 3, 0 ) | 0.79 0.20 0.79 |
| ( C, B, E ) | ( 1, 3, 0 ) | 0.76 0.20 0.79 |
| ( C, C, A ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( C, C, B ) | ( 0, 1, 2 ) | 0.76 0.73 0.30 |
| ( C, C, C ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( C, C, D ) | ( 0, 2, 1 ) | 0.76 0.30 0.73 |
| ( C, C, E ) | ( 1, 2, 1 ) | 0.70 0.70 0.70 |
| ( C, D, A ) | ( 1, 1, 0 ) | 0.40 0.40 0.73 |
| ( C, D, B ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( C, D, C ) | ( 2, 1, 0 ) | 0.30 0.73 0.76 |
| ( C, D, D ) | ( 1, 2, 0 ) | 0.73 0.30 0.76 |
| ( C, D, E ) | ( 2, 2, 0 ) | 0.30 0.30 0.76 |
| ( C, E, A ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( C, E, B ) | ( 1, 1, 2 ) | 0.70 0.70 0.70 |
| ( C, E, C ) | ( 2, 1, 1 ) | 0.70 0.70 0.70 |
| ( C, E, D ) | ( 1, 2, 1 ) | 0.70 0.70 0.70 |
| ( C, E, E ) | ( 2, 2, 1 ) | 0.40 0.40 0.73 |
| ( D, A, A ) | ( 0, 0, 1 ) | 0.73 0.73 0.40 |
| ( D, A, B ) | ( 0, 0, 2 ) | 0.76 0.76 0.30 |
| ( D, A, C ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( D, A, D ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( D, A, E ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( D, B, A ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( D, B, B ) | ( 0, 1, 2 ) | 0.76 0.73 0.30 |
| ( D, B, C ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( D, B, D ) | ( 0, 2, 1 ) | 0.76 0.30 0.73 |
| ( D, B, E ) | ( 1, 2, 1 ) | 0.70 0.70 0.70 |
| ( D, C, A ) | ( 0, 0, 2 ) | 0.76 0.76 0.30 |
| ( D, C, B ) | ( 0, 0, 3 ) | 0.79 0.79 0.20 |
| ( D, C, C ) | ( 1, 0, 2 ) | 0.73 0.76 0.30 |
| ( D, C, D ) | ( 0, 1, 2 ) | 0.76 0.73 0.30 |
| ( D, C, E ) | ( 1, 1, 2 ) | 0.70 0.70 0.70 |
| ( D, D, A ) | ( 1, 0, 1 ) | 0.40 0.73 0.40 |
| ( D, D, B ) | ( 1, 0, 2 ) | 0.73 0.76 0.30 |
| ( D, D, C ) | ( 2, 0, 1 ) | 0.30 0.76 0.73 |
| ( D, D, D ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( D, D, E ) | ( 2, 1, 1 ) | 0.70 0.70 0.70 |
| ( D, E, A ) | ( 1, 0, 2 ) | 0.73 0.76 0.30 |
| ( D, E, B ) | ( 1, 0, 3 ) | 0.76 0.79 0.20 |
| ( D, E, C ) | ( 2, 0, 2 ) | 0.30 0.76 0.30 |
| ( D, E, D ) | ( 1, 1, 2 ) | 0.70 0.70 0.70 |
| ( D, E, E ) | ( 2, 1, 2 ) | 0.40 0.73 0.40 |
| ( E, A, A ) | ( 0, 1, 1 ) | 0.73 0.40 0.40 |
| ( E, A, B ) | ( 0, 1, 2 ) | 0.76 0.73 0.30 |
| ( E, A, C ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( E, A, D ) | ( 0, 2, 1 ) | 0.76 0.30 0.73 |
| ( E, A, E ) | ( 1, 2, 1 ) | 0.70 0.70 0.70 |
| ( E, B, A ) | ( 0, 2, 1 ) | 0.76 0.30 0.73 |
| ( E, B, B ) | ( 0, 2, 2 ) | 0.76 0.30 0.30 |
| ( E, B, C ) | ( 1, 2, 1 ) | 0.70 0.70 0.70 |
| ( E, B, D ) | ( 0, 3, 1 ) | 0.79 0.20 0.76 |
| ( E, B, E ) | ( 1, 3, 1 ) | 0.76 0.30 0.76 |
| ( E, C, A ) | ( 0, 1, 2 ) | 0.76 0.73 0.30 |
| ( E, C, B ) | ( 0, 1, 3 ) | 0.79 0.76 0.20 |
| ( E, C, C ) | ( 1, 1, 2 ) | 0.70 0.70 0.70 |
| ( E, C, D ) | ( 0, 2, 2 ) | 0.76 0.30 0.30 |
| ( E, C, E ) | ( 1, 2, 2 ) | 0.73 0.40 0.40 |
| ( E, D, A ) | ( 1, 1, 1 ) | 0.60 0.60 0.60 |
| ( E, D, B ) | ( 1, 1, 2 ) | 0.70 0.70 0.70 |
| ( E, D, C ) | ( 2, 1, 1 ) | 0.70 0.70 0.70 |
| ( E, D, D ) | ( 1, 2, 1 ) | 0.70 0.70 0.70 |
| ( E, D, E ) | ( 2, 2, 1 ) | 0.40 0.40 0.73 |
| ( E, E, A ) | ( 1, 1, 2 ) | 0.70 0.70 0.70 |
| ( E, E, B ) | ( 1, 1, 3 ) | 0.76 0.76 0.30 |
| ( E, E, C ) | ( 2, 1, 2 ) | 0.40 0.73 0.40 |
| ( E, E, D ) | ( 1, 2, 2 ) | 0.73 0.40 0.40 |
| ( E, E, E ) | ( 2, 2, 2 ) | 0.50 0.50 0.50 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-J.; Naruse, M.; Aono, M. Harnessing the Computational Power of Fluids for Optimization of Collective Decision Making. Philosophies 2016, 1, 245-260. https://doi.org/10.3390/philosophies1030245
Kim S-J, Naruse M, Aono M. Harnessing the Computational Power of Fluids for Optimization of Collective Decision Making. Philosophies. 2016; 1(3):245-260. https://doi.org/10.3390/philosophies1030245
Chicago/Turabian StyleKim, Song-Ju, Makoto Naruse, and Masashi Aono. 2016. "Harnessing the Computational Power of Fluids for Optimization of Collective Decision Making" Philosophies 1, no. 3: 245-260. https://doi.org/10.3390/philosophies1030245
APA StyleKim, S.-J., Naruse, M., & Aono, M. (2016). Harnessing the Computational Power of Fluids for Optimization of Collective Decision Making. Philosophies, 1(3), 245-260. https://doi.org/10.3390/philosophies1030245






