Abstract
While substantial progress has been made in the field known as artificial consciousness, at the present time there is no generally accepted phenomenally conscious machine, nor even a clear route to how one might be produced should we decide to try. Here, we take the position that, from our computer science perspective, a major reason for this is a computational explanatory gap: our inability to understand/explain the implementation of high-level cognitive algorithms in terms of neurocomputational processing. We explain how addressing the computational explanatory gap can identify computational correlates of consciousness. We suggest that bridging this gap is not only critical to further progress in the area of machine consciousness, but would also inform the search for neurobiological correlates of consciousness and would, with high probability, contribute to demystifying the “hard problem” of understanding the mind–brain relationship. We compile a listing of previously proposed computational correlates of consciousness and, based on the results of recent computational modeling, suggest that the gating mechanisms associated with top-down cognitive control of working memory should be added to this list. We conclude that developing neurocognitive architectures that contribute to bridging the computational explanatory gap provides a credible and achievable roadmap to understanding the ultimate prospects for a conscious machine, and to a better understanding of the mind–brain problem in general.
1. Introduction
Can computational studies contribute to our understanding of phenomenal consciousness? By “phenomenal consciousness” we mean the subjective qualities (qualia) of sensory phenomena, emotions and mental imagery, such as the redness of an object or the pain from a skinned knee, that we experience when awake [1]. Consciousness1 is very poorly understood at present, and many people have argued that computational studies do not have a significant role to play in understanding it, or that there is no possibility of an artificial consciousness. For example, some philosophers have argued that phenomenal machine consciousness will never be possible for a variety of reasons: the non-organic nature of machines [2], it would imply panpsychism [3], the absence of a formal definition of consciousness [4], or the general insufficiency of computation to underpin consciousness [5,6]. More generally, it has been argued that the objective methods of science cannot shed light on phenomenal consciousness due to its subjective nature [7], making computational investigations irrelevant.
These arguments and similar ones are bolstered by the fact that no existing computational approach to artificial consciousness has yet presented a compelling demonstration or design of instantiated consciousness in a machine, or even clear evidence that machine consciousness will eventually be possible [8]. Yet at the same time, from our perspective in computer science, we believe that none of these arguments provide a compelling refutation of the possibility of a conscious machine, nor are they sufficient to account for the lack of progress that has occurred in this area. For example, concerning the absence of a good definition of consciousness, progress has been made in artificial intelligence and artificial life without having generally accepted definitions of either intelligence or life. The observation that only brains are known to be conscious does not appear to entail that artifacts never will be, any more than noting that only birds could fly in 1900 entailed that human-made heavier-than-air machines would never fly. The other minds problem, which is quite real [9,10], has not prevented studies of phenomenal consciousness and self-awareness in infants and animals, or routine decisions by doctors about the state/level of consciousness of apparently unresponsive patients, so why should it prevent studying consciousness in machines?
What then, from a purely computational viewpoint, is the main practical barrier at present to creating machine consciousness? In the following, we begin to answer this question by arguing that a critical barrier to advancement in this area is a computational explanatory gap, our current lack of understanding of how high-level cognitive computations can be captured in low-level neural computations [11]. If one accepts the existence of cognitive phenomenology, in other words, that our subjective experiences are not restricted to just traditional qualia but also encompass deliberative thought processes and high-level cognition [12], then developing neurocomputational architectures that bridge this gap may lead to a better understanding of consciousness. In particular, we propose a route to achieving this better understanding based on identifying possible computational correlates of consciousness, computational processes that are exclusively associated with phenomenally conscious information processing [13]. Here, our focus will be solely on neurocomputational correlates of high-level cognition that can be related to the computational explanatory gap. Identifying these correlates depends on neurocomputational implementation of high-level cognitive functions that are associated with subjective mental states. As a step in this direction, we provide a brief summary of potential computational correlates of consciousness that have been suggested/recognized during the last several years based on past work on neurocomputational architectures. We then propose, based on the results of recent computational modeling, that the gating mechanisms associated with top-down cognitive control of working memory should be added to this list, and we discuss this particular computational correlate in more detail. We conclude that developing neurocognitive architectures that contribute to bridging the computational explanatory gap provides a credible roadmap to better understanding the ultimate prospects for a conscious machine, and to a better understanding of phenomenal consciousness in general.
2. The Computational Explanatory Gap
There is a critically important barrier to understanding the prospects for machine consciousness that is not widely recognized. This barrier is the computational explanatory gap. We define the computational explanatory gap to be a lack of understanding of how high-level cognitive information processing can be mapped onto low-level neural computations [11]. By “high-level cognitive information processing” we mean aspects of cognition such as goal-directed problem solving, reasoning, executive decision making, cognitive control, planning, language understanding, and metacognition—cognitive processes that are widely accepted to at least in part be consciously accessible. By “low-level neural computations” we mean the kinds of computations that can be achieved by networks of artificial neurons such as those that are widely studied in contemporary computer science, engineering, psychology, and neuroscience.
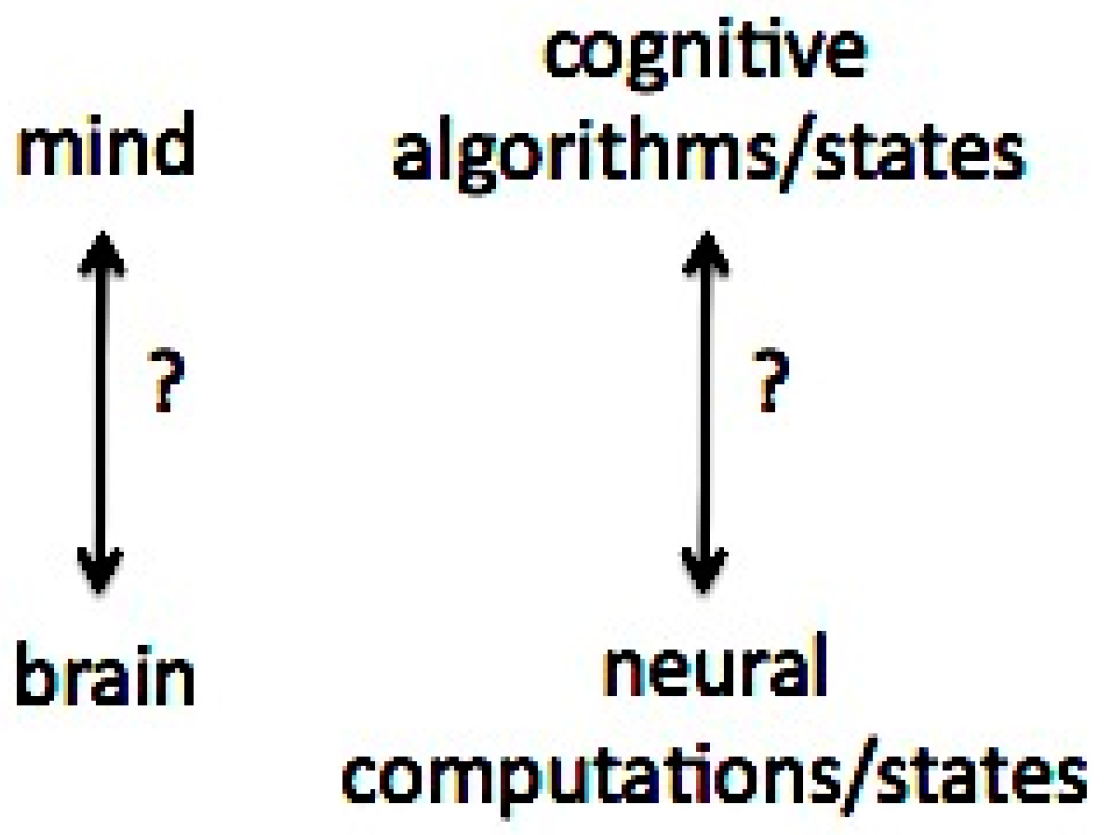
The computational explanatory gap can be contrasted with the well-known philosophical explanatory gap between a successful functional/computational account of consciousness and accounting for the subjective experiences that accompany it [14]. While we argue that the computational explanatory gap is ultimately relevant to the philosophical explanatory gap, the former is not a mind–brain issue per se. Rather, it is a gap in our general understanding of how computations (algorithms and dynamical processes) supporting goal-directed reasoning and problem solving at a high level of cognitive information processing can be mapped into the kinds of computations/algorithms/states that can be supported at the low level of neural networks. In other words, as illustrated in Figure 1, it is a purely computational issue, and thus may initially appear to be unrelated to understanding consciousness.
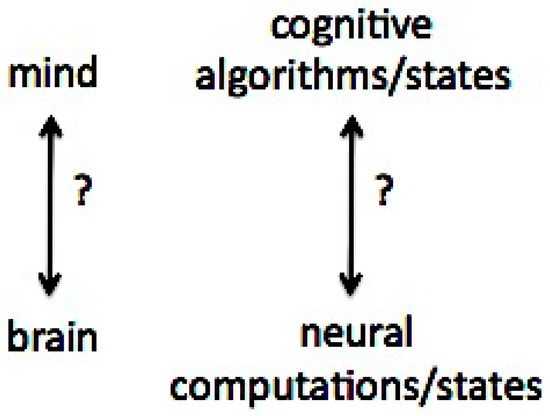
Figure 1.
The well-known philosophical explanatory gap (on the left) and less recognized computational explanatory gap (on the right). The arguments presented here are that the latter can also be viewed as a fundamental problem, and that focusing on solving it may be central to advancing future work on phenomenal machine consciousness.
The computational explanatory gap is also not an issue specific to computers or even computer science. It is a generic issue concerning how one type of computations at a high level (serial goal-directed deliberative reasoning algorithms associated with conscious aspects of cognition) can be mapped into a fundamentally different type of computations at a low level (parallel distributed neural computations and representational states). It is an abstraction independent of the hardware involved, be it the electronic circuits of a computer or the neural circuits of the brain.
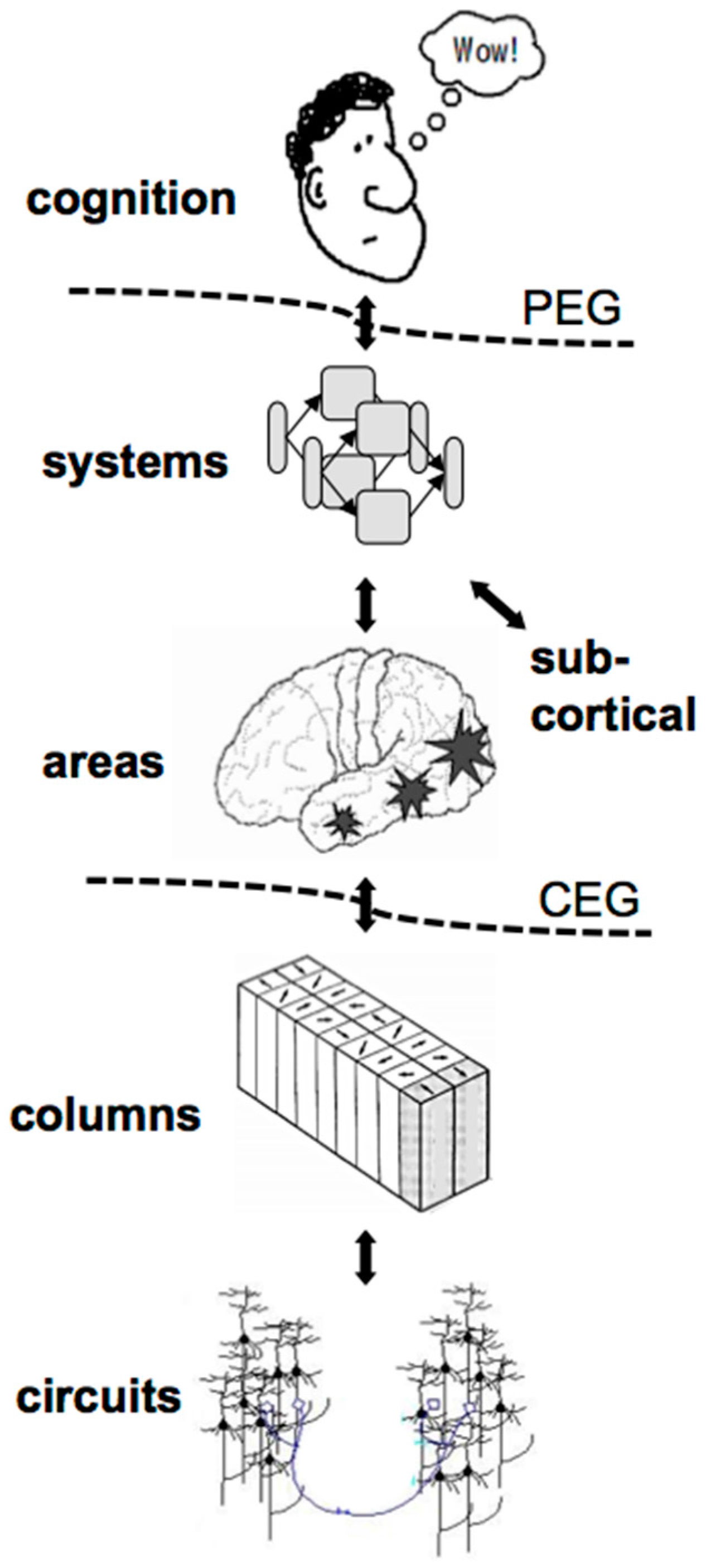
Further comparison of the computational explanatory gap and the philosophical explanatory gap is informative (see Figure 2). In philosophy, the computational explanatory gap relates to the long-standing discussion concerning the “easy problem” of accounting for cognitive information processing versus the “hard problem” of explaining subjective experience, the latter being associated with the philosophical explanatory gap [15]. This characterization of the easy problem is sometimes qualified by comments that the easy problem is not really viewed as being truly easy to solve, but that it is easy to imagine that a solution can be obtained via functional/computational approaches, while this is not the case for the hard problem (e.g., [1]). Nonetheless, the easy/hard contemporary philosophical distinction tends to largely dismiss solving the computational explanatory gap, as it is just part of the easy problem. Such a dismissal fails to explain why the computational explanatory gap has proven to be largely intractable during more than half a century of efforts (since McCulloch and Pitts [16] first captured propositional-level logical inferences using neural networks). This intractability is somewhat mysterious to us as computer scientists, given that the brain somehow readily bridges this gap. While the brain’s structure is of course quite complex, it appears unlikely that this complexity alone could be the whole explanation, given that mainstream top-down artificial intelligence (AI) systems (which are much simpler than brain structure/function) have been qualitatively more successful in modeling high-level cognition when compared to neurocomputational methods. We believe that something more fundamental is being missed here. From our perspective, the computational explanatory gap is actually a fundamental, difficult-to-resolve issue that is more relevant to the hard problem than is generally recognized, and that once the computational explanatory gap is bridged, the philosophical explanatory gap may prove to be much more tractable than it currently appears.
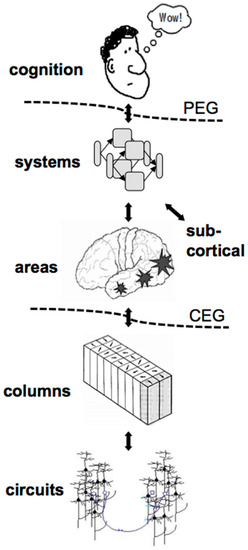
Figure 2.
The philosophical and computational explanatory gaps address different problems. The philosophical explanatory gap (top dashed line labeled PEG) refers to our inability to understand how subjective mental experiences can arise mechanistically from a material/physical substrate, the brain. In contrast, the computational explanatory gap (bottom dashed line labeled CEG) refers to our inability to understand how high-level cognitive algorithms and any macroscopic correspondences that they may have in the brain can be accounted for by the low-level computational mechanisms supported by the microscopic neurocomputational processes and algorithms of neural circuitry, artificial or otherwise.
Comparing the philosophical and computational explanatory gaps as above is closely related to what has been referred to as the “mind–mind problem” [17]. This framework takes the viewpoint that there are two senses of the word “mind”: the phenomenological mind involving conscious awareness and subjective experience, and the computational mind involving information processing. From this perspective, there are two mind–brain problems, and also a mind–mind problem that is concerned with how the phenomenological and computational minds relate to one another. Jackendoff suggests, inter alia, the theory that “The elements of conscious awareness are caused by/supported by/projected from information and processes of the computational mind that (1) are active and (2) have other (as yet unspecified) privileged properties.” The computational explanatory gap directly relates to this theoretical formulation of the mind–mind problem. In particular, the notion of “privileged properties” referenced here can be viewed as related to what we will call computational correlates of consciousness in the following. However, as we explain later, our perspective differs somewhat from that of Jackendoff: We are concerned more with cognitive phenomenology than with traditional sensory qualia, and our emphasis is on correlations between phenomenological and computational states rather than on causal relations.
The computational explanatory gap is also clarified by the efforts of cognitive psychologists to characterize the properties that distinguish human conscious versus unconscious cognitive information processing. Human conscious information processing has been characterized as being serial, relatively slow, and largely restricted to one task at a time [18,19,20]. In contrast, unconscious information processing is parallel, relatively fast, and can readily involve more than one task simultaneously with limited interference between the tasks. Conscious information processing appears to involve widespread “global” brain activity, while unconscious information processing appears to involve more localized activation of brain regions. Conscious information processing is often associated with inner speech and is operationally taken to be cognition that is reportable,2 while unconscious information processing has neither of these properties. The key point here is that psychologists explicitly trying to characterize the differences between conscious and unconscious information processing have implicitly, and perhaps unintentionally, identified the computational explanatory gap. The properties they have identified as characterizing unconscious information processing—parallel processing, efficient, modular, non-reportable—often match reasonably well with those of neural computation. For example, being “non-reportable” matches up well with the nature of neurocomputational models where, even once a neural network has learned to perform a task very successfully, what that network has learned remains largely opaque to outside observers and often requires a major effort to determine or express symbolically [21]. In contrast, the properties associated with conscious information processing—serial processing, relatively slow, holistic, reportable—are a much better match to symbolic top-down AI algorithms, and a poor match to the characteristics of neural computations. In this context, the unexplained gap between conscious cognition and the underlying neural computations that support it is strikingly evident.
Resolving the computational explanatory gap is complementary to substantial efforts in neuroscience that have focused on identifying neural correlates of consciousness [22]. Roughly, a neural correlate of consciousness is some minimal neurobiological state whose presence is sufficient for the occurrence of a corresponding state of consciousness [23]. Neurobiologists have identified several candidate neurobiological correlates, such as specific patterns in the brain’s electrical activity (e.g., synchronized cortical oscillations), activation of specific neuroanatomical structures (e.g., thalamic intra-laminar nuclei), widespread brain activation, etc. [24]. However, in spite of an enormous neuroscientific endeavor in general over more than a century, there remains a large difference between our understanding of unconscious versus conscious information processing in the brain, particularly in our limited understanding of the neural basis of the high-level cognitive functions. For example, a great deal is currently known at the macroscopic level about associating high-level cognitive functions with brain regions (pre-frontal cortex “executive” regions, language cortex areas, etc.), and a lot is known about the microscopic functionality of neural circuitry in these regions, all the way down to the molecular/genetic level. What remains largely unclear is how to put those two types of information processing together, or in other words, how the brain maps high-level cognitive functions into computations over the low-level neural circuits that are present, i.e., the computational explanatory gap (bottom dashed line CEG in Figure 2). It remains unclear why this mapping from cognitive computations to neural computations is so opaque today given the enormous resources that have been poured into understanding these issues. The key point here is that this large gap in our neuroscientific knowledge about how to relate the macroscopic and microscopic levels of information processing in the brain to one another is, at least in part, also a manifestation of the abstract underlying computational explanatory gap.
3. The Relevance to Consciousness
Why is bridging the computational explanatory gap of critical importance in developing a deeper understanding of phenomenal consciousness, and in addressing the possibility of phenomenal machine consciousness? The reason is that bridging this gap would allow us to do something that is currently beyond our reach: It would allow us to directly and cleanly compare (i) neurocomputational mechanisms associated with conscious high-level cognitive activities; and (ii) neurocomputational mechanisms associated with unconscious information processing. To understand this assertion, we need to first consider the issue of cognitive phenomenology.
The central assertion of cognitive phenomenology is that our subjective, first-person experience is not restricted to just traditional qualia involving sensory perception, emotions and visual imagery, but also encompasses deliberative thought and high-level cognition. Such an assertion might seem straightforward to the non-philosopher, but it has proven to be controversial in philosophy. Introductory overviews that explain this controversy in a historical context can be found in [25,26], and a balanced collection of essays arguing for and against the basic ideas of cognitive phenomenology is given in [12]. A recent detailed philosophical analysis of cognitive phenomenology is also available [27].
Most of this past discussion in the philosophy literature has focused on reasons for accepting or rejecting cognitive phenomenology. Philosophers generally appear to accept that some aspects of cognition are accessible to consciousness, so the arguments in the literature have focused on the specific issue of whether there are phenomenal aspects of cognition that cannot be accounted for by traditional sensory qualia and mental imagery. For example, an advocate of cognitive phenomenology might argue that there are different non-sensory subjective qualities associated with hearing the sentence “I’m tired” spoken in a foreign language if one understands that language than if one does not, given that the sensory experience is the same in both cases.
While there are those who do not agree with the idea of cognitive phenomenology, there appears to be increasing acceptance of the concept [28]. For our purposes, here, we will simply assume that cognitive phenomenology holds and ask what that might imply. In other words, we start by assuming that there exist distinct non-sensory subjective mental experiences associated with at least some aspects of cognition. What would follow from this assumption? One answer to this question is that cognitive phenomenology makes the computational explanatory gap, an apparently purely computational issue, of relevance to understanding consciousness. Since the computational explanatory gap focuses on mechanistically accounting for high-level cognitive information processing, and since at least some aspects of cognitive information processing are conscious, it means that computational efforts to mechanistically bridge the computational explanatory gap have direct relevance to the study of consciousness. In particular, we hypothesize that such neurocomputational studies provide a route to both a deeper understanding of human consciousness and also to a phenomenally conscious machine. This hypothesis makes a large body of research in cognitive science that is focused on developing neurocomputational implementations of high-level cognition pertinent to the issue of phenomenal consciousness. This work, while recognized as being relevant to intentional aspects of consciousness, has not generally been considered of direct relevance to phenomenology. This implication is an aspect of cognitive phenomenology that has apparently not been recognized previously.
4. A Roadmap to a Better Understanding of Consciousness
From a computational point of view, the recognition that high-level cognitive processes may have distinct subjective qualities associated with them has striking implications for computational research related to consciousness. Cognitive phenomenology implies that, in addition to past work explicitly studying “artificial consciousness”, other ongoing research focused on developing computational models of higher cognitive functions is directly relevant to understanding the nature of consciousness. Much of this work on neurocognitive architectures attempts to map higher cognitive functions into neurocomputational mechanisms independently of any explicit relationship between these functions and consciousness. Such work may, intentionally or inadvertently, identify neurocomputational mechanisms associated with phenomenally conscious information processing that are not observed with unconscious information processing. This would potentially provide examples of computational correlates of consciousness, and thus ideally would provide a deeper understanding of the nature of consciousness in general, just as molecular biology contributed to demystifying the nature of life and deprecating the theory of vitalism. In effect, this work may allow us to determine whether or not there are computational correlates of consciousness in the same sense that there are neurobiological correlates of consciousness.
A computational correlate of consciousness can, in general, be defined to be any principle of information processing that characterizes the differences between conscious and unconscious information processing [13]. Such a definition is quite broad: It could include, for example, symbolic AI logical reasoning and natural language processing algorithms. Consistent with this possibility, there have been past suggestions that intelligent information processing can be divided into symbolic processes that represent conscious aspects of the mind, and neurocomputational processes that represent unconscious aspects of cognition [29,30,31,32]. However, while such models/theories implicitly recognize the computational explanatory gap as we explained it above, they do not attempt to provide a solution to it, and they do not address serious objections to symbolic models of cognition in general [33]. The critical issue that we are concerned with here with respect to the computational explanatory gap is how to replace the high-level symbolic modules of such models with neurocomputational implementations. How such replacement is to be done remains stubbornly mysterious today.
Accordingly, in the following, we use the term “computational correlate of consciousness” to mean minimal neurocomputational processing mechanisms that are specifically associated with conscious aspects of cognition but not with unconscious aspects. In other words, in the context of the computational explanatory gap, we are specifically interested in neurocomputational correlates of consciousness, i.e., computational correlates related to the representation, storage, processing, and modification of information that occurs in neural networks. Computational correlates of consciousness are a priori distinct from neural correlates [13]. As noted above, proposed neural correlates have in practice included, for example, electrical/metabolic activity patterns, neuroanatomical regions of the brain, and biochemical phenomena [23]—correlates within the realm of biology that are not computational. Computational correlates are abstractions that may well find implementation in the brain, but as abstractions they are intended to be independent of the physical substrate that implements them (brain, silicon, etc.).
Our suggestion here is that, as computational correlates of consciousness as defined above become discovered, they will provide a direct route to investigating the possibility of phenomenal machine consciousness, to identifying candidate properties that could serve as objective criteria for the presence of phenomenal consciousness in machines, animals and people (the problem of other minds), and to a better understanding of the fundamental nature of consciousness. In other words, what we are suggesting is that a complete characterization of high-level cognition in neurocomputational terms may, along the way, show us how subjective experience arises mechanistically, based on the concepts of cognitive phenomenology discussed above.
5. Past Suggestions for Computational Correlates of Consciousness
If one allows the possibility that the computational explanatory gap is a substantial barrier both to a deeper understanding of phenomenal consciousness and to developing machine consciousness, then the immediate research program becomes determining how one can bridge this gap and identify computational correlates of consciousness. Encouragingly, cognitive phenomenology suggests that the substantial efforts by researchers working in artificial consciousness and by others developing neurocognitive architectures involving high-level cognitive functionality are beginning to provide a variety of potential computational correlates. Much of this past work can be interpreted as being founded upon specific candidates for computational correlates of consciousness, and this observation suggests that such models are directly related to addressing the computational explanatory gap. In the following, we give a description of past computational correlates that are identifiable from the existing literature, dividing them into five classes or categories:
- representation properties
- system-level properties
- self-modeling
- relational properties
- cognitive control
All of these correlates are based on neurocomputational systems. We give just a brief summary below, using only a single example of each class, to convey the general idea. Further, we will consider these potential correlates uncritically here, deferring the issue of whether they correlate exclusively with consciousness until the Discussion section. A more detailed technical characterization and many further examples in each class can be found in [34].
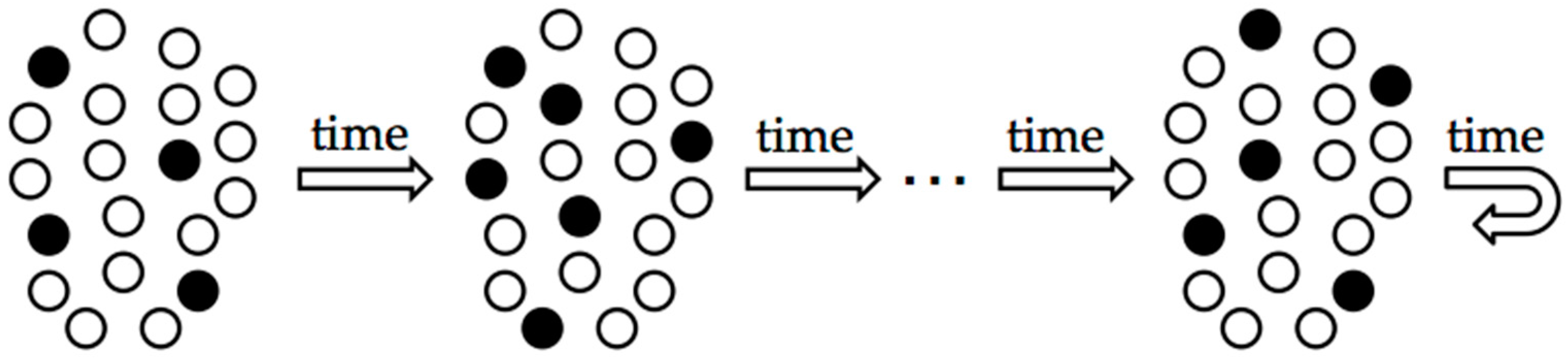
One class of computational correlates of consciousness is based on representation properties, i.e., on how information is encoded. This refers to the intrinsic properties of the neural representation of information used in cognitive states/processes. For example, a number of theoretical arguments and several early recurrent neural network models of consciousness were based on hypothesizing that neural activity attractor states are associated with or characterize consciousness [13,35,36,37,38,39]. At any point in time, a recurrent neural network has an activity state, a pattern of active and inactive neurons that represents/encodes the contents of the network’s current state (Figure 3). Over time, this pattern of activity typically changes from moment to moment as the activities of each neuron influence those of the other neurons. However, in networks that serve as models of short-term working memory, this evolution of the activity pattern stops and settles into a fixed, persistent activity state (Figure 3, right). This persisting activity state is referred to as an “attractor” of the network because other activity states of the network are “attracted” to be in this fixed state. It is these attractor states that have been proposed to enter conscious awareness and in this sense to be a computational correlate of consciousness. This claim appears to be consistent with at least some neurophysiological findings [40]. Of course, there are other types of attractor states in recurrent neural networks besides fixed activity patterns, such as periodically recurring activity patterns (limit cycles) [41], and they could also be potential computational correlates. In particular, it has been proposed that instantaneous activity states of a network are inadequate for realizing conscious experience—that qualia are correlated instead with a system’s activity space trajectory [35]. The term “trajectory” as used here refers to a temporal sequence of a neural system’s activity states, much as is pictured in Figure 3, rather than to a single instantaneous activity state. Viewing a temporal sequence of activity patterns as a correlate of subjective experience overcomes several objections that exist for single activity states as correlates [35].
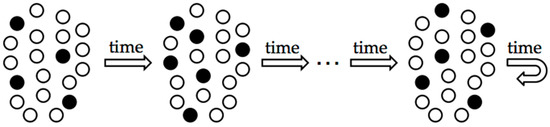
Figure 3.
On the left is a set of artificial neurons that are widely connected to one another (the connections are not shown to keep the diagram simple). An arbitrary initial activity state has been assigned to the network. This is shown schematically by indicating those neurons that are active (on, firing, excited, etc.) by filled circles and those neurons that are inactive (off, silent, inhibited, etc.) by unfilled circles. As time passes, the activity state typically changes repeatedly (middle), but under appropriate conditions, eventually reaches a state that no longer changes with time (rightmost). The network’s activity state is then said to have reached a fixed point, and this latter activity pattern is said to be an attractor state of the network because other transient states of the network are “attracted” to become this persistent state. Attractor states in neural networks of this sort often represent stored information in working memory or the solutions to problems.
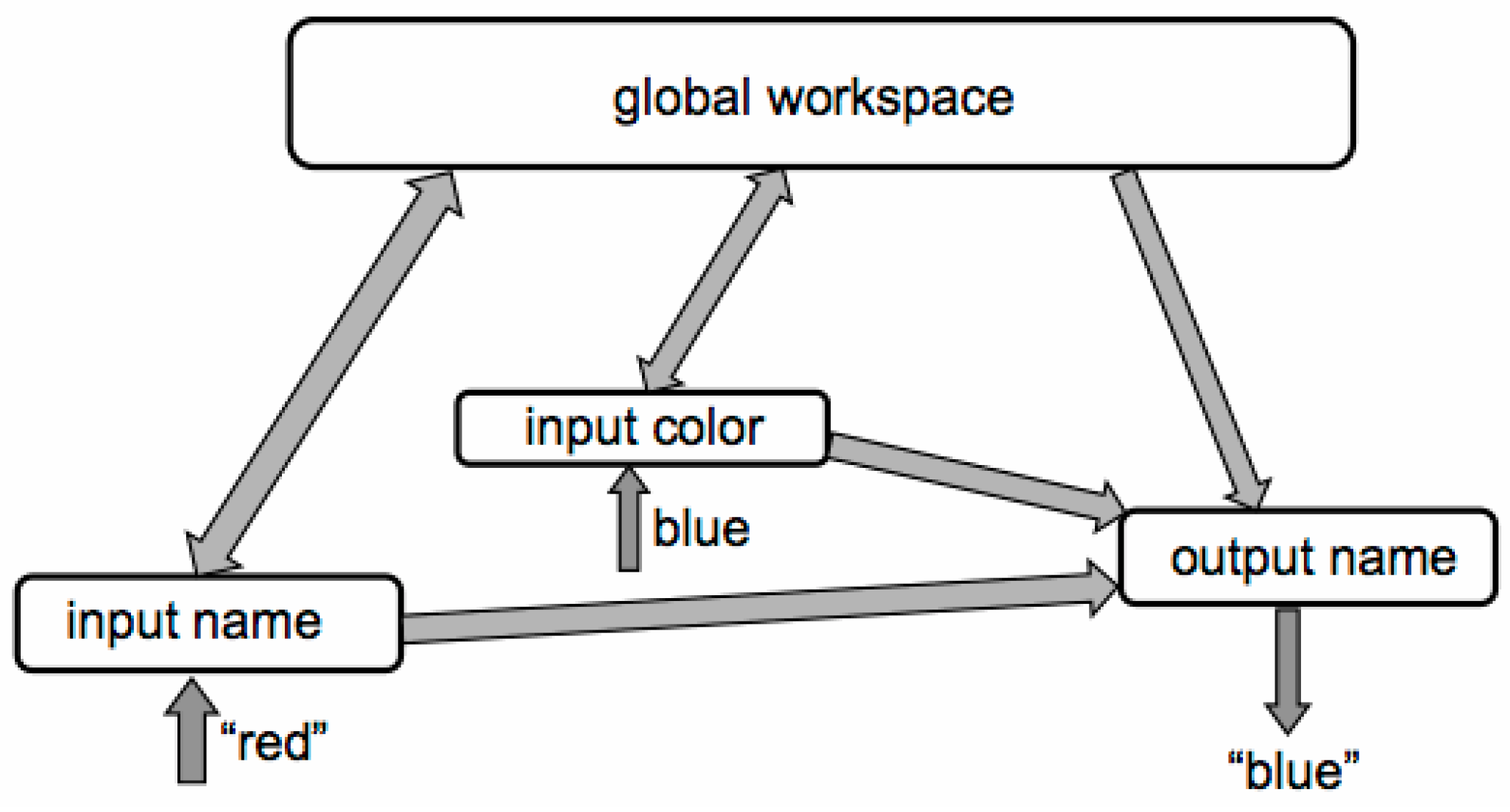
A second class of computational correlates of consciousness is based on system-level properties of a neurocomputational system. This term is used here to mean those computational properties that characterize a neurocomputational system as a whole rather than, as with representational properties, depend on the specific nature of neural activity patterns that represent/encode cognitive states and processes. We use global information processing as an example here. The terms local and global, when applied to neurocognitive architectures, generally refer to the spatial extent of information processing. A number of empirical studies have suggested that information processing during conscious mental activities is widely distributed (“global”) across cerebral cortex regions and also associated with increased inter-regional communication [42,43,44]. Inspired by this, a number of neural network models have been studied in which conscious/effortful information processing is associated with computational processes involving the recruitment of hidden layers and hence widespread network activation of a “global workspace” [45,46]. An example neural architecture of this type is illustrated schematically in Figure 4. This specific example concerns a Stroop task where one must either read aloud each seen word (“green”, “blue”, etc.) or name the color of the ink used in the word, the latter being more difficult and effortful with incongruous words. Significant widespread activation of the “global workspace” occurs when the model is dealing with a difficult naming task that requires conscious effort by humans, and not with the easier, more automatic word reading task, making global activation a potential computational correlate of consciousness. It has been suggested elsewhere that global information processing provides a plausible neurocomputational basis for both phenomenal and access consciousness [47].
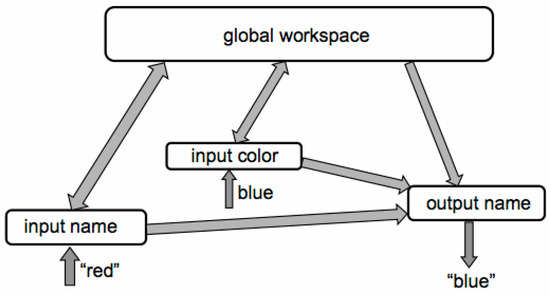
Figure 4.
A schematic representation of the architecture of a neural global workspace model for a word-color Stroop task [46]. Each box represents a set/layer of neurons. Local processing occurs in the input and output layers, while with global processing, substantial activation also occurs throughout the workspace layer.
A third class of computational correlates of consciousness involves self-modeling, that is, maintaining an internal model of self. Self-awareness has long been viewed as a central aspect of a conscious mind [48,49]. For example, analysis of the first-person perspective suggests that our mind includes a self-model (virtual model, body image) that is supported by neural activation patterns in the brain. The argument is that the subjective, conscious experience of a “self” arises because this model is always there due to the proprioceptive, somatic and other sensory input that the brain constantly receives, and because our cognitive processes do not recognize that the body image is a virtual representation of the physical body [50]. Accordingly, AI and cognitive science researchers have made a number of proposals for how subjective conscious experience could emerge in embodied agents from such self-models. An example of this type of work has studied “conscious robots” that are controlled by recurrent neural networks [51]. A central focus of this work is handling temporal sequences of stimuli, predicting the event that will occur at the next time step from past and current events. The predicted next state and the actual next state of the world are compared at each time step, and when these two states are the same a robot is declared to be conscious (“consistency of cognition and behavior generates consciousness”). In support of this concept of consciousness, these expectation-driven robots have been shown to be capable of self-recognition in a mirror [52], effectively passing the “mirror test” of self-awareness used with animals [53] and allowing the investigators to claim that it represents self-recognition. The predictive value of a self-model such as that used here has previously been argued by others to be associated with consciousness [54].
A fourth class of potential computational correlates of consciousness is based on relational properties: relationships between cognitive entities. Higher-order thought theory (HOT theory) of consciousness [55] provides a good example of a potential computational correlate of consciousness involving relational properties. HOT theory is relational: It postulates that a mental state S is conscious to the extent that there is some other mental state (a “higher-order thought”) that directly refers to S or is about S. In other words, consciousness occurs when there is a specific relationship such as this between two mental states. It has been suggested that artificial systems with higher-order representations consistent with HOT theory could be viewed as conscious, even to the extent of having qualia, if they use grounded symbols [56]. Further, HOT theory has served as a framework for developing metacognitive networks in which some components of a neurocomputational architecture, referred to as higher-order networks, are able to represent and access information about other lower-order networks [57], as illustrated in Figure 5. It is the second-order network’s learned reference to the first-order network’s internal representations that makes the latter at least functionally conscious, according to HOT theory. The claim is that “conscious experience occurs if and only if an information processing system has learned about its own representation of the world” [57], and that the higher-order representations formed in metacognitive models capture the core mechanisms of HOT theories of consciousness [58].
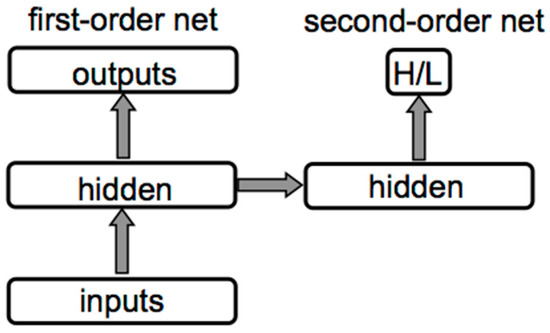
Figure 5.
A caricature of a typical metacognitive neural architecture. Boxes indicate network layers, and gray arrows indicate all-to-all adaptive connections between layers. The first-order network on the left is used to learn pattern classification tasks. The second-order network on the right monitors the first-order network’s hidden layer representation and outputs an estimate as to the correctness of the first-order network’s output for each input pattern. The correctness of this output over time reflects the extent to which the second-order network has learned a meta-representation of the first-order network’s representation.
A fifth class of computational correlates of consciousness is based on cognitive control, the executive processes that manage other cognitive processes [59]. Examples of cognitive control include directing attention, maintaining working memory, goal setting, and inhibiting irrelevant signals. Most past neurocomputational modeling work of relevance here has focused on attention mechanisms. While attention and conscious awareness are not equivalent processes, normally they are closely linked and highly correlated [60,61,62]. It is therefore not surprising that some computational studies have viewed attention mechanisms as computational correlates of consciousness. For example, Haikonen [63] has proposed a conscious machine based on a number of properties, including inner speech and the machine’s ability to report its inner states, in which consciousness is correlated with collective processing of a single topic. This machine is composed of a collection of inter-communicating modules. The distinction between a topic being conscious or not is based on whether the machine as a whole attends to that topic. At each moment of time, each specialized module of the machine broadcasts information about the topic it is addressing to the other modules. Each broadcasting module competes to recruit other modules to attend to the same topic that it is processing. The subject of this unified collective focus of attention is claimed to enter consciousness. In other words, it is the collective, cooperative attending to a single topic that represents a computational correlate of consciousness. Recently implemented in a robot [64], this idea suggests that a machine can only be conscious of one topic at a time, and like global workspace theory (from which it differs significantly), this hypothesis is consistent with empirical evidence that conscious brain states are associated with widespread communication between cerebral cortex regions.
6. Top-Down Gating of Working Memory
We have now seen that past research relevant to the computational explanatory gap has suggested or implied a variety of potential computational correlates of consciousness. It is highly likely that additional candidates will become evident in the future based on theoretical considerations, experimental evidence from cognitive science, the discovery of new neural correlates of consciousness, and so forth. In this section, we will consider a recently-introduced type of neural models focused on cognitive control of working memory. These models incorporate two potential computational correlates of consciousness: temporal sequences of attractor states, something that has been proposed previously as a computational correlate, and the top-down gating of working memory, something that we will propose below should also be considered as a computational correlate within the category of cognitive control. To understand this latter hypothesis, we need to first clarify the nature of working memory and characterize how it is controlled by cognitive processes.
6.1. Cognitive Control of Working Memory
The term working memory refers to the human memory system that temporarily retains and manipulates information over a short time period [65]. In contrast to the relatively limitless capacity of more permanent long-term memory, working memory has substantial capacity limitations. Evidence suggests that human working memory capacity is on the order of roughly four “chunks” of information under laboratory conditions [66]. For example, if you are playing the card game bridge, your working memory might contain information about some recent cards that have been played by your partner or by other players during the last few moves. Similarly, if you are asked to subtract 79 from 111 “in your head” without writing anything down, your working memory would contain these two numbers and often intermediate steps (borrowing, etc.) during your mental calculations. Items stored in working memory may interfere with each other, and they are eventually lost, or said to decay over time, reflecting the limited storage capacity. For example, if you do ten consecutive mental arithmetic problems, and then you are subsequently asked “What were the two numbers you subtracted in the third problem?”, odds are high that you would no longer be able to recall this information.
The operation of working memory is largely managed via cognitive control systems that, like working memory itself, are most clearly associated with prefrontal cortex regions. It is these top-down “executive processes” that are at issue here. Developing neural architectures capable of modeling cognitive control processes has proven to be surprisingly challenging, both for working memory and in general. What computational mechanisms might implement the control of working memory functionality?
One answer to this question is that top-down gating provides the mechanisms by which high-level cognitive processes control the operation of working memory, determining what is stored, retained and recalled. In general, the term “gating” in the context of neural information processing refers to any situation where one neurocomputational component controls the functionality of another. However, neural network practitioners use this term to refer to such control occurring at different levels in neurocomputational systems. At the “microscopic” level, gating can refer to local interactions between individual artificial neurons where, for example, one neuron controls whether or not another neuron retains or loses its current activity state, as in long short-term memory models [67]. While simulated evolution has shown that localized gating of individual neurons can sometimes contribute to the reproductive fitness of a neural system [68], we do not consider this type of localized gating further.
Instead, in the following, we are concerned solely with gating at a much more “macroscopic” level where one or more modules/networks as a whole controls the functionality of other modules/networks as a whole. Such large-scale gating apparently occurs widely in the brain. For example, if a person hears the word “elephant”, that person’s brain might turn on speech output modules such as Broca’s area (they repeat what they heard), or alternatively such output modules may be kept inactive (the person is just listening silently). In such situations, the modules not only exchange information via neural pathways, but they may also control the actions of one another. A module may, via gating, turn on/off the activity or connections of other modules as a whole, and may determine when other modules retain/discard their network activity state, when they learn/unlearn information, and when they generate output.
6.2. Modeling Top-Down Gating
To illustrate these ideas, we consider here a recently-developed neurocomputational model that addresses high-level cognitive functions and the computational explanatory gap. This model incorporates a control system that gates the actions of other modules and itself at a “macroscopic” level [69,70]. In this model, the control module learns to turn on/off (i.e., to gate) the actions of other modules, thereby determining when input patterns are saved or discarded, when to learn/unlearn information in working memory, when to generate outputs, and even when to update its own states.
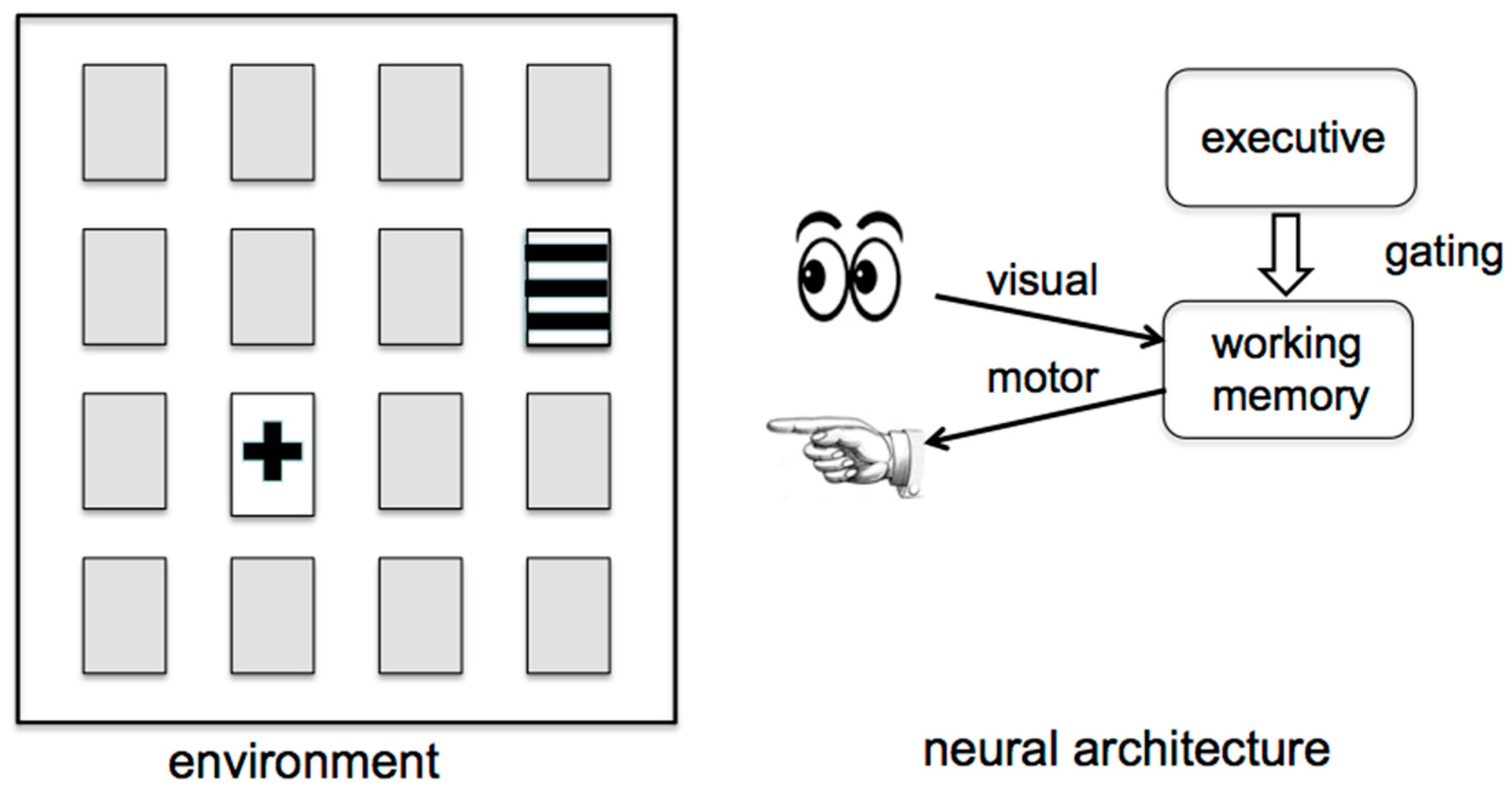
As a specific example, consider the situation depicted in Figure 6, which schematically illustrates a neural architecture described in [70]. On the left is an arrangement of 16 cards that each display a pattern on one face, where all but two of the cards shown are face down on a table top. On the right is pictured a neurocomputational agent that can see the card configuration and that has the ability to select specific cards on the table by pointing to them. The goal is for the neurocognitive agent to remove all of the cards from the table in as few steps as possible. On each step, the agent can select two cards to turn over and thereby reveal the identity of those two cards. If the two cards match, then they are removed from the table and progress is made towards the goal. If the selected cards reveal different patterns, as is the case illustrated in Figure 6, then they are turned back over and remain on the table. While it may appear that no progress has been made in this latter case, the agent’s neural networks include a working memory in which the patterns that have been seen and their locations are recorded and retained. Accordingly, if on the next step the agent first turns over the upper left card and discovers that it has horizontal stripes on its face, then rather than selecting the second card randomly, the agent would select the (currently face down) rightmost card in the second row to achieve a matching pair that can be removed.
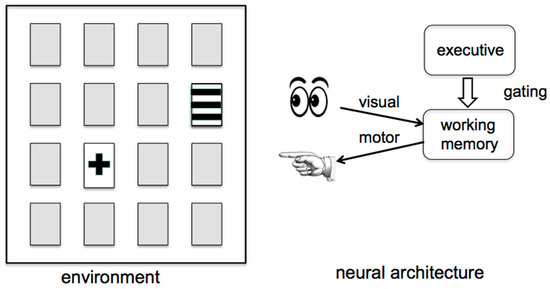
Figure 6.
On the left, a set of 16 cards is spread out on a table, with all but two of the cards face down. On the right, the top-level structure of a neurocomputational agent is shown schematically, where the agent can see the current card configuration and can act by pointing at face-down cards to indicate that they should be turned over. The agent has a working memory that allows it to retain in memory the identities and locations of a few recent cards that it has seen (subject to decay), and an executive control system that directs the agent’s working memory and output motor actions.
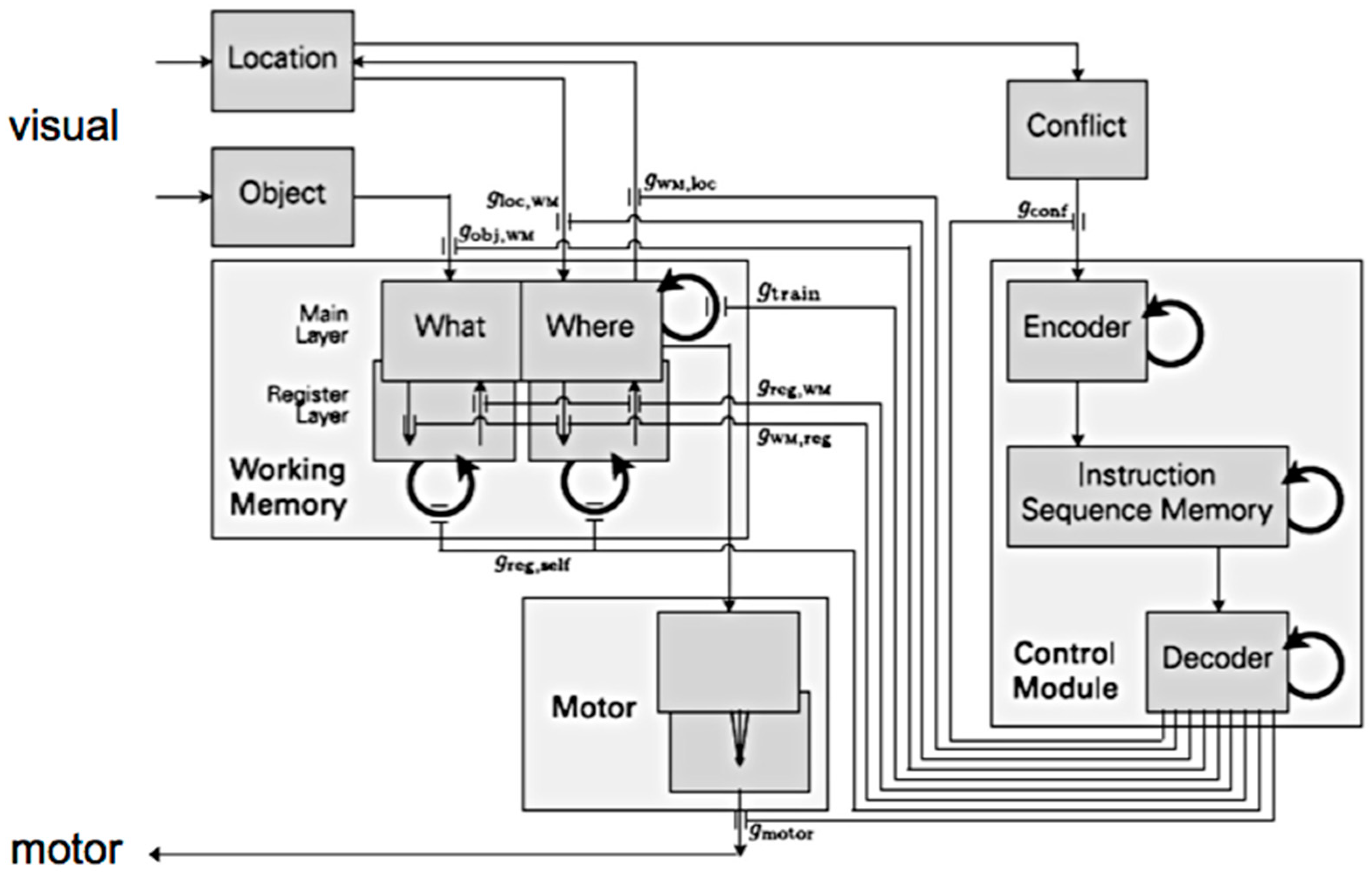
The most interesting aspect of our architecture’s underlying neurocomputational system is the executive module (upper right of Figure 6) that directs and controls the actions of the rest of the system. The executive module is initially trained to carry out the card removal task and acts via top-down gating mechanisms to control the sequence of operations that are performed by the agent. The agent’s neural architecture pictured on the right side of Figure 6 is expanded into a more detailed form in Figure 7, indicating the neurocomputational model’s actual components and connectivity. The visual input arrow of Figure 6 is implemented at the top left of Figure 7 by components modeling the human “what” (object) and “where” (location) visual pathways, while the motor output arrow of Figure 6 is implemented as a motor system at the bottom of Figure 7. The agent’s working memory in Figure 6 is seen on the left in Figure 7 to consist of multiple components, while the executive system is implemented as a multi-component control module on the right in Figure 7. The top-down gating arrow between executive and working memory systems in Figure 6 is implemented as nine gating outputs exiting the control module at the bottom right of Figure 7 and from there traveling to a variety of locations throughout the rest of the architecture.
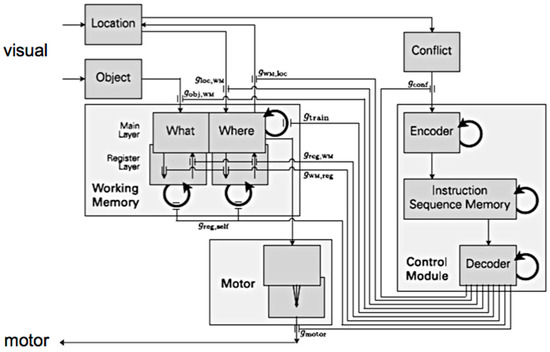
Figure 7.
A more detailed depiction of the neurocomputational mechanisms controlling the card matching task agent illustrated in Figure 6. Each gray-shaded box represents a neural network module, while the arrows represent connection pathways between these modules. On the left, an operational system consists of visual pathways feeding into the working memory, the latter driving the agent’s motor actions. Many of these modules are recurrently connected (broad circular arrows). The control module, or executive system, is pictured on the right. Its gating outputs, originating at the bottom right of the picture, control the operational system’s actions as described in the text.
In the neurocomputational architecture shown in Figure 7, incoming visual information passes through the visual pathways to the working memory, and can trigger motor actions (pointing at a specific card to turn over); these neural components form an “operational system” pictured on the left. The working memory stores information about which cards have been observed previously by learning, at appropriate times, the outputs of the location and object visual pathways. This allows the system subsequently to choose pairs of cards intelligently based on its past experience rather than blindly guessing the locations of potential matches, much as a person does. Working memory is implemented as an auto-associative neural network that uses Hebbian learning. It stores object-location pairs as attractor states. This allows the system to retrieve complete pairs when given just the object information alone or just the location information alone as needed during problem solving. This associating of objects and locations in memory can be viewed as addressing the binding problem [71].
The control module shown on the right in Figure 7 directs the actions of the operational system via a set of gating outputs. The core of the control module is an associative neural network called the instruction sequence memory. The purpose of this procedural memory module is to store simultaneously multiple instruction sequences that are to be used during problem solving, in this case simple instruction sequences for performing card matching tasks. Each instruction indicates to the control module which output gates should be opened at that point in time during problem solving. Informally, the instruction sequence memory allows the system to learn simple “programs” for what actions to take when zero, one, or two cards are face up on the table. The instruction sequence memory is trained via a special form of Hebbian learning to both store individual instructions as attractor states of the network, and to transition between these attractors/instructions during problem solving—it essentially learns to perform, autonomously, the card matching task.
The control module’s gating connections direct the flow of activity throughout the neural architecture, determine when output occurs, and decide when and where learning occurs. For example, the rightmost gating output labeled gmotor (bottom center in Figure 7) opens/closes the output from the motor module, thus determining when and where the agent points at a card to indicate that it should be turned over. Two of the other gating outputs, labeled gobj,WM and gloc,WM, determine when visually-observed information about a card’s identity and/or location, respectively, are stored in working memory. Other gates determine when learning occurs in working memory (gtrain), when comparison/manipulation of information stored in working memory occurs (greg,WM, gWM,reg, greg,self), when the top-down focus of visual attention shifts to a new location (gWM,loc), and when the executive control module switches to a new sequence of instructions (gconf).
The control module’s gating operations are implemented in the underlying neural networks of the architecture via what is sometimes referred to as multiplicative modulation [72]. At any point in time, each of the nine gating connections signals a value gx, where x is “motor” or “loc,WM” or other indices as pictured in Figure 7. These gx values multiplicatively enter into the equations governing the behaviors of the neural networks throughout the overall architecture. For example, if the output of a neuron j in the motor module has value oj at some point in time, then the actual gated output seen by the external environment at that time is the product gmotor × oj. If gmotor = 0 at that time, then no actual output is transmitted to the external environment; if on the other hand gmotor = 1, then oj is transmitted unchanged to the outside world. The detailed equations implementing activity and weight change dynamics and how they are influenced by these gating control signals for the card matching task can be found in [70].
When an appropriate rate of decay is used to determine how quickly items are lost from working memory, this specific architecture for solving card matching task produced accuracy and timing results reminiscent of those seen in humans performing similar tasks [70]. Specifically, this system successfully solved every one of hundreds of randomly-generated card matching tasks on which it was tested. We measured the number of rounds that the system needed to complete the task when 8, 12 or 16 cards were present, averaged over 200 runs. The result was 8.7, 13.0, and 21.2, respectively, increasing as the number of cards increased as would be expected. Interestingly, when we had 34 human subjects carry out the same task, the number of rounds measured was 7.9, 13.5, and 18.9 on average, respectively. While the agent’s performance was not an exact match to that of humans, it is qualitatively similar and exhibits the same trends, suggesting that this neural architecture may be capturing at least some important aspects of human cognitive control of working memory.
6.3. Top-Down Gating as a Computational Correlate of Consciousness
There are actually two innovative aspects of this agent’s neurocontroller that are potential computational correlates of consciousness, one a representational property proposed previously, the other a mechanism that relates to cognitive control. The first of these involves the instruction sequence memory that forms the heart of the control module (see Figure 7). Prior to problem solving, sequences of operations to carry out in various situations are stored in this memory, much as one stores a program in a computer’s memory [70]. Each operation/instruction is stored as an attractor state of this memory module, and during operation the instruction sequence memory cycles through these instructions/attractors consecutively to carry out the card matching or another task. In other words, the instruction sequence memory transitions through a sequence of attractor states in carrying out a task. As we discussed in Section 5, it has previously been hypothesized that an activity-space trajectory such as this is a computational correlate of consciousness [35]. Since the execution of stored instructions here is precisely a trajectory in the instruction sequence memory’s neural network activity-space, that aspect of the card-removal task agent’s functionality can be accepted as a potential computational correlate of consciousness based on the activity-space trajectory hypothesis.
However, our primary innovative suggestion here is that there is a second mechanism in this neurocontroller that can be viewed as a potential computational correlate of consciousness: the use of top-down gating of working memory that controls what is stored and manipulated in working memory. Arguably these gating operations, driven by sequences of attractor states in the executive control module, correspond to consciously reportable cognitive activities involving working memory, and thus they are a potential computational correlate of consciousness. To understand this suggestion, we need to clarify the relationship of working memory to consciousness. Working memory has long been considered to involve primarily conscious aspects of cognitive information processing. Specifically, psychologists widely believe that the working memory operations of input, rehearsal, manipulation, and recall are conscious and reportable [65,73,74,75]. Thus, on this basis alone any mechanisms involved in implementing or controlling these working memory operations merit inspection as potential correlates of consciousness.
In addition, cognitive phenomenology appears to be particularly supportive of our suggestion. Recall that cognitive phenomenology holds that our subjective first-person experience includes deliberative thought and high-level cognition. Our viewpoint here is that high-level cognitive processes become intimately associated with working memory via these top-down gating mechanisms. In particular, it seems intuitively reasonable that the controlling of cognitive activities involving working memory via top-down gating mechanisms might convey a conscious sense of ownership/self-control/agency to a system. Top-down gating of working memory may also relate to the concept of mental causation sometimes discussed in the philosophy of mind literature (especially the literature concerned with issues surrounding free will). The recent demonstration in neurocomputational models that goal-directed top-down gating of working memory can not only work effectively in problem-solving tasks such as the card matching application, but also that such models exhibit behaviors that match up with those observed in humans performing these tasks, supports the idea that something important about cognition (and hence consciousness, as per cognitive phenomenology) is being captured by such models.
Top-down gating of working memory is clearly a distinct potential correlate of consciousness that differs from those described previously (summarized in Section 5). It is obviously not a representational property, although gating can be used in conjunction with networks that employ attractor states as we described above. It is not a system property, like a global workspace or information integration, nor does it explicitly act via self-modeling. It is perhaps somewhat closer to relational properties in that gating can be viewed as relating high-level cognitive processes for problem-solving to working memory processes. However, top-down gating is quite different than relational models that have been previously proposed as computational correlates of consciousness. For example, unlike with past neurocomputational models based on HOT theory that are concerned with metacognitive networks/states that monitor one another, gating architectures are concerned with modules that control one another’s actions. Our view is that top-down gating fits best in the class of computational correlates of consciousness involving cognitive control. This latter class has previously focused primarily on aspects of attention mechanisms, such as the collective simultaneous attending of multiple modules to a single topic [63,64] or the generation of an “efference copy” of attention control signals [76]. Our proposed correlate of top-down gating of working memory differs from these, but appears to us to be complementary to these attention mechanisms rather than an alternative.
7. Discussion
Past progress in the field known as artificial consciousness has made significant strides over the last few decades, but has mainly involved computationally simulating various neural, behavioral, and cognitive aspects of consciousness, much as is done in using computers to simulate other natural processes [8]. There is nothing particularly mysterious about such work: Just as one does not claim that a computer used to simulate a nuclear reactor would actually become radioactive, there is no claim being made in such work that a computer used to model some aspect of conscious information processing would actually become phenomenally conscious. As noted earlier, there is currently no existing computational approach to artificial consciousness that has yet presented a compelling demonstration or design of phenomenal consciousness in a machine.
At the present time, our understanding of phenomenal consciousness in general remains incredibly limited. This is true not only for human consciousness but also for considerations about the possibility of animal and machine consciousness. Our central argument here is that this apparent lack of progress towards a deeper understanding of phenomenal consciousness is in part due to the computational explanatory gap: our current lack of understanding of how higher-level cognitive algorithms can be mapped onto neurocomputational algorithms/states. While those versed in mind–brain philosophy may generally be inclined to dismiss this gap as just part of the “easy problem”, such a view is at best misleading. This computational gap has proven surprisingly intractable to over half a century of research on neurocomputational methods, and existing philosophical works have provided no deep insight into why such an “easy problem” has proven to be so intractable. The view offered here is that the computational explanatory gap is a fundamental issue that needs a much larger collective effort to clarify and resolve. Doing so should go a long way in helping us pin down the computational correlates of consciousness.
Accordingly, we presented several examples of candidates for computational correlates of consciousness in this paper that have emerged from past work on artificial consciousness and neurocognitive architectures. Further, we suggested and described an additional possible correlate, top-down gating of working memory, based on our own recent neurocomputational studies of cognitive control [69,70]. It is interesting in this context to ask how such gating may be occurring in the brain. How one cortical region may directly/indirectly gate the activity of other cortical regions is currently only partially understood. This is an issue of much recent and ongoing interest in the cognitive neurosciences. Gating interactions might be brought about in part by direct connections between regions, such as the poorly understood ‘‘backwards’’ inter-regional connections that are well documented to exist in primate cortical networks [77]. Further, there is substantial evidence that gating may occur in part indirectly via a complex network of subcortical nuclei, including those in the basal ganglia and thalamus [78]. Another possibility is that gating may arise via functional mechanisms such as oscillatory activity synchronization [72,79]. In our related modeling work, the details of implementing gating actions have largely been suppressed, and a more detailed examination comparing alternative possible mechanisms could be an important direction for future research.
The examples that we presented above, and those suggested by other related studies, are very encouraging in suggesting that there now exist several potential computational correlates of consciousness. However, an important difficulty remains: Many hypothesized computational mechanisms identified so far as correlates of consciousness are either known to also occur in neurocomputational systems supporting non-conscious activities, or their occurrence has not yet been definitively excluded in such settings. In other words, the main difficulty in identifying computational correlates of consciousness at present is in establishing that proposed correlates are not also present with unconscious aspects of cognitive information processing. For example, viewing neural network activity attractor states as computational correlates of consciousness is problematic in that there are many physical systems with attractor states that are generally not viewed as conscious, leading to past suggestions that representing conscious aspects of cognition in such a fashion is not helpful: An attractor state may relate to the contents of consciousness, but it is arguably not a useful explanation of phenomenology because there is simply no reason to believe that it involves “internal experience” [80] or because it implies panpsychism [13]. Similarly, the metacognitive neural networks that HOT theory has inspired suggest that information processing in such neural architectures can be taken to be a computational correlate, but there are possibly analogous types of information processing in biological neural circuits at the level of the human brainstem and spinal cord that are associated with apparently unconscious processing. Thus, “second-order” information processing in neural architectures alone apparently would not fully satisfy our criteria for being a computational correlate of consciousness. Similarly, global/widespread neural activity per se does not appear to fully satisfy our criteria because such processing also occurs in apparently unconscious neural systems (e.g., interacting central pattern generators in isolated lamprey eel spinal cord preparations produce coordinated movements involving widespread distributed neural interactions [81], but it is improbable that an isolated eel spinal cord should be viewed as being conscious). Very similar points can be made about HOT theories, gating mechanisms, integrated information processing, and self-modeling.
For this reason, it remains unclear at present which, if any, of the currently hypothesized candidates for neurocomputational correlates of consciousness will ultimately prove to be satisfactory without further qualifications/refinements. This is not because they fail to capture important aspects of conscious information processing, but primarily because similar computational mechanisms have not yet been proven to be absent in unconscious information processing situations. These computational mechanisms are thus not yet specifically identifiable only with conscious cognitive activities. Future work is needed to resolve such issues, to pin down more clearly which aspects of cognition enter conscious awareness and which do not, and to further consider other types of potential computational correlates (quantum computing, massively parallel symbol processing, etc.).
Acknowledgments
This work was supported in part by ONR award N000141310597.
Author Contributions
The authors contributed jointly to all aspects of this work.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Block, N. On a Confusion about a Function of Consciousness. Behav. Brain Sci. 1995, 18, 227–247. [Google Scholar] [CrossRef]
- Schlagel, R. Why not Artificial Consciousness or Thought? Minds Mach. 1999, 9, 3–28. [Google Scholar] [CrossRef]
- Bishop, M. Why Computers Can’t Feel Pain. Minds Mach. 2009, 19, 507–516. [Google Scholar] [CrossRef]
- Bringsjord, S. Offer: One Billion Dollars for a Conscious Robot; If You’re Honest, You Must Decline. J. Conscious. Stud. 2007, 14, 28–43. [Google Scholar]
- Manzotti, R. The Computational Stance is Unfit for Consciousness. Int. J. Mach. Conscious. 2012, 4, 401–420. [Google Scholar] [CrossRef]
- Piper, M. You Can’t Eat Causal Cake with an Abstract Fork. J. Conscious. Stud. 2012, 19, 154–180. [Google Scholar]
- McGinn, C. Consciousness and Its Origins; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Reggia, J. The Rise of Machine Consciousness. Neural Netw. 2013, 44, 112–131. [Google Scholar] [CrossRef] [PubMed]
- Harnad, S. Animal Sentience: The Other-Minds Problem. Anim. Sentience 2016, 1, 1–11. [Google Scholar]
- Reggia, J.; Huang, D.; Katz, G. Beliefs Concerning the Nature of Consciousness. J. Conscious. Stud. 2015, 22, 146–171. [Google Scholar]
- Reggia, J.; Monner, D.; Sylvester, J. The Computational Explanatory Gap. J. Conscious. Stud. 2014, 21, 153–178. [Google Scholar]
- Bayne, T.; Montague, M. (Eds.) Cognitive Phenomenology; Oxford University Press: Oxford, UK, 2011.
- Cleeremans, A. Computational Correlates of Consciousness. Prog. Brain Res. 2005, 150, 81–98. [Google Scholar] [PubMed]
- Levine, J. Materialism and Qualia: The Explanatory Gap. Pac. Philos. Q. 1983, 64, 354–361. [Google Scholar]
- Chalmers, D. The Conscious Mind; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- McCulloch, W.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Jackendoff, R. Consciousness and the Computational Mind; MIT Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Baars, B. A Cognitive Theory of Consciousness; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Baars, B. The Conscious Access Hypothesis. Trends Cognit. Sci. 2002, 6, 47–52. [Google Scholar] [CrossRef]
- Dehaene, S.; Naccache, L. Towards a Cognitive Neuroscience of Consciousness. Cognition 2001, 79, 1–37. [Google Scholar] [CrossRef]
- Huynh, T.; Reggia, J. Symbolic Representation of Recurrent Neural Network Dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1649–1658. [Google Scholar] [CrossRef] [PubMed]
- Crick, F.; Koch, C. Towards a Neurobiological Theory of Consciousness. Semin. Neurosci. 1990, 2, 263–275. [Google Scholar]
- Chalmers, D. What is a Neural Correlate of Consciousness? In Neural Correlates of Consciousness; Metzinger, T., Ed.; MIT Press: Cambridge, MA, USA, 2000; pp. 17–39. [Google Scholar]
- Metzinger, T. Neural Correlates of Consciousness; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Bayne, T.; Montague, M. Cognitive Phenomenology: An Introduction. In Cognitive Phenomenology; Bayne, T., Montague, M., Eds.; Oxford University Press: Oxford, UK, 2011; pp. 1–34. [Google Scholar]
- Siewert, C. Phenomenal Thought. In Cognitive Phenomenology; Bayne, T., Montague, M., Eds.; Oxford University Press: Oxford, UK, 2011; pp. 236–267. [Google Scholar]
- Chudnoff, E. Cognitive Phenomenology; Routledge Press: Abingdon-on-Thames UK, 2015. [Google Scholar]
- Jorba, M.; Vincente, A. Cognitive Phenomenology, Access to Contents, and Inner Speech. J. Conscious. Stud. 2014, 21, 74–99. [Google Scholar]
- Chella, A. Towards Robot Conscious Perception. In Artificial Consciousness; Chella, A., Manzotti, R., Eds.; Imprint Academic: Charlottesville VA, 2007; pp. 124–140. [Google Scholar]
- Kitamura, T.; Tahara, T.; Asami, K. How Can a Robot Have Consciousness? Adv. Robot. 2000, 14, 263–275. [Google Scholar] [CrossRef]
- Sun, R. Accounting for the Computational Basis of Consciousness. Conscious. Cognit. 1999, 8, 529–565. [Google Scholar] [CrossRef] [PubMed]
- Sun, R. Duality of the Mind; Erlbaum: Hillsdale, NJ, USA, 2002. [Google Scholar]
- Dodig-Crakovic, G. The Architecture of Mind as a Network of Networks of Natural Computational Processes. Philosophies 2016, 1, 111–125. [Google Scholar] [CrossRef]
- Reggia, J.; Katz, G.; Huang, D. What are the Computational Correlates of Consciousness? Biolog. Inspir. Cognit. Archit. 2016, in press. [Google Scholar] [CrossRef]
- Fekete, T.; Edelman, S. Towards a Computational Theory of Experience. Conscious. Cognit. 2011, 20, 807–827. [Google Scholar] [CrossRef] [PubMed]
- Grossberg, S. The Link between Brain Learning, Attention, and Consciousness. Conscious. Cognit. 1999, 8, 1–44. [Google Scholar] [CrossRef] [PubMed]
- Mathis, D.; Mozer, M. On the Computational Utility of Consciousness. In Advances in Neural Information Processing Systems; Tesauro, G., Touretzky, D., Leen, T., Eds.; MIT Press: Cambridge, MA, USA, 1995; Volume 7, pp. 10–18. [Google Scholar]
- O’Brien, G.; Opie, J. A Connectionist Theory of Phenomenal Experience. Behav. Brain Sci. 1999, 22, 127–196. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J. Neural Networks for Consciousness. Neural Netw. 1997, 10, 1207–1225. [Google Scholar] [CrossRef]
- Libet, B. The Neural Time Factor in Conscious and Unconscious Events. In Experimental and Theoretical Studies of Consciousness; Wiley: New York, NY, USA, 1993; pp. 123–137. [Google Scholar]
- Huang, D.; Gentili, R.; Reggia, J. Self-Organizing Maps Based on Limit Cycle Attractors. Neural Netw. 2015, 63, 208–222. [Google Scholar] [CrossRef] [PubMed]
- Baars, B.; Ramsey, T.; Laureys, S. Brain, Conscious Experience, and the Observing Self. Trends Neurosci. 2003, 26, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Massimini, M.; Ferrarelli, F.; Huber, R.; Esser, S.K.; Singh, H.; Tononi, G. Breakdown of Cortical Effective Connectivity during Sleep. Science 2005, 309, 2228–2232. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E.; Chialvo, D.; Siniatchkin, M.; Amico, E.; Brichant, J.F.; Bonhomme, V.; Noirhomme, Q.; Laufs, H.; Laureys, S. Large-Scale Signatures of Unconsciousness are Consistent with a Departure from Critical Dynamics. J. R. Soc. Interface 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Connor, D.; Shanahan, M. A Computational Model of a Global Neuronal Workspace with Stochastic Connections. Neural Netw. 2010, 23, 1139–1154. [Google Scholar] [CrossRef] [PubMed]
- Dehaene, S.; Kerszberg, M.; Changeux, J. A Neuronal Model of a Global Workspace in Effortful Cognitive Tasks. Proc. Natl. Acad. Sci. USA 1998, 95, 14529–14534. [Google Scholar] [CrossRef] [PubMed]
- Raffone, A.; Pantani, M. A Global Workspace Model for Phenomenal and Access Consciousness. Conscious. Cognit. 2010, 19, 580–596. [Google Scholar] [CrossRef] [PubMed]
- Samsonovich, A.; Nadel, L. Fundamental Principles and Mechanisms of the Conscious Self. Cortex 2005, 41, 669–689. [Google Scholar] [CrossRef]
- Searle, J. Mind; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Metzinger, T. The Subjectivity of Subjective Experience. In Neural Correlates of Consciousness; Metzinger, T., Ed.; MIT Press: Cambridge, MA, USA, 2000; pp. 285–306. [Google Scholar]
- Takeno, J. Creation of a Conscious Robot; Pan Stanford: Singapore, 2013. [Google Scholar]
- Takeno, J. A Robot Succeeds in 100% Mirror Image Cognition. Int. J. Smart Sens. Intell. Syst. 2008, 1, 891–911. [Google Scholar]
- Gallup, G. Chimpanzees: Self-Recognition. Science 1970, 167, 86–87. [Google Scholar] [CrossRef]
- Ascoli, G. Brain and Mind at the Crossroads of Time. Cortex. 2005, 41, 619–620. [Google Scholar] [CrossRef]
- Rosenthal, D. A Theory of Consciousness. In The Nature of Consciousness; Block, N., Flanagan, O., Guzeldere, G., Eds.; MIT Press: Cambridge, MA, USA, 1996; pp. 729–753. [Google Scholar]
- Rolls, E. A Computational Neuroscience Approach to Consciousness. Neural Netw. 2007, 20, 962–982. [Google Scholar] [CrossRef] [PubMed]
- Cleeremans, A.; Timmermans, B.; Pasquali, A. Consciousness and Metarepresentation: A Computational Sketch. Neural Netw. 2007, 20, 1032–1039. [Google Scholar] [CrossRef] [PubMed]
- Pasquali, A.; Timmermans, B.; Cleeremans, A. Know Thyself: Metacognitive Networks and Measures of Consciousness. Cognition 2010, 117, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Schneider, W.; Chein, J.M. Controlled and Automatic Processing: Behavior, Theory, and Biological Mechanisms. Cognit. Sci. 2003, 27, 525–559. [Google Scholar] [CrossRef]
- Graziano, M.; Webb, T. A Mechanistic Theory of Consciousness. Int. J. Mach. Conscious. 2014, 6, 163–175. [Google Scholar] [CrossRef]
- Koch, C.; Tsuchiya, N. Attention and Consciousness: Two Distinct Brain Processes. Trends Cognit. Sci. 2006, 11, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Lamme, V. Why Visual Attention and Awareness are Different. Trends Cognit. Sci. 2003, 7, 12–18. [Google Scholar] [CrossRef]
- Haikonen, P. Essential Issues of Conscious Machines. J. Conscious. Stud. 2007, 14, 72–84. [Google Scholar]
- Haikonen, P. Consciousness and Robot Sentience; World Scientific: Singapore, 2012. [Google Scholar]
- Baddeley, A. Working Memory and Conscious Awareness. In Theories of Memory; Collins, A., Conway, M., and Morris, P., Eds.; Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar]
- Cowan, N.; Elliott, E.; Scott Saults, J.; Morey, C.; Mattox, S.; Hismjatullina, A.; Conway, A. On the Capacity of Attention: Its Estimation and Its Role in Working Memory and Cognitive Aptitudes. Cognit. Psychol. 2005, 51, 42–100. [Google Scholar] [CrossRef] [PubMed]
- Monner, D.; Reggia, J. Emergent Latent Symbol Systems in Recurrent Neural Networks. Connect. Sci. 2012, 24, 193–225. [Google Scholar] [CrossRef]
- Chabuk, T.; Reggia, J. The Added Value of Gating in Evolved Neurocontrollers. In Proceedings of the International Joint Conference on Neural Networks, Dallas, TX, USA, 4–9 August 2013; pp. 1335–1342.
- Sylvester, J.; Reggia, J.; Weems, S.; Bunting, M. Controlling Working Memory with Learned Instructions. Neural Netw. 2013, 41, 23–38. [Google Scholar] [CrossRef] [PubMed]
- Sylvester, J.; Reggia, J. Engineering Neural Systems for High-Level Problem Solving. Neural Netw. 2016, 79, 37–52. [Google Scholar] [CrossRef] [PubMed]
- Feldman, J. The Neural Binding Problem. Cognit. Neurodyn. 2013, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Akam, T.; Kullmann, D. Oscillatory Multiplexing of Population Codes for Selective Communication in the Mammalian Brain. Nat. Rev. Neurosci. 2014, 15, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Baddeley, A. Working Memory: Theories, Models and Controversies. Annu. Rev. Psychol. 2012, 63, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Baars, B.; Franklin, S. How Conscious Experience and Working Memory Interact. Trends Cognit. Sci. 2003, 7, 166–172. [Google Scholar] [CrossRef]
- Block, N. Perceptual Consciousness Overflows Cognitive Access. Trends Cognit. Sci. 2011, 15, 567–575. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J. CODAM: A Neural Network Model of Consciousness. Neural Netw. 2007, 20, 983–992. [Google Scholar] [CrossRef] [PubMed]
- Van Essen, D. Corticocortical and Thalamocortical Information Flow in the Primate Visual System. Prog. Brain Res. 2005, 149, 173–185. [Google Scholar] [PubMed]
- Sherman, S.; Guillery, R. Exploring the Thalamus and its Role in Cortical Function; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Singer, W. Dynamic Formation of Functional Networks by Synchronization. Neuron 2011, 69, 191–193. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J. Neural Models of Consciousness. In Handbook of Brain Theory and Neural Networks; Arbib, M., Ed.; MIT Press: Cambridge, MA, USA, 2003; pp. 263–267. [Google Scholar]
- Ijspeert, A. Central Pattern Generators for Locomotion Control in Animals and Robots. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef] [PubMed]
- 1Here and below, we use the term “consciousness” to mean “phenomenal consciousness” unless specifically indicated otherwise.
- 2Although such a criterion has substantial limitations, being verbally reportable has long been widely used in experimental psychology as a major objective criterion for accepting that a person is conscious of (subjectively aware of) an event [18,20].
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).