On the Interpretation of Denotational Semantics
Abstract
1. The Need for Interpretations of Semantics
the theory has been presented as an abstract mathematical development from assumptions which are only informally and intuitively justified. However, since these assumptions lead to conclusions which are quite different from the conventional theory of computation, it is important to understand their precise interpretation in terms of real computation.
2. Information in Computation: The Rise of Domains
2.1. Axiomatizing Domains
Scott introduced an element, ⊥, into the value domain […] rather than worrying about partial functions and undefined results: to coin a phrase, he objectifies (some of) the metalanguage.
if f were a function defined by a program in any of the usual ways, it would be sensitive to the accuracy of the arguments (inputs) in a special way: the more accurate the input, the more accurate the output [4].
It is reasonably self-evident that any physically feasible function must be monotonic and obey the condition proved equivalent to continuity as an output event could hardly depend on infinitely many input events as a machine should only be able to do a finite amount of computation before causing a given output event [18]We can even state an abstract counterpart to Church’s Thesis:Scott’s Thesis: Computable functions are continuous [19].
2.2. Domains as Abstract Physical Models of Computation
- Events are meant as event occurrences at specific places, and causality turns out to be a partial-order relation on events.
- There is a natural notion of conflict between events that happen at the same place, and are therefore mutually exclusive. This notion is derived from the corresponding notion for Petri nets:an event is imagined to occur at a fixed point in space and time; conflict between events is localised in that two conflicting events are enabled at the same time and are competing for the same point in space and time [29]
- A state that is finite as a set can only be preceded by finitely many other states. This important property is not true in all Scott domains, but is fairly natural wheninformation has to do with (occurrences of) events: namely the information that those events occurred. For example […], ⊥ might mean that no event occurred and an integer n, might mean that the event occurred of the integer n being output (or, in another circumstance being input) [18]
- If a state x can evolve into two different states by the happening of two non-conflicting, causally independent events a and , then there is a state to which both and can evolve (by performing and a, respectively). In this situation, events a and are concurrent in x—this, again, is related to the way concurrency is defined in Petri nets [31].
a domain is physically concrete iff it can be implemented as a collection of digital events spread through space–time according to some rules (such domains should be suitable for communication between processes) [36].A companion to Scott’s Thesis in this restricted context is then thata domain is concrete iff it is physically concrete (ibidem).
- A collection of places p that may be filled with values 0 and s. Filling of a place p with a value v is an event, represented by the pair ;
- A relation of enabling between (finite sets of) events and places that describes the causal structure of events.
- to fill Bread the value of Nif it is 0fill B with tif it is sfill B with f
2.3. From Physics to Communication
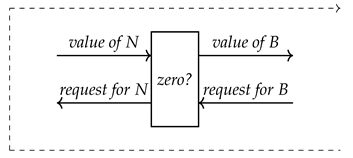
3. From Semantics to Pragmatics
3.1. The Basic Structure of Intentionality
they have just like acts of knowing the characteristic that they have an object, an object towards which they are directed, which is the result of the action [49] (p. 145)
The affirmation of a proposition means the fulfillment of an intention [51] (Eng. translation, p. 59)
3.2. Digression: Proofs and Contracts
[T]o define the inferential role of an expression ‘&’ of Boolean conjunction, one specifies that anyone who is committed to p, and committed to q, is thereby to count also as committed to , and that anyone who is committed to is thereby committed both to p and to q. For a commitment to become explicit is for it to be thrown into the game of giving and asking for reasons as something whose justification, in terms of other commitments and entitlements, is liable to question [54] (Ch. 1)
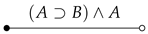
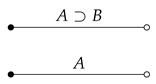

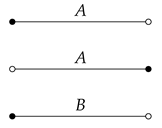
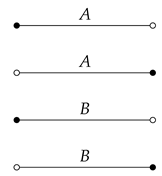
3.3. Program Semantics as Dialogue
4. Further Developments
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scott, D.S.; Strachey, C. Toward a mathematical semantics for computer languages. In Proceedings of the Symposium on Computers and Automata, New York, NY, USA, 13–15 April 1971; Fox, J., Ed.; Polytechnic Press: New York, NY, USA, 1971; pp. 19–46. [Google Scholar]
- Walters, R.F.C. Categories and Computer Science; Cambridge Computer Science Texts, Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Reynolds, J.C. On the interpretation of Scott domains. In Symposia Mathematica; Academic Press: Cambridge, MA, USA, 1975; Volume 15, pp. 123–135. [Google Scholar]
- Scott, D.S. Outline of a mathematical theory of computation. In Proceedings of the Fourth Annual Princeton Conference on Information Sciences and Systems, Princeton, NJ, USA, 25–26 March 1970; pp. 169–176. [Google Scholar]
- Milner, R. Fully abstract models of typed λ-calculi. Theor. Comput. Sci. 1977, 4, 1–22. [Google Scholar] [CrossRef]
- Plotkin, G. LCF considered as a programming language. Theor. Comput. Sci. 1977, 5, 223–257. [Google Scholar] [CrossRef]
- Berry, G.; Curien, P.L.; Lévy, J.J. Full abstraction for sequential languages: The state of the art. In Proceedings of the Algebraic Methods in Semantics, Fontainebleau, France, 8–15 June 1982; Nivat, M., Reynolds, J., Eds.; Cambridge University Press: Cambridge, UK, 1985; pp. 89–132. [Google Scholar]
- Ong, C.H.L. Correspondence between operational and denotational semantics. In Handbook of Logic in Computer Science; Abramsky, S., Gabbay, D., Maibaum, T.S.E., Eds.; Oxford University Press: Oxford, UK, 1995; Volume 4, pp. 269–356. [Google Scholar]
- Abramsky, S. Semantics of Interaction: An Introduction to Game Semantics. In Semantics and Logics of Computation; Pitts, A.M., Dybjer, P., Eds.; Publications of the Newton Institute, Cambridge University Press: Cambridge, UK, 1997; pp. 1–32. [Google Scholar]
- Martin-Löf, P. On the meanings of the logical constants and the justifications of the logical laws. In Atti degli Incontri di Logica Matematica; Bernardi, C., Pagli, P., Eds.; University di Siena: Siena, Italy, 1985; pp. 203–281. [Google Scholar]
- Tieszen, R.L. Phenomenology, Logic, and the Philosophy of Mathematics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Tieszen, R. Intentionality, Intuition, and Proof in Mathematics. In Foundational Theories of Classical and Constructive Mathematics; Sommaruga, G., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 245–263. [Google Scholar]
- van Atten, M. The Development of Intuitionistic Logic. In The Stanford Encyclopedia of Philosophy, Fall, 2023rd ed.; Zalta, E.N., Nodelman, U., Eds.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2023. [Google Scholar]
- Bentzen, B. Propositions as Intentions. Husserl Stud. 2023, 39, 143–160. [Google Scholar] [CrossRef]
- Gunter, C.A. Semantics of Programming Languages. Structures and Techniques; Foundations of Computing; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Winskel, G. The Formal Semantics of Programming Languages—An Introduction; Foundation of Computing Series; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Amadio, R.; Curien, P.L. Domains and Lambda-Calculi. In Cambridge Tracts in Theoretical Computer Science; Cambridge University Press: Cambridge, UK, 1998; Volume 46. [Google Scholar]
- Plotkin, G. The Category of Complete Partial Orders: A Tool for Making Meanings; Summer School on Foundations of Artificial Intelligence and Computer Science; Istituto di Scienze dell’Informazione, Università di Pisa: Pisa, Italy, 1978. [Google Scholar]
- Winskel, G. Events in Computation. Ph.D. Thesis, Department of Computer Science, University of Edinburgh, Edinburgh, UK, 1980. [Google Scholar]
- Sokolowski, R. Introduction to Phenomenology; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Manna, Z. Mathematical Theory of Computation; Dover Publications, Inc.: Mineola, NY, USA, 2003. [Google Scholar]
- Kleene, S.C. On notation for ordinal numbers. J. Symb. Log. 1938, 3, 150–155. [Google Scholar] [CrossRef]
- Kleene, S.C. Introduction to Metamathematics; Van Nostrand: New York, NY, USA, 1952. [Google Scholar]
- Scott, D.S. A type-theoretical alternative to ISWIM, CUCH, OWHY. Theor. Comput. Sci. 1993, 121, 411–420. [Google Scholar] [CrossRef]
- Berry, G. Stable models of typed λ-calculi. In Automata, Languages and Programming, Fifth Colloquium; Ausiello, G., Böhm, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1978; Volume 62, pp. 72–89. [Google Scholar]
- Berry, G. Séquentialité de l’évaluation formelle des lambda-expressions. In Program Transformations, Proceedings of the 3rd International Colloquium on Programming, Paris, France, 28–30 March 1978; Robinet, B., Ed.; Dunod: Paris, France, 1978; pp. 67–80. [Google Scholar]
- Vuillemin, J. Correct and optimal implementations of recursion in a simple programming language. J. Comput. Syst. Sci. 1974, 9, 332–354. [Google Scholar] [CrossRef]
- Kahn, G.; Plotkin, G. Domaines Concrets. Theor. Comput. Sci. 1978, 1993, 187–277. [Google Scholar]
- Nielsen, M.; Plotkin, G.; Winskel, G. Petri nets, event structures and domains, Part I. Theor. Comput. Sci. 1981, 13, 85–108. [Google Scholar] [CrossRef]
- Lamport, L. Time, clocks and the ordering of events in a distributed system. Commun. ACM 1978, 21, 558–565. [Google Scholar] [CrossRef]
- Holt, A. Final Report of the Information System Theory Project; Technical Report RADC-TR-68-305; Rome Air Development Center, Air Force Systems Command, Griffiss Air Force Base: Rome, NY, USA, 1968. [Google Scholar]
- Holt, A.; Commoner, F. Events and conditions. In Proceedings of the MIT Conference on Concurrent Systems and Parallel Computation, Woods Hole, MA, USA, 2–5 June 1970; Association for Computing Machinery: New York, NY, USA, 1970; pp. 3–52. [Google Scholar]
- Petri, C.A. Non-Sequential Processes; Interner Bericht ISF-77-5; Gesellschaft für Mathematik und Datenverarbeitung: Bonn, Germany, 1977. [Google Scholar]
- Brookes, S. Historical introduction to “concrete domains” by G. Kahn and G. Plotkin. Theor. Comput. Sci. 1993, 121, 179–186. [Google Scholar] [CrossRef]
- Berry, G.; Curien, P.L. Sequential algorithms on concrete data structures. Theor. Comput. Sci. 1982, 20, 265–321. [Google Scholar] [CrossRef]
- Plotkin, G. Gilles Kahn and concrete domains, January 2007. In Proceedings of the Slides of a Presentation at the Colloquium in Memory of Gilles Kahn, Paris, France, 12 January 2007. [Google Scholar]
- Abramsky, S.; Jagadeesan, R.; Malacaria, P. Full Abstraction for PCF. Inf. Comput. 2000, 163, 409–470. [Google Scholar] [CrossRef]
- Hyland, J.M.E.; Ong, C.H.L. On full abstraction for PCF: I. Models, observables and the full abstraction problem, II. Dialogue games and innocent strategies, III. A fully abstract and universal game model. Inf. Comput. 2000, 163, 285–408. [Google Scholar] [CrossRef]
- Abramsky, S.; Jagadeesan, R. Games and Full Completeness for Multiplicative Linear Logic. J. Symb. Log. 1994, 59, 543–574. [Google Scholar] [CrossRef]
- Abramsky, S. Information, processes and games. In Handbook of the Pilosophy of Science, Volume 8: Philosophy of Information; van Benthem, J., Adriaans, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 483–549. [Google Scholar]
- Conway, J.H. On Numbers and Games. In London Mathematical Society Monographs; Academic Press: London, UK, 1976; Volume 6. [Google Scholar]
- Joyal, A. Remarques sur la théorie des jeux a deux personnes. Gaz. Sci. Math. Que. 1977, 1, 46–52. [Google Scholar]
- Curien, P.L. Symmetry and Interactivity in Programming. Bull. Symb. Log. 2003, 9, 169–180. [Google Scholar] [CrossRef]
- Girard, J.Y. Linear logic. Theor. Comput. Sci. 1987, 50, 1–102. [Google Scholar] [CrossRef]
- Blass, A. A game semantics for linear logic. Ann. Pure Appl. Log. 1992, 56, 183–220. [Google Scholar] [CrossRef]
- Lorenzen, P. Ein dialogisches Konstructivitätskriterium. In Infinitistic Methods; Pergamon Press and PWN: Oxford, UK; Warsaw, Poland, 1961; pp. 193–200. [Google Scholar]
- van Berkel, K. Handshake Circuits: An Asynchronous Architecture for VLSI Programming; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Krifka, M. The Origins of Telicity. In Events and Grammar; Rothstein, S., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 197–235. [Google Scholar]
- Martin-Löf, P. A path from logic to metaphysics. In Atti del Congresso: Nuovi Problemi della Logica e della Filosofia della Scienza, Viareggio 8–13 Gennaio 1990; CLUEB: Bologna, Italy, 1991; Volume II, pp. 141–149. [Google Scholar]
- Kosman, A. The Activity of Being: An Essay on Aristotle’s Ontology; Harvard: Cambridge, MA, USA, 2013. [Google Scholar]
- Heyting, A. Die Intuitionistische Grundlegung der Mathematik. Erkenntnis 1931, 2, 106–115. [Google Scholar] [CrossRef]
- Brandom, R. Asserting. Noûs 1983, 17, 637–650. [Google Scholar] [CrossRef]
- Brandom, R. Making It Explicit: Reasoning, Representing, and Discursive Commitment; Harvard University Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Brandom, R. Articulating Reasons: An Introduction to Inferentialism; Harvard University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Brandom, R. Between Saying and Doing: Towards an Analytic Pragmatism; Oxford University Press UK: Oxford, UK, 2008. [Google Scholar]
- Gallagher, S. Phenomenology; Palgrave-Macmillan: New York, NY, USA, 2012. [Google Scholar]
- Marion, M. Why Play Logical Games? In Games: Unifying Logic, Language, and Philosophy; Majer, O., Pietarinen, A., Tulenheimo, T., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 3–26. [Google Scholar]
- Marion, M. Game Semantics and the Manifestation Thesis. In The Realism-Antirealism Debate in the Age of Alternative Logics; Rahman, S., Primiero, G., Marion, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 141–168. [Google Scholar]
- Cardone, F. The algebra and geometry of commitment. In Ludics, Dialogue and Interaction; Lecomte, A., Tronçon, S., Eds.; Lecture Notes in Artificial intelligence FoLLI; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6505, pp. 147–160. [Google Scholar]
- Martin-Löf, P. Logic and ethics. In Meaning and understanding; Sedlár, I., Blicha, M., Eds.; College Publications: London, UK, 2020; pp. 83–92. [Google Scholar]
- Pagin, P.; Marsili, N. Assertion. In The Stanford Encyclopedia of Philosophy, Winter, 2021st ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2021. [Google Scholar]
- Barth, E.M.; Krabbe, E.C. From Axiom to Dialogue; De Gruyter: Berlin, Germany; New York, NY, USA, 1982. [Google Scholar]
- Husserl, E. Logical Investigations; Moran, D., Ed.; Routledge: New York, NY, USA, 1970. [Google Scholar]
- Abramsky, S.; McCusker, G. Games for recursive types. In Proceedings of the 1994 Workshop on Theory and Formal Methods, London, UK, 28–30 March 1994; Hankin, C.L., Ed.; Imperial College Press: London, UK, 1995; pp. 1–20. [Google Scholar]
- Verbeek, P.P. Beyond interaction: A short introduction to mediation theory. Interactions 2015, 22, 26–31. [Google Scholar] [CrossRef]
- Turner, R. Programming Languages as Technical Artifacts. Philos. Technol. 2013, 27, 377–397. [Google Scholar] [CrossRef]
- van Atten, M. Brouwer Meets Husserl: On the Phenomenology of Choice Sequences; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Sundholm, G. Questions of proof. Manuscrito 1993, XVI, 47–70. [Google Scholar]
- Sundholm, G. “Inference Versus Consequence” Revisited: Inference, Consequence, Conditional, Implication. Synthese 2012, 187, 943–956. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardone, F. On the Interpretation of Denotational Semantics. Philosophies 2025, 10, 54. https://doi.org/10.3390/philosophies10030054
Cardone F. On the Interpretation of Denotational Semantics. Philosophies. 2025; 10(3):54. https://doi.org/10.3390/philosophies10030054
Chicago/Turabian StyleCardone, Felice. 2025. "On the Interpretation of Denotational Semantics" Philosophies 10, no. 3: 54. https://doi.org/10.3390/philosophies10030054
APA StyleCardone, F. (2025). On the Interpretation of Denotational Semantics. Philosophies, 10(3), 54. https://doi.org/10.3390/philosophies10030054





