Estimation of Cardiac Short Axis Slice Levels with a Cascaded Deep Convolutional and Recurrent Neural Network Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Data Labeling
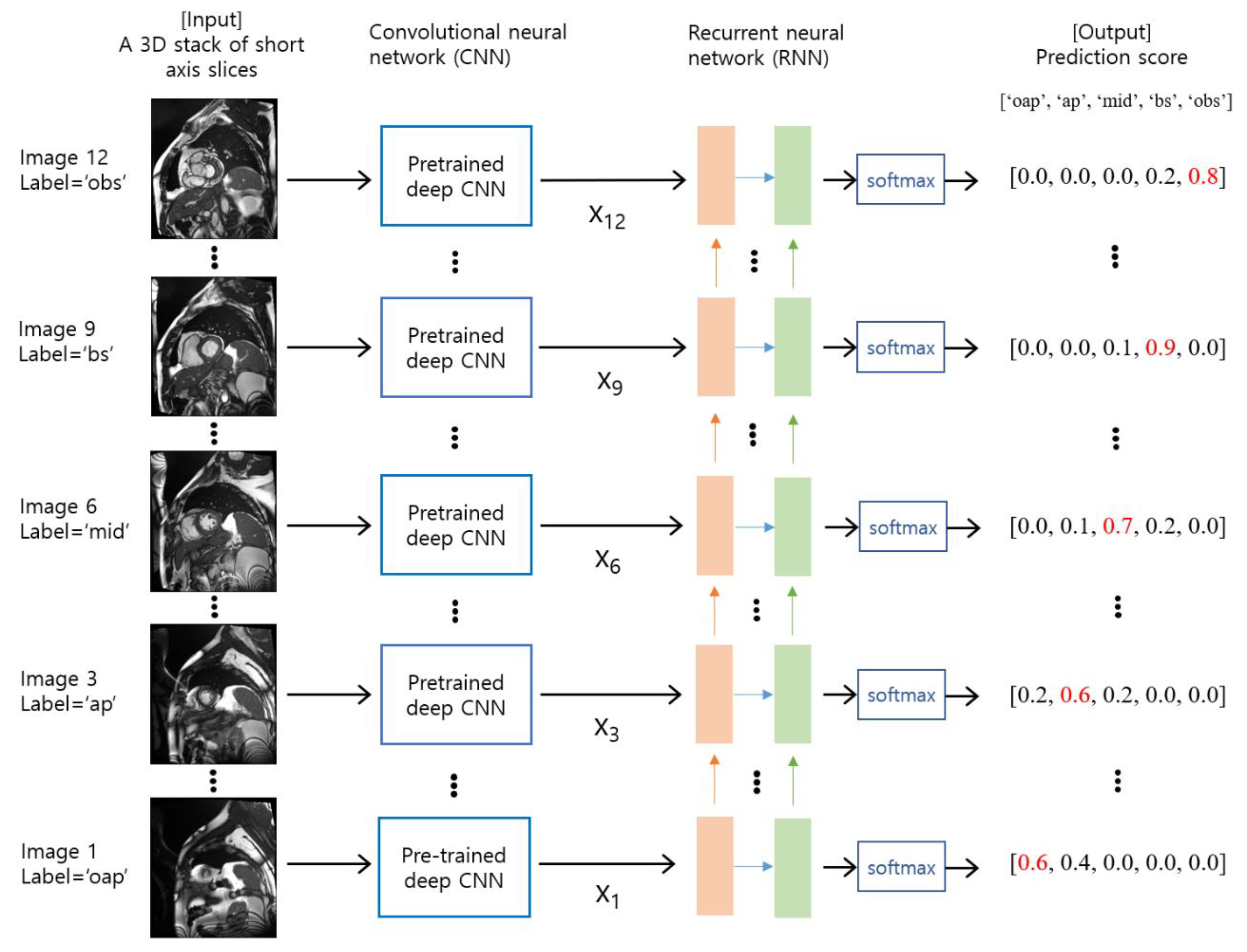
2.3. Deep Learning Model Training and Validation
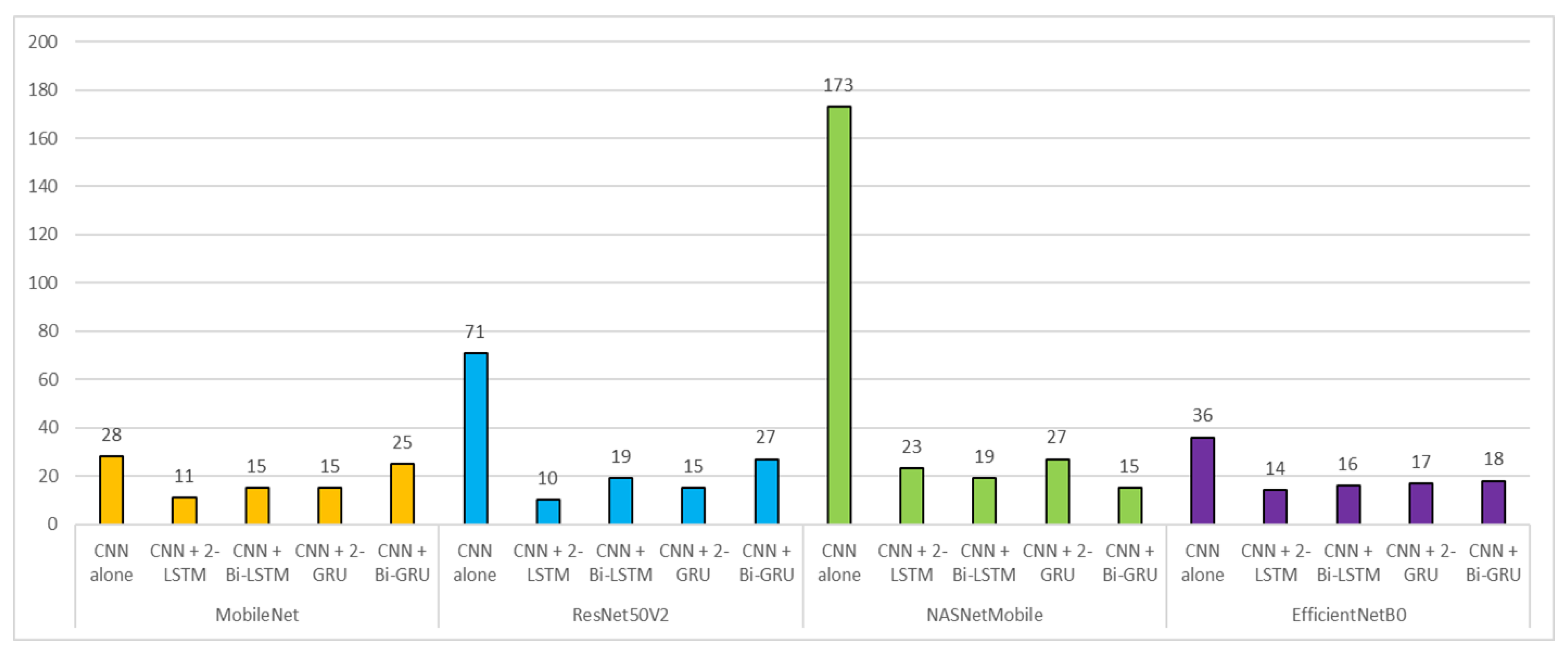
2.4. Evaluation
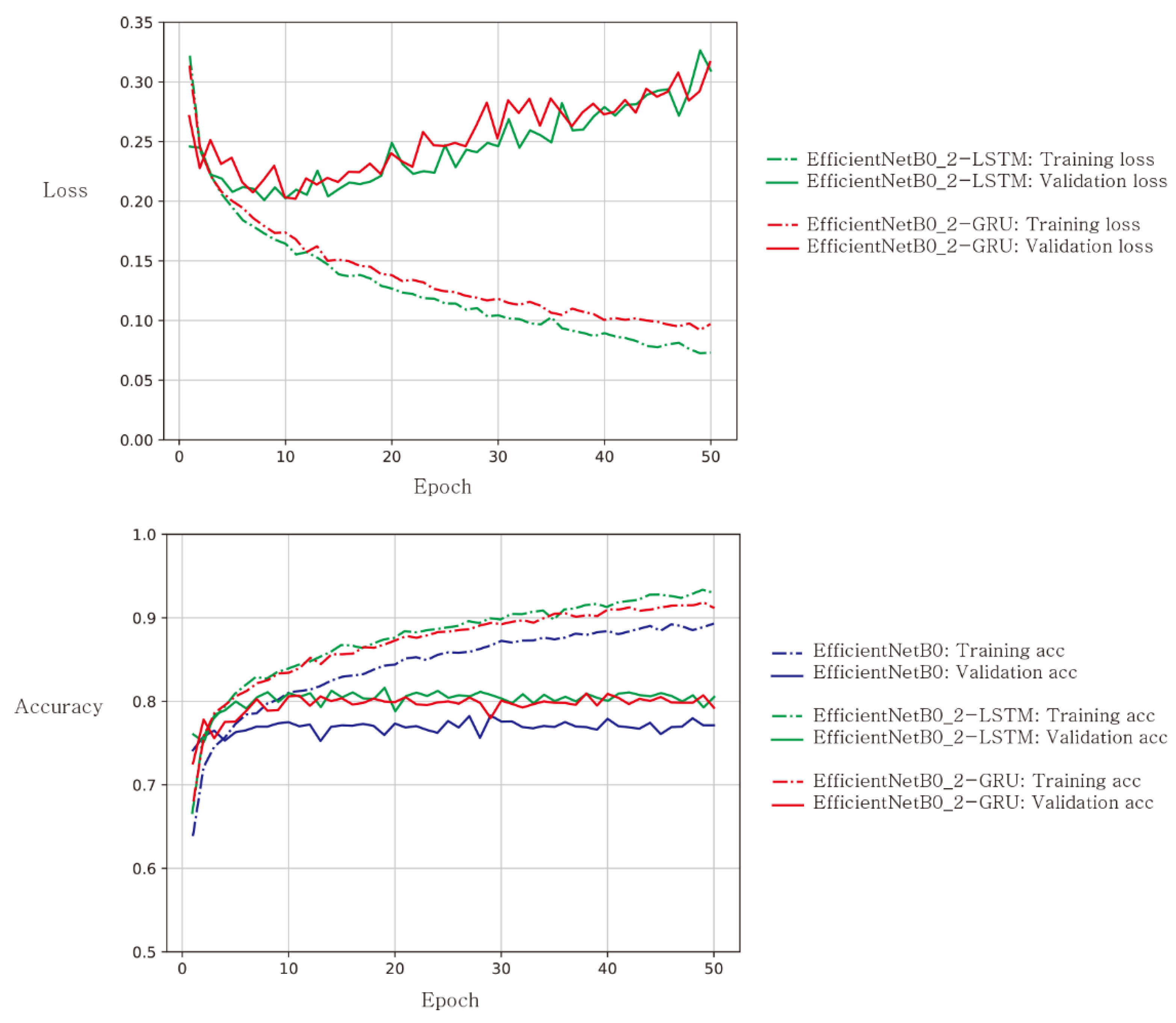
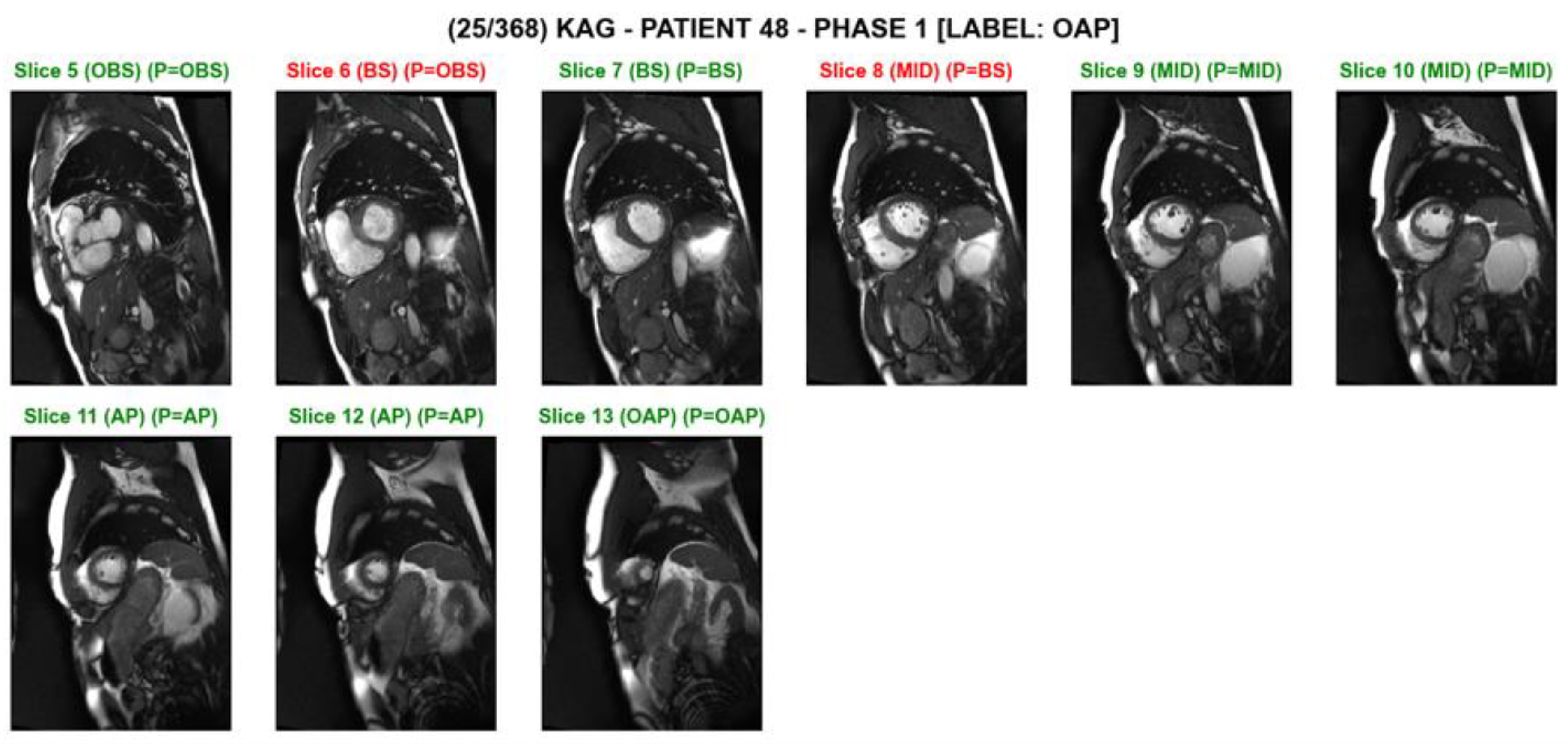
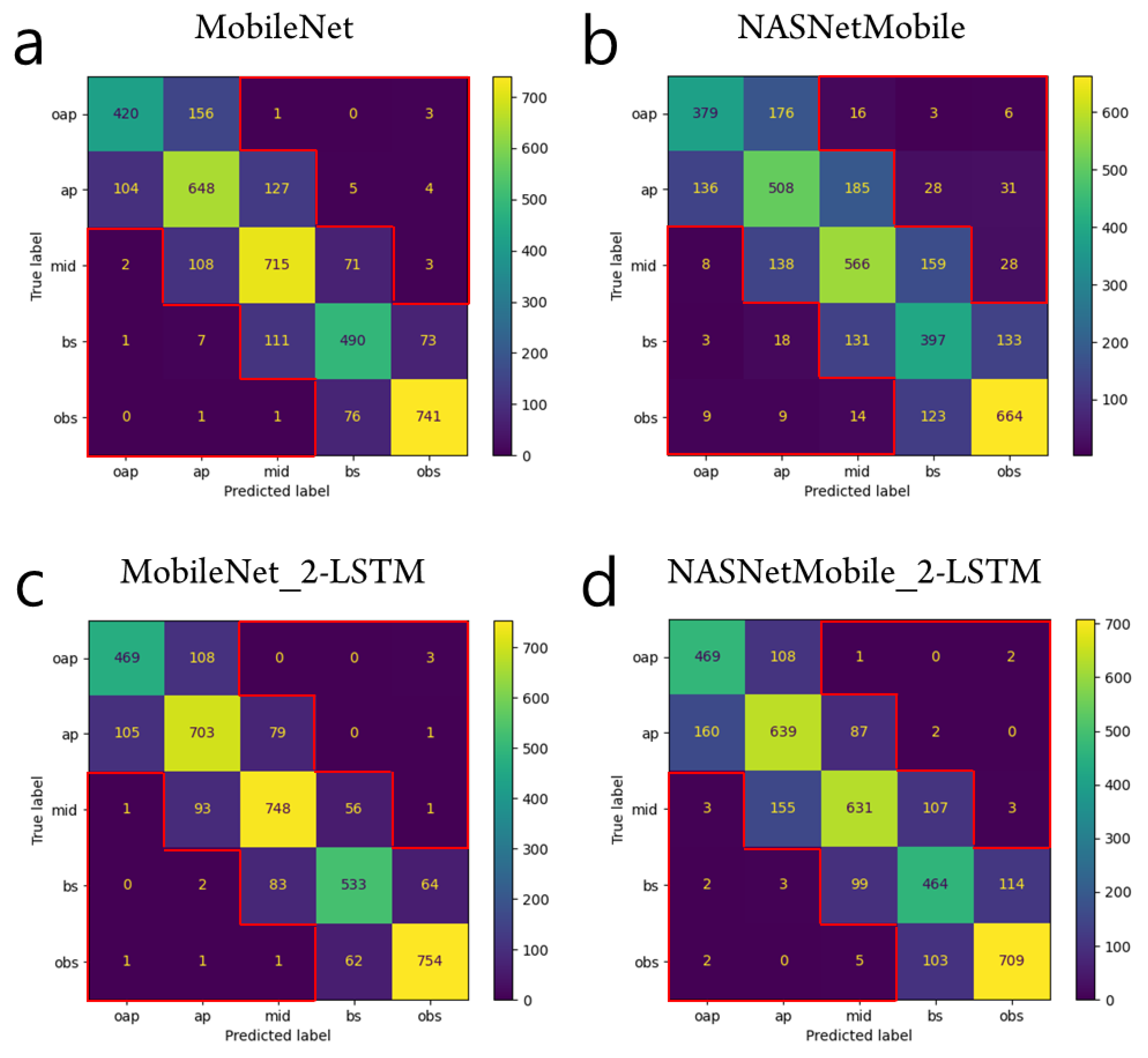
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Higgins, C.B.; de Roos, A. MRI and CT of the Cardiovascular System; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2006. [Google Scholar]
- Ainslie, M.; Miller, C.; Brown, B.; Schmitt, M. Cardiac MRI of patients with implanted electrical cardiac devices. Heart 2014, 100, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Petitjean, C.; Dacher, J.-N. A review of segmentation methods in short axis cardiac MR images. Med. Image Anal. 2011, 15, 169–184. [Google Scholar] [CrossRef] [PubMed]
- Cerqueira, M.D.; Weissman, N.J.; Dilsizian, V.; Jacobs, A.K.; Kaul, S.; Laskey, W.K.; Pennell, D.J.; Rumberger, J.A.; Ryan, T.; Verani, M.S.; et al. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart. A statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation 2002, 105, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Margeta, J.; Criminisi, A.; Cabrera Lozoya, R.; Lee, D.C.; Ayache, N. Fine-tuned convolutional neural nets for cardiac MRI acquisition plane recognition. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2017, 5, 339–349. [Google Scholar] [CrossRef]
- Zhang, L.; Gooya, A.; Dong, B.; Hua, R.; Petersen, S.E.; Medrano-Gracia, P.; Frangi, A.F. Automated quality assessment of cardiac MR images using convolutional neural networks. In Proceedings of the International Workshop on Simulation and Synthesis in Medical Imaging, Athens, Greece, 21 October 2016; pp. 138–145. [Google Scholar]
- Ho, N.; Kim, Y.C. Evaluation of transfer learning in deep convolutional neural network models for cardiac short axis slice classification. Sci. Rep. 2021, 11, 1839. [Google Scholar] [CrossRef]
- Dezaki, F.T.; Liao, Z.B.; Luong, C.; Girgis, H.; Dhungel, N.; Abdi, A.H.; Behnami, D.; Gin, K.; Rohling, R.; Abolmaesumi, P.; et al. Cardiac Phase Detection in Echocardiograms With Densely Gated Recurrent Neural Networks and Global Extrema Loss. IEEE Trans Med. Imaging 2019, 38, 1821–1832. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.; Van De Leemput, S.C.; Prokop, M.; Van Ginneken, B.; Manniesing, R. Image level training and prediction: Intracranial hemorrhage identification in 3D non-contrast CT. IEEE Access 2019, 7, 92355–92364. [Google Scholar] [CrossRef]
- Ye, H.; Gao, F.; Yin, Y.; Guo, D.; Zhao, P.; Lu, Y.; Wang, X.; Bai, J.; Cao, K.; Song, Q. Precise diagnosis of intracranial hemorrhage and subtypes using a three-dimensional joint convolutional and recurrent neural network. Eur. Radiol. 2019, 29, 6191–6201. [Google Scholar] [CrossRef]
- Islam, M.Z.; Islam, M.M.; Asraf, A. A combined deep CNN-LSTM network for the detection of novel coronavirus (COVID-19) using X-ray images. Inform. Med. Unlocked 2020, 20, 100412. [Google Scholar] [CrossRef]
- Yao, H.; Zhang, X.; Zhou, X.; Liu, S. Parallel structure deep neural network using CNN and RNN with an attention mechanism for breast cancer histology image classification. Cancers 2019, 11, 1901. [Google Scholar] [CrossRef]
- Lee, J.W.; Hur, J.H.; Yang, D.H.; Lee, B.Y.; Im, D.J.; Hong, S.J.; Kim, E.Y.; Park, E.-A.; Jo, Y.; Kim, J.J. Guidelines for cardiovascular magnetic resonance imaging from the Korean Society of Cardiovascular Imaging (KOSCI)-Part 2: Interpretation of cine, flow, and angiography data. Investig. Magn. Reson. Imaging 2019, 23, 316–327. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Schulz-Menger, J.; Bluemke, D.A.; Bremerich, J.; Flamm, S.D.; Fogel, M.A.; Friedrich, M.G.; Kim, R.J.; von Knobelsdorff-Brenkenhoff, F.; Kramer, C.M.; Pennell, D.J.; et al. Standardized image interpretation and post processing in cardiovascular magnetic resonance: Society for Cardiovascular Magnetic Resonance (SCMR) board of trustees task force on standardized post processing. J. Cardiovasc. Magn. Reson. 2013, 15, 35. [Google Scholar] [CrossRef] [PubMed]
- Selvadurai, B.S.N.; Puntmann, V.O.; Bluemke, D.A.; Ferrari, V.A.; Friedrich, M.G.; Kramer, C.M.; Kwong, R.Y.; Lombardi, M.; Prasad, S.K.; Rademakers, F.E.; et al. Definition of Left Ventricular Segments for Cardiac Magnetic Resonance Imaging. JACC Cardiovasc. Imaging 2018, 11, 926–928. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Chollet, F. Deep Learning with Python; Simon and Schuster: New York, NY, USA, 2021. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8697–8710. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fonseca, C.G.; Backhaus, M.; Bluemke, D.A.; Britten, R.D.; Chung, J.D.; Cowan, B.R.; Dinov, I.D.; Finn, J.P.; Hunter, P.J.; Kadish, A.H. The Cardiac Atlas Project—An imaging database for computational modeling and statistical atlases of the heart. Bioinformatics 2011, 27, 2288–2295. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Wang, H.; Shen, Y.; Wang, S.; Xiao, T.; Deng, L.; Wang, X.; Zhao, X. Ensemble of 3D densely connected convolutional network for diagnosis of mild cognitive impairment and Alzheimer’s disease. Neurocomputing 2019, 333, 145–156. [Google Scholar] [CrossRef]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Jianming, L. Convolutional Neural Networks for Medical Image Analysis: Full Training or Fine Tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Luo, W.; Li, Y.; Urtasun, R.; Zemel, R. Understanding the effective receptive field in deep convolutional neural networks. In Proceedings of the Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Im, D.J.; Hong, S.J.; Park, E.-A.; Kim, E.Y.; Jo, Y.; Kim, J.; Park, C.H.; Yong, H.S.; Lee, J.W.; Hur, J.H. Guidelines for cardiovascular magnetic resonance imaging from the Korean Society of Cardiovascular Imaging—Part 3: Perfusion, delayed enhancement, and T1-and T2 mapping. Korean J. Radiol. 2019, 20, 1562–1582. [Google Scholar] [CrossRef]
- Fair, M.J.; Gatehouse, P.D.; DiBella, E.V.; Firmin, D.N. A review of 3D first-pass, whole-heart, myocardial perfusion cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2015, 17, 68. [Google Scholar] [CrossRef]
- Qi, H.; Jaubert, O.; Bustin, A.; Cruz, G.; Chen, H.; Botnar, R.; Prieto, C. Free-running 3D whole heart myocardial T1 mapping with isotropic spatial resolution. Magn. Reson. Med. 2019, 82, 1331–1342. [Google Scholar] [CrossRef]
| Training | Validation | Testing | Total | |
|---|---|---|---|---|
| Number of subjects | 576 | 214 | 184 | 974 |
| Percentage (%) | 59.1 | 22.0 | 18.9 | 100 |
| Model Type | Training | Validation | Testing | Total | |
|---|---|---|---|---|---|
| CNN * | Number of samples | 12,070 | 4594 | 3868 | 20,532 |
| Percentage (%) | 58.8 | 22.4 | 18.8 | 100 | |
| CNN-RNN ** | Number of samples | 1152 | 428 | 368 | 1948 |
| Percentage (%) | 59.1 | 22.0 | 18.9 | 100 |
| Class Label | Total | ||||||
|---|---|---|---|---|---|---|---|
| oap | ap | mid | bs | obs | |||
| Training | Number of images | 1878 | 2784 | 2800 | 2132 | 2476 | 12,070 |
| Percentage (%) | 15.5 | 23.1 | 23.2 | 17.7 | 20.5 | 100 | |
| Validation | Number of images | 710 | 1086 | 1114 | 751 | 933 | 4594 |
| Percentage (%) | 15.5 | 23.6 | 24.2 | 16.4 | 20.3 | 100 | |
| CNN Base Network | Number of Model Parameters | ImageNet Top-1 Accuracy | Number of Features after GAP * | Batch Size for CNN | Batch Size for CNN-RNN |
|---|---|---|---|---|---|
| EfficientNetB0 | 5.3 M | 77.1% | 1280 | 32 | 2 |
| MobileNet | 4.2 M | 70.6% | 1024 | 32 | 2 |
| NASNetMobile | 5.3 M | 74.4% | 1056 | 32 | 2 |
| ResNet50V2 | 25.6 M | 76.0% | 2048 | 16 | 2 |
| CNN Base Network | RNN Type | F1-Score | AUC * | Accuracy | |||||
|---|---|---|---|---|---|---|---|---|---|
| oap | ap | mid | bs | obs | |||||
| CNN | MobileNet | - | 0.759 | 0.717 | 0.771 | 0.740 | 0.902 | 0.957 | 0.779 |
| ResNet50V2 | - | 0.748 | 0.668 | 0.726 | 0.688 | 0.868 | 0.944 | 0.740 | |
| NASNetMobile | - | 0.680 | 0.585 | 0.625 | 0.570 | 0.790 | 0.904 | 0.650 | |
| EfficientNetB0 | - | 0.761 | 0.696 | 0.729 | 0.716 | 0.889 | 0.946 | 0.757 | |
| CNN-RNN | MobileNet | 2-LSTM | 0.811 | 0.783 | 0.827 | 0.800 | 0.918 | 0.972 | 0.829 |
| Bi-LSTM | 0.825 | 0.779 | 0.812 | 0.793 | 0.922 | 0.972 | 0.827 | ||
| 2-GRU | 0.808 | 0.769 | 0.814 | 0.785 | 0.909 | 0.970 | 0.817 | ||
| Bi-GRU | 0.819 | 0.784 | 0.801 | 0.784 | 0.907 | 0.970 | 0.819 | ||
| ResNet50V2 | 2-LSTM | 0.759 | 0.763 | 0.804 | 0.759 | 0.904 | 0.966 | 0.801 | |
| Bi-LSTM | 0.821 | 0.781 | 0.782 | 0.769 | 0.908 | 0.968 | 0.812 | ||
| 2-GRU | 0.781 | 0.772 | 0.788 | 0.721 | 0.882 | 0.963 | 0.791 | ||
| Bi-GRU | 0.816 | 0.746 | 0.755 | 0.758 | 0.909 | 0.962 | 0.796 | ||
| NASNetMobile | 2-LSTM | 0.771 | 0.713 | 0.733 | 0.683 | 0.861 | 0.952 | 0.753 | |
| Bi-LSTM | 0.809 | 0.713 | 0.772 | 0.711 | 0.874 | 0.960 | 0.777 | ||
| 2-GRU | 0.738 | 0.721 | 0.740 | 0.667 | 0.853 | 0.947 | 0.746 | ||
| Bi-GRU | 0.806 | 0.747 | 0.770 | 0.712 | 0.869 | 0.958 | 0.780 | ||
| EfficientNetB0 | 2-LSTM | 0.805 | 0.772 | 0.800 | 0.777 | 0.901 | 0.967 | 0.811 | |
| Bi-LSTM | 0.827 | 0.772 | 0.800 | 0.764 | 0.904 | 0.969 | 0.814 | ||
| 2-GRU | 0.811 | 0.763 | 0.793 | 0.764 | 0.909 | 0.965 | 0.808 | ||
| Bi-GRU | 0.822 | 0.785 | 0.801 | 0.767 | 0.910 | 0.969 | 0.817 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, N.; Kim, Y.-C. Estimation of Cardiac Short Axis Slice Levels with a Cascaded Deep Convolutional and Recurrent Neural Network Model. Tomography 2022, 8, 2749-2760. https://doi.org/10.3390/tomography8060229
Ho N, Kim Y-C. Estimation of Cardiac Short Axis Slice Levels with a Cascaded Deep Convolutional and Recurrent Neural Network Model. Tomography. 2022; 8(6):2749-2760. https://doi.org/10.3390/tomography8060229
Chicago/Turabian StyleHo, Namgyu, and Yoon-Chul Kim. 2022. "Estimation of Cardiac Short Axis Slice Levels with a Cascaded Deep Convolutional and Recurrent Neural Network Model" Tomography 8, no. 6: 2749-2760. https://doi.org/10.3390/tomography8060229
APA StyleHo, N., & Kim, Y.-C. (2022). Estimation of Cardiac Short Axis Slice Levels with a Cascaded Deep Convolutional and Recurrent Neural Network Model. Tomography, 8(6), 2749-2760. https://doi.org/10.3390/tomography8060229






