Detection of Lung Nodules in Micro-CT Imaging Using Deep Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Animal Model and Datasets
2.2. Micro-CT Imaging
2.3. Lung Segmentation
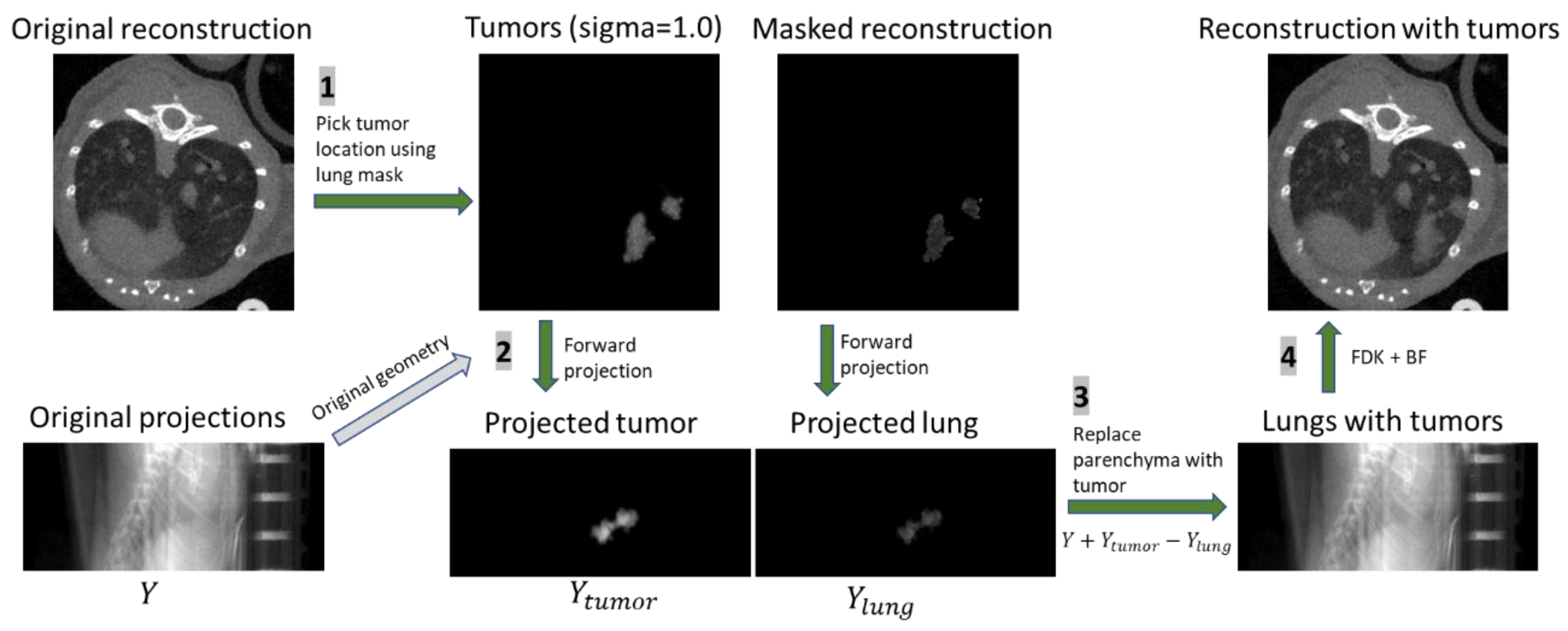
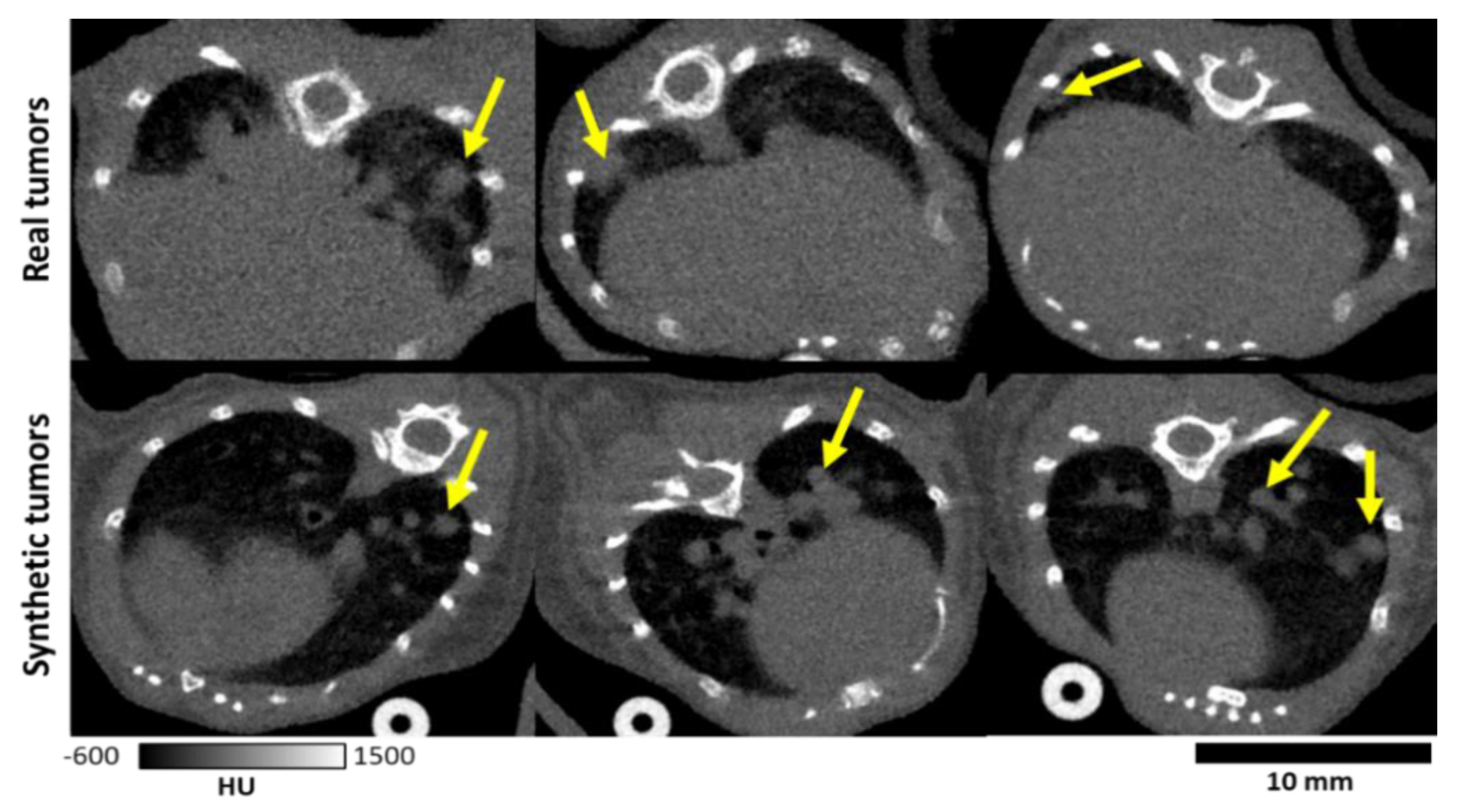
2.4. Data Augmentation with Simulated Image Generation
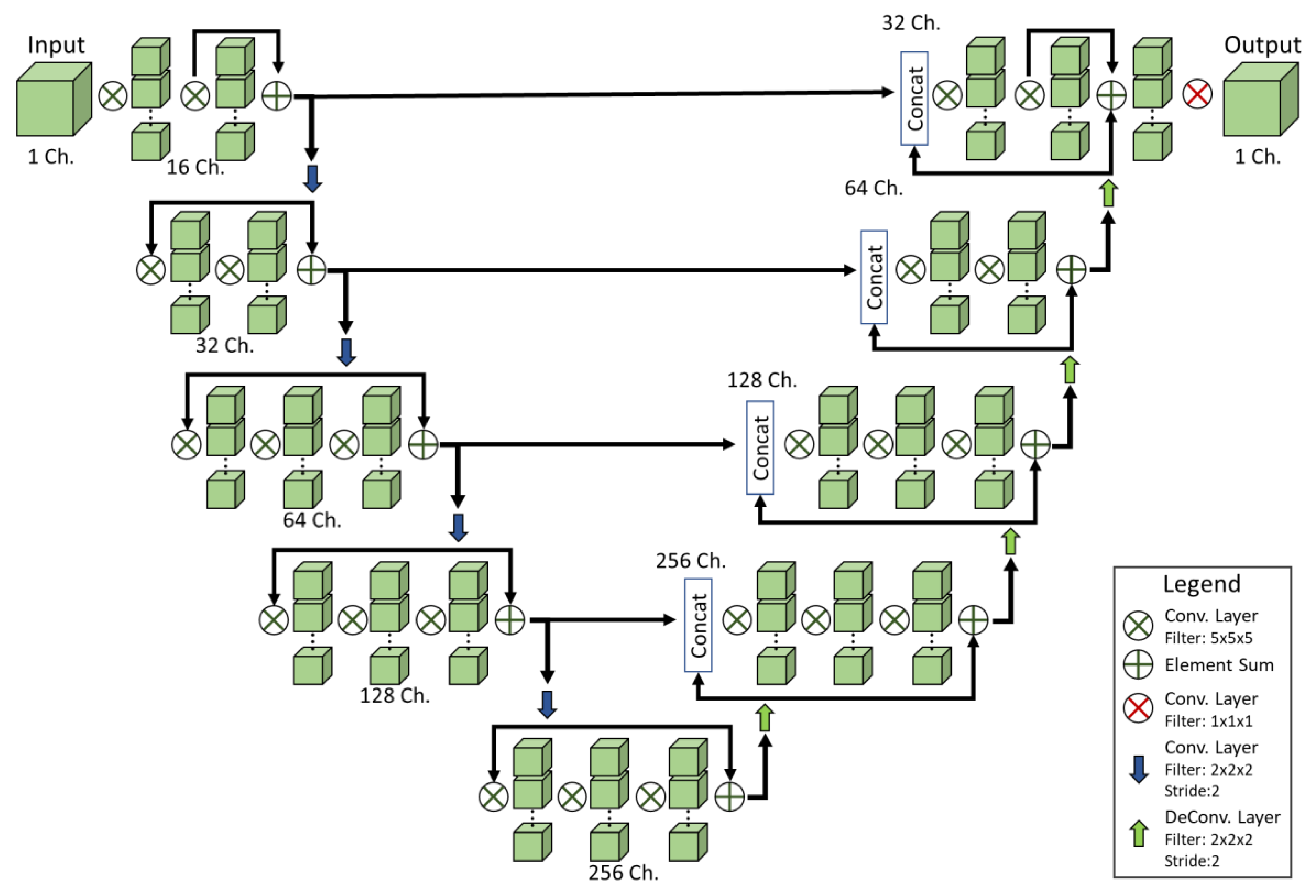
2.5. Network Structure
2.6. Detection Post Processing
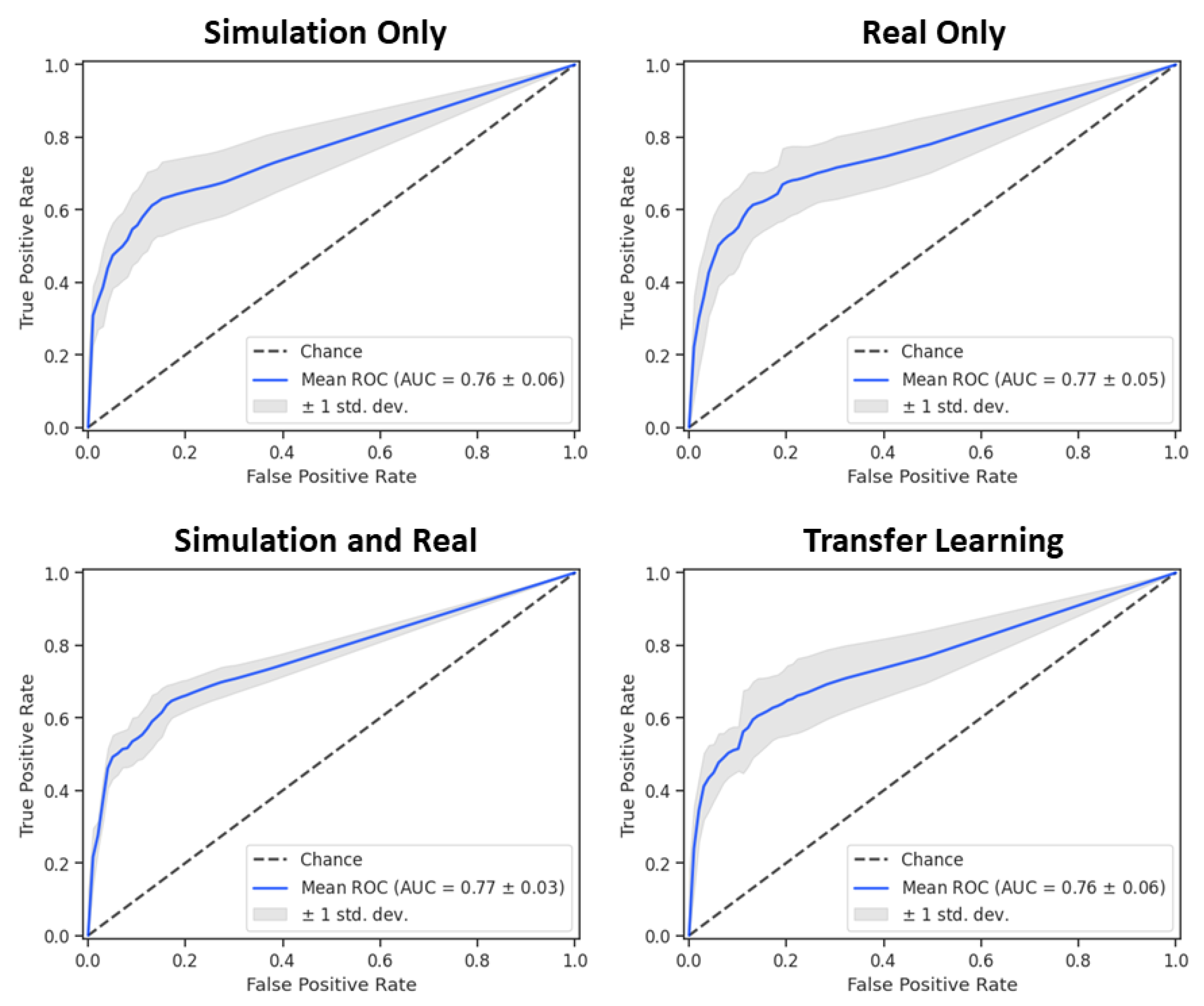
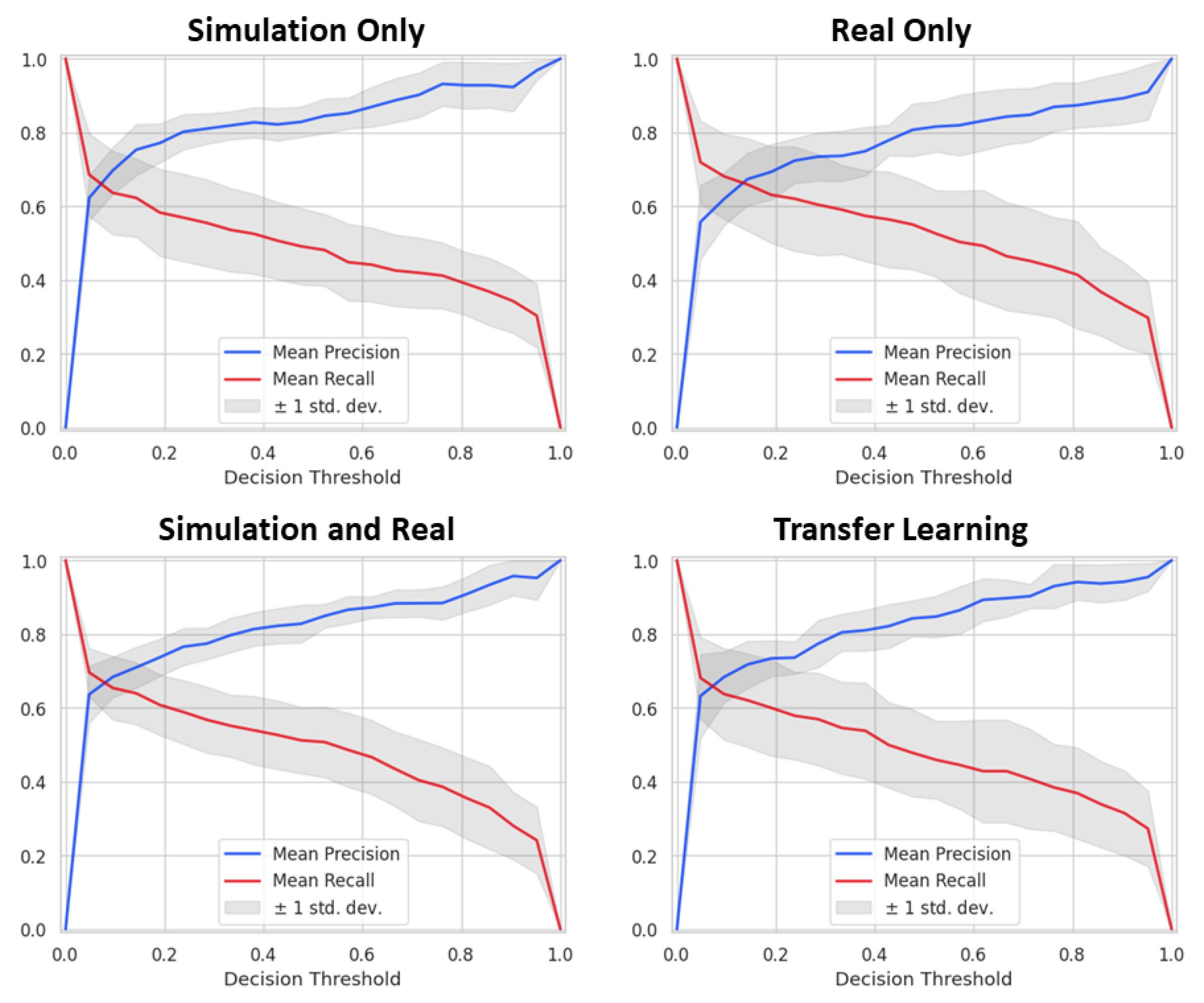
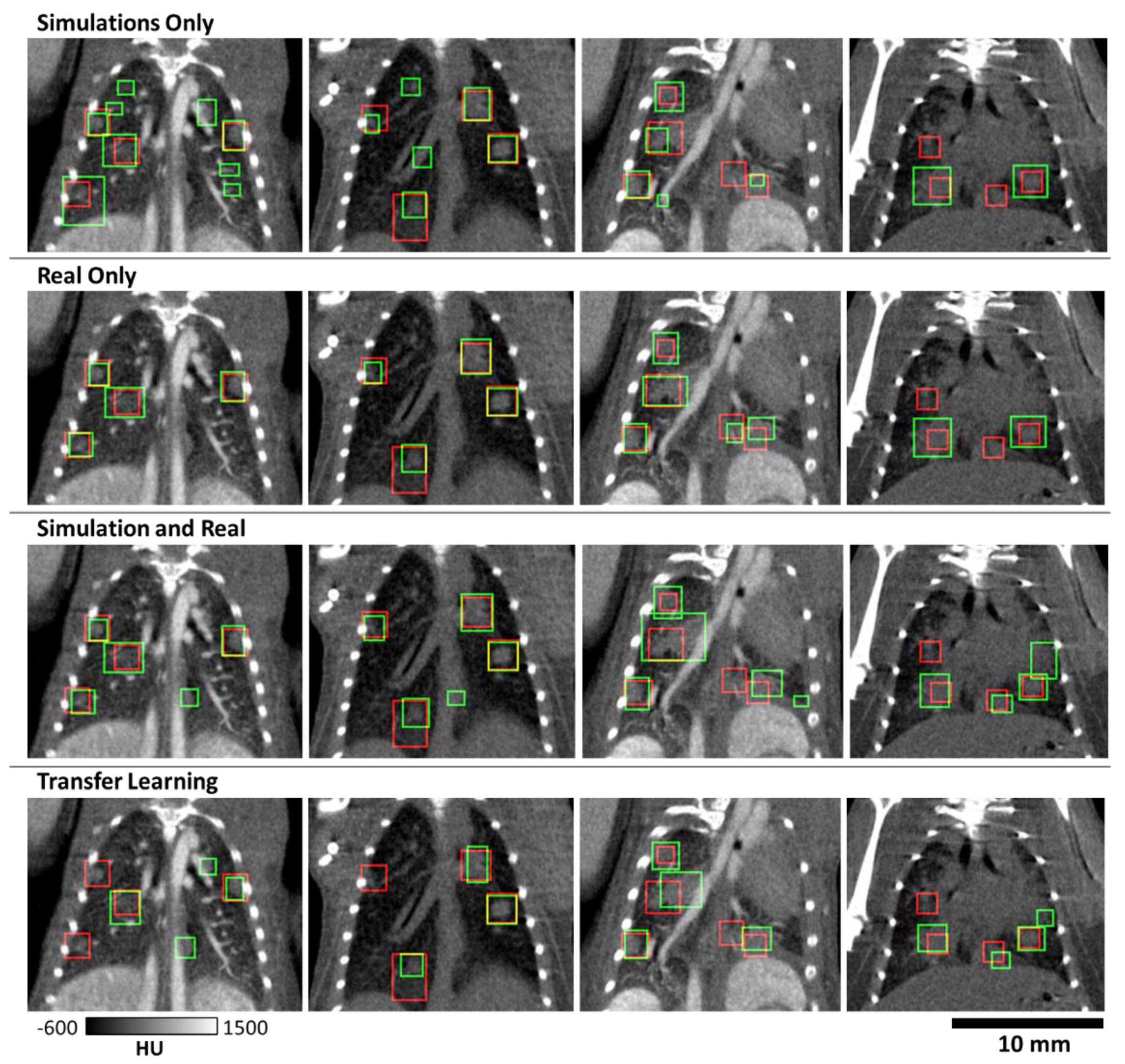
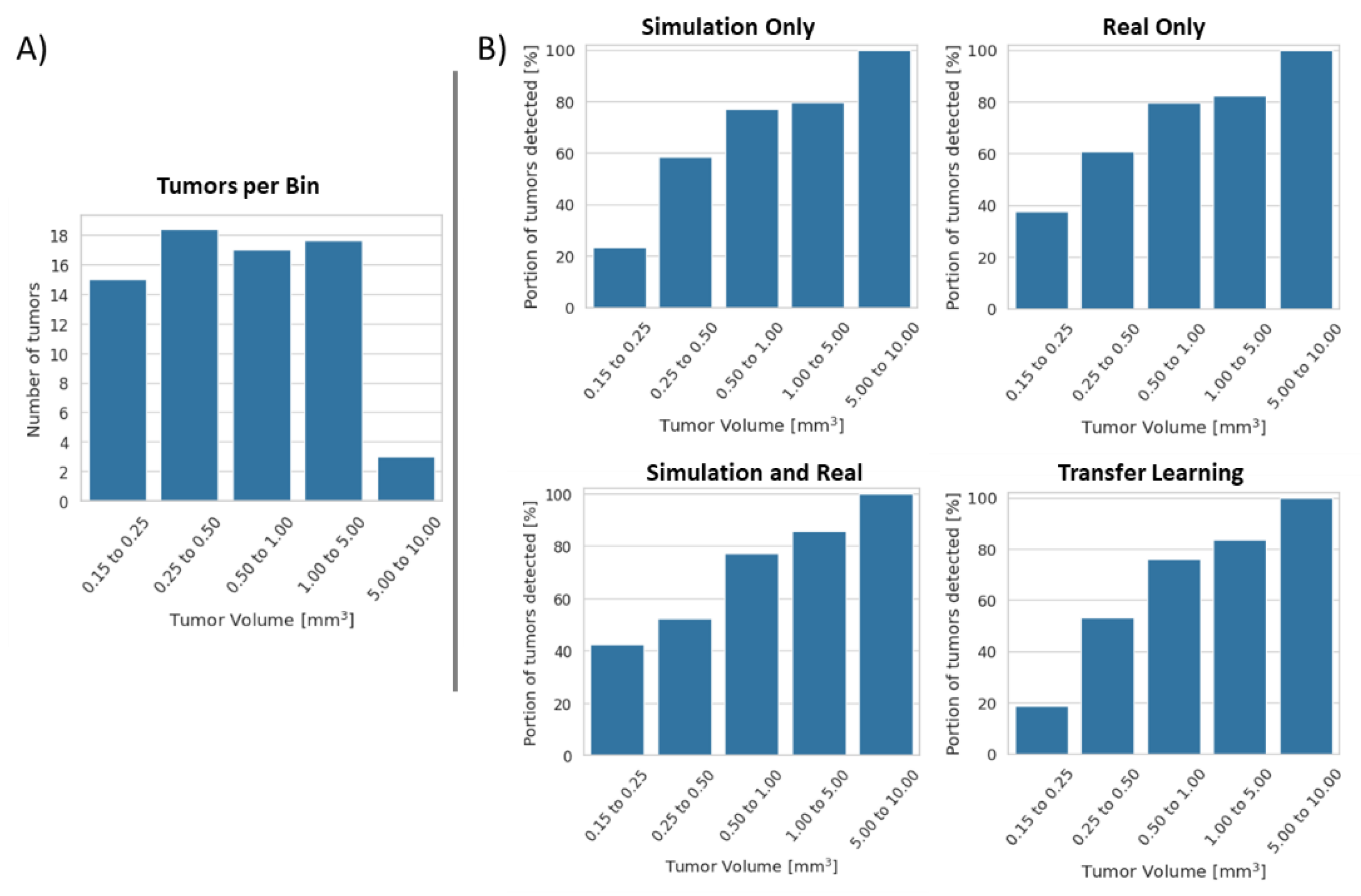
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Cheng, K.; Walton, Z.; Wang, Y.; Ebi, H.; Shimamura, T.; Liu, Y.; Tupper, T.; Ouyang, J.; Li, J.; et al. A murine lung cancer co-clinical trial identifies genetic modifiers of therapeutic response. Nature 2012, 483, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Nishino, M.; Sacher, A.G.; Gandhi, L.; Chen, Z.; Akbay, E.; Fedorov, A.; Westin, C.F.; Hatabu, H.; Johnson, B.E.; Hammerman, P.; et al. Co-clinical quantitative tumor volume imaging in ALK-rearranged NSCLC treated with crizotinib. Eur. J. Radiol. 2017, 88, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Ruggeri, B.A.; Camp, F.; Miknyoczki, S. Animal models of disease: Pre-clinical animal models of cancer and their applications and utility in drug discovery. Biochem. Pharmacol. 2014, 87, 150–161. [Google Scholar] [CrossRef] [PubMed]
- Blocker, S.J.; Mowery, Y.M.; Holbrook, M.D.; Qi, Y.; Kirsch, D.G.; Johnson, G.A.; Badea, C.T. Bridging the translational gap: Implementation of multimodal small animal imaging strategies for tumor burden assessment in a co-clinical trial. PLoS ONE 2019, 14, e0207555. [Google Scholar] [CrossRef]
- Blocker, S.J.; Holbrook, M.D.; Mowery, Y.M.; Sullivan, D.C.; Badea, C.T. The impact of respiratory gating on improving volume measurement of murine lung tumors in micro-CT imaging. PLoS ONE 2020, 15, e0225019. [Google Scholar] [CrossRef]
- Bidola, P.; e Silva, J.M.d.S.; Achterhold, K.; Munkhbaatar, E.; Jost, P.J.; Meinhardt, A.-L.; Taphorn, K.; Zdora, M.-C.; Pfeiffer, F.; Herzen, J. A step towards valid detection and quantification of lung cancer volume in experimental mice with contrast agent-based X-ray microtomography. Sci. Rep. 2019, 9, 1325. [Google Scholar] [CrossRef]
- Deng, L.; Tang, H.; Qiang, J.; Wang, J.; Xiao, S. Blood Supply of Early Lung Adenocarcinomas in Mice and the Tumor-supplying Vessel Relationship: A Micro-CT Angiography Study. Cancer Prev. Res. 2020, 13, 989–996. [Google Scholar] [CrossRef]
- Cavanaugh, D.; Johnson, E.; Price, R.E.; Kurie, J.; Travis, E.L.; Cody, D.D. In vivo respiratory-gated micro-CT imaging in small-animal oncology models. Mol. Imaging 2004, 3, 55–62. [Google Scholar] [CrossRef]
- De Clerck, N.M.; Meurrens, K.; Weiler, H.; Van Dyck, D.; Van Houtte, G.; Terpstra, P.; Postnov, A.A. High-resolution X-ray microtomography for the detection of lung tumors in living mice. Neoplasia 2004, 6, 374–379. [Google Scholar] [CrossRef] [PubMed]
- Namati, E.; Thiesse, J.; Sieren, J.C.; Ross, A.; Hoffman, E.A.; McLennan, G. Longitudinal assessment of lung cancer progression in the mouse using in vivo micro-CT imaging. Med. Phys. 2010, 37, 4793–4805. [Google Scholar] [CrossRef]
- Gruetzemacher, R.; Gupta, A.; Paradice, D. 3D deep learning for detecting pulmonary nodules in CT scans. J. Am. Med. Inform. Assoc. 2018, 25, 1301–1310. [Google Scholar] [CrossRef]
- Liu, M.; Dong, J.; Dong, X.; Yu, H.; Qi, L. Segmentation of Lung Nodule in CT Images Based on Mask R-CNN. In Proceedings of the 2018 9th International Conference on Awareness Science and Technology (iCAST), Fukuoka, Japan, 19–21 September 2018; pp. 1–6. [Google Scholar]
- Pehrson, L.M.; Nielsen, M.B.; Ammitzbøl Lauridsen, C. Automatic Pulmonary Nodule Detection Applying Deep Learning or Machine Learning Algorithms to the LIDC-IDRI Database: A Systematic Review. Diagnostics 2019, 9, 29. [Google Scholar] [CrossRef]
- Shaukat, F.; Raja, G.; Gooya, A.; Frangi, A.F. Fully automatic detection of lung nodules in CT images using a hybrid feature set. Med. Phys. 2017, 44, 3615–3629. [Google Scholar] [CrossRef]
- Su, Y.; Li, D.; Chen, X. Lung Nodule Detection based on Faster R-CNN Framework. Comput. Methods Programs Biomed. 2021, 200, 105866. [Google Scholar] [CrossRef]
- Zhang, G.; Jiang, S.; Yang, Z.; Gong, L.; Ma, X.; Zhou, Z.; Bao, C.; Liu, Q. Automatic nodule detection for lung cancer in CT images: A review. Comput. Biol. Med. 2018, 103, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Armato, S.G.; McLennan, G.; Bidaut, L.; McNitt-Gray, M.F.; Meyer, C.R.; Reeves, A.P.; Zhao, B.; Aberle, D.R.; Henschke, C.I.; Hoffman, E.A.; et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): A Completed Reference Database of Lung Nodules on CT Scans. Med. Phys. 2011, 38, 915–931. [Google Scholar] [CrossRef] [PubMed]
- Setio, A.A.A.; Traverso, A.; de Bel, T.; Berens, M.S.N.; van den, B.C.; Cerello, P.; Chen, H.; Dou, Q.; Fantacci, M.E.; Geurts, B.; et al. Validation, comparison, and combination of algorithms for automatic detection of pulmonary nodules in computed tomography images: The LUNA16 challenge. Med. Image Anal. 2017, 42, 1–13. [Google Scholar] [CrossRef]
- Holbrook, M.D.; Clark, D.P.; Patel, R.; Qi, Y.; Mowery, Y.M.; Badea, C.T. Towards deep learning segmentation of lung nodules using micro-CT data. In Proceedings of the Medical Imaging 2021: Biomedical Applications in Molecular, Structural, and Functional Imaging; International Society for Optics and Photonics, San Diego, CA, USA, 1–5 AUgust 2021; Volume 11600, p. 116000. [Google Scholar]
- DuPage, M.; Dooley, A.L.; Jacks, T. Conditional mouse lung cancer models using adenoviral or lentiviral delivery of Cre recombinase. Nat. Protoc. 2009, 4, 1064–1072. [Google Scholar] [CrossRef] [PubMed]
- Perez, B.A.; Ghafoori, A.P.; Lee, C.-L.; Johnston, S.M.; Li, Y.I.; Moroshek, J.G.; Ma, Y.; Mukherjee, S.; Kim, Y.; Badea, C.T.; et al. Assessing the Radiation Response of Lung Cancer with Different Gene Mutations Using Genetically Engineered Mice. Front. Oncol. 2013, 3, 72. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.P.; Ghaghada, K.; Moding, E.J.; Kirsch, D.G.; Badea, C.T. In vivo characterization of tumor vasculature using iodine and gold nanoparticles and dual energy micro-CT. Phys. Med. Biol. 2013, 58, 1683–1704. [Google Scholar] [CrossRef] [PubMed]
- Mukundan, S.; Ghaghada, K.B.; Badea, C.T.; Kao, C.-Y.; Hedlund, L.W.; Provenzale, J.M.; Johnson, G.A.; Chen, E.; Bellamkonda, R.V.; Annapragada, A. A Liposomal Nanoscale Contrast Agent for Preclinical CT in Mice. Am. J. Roentgenol. 2006, 186, 300–307. [Google Scholar] [CrossRef]
- Feldkamp, L.A.; Davis, L.C.; Kress, J.W. Practical cone-beam algorithm. J. Opt. Soc. Am. A 1984, 1, 612–619. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat. No.98CH36271), Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar]
- Robins, M.; Solomon, J.; Sahbaee, P.; Sedlmair, M.; Choudhury, K.R.; Pezeshk, A.; Sahiner, B.; Samei, E. Techniques for virtual lung nodule insertion: Volumetric and morphometric comparison of projection-based and image-based methods for quantitative CT. Phys. Med. Biol. 2017, 62, 7280–7299. [Google Scholar] [CrossRef][Green Version]
- Yushkevich, P.A.; Piven, J.; Hazlett, H.C.; Smith, R.G.; Ho, S.; Gee, J.C.; Gerig, G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. NeuroImage 2006, 31, 1116–1128. [Google Scholar] [CrossRef]
- Milletari, F.; Navab, N.; Ahmadi, S. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning Research, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Hossain, S.; Najeeb, S.; Shahriyar, A.; Abdullah, Z.R.; Haque, M.A. A Pipeline for Lung Tumor Detection and Segmentation from CT Scans Using Dilated Convolutional Neural Networks. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 1348–1352. [Google Scholar]
- Opfer, R.; Wiemker, R. Performance analysis for computer-aided lung nodule detection on LIDC data. In Proceedings of the Medical Imaging 2007: Image Perception, Observer Performance, and Technology Assessment; International Society for Optics and Photonics, San Diego, CA, USA, 20 March 2007; Volume 6515, p. 65151C. [Google Scholar]
- Jacobs, C.; van Rikxoort, E.M.; Murphy, K.; Prokop, M.; Schaefer-Prokop, C.M.; van Ginneken, B. Computer-aided detection of pulmonary nodules: A comparative study using the public LIDC/IDRI database. Eur. Radiol. 2016, 26, 2139–2147. [Google Scholar] [CrossRef] [PubMed]

| Training | True Positives | False Positives | False Negatives | Precision | Recall | Dice |
|---|---|---|---|---|---|---|
| Simulation Only | 138 | 84 | 69 | 0.622 | 0.667 | 0.643 |
| Real Only | 148 | 120 | 59 | 0.552 | 0.715 | 0.623 |
| Simulation and Real | 147 | 91 | 60 | 0.618 | 0.710 | 0.661 |
| Transfer Learning | 139 | 72 | 68 | 0.659 | 0.671 | 0.665 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holbrook, M.D.; Clark, D.P.; Patel, R.; Qi, Y.; Bassil, A.M.; Mowery, Y.M.; Badea, C.T. Detection of Lung Nodules in Micro-CT Imaging Using Deep Learning. Tomography 2021, 7, 358-372. https://doi.org/10.3390/tomography7030032
Holbrook MD, Clark DP, Patel R, Qi Y, Bassil AM, Mowery YM, Badea CT. Detection of Lung Nodules in Micro-CT Imaging Using Deep Learning. Tomography. 2021; 7(3):358-372. https://doi.org/10.3390/tomography7030032
Chicago/Turabian StyleHolbrook, Matthew D., Darin P. Clark, Rutulkumar Patel, Yi Qi, Alex M. Bassil, Yvonne M. Mowery, and Cristian T. Badea. 2021. "Detection of Lung Nodules in Micro-CT Imaging Using Deep Learning" Tomography 7, no. 3: 358-372. https://doi.org/10.3390/tomography7030032
APA StyleHolbrook, M. D., Clark, D. P., Patel, R., Qi, Y., Bassil, A. M., Mowery, Y. M., & Badea, C. T. (2021). Detection of Lung Nodules in Micro-CT Imaging Using Deep Learning. Tomography, 7(3), 358-372. https://doi.org/10.3390/tomography7030032







