Single Sequential Trajectory Optimization with Centroidal Dynamics and Whole-Body Kinematics for Vertical Jump of Humanoid Robot
Abstract
1. Introduction
- (1)
- A single sequential kino-dynamic trajectory optimization framework is proposed to solve the optimal jumping motion problem. The whole-body trajectory is effectively generated by a single sequential optimization, which is an efficient solution.
- (2)
- This optimization framework can generate vertical jumping motions with launching and flight phases, which are essential for highly dynamic motions.
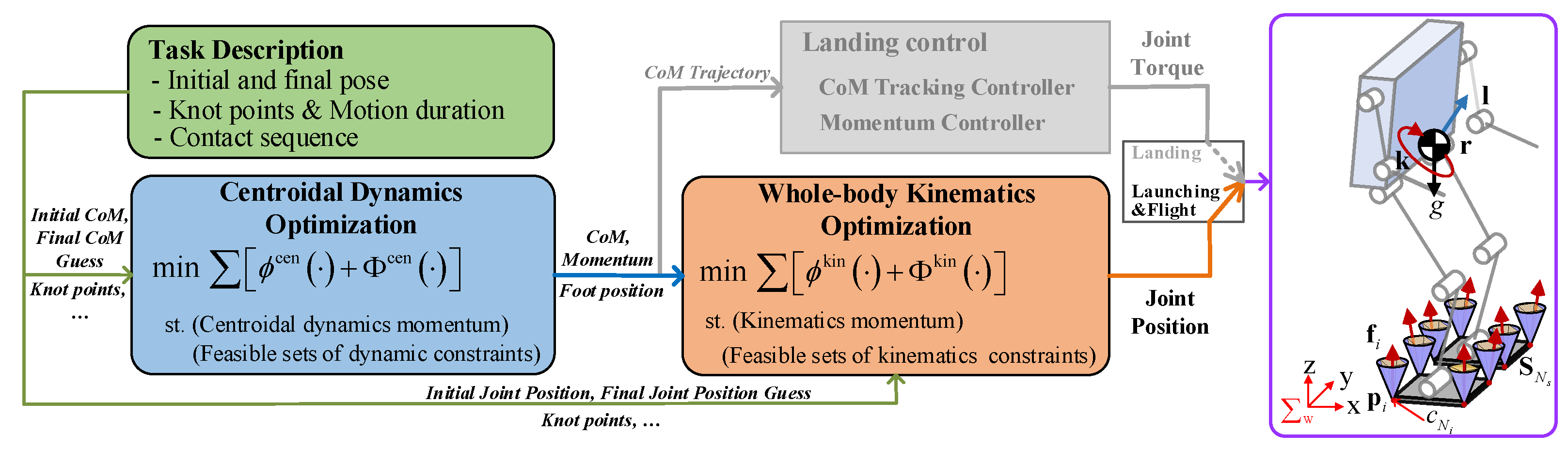
2. Single Sequential Kino-Dynamic Trajectory Optimization
2.1. Centroidal Dynamics Optimization
2.2. Whole-Body Kinematics Optimization
3. Simulation and Experimental Results
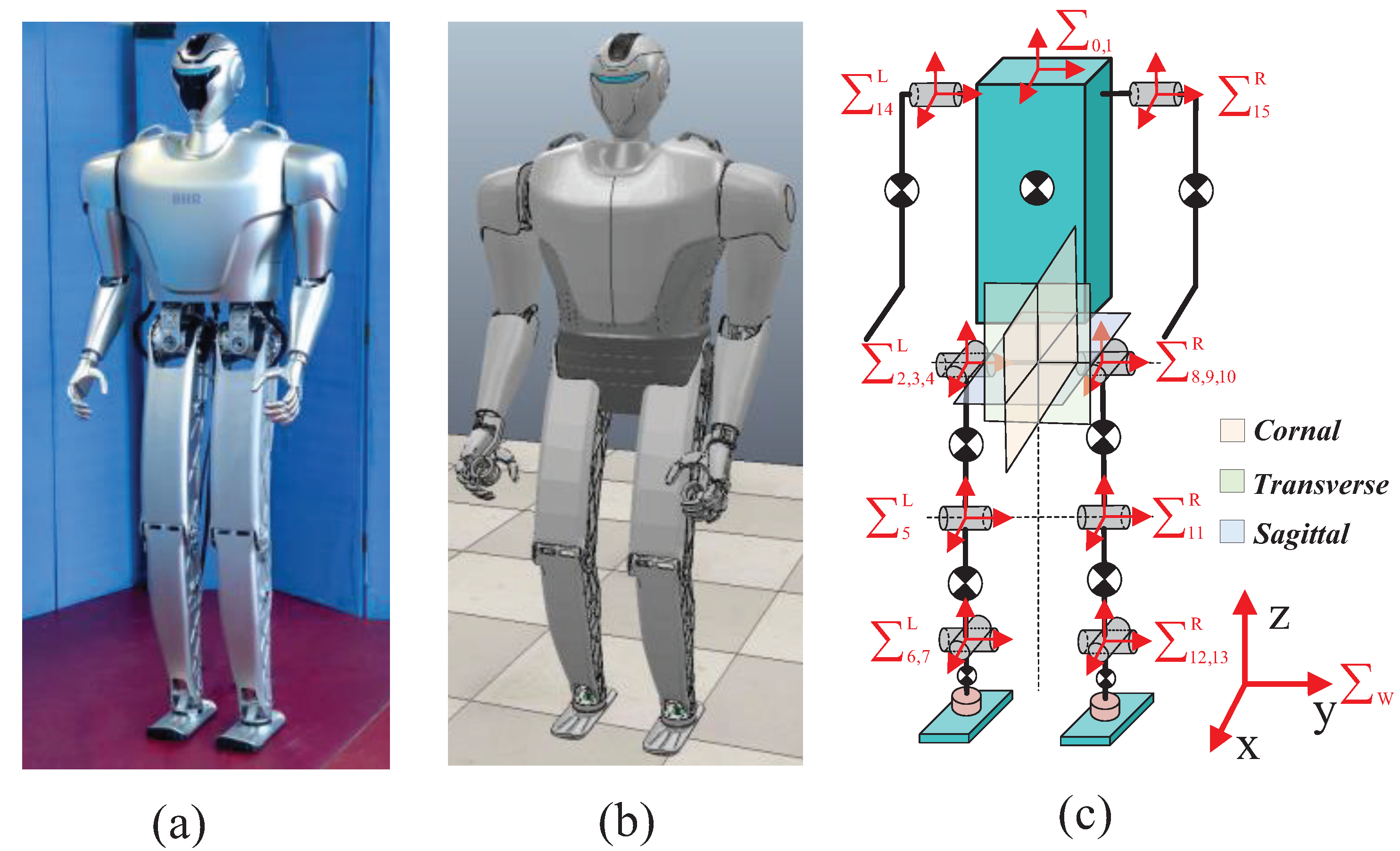
3.1. Validation Setup
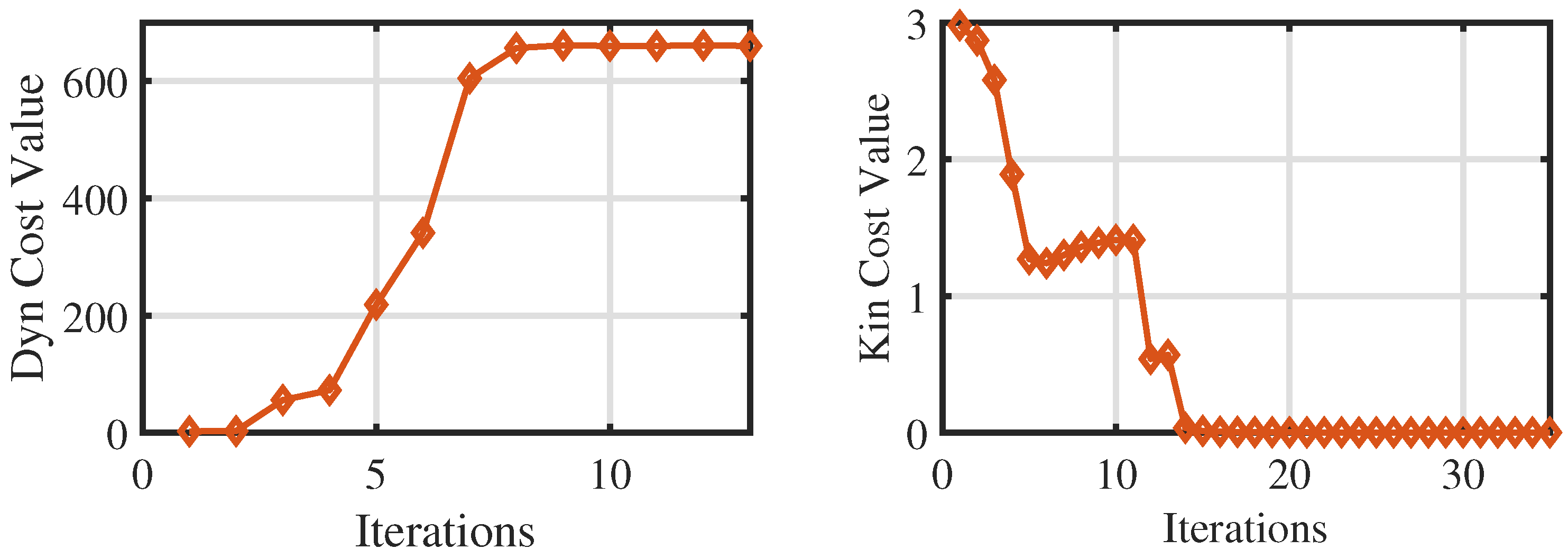
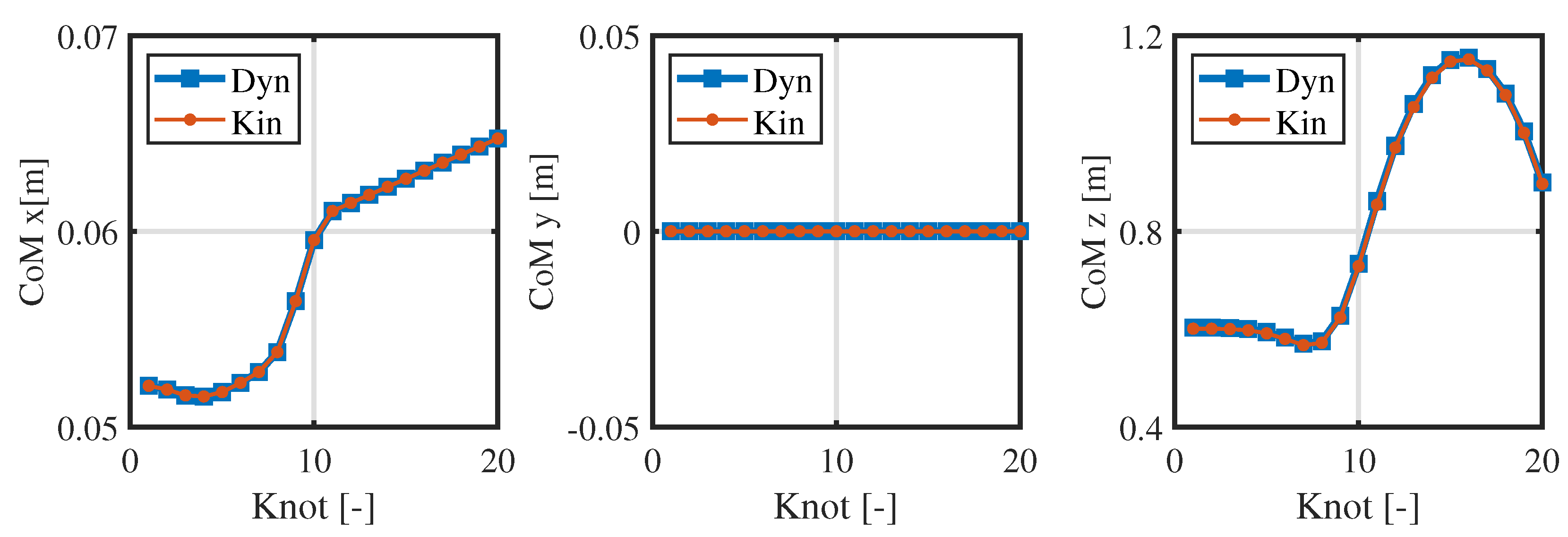
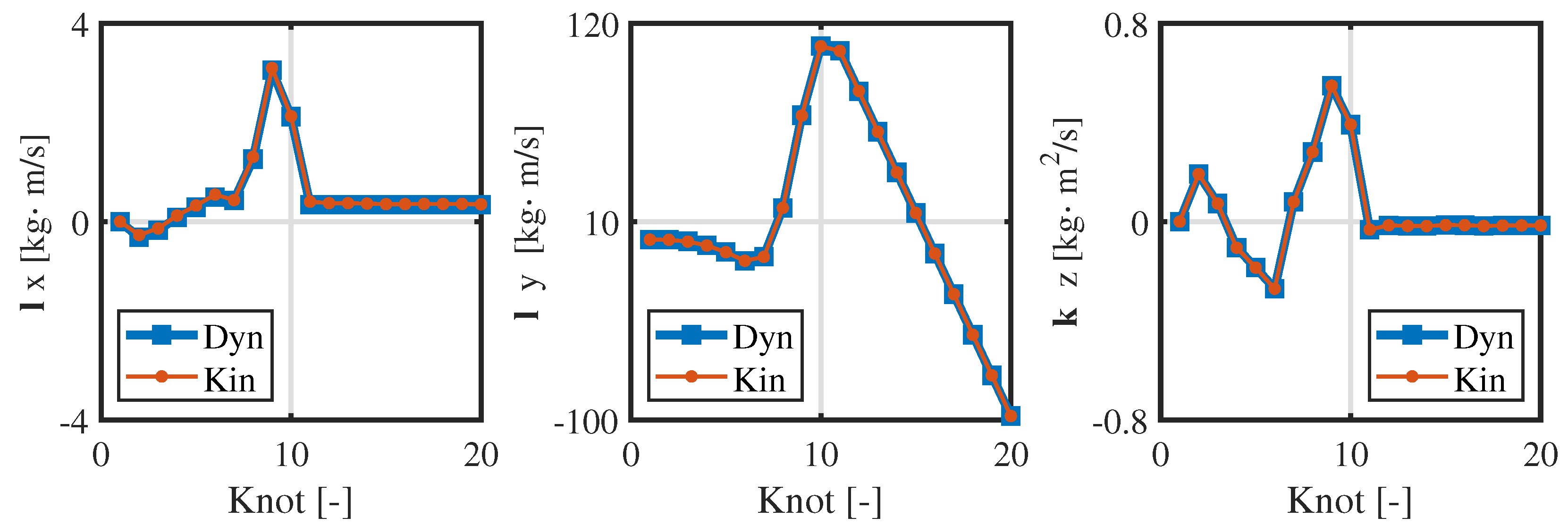
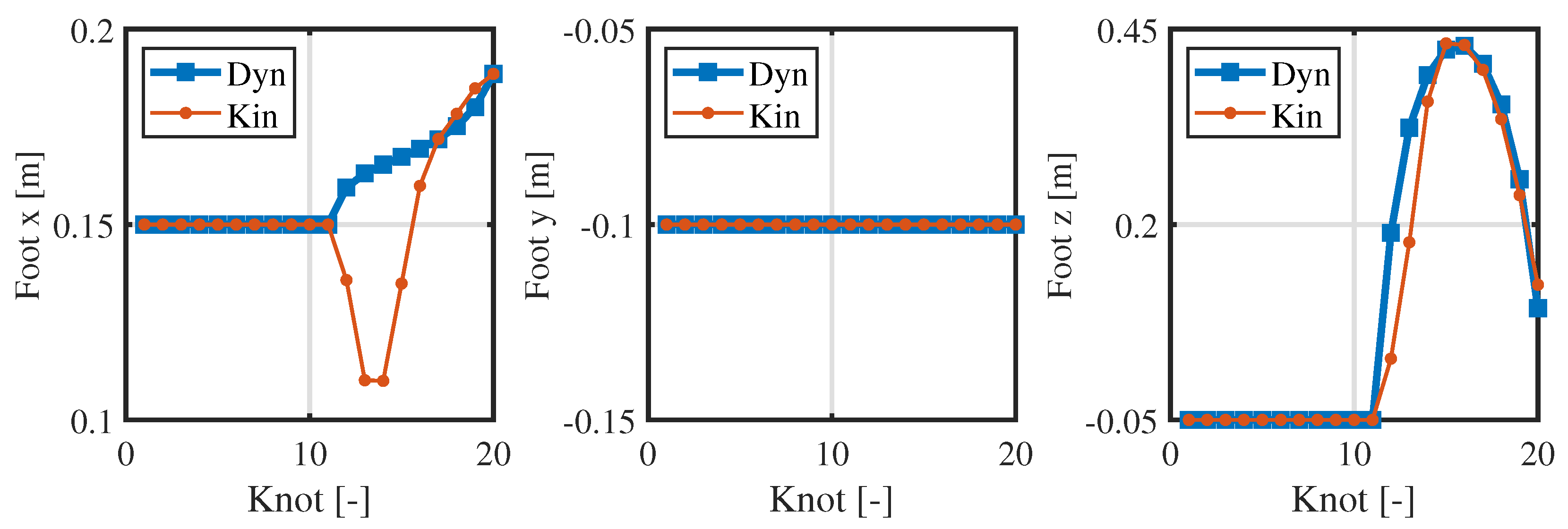
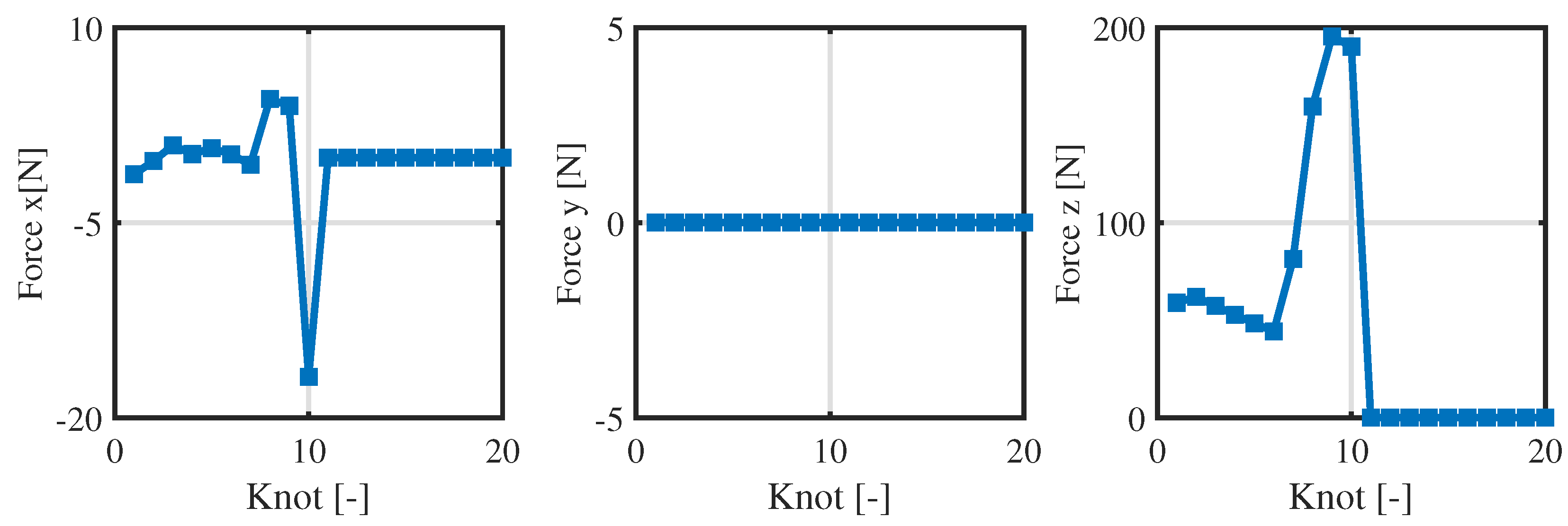
3.2. Numerical Optimization
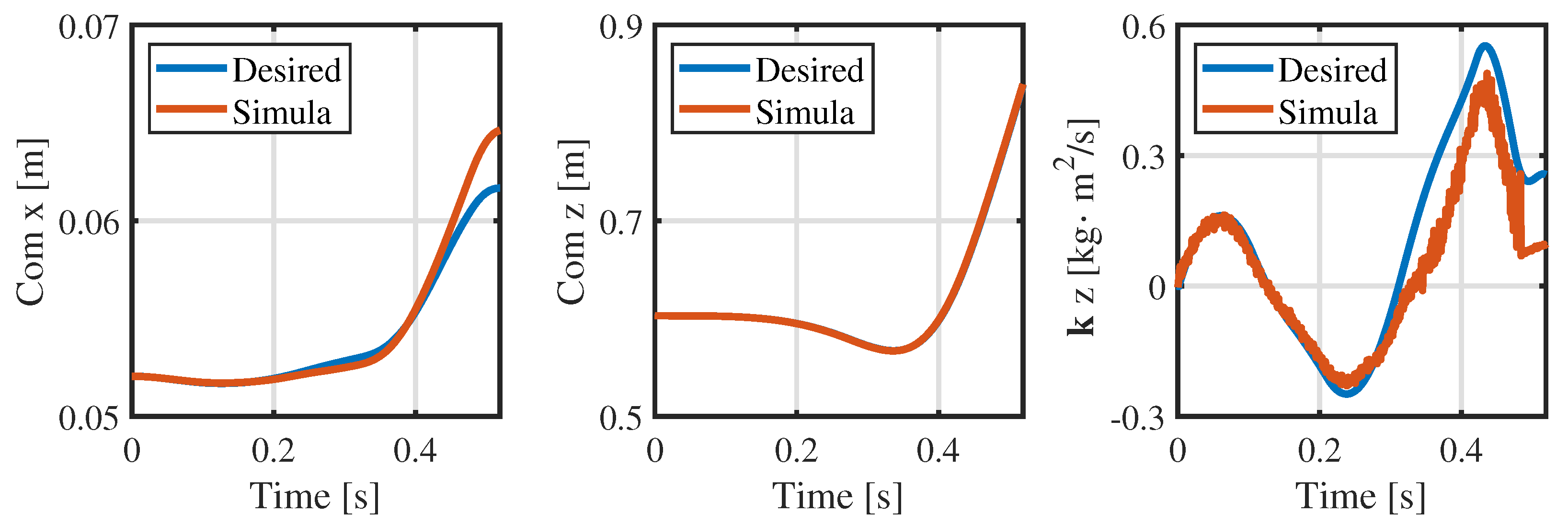
3.3. Simulations
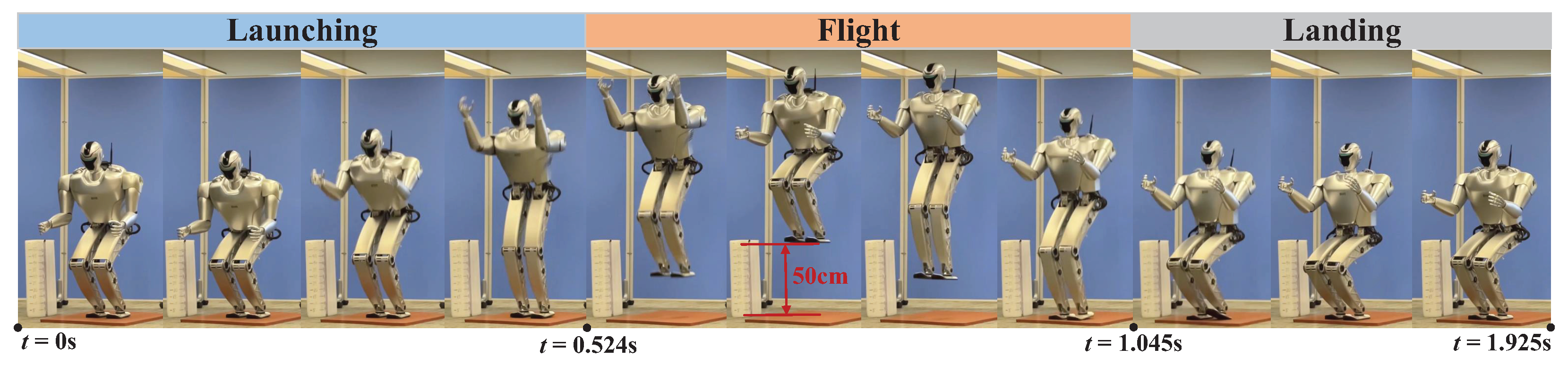
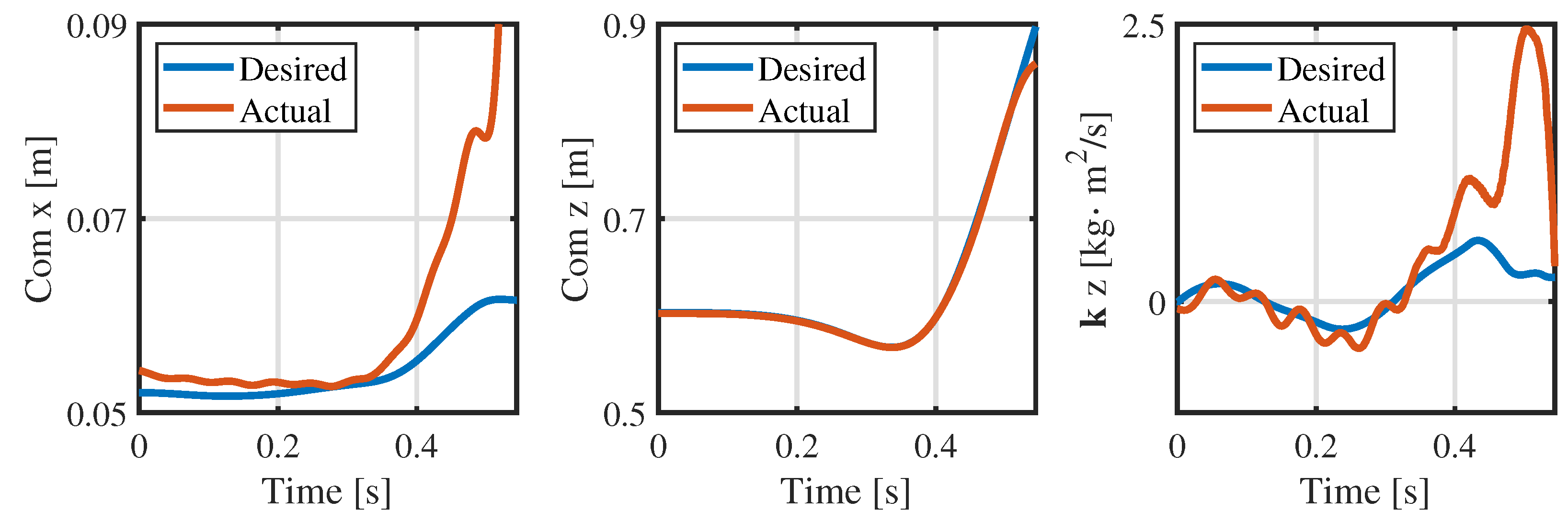
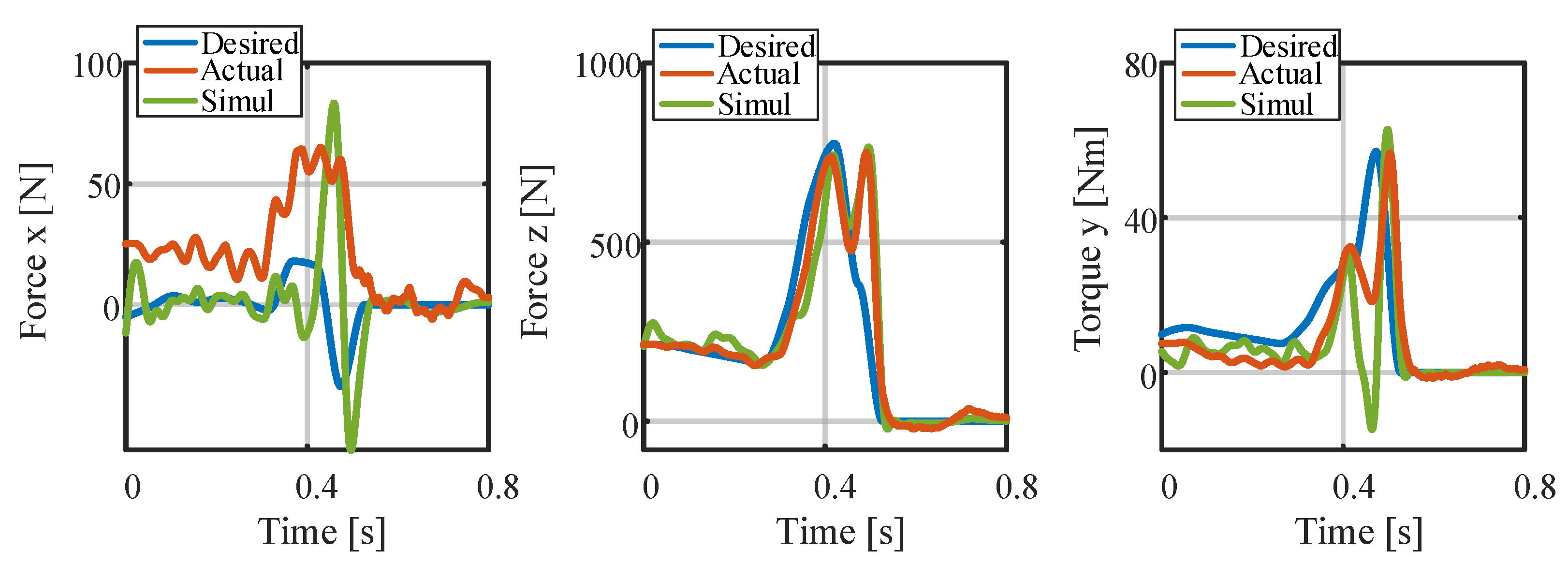
3.4. Experiments

4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Choi, B.; Lee, W.; Park, G.; Lee, Y.; Min, J.; Hong, S. Development and control of a military rescue robot for casualty extraction task. J. Field Robot. 2019, 36, 656–676. [Google Scholar] [CrossRef]
- Kumagai, I.; Morisawa, M.; Sakaguchi, T.; Nakaoka, S.; Kaneko, K.; Kaminaga, H.; Kajita, S.; Benallegue, M.; Cisneros, R.; Kanehiro, F. Toward industrialization of humanoid robots: Autonomous plasterboard installation to improve safety and efficiency. IEEE Robot. Autom. Mag. 2019, 26, 20–29. [Google Scholar] [CrossRef]
- Yoshiike, T.; Kuroda, M.; Ujino, R.; Kanemoto, Y.; Kaneko, H.; Higuchi, H.; Komura, S.; Iwasaki, S.; Asatani, M.; Koshiishi, T. The experimental humanoid robot e2-dr: A design for inspection and disaster response in industrial environments. IEEE Robot. Autom. Mag. 2019, 26, 46–58. [Google Scholar] [CrossRef]
- Cai, Z.; Zhu, X.; Gergondet, P.; Chen, X.; Yu, Z. A Friction-Driven Strategy for Agile Steering Wheel Manipulation by Humanoid Robots. Cyborg Bionic Syst. 2023, 4, 0064. [Google Scholar] [CrossRef] [PubMed]
- Wensing, P.M.; Orin, D.E. Generation of dynamic humanoid behaviors through task-space control with conic optimization. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscateville, NJ, USA, 2013; pp. 3103–3109. [Google Scholar]
- Ahn, D.; Cho, B.K. Optimal standing jump trajectory generation for biped robots. Int. J. Precis. Eng. Manuf. 2020, 21, 1459–1467. [Google Scholar] [CrossRef]
- Vatavuk, I.; Kovačić, Z. Precise Jump Planning using Centroidal Dynamics based Bilevel Optimization. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscateville, NJ, USA, 2021; pp. 3026–3032. [Google Scholar]
- Zhu, Q.; Wu, W.; Zhao, Y.; Wu, J.; Xiong, R. Design and control of stiffness coordination between knee and ankle joints for a hopping legged robot. In Proceedings of the 2017 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 27–29 October 2017; IEEE: Piscateville, NJ, USA, 2017; pp. 624–630. [Google Scholar]
- Wensing, P.M.; Orin, D.E. Improved computation of the humanoid centroidal dynamics and application for whole-body control. Int. J. Humanoid Robot. 2016, 13, 1550039. [Google Scholar] [CrossRef]
- Chignoli, M.; Kim, D.; Stanger-Jones, E.; Kim, S. The MIT humanoid robot: Design, motion planning, and control for acrobatic behaviors. In Proceedings of the 2020 IEEE-RAS 20th International Conference on Humanoid Robots (Humanoids), Munich, Germany, 19–21 July 2021; IEEE: Piscateville, NJ, USA, 2021; pp. 1–8. [Google Scholar]
- Wan, X.; Urakubo, T.; Tada, Y. Optimization of jumping motion of a legged robot for different take-off postures. J. Mech. Sci. Technol. 2015, 29, 1391–1397. [Google Scholar] [CrossRef]
- Xiong, X.; Ames, A.D. Sequential motion planning for bipedal somersault via flywheel slip and momentum transmission with task space control. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: Piscateville, NJ, USA, 2020; pp. 3510–3517. [Google Scholar]
- Dynamics, B. What’s New, Atlas? 2017. Available online: https://youtube.com/watch?v=fRj34o4hN4I/ (accessed on 27 April 2024).
- Kojima, K.; Kojio, Y.; Ishikawa, T.; Sugai, F.; Kakiuchi, Y.; Okada, K.; Inaba, M. A robot design method for weight saving aimed at dynamic motions: Design of humanoid JAXON3-P and realization of jump motions. In Proceedings of the 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), Toronto, ON, Canada, 15–17 October 2019; IEEE: Piscateville, NJ, USA, 2019; pp. 586–593. [Google Scholar]
- Ahn, D.; Cho, B.K. Online Jumping Motion Generation via Model Predictive Control. IEEE Trans. Ind. Electron. 2021, 69, 4957–4965. [Google Scholar] [CrossRef]
- Xiong, X.; Ames, A.D. Bipedal hopping: Reduced-order model embedding via optimization-based control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscateville, NJ, USA, 2018; pp. 3821–3828. [Google Scholar]
- Qi, H.; Chen, X.; Yu, Z.; Huang, G.; Liu, Y.; Meng, L.; Huang, Q. Vertical Jump of a Humanoid Robot with CoP-Guided Angular Momentum Control and Impact Absorption. IEEE Trans. Robot. 2023, 39, 3154–3166. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, J.; Liu, Y.; Hong, D. Design of a jumping control framework with heuristic landing for bipedal robots. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; IEEE: Piscateville, NJ, USA, 2023; pp. 8502–8509. [Google Scholar]
- Xiang, P.; Yan, L.; Guo, Y.; He, X.; Gerada, C.; Chen, I.M. A concentrated-flux-type pm machine with irregular magnets and iron poles. IEEE/ASME Trans. Mechatron. 2023, 29, 691–702. [Google Scholar] [CrossRef]
- Zhou, Z.; Wingo, B.; Boyd, N.; Hutchinson, S.; Zhao, Y. Momentum-aware trajectory optimization and control for agile quadrupedal locomotion. IEEE Robot. Autom. Lett. 2022, 7, 7755–7762. [Google Scholar] [CrossRef]
- Chen, H.; Wang, B.; Hong, Z.; Shen, C.; Wensing, P.M.; Zhang, W. Underactuated motion planning and control for jumping with wheeled-bipedal robots. IEEE Robot. Autom. Lett. 2020, 6, 747–754. [Google Scholar] [CrossRef]
- Bledt, G.; Kim, S. Implementing regularized predictive control for simultaneous real-time footstep and ground reaction force optimization. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: Piscateville, NJ, USA, 2019; pp. 6316–6323. [Google Scholar]
- Jeon, S.H.; Kim, S.; Kim, D. Online Optimal Landing Control of the MIT Mini Cheetah. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Piscateville, NJ, USA, 2022; pp. 178–184. [Google Scholar]
- Winkler, A.W.; Bellicoso, C.D.; Hutter, M.; Buchli, J. Gait and trajectory optimization for legged systems through phase-based end-effector parameterization. IEEE Robot. Autom. Lett. 2018, 3, 1560–1567. [Google Scholar] [CrossRef]
- Dai, H.; Valenzuela, A.; Tedrake, R. Whole-body motion planning with centroidal dynamics and full kinematics. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; IEEE: Piscateville, NJ, USA, 2014; pp. 295–302. [Google Scholar]
- Ponton, B.; Khadiv, M.; Meduri, A.; Righetti, L. Efficient multicontact pattern generation with sequential convex approximations of the centroidal dynamics. IEEE Trans. Robot. 2021, 37, 1661–1679. [Google Scholar] [CrossRef]
- Budhiraja, R.; Carpentier, J.; Mansard, N. Dynamics consensus between centroidal and whole-body models for locomotion of legged robots. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscateville, NJ, USA, 2019; pp. 6727–6733. [Google Scholar]
- Nguyen, C.; Nguyen, Q. Contact-timing and trajectory optimization for 3d jumping on quadruped robots. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscateville, NJ, USA, 2022; pp. 11994–11999. [Google Scholar]
- Neunert, M.; Farshidian, F.; Winkler, A.W.; Buchli, J. Trajectory optimization through contacts and automatic gait discovery for quadrupeds. IEEE Robot. Autom. Lett. 2017, 2, 1502–1509. [Google Scholar] [CrossRef]
- Deits, R.; Tedrake, R. Footstep planning on uneven terrain with mixed-integer convex optimization. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; IEEE: Piscateville, NJ, USA, 2014; pp. 279–286. [Google Scholar]
- Aceituno-Cabezas, B.; Mastalli, C.; Dai, H.; Focchi, M.; Radulescu, A.; Caldwell, D.G.; Cappelletto, J.; Grieco, J.C.; Fernández-López, G.; Semini, C. Simultaneous contact, gait, and motion planning for robust multilegged locomotion via mixed-integer convex optimization. IEEE Robot. Autom. Lett. 2017, 3, 2531–2538. [Google Scholar]
- Herzog, A.; Schaal, S.; Righetti, L. Structured contact force optimization for kino-dynamic motion generation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscateville, NJ, USA, 2016; pp. 2703–2710. [Google Scholar]
- Caron, S.; Pham, Q.C.; Nakamura, Y. Stability of surface contacts for humanoid robots: Closed-form formulae of the contact wrench cone for rectangular support areas. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscateville, NJ, USA, 2015; pp. 5107–5112. [Google Scholar]
- Caron, S.; Kheddar, A. Multi-contact walking pattern generation based on model preview control of 3D COM accelerations. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; IEEE: Piscateville, NJ, USA, 2016; pp. 550–557. [Google Scholar]
- Chignoli, M.; Kim, S. Online trajectory optimization for dynamic aerial motions of a quadruped robot. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscateville, NJ, USA, 2021; pp. 7693–7699. [Google Scholar]
- Kelly, M. An Introduction to Trajectory Optimization: How to Do Your Own Direct Collocation. SIAM Rev. 2017, 59, 849–904. [Google Scholar] [CrossRef]
- Lee, S.H.; Goswami, A. A momentum-based balance controller for humanoid robots on non-level and non-stationary ground. Auton. Robot. 2012, 33, 399–414. [Google Scholar] [CrossRef]



| Main Parameter | Value |
|---|---|
| Knot points, N | 20 |
| Motion duration, T | 1 s |
| Contact sequence of , , … and | [] |
| Optimality tolerance | <1 × 10−5 |
| diag (0.001, 0.001, 0.001, …, 0.001, 0.001, 0.001) | |
| diag (40, 40, 40) | |
| diag (30, 10, 10, 10, 50, 10) | |
| diag (0.01, 0.01, 0.01, …, 0.01, 0.01, 0.01) | |
| diag (0.0001, 0.0001, 0.0001, …, 0.0001) | |
| diag (1, 1, 1, 1, 1, 1) | |
| diag (0.01, 0.01, 0.01) | |
| diag (0.02, 0.02, 0.02, …, 0.02, 0.02, 0.02) | |
| diag (0.01, 0, 0.001, …, 0.01, 0, 0.001) |
| Optimization Project | Centroidal Dynamics | Whole-Body Kinematics |
|---|---|---|
| Number of variables | 720 | 1200 |
| Duration of motion | 1 s | 1 s |
| Number of equality constraints | 1036 | 720 |
| Number of inequality constraints | 3102 | 4250 |
| Solving time | 0.230 s | 3.2 s |
| Number of iterations | 12 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, X.; Yu, Z.; Qi, H.; Yi, C. Single Sequential Trajectory Optimization with Centroidal Dynamics and Whole-Body Kinematics for Vertical Jump of Humanoid Robot. Biomimetics 2024, 9, 274. https://doi.org/10.3390/biomimetics9050274
Liu Y, Chen X, Yu Z, Qi H, Yi C. Single Sequential Trajectory Optimization with Centroidal Dynamics and Whole-Body Kinematics for Vertical Jump of Humanoid Robot. Biomimetics. 2024; 9(5):274. https://doi.org/10.3390/biomimetics9050274
Chicago/Turabian StyleLiu, Yaliang, Xuechao Chen, Zhangguo Yu, Haoxiang Qi, and Chuanku Yi. 2024. "Single Sequential Trajectory Optimization with Centroidal Dynamics and Whole-Body Kinematics for Vertical Jump of Humanoid Robot" Biomimetics 9, no. 5: 274. https://doi.org/10.3390/biomimetics9050274
APA StyleLiu, Y., Chen, X., Yu, Z., Qi, H., & Yi, C. (2024). Single Sequential Trajectory Optimization with Centroidal Dynamics and Whole-Body Kinematics for Vertical Jump of Humanoid Robot. Biomimetics, 9(5), 274. https://doi.org/10.3390/biomimetics9050274







