A New Approach Based on Collective Intelligence to Solve Traveling Salesman Problems
Abstract
1. Introduction
2. Material and Methods
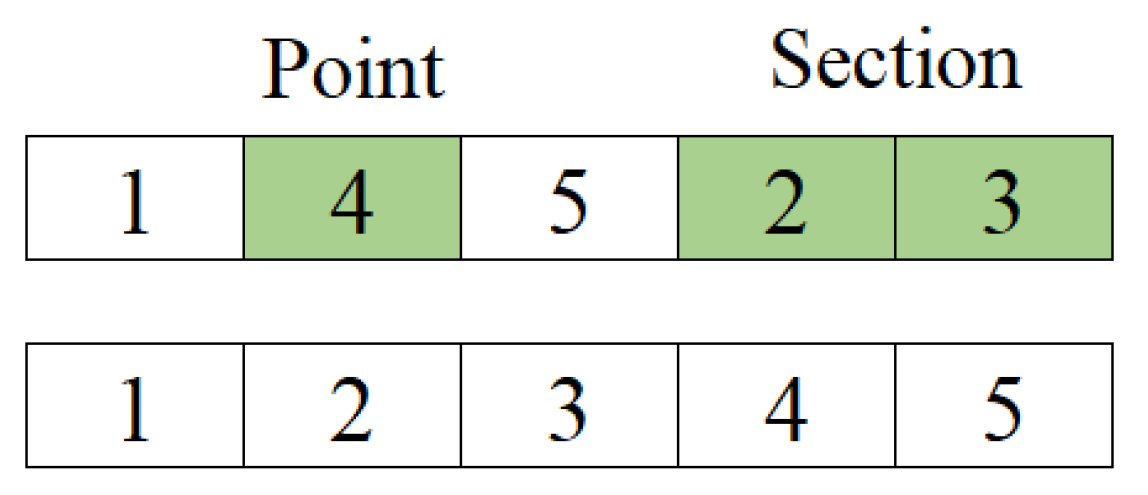
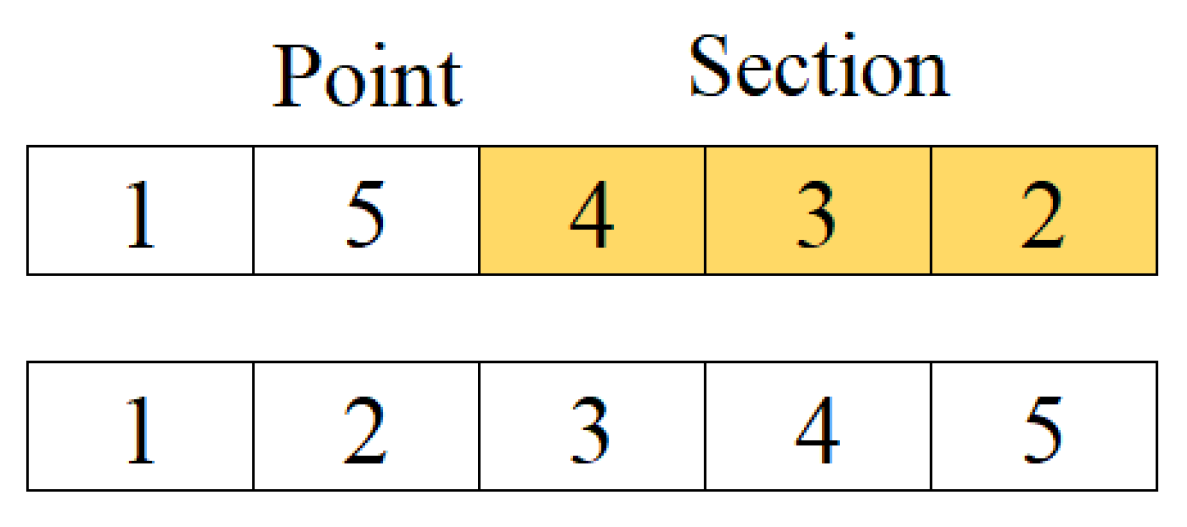
2.1. Path Construction Phase
2.2. Path Improvement Phase
3. Experimental Results
4. Results and Discussion
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beşkirli, A.; Dağ, İ. A new binary variant with transfer functions of Harris Hawks Optimization for binary wind turbine micrositing. Energy Rep. 2020, 6, 668–673. [Google Scholar] [CrossRef]
- Gunduz, M.; Aslan, M. DJAYA: A discrete Jaya algorithm for solving traveling salesman problem. Appl. Soft Comput. 2021, 105, 107275. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. An efficient tree seed inspired algorithm for parameter estimation of Photovoltaic models. Energy Rep. 2022, 8, 291–298. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. I-CPA: An Improved Carnivorous Plant Algorithm for Solar Photovoltaic Parameter Identification Problem. Biomimetics 2023, 8, 569. [Google Scholar] [CrossRef] [PubMed]
- Maniezzo, V.; Dorigo, M.; Colorni, A. The ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95. the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the Proceedings of IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Akay, B. Performance Analysis of Artificial Bee Colony Algorithm on Numerical Optimization Problems. Ph.D. Thesis, Erciyes University, Kayseri, Turkey, 2009. [Google Scholar]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Zhong, W.H.; Zhang, J.; Chen, W.N. A novel discrete particle swarm optimization to solve traveling salesman problem. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3283–3287. [Google Scholar]
- Uğur, A.; Aydin, D. An interactive simulation and analysis software for solving TSP using Ant Colony Optimization algorithms. Adv. Eng. Softw. 2009, 40, 341–349. [Google Scholar] [CrossRef]
- Langevin, A.; Soumis, F.; Desrosiers, J. Classification of travelling salesman problem formulations. Oper. Res. Lett. 1990, 9, 127–132. [Google Scholar] [CrossRef]
- Laporte, G. The traveling salesman problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Punnen, A.P. Traveling salesman problem under categorization. Oper. Res. Lett. 1992, 12, 89–95. [Google Scholar] [CrossRef]
- Bektas, T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega 2006, 34, 209–219. [Google Scholar] [CrossRef]
- Rego, C.; Gamboa, D.; Glover, F.; Osterman, C. Traveling salesman problem heuristics: Leading methods, implementations and latest advances. Eur. J. Oper. Res. 2011, 211, 427–441. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A. A double-adaptive general variable neighborhood search algorithm for the solution of the traveling salesman problem. Appl. Soft Comput. 2022, 121, 108746. [Google Scholar] [CrossRef]
- Papalitsas, C.; Karakostas, P.; Andronikos, T. A performance study of the impact of different perturbation methods on the efficiency of GVNS for solving TSP. Appl. Syst. Innov. 2019, 2, 31. [Google Scholar] [CrossRef]
- Cook, W.J.; Applegate, D.L.; Bixby, R.E.; Chvatal, V. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Johnson, D.S.; McGeoch, L.A. The traveling salesman problem: A case study in local optimization. Local Search Comb. Optim. 1997, 1, 215–310. [Google Scholar]
- Zhang, P.; Wang, J.; Tian, Z.; Sun, S.; Li, J.; Yang, J. A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem. Appl. Soft Comput. 2022, 127, 109339. [Google Scholar] [CrossRef]
- Kıran, M.S.; İşcan, H.; Gündüz, M. The analysis of discrete artificial bee colony algorithm with neighborhood operator on traveling salesman problem. Neural Comput. Appl. 2013, 23, 9–21. [Google Scholar] [CrossRef]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, Q.X. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Q.; Tang, Z. A discrete chicken swarm optimization for traveling salesman problem. J. Phys. Conf. Ser. 2021, 1978, 012034. [Google Scholar] [CrossRef]
- Panwar, K.; Deep, K. Discrete Grey Wolf Optimizer for symmetric travelling salesman problem. Appl. Soft Comput. 2021, 105, 107298. [Google Scholar] [CrossRef]
- Saji, Y.; Barkatou, M. A discrete bat algorithm based on Lévy flights for Euclidean traveling salesman problem. Expert Syst. Appl. 2021, 172, 114639. [Google Scholar] [CrossRef]
- Baş, E.; Ülker, E. Dıscrete socıal spıder algorıthm for the travelıng salesman problem. Artif. Intell. Rev. 2021, 54, 1063–1085. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, Y. Discrete sparrow search algorithm for symmetric traveling salesman problem. Appl. Soft Comput. 2022, 118, 108469. [Google Scholar] [CrossRef]
- Kanna, S.R.; Sivakumar, K.; Lingaraj, N. Development of deer hunting linked earthworm optimization algorithm for solving large scale traveling salesman problem. Knowl. Based Syst. 2021, 227, 107199. [Google Scholar] [CrossRef]
- Jati, G.K.; Kuwanto, G.; Hashmi, T.; Widjaja, H. Discrete komodo algorithm for traveling salesman problem. Appl. Soft Comput. 2023, 139, 110219. [Google Scholar] [CrossRef]
- Akhand, M.A.H.; Ayon, S.I.; Shahriyar, S.A.; Siddique, N.; Adeli, H. Discrete Spider Monkey Optimization for Travelling Salesman Problem. Appl. Soft Comput. 2020, 86, 105887. [Google Scholar] [CrossRef]
- Mzili, T.; Riffi, M.E.; Mzili, I.; Dhiman, G. A novel discrete Rat swarm optimization (DRSO) algorithm for solving the traveling salesman problem. Decis. Mak. Appl. Manag. Eng. 2022, 5, 287–299. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.; Luan, S.; Li, X.; Sun, Y. Opposition-Based Ant Colony Optimization Algorithm for the Traveling Salesman Problem. Mathematics 2020, 8, 1650. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Abdollahzadeh, B. An efficient harris hawk optimization algorithm for solving the travelling salesman problem. Clust. Comput. 2022, 25, 1981–2005. [Google Scholar] [CrossRef]
- Al-Gaphari, G.H.; Al-Amry, R.; Al-Nuzaili, A.S. Discrete crow-inspired algorithms for traveling salesman problem. Eng. Appl. Artif. Intell. 2021, 97, 104006. [Google Scholar] [CrossRef]
- Krishna, M.M.; Majhi, S.K.; Panda, N. A MapReduce hybridized spotted hyena optimizer algorithm for travelling salesman problem. Int. J. Inf. Technol. 2023, 15, 3873–3887. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J. A discrete cuckoo search algorithm for traveling salesman problem and its application in cutting path optimization. Comput. Ind. Eng. 2022, 169, 108157. [Google Scholar] [CrossRef]
- Almazini, H.F.; Mortada, S.; Al-Mazini, H.F.A.; Al-Behadili, H.N.K.; Alkenani, J. Improved discrete plant propagation algorithm for solving the traveling salesman problem. IAES Int. J. Artif. Intell. 2022, 11, 13. [Google Scholar] [CrossRef]
- Zheng, J.; Zhong, J.; Chen, M.; He, K. A reinforced hybrid genetic algorithm for the traveling salesman problem. Comput. Oper. Res. 2023, 157, 106249. [Google Scholar] [CrossRef]
- Nayyef, H.M.; Ibrahim, A.A.; Mohd Zainuri, M.A.A.; Zulkifley, M.A.; Shareef, H. A Novel Hybrid Algorithm Based on Jellyfish Search and Particle Swarm Optimization. Mathematics 2023, 11, 3210. [Google Scholar] [CrossRef]
- Goel, L.; Vaishnav, G.; Ramola, S.C.; Purohit, T. A Modified Ant Colony Optimization Algorithm with Pheromone Mutations for Dynamic Travelling Salesman Problem. IETE Tech. Rev. 2023, 40, 767–782. [Google Scholar] [CrossRef]
- Kiran, M.S.; Gündüz, M. XOR-based artificial bee colony algorithm for binary optimization. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 2307–2328. [Google Scholar] [CrossRef]
- TSPLIB. Available online: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/ (accessed on 13 December 2023).
- Oliver, I.; Smith, D.; Holland, J.R. Study of permutation crossover operators on the traveling salesman problem. In Genetic Algorithms and Their Applications: Proceedings of the Second International Conference on Genetic Algorithms: 28–31 July 1987; Massachusetts Institute of Technology: Cambridge, MA, USA, 1987. [Google Scholar]
- Gündüz, M.; Kiran, M.S.; Özceylan, E. A hierarchic approach based on swarm intelligence to solve the traveling salesman problem. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 103–117. [Google Scholar] [CrossRef]
- Cinar, A.C.; Korkmaz, S.; Kiran, M.S. A discrete tree-seed algorithm for solving symmetric traveling salesman problem. Eng. Sci. Technol. Int. J. 2020, 23, 879–890. [Google Scholar] [CrossRef]





| Problem | Optimum | Problem | Optimum |
|---|---|---|---|
| Oliver30 | 423.74 | Eil51 | 428.87 |
| Berlin52 | 7544.37 | St70 | 677.11 |
| Pr76 | 108,159.44 | Eil76 | 545.39 |
| Rat99 | 1211 | Rd100 | 7910 |
| KroA100 | 21,285.44 | KroB100 | 22,141 |
| KroC100 | 20,749 | KroD100 | 21,294 |
| KroE100 | 22,068 | Bier127 | 118,282 |
| Lin105 | 14,379 | Eil101 | 642.31 |
| Pr124 | 59,030 | Pr107 | 44,307 |
| Pr136 | 96,772 | Ch130 | 6110 |
| Ch150 | 6532.28 | Pr144 | 58,537 |
| KroA150 | 26,524 | TSP225 | 3859 |
| KroB150 | 26,130 |
| Parameter | Ant System | Proposed Method |
|---|---|---|
| Population Size (P) | D * | D * |
| Maximum Cycle Number | 500 | 500 |
| Alpha (α) | 1.0 | N/A |
| Beta (β) | 5.0 | N/A |
| a | N/A | 1.0 |
| b | N/A | 5.0 |
| Rho (ρ) | 0.65 | N/A |
| Q | 100 | 10 |
| Problem | Ant System Algorithm | Proposed Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Optimum | Best | Worst | Average | Std. Dev. | RE (%) | Best | Worst | Average | Std. Dev. | RE (%) |
| Oliver30 | 423.74 | 423.91 | 433.07 | 425.81 | 2.03 | 0.49 | 423.74 | 424.46 | 423.84 | 0.20 | 0.02 |
| Eil51 | 428.87 | 447.37 | 463.42 | 456.52 | 3.83 | 6.45 | 434.80 | 454.88 | 444.78 | 4.91 | 3.71 |
| Berlin52 | 7544.37 | 7663.59 | 7872.49 | 7694.30 | 45.53 | 1.99 | 7544.37 | 7819.59 | 7596.93 | 70.62 | 0.70 |
| St70 | 677.11 | 697.02 | 719.27 | 710.54 | 5.91 | 4.94 | 689.69 | 718.37 | 706.16 | 7.86 | 4.29 |
| Pr76 | 108,159.44 | 114,674.63 | 118,727.64 | 116,898.74 | 977.97 | 8.08 | 113,406.81 | 119,641.27 | 116,964.07 | 1617.86 | 8.14 |
| Eil76 | 545.39 | 559.17 | 570.36 | 565.36 | 3.35 | 3.66 | 553.53 | 581.84 | 566.18 | 5.78 | 3.81 |
| Rat99 | 1211.00 | 1269.82 | 1307.81 | 1290.49 | 8.29 | 6.56 | 1242.59 | 1316.05 | 1285.80 | 18.29 | 6.18 |
| Rd100 | 7910.00 | 8214.34 | 8468.61 | 8359.81 | 60.39 | 5.69 | 8070.45 | 8403.07 | 8217.68 | 79.46 | 3.89 |
| KroA100 | 21,285.44 | 22,455.89 | 23,271.16 | 22,882.11 | 232.25 | 7.50 | 21,575.98 | 22,321.42 | 21,986.93 | 213.88 | 3.30 |
| KroB100 | 22,141.00 | 22,693.38 | 23,043.60 | 22,929.66 | 72.19 | 3.56 | 22,486.55 | 23,138.72 | 22,763.13 | 171.27 | 2.81 |
| KroC100 | 20,749.00 | 21,218.38 | 21,629.82 | 21,479.12 | 109.41 | 3.52 | 21,103.32 | 21,580.70 | 21,401.25 | 132.99 | 3.14 |
| KroD100 | 21,294.00 | 22,681.23 | 23,034.26 | 22,857.46 | 92.72 | 7.34 | 22,057.57 | 22,784.83 | 22,408.96 | 176.76 | 5.24 |
| KroE100 | 22,068.00 | 22,893.72 | 24,020.36 | 23,624.95 | 226.28 | 7.06 | 22,429.60 | 23,681.80 | 23,075.59 | 293.60 | 4.57 |
| Bier127 | 118,282.00 | 122,170.98 | 124,011.82 | 123,173.65 | 487.68 | 4.14 | 120,608.54 | 124,215.06 | 122,415.63 | 974.55 | 3.49 |
| Eil101 | 642.31 | 674.41 | 704.14 | 693.02 | 7.75 | 7.89 | 656.14 | 701.46 | 676.76 | 9.23 | 5.36 |
| Lin105 | 14,379.00 | 14,706.08 | 14,930.62 | 14807.13 | 66.35 | 2.98 | 14,501.10 | 14,953.92 | 14,689.60 | 116.37 | 2.16 |
| Pr107 | 44,307.00 | 46,034.75 | 46,838.57 | 46,368.35 | 180.75 | 4.65 | 44,781.22 | 46,053.97 | 45,364.00 | 301.81 | 2.39 |
| Pr124 | 59,030.00 | 59,731.20 | 60,700.56 | 60,059.94 | 214.25 | 1.74 | 59,553.62 | 60,830.49 | 60,316.46 | 322.43 | 2.18 |
| Ch130 | 6110.00 | 6419.15 | 6579.30 | 6482.77 | 43.58 | 6.10 | 6276.59 | 6414.22 | 6331.80 | 37.52 | 3.63 |
| Pr136 | 96,772.00 | 104,670.51 | 108,272.22 | 106,807.35 | 734.25 | 10.37 | 102,771.33 | 108,650.39 | 105,825.77 | 1446.93 | 9.36 |
| Pr144 | 58,537.00 | 58,816.80 | 58,868.72 | 58,820.60 | 10.01 | 0.48 | 58,820.96 | 59,617.26 | 59,138.08 | 188.42 | 1.03 |
| KroA150 | 26,524.00 | 27,727.74 | 29,006.01 | 28,518.77 | 251.62 | 7.52 | 27,801.51 | 28,979.46 | 28,458.39 | 334.31 | 7.29 |
| KroB150 | 26,130.00 | 27,309.28 | 28,314.81 | 27,948.45 | 178.94 | 6.96 | 27,133.53 | 28,211.93 | 27,724.68 | 256.21 | 6.10 |
| Ch150 | 6532.28 | 6648.51 | 6726.27 | 6702.87 | 24.65 | 2.61 | 6611.95 | 6788.13 | 6704.08 | 37.29 | 2.63 |
| TSP225 | 3859.00 | 4112.35 | 4236.84 | 4176.08 | 22.65 | 8.22 | 4066.95 | 4174.39 | 4130.64 | 26.49 | 7.04 |
| Problem | Algorithm | Best | Worst | Mean | Std. Dev. | RE | Rank |
|---|---|---|---|---|---|---|---|
| Oliver30 | ACO | 423.74 | 429.36 | 424 68 | 1.41 | 0.22 | 3 |
| ABC | 439.49 | 484.83 | 462.55 | 12.47 | 9.16 | 5 | |
| HA | 423.74 | 423.74 | 423.74 | 0 | 0 | 1 | |
| DTSA | N/A | N/A | 428.5 | 4.21 | 1.12 | 4 | |
| PM | 423.74 | 424.46 | 423.84 | 0.2 | 0.02 | 2 | |
| Eil51 | ACO | 450.59 | 463.55 | 457.86 | 4.07 | 6.76 | 4 |
| ABC | 563.75 | 619.44 | 590.49 | 15.79 | 37.68 | 5 | |
| HA | 431.74 | 454.97 | 443.39 | 5.25 | 3.39 | 1 | |
| DTSA | N/A | N/A | 443.93 | 4.04 | 3.51 | 2 | |
| PM | 434.8 | 454.88 | 444 78 | 4.91 | 3.71 | 3 | |
| Berlin52 | ACO | 7548.99 | 7681.75 | 7659.31 | 38.7 | 1.52 | 4 |
| ABC | 9479.11 | 11,021.99 | 10,390.26 | 439.69 | 37.72 | 5 | |
| HA | 7544.37 | 7544.37 | 7544.37 | 0 | 0 | 1 | |
| DTSA | N/A | N/A | 7545.83 | 21.00 | 0.02 | 2 | |
| PM | 7544.37 | 7819.59 | 7596.93 | 70.62 | 0.7 | 3 | |
| St70 | ACO | 696.05 | 725.26 | 709.16 | 8.27 | 4.73 | 4 |
| ABC | 1162.12 | 1339.24 | 1230.49 | 41.79 | 81.73 | 5 | |
| HA | 687.24 | 716.52 | 700.58 | 7.51 | 3.47 | 1 | |
| DTSA | N/A | N/A | 708.65 | 6.77 | 4.66 | 3 | |
| PM | 689.69 | 718.37 | 706.16 | 7.86 | 4.29 | 2 | |
| Eil76 | ACO | 554.46 | 568.62 | 561.98 | 3.5 | 3.04 | 2 |
| ABC | 877.28 | 971.36 | 931.44 | 24.86 | 70.78 | 5 | |
| HA | 551.07 | 565.51 | 557.98 | 4.1 | 2.31 | 1 | |
| DTSA | N/A | N/A | 578.58 | 3.93 | 6.09 | 4 | |
| PM | 553.53 | 581.84 | 566.18 | 5.78 | 3.81 | 3 | |
| Pr76 | ACO | 115,166.66 | 118,227.41 | 116,321.22 | 885.79 | 7.55 | 3 |
| ABC | 195,198.9 | 219,173.64 | 205,119.61 | 7379.16 | 89.65 | 5 | |
| HA | 113,798.56 | 116,353.01 | 115,072.29 | 742.9 | 6.39 | 2 | |
| DTSA | N/A | N/A | 114,930.03 | 1545.64 | 6.26 | 1 | |
| PM | 113,406.81 | 119,641.27 | 116,964.07 | 1617.86 | 8.14 | 4 | |
| KroA100 | ACO | 22,455.89 | 23,365.46 | 22,880.12 | 235.18 | 7.49 | 4 |
| ABC | 49,519.51 | 57,566.05 | 53,840.03 | 2198.36 | 152.94 | 5 | |
| HA | 22,122.75 | 23,050.81 | 22,435.31 | 231.34 | 5.4 | 3 | |
| DTSA | N/A | N/A | 21,728.4 | 358.13 | 2.08 | 1 | |
| PM | 21,575.98 | 22,321.42 | 21,986.93 | 213.88 | 3.3 | 2 | |
| Eil101 | ACO | 678.04 | 705.65 | 693.42 | 6.8 | 7.96 | 4 |
| ABC | 1237.31 | 1392.64 | 1315.95 | 35.28 | 104.88 | 5 | |
| HA | 672.71 | 696.04 | 683.39 | 6.56 | 6.39 | 2 | |
| DTSA | N/A | N/A | 689.91 | 4.47 | 7.41 | 3 | |
| PM | 656.14 | 701.46 | 676.76 | 9.23 | 5.36 | 1 | |
| Ch150 | ACO | 6648.51 | 6726.27 | 6702.87 | 20.73 | 2.61 | 2 |
| ABC | 20,908.89 | 22,574.99 | 21,61748 | 453.71 | 230.93 | 5 | |
| HA | 6641.69 | 6707.86 | 6677.12 | 19.3 | 2.21 | 1 | |
| DTSA | N/A | N/A | 6748.99 | 32.63 | 3.32 | 4 | |
| PM | 6611.95 | 6788.13 | 6704.08 | 37.29 | 2.63 | 3 | |
| Tsp225 | ACO | 4112.35 | 4236.85 | 4176.08 | 28.34 | 8.22 | 3 |
| ABC | 16,998.41 | 18,682.56 | 17,955.12 | 387.35 | 365.2792 | 5 | |
| HA | 4090.54 | 4212.08 | 4157.85 | 26.27 | 7.74 | 2 | |
| DTSA | N/A | N/A | 4230.45 | 58.76 | 9.63 | 4 | |
| PM | 4066.95 | 4174.39 | 4130.64 | 26.49 | 7.04 | 1 |
| Problem | Algorithm | Mean | Std. Dev. | RE (%) | Rank |
|---|---|---|---|---|---|
| KroA100 | PM | 21,986.93 | 213.88 | 3.3 | 3 |
| SA | 22,635 | 778.72 | 6.36 | 4 | |
| DSTA0 | 23,213 | 906.11 | 9.07 | 6 | |
| DSTAI | 22,835 | 715.85 | 7.3 | 5 | |
| DSTAII | 21,767 | 221.64 | 2.28 | 2 | |
| DTSA | 21,506.78 | 260.55 | 1.06 | 1 | |
| KroB100 | PM | 22,763.13 | 171.27 | 2.81 | 1 |
| SA | 23,657 | 445.78 | 6.85 | 4 | |
| DSTA0 | 23,794 | 517.05 | 7.47 | 6 | |
| DSTAI | 23,734 | 507.38 | 7.19 | 5 | |
| DSTAII | 22,880 | 302.14 | 3.34 | 2 | |
| DTSA | 23,139.26 | 181.74 | 4.51 | 3 | |
| KroC100 | PM | 21,401.25 | 132.99 | 3.14 | 2 |
| SA | 22,223 | 522.2 | 7.1 | 5 | |
| DSTA0 | 22,877 | 709.87 | 10.26 | 6 | |
| DSTAI | 21,891 | 536.88 | 5.5 | 4 | |
| DSTAII | 21,378 | 246.34 | 3.03 | 1 | |
| DTSA | 21,817.08 | 217.77 | 5.15 | 3 | |
| KroD100 | PM | 22,408.96 | 176.76 | 5.24 | 2 |
| SA | 22,911 | 483.01 | 7.59 | 4 | |
| DSTA0 | 23,043 | 565.8 | 8.21 | 6 | |
| DSTAI | 22,665 | 592.53 | 6.44 | 3 | |
| DSTAII | 21,991 | 315.32 | 3.27 | 1 | |
| DTSA | 22,972.26 | 390.5 | 7.88 | 5 | |
| KroE100 | PM | 23,075.59 | 293.6 | 4.57 | 4 |
| SA | 23,125 | 389.42 | 4.44 | 3 | |
| DSTA0 | 23,738 | 450.82 | 7.21 | 6 | |
| DSTAI | 23,371 | 678.69 | 5.56 | 5 | |
| DSTAII | 22,637 | 166.82 | 2.24 | 2 | |
| DTSA | 22,547 | 121.96 | 1.83 | 1 |
| Problem | PM | M-ACO-SM [43] | M-ACO-RM [43] | E-ACO [43] | E-M-ACO [43] | E-SM-ACO [43] | P-ACO [43] | P-M-ACO [43] |
|---|---|---|---|---|---|---|---|---|
| Eil51 | 444.78 | 456 | 452 | - | - | - | - | - |
| Berlin52 | 7596.93 | 8093 | 8093 | 8417 | 8091 | 8054 | 8201 | 8291 |
| St70 | 706.16 | 742 | 734 | 743 | 726 | 744 | 774 | 760 |
| Pr76 | 119,641 | 122,436 | 122,331 | - | - | - | - | - |
| Eil76 | 566.18 | 566 | 585 | - | - | - | - | - |
| Rat99 | 1285.80 | 1369 | 1369 | 1380 | 1322 | 1369 | 1389 | 1368 |
| Eil101 | 676.76 | 702 | 754 | 698 | 703 | 726 | 748 | 736 |
| Lin105 | 14,689.60 | 15,662 | 15,650 | 16,499 | 15,470 | 15,358 | 16,998 | 16,255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiran, M.S.; Beskirli, M. A New Approach Based on Collective Intelligence to Solve Traveling Salesman Problems. Biomimetics 2024, 9, 118. https://doi.org/10.3390/biomimetics9020118
Kiran MS, Beskirli M. A New Approach Based on Collective Intelligence to Solve Traveling Salesman Problems. Biomimetics. 2024; 9(2):118. https://doi.org/10.3390/biomimetics9020118
Chicago/Turabian StyleKiran, Mustafa Servet, and Mehmet Beskirli. 2024. "A New Approach Based on Collective Intelligence to Solve Traveling Salesman Problems" Biomimetics 9, no. 2: 118. https://doi.org/10.3390/biomimetics9020118
APA StyleKiran, M. S., & Beskirli, M. (2024). A New Approach Based on Collective Intelligence to Solve Traveling Salesman Problems. Biomimetics, 9(2), 118. https://doi.org/10.3390/biomimetics9020118






