Modeling and Analysis of Bio-Inspired, Reconfigurable, Piezo-Driven Vibration Isolator for Spacecraft
Abstract
1. Introduction
- the ability to stabilize the payload in inertial space, effectively counteracting the low-frequency vibration transmitted by the base structure, and
- the ability to resist the internal disturbance inside the payload to prevent vibration level deterioration.
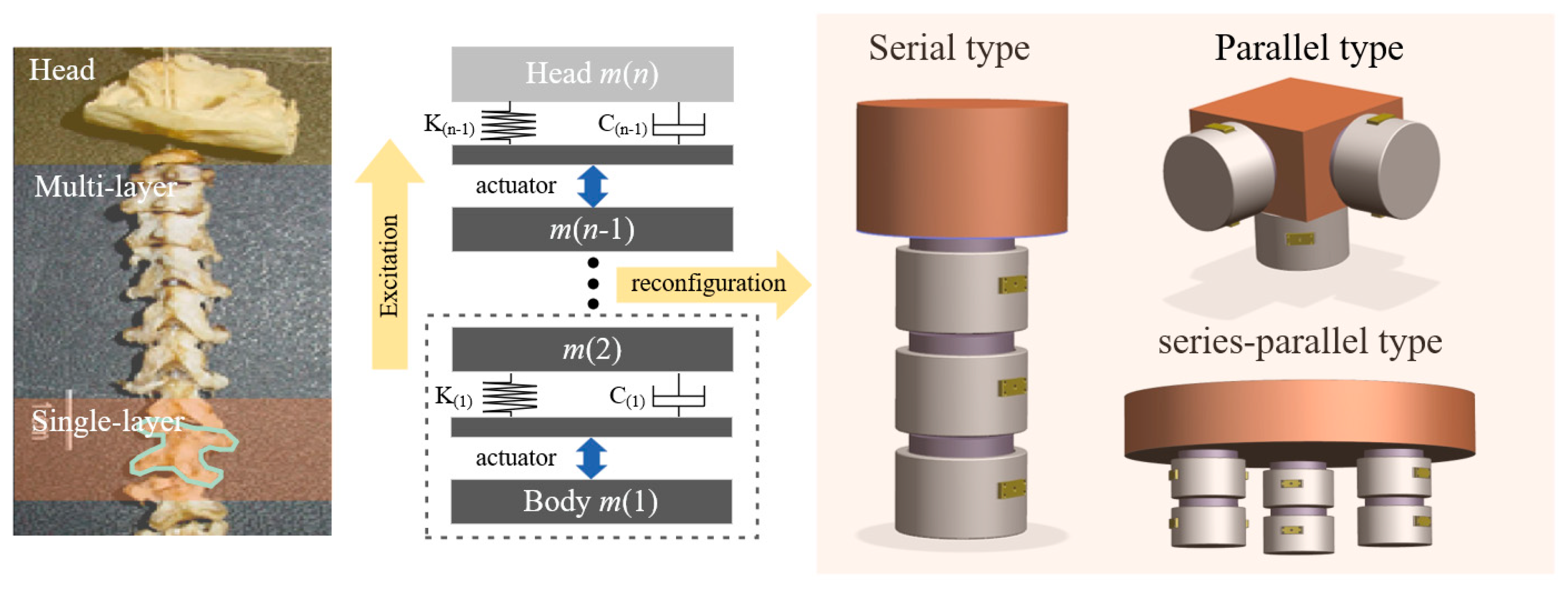
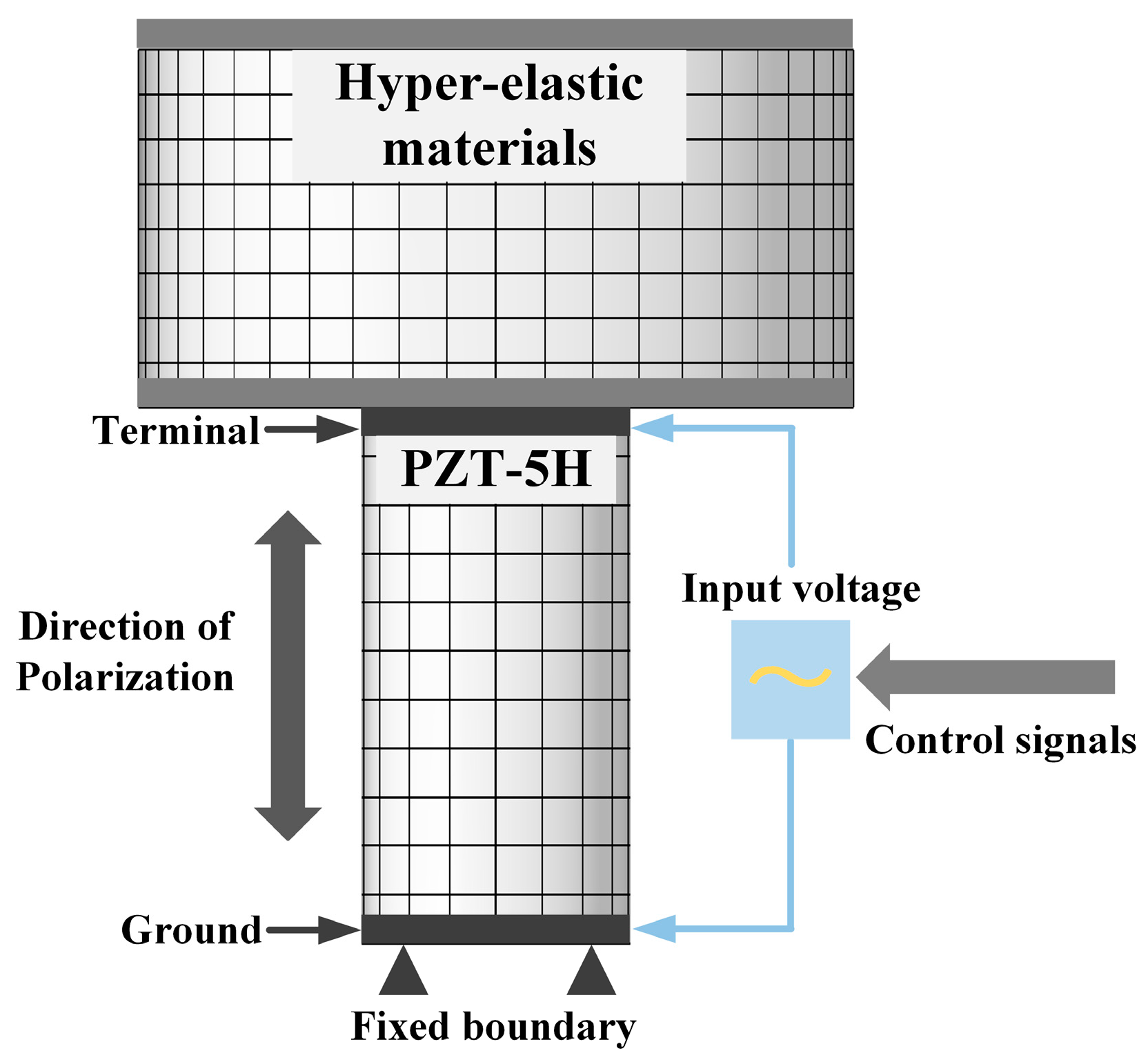
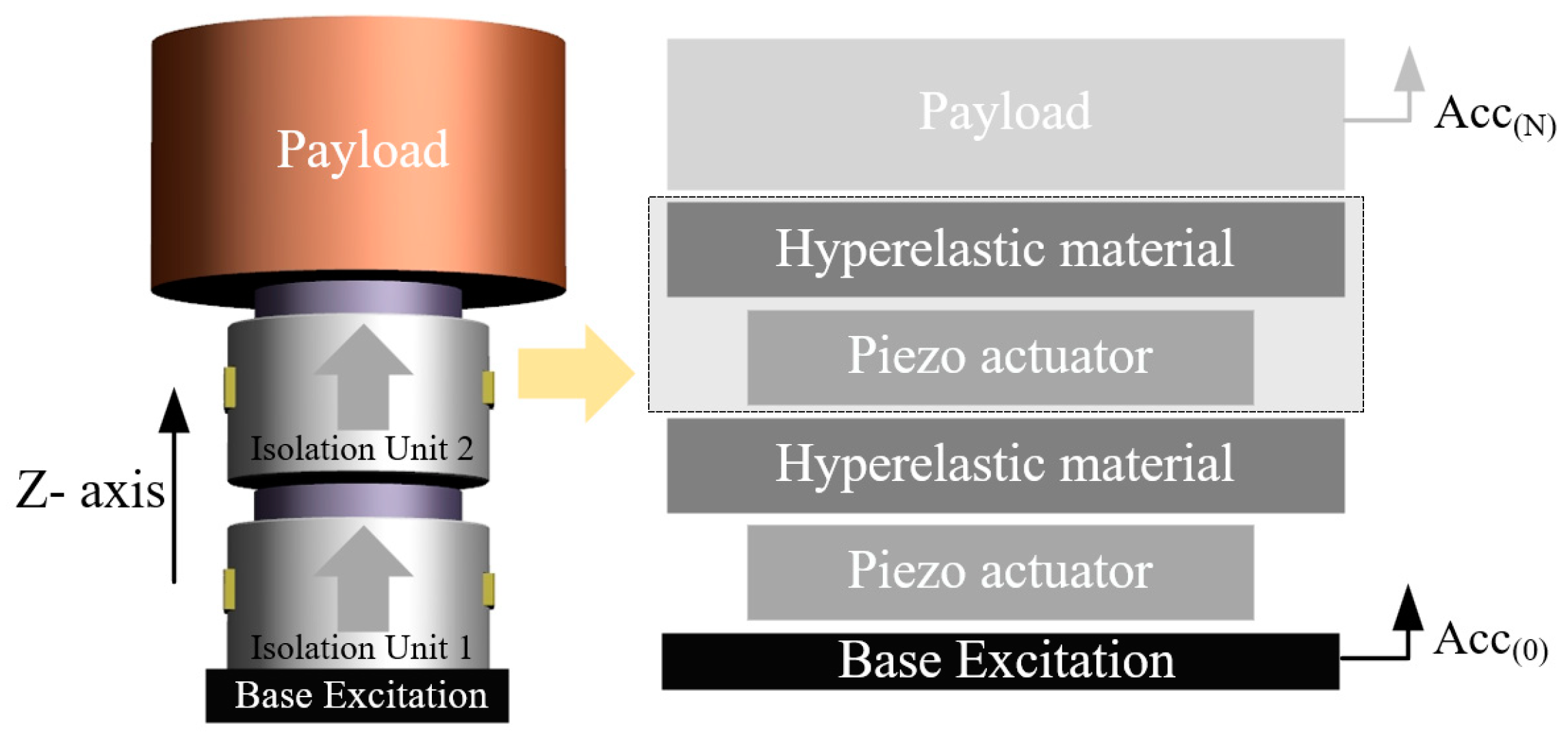
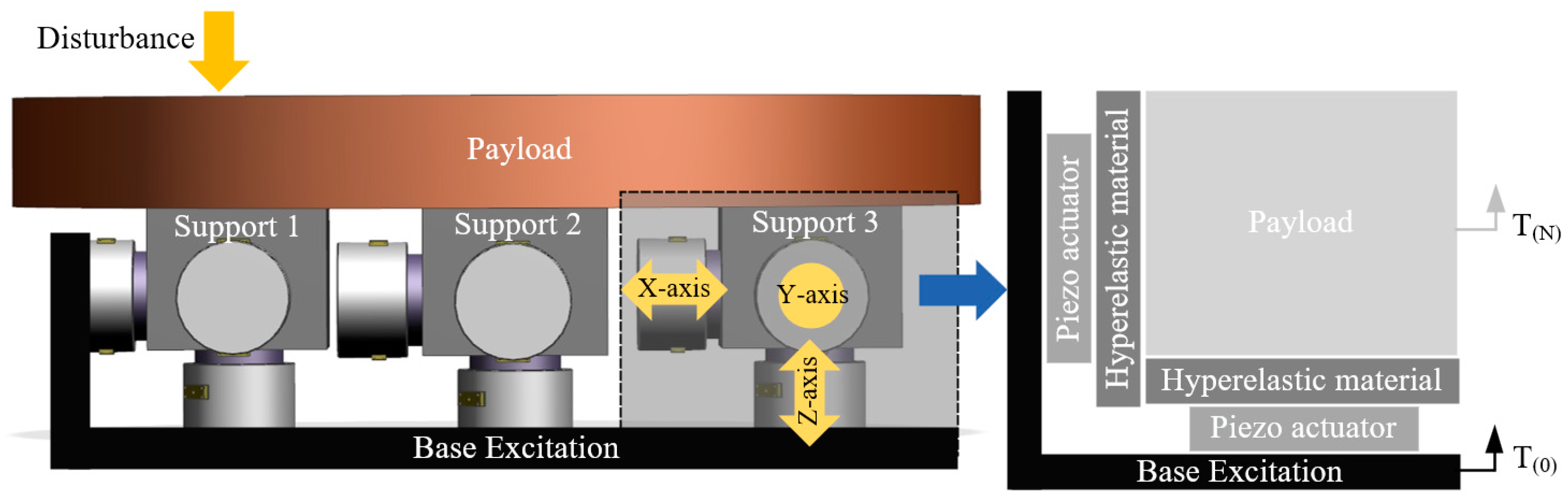
2. Active Isolation Unit
2.1. Dynamic Model
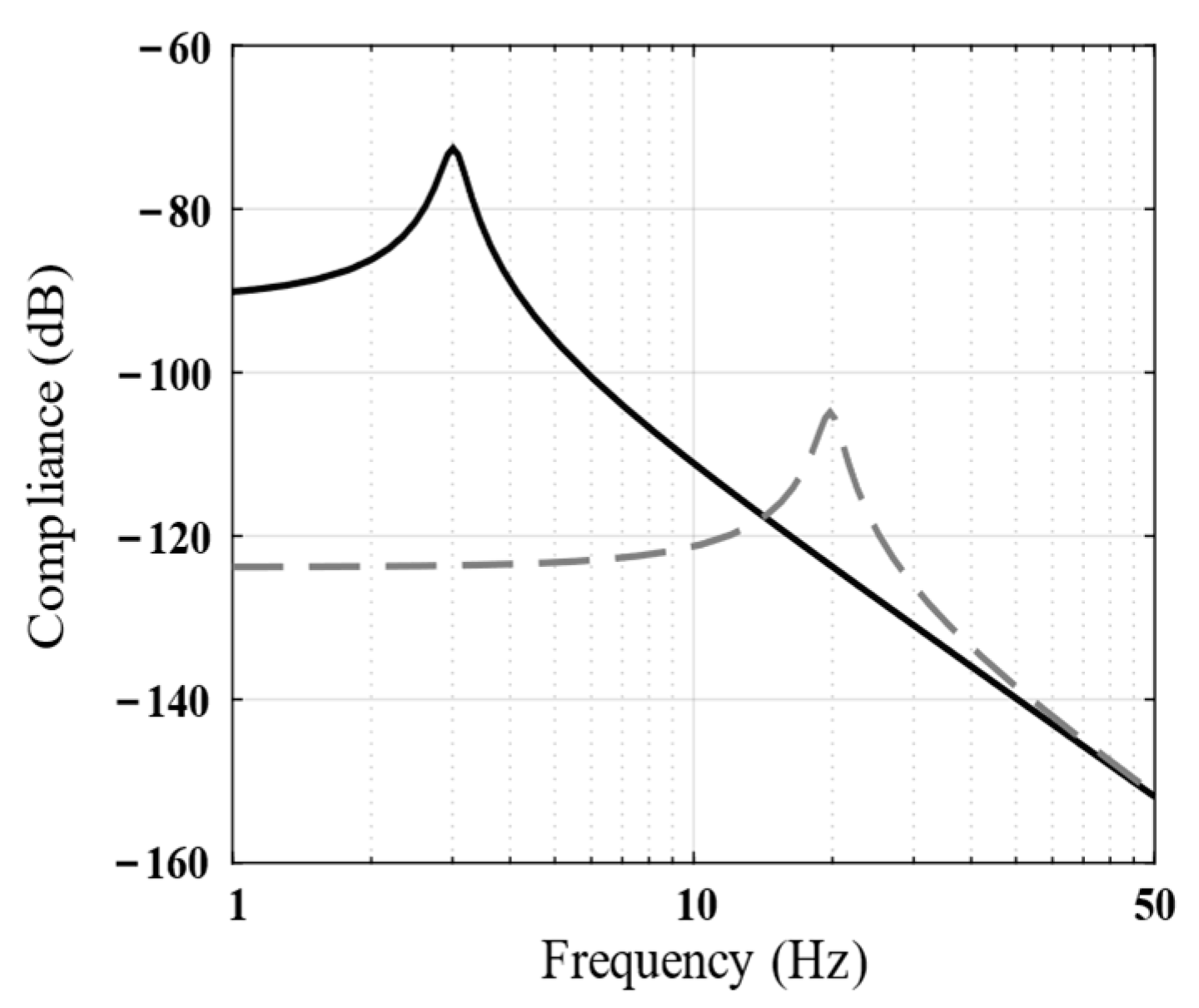
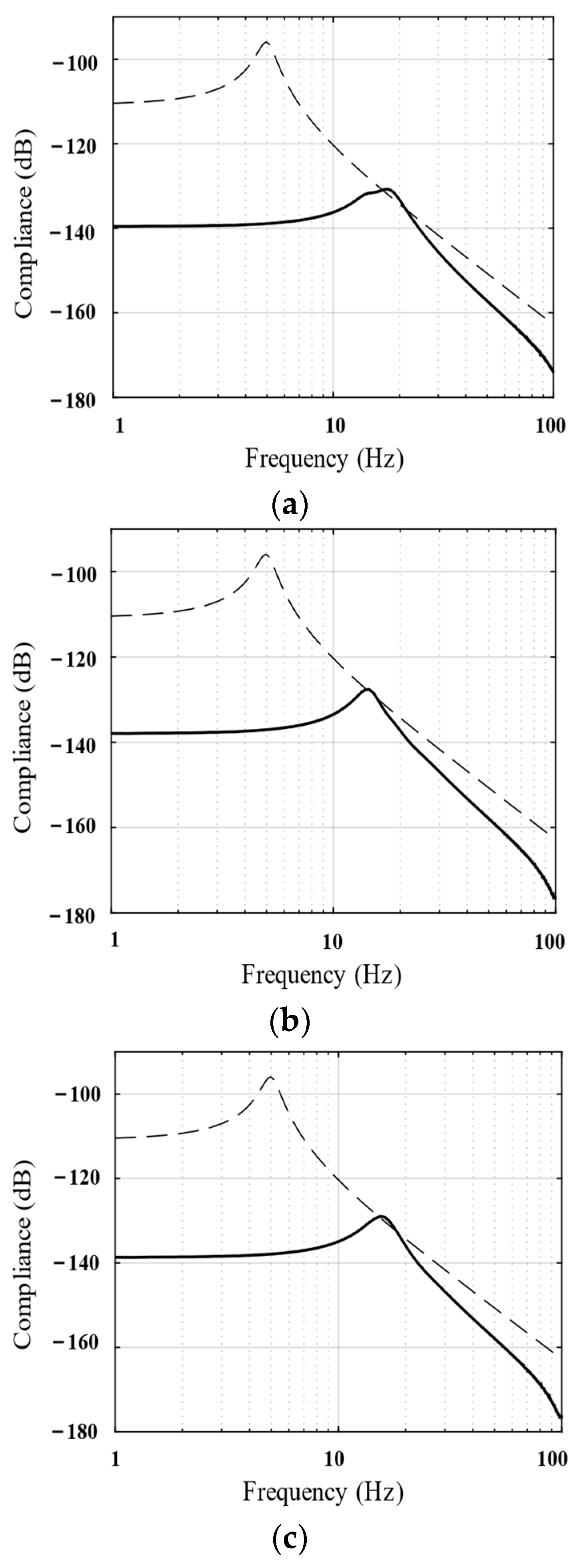
2.2. Dynamic Analysis
2.3. Anti-Disturbance Characteristics
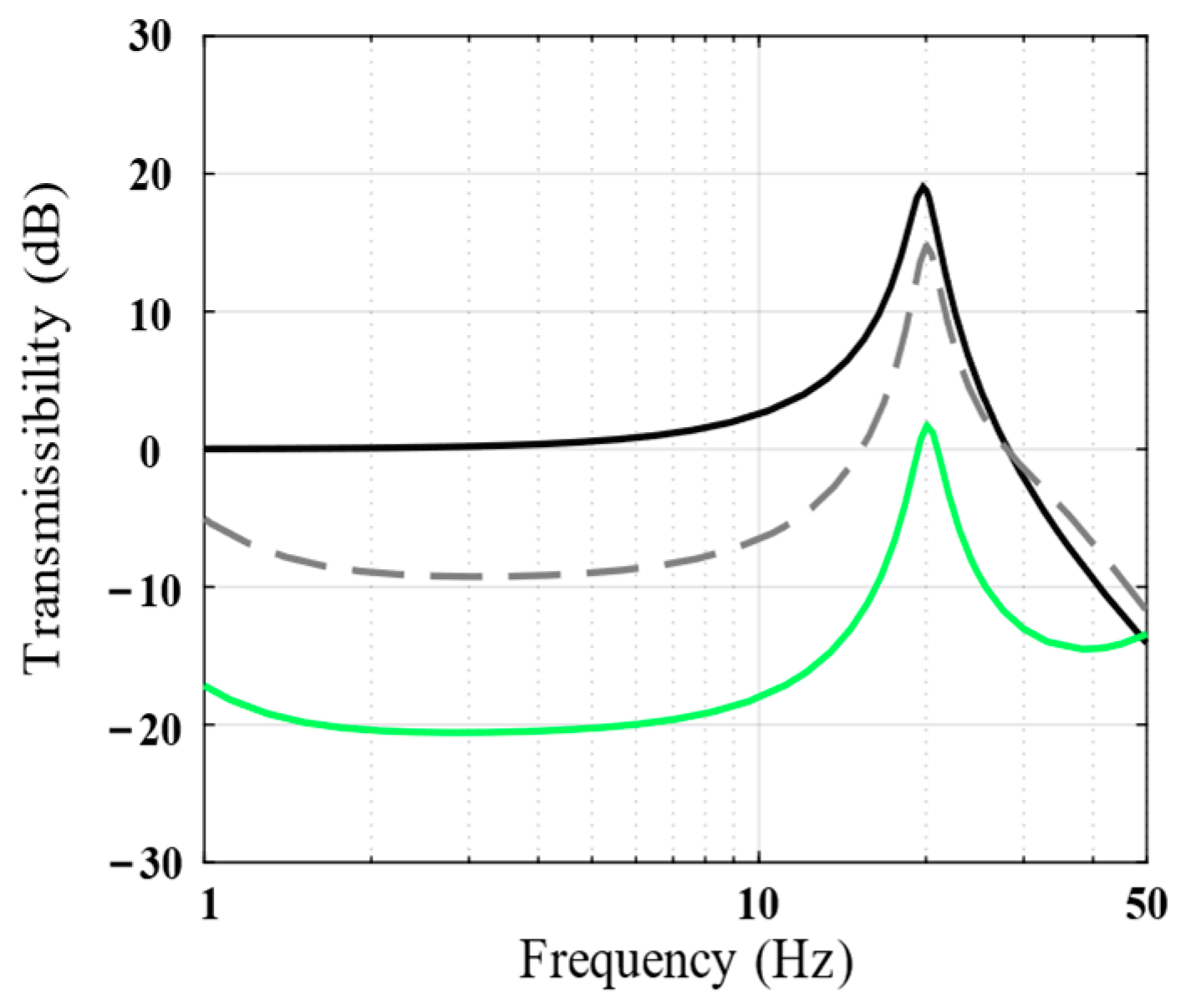
2.4. Feedback Control
2.4.1. Absolute Displacement Feedback
2.4.2. Integral Force Feedback
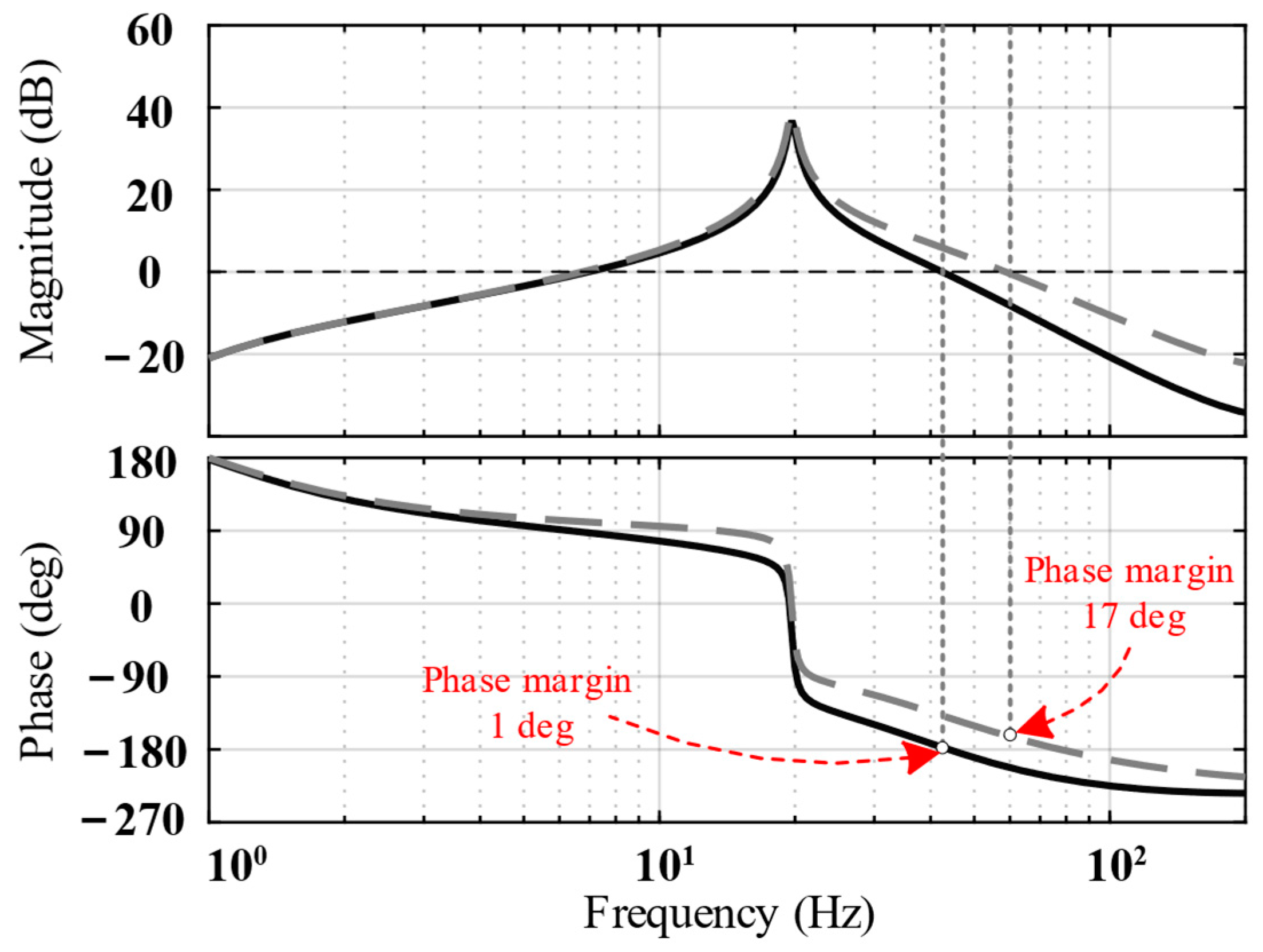
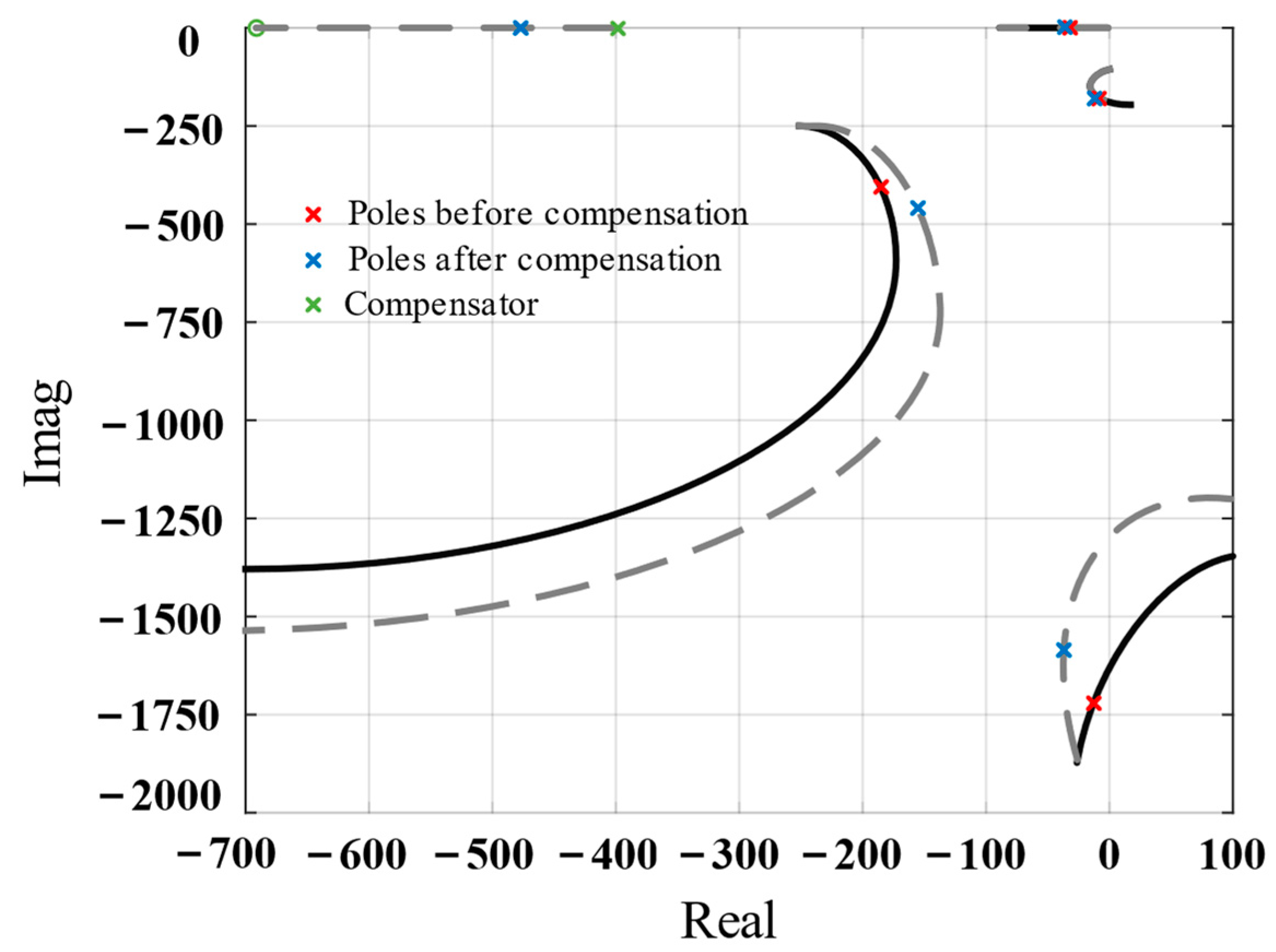
3. Stability Analysis
3.1. Force Sensor Feedback Loop
3.2. Absolute Displacement Feedback Loop
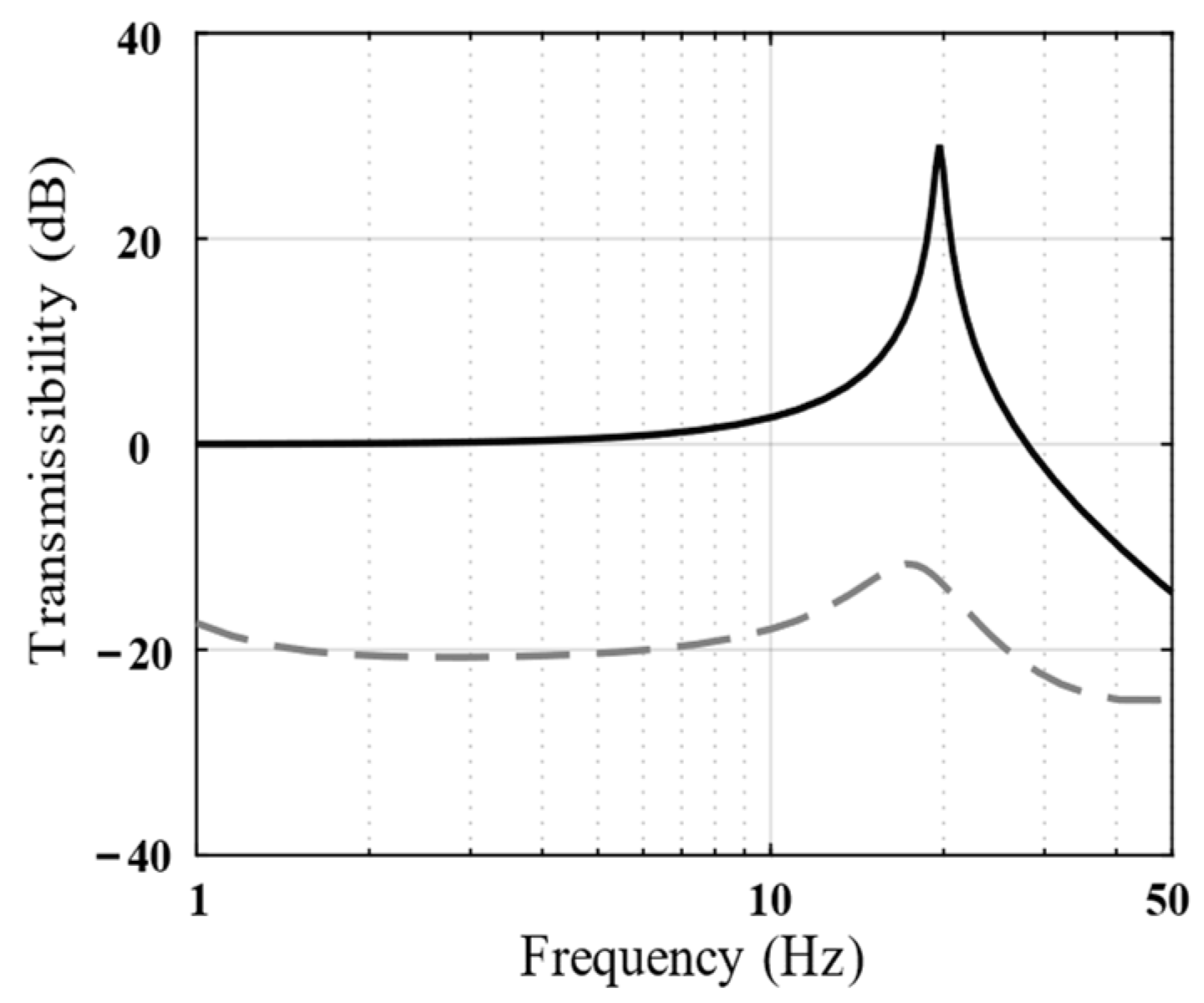
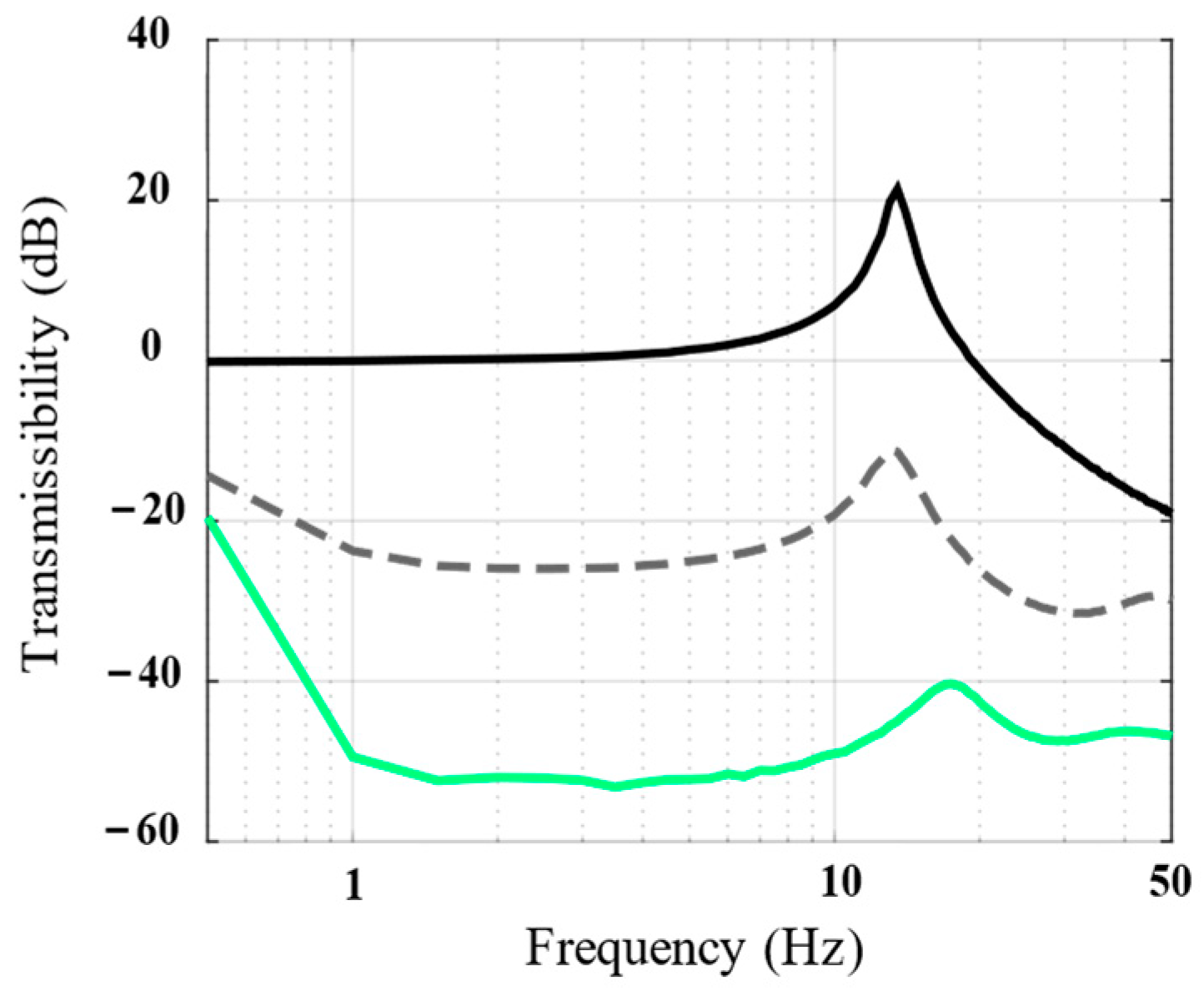
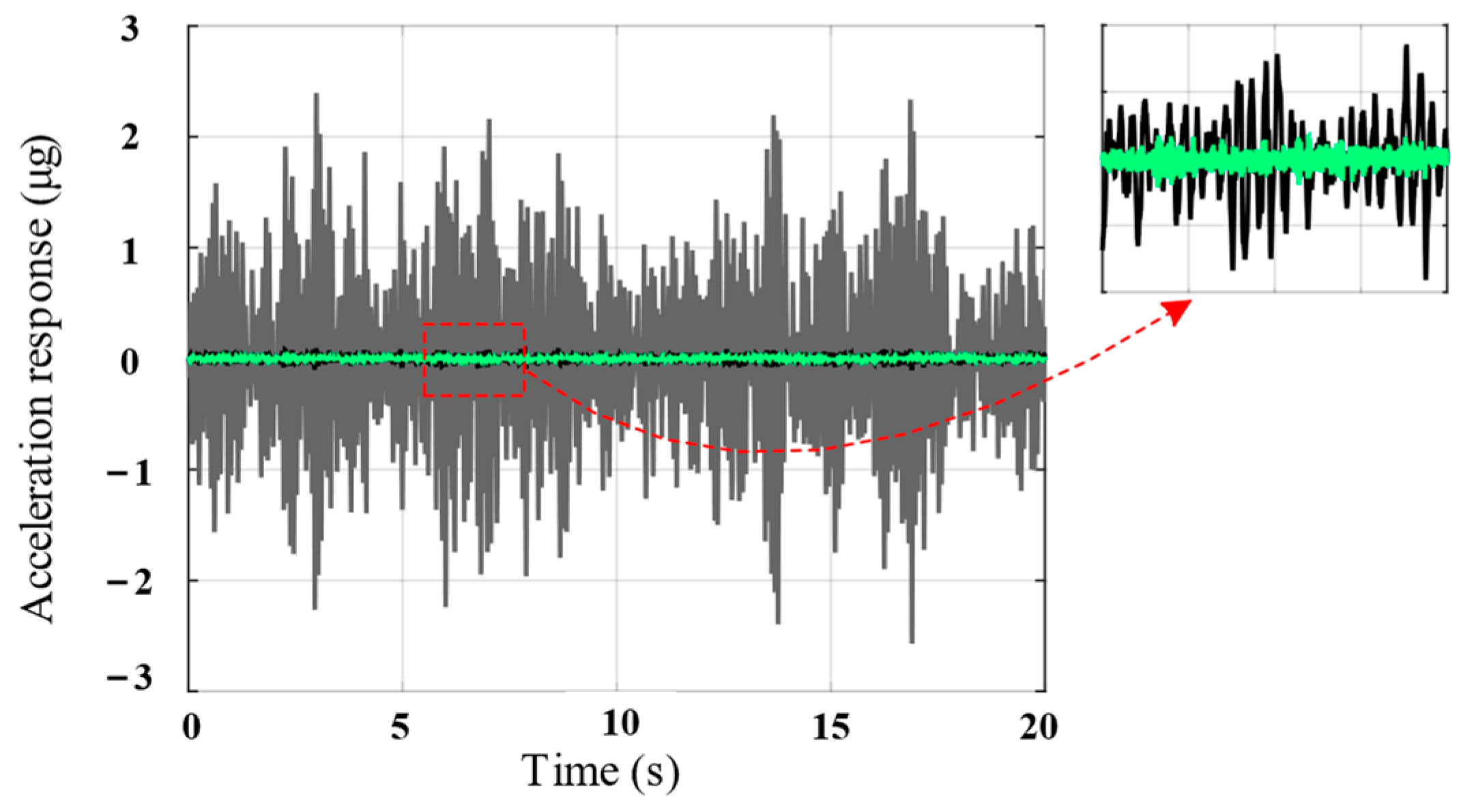
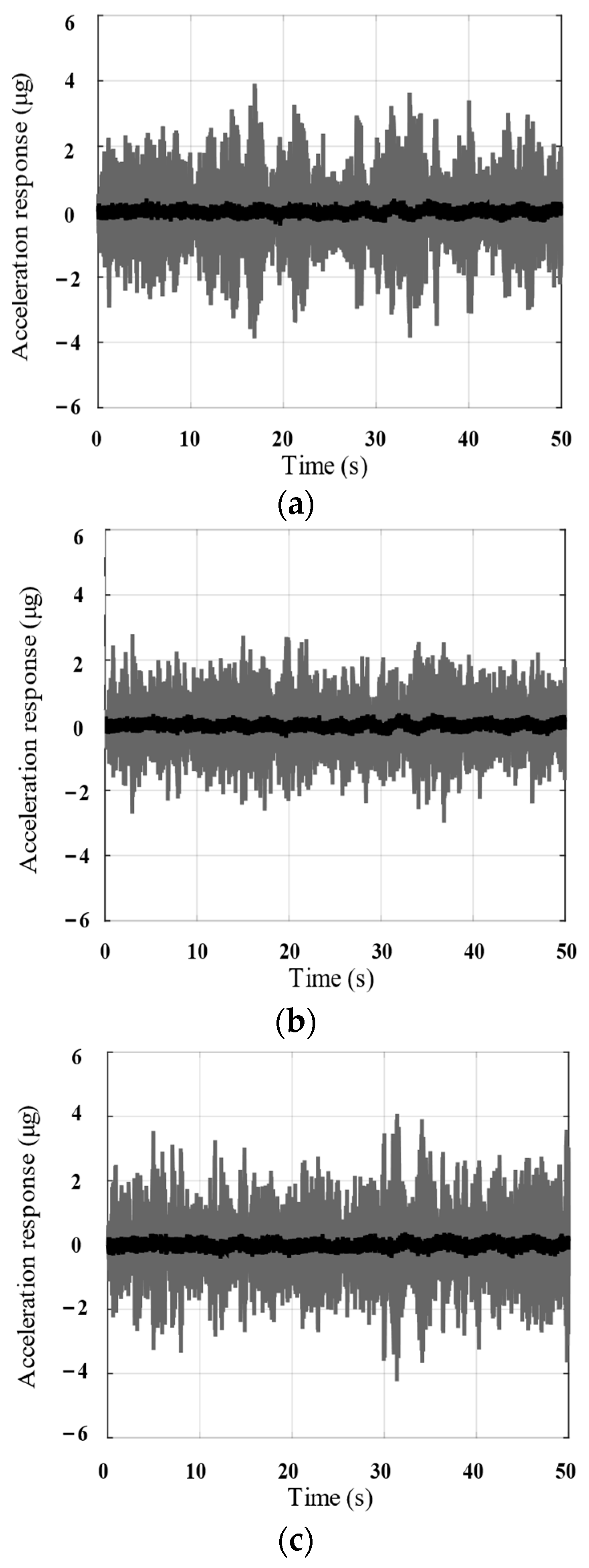
4. Simulation
4.1. Serial System
4.2. Parallel System
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, Q.; Ma, G. Variable Structure Control and Active Vibration Suppression of Flexible Spacecraft during Attitude Maneuver. Aerosp. Sci. Technol. 2005, 9, 307–317. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, Y.; He, W.; Hui, Q. Modeling and Observer-Based Vibration Control of a Flexible Spacecraft with External Disturbances. IEEE Trans. Ind. Electron. 2018, 66, 8648–8658. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, Y.-W.; Ding, H.; Yang, T.-Z.; Li, Y.; Chen, L.-Q. Nonlinear Energy Sink for Whole-Spacecraft Vibration Reduction. J. Vib. Acoust. 2017, 139, 021011. [Google Scholar] [CrossRef]
- Connolly, C. Vibration Isolation Theory and Practice. Assem. Autom. 2009, 29, 8–13. [Google Scholar] [CrossRef]
- Di Gennaro, S. Output Stabilization of Flexible Spacecraft with Active Vibration Suppression. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 747–759. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Zhang, J. Vibration Control for Rapid Attitude Stabilization of Spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1308–1320. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, H.Y.; Kim, K.H.; Kim, M.H.; Lee, S.W. Control of a Hybrid Active-Passive Vibration Isolation System. J. Mech. Sci. Technol. 2017, 31, 5711–5719. [Google Scholar] [CrossRef]
- Abhilash, M.; Rajendran, D.; Sharma, G. Passive Flexural Ring Micro-Vibration Isolator for Spacecraft Actuators. In Proceedings of the 11th National Conference and Exhibition on Aerospace & Defense Related Mechanisms, Hyderabad, India, 16–17 November 2018. [Google Scholar]
- Balaji, P.S.; Rahman, M.E.; Moussa, L.; Lau, H.H. Wire Rope Isolators for Vibration Isolation of Equipment and Structures–A Review. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 9th Curtin University of Technology Science and Engineering International Conference 2014 (CUTSE2014), Sarawak, Malaysia, 3–4 December 2014; IOP Publishing: Bristol, UK, 2015; Volume 78, p. 012001. [Google Scholar]
- Lai, A.; Du, Z.; Gan, C.L.; Schuh, C.A. Shape Memory and Superelastic Ceramics at Small Scales. Science 2013, 341, 1505–1508. [Google Scholar] [CrossRef] [PubMed]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A Study of a Nonlinear Vibration Isolator with a Quasi-Zero Stiffness Characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- Asadi Jafari, M.H.; Zarastvand, M.; Zhou, J. Doubly Curved Truss Core Composite Shell System for Broadband Diffuse Acoustic Insulation. J. Vib. Control 2023, 10775463231206229. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, X.; Bian, J.; Li, F.; Allen, R. Vibration Isolation by Exploring Bio-Inspired Structural Nonlinearity. Bioinspir. Biomim. 2015, 10, 056015. [Google Scholar] [CrossRef] [PubMed]
- Gatti, G.; Ledezma-Ramirez, D.F.; Brennan, M.J. Performance of a Shock Isolator Inspired by Skeletal Muscles. Int. J. Mech. Sci. 2023, 244, 108066. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Wang, Y.; Yue, X.; Yuan, J. Post-Capture Vibration Suppression of Spacecraft via a Bio-Inspired Isolation System. Mech. Syst. Signal Process. 2018, 105, 214–240. [Google Scholar] [CrossRef]
- Yan, G.; Wang, S.; Zou, H.; Zhao, L.; Gao, Q.; Zhang, W. Bio-Inspired Polygonal Skeleton Structure for Vibration Isolation: Design, Modelling, and Experiment. Sci. China Technol. Sci. 2020, 63, 2617–2630. [Google Scholar] [CrossRef]
- Jiao, X.; Zhang, J.; Li, W.; Wang, Y.; Ma, W.; Zhao, Y. Advances in Spacecraft Micro-Vibration Suppression Methods. Prog. Aerosp. Sci. 2023, 138, 100898. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent Advances in Micro-Vibration Isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Fuller, C.R.; von Flotow, A.H. Active Control of Sound and Vibration. IEEE Control Syst. Mag. 1995, 15, 9–19. [Google Scholar] [CrossRef]
- Shang, J.; Tian, Y.; Li, Z.; Wang, F.; Cai, K. A Novel Voice Coil Motor-Driven Compliant Micropositioning Stage Based on Flexure Mechanism. Rev. Sci. Instrum. 2015, 86, 095001. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Hsieh, H.-E.; Wu, W.-H. An Active Vibration Isolation System Using Adaptive Proportional Control Method; Liao, W.-H., Ed.; SPIE: San Diego, CA, USA, 2014; p. 90572W. [Google Scholar]
- Liu, J.; Li, Y.; Zhang, Y.; Gao, Q.; Zuo, B. Dynamics and Control of a Parallel Mechanism for Active Vibration Isolation in Space Station. Nonlinear Dyn. 2014, 76, 1737–1751. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, W. Data-Driven Feedforward Control on Active Vibration Isolation System. In Proceedings of the 2017 17th International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 18–21 October 2017; pp. 562–567. [Google Scholar]
- Beijen, M.A.; Heertjes, M.F.; Van Dijk, J.; Hakvoort, W.B.J. Self-Tuning MIMO Disturbance Feedforward Control for Active Hard-Mounted Vibration Isolators. Control Eng. Pract. 2018, 72, 90–103. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. Mixed Feedback and Feedforward Control Design for Multi-Axis Vibration Isolation Systems. Mechatronics 2019, 61, 106–116. [Google Scholar] [CrossRef]
- Sui, L.; Xiong, X.; Shi, G. Piezoelectric Actuator Design and Application on Active Vibration Control. Phys. Procedia 2012, 25, 1388–1396. [Google Scholar] [CrossRef]
- Li, P.; Fu, J.; Wang, Y.; Xing, Z.; Yu, M. Dynamic Model and Parameters Identification of Piezoelectric Stack Actuators. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 1918–1923. [Google Scholar]
- Wang, C.; Xie, X.; Chen, Y.; Zhang, Z. Investigation on Active Vibration Isolation of a Stewart Platform with Piezoelectric Actuators. J. Sound Vib. 2016, 383, 1–19. [Google Scholar] [CrossRef]
- Du, L.; Ji, L.; Luo, Y.; Shao, S.; Xu, M. Simulation and Experiment of an Active-Passive Isolator for Micro-Vibration Control of Spacecraft. In Proceedings of the 2020 15th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Zhengzhou, China, 16 April 2021; pp. 227–232. [Google Scholar]
- Song, H.; Shan, X.; Hou, W.; Wang, C.; Sun, K.; Xie, T. A Novel Piezoelectric-Based Active-Passive Vibration Isolator for Low-Frequency Vibration System and Experimental Analysis of Vibration Isolation Performance. Energy 2023, 278, 127870. [Google Scholar] [CrossRef]
- Hanieh, A.A.; Preumont, A. Multi-Axis Vibration Isolation Using Different Active Techniques of Frequency Reduction. J. Vib. Control 2011, 17, 759–768. [Google Scholar] [CrossRef]
- Sun, X.; Wang, F.; Xu, J. A Novel Dynamic Stabilization and Vibration Isolation Structure Inspired by the Role of Avian Neck. Int. J. Mech. Sci. 2021, 193, 106166. [Google Scholar] [CrossRef]
- Chin, D.D.; Lentink, D. Flapping Wing Aerodynamics: From Insects to Vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef]
- Deng, T.; Wen, G.; Ding, H.; Lu, Z.-Q.; Chen, L.-Q. A Bio-Inspired Isolator Based on Characteristics of Quasi-Zero Stiffness and Bird Multi-Layer Neck. Mech. Syst. Signal Process. 2020, 145, 106967. [Google Scholar] [CrossRef]
- Shyy, W.; Aono, H.; Kang, C.; Liu, H. An Introduction to Flapping Wing Aerodynamics; Cambridge University Press: Cambridge, UK, 2013; Volume 37. [Google Scholar]
- Mazaheri, K.; Ebrahimi, A. Experimental Investigation on Aerodynamic Performance of a Flapping Wing Vehicle in Forward Flight. J. Fluids Struct. 2011, 27, 586–595. [Google Scholar] [CrossRef]
- McArthur, K.L.; Dickman, J.D. State-Dependent Sensorimotor Processing: Gaze and Posture Stability during Simulated Flight in Birds. J. Neurophysiol. 2011, 105, 1689–1700. [Google Scholar] [CrossRef]
- Kress, D.; Van Bokhorst, E.; Lentink, D. How Lovebirds Maneuver Rapidly Using Super-Fast Head Saccades and Image Feature Stabilization. PLoS ONE 2015, 10, e0129287. [Google Scholar] [CrossRef]
- Hedenström, A.; Johansson, L.C. Bat Flight: Aerodynamics, Kinematics and Flight Morphology. J. Exp. Biol. 2015, 218, 653–663. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H.; Fatikow, S. Modeling and Control of Piezo-Actuated Nanopositioning Stages: A Survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Adriaens, H.; De Koning, W.L.; Banning, R. Modeling Piezoelectric Actuators. IEEEASME Trans. Mechatron. 2000, 5, 331–341. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Wang, L.; Yuan, L.; Zhang, L.; Gong, X.; Wu, Y.; Zheng, R. Modeling and Analysis of the Influence Caused by Micro-Vibration on Satellite Attitude Control System. Acta Astronaut. 2023, 213, 71–80. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, T.; Du, H.; Zhou, S. Wideband Vibration Isolation and Energy Harvesting Based on a Coupled Piezoelectric-Electromagnetic Structure. Mech. Syst. Signal Process. 2023, 184, 109689. [Google Scholar] [CrossRef]
- Zhou, S.; Lallart, M.; Erturk, A. Multistable Vibration Energy Harvesters: Principle, Progress, and Perspectives. J. Sound Vib. 2022, 528, 116886. [Google Scholar] [CrossRef]




| Parameter | Numerical Value |
|---|---|
| mp | 200 kg |
| kr | 3,400,000 N/m |
| cr | 150 N/(m/s) |
| mi | 30 kg |
| kc | 100,000,000 N/m |
| cc | 1500 N/(m/s) |
| Parameter | Numerical Value |
|---|---|
| Mass of payload | 196 kg |
| Z-axis stiffness of hyperelastic material | 3,000,000 N/m |
| Z-axis damping of hyperelastic material | 3000 N/(m/s) |
| Mass of intermediate | 16 kg |
| Z-axis stiffness of the piezo actuator | 80,000,000 N/m |
| Parameter | Numerical Value |
|---|---|
| Mass of payload | 646 kg |
| single-axis stiffness of hyperelastic material | 3,400,000 N/m |
| single-axis damping of hyperelastic material | 1000 N/(m/s) |
| Mass of intermediate | 27 kg |
| Z-axis stiffness of the piezo actuator | 100,000,000 N/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, L.; Li, L.; Wang, X.; He, S. Modeling and Analysis of Bio-Inspired, Reconfigurable, Piezo-Driven Vibration Isolator for Spacecraft. Biomimetics 2024, 9, 29. https://doi.org/10.3390/biomimetics9010029
Zhang Y, Wang L, Li L, Wang X, He S. Modeling and Analysis of Bio-Inspired, Reconfigurable, Piezo-Driven Vibration Isolator for Spacecraft. Biomimetics. 2024; 9(1):29. https://doi.org/10.3390/biomimetics9010029
Chicago/Turabian StyleZhang, Yubo, Lintao Wang, Lin Li, Xiaoming Wang, and Shuai He. 2024. "Modeling and Analysis of Bio-Inspired, Reconfigurable, Piezo-Driven Vibration Isolator for Spacecraft" Biomimetics 9, no. 1: 29. https://doi.org/10.3390/biomimetics9010029
APA StyleZhang, Y., Wang, L., Li, L., Wang, X., & He, S. (2024). Modeling and Analysis of Bio-Inspired, Reconfigurable, Piezo-Driven Vibration Isolator for Spacecraft. Biomimetics, 9(1), 29. https://doi.org/10.3390/biomimetics9010029





