A High-Efficient Reinforcement Learning Approach for Dexterous Manipulation
Abstract
1. Introduction
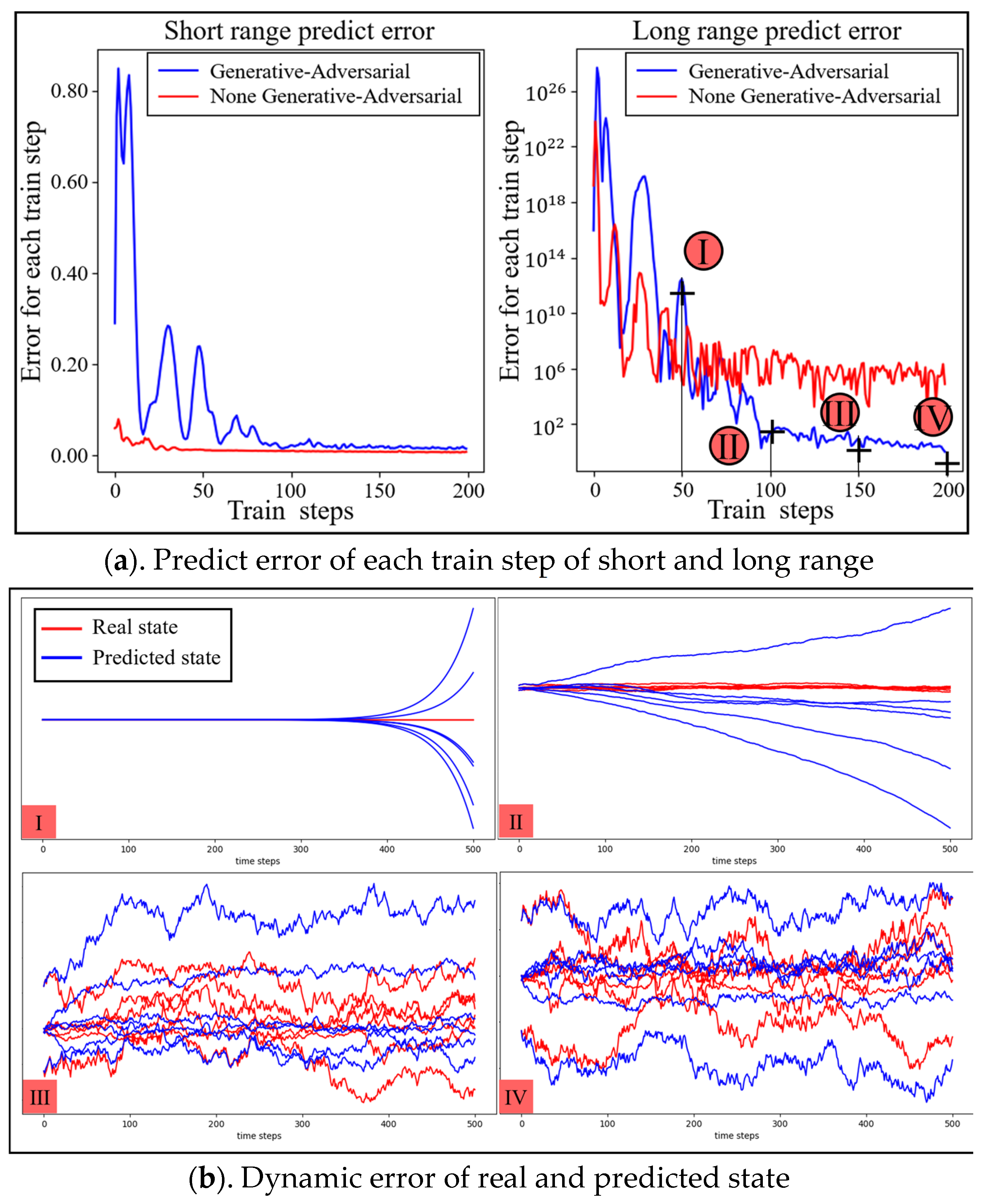
- To address the problem of prediction error explosion over long spans, the state of the dexterous hand is learned through generative adversarial architecture with high prediction accuracy.
- An adaptive trajectory planning method is proposed. Moreover, an adaptive trajectory programming kernel is built to generate High Value Area Trajectory (HVAT) based on the dexterous dynamic model and object. A smooth distance loss function and a U-shaped loss function are designed to calculate the loss value of the dexterous hand system at the reference point.
- A new Actor–Critic-based reinforcement learning algorithm is proposed for the control of the dexterous hand.
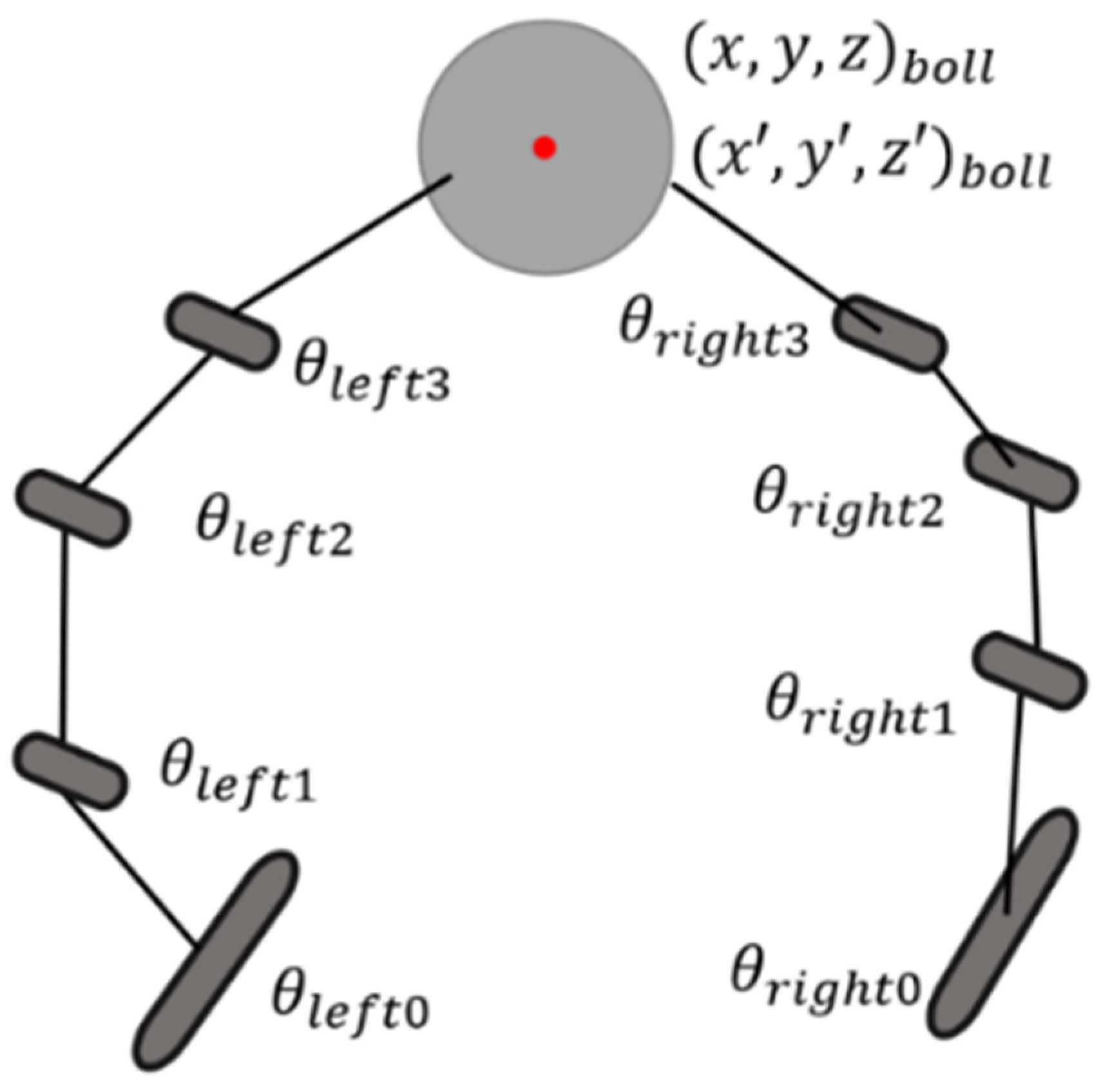
2. Methodologies
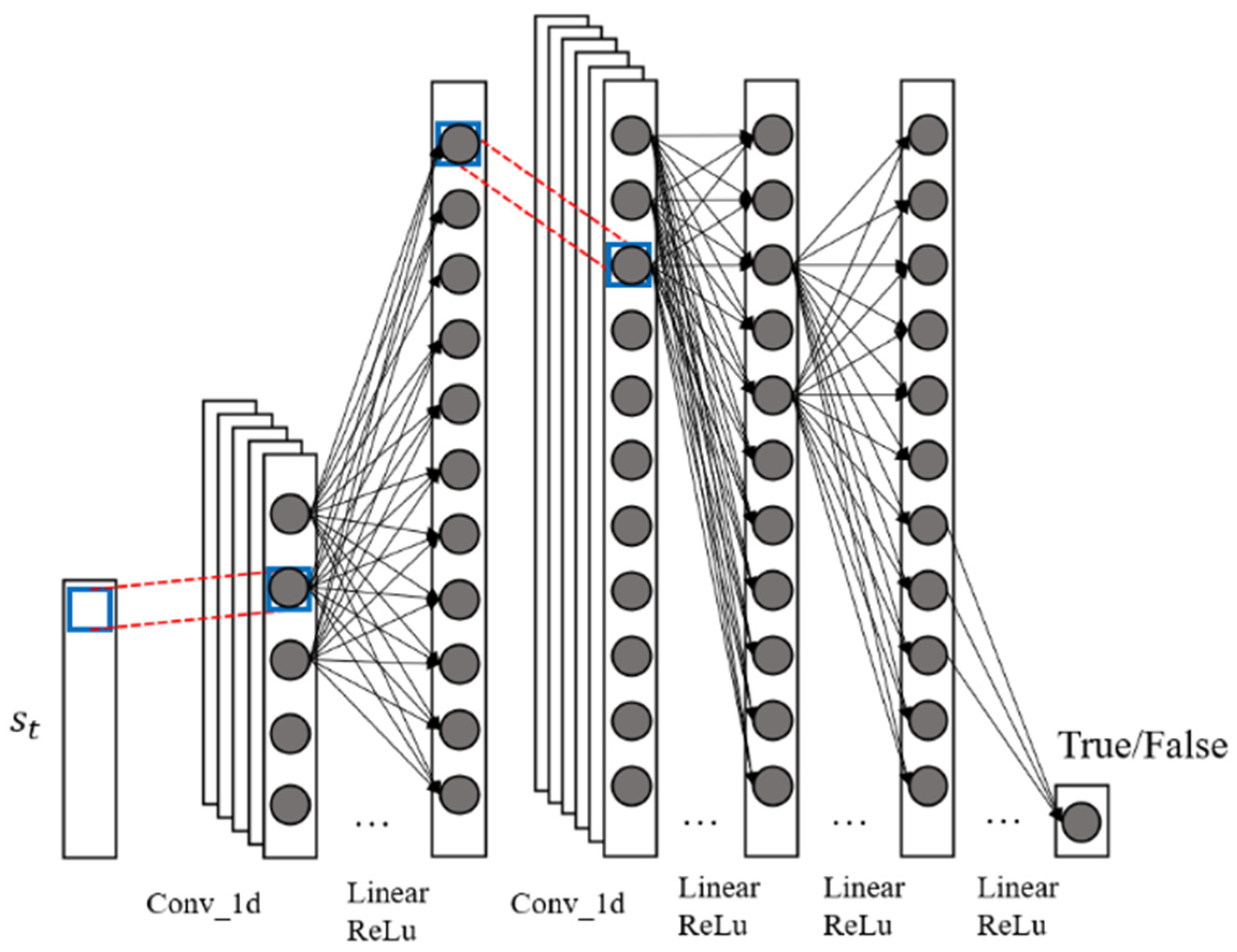
2.1. Generative Adversarial Architecture
2.2. Theoretical Analysis of Trajectory Planning Algorithm
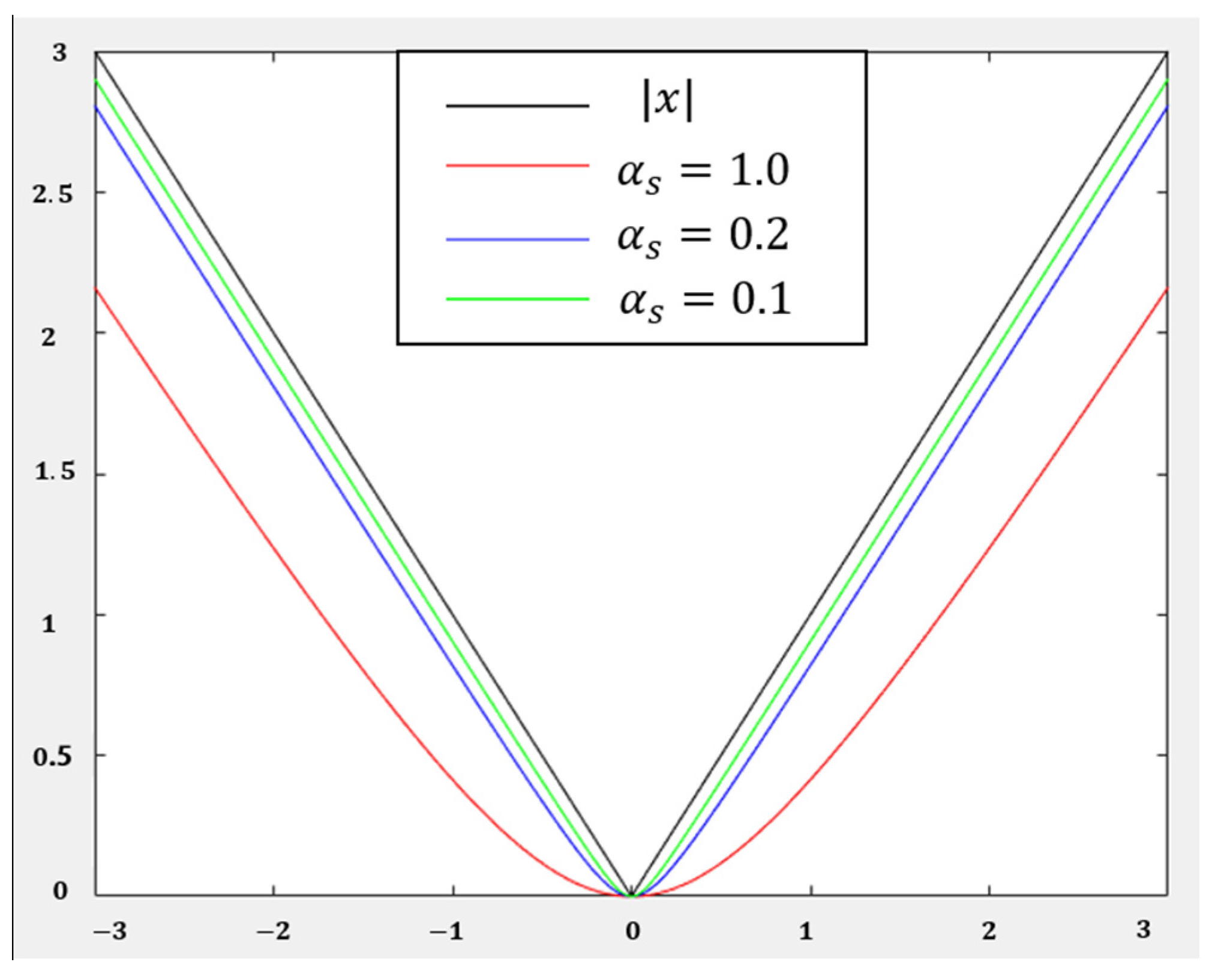
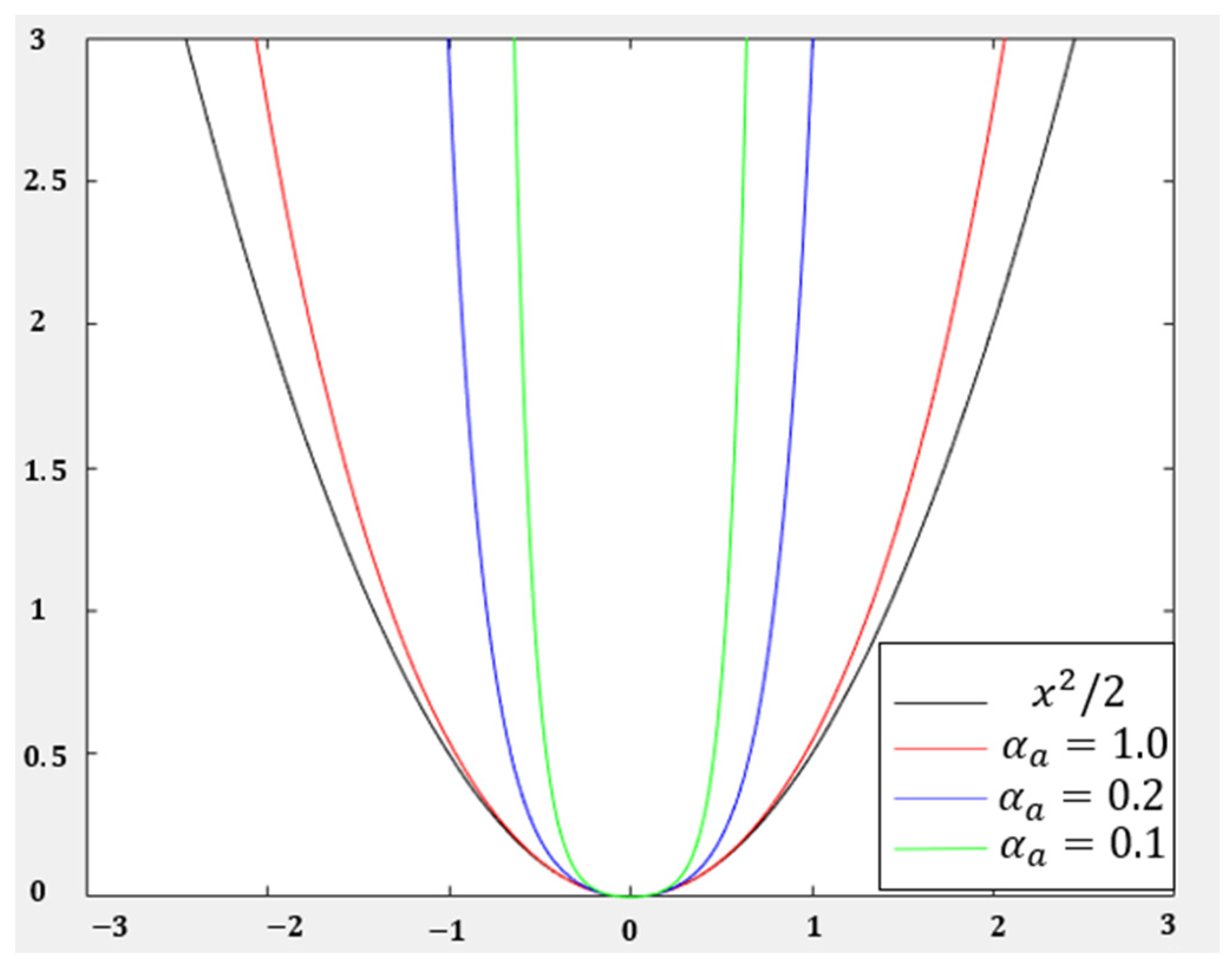
2.3. Design of Loss Function
2.4. Kernel Design of Adaptive Trajectory Planning
2.5. Improved SAC Algorithm
Iteration of Control Policies
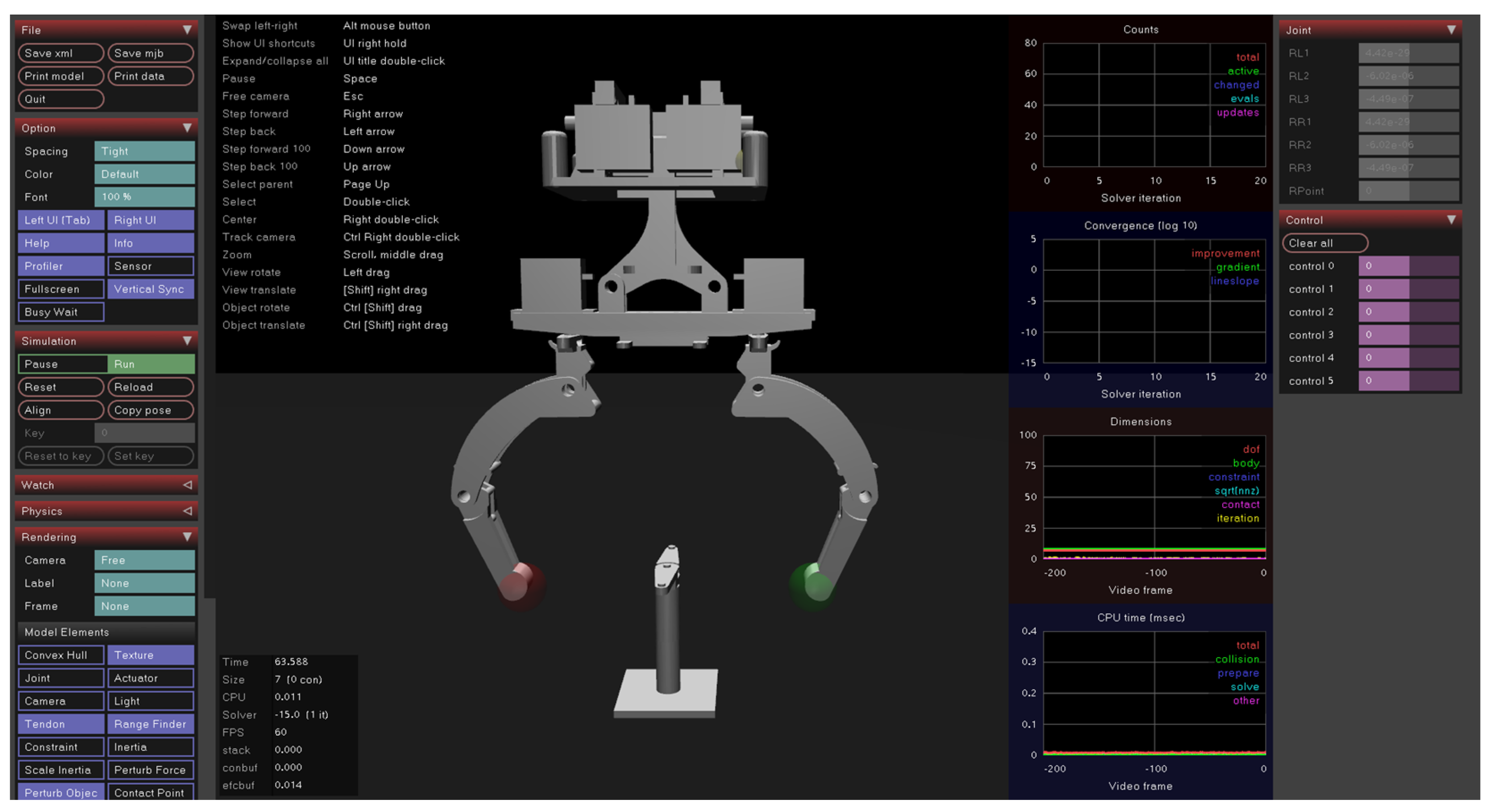
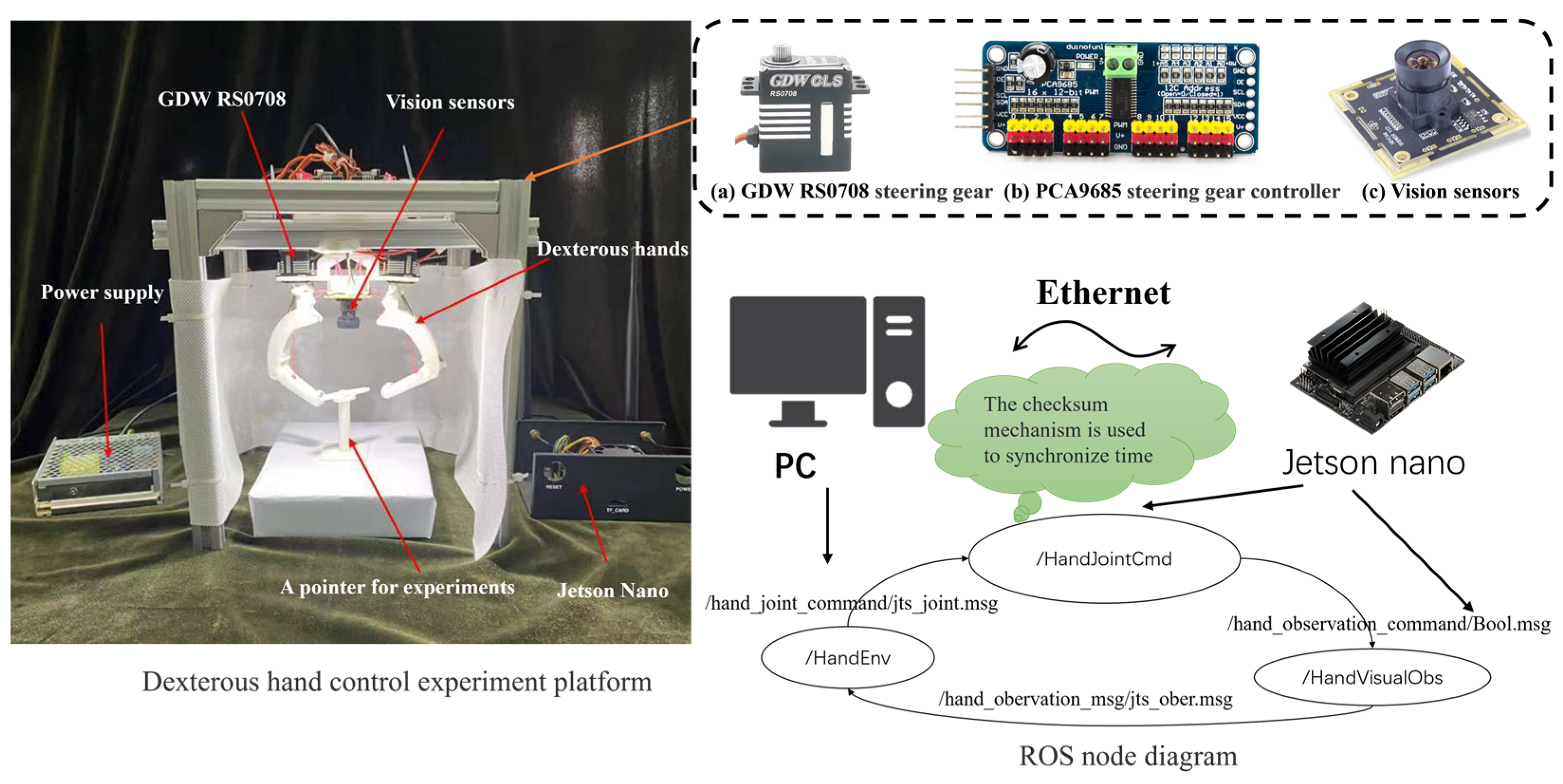
3. Experiments
3.1. Model-Fitting Experiments for Dynamic Processes
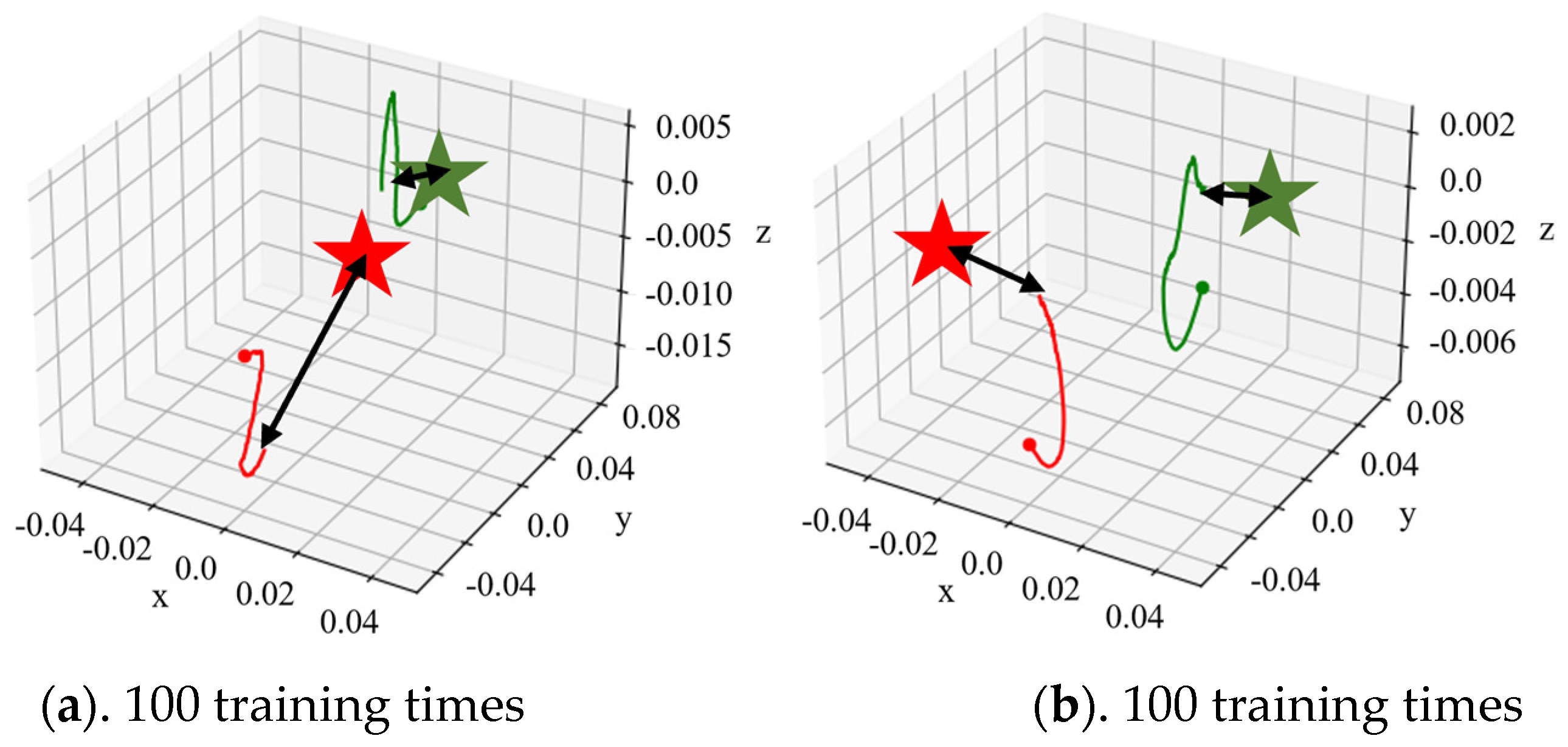
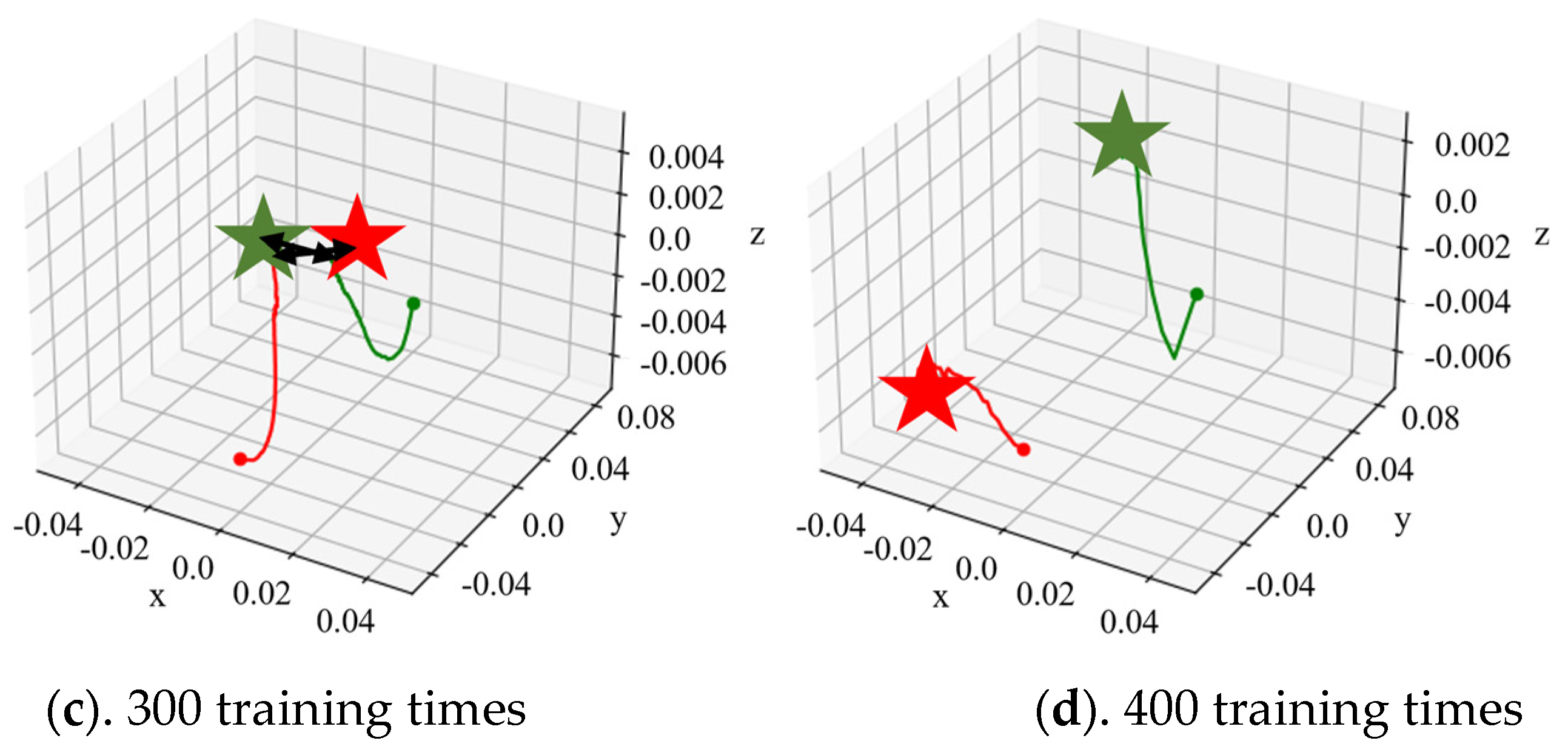
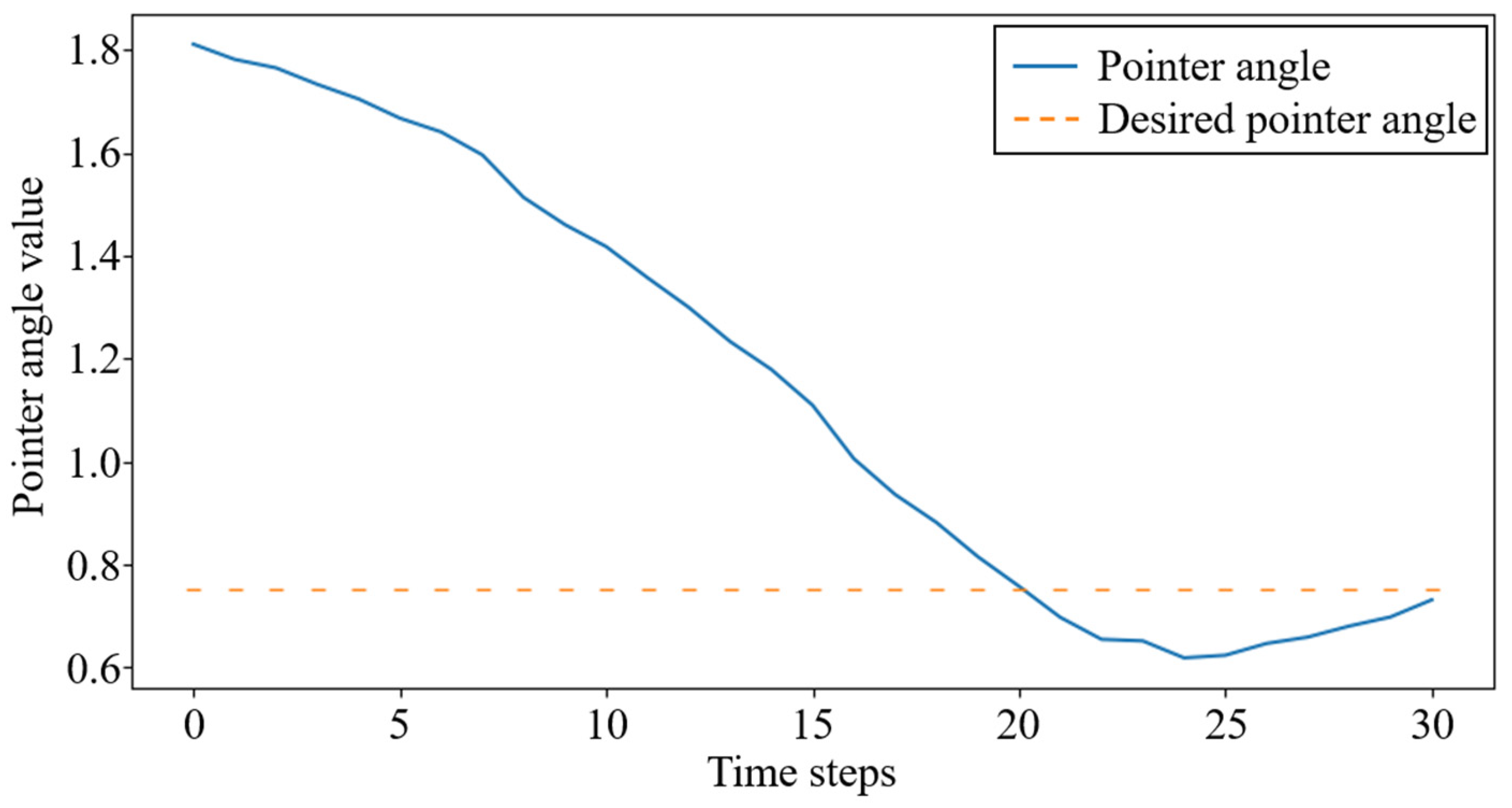
3.2. Adaptive Trajectory Planning Experiments of the Dexterous Hand
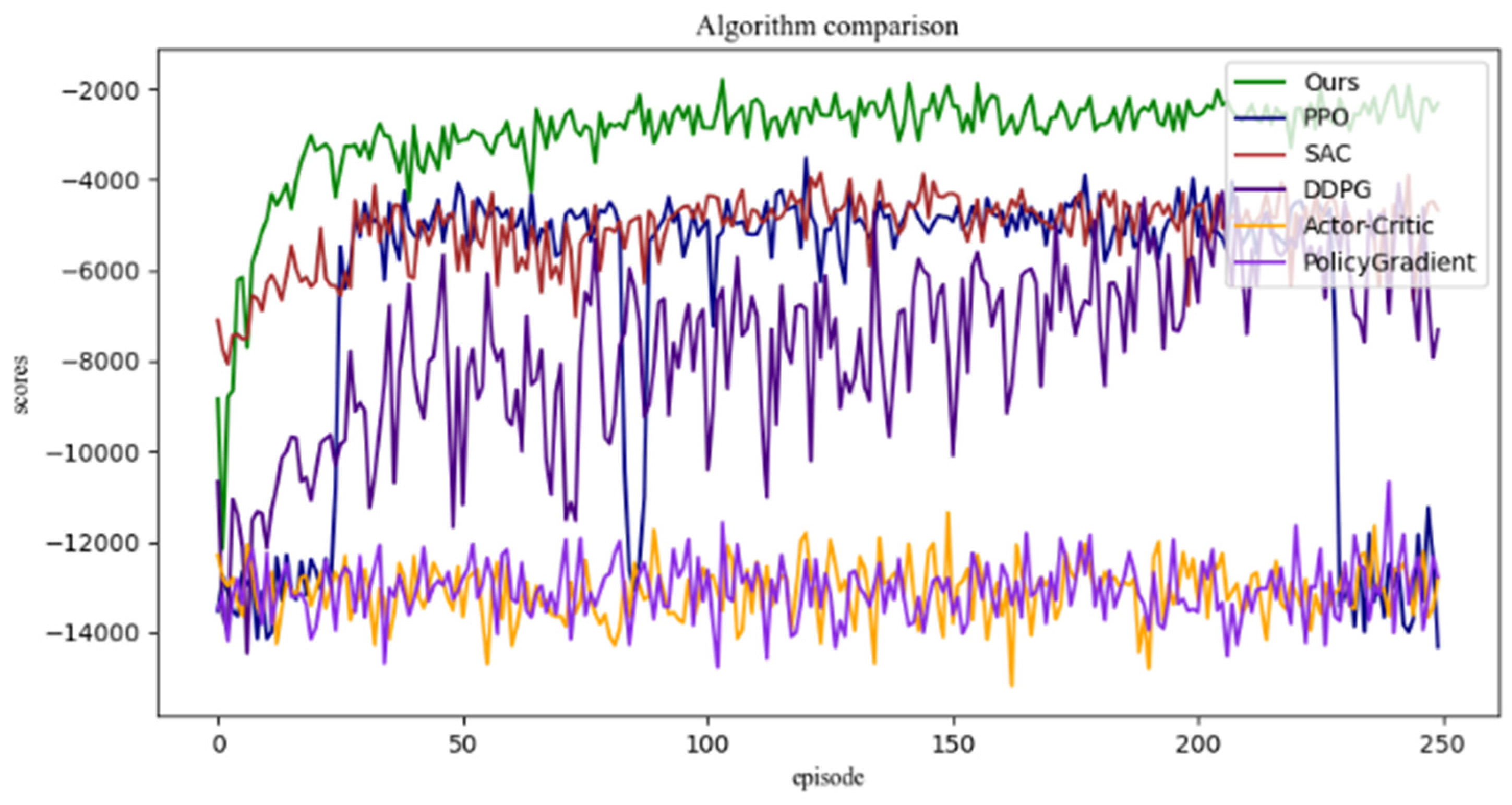
3.3. Controlling Experiments of the Dexterous Hand
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, G.; Gorjup, G.; Yu, R.B.; Jarvis, P.; Liarokapis, M. Modular, Accessible, Sensorized Objects for Evaluating the Grasping and Manipulation Capabilities of Grippers and Hands. IEEE Robot. Autom. Lett. 2020, 5, 6105–6112. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [PubMed]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Li, X.; Serlin, Z.; Yang, G.; Belta, C. A formal methods approach to interpretable reinforcement learning for robotic planning. Sci. Robot. 2019, 4, eaay6276. [Google Scholar] [CrossRef] [PubMed]
- Kormushev, P.; Calinon, S.; Caldwell, D.G. Reinforcement learning in robotics: Applications and real-world challenges. Robotics 2013, 2, 122–148. [Google Scholar] [CrossRef]
- Iwata, T.; Shibuya, T. Adaptive modular reinforcement learning for robot controlled in multiple environments. IEEE Access 2021, 9, 103032–103043. [Google Scholar] [CrossRef]
- Wiedemann, T.; Vlaicu, C.; Josifovski, J.; Viseras, A. Robotic Information Gathering With Reinforcement Learning Assisted by Domain Knowledge: An Application to Gas Source Localization. IEEE Access 2021, 9, 13159–13172. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Al Sallab, A.A.; Yogamani, S.; Perez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Tsurumine, Y.; Cui, Y.; Uchibe, E.; Matsubara, T. Deep reinforcement learning with smooth policy update: Application to robotic cloth manipulation. Robot. Auton. Syst. 2019, 112, 72–83. [Google Scholar] [CrossRef]
- Rombokas, E.; Malhotra, M.; Theodorou, E.A.; Todorov, E.; Matsuoka, Y. Reinforcement Learning and Synergistic Control of the ACT Hand. IEEE-Asme Trans. Mechatron. 2013, 18, 569–577. [Google Scholar] [CrossRef]
- Rothmann, M.; Porrmann, M. A Survey of Domain-Specific Architectures for Reinforcement Learning. IEEE Access 2022, 10, 13753–13767. [Google Scholar] [CrossRef]
- Zhu, H.; Gupta, A.; Rajeswaran, A.; Levine, S.; Kumar, V. Dexterous Manipulation with Deep Reinforcement Learning: Efficient, General, and Low-Cost. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Andrychowicz, M.; Baker, B.; Chociej, M.; Jozefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 2020, 39, 3–20. [Google Scholar] [CrossRef]
- Gao, Y.; Ma, S.W.; Liu, J.J.; Xiu, X.C. Fusion-UDCGAN: Multifocus Image Fusion via a U-Type Densely Connected Generation Adversarial Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Jain, D.; Li, A.; Singhal, S.; Rajeswaran, A.; Kumar, V.; Todorov, E. Learning Deep Visuomotor Policies for Dexterous Hand Manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Montreal, CA, Canada, 20–24 May 2019; pp. 3636–3643. [Google Scholar]
- Fu, Q.; Santello, M. Chapter 3—Sensorimotor Learning of Dexterous Manipulation. In Human Inspired Dexterity in Robotic Manipulation; Watanabe, T., Harada, K., Tada, M., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 27–52. [Google Scholar]
- Kim, C.I.; Kim, M.; Jung, S.; Hwang, E. Simplified Frechet Distance for Generative Adversarial Nets. Sensors 2020, 20, 1548. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.J.; Wang, P.; Wang, J.H.; An, W. The research process of generative adversarial networks. In Proceedings of the International Seminar on Computer Science and Engineering Technology (SCSET), Shanghai, China, 17–18 December 2018. [Google Scholar]
- Abdelgader, A.A.; Viriri, S. Deep Residual Learning for Human Identification Based on Facial Landmarks. In Proceedings of the 15th International Work-Conference on Artificial Neural Networks (IWANN), Gran Canaria, Spain, 12–14 June 2019; pp. 61–72. [Google Scholar]
- Xu, Z.; Zhou, X.; Bai, X.; Li, C.; Chen, J.; Ni, Y. Attacking asymmetric cryptosystem based on phase truncated Fourier fransform by deep learning. Acta Phys. Sin. 2021, 70, 144202. [Google Scholar] [CrossRef]
- Dolanc, G.; Strmčnik, S. Design of a nonlinear controller based on a piecewise-linear Hammerstein model. Syst. Control Lett. 2008, 57, 332–339. [Google Scholar] [CrossRef]
- Hamalainen, P.; Babadi, A.; Xiaoxiao, M.; Lehtinen, J. PPO-CMA: Proximal Policy Optimization with Covariance Matrix Adaptation. In Proceedings of the 2020 IEEE 30th International Workshop on Machine Learning for Signal Processing (MLSP), Espoo, Finland, 21–24 September 2020; p. 6. [Google Scholar] [CrossRef]
- Bernat, J.; Apanasiewicz, D. Model Free DEAP Controller Learned by Reinforcement Learning DDPG Algorithm. In Proceedings of the 2020 IEEE Congreso Bienal de Argentina (ARGENCON), Resistencia, Argentina, 1–4 December 2020; p. 6. [Google Scholar] [CrossRef]
- de Jesus, J.C.; Kich, V.A.; Kolling, A.H.; Grando, R.B.; Cuadros, M.A.d.S.L.; Gamarra, D.F.T. Soft Actor-Critic for Navigation of Mobile Robots. J. Intell. Robot. Syst. 2021, 102, 31. [Google Scholar] [CrossRef]
- Ju-Seung, B.; Byungmoon, K.; Huamin, W. Proximal Policy Gradient: PPO with Policy Gradient. arXiv 2020, arXiv:2010.09933. [Google Scholar]




| Parameter | Symbol | Value |
|---|---|---|
| Learning rate | 0.0003 | |
| Hidden layer | 2 | |
| Number of monolayer neurons | 256 | |
| The entropy coefficient | 10 | |
| Discount factor | 0.99 | |
| Batch size | 256 |
| Parameter | Symbol | Value |
|---|---|---|
| Learning rate | 0.0001 | |
| Number of monolayer neurons | 256 | |
| Number of polar layers | 2 | |
| Adversarial coefficient | 0.4 | |
| Weight decay | 0.0001 |
| Parameter | Symbol | Value |
|---|---|---|
| Initial LM coefficient | 0.1 | |
| Maximum LM coefficient | 10 | |
| Gain coefficient | 1.2 | |
| Initial gain coefficient | 1.5 | |
| Maximum number of iterations | 20 | |
| Predicted steps to control | 15 |
| 01: Initialize these network parameters and DataBuffer, such as , , , |
| 02: Collect transfer data for the initial system state |
| 03: Each episode executes in the iteration loop |
| 04: Sample control targets randomly |
| 05: The number of steps at each time t is executed in the iteration loop |
| 06: Obtain with the sampling motion |
| 07: Policy updates in the iteration loop |
| 08: Sample batch data from DataBuffer |
| 09: Update the network parameters of , , , |
| 10: Dynamic model updates in the iteration loop: |
| 11: Sample batch data from DataBuffer |
| 12: Update and |
| 13: The HVAT sample is taken from the iteration loop |
| 14: Sample the initial data from DataBuffer |
| 15: The optimal trajectory planning is carried out to generate HVAT data |
| Methodology | Reward-10,000 | Reward-8000 | Reward-6000 | Reward-4000 |
|---|---|---|---|---|
| Ours | 6 | 10 | 20 | 25 |
| SAC | 7 | 12 | 21 | 30 |
| PPO | 135 | 151 | 162 | N.A. |
| DDPG | 7 | 18 | 63 | N.A. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhou, X.; Zhou, J.; Qiu, S.; Liang, G.; Cai, S.; Bao, G. A High-Efficient Reinforcement Learning Approach for Dexterous Manipulation. Biomimetics 2023, 8, 264. https://doi.org/10.3390/biomimetics8020264
Zhang J, Zhou X, Zhou J, Qiu S, Liang G, Cai S, Bao G. A High-Efficient Reinforcement Learning Approach for Dexterous Manipulation. Biomimetics. 2023; 8(2):264. https://doi.org/10.3390/biomimetics8020264
Chicago/Turabian StyleZhang, Jianhua, Xuanyi Zhou, Jinyu Zhou, Shiming Qiu, Guoyuan Liang, Shibo Cai, and Guanjun Bao. 2023. "A High-Efficient Reinforcement Learning Approach for Dexterous Manipulation" Biomimetics 8, no. 2: 264. https://doi.org/10.3390/biomimetics8020264
APA StyleZhang, J., Zhou, X., Zhou, J., Qiu, S., Liang, G., Cai, S., & Bao, G. (2023). A High-Efficient Reinforcement Learning Approach for Dexterous Manipulation. Biomimetics, 8(2), 264. https://doi.org/10.3390/biomimetics8020264






