Abstract
Flight range, endurance, maneuverability, and agility are the key elements that determine an aircraft’s performance. Both conventional and morphing wing aircraft have been well studied and estimated in all aspects of performance. When considering the performance of morphing aircraft, most works address aspects of the aerodynamical performance such as and as well as flight envelopes for flight dynamics and control perspectives. However, the actual benefits of adopting morphing technologies in practical aspects such as aircraft operation, mission planning, and sustainability have not been addressed so far. Thus, this paper addresses the practical aspect of the benefits when adopting a camber morphing wing aircraft. Identical geometrical and computational conditions were applied to an already-existing aircraft: the RQ-7a Shadow. The wing structure was switched between a fixed wing and a camber morphing wing to generate conventional and morphing wing geometries. The fixed-wing cases had varying flap deflection angles, and the camber morphing wing cases had varying camber rates from 4% to 8%. Once the values of the fixed and morphing wing cases were matched up to two significant figures, the and were analyzed for these matching cases to calculate the flight endurance, range, and improvement. When NACA 6410 is adopted, a 17% improvement in flight range and endurance average was expected. In the case of NACA 8410, an average 60% improvement was expected.
1. Introduction
The word ‘morph’ comes from the Greek word ‘metamorphosis’, as in ‘to change shape and form’—a biological development process in which forms change [1,2,3,4]. In engineering, morphing is a discipline of smart structures or an either compliant or rigid body mechanism-based approach. It is associated with providing systems with additional capabilities to adapt to external changes [5]. In engineering, morphing technologies refer to sustainable technologies that enhance flight performance, including maneuverability and the flight envelope, by actively adjusting aircraft wing shapes that correspond to different flight modes [6]. Whereas conventional aircraft adjust wing shapes using discrete and deployable control surfaces such as flaps, ailerons, and rudders, morphing wing aircraft use an internal morphing mechanism, thereby possibly generating more substantial wing-shaped changes toward optimal shapes [7,8,9,10,11,12,13,14,15].
Additional advantages of the absence of jointed control surfaces that conventional aircraft have include reduced assembly complexities and costs [13,16,17,18,19,20,21] and aerodynamical performance aspects. Morphing aircraft have also been verified to have improved roll control motions, a reduced , an increased range, an expanded operational envelope, reduced fuel consumption and airframe noise, etc. [22,23,24,25,26,27,28,29,30,31].
The research and development of morphing technologies span almost all engineering topics and approaches. In wing design itself, some major topics include (1) design for shape optimization [32,33,34,35,36], (2) design for aerodynamic optimization [37,38,39], (3) design for aero-structure optimization [40,41,42], and (4) manufacturing process development [43,44,45]. In the focus of morphing mechanism development, topics such as (1) material selection and analysis [46,47,48,49,50,51], (2) structure and solid mechanics development [50,52,53,54,55,56,57,58,59], (3) smart materials for actuation [60,61,62,63,64,65,66,67], and (4) conventional actuators for morphing [61,66,67] are primary. In morphing wing analysis regarding design and implementation, (1) analytical or experimental modeling, (2) validation [43,68,69,70,71], (3) performance and characteristics analysis [72,73,74,75,76,77], and (4) aeroelasticity analysis [78,79,80] are the topics being investigated. Other than those previously mentioned, control systems and flight control and dynamics for morphing wing aircraft [81,82,83] are also seriously studied. In the sense of the technology readiness level (TRL) of morphing aircraft, various levels of analysis and validation have been performed that range from analytical and numerical works to large-scale wind tunnel and flight tests [43,71,84]. Emphasizing manufacturability and feasibility according to implementation aspects, skin structure design and analysis of morphing wings is probably one of the most popular studied subjects [85,86,87,88].
Among many topics, this paper relates to morphing wing analysis regarding design and implementation topic (3)—performance and characteristics analysis of morphing wing aircraft [89,90,91]. Moreover, among the many types of morphing, this paper mainly targets camber morphing in the airfoil.
2. Motivation
The performance of an aircraft is determined by the key elements: flight range, endurance, maneuverability, and agility [92]. Conventional and morphing wing aircraft have been studied and estimated [93,94]. Studies that investigated the performance of morphing aircraft addressed aerodynamical performance aspects such as and as well as flight envelopes for flight dynamics and control [27,31,90,91,95,96,97,98,99]. Some representative works of a camber morphing wing aircraft’s aerodynamical characteristics compared their performance to those of conventional wing aircraft [72,73]. However, the flight range and endurance of a camber morphing wing aircraft have been overlooked.
Another motivation for this work regarded a more practical aspect of research on morphing wings and aircraft toward realization in commercial or military lines. Unfortunately, most of the literature is not based on a practical aircraft model, which implies a lack of practicability and feasibility for actual flight. However, we began from an already existing UAV model with a fixed wing. We then switched to the same UAV model with a camber morphing wing with the same geometric parameters (chord length, etc.), specifications, and operational conditions. This was done to investigate the benefits of morphing wing aircraft regarding enhanced flight range and endurance. The flight range and endurance are directly related to energy efficiencies, fuel consumption, and sustainability for futuristic applications.
In the aircraft design process, the first step is to configure the aerodynamical performance metrics, including the flight ranges and endurances. Thus, it is crucial to precisely understand and acknowledge the actual benefits of flight while adopting morphing wings instead of conventional fixed wings. The flowchart shown in Figure 1 explains the aircraft design cycle.
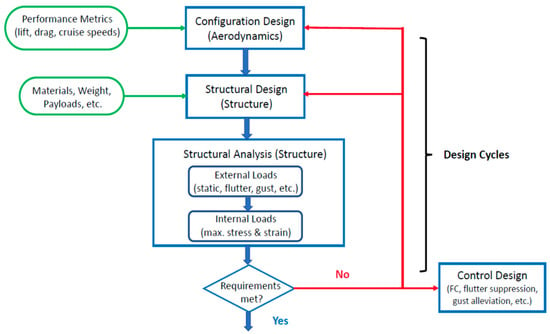
Figure 1.
Flowchart of aircraft design and analysis cycle (image courtesy of J.T. Kim).
3. Problem Statement
This paper analyzes and explains the expected benefits of a morphing wing aircraft through a comparative study with conventional, fixed-wing aircraft under identical conditions. To emphasize the aspect of real-world applications, we adopted an already-existing UAV model and operational conditions. The flight range and endurance are the two elements that determine flight performance, and they are functions of , or To maintain and guarantee a precise analysis, we matched on cases of both a camber morphing wing and a fixed wing under identical geometrical and aerodynamical conditions. Then, we analyzed differentiations of , and the flight range and endurance were analyzed using .
Thus, the main objectives of this work were: (1) to match L with the flap-deflection angle from a fixed wing and a camber rate from a morphing wing; and then (2) to compare , and between these two types of wings. The differentiated flight ranges and endurance from both cases were computed under the same operational conditions.
4. Computational Model
Computational models for morphing and conventional wings were constructed to satisfy identical geometries. Then, a computational analysis using ANSYS FLUENT was adopted to match L values to determine differences in their L, D, and L/D. Table 1 below shows the operational parameters and conditions that were applied to both models to determine the Re, speed, and other external conditions. As categorized in the review of modeling and analysis of morphing wings [70], linear and non-linear methods are used for computing steady-state aerodynamics. Linear methods are better suited for thin lifting surfaces such as an airfoil at a small AoA. Since this study was conducted over a range of AoAs that included higher AoAs, the CFD method was chosen over linear methods.

Table 1.
UAV model and flight specification.
The CFD simulation software ANSYS FLUENT was employed with the RANS-based Spalart–Allmaras (SA) turbulence model. A C-type unstructured mesh was used in the FLUENT setup in which the dimensions of the fluid domain were set based on the recommended length [100]. First, the FLUENT setup was benchmarked. Then, the settings were maintained as identical to those of a previous study described in [73]. The values for the air density () and velocity () inputs corresponded to the cruising conditions of our RQ-7a Shadow UAV model as shown in Table 1.
For the wall boundary conditions, ANSYS FLUENT has a built-in enhanced wall treatment (EWT) feature available in its Spalart–Allmaras model that automatically blends all solution variables from their viscous sublayer formulation to the corresponding logarithmic layer values depending on as shown in Equation (1):
where u is the velocity parallel to the wall, is the shear velocity, y is the distance from the wall, is the von Kármán constant (0.4187), and E = 9.793.
However, it should be noted that EWT alone is not sufficient to generate wall values of less than one at the airfoil boundary, so inflation layers had to be generated to resolve the viscous sublayer in the near-wall region. A total of 25 inflation layers were generated around the airfoil with a growth rate of 1.1 to resolve the viscous sublayer in the near-wall region. The first layer thickness (y) was computed using Equation (2) to maintain a value of less than one at the wall:
where is the dynamic viscosity, is the air density, and is the cruise velocity as shown in Table 1.
The skin friction was calculated using Equation (3):
The AoA () was made a parameter in the FLUENT setup, and the value of varied from 0° to 15°. The and computed by ANSYS ( and ) were further manipulated using Equation (4):
FLUENT does not have the option to set the direction vector of L and D as a parameter, so the normal x and y components obtained for each ( and ) had to be transformed.
Various morphed and deflected geometries were generated to mimic the behavior of a morphing wing and a conventional wing with a deflecting flap. These airfoil geometries were drawn in Fusion 360 and imported into the ANSYS Workbench Design Modeler in step format.
5. Methodology
The UAV model (RQ-7 Shadow) used a NACA 2410 airfoil with a chord length of 0.54 m. Correspondingly, the morphed configurations were generated by varying the camber rate (the first digit of the four-digit NACA series) in increments of 2% to generate three configurations: NACA 4410, NACA 6410, and NACA 8410. In contrast, the conventional airfoil configurations were generated by rotating the trailing edge flap clockwise at the joint. The flap joint rested at 0.7c from the leading edge of the baseline airfoil (NACA 2410) with a chord length of 0.54 m. The value of the flap or deflection angle was set by matching the generated by the morphed configurations.
For these matching morphing and conventional airfoils, the values were also computed and compared. The aerodynamic parameter of interest was or /, which in aeronautics is used synonymously with aerodynamic performance. or / measures the aerodynamic cruising efficiency and can affect the fuel consumption, range, endurance, etc. The Breguet range equation is written as:
where R is the cruise segment range, is the constant cruise speed, is the fuel weight, is the fixed weight of the aircraft, and is the thrust-specific fuel consumption for specific operating conditions. When taking other terms in Equation (5) to be constant, the maximum range can be achieved by maximizing the quantity / on a particular cruise operation.
Similarly, based on Equation (5), to minimize the environmental impact of fuel consumption and reduce the carbon emission rate, the amount of fuel used should be as small as possible; by looking strictly at the aerodynamics, the quantity should be maximized in order to minimize the amount of fuel burned.
The endurance of an aircraft can be calculated as range divided by speed, which is denoted as:
where is the propulsion system efficiency and S is the wing planform area. The endurance of an aircraft is a function of its power output; thus, the total propulsive power must be minimized to maximize the endurance. Assuming the specific fuel consumption is nearly constant in Equation (2), the fuel flow per unit time and the must be minimized to maximize the endurance, which can be achieved when (the endurance factor) is maximized across all points of the mission.
For airfoil cases, four camber rates were analyzed: NACA 2410 was used for the baseline; and NACA 4410, NACA 6410, and NACA 8410, were used for comparison.
6. Results
Figure 2 below shows the case of NACA 2410 with the baseline of the and varying the AoA by up to 15°. As noted, both the and increased as the AoA increased, and the stall angle was around 11°. The operational condition was Re at 778,179 for the RQ-7a Shadow. Through this, we confirmed the that computational models were sufficiently accurate to run other cases and that the and were reliable compared to the benchmark data [72,73,77].
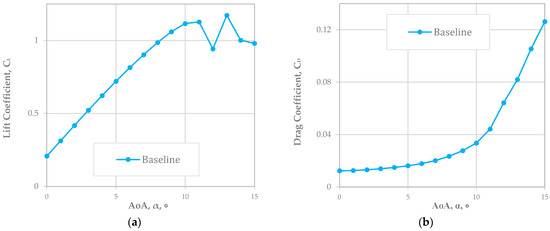
Figure 2.
(a) and (b) plots of baseline NACA 2410 airfoil (Re = 778,179).
Once the computational model for the airfoil was verified, the simulations for comparison were run for the three morphed configurations when the AoA changed from 0 to 15°. The morphed configurations were adequately matched against the conventional airfoil using flap-angle variations and by computing the L values of deflected configurations at each AoA to match the values. The relationships between the camber rate and the flap-deflection angle are also presented in Table 2, Table 3 and Table 4. Additionally, Table 2, Table 3 and Table 4 present data for the and for the endurance ratio ().

Table 2.
Morphing (NACA 4410) and matching conventional airfoils.

Table 3.
Aerodynamic data of morphing (NACA 6410) and matching conventional airfoils.

Table 4.
Aerodynamic data of morphing (NACA 8410) and matching conventional airfoils.
For NACA 4410, Figure 3a shows the was well matched for both the conventional and morphing wings. The offset value of about 0.21 in implied that the NACA 4410 had a 0.21 greater than NACA 2410 (or a 2% higher camber rate was around a 0.21 increment). Based on the graph in Figure 3a, the reliable AoA was up to 10° because the stall began right after 10°. As shown in Figure 3b, we analyzed ; the results implied that a camber morphing wing at a 4% camber rate (NACA 4410) had an almost identical to that of the conventional fixed wing. However, the graph separation began around 7° for the AoA when the of the fixed wing was less than that of the camber morphing wing.
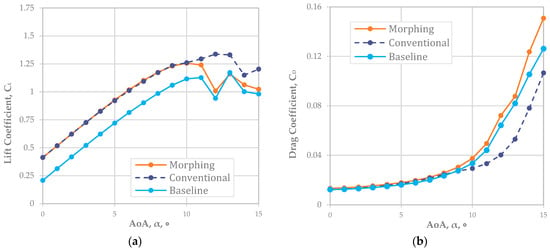
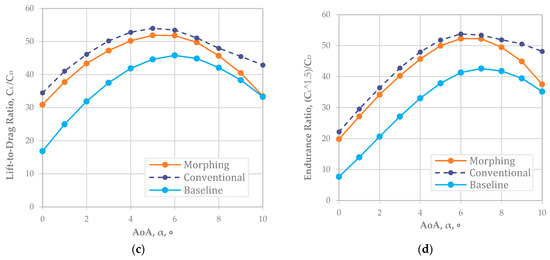
Figure 3.
Matching L morphing (NACA 4410) and conventional airfoil plots (Re = 778,179): (a) plot; (b) D plot; (c) L/D; (d) endurance ratio.
Figure 3c,d are directly related to , , and . The indicated the improvement in the flight range; Figure 3d does so for the endurance improvement. We noted that conventional fixed-wing aircraft still had a better flight range and endurance when the NACA 4410 airfoil was adopted.
The improvement rate of the flight range was maximized to about 11.5% at a 2° AoA and minimized to about 2.7% at a 9° AoA. On average, an approximately 5.9% improvement in the flight range was expected when NACA 4410—the baseline airfoil—adopted a deflecting flap rather than a camber morphing wing.
In endurance, the improvement rate was maximized to about 11.7% at a 2° AOA and minimized to about 2.25% at a 9° AoA. An average of about a 5.8% improvement in the flight endurance was expected with NACA 2410 with a deflecting flap adopted rather than a 2% camber morphed wing (NACA 4410).
For NACA 6410, Figure 4a shows the was well matched for both the conventional and morphing wings. The offset value of about 0.5 in implied that the NACA 6410 had a 0.5 greater than NACA 2410 (or a 4% higher camber rate was around a 0.5 increment). Based on the graph in Figure 4a, the reliable AoA was up to 10° because the airfoil began to stall after 10°. As shown in Figure 4b, we analyzed ; the results implied that a camber morphing wing at a 6% camber rate (NACA 6410) had an almost identical to that of the conventional fixed wing. However, the graph began to separate at an AoA of around 5° when the of the camber morphing wing was less than that of the fixed wing.
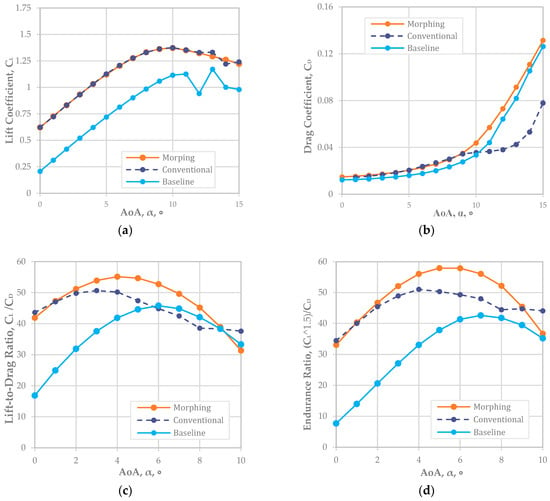
Figure 4.
Matching morphing (NACA 6410) and conventional airfoil plots (Re = 778,179): (a); (b); (c); (d) endurance ratio.
Similarly, and graphs are as shown in Figure 4a,b, an improvement in the flight range in Figure 4c, and endurance improvement in Figure 4d. In addition, we noted that the camber morphing wing aircraft had a better flight range and endurance when the NACA 6410 airfoil was adopted.
The improvement rate of the flight range was maximized to about 17.6% at an 8-degree AoA and was minimized to about 0.5% at a 1° AoA. On average, an approximately 4.7% extension in the flight range was expected with a 6% camber morphed wing compared to a fixed wing with a deflecting flap.
The endurance factor maximized to about 17.4% at an 8° AoA and minimized to about 0.85% at a 2° AoA. This resulted in about a 7.8% improvement in the flight endurance with a morphing wing with a NACA 6410 airfoil rather than a fixed-wing airfoil with a NACA 2410 baseline configuration with a deflecting flap.
For NACA 8410, Figure 5a shows the was well matched for both the conventional and morphing wings, with an offset of about 0.6 against the baseline airfoil that implies that the NACA 8410 airfoil has a 0.6 greater than NACA 2410 (or a 6% higher camber rate was around a 0.6 increment). Based on the graph in Figure 5a, the reliable AoA is up to 10° because the stall began right after 10°. As shown in Figure 5b, we analyzed ; the results implied that a camber morphing wing at an 8% camber rate (NACA 8410) had an almost identical to that of the conventional fixed wing. However, the graph separation began at 0° of the AoA when the of the camber morphing wing was much less than that of the fixed wing.
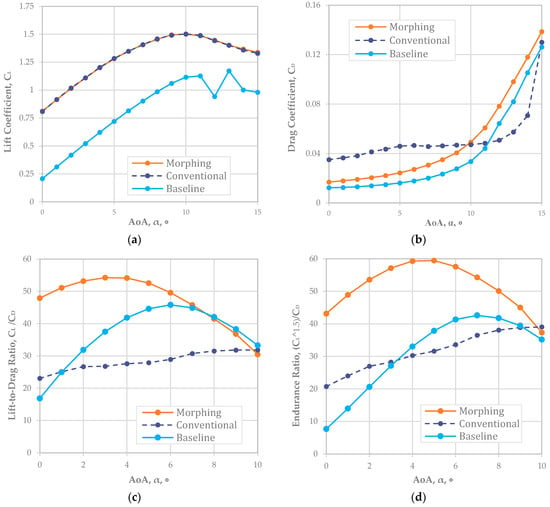
Figure 5.
Matching morphing (NACA 8410) and conventional airfoil plots (Re = 778,179): (a); (b); (c); (d) endurance ratio.
As shown in Table 4, the improvement rate of the flight range was observed in the entire range of AoAs with a large number. On average, an approximately 60% improvement in the flight range was expected when the morphing wing with a NACA 8410 airfoil was adopted rather than a fixed-wing NACA 2410 baseline airfoil with a deflecting flap.
Regarding the endurance, the improvement rate was expected in the entire range of AoAs with a large number. An average improvement of approximately 61% in the flight endurance was expected when the morphing wing with a NACA 8410 airfoil was adopted.
Table 5 and Table 6 summarize all the results above with an additional improvement percentage in the flight range and endurance. For NACA 4410, the improvement rates were negative, which implied that the conventional fixed wing performed better in the flight range and endurance; however, other cases (NACA 6410 and NACA 8410) showed improvement rates and performed substantially better in terms of the flight range and endurance in the entire range of AoAs.

Table 5.
Comparison of the or of morphing and conventional airfoils.

Table 6.
Comparison of the endurance ratio of morphing and conventional airfoils.
7. Summary
The NACA 2410 (the baseline of the and ) when varying the AoA by up to 15° was verified. Both the and increased as the AoA increased, and the stall angle was around 11°. Based on this, we confirmed that the computational models were sufficiently accurate to run other cases and that the and were reliable compared to the benchmark data.
For NACA 4410, the was well matched for both the conventional and morphing wings. The offset value of about 0.25 in the implied that the NACA 4410 has a 0.25 greater than NACA 2410 (or a 2% higher camber rate was around a 0.25 increment). We also analyzed ; the results implied that a camber morphing wing at a 4% camber rate (NACA 4410) had an almost identical to that of the conventional fixed wing. We noted that the conventional fixed-wing aircraft still had a better flight range and endurance when the NACA 4410 airfoil was adopted. The improvement rate of the flight range was maximized at about 11.5% at a 2° AoA and was minimized at about 2.7% at a 9° AoA. On average, an approximately 5.9% improvement in the flight range was expected when NACA 4410 with flap deflection was adopted rather than a morphing wing. Regarding endurance, the improvement rate was maximized at about 11.7% at a 2° AoA and minimized to about 2.25% at a 9° AoA. On average, an approximately 5.8% flight endurance improvement was expected when NACA 4410 with flap deflection is adopted rather than a morphing wing.
For NACA 6410, the offset value of about 0.5 in implied that the NACA 6410 has an 0.5 larger than NACA 2410 (or a 4% higher camber rate was around a 0.5 increment). We also analyzed ; the results implied that a camber morphing wing at a 6% camber rate (NACA 6410) had an almost identical to that of the conventional fixed wing. However, the graph separation began around a 5° AoA when the of the camber morphing wing was less than that of the fixed wing. We noted that the camber morphing wing aircraft had a better flight range and endurance when the NACA 6410 airfoil was adopted. The improvement rate of the flight range was maximized at about 17.6% at an 8-degree AoA and minimized by about 0.5% at a 1° AoA. On average, about a 4.7% higher flight range improvement was expected when the morphing wing with a NACA 6410 airfoil was adopted rather than a NACA 6410 fixed-wing airfoil with flap deflection. In endurance, the improvement rate was maximized at about 17.4% at an 8° AoA and minimized to about 0.85% at a 2° AoA. On average, an approximately 7.8% higher flight endurance improvement was expected when the morphing wing with a NACA 6410 airfoil was adopted rather than a fixed wing with a NACA 6410 airfoil with flap deflection.
For NACA 8410, the offset value of about 0.7 in implied that the NACA 8410 had a 0.7 larger larger than NACA 2410 (or a 6% higher camber rate was around a 0.7 increment). We also analyzed ; the results implied that the camber morphing wing at an 8% camber rate (NACA 8410) had an almost identical to that of the conventional fixed wing. We noted that the camber morphing wing aircraft had a better flight range and endurance when the NACA 8410 airfoil was adopted. The improvement rate of the flight range was observed in the entire range of AoAs with a large number. On average, an approximately 60% higher flight range improvement was expected when the morphing wing with a NACA 8410 airfoil was adopted rather than the fixed wing with a NACA 8410 airfoil with flap deflection. In endurance, the improvement rate was expected in the entire range of AoAs with a large number. On average, an approximately 61% higher flight endurance improvement was expected when the morphing wing with a NACA 8410 airfoil was adopted rather than a fixed wing with a NACA 8410 airfoil with flap deflection.
8. Conclusions
This paper addressed the practical aspects of adopting a camber morphing wing aircraft compared to a conventional fixed-wing aircraft. Identical geometrical and computational conditions were applied to an already-existing aircraft model: the RQ-7a Shadow. The model’s original wing structure was a NACA 2410 airfoil geometry with a trailing edge flap. In this study, the deflection angle of the flap was changed to generate the different geometric configurations of conventional wings; whereas for the morphing wing configurations, NACA 4410, NACA 6410, and NACA 8410 airfoil geometries with the same chord length were used. The corresponding matching cases were identified along with the and ; these were analyzed to calculate any improvements in flight endurance and range. Morphing the camber by 2% from the baseline airfoil (NACA 2410 to NACA 4410) did not improve the aircraft’s performance; the conventional wing with a deflecting flap performed better. However, morphing by 4% and 6% from the baseline airfoil; i.e., using NACA 6410 or NACA 8410 configurations, improvements in the flight range and endurance ratio were seen compared to conventional ones. When NACA 6410 was adopted, an average 17% improvement in the flight range and endurance was expected. By morphing 6% to generate the NACA 8410 configuration, an average improvement of 60% was seen compared to the conventional aircraft wing design. The camber morphing wing aircraft contributed mainly to the reduced compared to the fixed-wing aircraft, which could eventually increase the fuel efficiency and sustainability. The improvements seen in the computed lift-to-drag and endurance ratios supported this.
Author Contributions
Conceptualization, B.W.J. and TM; methodology, B.W.J. and T.M.; software, T.M.; validation, B.W.J. and T.M.; formal analysis, B.W.J. and T.M.; investigation, B.W.J. and T.M.; data curation, T.M.; writing—original draft preparation, T.M. and B.W.J.; writing—review and editing, B.W.J. and T.M.; visualization, T.M.; supervision, B.W.J.; project administration, B.W.J.; funding acquisition, B.W.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially sponsored by InnoScience Co., Ltd. (20210901) and was under the framework of the international cooperation program managed by the National Research Foundation (NRF) of Korea (2021K2A9A2A06049018).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors greatly appreciate SUNY Korea for their sincere efforts and technical advice.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Nomenclature | |
| L | Lift force |
| D | Drag force |
| Lift coefficient | |
| Drag coefficient | |
| AoA | Angle of attack |
| Skin friction coefficient | |
| Distance between the airfoil wall and the first layer | |
| Re | Reynolds number |
| Cruise velocity | |
| Greek Symbols | |
| μ | Dynamic viscosity |
| ρ | Density of air |
| Shear velocity | |
| von Kármán constant | |
| Abbreviations | |
| CFD | Computational fluid dynamics |
| RANS | Reynolds-averaged Navier–Stokes |
| EWT | Enhanced wall treatment |
| NACA | National Advisory Committee for Aeronautics |
References
- Bishop, C.; Erezyilmaz, D.; Flatt, T.; Georgiou, C.; Hadfield, M.; Heyland, A.; Hodin, J.; Jacobs, M.; Maslakova, S.; Pires, A. What is metamorphosis? Integr. Comp. Biol. 2006, 46, 655–661. [Google Scholar] [CrossRef]
- Dodd, M.; Dodd, J. The biology of metamorphosis. Physiol. Amphib. 1976, 3, 467–599. [Google Scholar]
- Harvey, C.; Gamble, L.L.; Bolander, C.R.; Hunsaker, D.F.; Joo, J.J.; Inman, D.J. A review of avian-inspired morphing for UAV flight control. Prog. Aerosp. Sci. 2022, 132, 100825. [Google Scholar] [CrossRef]
- Truman, J.W.; Riddiford, L.M. The origins of insect metamorphosis. Nature 1999, 401, 447–452. [Google Scholar] [CrossRef]
- Sofla, A.; Meguid, S.; Tan, K.; Yeo, W. Shape morphing of aircraft wing: Status and challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, C.; Song, Z. Discussion on research status and key technologies of morphing aircraft. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; p. 012021. [Google Scholar]
- Jha, A.K.; Kudva, J.N. Morphing aircraft concepts, classifications, and challenges. In Proceedings of the Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologie, San Diego, CA, USA, 14–18 March 2004; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; pp. 213–224. [Google Scholar]
- Reich, G.; Sanders, B. Introduction to morphing aircraft research. J. Aircr. 2007, 44, 1059. [Google Scholar] [CrossRef]
- Rodriguez, A. Morphing aircraft technology survey. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 8–11 January 2007; p. 1258. [Google Scholar]
- Tsushima, N.; Tamayama, M. Recent researches on morphing aircraft technologies in Japan and other countries. Mech. Eng. Rev. 2019, 6, 19–00197. [Google Scholar] [CrossRef]
- Weisshaar, T.A. Morphing Aircraft Technology—New Shapes for Aircraft Design; Defense Technical Information Center: Fort Belvoir, VA, USA, 2006. [Google Scholar]
- Weisshaar, T.A. Morphing aircraft systems: Historical perspectives and future challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Beaverstock, C.S.; Friswell, M.I. Morphing aircraft: The need for a new design philosophy. Aerosp. Sci. Technol. 2016, 49, 154–166. [Google Scholar] [CrossRef]
- Gomez, J.C.; Garcia, E. Morphing unmanned aerial vehicles. Smart Mater. Struct. 2011, 20, 103001. [Google Scholar] [CrossRef]
- Martin, J.; Heyder-Bruckner, J.J.; Remillat, C.; Scarpa, F.; Potter, K.; Ruzzene, M. The hexachiral prismatic wingbox concept. Phys. Status Solidi B 2008, 245, 570–577. [Google Scholar] [CrossRef]
- McGowan, A.-M.R.; Vicroy, D.D.; Busan, R.C.; Hahn, A.S. Perspectives on Highly Adaptive or Morphing Aircraft. In the Symposium, NATO RTO AVT-169, No. RTO-MP-AVT-168, 2009. Available online: https://ntrs.nasa.gov/citations/20090017845 (accessed on 4 January 2023).
- Parker, H. The Parker Variable Camber Wing. Technical Report, No. NACA-TR-77. 1920. Available online: https://digital.library.unt.edu/ark:/67531/metadc65726/ (accessed on 4 January 2023).
- Pettit, G.W.; Robertshaw, H.H.; Inman, D.J. Morphing wings for unmanned aircraft. Smart Mater. Bull. 2001, 2001, 7–12. [Google Scholar] [CrossRef]
- Szodruch, J.; Hilbig, R. Variable wing camber for transport aircraft. Prog. Aerosp. Sci. 1988, 25, 297–328. [Google Scholar] [CrossRef]
- Panagiotou, P.; Yakinthos, K. Aerodynamic efficiency and performance enhancement of fixed-wing UAVs. Aerosp. Sci. Technol. 2020, 99, 105575. [Google Scholar] [CrossRef]
- Previtali, F.; Arrieta, A.F.; Ermanni, P. Performance of a three-dimensional morphing wing and comparison with a conventional wing. AIAA J. 2014, 52, 2101–2113. [Google Scholar] [CrossRef]
- Béguin, B.; Breitsamter, C. Effects of membrane pre-stress on the aerodynamic characteristics of an elasto-flexible morphing wing. Aerosp. Sci. Technol. 2014, 37, 138–150. [Google Scholar] [CrossRef]
- Della Vecchia, P.; Corcione, S.; Pecora, R.; Nicolosi, F.; Dimino, I.; Concilio, A. Design and integration sensitivity of a morphing trailing edge on a reference airfoil: The effect on high-altitude long-endurance aircraft performance. J. Intell. Mater. Syst. Struct. 2017, 28, 2933–2946. [Google Scholar] [CrossRef]
- Kuya, Y.; Ito, R.; Maki, M.; Sawada, K. Numerical Study of Flowfield Around a Multislotted High-Lift Wing. J. Aircr. 2021, 58, 383–389. [Google Scholar] [CrossRef]
- Molinari, G.; Arrieta, A.F.; Guillaume, M.; Ermanni, P. Aerostructural performance of distributed compliance morphing wings: Wind tunnel and flight testing. AIAA J. 2016, 54, 3859–3871. [Google Scholar] [CrossRef]
- Pankonien, A.M.; Faria, C.T.; Inman, D.J. Synergistic smart morphing aileron: Experimental quasi-static performance characterization. J. Intell. Mater. Syst. Struct. 2015, 26, 1179–1190. [Google Scholar] [CrossRef]
- Pecora, R.; Amoroso, F.; Lecce, L. Effectiveness of wing twist morphing in roll control. J. Aircr. 2012, 49, 1666–1674. [Google Scholar] [CrossRef]
- Vale, J.; Leite, A.; Lau, F.; Suleman, A. Aero-structural optimization and performance evaluation of a morphing wing with variable span and camber. J. Intell. Mater. Syst. Struct. 2011, 22, 1057–1073. [Google Scholar] [CrossRef]
- Vasista, S.; Riemenschneider, J.; Van De Kamp, B.; Monner, H.P.; Cheung, R.C.; Wales, C.; Cooper, J.E. Evaluation of a compliant droop-nose morphing wing tip via experimental tests. J. Aircr. 2017, 54, 519–534. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Optimization and Design of a Flexible Droop-Nose Leading-Edge Morphing Wing Based on a Novel Black Widow Optimization Algorithm—Part I. Designs 2022, 6, 10. [Google Scholar] [CrossRef]
- Dexl, F.; Hauffe, A.; Wolf, K. Comparison of structural parameterization methods for the multidisciplinary optimization of active morphing wing sections. Comput. Struct. 2022, 263, 106743. [Google Scholar] [CrossRef]
- Koreanschi, A.; Gabor, O.S.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M.; Mamou, M.; Mebarki, Y. Optimization and design of an aircraft’s morphing wing-tip demonstrator for drag reduction at low speeds, Part II-Experimental validation using Infra-Red transition measurement from Wind Tunnel tests. Chin. J. Aeronaut. 2017, 30, 164–174. [Google Scholar] [CrossRef]
- Liu, B.; Liang, H.; Han, Z.-H.; Yang, G. Surrogate-based aerodynamic shape optimization of a morphing wing considering a wide Mach-number range. Aerosp. Sci. Technol. 2022, 124, 107557. [Google Scholar] [CrossRef]
- Murugan, S.; Woods, B.; Friswell, M. Hierarchical modeling and optimization of camber morphing airfoil. Aerosp. Sci. Technol. 2015, 42, 31–38. [Google Scholar] [CrossRef]
- Andrejašič, M.; Eržen, D.; Costa, E.; Porziani, S.; Biancolini, M.; Groth, C. A mesh morphing based FSI method used in aeronautical optimization applications. In Proceedings of the ECCOMAS Congress, VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- Gabor, O.Ş.; Koreanschi, A.; Botez, R.M. A new non-linear vortex lattice method: Applications to wing aerodynamic optimizations. Chin. J. Aeronaut. 2016, 29, 1178–1195. [Google Scholar] [CrossRef]
- Namgoong, H.; Crossley, W.A.; Lyrintzis, A.S. Aerodynamic optimization of a morphing airfoil using energy as an objective. AIAA J. 2007, 45, 2113–2124. [Google Scholar] [CrossRef]
- Burdette, D.A.; Kenway, G.K.; Lyu, Z.; Martins, J.R. Aerostructural design optimization of an adaptive morphing trailing edge wing. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1129. [Google Scholar]
- Keidel, D.; Molinari, G.; Ermanni, P. Aero-structural optimization and analysis of a camber-morphing flying wing: Structural and wind tunnel testing. J. Intell. Mater. Syst. Struct. 2019, 30, 908–923. [Google Scholar] [CrossRef]
- Molinari, G.; Arrieta, A.F.; Ermanni, P. Aero-structural optimization of three-dimensional adaptive wings with embedded smart actuators. AIAA J. 2014, 52, 1940–1951. [Google Scholar] [CrossRef]
- De Gaspari, A.; Riccobene, L.; Ricci, S. Design, manufacturing and wind tunnel validation of a morphing compliant wing. J. Aircr. 2018, 55, 2313–2326. [Google Scholar] [CrossRef]
- Fasel, U.; Keidel, D.; Baumann, L.; Cavolina, G.; Eichenhofer, M.; Ermanni, P. Composite additive manufacturing of morphing aerospace structures. Manuf. Lett. 2020, 23, 85–88. [Google Scholar] [CrossRef]
- Yang, B.; Ouyang, J.; Li, X. Simulation of fiber reinforced composite materials mold filling process and mechanical properties analysis. J. Non-Newton. Fluid Mech. 2011, 166, 1129–1136. [Google Scholar] [CrossRef]
- Somnic, J.; Jo, B.W. Status and Challenges in Homogenization Methods for Lattice Materials. Materials 2022, 15, 605. [Google Scholar] [CrossRef]
- Arrieta, A.F.; Kuder, I.K.; Waeber, T.; Ermanni, P. Variable stiffness characteristics of embeddable multi-stable composites. Compos. Sci. Technol. 2014, 97, 12–18. [Google Scholar] [CrossRef]
- Barbarino, S.; Flores, E.S.; Ajaj, R.M.; Dayyani, I.; Friswell, M.I. A review on shape memory alloys with applications to morphing aircraft. Smart Mater. Struct. 2014, 23, 063001. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Stefanou, G. Multiscale Modeling and Uncertainty Quantification of Materials and Structures; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Sun, J.; Guan, Q.; Liu, Y.; Leng, J. Morphing aircraft based on smart materials and structures: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2016, 27, 2289–2312. [Google Scholar] [CrossRef]
- Tong, X.; Ge, W.; Sun, C.; Liu, X. Topology optimization of compliant adaptive wing leading edge with composite materials. Chin. J. Aeronaut. 2014, 27, 1488–1494. [Google Scholar] [CrossRef]
- Katagiri, K.; Park, C.S.; Kawakita, S.; Kim, D.; Tamayama, M.; Honda, S.; Sasaki, K.; Yamazaki, M. Mechanical properties of the skeletal structure for UAV morphing wing by using CFRP with applying the electrodeposition resin molding method. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0865. [Google Scholar]
- Rivero, A.E.; Weaver, P.M.; Cooper, J.E.; Woods, B.K. Structural Modeling of Compliance-Based Camber Morphing Structures Under Transverse Shear Loading. AIAA J. 2020, 58, 4941–4951. [Google Scholar] [CrossRef]
- Jenett, B.; Calisch, S.; Cellucci, D.; Cramer, N.; Gershenfeld, N.; Swei, S.; Cheung, K.C. Digital morphing wing: Active wing shaping concept using composite lattice-based cellular structures. Soft Robot. 2017, 4, 33–48. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Zhang, Q.; Scarpa, F.; Liu, Y.; Leng, J. In-plane elasticity of a novel auxetic honeycomb design. Compos. Part B Eng. 2017, 110, 72–82. [Google Scholar] [CrossRef]
- Zhou, J.; Guan, Z.; Cantwell, W. Scaling effects in the mechanical response of sandwich structures based on corrugated composite cores. Compos. Part B Eng. 2016, 93, 88–96. [Google Scholar] [CrossRef]
- Woods, B.K.; Friswell, M.I. Multi-objective geometry optimization of the Fish Bone Active Camber morphing airfoil. J. Intell. Mater. Syst. Struct. 2016, 27, 808–819. [Google Scholar] [CrossRef]
- Vasista, S.; De Gaspari, A.; Ricci, S.; Riemenschneider, J.; Monner, H.P.; van de Kamp, B. Compliant structures-based wing and wingtip morphing devices. Aircr. Eng. Aerosp. Technol. Int. J. 2016, 88, 311–330. [Google Scholar] [CrossRef]
- Takahashi, H.; Yokozeki, T.; Hirano, Y. Development of variable camber wing with morphing leading and trailing sections using corrugated structures. J. Intell. Mater. Syst. Struct. 2016, 27, 2827–2836. [Google Scholar] [CrossRef]
- Barbarino, S.; Pecora, R.; Lecce, L.; Concilio, A.; Ameduri, S.; De Rosa, L. Airfoil structural morphing based on SMA actuator series: Numerical and experimental studies. J. Intell. Mater. Syst. Struct. 2011, 22, 987–1004. [Google Scholar] [CrossRef]
- Basaeri, H.; Yousefi-Koma, A.; Zakerzadeh, M.R.; Mohtasebi, S.S. Experimental study of a bio-inspired robotic morphing wing mechanism actuated by shape memory alloy wires. Mechatronics 2014, 24, 1231–1241. [Google Scholar] [CrossRef]
- Bil, C.; Massey, K.; Abdullah, E.J. Wing morphing control with shape memory alloy actuators. J. Intell. Mater. Syst. Struct. 2013, 24, 879–898. [Google Scholar] [CrossRef]
- Brailovski, V.; Terriault, P.; Georges, T.; Coutu, D. SMA actuators for morphing wings. Phys. Procedia 2010, 10, 197–203. [Google Scholar] [CrossRef]
- Icardi, U.; Ferrero, L. Preliminary study of an adaptive wing with shape memory alloy torsion actuators. Mater. Des. 2009, 30, 4200–4210. [Google Scholar] [CrossRef]
- Kang, W.-R.; Kim, E.-H.; Jeong, M.-S.; Lee, I.; Ahn, S.-M. Morphing wing mechanism using an SMA wire actuator. Int. J. Aeronaut. Space Sci. 2012, 13, 58–63. [Google Scholar] [CrossRef]
- Karagiannis, D.; Stamatelos, D.; Kappatos, V.; Spathopoulos, T. An investigation of shape memory alloys as actuating elements in aerospace morphing applications. Mech. Adv. Mater. Struct. 2017, 24, 647–657. [Google Scholar] [CrossRef]
- Ko, S.-H.; Bae, J.-S.; Rho, J.-H. Development of a morphing flap using shape memory alloy actuators: The aerodynamic characteristics of a morphing flap. Smart Mater. Struct. 2014, 23, 074015. [Google Scholar] [CrossRef]
- Communier, D.; Botez, R.M.; Wong, T. Design and Validation of a New Morphing Camber System by Testing in the Price—Païdoussis Subsonic Wind Tunnel. Aerospace 2020, 7, 23. [Google Scholar] [CrossRef]
- Rivero, A.E.; Weaver, P.M.; Cooper, J.E.; Woods, B.K. Parametric structural modelling of fish bone active camber morphing aerofoils. J. Intell. Mater. Syst. Struct. 2018, 29, 2008–2026. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Chanzy, Q.; Keane, A. Analysis and experimental validation of morphing UAV wings. Aeronaut. J. 2018, 122, 390–408. [Google Scholar] [CrossRef]
- Jo, B.W.; Majid, T. Aerodynamic Analysis of Camber Morphing Airfoils in Transition via Computational Fluid Dynamics. Biomimetics 2022, 7, 52. [Google Scholar] [CrossRef] [PubMed]
- Majid, T.; Jo, B.W. Comparative Aerodynamic Performance Analysis of Camber Morphing and Conventional Airfoils. Appl. Sci. 2021, 11, 10663. [Google Scholar] [CrossRef]
- Kumar, T.; Venugopal, S.; Ramakrishnananda, B.; Vijay, S. Aerodynamic performance estimation of camber morphing airfoils for small unmanned aerial vehicle. J. Aerosp. Technol. Manag. 2020, 12. [Google Scholar] [CrossRef]
- Eguea, J.P.; da Silva, G.P.G.; Catalano, F.M. Fuel efficiency improvement on a business jet using a camber morphing winglet concept. Aerosp. Sci. Technol. 2020, 96, 105542. [Google Scholar] [CrossRef]
- Sato, K.; Yokozeki, T. Aero-structural evaluation of morphing control surface using corrugated panels. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2017, 15, a7–a15. [Google Scholar] [CrossRef]
- Alsulami, A.; Akbar, M.; Joe, W.Y. A Comparative Study: Aerodynamics of Morphed Airfoils Using CFD Techniques and Analytical Tools. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; p. V001T003A010. [Google Scholar]
- Sabri, F.; Elzaabalawy, A.; Meguid, S. Aeroelastic behaviour of a flexible morphing wing design for unmanned aerial vehicle. Acta Mech. 2022, 233, 851–867. [Google Scholar] [CrossRef]
- Gillebaart, E.; De Breuker, R. Low-fidelity 2D isogeometric aeroelastic analysis and optimization method with application to a morphing airfoil. Comput. Methods Appl. Mech. Eng. 2016, 305, 512–536. [Google Scholar] [CrossRef]
- Woods, B.K.; Dayyani, I.; Friswell, M.I. Fluid/structure-interaction analysis of the fish-bone-active-camber morphing concept. J. Aircr. 2015, 52, 307–319. [Google Scholar] [CrossRef]
- Kammegne, M.J.T.; Botez, R.M.; Grigorie, L.T.; Mamou, M.; Mébarki, Y. Proportional fuzzy feed-forward architecture control validation by wind tunnel tests of a morphing wing. Chin. J. Aeronaut. 2017, 30, 561–576. [Google Scholar] [CrossRef]
- Li, D.; Guo, S.; Aburass, T.O.; Yang, D.; Xiang, J. Active control design for an unmanned air vehicle with a morphing wing. Aircr. Eng. Aerosp. Technol. Int. J. 2016, 88, 168–177. [Google Scholar] [CrossRef]
- Shi, R.; Song, J.; Wan, W. Active disturbance rejection control system design for a morphing wing structure. Asian J. Control. 2015, 17, 832–841. [Google Scholar] [CrossRef]
- Keidel, D.; Fasel, U.; Molinari, G.; Ermanni, P. Design, Development, and Structural Testing of a Camber-Morphing Flying Wing Airplane. In Proceedings of the Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 18–20 September 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; p. V002T004A013. [Google Scholar]
- Yu, J.; Ma, J. Design and Shear Analysis of an Angled Morphing Wing Skin Module. Appl. Sci. 2022, 12, 3092. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Computational analysis of 3D lattice structures for skin in real-scale camber morphing aircraft. Aerospace 2019, 6, 79. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Simplified 2D skin lattice models for multi-axial camber morphing wing aircraft. Aerospace 2019, 6, 90. [Google Scholar] [CrossRef]
- La, S.; Joe, W.Y.; Akbar, M.; Alsaidi, B. Surveys on skin design for morphing wing aircraft: Status and challenges. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0315. [Google Scholar]
- Wong, A.; Bil, C.; Marino, M. Design and Aerodynamic Performance of a FishBAC Morphing Wing. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1298. [Google Scholar]
- Azzawi, W.A. Development and performance evaluation of a morphing wing design using shape memory polymer and composite corrugated structure. Aust. J. Mech. Eng. 2022. [Google Scholar] [CrossRef]
- Auteri, F.; Savino, A.; Zanotti, A.; Gibertini, G.; Zagaglia, D.; Tekap, Y.B.; Braza, M. Experimental evaluation of the aerodynamic performance of a large-scale high-lift morphing wing. Aerosp. Sci. Technol. 2022, 124, 107515. [Google Scholar] [CrossRef]
- Anderson, J.D.; Bowden, M.L. Introduction to Flight; McGraw-Hill Higher Education: New York, NY, USA, 2005. [Google Scholar]
- Eshelby, M. Aircraft Performance: Theory and Practice; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2000. [Google Scholar]
- Mair, W.A.; Birdsall, D.L. Aircraft Performance; Cambridge University Press: Cambridge, UK, 1996; Volume 5. [Google Scholar]
- Ai, Q.; Kamliya Jawahar, H.; Azarpeyvand, M. Experimental investigation of aerodynamic performance of airfoils fitted with morphing trailing edges. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1563. [Google Scholar]
- Bowman, J.; Sanders, B.; Weisshaar, T. Evaluating the impact of morphing technologies on aircraft performance. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002; p. 1631. [Google Scholar]
- Hui, Z.; Zhang, Y.; Chen, G. Aerodynamic performance investigation on a morphing unmanned aerial vehicle with bio-inspired discrete wing structures. Aerosp. Sci. Technol. 2019, 95, 105419. [Google Scholar]
- Jawahar, H.K.; Ai, Q.; Azarpeyvand, M. Experimental and numerical investigation of aerodynamic performance for airfoils with morphed trailing edges. Renew. Energy 2018, 127, 355–367. [Google Scholar] [CrossRef]
- Joshi, S.; Tidwell, Z.; Crossley, W.; Ramakrishnan, S. Comparison of morphing wing stategies based upon aircraft performance impacts. In Proceedings of the 45th the AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; p. 1722. [Google Scholar]
- Goetten, F.; Finger, D.; Marino, M.; Bil, C.; Havermann, M.; Braun, C. A review of guidelines and best practices for subsonic aerodynamic simulations using RANS CFD. In Proceedings of the APISAT 2019: Asia Pacific International Symposium on Aerospace Technology, Gold Coast, Australia, 4–6 December 2019; Engineers Australia: Barton, Australia, 2019; p. 227. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
