Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems
Abstract
1. Introduction
- GAO is designed based on mimicking the behavior of green anacondas in the wild.
- The fundamental inspiration for GAO is the green anaconda’s tracking mechanism during the mating season and the hunting strategy they have when attacking prey.
- The mathematical model of GAO is presented in two phases with the aim of forming exploration and exploitation in the search process.
- GAO’s performance on optimization tasks is tested on twenty-nine benchmark functions from the CEC 2017 test suite and CEC 2019 test suite.
- GAO’s ability to handle real-world applications is evaluated on twenty-one optimization problems from the CEC 2011 test suite.
- The results obtained from GAO are compared with the performance of twelve well-known metaheuristic algorithms.
2. Literature Review
3. Green Anaconda Optimization
3.1. Inspiration of GAO
3.2. Algorithm Initialization
3.3. Mathematical Modelling of GAO
3.3.1. Phase 1: Mating Season (Exploration)
3.3.2. Phase 2: Hunting Strategy (Exploitation)
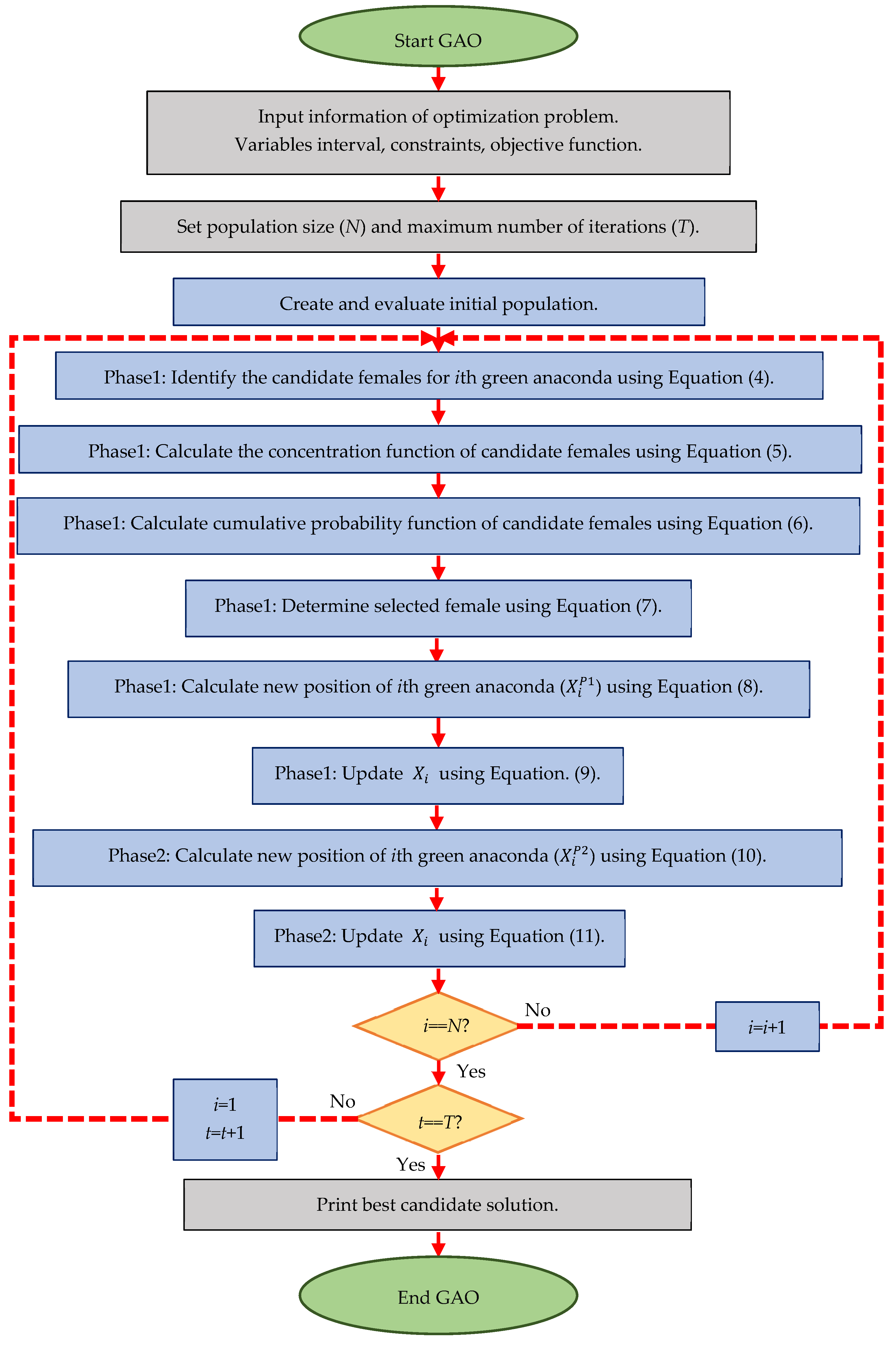
3.4. Repetition Process, Pseudocode, and Flowchart of GAO
| Algorithm 1. Pseudocode of GAO | |
| Start GAO. | |
| 1. | Input problem information: variables, objective function, and constraints. |
| 2. | Set GAO population size (N) and iterations (T). |
| 3. | Generate the initial population matrix at random using Equation (2). |
| 4. | Evaluate the objective function. |
| 5. | For to T |
| 6. | For to |
| 7. | Phase 1: mating season (exploration) |
| 8. | Identify the candidate females using Equation (4). |
| 9. | Calculate the concentration function of candidate females using Equation (5). |
| 10. | Calculatethe cumulative probability function candidate females using Equation (6). |
| 11. | Determine the selected female using Equation (7). |
| 12. | Calculate the new position of ith GAO member using Equation (8). |
| 13. | Update ith GAO member using Equation (9). |
| 14. | Phase 2: hunting strategy (exploitation) |
| 15. | Calculate the new position of ith GAO member using Equation (10). |
| 16. | Update the th GAO member using Equation (11). |
| 17. | End |
| 18. | Save the best candidate solution so far. |
| 19. | End |
| 20. | Output the best quasi-optimal solution obtained with the GAO. |
| End GAO. | |
3.5. Computational Complexity of GAO
4. Simulation Studies and Results
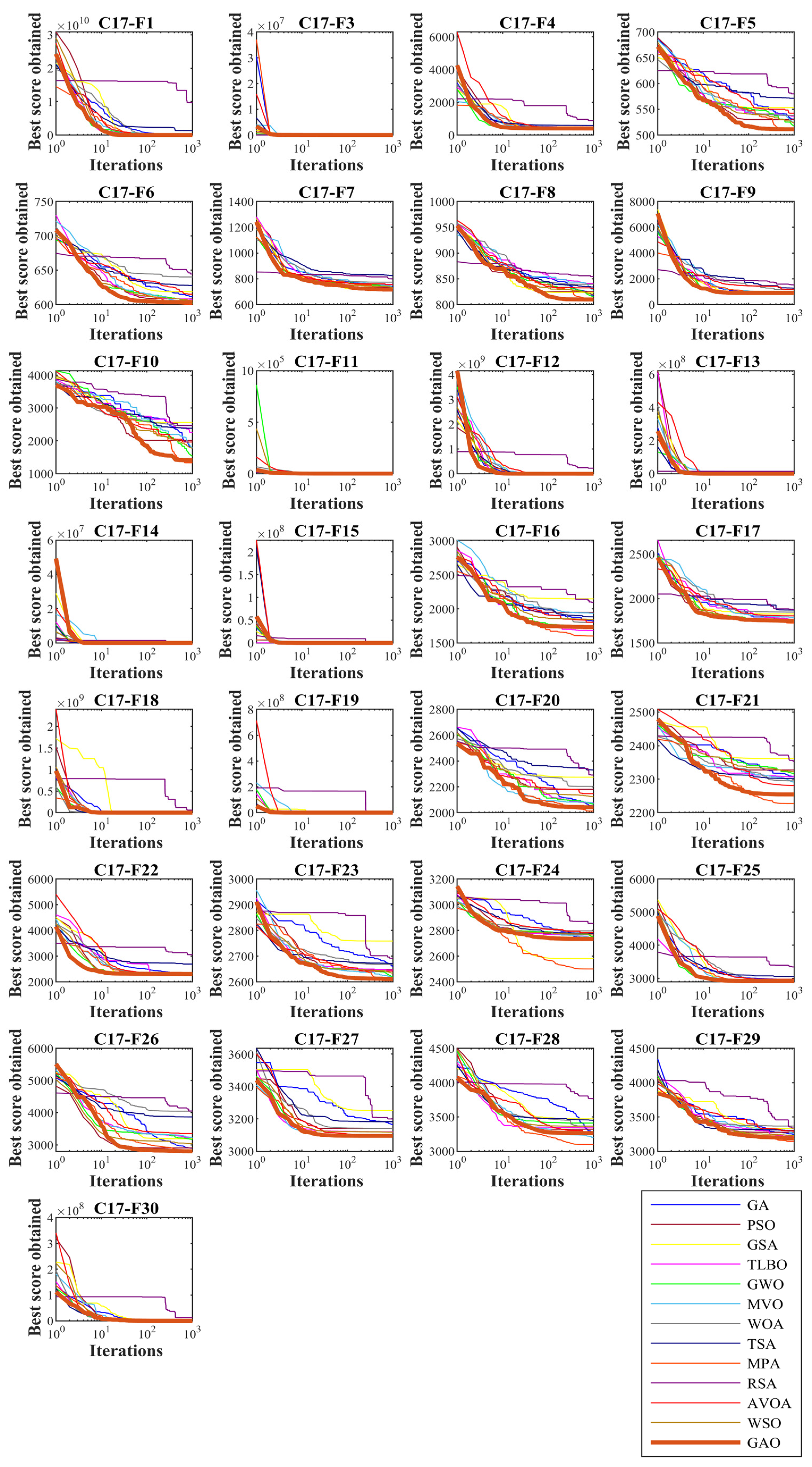
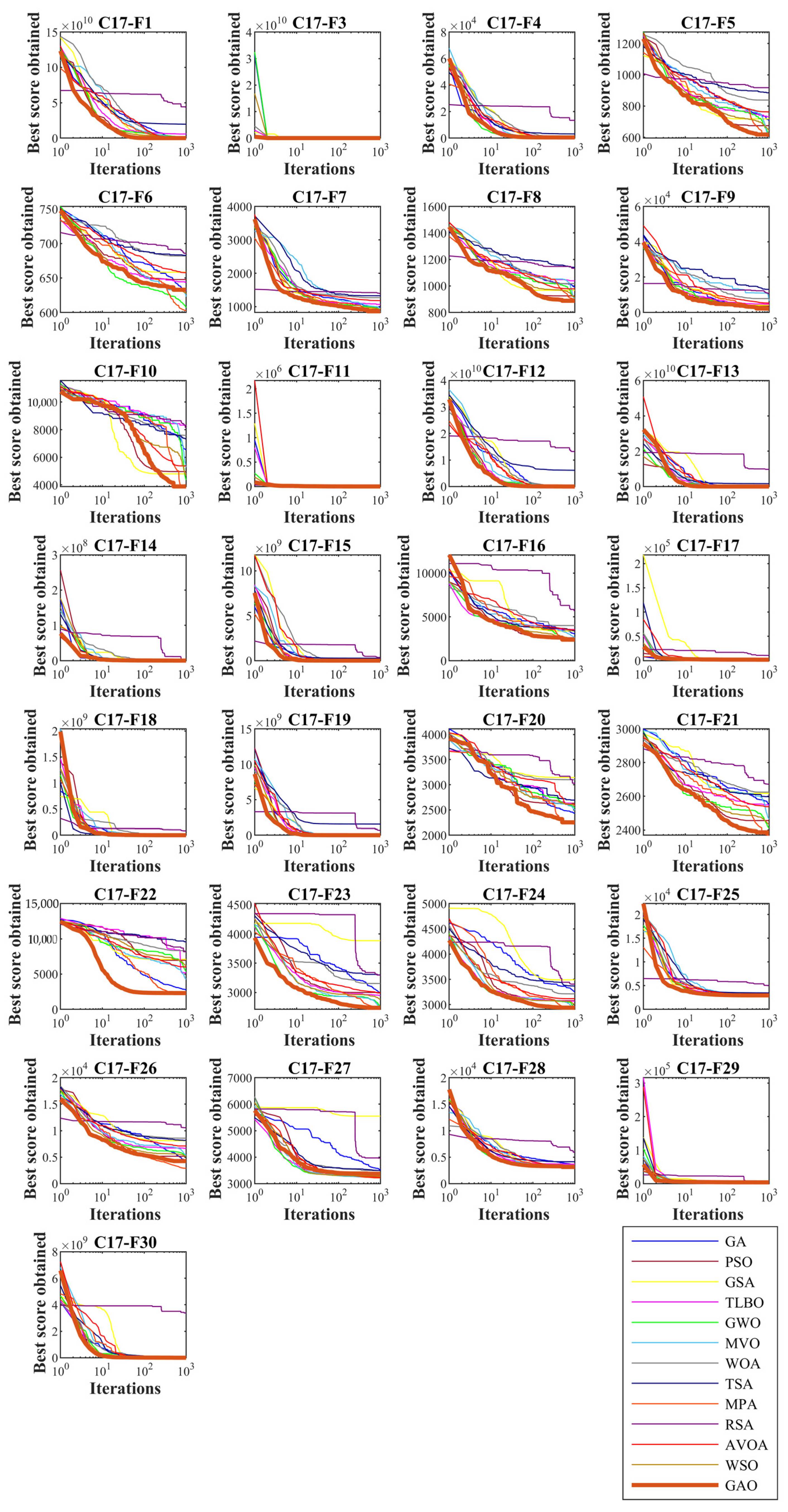
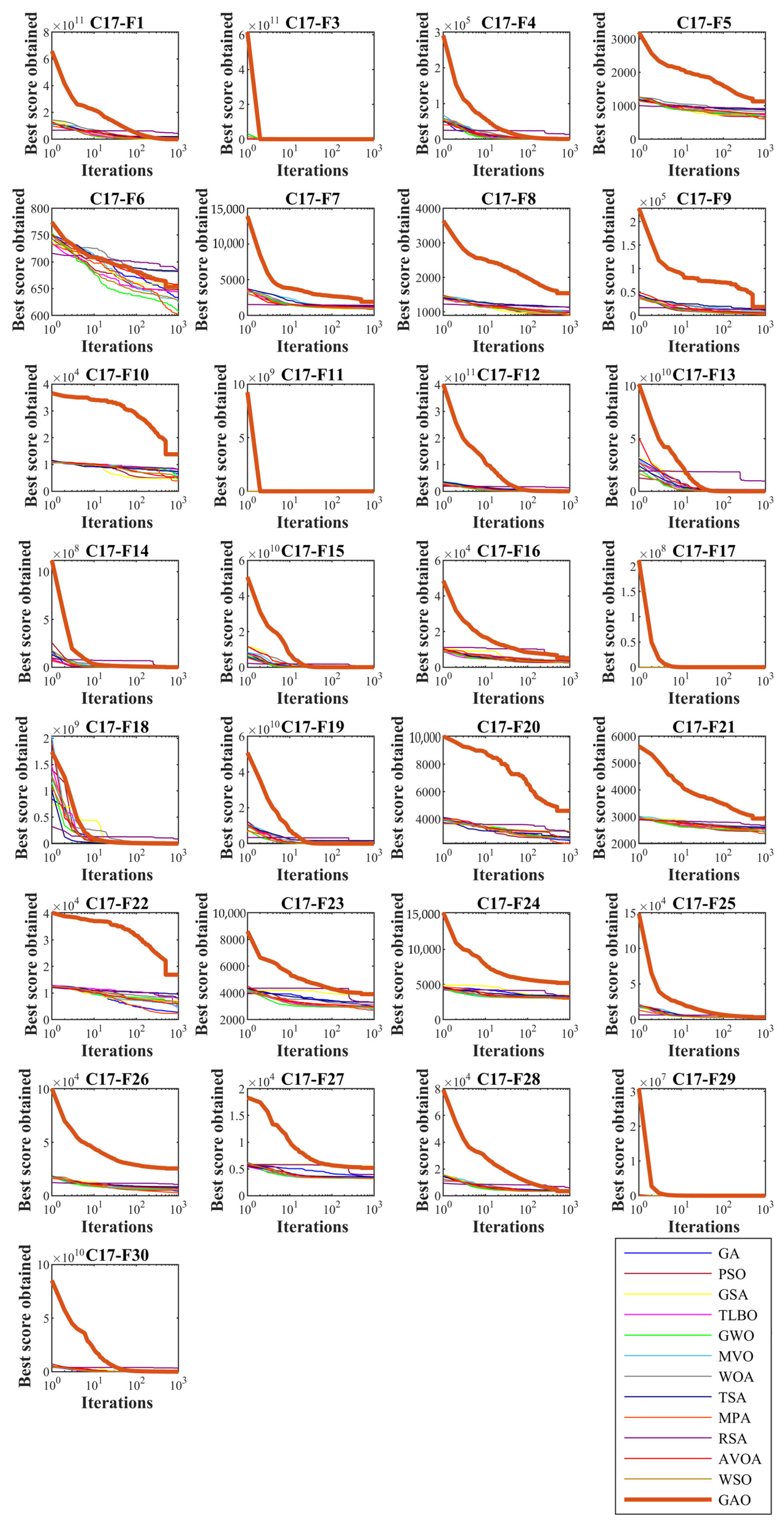
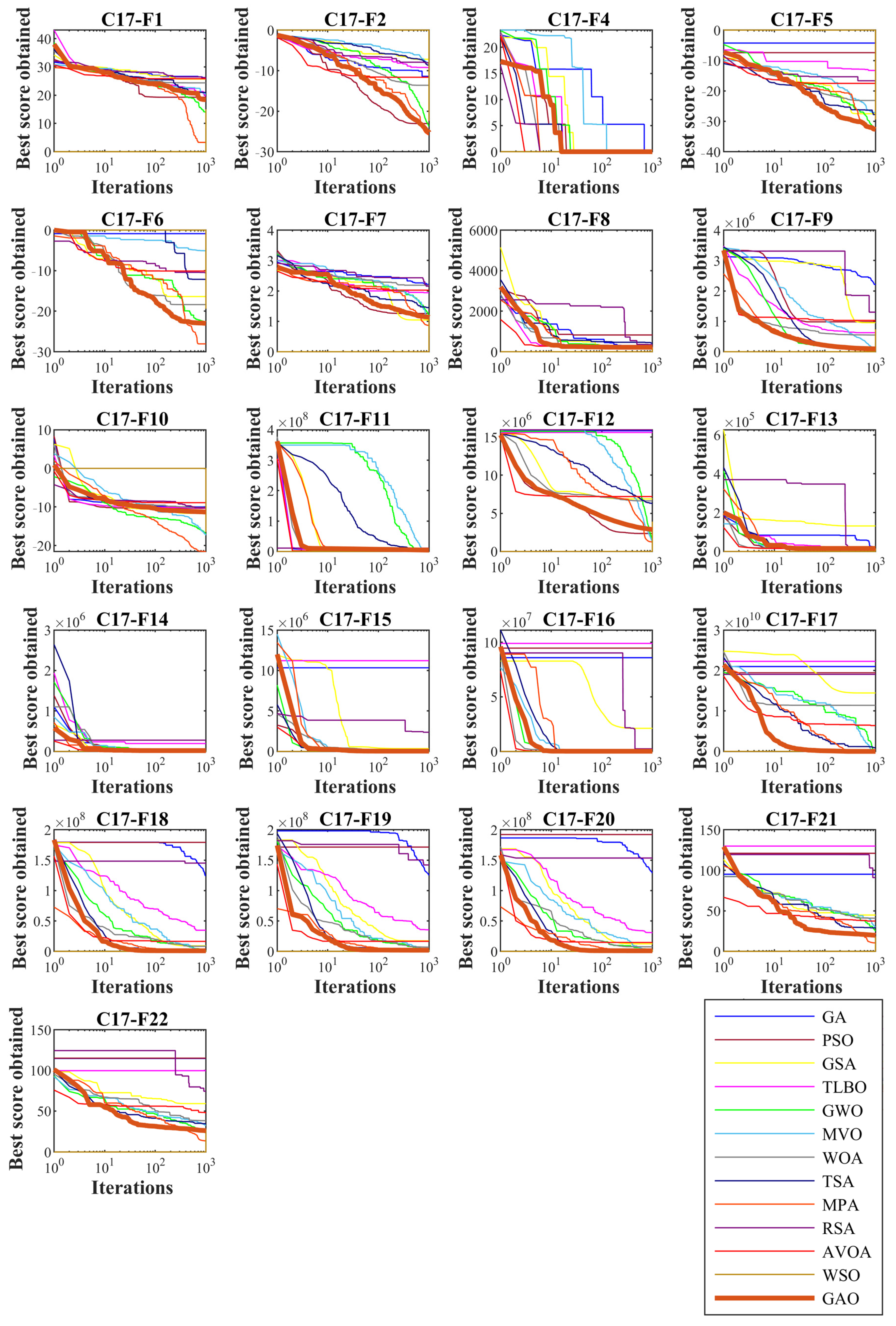
4.1. Evaluation the CEC 2017 Test Suite
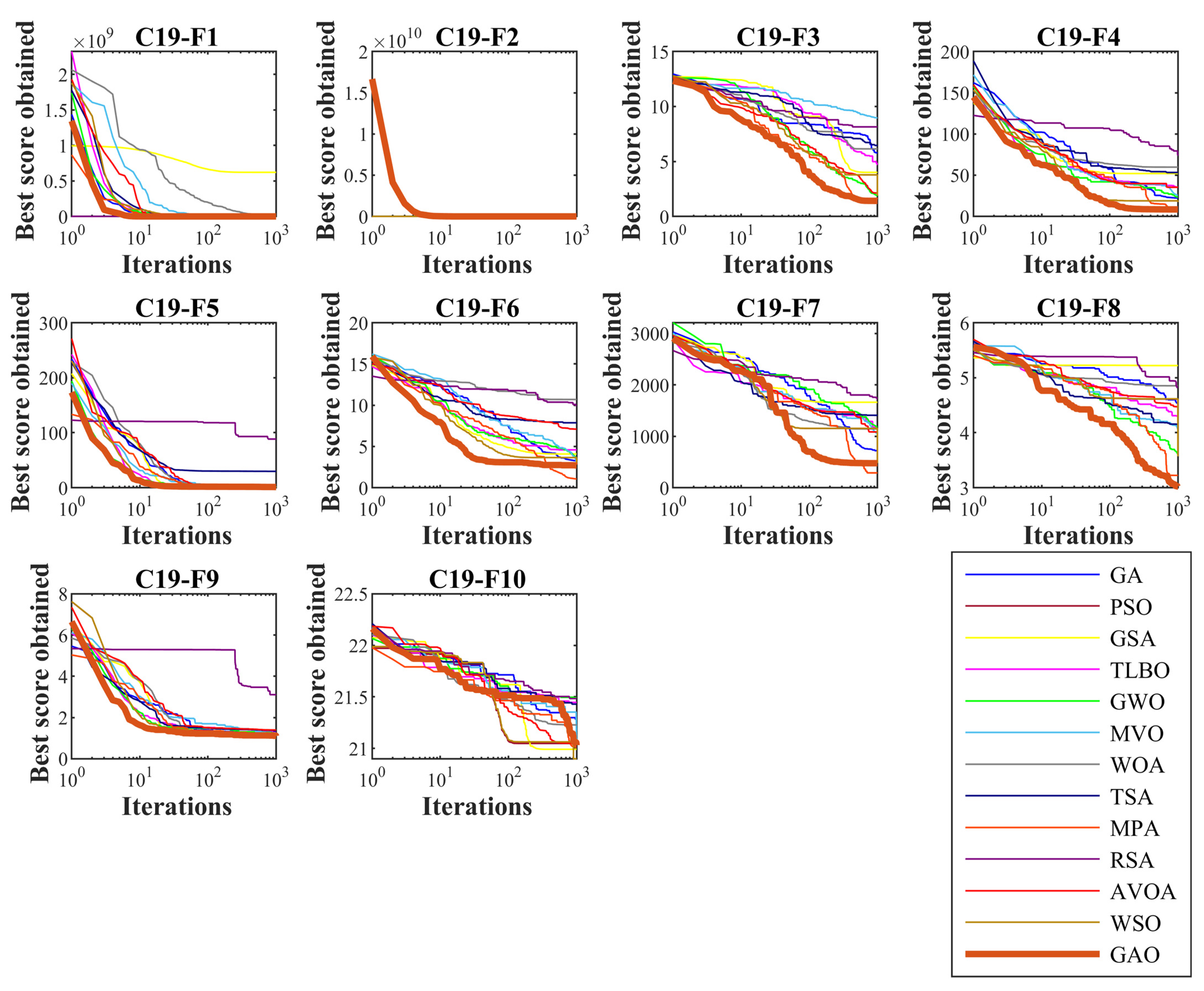
4.2. Evaluation the CEC 2019 Test Suite
4.3. Statistical Analysis
5. GAO for Real-World Applications
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Jahani, E.; Chizari, M. Tackling global optimization problems with a novel algorithm–Mouth Brooding Fish algorithm. Appl. Soft Comput. 2018, 62, 987–1002. [Google Scholar] [CrossRef]
- Sergeyev, Y.D.; Kvasov, D.; Mukhametzhanov, M. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018, 8, 453. [Google Scholar] [CrossRef]
- Liberti, L.; Kucherenko, S. Comparison of deterministic and stochastic approaches to global optimization. Int. Trans. Oper. Res. 2005, 12, 263–285. [Google Scholar] [CrossRef]
- Koc, I.; Atay, Y.; Babaoglu, I. Discrete tree seed algorithm for urban land readjustment. Eng. Appl. Artif. Intell. 2022, 112, 104783. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 2022, 12, 9924. [Google Scholar] [CrossRef]
- Zeidabadi, F.-A.; Dehghani, M.; Trojovský, P.; Hubálovský, Š.; Leiva, V.; Dhiman, G. Archery Algorithm: A Novel Stochastic Optimization Algorithm for Solving Optimization Problems. Comput. Mater. Contin. 2022, 72, 399–416. [Google Scholar] [CrossRef]
- de Armas, J.; Lalla-Ruiz, E.; Tilahun, S.L.; Voß, S. Similarity in metaheuristics: A gentle step towards a comparison methodology. Nat. Comput. 2022, 21, 265–287. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra Optimization Algorithm: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Malik, O.P.; Morales-Menendez, R.; Dhiman, G.; Nouri, N.; Ehsanifar, A.; Guerrero, J.M.; Ramirez-Mendoza, R.A. Binary spring search algorithm for solving various optimization problems. Appl. Sci. 2021, 11, 1286. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Karaboga, D.; Basturk, B. Artificial Bee Colony (ABC) Optimization Algorithm for Solving Constrained Optimization Problems. In International Fuzzy Systems Association World Congress; Springer: Berlin/Heidelberg, Germany, 2007; pp. 789–798. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Perth, WA, Australia, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, Q.; Zhu, S.; Zhang, L. Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Syst. Appl. 2022, 188, 116026. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl. Based Syst. 2022, 234, 108457. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden Jackal Optimization: A Novel Nature-Inspired Optimizer for Engineering Applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dhiman, G.; Malik, O.; Morales-Menendez, R.; Ramirez-Mendoza, R.A.; Dehghani, A.; Guerrero, J.M.; Parra-Arroyo, L. A spring search algorithm applied to engineering optimization problems. Appl. Sci. 2020, 10, 6173. [Google Scholar] [CrossRef]
- Dehghani, M.; Samet, H. Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Appl. Sci. 2020, 2, 1720. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Francisco, M.B.; Diniz, C.A.; Oliver, G.A.; Cunha Jr, S.S.; Gomes, G.F. Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Syst. Appl. 2021, 170, 114522. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, C.; Wang, X.; Han, T.; Li, Y. Nuclear reaction optimization: A novel and powerful physics-based algorithm for global optimization. IEEE Access 2019, 7, 66084–66109. [Google Scholar] [CrossRef]
- Cuevas, E.; Oliva, D.; Zaldivar, D.; Pérez-Cisneros, M.; Sossa, H. Circle detection using electro-magnetism optimization. Inf. Sci. 2012, 182, 40–55. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Guerrero, J.M.; Malik, O.P.; Ramirez-Mendoza, R.A.; Matas, J.; Vasquez, J.C.; Parra-Arroyo, L. A new “Doctor and Patient” optimization algorithm: An application to energy commitment problem. Appl. Sci. 2020, 10, 5791. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Malik, O. FOA:‘Following’Optimization Algorithm for solving Power engineering optimization problems. J. Oper. Autom. Power Eng. 2020, 8, 57–64. [Google Scholar]
- Ayyarao, T.L.; RamaKrishna, N.; Elavarasam, R.M.; Polumahanthi, N.; Rambabu, M.; Saini, G.; Khan, B.; Alatas, B. War Strategy Optimization Algorithm: A New Effective Metaheuristic Algorithm for Global Optimization. IEEE Access 2022, 10, 25073–25105. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovský, P. Teamwork Optimization Algorithm: A New Optimization Approach for Function Minimization/Maximization. Sensors 2021, 21, 4567. [Google Scholar] [CrossRef]
- Braik, M.; Ryalat, M.H.; Al-Zoubi, H. A novel meta-heuristic algorithm for solving numerical optimization problems: Ali Baba and the forty thieves. Neural Comput. Appl. 2022, 34, 409–455. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Alyasseri, Z.A.A.; Awadallah, M.A.; Abu Doush, I. Coronavirus herd immunity optimizer (CHIO). Neural Comput. Appl. 2021, 33, 5011–5042. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, M.; Montazeri, Z.; Saremi, S.; Dehghani, A.; Malik, O.P.; Al-Haddad, K.; Guerrero, J.M. HOGO: Hide objects game optimization. Int. J. Intell. Eng. Syst. 2020, 13, 4. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Malik, O.P.; Ehsanifar, A.; Dehghani, A. OSA: Orientation search algorithm. Int. J. Ind. Electron. Control. Optim. 2019, 2, 99–112. [Google Scholar]
- Moghdani, R.; Salimifard, K. Volleyball premier league algorithm. Appl. Soft Comput. 2018, 64, 161–185. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Guerrero, J.M.; Malik, O.; Kumar, V. Football game based optimization: An application to solve energy commitment problem. Int. J. Intell. Eng. Syst. 2020, 13, 514–523. [Google Scholar] [CrossRef]
- DEHGHANI, M.; MONTAZERI, Z.; MALIK, O.P. DGO: Dice game optimizer. Gazi Univ. J. Sci. 2019, 32, 871–882. [Google Scholar] [CrossRef]
- Doumari, S.A.; Givi, H.; Dehghani, M.; Malik, O.P. Ring Toss Game-Based Optimization Algorithm for Solving Various Optimization Problems. Int. J. Intell. Eng. Syst. 2021, 14, 545–554. [Google Scholar] [CrossRef]
- Zeidabadi, F.A.; Dehghani, M. POA: Puzzle Optimization Algorithm. Int. J. Intell. Eng. Syst. 2022, 15, 273–281. [Google Scholar]
- Hsiou, A.S.; Winck, G.R.; Schubert, B.W.; Avilla, L. On the presence of Eunectes murinus (Squamata, Serpentes) from the late Pleistocene of northern Brazil. Rev. Bras. De Paleontol. 2013, 16, 77–82. [Google Scholar] [CrossRef]
- Rivas, J.A. The Life History of the Green Anaconda (Eunectes murinus), with Emphasis on Its Reproductive Biology. Ph.D. Thesis, The University of Tennessee, Knoxville, TN, USA, 1999. [Google Scholar]
- Rivas, J.A.; Burghardt, G.M. Understanding sexual size dimorphism in snakes: Wearing the snake’s shoes. Anim. Behav. 2001, 62, F1–F6. [Google Scholar] [CrossRef]
- Pope, C.H. The Giant Snakes: The Natural History of the Boa Constrictor, the Anaconda, and the Largest Pythons, Including Comparative Facts about Other Snakes and Basic Information on Reptiles in General; Knopf: New York, NY, USA, 1961. [Google Scholar]
- Harvey, D. Smithsonian Super Nature Encyclopedia; Dorling Kindersley Publishing: London, UK, 2012. [Google Scholar]
- Thomas, O.; Allain, S. Review of prey taken by anacondas (Squamata, Boidae: Eunectes). Reptiles Amphib. 2021, 28, 329–334. [Google Scholar] [CrossRef]
- Strimple, P. The Green Anaconda Eunectes murinus (Linnaeus). Liyyeratura Serpentium 1993, 13, 46–50. [Google Scholar]
- Burton, M.; Burton, R. International Wildlife Encyclopedia; Marshall Cavendish: New York, NY, USA, 2002; Volume 1. [Google Scholar]
- Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P.; Definitions, P. Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Technology Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Price, K.V.; Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the 100-Digit Challenge Special Session and Competition on Single Objective Numerical Optimization; Nanyang Technological University: Singapore, 2018. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 196–202. [Google Scholar]
- Das, S.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Jadavpur University: Kolkata, India; Nanyang Technological University: Singapore, 2010; pp. 341–359. [Google Scholar]


| Algorithm | Parameter | Value |
|---|---|---|
| GA | ||
| Type | Real coded | |
| Selection | Roulette wheel (proportionate) | |
| Crossover | Whole arithmetic (probability = 0.8, ) | |
| Mutation | Gaussian (probability = 0.05) | |
| PSO | ||
| Topology | Fully connected | |
| Cognitive and social constant | (C1, C2) | |
| Inertia weight | Linear reduction from 0.9 to 0.1 | |
| Velocity limit | 10% of dimension range | |
| GSA | ||
| Alpha, G0, Rnorm, Rpower | 20, 100, 2, 1 | |
| TLBO | ||
| TF: Teaching factor | TF = round | |
| random number | rand is a random number between | |
| GWO | ||
| Convergence parameter (a) | a: Linear reduction from 2 to 0. | |
| MVO | ||
| Wormhole existence probability (WEP) | Min(WEP) = 0.2 and Max(WEP) = 1. | |
| Exploitation accuracy over the iterations (p) | . | |
| WOA | ||
| Convergence parameter (a) | a: Linear reduction from 2 to 0. | |
| r is a random vector in | ||
| l is a random number in | ||
| TSA | ||
| Pmin and Pmax | 1, 4 | |
| c1, c2, c3 | random numbers lie in the range of | |
| MPA | ||
| Constant number | ||
| Random vector | R is a vector of uniform random numbers in | |
| Fish aggregating devices (FADs) | ||
| Binary vector | or 1 | |
| RSA | ||
| Sensitive parameter | ||
| Sensitive parameter | ||
| Evolutionary sense (ES) | ES: randomly decreasing values between 2 and −2 | |
| AVOA | ||
| L1, L2 | 0.8, 0.2 | |
| W | 2.5 | |
| P1, P2, P3 | 0.6, 0.4, 0.6 | |
| WSO | ||
| Fmin and Fmax | 0.07, 0.75 | |
| τ, ao, a1, a2 | 4.125, 6.25, 100, 0.0005 |
| GAO | WSO | AVOA | RSA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C17-F1 | mean | 100 | 6977.111 | 1822.634 | 9.72 × 109 | 104.6622 | 1.33 × 109 | 7,296,302 | 11,776.52 | 18,952.96 | 1.57 × 108 | 328.9346 | 3347.233 | 20,023,383 |
| best | 100 | 345.9705 | 754.1327 | 7.3 × 109 | 102.4063 | 11,665,981 | 3,349,288 | 6355.289 | 11,697.02 | 69,930,767 | 109.1846 | 362.021 | 6,675,925 | |
| worst | 100 | 12,471.59 | 3882.122 | 1.27 × 1010 | 106.0517 | 3.8 × 109 | 10,244,428 | 15,855.06 | 28,173.75 | 3.79 × 108 | 747.2462 | 9924.345 | 36,691,453 | |
| std | 1.76 × 10−5 | 6313.97 | 1440.855 | 2.69 × 109 | 1.615877 | 1.69 × 109 | 3,442,725 | 4085.323 | 7694.896 | 1.49 × 108 | 290.3269 | 4427.81 | 12,404,106 | |
| median | 100 | 7545.442 | 1327.14 | 9.47 × 109 | 105.0955 | 7.46 × 108 | 7,795,746 | 12,447.86 | 17,970.54 | 89,666,699 | 229.6539 | 1551.284 | 18,363,078 | |
| rank | 1 | 6 | 4 | 13 | 2 | 12 | 9 | 7 | 8 | 11 | 3 | 5 | 10 | |
| C17-F3 | mean | 300 | 349.9638 | 333.4122 | 11,479.03 | 300 | 11,447.37 | 1003.998 | 300.0247 | 3182.624 | 754.5378 | 11,414.77 | 314.1376 | 15,733.23 |
| best | 300 | 302.6537 | 300.001 | 7421.598 | 300 | 7260.632 | 501.6584 | 300.0095 | 612.137 | 482.5901 | 9317.412 | 311.5075 | 4618.157 | |
| worst | 300 | 394.8162 | 375.47 | 15,834.53 | 300 | 15,343.09 | 1755.01 | 300.0433 | 7521.755 | 932.1847 | 12,906.36 | 317.3719 | 24,879.84 | |
| std | 4.64 × 10−14 | 50.70352 | 31.21843 | 4674.285 | 5.43 × 10−11 | 3304.026 | 552.1851 | 0.014095 | 3284.596 | 197.091 | 1554.807 | 2.491209 | 10,584.32 | |
| median | 300 | 351.1926 | 329.0889 | 11,329.99 | 300 | 11,592.88 | 879.6611 | 300.023 | 2298.302 | 801.6882 | 11,717.65 | 313.8355 | 16,717.47 | |
| rank | 1 | 6 | 5 | 12 | 2 | 11 | 8 | 3 | 9 | 7 | 10 | 4 | 13 | |
| C17-F4 | mean | 400.002 | 407.7045 | 418.5456 | 881.8049 | 417.7576 | 582.4649 | 430.8554 | 404.3984 | 423.2437 | 409.7871 | 406.2592 | 421.6779 | 415.7083 |
| best | 400 | 400.0125 | 401.1698 | 586.4966 | 414.2066 | 406.9075 | 406.8525 | 403.2745 | 407.2344 | 408.9495 | 405.0984 | 400.1128 | 412.4635 | |
| worst | 400.008 | 424.6187 | 468.8402 | 1517.016 | 423.186 | 947.3914 | 456.5312 | 405.4712 | 470.4305 | 410.3159 | 406.799 | 475.105 | 419.6784 | |
| std | 0.004024 | 11.63975 | 33.53654 | 427.6431 | 4.118432 | 246.3324 | 27.24021 | 0.898639 | 31.45858 | 0.585883 | 0.781423 | 35.98526 | 3.157633 | |
| median | 400 | 403.0934 | 402.0862 | 711.8537 | 416.8188 | 487.7803 | 430.019 | 404.4239 | 407.655 | 409.9415 | 406.5697 | 405.7469 | 415.3457 | |
| rank | 1 | 4 | 8 | 13 | 7 | 12 | 11 | 2 | 10 | 5 | 3 | 9 | 6 | |
| C17-F5 | mean | 520.5609 | 519.1534 | 542.2855 | 580.0791 | 521.6225 | 571.2951 | 538.0164 | 524.0977 | 517.8573 | 536.616 | 553.2224 | 529.9867 | 530.1072 |
| best | 507.9597 | 509.9497 | 520.8941 | 561.3768 | 509.9496 | 534.1875 | 514.506 | 514.9287 | 510.3157 | 530.7196 | 539.7681 | 511.9395 | 525.052 | |
| worst | 534.983 | 528.8541 | 563.6767 | 591.9163 | 544.5154 | 593.0703 | 562.2668 | 542.6545 | 528.6164 | 540.4401 | 566.6616 | 555.7175 | 536.3365 | |
| std | 14.10965 | 8.72578 | 17.58362 | 13.27221 | 15.63282 | 25.97608 | 19.84514 | 12.60888 | 8.11889 | 4.272868 | 12.55651 | 20.21898 | 5.109001 | |
| median | 519.6504 | 518.905 | 542.2856 | 583.5117 | 516.0124 | 578.9613 | 537.6464 | 519.4038 | 516.2485 | 537.6521 | 553.2301 | 526.145 | 529.5201 | |
| rank | 3 | 2 | 10 | 13 | 4 | 12 | 9 | 5 | 1 | 8 | 11 | 6 | 7 | |
| C17-F6 | mean | 603.01 | 600.5606 | 614.929 | 644.2993 | 600.0003 | 627.6556 | 640.0763 | 600.5326 | 601.6492 | 607.426 | 618.4222 | 608.0398 | 611.1025 |
| best | 601.6233 | 600.0005 | 605.396 | 641.2874 | 600.0001 | 612.1762 | 634.9033 | 600.2196 | 601.1107 | 605.1494 | 609.0575 | 601.4659 | 607.472 | |
| worst | 604.6321 | 602.0417 | 635.5747 | 647.7859 | 600.0004 | 644.1825 | 650.7377 | 601.0412 | 603.1359 | 610.9759 | 629.7345 | 620.8405 | 615.6957 | |
| std | 1.3499 | 0.991847 | 13.93839 | 2.8917 | 0.000133 | 13.3633 | 7.437235 | 0.385881 | 0.991826 | 2.656369 | 8.639876 | 8.788191 | 3.64533 | |
| median | 602.8922 | 600.1001 | 609.3725 | 644.0619 | 600.0004 | 627.1318 | 637.332 | 600.4348 | 601.1752 | 606.7894 | 617.4483 | 604.9264 | 610.6212 | |
| rank | 5 | 3 | 9 | 13 | 1 | 11 | 12 | 2 | 4 | 6 | 10 | 7 | 8 | |
| C17-F7 | mean | 714.9746 | 727.3328 | 753.8474 | 799.9577 | 720.073 | 824.0926 | 772.6133 | 721.9245 | 730.1478 | 755.4194 | 716.7679 | 734.5213 | 738.9913 |
| best | 714.4159 | 716.9793 | 727.955 | 790.3283 | 715.4835 | 794.2034 | 751.0108 | 711.5214 | 721.8083 | 750.5447 | 711.4275 | 726.7135 | 727.7346 | |
| worst | 715.7112 | 737.1411 | 801.0858 | 810.4362 | 724.3538 | 863.1991 | 802.0857 | 728.4637 | 749.7124 | 764.2491 | 725.9128 | 747.0726 | 743.9886 | |
| std | 0.628096 | 8.631729 | 32.39556 | 8.435769 | 3.767197 | 28.68428 | 25.18788 | 7.555293 | 13.11915 | 6.146001 | 6.368765 | 9.270855 | 7.625192 | |
| median | 714.8856 | 727.6054 | 743.1745 | 799.5332 | 720.2273 | 819.4839 | 768.6783 | 723.8564 | 724.5352 | 753.4418 | 714.8658 | 732.1495 | 742.121 | |
| rank | 1 | 5 | 9 | 12 | 3 | 13 | 11 | 4 | 6 | 10 | 2 | 7 | 8 | |
| C17-F8 | mean | 818.8348 | 817.5792 | 830.8799 | 854.2832 | 833.2392 | 834.1207 | 839.1509 | 827.6156 | 815.564 | 840.7119 | 823.3815 | 824.5363 | 818.0629 |
| best | 804.9748 | 807.9599 | 822.034 | 840.3486 | 809.9496 | 812.4518 | 825.8119 | 808.9582 | 810.3711 | 833.2718 | 815.9193 | 816.9143 | 813.7883 | |
| worst | 851.46 | 841.4628 | 837.8083 | 860.4043 | 863.7533 | 856.0983 | 854.1837 | 855.7292 | 822.351 | 849.4086 | 831.8386 | 831.483 | 826.546 | |
| std | 21.88629 | 16.01194 | 8.152015 | 9.478211 | 26.18452 | 18.60264 | 11.62491 | 19.87598 | 5.278038 | 8.256642 | 7.685449 | 7.212869 | 5.753112 | |
| median | 809.4521 | 810.4471 | 831.8386 | 858.19 | 829.6269 | 833.9664 | 838.3041 | 822.8875 | 814.767 | 840.0837 | 822.884 | 824.8739 | 815.9586 | |
| rank | 4 | 2 | 8 | 13 | 9 | 10 | 11 | 7 | 1 | 12 | 5 | 6 | 3 | |
| C17-F9 | mean | 900 | 958.0246 | 1183.273 | 1521.471 | 900 | 1272.429 | 1145.44 | 900.1154 | 900.5917 | 912.8054 | 926.2937 | 904.5932 | 905.5344 |
| best | 900 | 906.8134 | 1031.947 | 1377.821 | 900 | 931.1214 | 1005.691 | 900.0008 | 900.0569 | 907.8307 | 920.4252 | 900.9737 | 903.0297 | |
| worst | 900 | 1056.588 | 1387.365 | 1784.32 | 900 | 1701.296 | 1460.087 | 900.4561 | 900.9171 | 921.6602 | 931.8898 | 913.3387 | 909.8295 | |
| std | 0 | 70.4426 | 148.8524 | 184.2871 | 6.63 × 10−8 | 336.066 | 211.231 | 0.227138 | 0.376198 | 6.077825 | 5.95763 | 5.904611 | 3.075444 | |
| median | 900 | 934.3484 | 1156.889 | 1461.871 | 900 | 1228.649 | 1057.991 | 900.0023 | 900.6964 | 910.8653 | 926.4299 | 902.0301 | 904.6392 | |
| rank | 1 | 9 | 11 | 13 | 2 | 12 | 10 | 3 | 4 | 7 | 8 | 5 | 6 | |
| C17-F10 | mean | 1301.559 | 1482.241 | 1963.686 | 2463.959 | 1343.128 | 2384.889 | 2464.88 | 1794.25 | 1535.89 | 2256.198 | 2564.708 | 2013.59 | 1766.646 |
| best | 1148.146 | 1240.525 | 1532.027 | 2279.151 | 1189.366 | 2194.314 | 2123.467 | 1606.638 | 1410.302 | 1836.742 | 2149.315 | 1599.934 | 1443.475 | |
| worst | 1457.885 | 1761.604 | 2178.649 | 2817.449 | 1472.816 | 2769.978 | 2906.585 | 2041.969 | 1721.165 | 2565.7 | 2887.991 | 2449.501 | 2191.037 | |
| std | 133.5989 | 219.3419 | 292.3638 | 240.3721 | 116.9823 | 260.9104 | 329.2918 | 213.5238 | 132.1632 | 309.9574 | 332.2394 | 348.9919 | 320.4534 | |
| median | 1300.103 | 1463.417 | 2072.033 | 2379.618 | 1355.166 | 2287.633 | 2414.733 | 1764.196 | 1506.047 | 2311.176 | 2610.763 | 2002.462 | 1716.037 | |
| rank | 1 | 3 | 7 | 11 | 2 | 10 | 12 | 6 | 4 | 9 | 13 | 8 | 5 | |
| C17-F11 | mean | 1110.291 | 1129.294 | 1216.327 | 2847.161 | 1101.951 | 3448.614 | 1271.237 | 1117.426 | 1129.288 | 1154.533 | 1132.152 | 1146.624 | 2474.015 |
| best | 1109.37 | 1112.659 | 1137.215 | 2190.264 | 1100.106 | 1227.421 | 1131.339 | 1103.416 | 1113.949 | 1140.523 | 1123.071 | 1134.545 | 1116.115 | |
| worst | 1110.713 | 1155.055 | 1382.588 | 3615.403 | 1103.709 | 5693.758 | 1472.267 | 1139.468 | 1144.24 | 1177.45 | 1138.753 | 1169.648 | 6326.297 | |
| std | 0.631109 | 20.42284 | 112.1149 | 598.7897 | 1.471866 | 2486.253 | 151.1479 | 15.44328 | 13.40317 | 15.94047 | 6.927099 | 15.80819 | 2568.811 | |
| median | 1110.54 | 1124.73 | 1172.752 | 2791.489 | 1101.994 | 3436.639 | 1240.671 | 1113.41 | 1129.481 | 1150.079 | 1133.392 | 1141.152 | 1226.824 | |
| rank | 2 | 5 | 9 | 12 | 1 | 13 | 10 | 3 | 4 | 8 | 6 | 7 | 11 | |
| C17-F12 | mean | 1236.271 | 5504.867 | 2,486,523 | 2.2 × 108 | 1290.268 | 271,235.9 | 8,310,292 | 182,122.5 | 1,523,242 | 5,426,363 | 526,882.7 | 8588.212 | 649,676 |
| best | 1200.472 | 2544.855 | 1,327,937 | 71,378,713 | 1258.491 | 90,040.82 | 1,024,361 | 52,968.26 | 348,583.1 | 1,452,091 | 86,253.94 | 2606.745 | 188,110.4 | |
| worst | 1320.393 | 8397.613 | 4,285,351 | 3.92 × 108 | 1351.6 | 366,131.1 | 18,484,802 | 401,267.3 | 2,123,298 | 9,606,371 | 1,163,364 | 14,841.02 | 1,146,930 | |
| std | 56.3488 | 2509.074 | 1,363,601 | 1.52 × 108 | 42.41378 | 126,890.6 | 7,346,263 | 152,346.3 | 821,342.4 | 4,319,261 | 485,164.3 | 5574.514 | 393,704.8 | |
| median | 1212.11 | 5538.5 | 2,166,401 | 2.08 × 108 | 1275.49 | 314,385.8 | 6,866,002 | 137,127.3 | 1,810,543 | 5,323,495 | 428,956.2 | 8452.54 | 631,832 | |
| rank | 1 | 3 | 10 | 13 | 2 | 6 | 12 | 5 | 9 | 11 | 7 | 4 | 8 | |
| C17-F13 | mean | 1304.993 | 1331.056 | 8036.958 | 14,569,791 | 1381.022 | 7034.525 | 20,801.23 | 23,724.72 | 13,550.53 | 17,865.5 | 11,709.24 | 7013.944 | 58,378.41 |
| best | 1300.267 | 1313.111 | 3973.009 | 557,392.2 | 1369.765 | 3401.616 | 8156.543 | 1416.265 | 1737.605 | 16,864.65 | 9814.234 | 2458.308 | 9078.56 | |
| worst | 1307.311 | 1374.61 | 12,181.24 | 38,425,092 | 1393.283 | 9616.915 | 33,543.16 | 32,645.07 | 29,200.54 | 20,310.85 | 13,162.4 | 17,853.43 | 193,258.2 | |
| std | 3.216697 | 29.23646 | 3392.984 | 17,876,504 | 9.930585 | 3048.989 | 11,159.08 | 14,913.04 | 12,554.77 | 1645.737 | 1390.591 | 7306.492 | 89,972.56 | |
| median | 1306.198 | 1318.252 | 7996.789 | 9,648,339 | 1380.521 | 7559.784 | 20,752.61 | 30,418.78 | 11,631.99 | 17,143.25 | 11,930.17 | 3872.02 | 15,588.43 | |
| rank | 1 | 2 | 6 | 13 | 3 | 5 | 10 | 11 | 8 | 9 | 7 | 4 | 12 | |
| C17-F14 | mean | 1402.488 | 1429.937 | 2267.222 | 4189.987 | 1458.09 | 2493.258 | 2004.287 | 1444.479 | 2191.108 | 1605.133 | 6961.758 | 3115.468 | 13,829.69 |
| best | 1400.997 | 1422.745 | 1465.467 | 1759.231 | 1451.345 | 1483.963 | 1540.274 | 1436.906 | 1505.748 | 1524.797 | 4027.829 | 1434.97 | 3901.489 | |
| worst | 1404.975 | 1447.049 | 4113.275 | 5019.092 | 1467.112 | 5421.258 | 2633.201 | 1452.614 | 4188.18 | 1637.676 | 9408.754 | 7252.678 | 27,663.3 | |
| std | 1.722924 | 11.45666 | 1238.764 | 1620.565 | 7.945331 | 1952.273 | 456.8535 | 8.481639 | 1331.488 | 53.81531 | 2846.787 | 2780.418 | 10,065.91 | |
| median | 1401.99 | 1424.977 | 1745.074 | 4990.812 | 1456.951 | 1533.905 | 1921.836 | 1444.197 | 1535.253 | 1629.029 | 7205.224 | 1887.112 | 11,876.98 | |
| rank | 1 | 2 | 8 | 11 | 4 | 9 | 6 | 3 | 7 | 5 | 12 | 10 | 13 | |
| C17-F15 | mean | 1511.413 | 1528.001 | 6200.738 | 11,809.76 | 1500.735 | 8083.926 | 10,091.39 | 3322.012 | 8029.693 | 1724.884 | 22,527.21 | 9559.728 | 4778.883 |
| best | 1508.477 | 1501.587 | 2569.987 | 7105.858 | 1500.42 | 1606.064 | 2309.799 | 1533.502 | 1610.261 | 1590.433 | 9704.224 | 2974.495 | 1919.88 | |
| worst | 1514.151 | 1561.085 | 10,787.13 | 18,686.75 | 1501.47 | 23,704.43 | 18,933.6 | 6377.536 | 13,679.32 | 1821.273 | 31,769.43 | 15,791.91 | 8502.898 | |
| std | 2.335106 | 28.10815 | 3584.793 | 5429.859 | 0.492915 | 10,485.67 | 6814.4 | 2309.765 | 5227.34 | 113.2876 | 10,706.11 | 5356.91 | 3272.896 | |
| median | 1511.512 | 1524.667 | 5722.919 | 10,723.22 | 1500.525 | 3512.605 | 9561.076 | 2688.506 | 8414.598 | 1743.915 | 24,317.6 | 9736.253 | 4346.377 | |
| rank | 2 | 3 | 7 | 12 | 1 | 9 | 11 | 5 | 8 | 4 | 13 | 10 | 6 | |
| C17-F16 | mean | 1601.491 | 1633.587 | 1803.613 | 2096.509 | 1659.379 | 1883.829 | 1801.984 | 1935.052 | 1740.482 | 1682.598 | 2148.203 | 1947.807 | 1817.44 |
| best | 1600.891 | 1602.605 | 1729.091 | 1912.598 | 1646.361 | 1687.047 | 1645.957 | 1843.116 | 1659.908 | 1654.683 | 1982.965 | 1839.08 | 1727.547 | |
| worst | 1602.221 | 1723.653 | 1908.663 | 2254.739 | 1673.281 | 2182.963 | 1909.181 | 2069.264 | 1867.991 | 1740.941 | 2270.276 | 2119.513 | 1850.824 | |
| std | 0.559227 | 60.05047 | 88.07985 | 173.5591 | 14.04957 | 223.369 | 126.0866 | 110.7665 | 95.72114 | 40.19961 | 120.5145 | 129.9046 | 59.98088 | |
| median | 1601.426 | 1604.046 | 1788.349 | 2109.349 | 1658.936 | 1832.652 | 1826.399 | 1913.913 | 1717.016 | 1667.383 | 2169.786 | 1916.318 | 1845.695 | |
| rank | 1 | 2 | 7 | 12 | 3 | 9 | 6 | 10 | 5 | 4 | 13 | 11 | 8 | |
| C17-F17 | mean | 1736.831 | 1747.593 | 1805.19 | 1874.792 | 1723.586 | 1869.789 | 1847.103 | 1780.828 | 1743.952 | 1762.775 | 1827.495 | 1756.302 | 1760.194 |
| best | 1730.528 | 1725.836 | 1771.453 | 1802.824 | 1720.806 | 1768.912 | 1768.602 | 1731.348 | 1730.034 | 1751.879 | 1749.789 | 1749.136 | 1756.835 | |
| worst | 1740.08 | 1759.723 | 1868.404 | 1931.055 | 1726.376 | 2008.081 | 1910.392 | 1803.882 | 1754.053 | 1773.479 | 2038.379 | 1763.5 | 1762.82 | |
| std | 4.42058 | 14.96716 | 45.71854 | 61.71314 | 2.675517 | 108.6038 | 70.05953 | 33.45616 | 10.06638 | 10.69879 | 140.7927 | 6.142389 | 2.707453 | |
| median | 1738.357 | 1752.406 | 1790.452 | 1882.645 | 1723.581 | 1851.081 | 1854.708 | 1794.041 | 1745.86 | 1762.871 | 1760.905 | 1756.286 | 1760.561 | |
| rank | 2 | 4 | 9 | 13 | 1 | 12 | 11 | 8 | 3 | 7 | 10 | 5 | 6 | |
| C17-F18 | mean | 1800.837 | 1841.26 | 13,800.96 | 58,981,931 | 1877.88 | 22,558.16 | 11,714.7 | 16,999.55 | 28,058.53 | 31,504.64 | 6693.863 | 23,325.42 | 13,609.97 |
| best | 1800.382 | 1813.308 | 7389.737 | 1,161,205 | 1855.98 | 7482.826 | 4795.665 | 3018.931 | 6287.974 | 25,593.54 | 2757.193 | 2958.931 | 3554.508 | |
| worst | 1801.23 | 1866.786 | 30,487.91 | 2.29 × 108 | 1925.128 | 38,281.51 | 18,261.51 | 28,200.17 | 43,428.11 | 39,435.71 | 11,618.87 | 43,550.36 | 19,687.74 | |
| std | 0.425238 | 23.52028 | 11,179.23 | 1.13 × 108 | 32.02221 | 16,834.36 | 5938.542 | 10,954.3 | 16,105.16 | 6367.121 | 3682.255 | 20,955.05 | 7046.641 | |
| median | 1800.869 | 1842.473 | 8663.093 | 2,922,614 | 1865.207 | 22,234.15 | 11,900.81 | 18,389.54 | 31,259.02 | 30,494.65 | 6199.696 | 23,396.19 | 15,598.82 | |
| rank | 1 | 2 | 7 | 13 | 3 | 9 | 5 | 8 | 11 | 12 | 4 | 10 | 6 | |
| C17-F19 | mean | 1900.699 | 1907.221 | 17,358.96 | 878,425.8 | 1988.542 | 69,005.95 | 90,424.78 | 2040.642 | 9820.11 | 4898.742 | 36,643.02 | 26,610.54 | 6492.073 |
| best | 1900.02 | 1901.521 | 11,828.97 | 259,265.4 | 1939.983 | 1970.087 | 2408.219 | 1915.575 | 1928.924 | 2053.504 | 19,411.47 | 2676.945 | 2235.907 | |
| worst | 1901.018 | 1917.582 | 22,721.81 | 1,443,245 | 2029.189 | 26,983.7 | 299,607.6 | 2164.619 | 14,822.13 | 13,254.21 | 55,613.04 | 82,298.3 | 10,459.09 | |
| std | 0.469791 | 7.145903 | 4482.402 | 563,481.2 | 37.74168 | 131,992.5 | 140,090.8 | 137.2124 | 5786.879 | 5570.514 | 16,664.04 | 37,542.78 | 3392.754 | |
| median | 1900.878 | 1904.891 | 17,442.54 | 905,596.3 | 1992.498 | 3535.02 | 29,841.65 | 2041.187 | 11,264.69 | 2143.627 | 35,773.79 | 10,733.45 | 6636.648 | |
| rank | 1 | 2 | 8 | 13 | 3 | 11 | 12 | 4 | 7 | 5 | 10 | 9 | 6 | |
| C17-F20 | mean | 2026.662 | 2034.642 | 2147.227 | 2292.086 | 2012.062 | 2331.222 | 2203.439 | 2070.82 | 2063.92 | 2077.176 | 2275.049 | 2181.152 | 2053.815 |
| best | 2013.865 | 2021.307 | 2076.582 | 2232.916 | 2000.995 | 2226.58 | 2194.177 | 2040.177 | 2040.405 | 2065.354 | 2190.026 | 2155.286 | 2038.374 | |
| worst | 2038.307 | 2044.877 | 2266.378 | 2360.461 | 2022.277 | 2500.44 | 2222.75 | 2152.489 | 2101.134 | 2088.349 | 2394.247 | 2215.298 | 2062.141 | |
| std | 13.07228 | 11.03511 | 84.87342 | 54.33571 | 10.64651 | 129.4526 | 13.04085 | 54.64582 | 26.46466 | 9.641058 | 98.96337 | 29.82688 | 10.95787 | |
| median | 2027.237 | 2036.192 | 2122.974 | 2287.484 | 2012.488 | 2298.934 | 2198.414 | 2045.306 | 2057.07 | 2077.501 | 2257.962 | 2177.013 | 2057.373 | |
| rank | 2 | 3 | 8 | 12 | 1 | 13 | 10 | 6 | 5 | 7 | 11 | 9 | 4 | |
| C17-F21 | mean | 2230.958 | 2255.077 | 2281.079 | 2353.337 | 2300.981 | 2301.662 | 2295.278 | 2291.145 | 2317.044 | 2306.962 | 2362.034 | 2327.466 | 2305.331 |
| best | 2200 | 2201.126 | 2203.848 | 2268.27 | 2276.646 | 2206.365 | 2238.668 | 2200.011 | 2305.236 | 2203.991 | 2342.354 | 2318.817 | 2228.495 | |
| worst | 2323.833 | 2308.936 | 2367.125 | 2393.638 | 2319.224 | 2398.948 | 2357.396 | 2332.814 | 2323.9 | 2348.473 | 2373.923 | 2335.569 | 2342.504 | |
| std | 61.91636 | 60.47791 | 89.24471 | 57.35467 | 18.20708 | 102.8811 | 62.9355 | 61.28073 | 8.151 | 69.14021 | 13.6687 | 8.239775 | 51.87787 | |
| median | 2200 | 2255.124 | 2276.672 | 2375.72 | 2304.028 | 2300.667 | 2292.523 | 2315.878 | 2319.52 | 2337.692 | 2365.929 | 2327.739 | 2325.162 | |
| rank | 1 | 2 | 3 | 12 | 6 | 7 | 5 | 4 | 10 | 9 | 13 | 11 | 8 | |
| C17-F22 | mean | 2266.732 | 2309.061 | 2307.691 | 3057.272 | 2301.898 | 2714.923 | 2319.448 | 2304.337 | 2311.086 | 2321.01 | 2361.062 | 2314.243 | 2319.245 |
| best | 2225.162 | 2304.818 | 2302.728 | 2789.931 | 2300.346 | 2334.84 | 2312.699 | 2303.309 | 2301.875 | 2314.271 | 2300 | 2300.685 | 2316.136 | |
| worst | 2300 | 2313.926 | 2319.708 | 3303.004 | 2306.031 | 3150.748 | 2327.601 | 2305.381 | 2325.309 | 2333.618 | 2445.235 | 2348.82 | 2324.026 | |
| std | 39.00767 | 3.810058 | 8.080836 | 227.6039 | 2.763264 | 410.991 | 6.415496 | 0.846824 | 11.19175 | 8.848757 | 72.99001 | 23.1002 | 3.37026 | |
| median | 2270.884 | 2308.75 | 2304.165 | 3068.076 | 2300.607 | 2687.051 | 2318.745 | 2304.328 | 2308.58 | 2318.076 | 2349.508 | 2303.733 | 2318.408 | |
| rank | 1 | 5 | 4 | 13 | 2 | 12 | 9 | 3 | 6 | 10 | 11 | 7 | 8 | |
| C17-F23 | mean | 2573.243 | 2573.12 | 2641.556 | 2691.514 | 2634.124 | 2671.267 | 2667.856 | 2655.194 | 2619.849 | 2645.742 | 2758.891 | 2647.616 | 2660.372 |
| best | 2300.003 | 2377.404 | 2624.533 | 2680.076 | 2609.415 | 2628.779 | 2650.955 | 2614.194 | 2610.113 | 2634.093 | 2688.971 | 2639.73 | 2638.96 | |
| worst | 2776.963 | 2646.48 | 2672.977 | 2714.233 | 2699.371 | 2720.796 | 2687.563 | 2759.569 | 2626.772 | 2655.608 | 2923.019 | 2660.513 | 2669.42 | |
| std | 198.8117 | 130.6378 | 21.45668 | 15.59204 | 43.6031 | 40.64644 | 15.13134 | 69.72568 | 8.312072 | 9.556135 | 109.9465 | 9.372923 | 14.49226 | |
| median | 2608.003 | 2634.299 | 2634.356 | 2685.874 | 2613.855 | 2667.747 | 2666.454 | 2623.507 | 2621.255 | 2646.634 | 2711.786 | 2645.111 | 2666.553 | |
| rank | 2 | 1 | 5 | 12 | 4 | 11 | 10 | 8 | 3 | 6 | 13 | 7 | 9 | |
| C17-F24 | mean | 2517.265 | 2628.48 | 2782.755 | 2853.722 | 2500 | 2779.188 | 2796.677 | 2743.409 | 2751.65 | 2765.308 | 2582.671 | 2775.772 | 2730.119 |
| best | 2513.188 | 2500.074 | 2762.559 | 2835.68 | 2500 | 2643.075 | 2767.067 | 2739.998 | 2734.241 | 2760.859 | 2500 | 2757.415 | 2523.272 | |
| worst | 2520.307 | 2751.903 | 2814.627 | 2869.479 | 2500 | 2870.335 | 2829 | 2752.217 | 2778.471 | 2769.47 | 2830.685 | 2790.675 | 2817.267 | |
| std | 2.967858 | 140.9207 | 22.81526 | 15.09578 | 0.000208 | 97.28497 | 25.56641 | 5.900329 | 19.28029 | 3.526871 | 165.3426 | 14.04169 | 138.498 | |
| median | 2517.783 | 2630.972 | 2776.916 | 2854.864 | 2500 | 2801.671 | 2795.32 | 2740.711 | 2746.944 | 2765.451 | 2500 | 2777.5 | 2789.97 | |
| rank | 2 | 4 | 11 | 13 | 1 | 10 | 12 | 6 | 7 | 8 | 3 | 9 | 5 | |
| C17-F25 | mean | 2862.423 | 2910.104 | 2973.2 | 3346.147 | 2980.623 | 3053.727 | 2933.158 | 2921.475 | 2938.295 | 2933.596 | 2932.066 | 2922.641 | 2953.708 |
| best | 2756.464 | 2897.743 | 2948.764 | 3256.737 | 2897.743 | 2949.278 | 2907.26 | 2897.897 | 2913.367 | 2913.96 | 2897.94 | 2898.714 | 2941.202 | |
| worst | 2897.743 | 2945.28 | 3024.363 | 3420.107 | 3093.93 | 3308.727 | 2957.932 | 2946.111 | 2947.324 | 2952.974 | 2943.456 | 2946.61 | 2964.225 | |
| std | 70.63967 | 23.4674 | 35.52094 | 69.42892 | 82.11035 | 171.5326 | 28.38164 | 27.07956 | 16.62652 | 20.74106 | 22.7505 | 27.11627 | 9.803424 | |
| median | 2897.743 | 2898.696 | 2959.837 | 3353.872 | 2965.409 | 2978.451 | 2933.72 | 2920.945 | 2946.245 | 2933.724 | 2943.434 | 2922.619 | 2954.702 | |
| rank | 1 | 2 | 10 | 13 | 11 | 12 | 6 | 3 | 8 | 7 | 5 | 4 | 9 | |
| C17-F26 | mean | 2754.982 | 2943.073 | 3351.736 | 4051.78 | 2825.003 | 3869.985 | 4044.972 | 3225.067 | 3169.235 | 3229.716 | 3254.197 | 2904.365 | 2947.415 |
| best | 2692.913 | 2800.885 | 3053.663 | 3728.9 | 2800.002 | 3472.705 | 3115.481 | 2900.125 | 2900.207 | 2912.962 | 2800 | 2800 | 2773.079 | |
| worst | 2800 | 3133.611 | 4095.261 | 4287.423 | 2900 | 4259.634 | 4697.221 | 4199.868 | 3803.627 | 3949.226 | 4356.049 | 3017.461 | 3125.39 | |
| std | 53.81419 | 167.603 | 500.4959 | 235.0147 | 49.99818 | 428.5773 | 676.5947 | 649.8669 | 424.9744 | 482.8277 | 738.0429 | 88.92102 | 164.2531 | |
| median | 2763.508 | 2918.898 | 3129.009 | 4095.399 | 2800.005 | 3873.799 | 4183.593 | 2900.139 | 2986.552 | 3028.338 | 2930.37 | 2900 | 2945.596 | |
| rank | 1 | 4 | 10 | 13 | 2 | 11 | 12 | 7 | 6 | 8 | 9 | 3 | 5 | |
| C17-F27 | mean | 3095.651 | 3155.778 | 3100.402 | 3198.815 | 3089.302 | 3181.938 | 3139.425 | 3092.936 | 3096.247 | 3117.018 | 3252.796 | 3139.581 | 3165.314 |
| best | 3093.138 | 3107.813 | 3094.856 | 3132.671 | 3088.978 | 3153.813 | 3092.968 | 3089.738 | 3092.809 | 3095.827 | 3241.634 | 3097.666 | 3121.59 | |
| worst | 3096.979 | 3188.745 | 3104.844 | 3327.562 | 3089.706 | 3211.238 | 3246.443 | 3095.297 | 3103.359 | 3177.422 | 3260.285 | 3190.464 | 3228.683 | |
| std | 1.711133 | 34.28873 | 5.10199 | 87.45869 | 0.366278 | 27.96866 | 71.87095 | 2.364432 | 4.918617 | 40.27925 | 8.221604 | 39.02481 | 45.27772 | |
| median | 3096.244 | 3163.277 | 3100.954 | 3167.514 | 3089.262 | 3181.35 | 3109.144 | 3093.354 | 3094.41 | 3097.412 | 3254.632 | 3135.097 | 3155.491 | |
| rank | 3 | 9 | 5 | 12 | 1 | 11 | 7 | 2 | 4 | 6 | 13 | 8 | 10 | |
| C17-F28 | mean | 3113.935 | 3177.694 | 3259.269 | 3768.182 | 3100 | 3451.178 | 3368.732 | 3199.942 | 3410.869 | 3341.745 | 3473.798 | 3320.885 | 3257.183 |
| best | 3100.15 | 3100.001 | 3100 | 3605.245 | 3100 | 3217.585 | 3174.627 | 3100.127 | 3383.764 | 3222.407 | 3413.862 | 3182.82 | 3148.201 | |
| worst | 3130.273 | 3217.332 | 3411.822 | 4044.617 | 3100 | 3652.941 | 3475.963 | 3383.75 | 3434.275 | 3412.081 | 3510.006 | 3412.053 | 3543.984 | |
| std | 16.04256 | 54.9365 | 130.9643 | 198.0034 | 7.84 × 10−5 | 178.7025 | 132.8519 | 134.107 | 20.73145 | 90.53327 | 42.51919 | 103.9299 | 191.9303 | |
| median | 3112.659 | 3196.722 | 3262.628 | 3711.433 | 3100 | 3467.092 | 3412.168 | 3157.946 | 3412.719 | 3366.247 | 3485.663 | 3344.334 | 3168.273 | |
| rank | 2 | 3 | 6 | 13 | 1 | 11 | 9 | 4 | 10 | 8 | 12 | 7 | 5 | |
| C17-F29 | mean | 3144.189 | 3217.825 | 3295.537 | 3338.434 | 3236.274 | 3303.244 | 3368.142 | 3262.597 | 3176.277 | 3218.734 | 3328.987 | 3276.182 | 3245.186 |
| best | 3136.956 | 3165.889 | 3189.716 | 3274.636 | 3152.918 | 3217.457 | 3258.78 | 3200.595 | 3160.275 | 3168.356 | 3236.83 | 3170.757 | 3192.605 | |
| worst | 3153.72 | 3349.479 | 3456.253 | 3373.345 | 3303.413 | 3456.374 | 3507.331 | 3310.243 | 3196.453 | 3242.962 | 3525.19 | 3365.159 | 3298.151 | |
| std | 7.730902 | 87.95734 | 124.8115 | 43.68494 | 64.01218 | 108.1025 | 103.1848 | 51.8816 | 15.04045 | 35.00934 | 132.3611 | 88.34778 | 44.37193 | |
| median | 3143.039 | 3177.967 | 3268.089 | 3352.879 | 3244.383 | 3269.572 | 3353.228 | 3269.775 | 3174.189 | 3231.809 | 3276.964 | 3284.406 | 3244.995 | |
| rank | 1 | 3 | 9 | 12 | 5 | 10 | 13 | 7 | 2 | 4 | 11 | 8 | 6 | |
| C17-F30 | mean | 3422.278 | 9969.272 | 284,851.7 | 11,811,886 | 3399.757 | 803,656.6 | 1,269,588 | 390,395.5 | 778,432.3 | 64,677.52 | 925,304.9 | 414,393.2 | 1,635,020 |
| best | 3418.586 | 4191.371 | 30,391.26 | 1,919,018 | 3395.483 | 20,061.19 | 228,475.9 | 15,899.26 | 6287.419 | 31,122.82 | 570,711.4 | 6603.207 | 562,734.7 | |
| worst | 3426.636 | 23,642.72 | 677,453.5 | 30,929,943 | 3406.359 | 1,678,417 | 3,019,728 | 1,479,145 | 2,878,412 | 108,709.8 | 1,272,741 | 821,874.7 | 3,725,142 | |
| std | 3.707695 | 9240.159 | 313,955.1 | 13,044,105 | 4.745776 | 901,821.7 | 1,308,347 | 726,003.4 | 1,402,476 | 37,893.81 | 286,632.7 | 469,896.9 | 1,490,657 | |
| median | 3421.945 | 6021.499 | 215,781 | 7,199,292 | 3398.593 | 758,074.1 | 915,074.1 | 33,268.63 | 114,515 | 59,438.72 | 928,883.5 | 414,547.5 | 1,126,102 | |
| rank | 2 | 3 | 5 | 13 | 1 | 9 | 11 | 6 | 8 | 4 | 10 | 7 | 12 | |
| Sum rank | 48 | 104 | 218 | 363 | 88 | 303 | 280 | 152 | 178 | 217 | 258 | 207 | 223 | |
| Mean rank | 1.655172 | 3.586207 | 7.517241 | 12.51724 | 3.034483 | 10.44828 | 9.655172 | 5.241379 | 6.137931 | 7.482759 | 8.896552 | 7.137931 | 7.689655 | |
| Total rank | 1 | 3 | 8 | 13 | 2 | 12 | 11 | 4 | 5 | 7 | 10 | 6 | 9 | |
| GAO | WSO | AVOA | RSA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C17-F1 | mean | 2965.641 | 5.61 × 109 | 96,586.16 | 4.35 × 1010 | 86,759 | 1.96 × 1010 | 1.67 × 109 | 505,100.8 | 1.3 × 109 | 5.71 × 109 | 32,552,559 | 4.2 × 108 | 1.92 × 108 |
| best | 105.4059 | 1.63 × 109 | 3775.707 | 3.92 × 1010 | 7863.15 | 1.85 × 1010 | 9.03 × 108 | 347,301.5 | 5.83 × 108 | 3.66 × 109 | 104.8029 | 6710.215 | 1.56 × 108 | |
| worst | 6756.63 | 8.1 × 109 | 363,121.4 | 4.78 × 1010 | 217,079.1 | 2.11 × 1010 | 2.61 × 109 | 809,113.2 | 1.73 × 109 | 1.01 × 1010 | 1.3 × 108 | 1.03 × 109 | 2.35 × 108 | |
| std | 2967.156 | 2.79 × 109 | 177,756.2 | 3.59 × 109 | 99,555.51 | 1.16 × 109 | 7.07 × 108 | 208,219 | 5.09 × 108 | 2.94 × 109 | 65,065,475 | 5.08 × 108 | 33,433,720 | |
| median | 2500.265 | 6.36 × 109 | 9723.769 | 4.34 × 1010 | 61,046.89 | 1.95 × 1010 | 1.59 × 109 | 431,994.3 | 1.45 × 109 | 4.55 × 109 | 29,684.6 | 3.26 × 108 | 1.89 × 108 | |
| rank | 1 | 10 | 3 | 13 | 2 | 12 | 9 | 4 | 8 | 11 | 5 | 7 | 6 | |
| C17-F3 | mean | 742.8731 | 57,920.14 | 52,951.58 | 77,211.19 | 789.4722 | 62,088.78 | 210,060.4 | 1624.497 | 65,596.78 | 35,343.56 | 103,615.2 | 44,565.91 | 149,306.7 |
| best | 513.4013 | 48,314.06 | 42,383.07 | 70,955.93 | 540.9163 | 44,706.74 | 154,454.5 | 726.4012 | 56,524.54 | 28,173.29 | 98,570.69 | 15,600.4 | 111,040.5 | |
| worst | 1141.321 | 81,363.34 | 63,002.48 | 82,275.53 | 1214.161 | 73,753.25 | 254,369.3 | 2486.051 | 79,838.62 | 44,107.98 | 108,512.9 | 88,268.11 | 182,709.5 | |
| std | 289.4161 | 15,759.39 | 8486.713 | 4692.112 | 309.0768 | 12,486.41 | 48,983.66 | 787.5179 | 10,425.3 | 7060.413 | 4665.24 | 32,704.73 | 37,175.16 | |
| median | 658.3851 | 51,001.57 | 53,210.38 | 77,806.65 | 701.4055 | 64,947.56 | 215,709 | 1642.768 | 63,011.97 | 34,546.48 | 103,688.7 | 37,197.58 | 151,738.5 | |
| rank | 1 | 7 | 6 | 10 | 2 | 8 | 13 | 3 | 9 | 4 | 11 | 5 | 12 | |
| C17-F4 | mean | 491.1351 | 837.3914 | 534.7466 | 13,336.8 | 509.4025 | 3117.836 | 848.5098 | 503.0084 | 661.7039 | 748.9401 | 624.7152 | 675.6909 | 735.2118 |
| best | 468.6344 | 725.9771 | 521.2662 | 7325.298 | 486.7772 | 868.6846 | 745.6112 | 488.4792 | 538.4455 | 668.2051 | 567.1673 | 499.2964 | 707.5575 | |
| worst | 512.6268 | 1058.681 | 549.2611 | 26,000.81 | 542.6027 | 5006.098 | 936.1373 | 517.528 | 754.3157 | 849.7198 | 752.0121 | 1076.728 | 761.2708 | |
| std | 18.01092 | 154.883 | 12.25453 | 8716.748 | 25.44004 | 1808.51 | 95.9796 | 15.12204 | 92.02884 | 80.56382 | 86.61078 | 271.7502 | 26.1284 | |
| median | 491.6396 | 782.4537 | 534.2294 | 10,010.54 | 504.115 | 3298.28 | 856.1454 | 503.0133 | 677.0271 | 738.9177 | 589.8407 | 563.3699 | 736.0095 | |
| rank | 1 | 10 | 4 | 13 | 3 | 12 | 11 | 2 | 6 | 9 | 5 | 7 | 8 | |
| C17-F5 | mean | 585.6623 | 644.6729 | 762.3586 | 917.5582 | 604.7663 | 884.8544 | 838.1558 | 594.886 | 619.214 | 731.8464 | 717.6456 | 674.1303 | 706.7469 |
| best | 582.592 | 616.8786 | 735.8031 | 894.1469 | 594.6117 | 796.6634 | 807.3832 | 579.0498 | 588.317 | 719.8893 | 702.9702 | 660.1907 | 686.0723 | |
| worst | 591.1983 | 687.2621 | 786.545 | 948.5521 | 629.3993 | 1049.042 | 900.7655 | 631.5963 | 646.9154 | 747.028 | 727.844 | 685.1118 | 720.6189 | |
| std | 4.041704 | 31.89212 | 22.97672 | 23.33033 | 16.49975 | 112.9375 | 43.3928 | 24.77706 | 26.59695 | 12.88375 | 11.92192 | 11.58915 | 14.84429 | |
| median | 584.4295 | 637.2754 | 763.5432 | 913.7669 | 597.527 | 846.8561 | 822.2373 | 584.4489 | 620.8117 | 730.2343 | 719.8841 | 675.6094 | 710.1482 | |
| rank | 1 | 5 | 10 | 13 | 3 | 12 | 11 | 2 | 4 | 9 | 8 | 6 | 7 | |
| C17-F6 | mean | 606.7204 | 637.6933 | 657.7141 | 685.7894 | 602.6388 | 682.6748 | 681.8045 | 622.9356 | 606.9295 | 643.482 | 658.2771 | 647.6491 | 631.1395 |
| best | 605.1486 | 633.5361 | 641.1756 | 679.3235 | 600.8551 | 671.0576 | 669.5708 | 615.361 | 604.7665 | 632.1329 | 653.7776 | 637.6309 | 630.2327 | |
| worst | 607.4042 | 644.45 | 667.264 | 688.9118 | 603.6152 | 695.4225 | 697.3843 | 628.5635 | 608.055 | 659.2047 | 662.2351 | 661.9608 | 632.1984 | |
| std | 1.05629 | 4.867309 | 11.70441 | 4.513135 | 1.261537 | 10.19072 | 12.05372 | 5.52481 | 1.476224 | 11.71106 | 3.483087 | 10.33603 | 0.976799 | |
| median | 607.1643 | 636.3935 | 661.2084 | 687.4612 | 603.0425 | 682.1095 | 680.1315 | 623.9089 | 607.4483 | 641.2951 | 658.5478 | 645.5023 | 631.0635 | |
| rank | 2 | 6 | 9 | 13 | 1 | 12 | 11 | 4 | 3 | 7 | 10 | 8 | 5 | |
| C17-F7 | mean | 820.8024 | 1089.043 | 1182.495 | 1395.582 | 854.1701 | 1325.59 | 1270.217 | 845.7349 | 881.1955 | 1068.159 | 949.8174 | 930.2214 | 984.2242 |
| best | 813.7177 | 995.5985 | 1059.063 | 1322.22 | 835.6078 | 1266.912 | 1240.955 | 833.2816 | 854.9027 | 1041.927 | 922.6795 | 868.6313 | 961.3759 | |
| worst | 827.619 | 1184.217 | 1248.513 | 1438.018 | 869.8823 | 1349.314 | 1329.113 | 860.5127 | 902.7389 | 1092.014 | 976.0323 | 992.083 | 1011.485 | |
| std | 6.229666 | 77.96311 | 88.58013 | 50.57298 | 17.30967 | 39.38619 | 40.02886 | 13.81518 | 19.79133 | 26.48992 | 26.05838 | 50.43402 | 23.39094 | |
| median | 820.9365 | 1088.178 | 1211.201 | 1411.044 | 855.5951 | 1343.067 | 1255.4 | 844.5726 | 883.5701 | 1069.347 | 950.2788 | 930.0856 | 982.0181 | |
| rank | 1 | 9 | 10 | 13 | 3 | 12 | 11 | 2 | 4 | 8 | 6 | 5 | 7 | |
| C17-F8 | mean | 877.6456 | 916.3291 | 978.0973 | 1133.102 | 901.0738 | 1140.52 | 1017.573 | 902.8113 | 902.7396 | 1038.544 | 966.9033 | 924.7556 | 993.9056 |
| best | 866.6767 | 887.4457 | 936.3094 | 1125.885 | 884.5957 | 1053.955 | 979.1085 | 863.1024 | 872.8583 | 1023.917 | 946.2582 | 887.5568 | 959.312 | |
| worst | 892.3077 | 942.7474 | 1015.905 | 1146.021 | 911.7185 | 1205.168 | 1089.695 | 917.7493 | 928.7814 | 1053.247 | 1004.96 | 976.1195 | 1021.463 | |
| std | 12.03403 | 24.70294 | 32.73762 | 8.879199 | 11.97364 | 64.32434 | 49.15648 | 26.50395 | 29.49711 | 12.9849 | 27.48129 | 43.15555 | 26.37234 | |
| median | 875.7989 | 917.5616 | 980.0876 | 1130.251 | 903.9904 | 1151.478 | 1000.745 | 915.1968 | 904.6592 | 1038.506 | 958.1975 | 917.6731 | 997.4234 | |
| rank | 1 | 5 | 8 | 12 | 2 | 13 | 10 | 4 | 3 | 11 | 7 | 6 | 9 | |
| C17-F9 | mean | 1165.65 | 6118.317 | 5285.631 | 10,677.51 | 1310.315 | 13,059.8 | 7819.018 | 6584.038 | 2283.474 | 4651.679 | 4123.625 | 3535.136 | 1379.814 |
| best | 1048.058 | 3812.091 | 4583.34 | 8370.654 | 1103.222 | 8931.468 | 6525.942 | 1125.644 | 1241.751 | 3242.499 | 3402.813 | 2404.144 | 1225.076 | |
| worst | 1337.301 | 7705.346 | 5737.959 | 12,502.83 | 1788.264 | 19,283.94 | 9256.488 | 11,627.78 | 3578.942 | 5837.91 | 4747.383 | 5875.287 | 1543.585 | |
| std | 130.0098 | 1697.137 | 556.4414 | 1715.525 | 325.1294 | 4428.538 | 1255.761 | 4991.033 | 982.1215 | 1196.281 | 613.4941 | 1593.562 | 137.1979 | |
| median | 1138.621 | 6477.916 | 5410.614 | 10,918.27 | 1174.887 | 12,011.89 | 7746.822 | 6791.365 | 2156.601 | 4763.153 | 4172.152 | 2930.556 | 1375.297 | |
| rank | 1 | 9 | 8 | 12 | 2 | 13 | 11 | 10 | 4 | 7 | 6 | 5 | 3 | |
| C17-F10 | mean | 3686.42 | 5097.435 | 5376.248 | 8165.39 | 3966.598 | 7339.579 | 7588.39 | 5284.051 | 4409.938 | 8329.399 | 4799.841 | 4968.059 | 6555.299 |
| best | 3486.984 | 4046.474 | 5210.865 | 8063.814 | 3600.688 | 6817.31 | 6285.025 | 4499.451 | 4009.121 | 8216.554 | 4150.098 | 4099.397 | 5554.57 | |
| worst | 3851.9 | 7007.736 | 5672.714 | 8257.688 | 4371.786 | 7861.61 | 8551.306 | 6421.91 | 5039.747 | 8519.895 | 5515.315 | 5511.443 | 7161.94 | |
| std | 189.092 | 1365.454 | 209.6517 | 80.84512 | 346.6865 | 426.3938 | 989.7159 | 811.0246 | 458.9879 | 131.8935 | 622.5674 | 670.3383 | 706.2351 | |
| median | 3703.398 | 4667.766 | 5310.706 | 8170.029 | 3946.959 | 7339.699 | 7758.615 | 5107.422 | 4295.441 | 8290.573 | 4766.976 | 5130.698 | 6752.344 | |
| rank | 1 | 6 | 8 | 12 | 2 | 10 | 11 | 7 | 3 | 13 | 4 | 5 | 9 | |
| C17-F11 | mean | 1176.86 | 1510.898 | 1316.714 | 7335.945 | 1209.9 | 3557.005 | 7893.704 | 1361.737 | 1683.239 | 1916.548 | 3506.789 | 1349.558 | 5022.123 |
| best | 1156.088 | 1422.613 | 1266.473 | 6658.404 | 1160.183 | 2246.748 | 3014.369 | 1289.335 | 1556.019 | 1726.753 | 3036.57 | 1298.049 | 3707.247 | |
| worst | 1200.911 | 1658.534 | 1437.228 | 8165.895 | 1237.557 | 4990.051 | 12,541.55 | 1445.222 | 1913.274 | 2124.247 | 4371.403 | 1394.515 | 7220.175 | |
| std | 18.56114 | 109.8245 | 81.3137 | 622.5615 | 34.54917 | 1165.235 | 3987.813 | 71.07825 | 158.4847 | 166.7819 | 629.2975 | 51.30956 | 1525.397 | |
| median | 1175.22 | 1481.223 | 1281.577 | 7259.74 | 1220.931 | 3495.611 | 8009.447 | 1356.196 | 1631.832 | 1907.597 | 3309.592 | 1352.835 | 4580.536 | |
| rank | 1 | 6 | 3 | 12 | 2 | 10 | 13 | 5 | 7 | 8 | 9 | 4 | 11 | |
| C17-F12 | mean | 85,555.87 | 25,949,230 | 10,375,592 | 1.32 × 1010 | 89,184.91 | 6.12 × 109 | 3.34 × 108 | 28,219,307 | 1.35 × 108 | 3.08 × 108 | 84,031,918 | 62,898,515 | 8,506,616 |
| best | 25,576.26 | 1,213,875 | 1,853,642 | 9.56 × 109 | 26,351.25 | 4.1 × 109 | 44,146,877 | 9,447,872 | 77,445,909 | 1.76 × 108 | 3,464,275 | 201,962.8 | 3,266,660 | |
| worst | 191,112.3 | 73,085,854 | 30,139,971 | 1.66 × 1010 | 200,262 | 8.4 × 109 | 8.95 × 108 | 71,379,451 | 2.74 × 108 | 4.53 × 108 | 1.6 × 108 | 2 × 108 | 12,986,786 | |
| std | 72,522.38 | 32,367,345 | 13,248,399 | 2.96 × 109 | 76,266.98 | 2.02 × 109 | 3.84 × 108 | 29,109,113 | 93,894,353 | 1.37 × 108 | 77,920,027 | 94,482,882 | 5,007,932 | |
| median | 62,767.48 | 14,748,596 | 4,754,377 | 1.34 × 1010 | 65,063.21 | 5.98 × 109 | 1.99 × 108 | 16,024,953 | 93,914,719 | 3.01 × 108 | 86,487,233 | 25,671,885 | 8,886,510 | |
| rank | 1 | 5 | 4 | 13 | 2 | 12 | 11 | 6 | 9 | 10 | 8 | 7 | 3 | |
| C17-F13 | mean | 1679.051 | 65,307.57 | 196,312.1 | 9.71 × 109 | 1663.41 | 1.62 × 109 | 1,218,387 | 169,962.5 | 107,891.8 | 1.05 × 108 | 34,883.97 | 1,140,606 | 9,001,402 |
| best | 1509.439 | 10,167.41 | 64,177.33 | 5.02 × 109 | 1496.899 | 9,775,852 | 190,877.6 | 61,271.86 | 80,912.23 | 73,593,614 | 29,396.19 | 27,575.57 | 2,238,017 | |
| worst | 1846.767 | 222,691.8 | 385,695.2 | 1.73 × 1010 | 1828.612 | 4.01 × 109 | 3,666,218 | 384,298.9 | 157,114.6 | 1.61 × 108 | 47,660 | 4,444,295 | 13,874,918 | |
| std | 138.2768 | 104,969.9 | 146,282.3 | 5.43 × 109 | 136.0205 | 1.9 × 109 | 1,643,068 | 146,086.5 | 34,141.59 | 38,514,757 | 8575.928 | 2,202,480 | 5,734,672 | |
| median | 1679.999 | 14,185.55 | 167,687.9 | 8.27 × 109 | 1664.065 | 1.23 × 109 | 508,225.6 | 117,139.5 | 96,770.14 | 92,927,829 | 31,239.85 | 45,277.58 | 9,946,336 | |
| rank | 2 | 4 | 7 | 13 | 1 | 12 | 9 | 6 | 5 | 11 | 3 | 8 | 10 | |
| C17-F14 | mean | 1445.686 | 5029.534 | 310,318 | 3,166,786 | 1506.721 | 944,929.1 | 1,449,403 | 8360.852 | 312,592.2 | 104,927.4 | 1,488,236 | 17,259.01 | 2,471,053 |
| best | 1439.939 | 1874.271 | 190,232.1 | 1,938,929 | 1490.417 | 43,337.9 | 831,823.4 | 5657.736 | 44,267.26 | 55,063.1 | 589,278.8 | 5235.579 | 1,453,463 | |
| worst | 1458.422 | 13,681.86 | 385,275.7 | 5,133,496 | 1521.294 | 1,897,719 | 1,916,237 | 11,991.96 | 1,004,397 | 156,646 | 2,344,763 | 25,836.68 | 3,521,220 | |
| std | 8.727275 | 5779.772 | 87,907.64 | 1,445,810 | 13.57225 | 1,040,334 | 532,404.3 | 3010.837 | 464,006.7 | 57,133.45 | 881,268.4 | 9220.18 | 1,034,268 | |
| median | 1442.191 | 2281.001 | 332,882.1 | 2,797,359 | 1507.587 | 919,329.9 | 1,524,776 | 7896.855 | 100,852.1 | 104,000.2 | 1,509,451 | 18,981.88 | 2,454,764 | |
| rank | 1 | 3 | 7 | 13 | 2 | 9 | 10 | 4 | 8 | 6 | 11 | 5 | 12 | |
| C17-F15 | mean | 1588.785 | 2511.297 | 45,133.53 | 3.52 × 108 | 1577.262 | 2.66 × 108 | 1,282,549 | 56,902.87 | 629,660.2 | 2,881,979 | 18,208.94 | 8283.199 | 986,862.4 |
| best | 1560.073 | 1925.339 | 26,535.07 | 2.27 × 108 | 1550.94 | 206,063.4 | 348,434.1 | 38,106.18 | 21,681.95 | 1,030,920 | 8605.33 | 2205.324 | 367,843.7 | |
| worst | 1624.03 | 3215.395 | 59,058.66 | 5.16 × 108 | 1612.701 | 1.03 × 109 | 2,123,573 | 96,468.19 | 2,007,235 | 4,849,628 | 22,396.17 | 15,491.71 | 1,359,201 | |
| std | 26.94309 | 601.986 | 14,789.58 | 1.28 × 108 | 26.55107 | 5.06 × 108 | 948,175.3 | 27,305.97 | 939,116.3 | 1,581,134 | 6440.914 | 5566.237 | 447,634.1 | |
| median | 1585.518 | 2452.228 | 47,470.2 | 3.32 × 108 | 1572.705 | 19,428,469 | 1,329,094 | 46,518.56 | 244,862 | 2,823,685 | 20,917.14 | 7717.879 | 1,110,203 | |
| rank | 2 | 3 | 6 | 13 | 1 | 12 | 10 | 7 | 8 | 11 | 5 | 4 | 9 | |
| C17-F16 | mean | 2157.589 | 2621.237 | 3504.832 | 5684.392 | 2411.321 | 3393.39 | 4006.918 | 2640.575 | 2419.743 | 3554.599 | 3382.484 | 2628.98 | 3048.951 |
| best | 2037.231 | 2230.767 | 3285.167 | 4800.654 | 2317.615 | 2965.308 | 3410.842 | 2505.972 | 2097.616 | 3255.021 | 3093.147 | 2304.9 | 2816.301 | |
| worst | 2228.757 | 2887.896 | 3750.51 | 7790.203 | 2527.256 | 3870.972 | 4848.864 | 2829.698 | 2713.406 | 4153.135 | 3550.905 | 3171.968 | 3285.631 | |
| std | 87.98998 | 277.6318 | 202.3443 | 1409.831 | 88.86949 | 388.2075 | 675.2394 | 145.1525 | 262.9818 | 420.4846 | 201.6026 | 375.8814 | 209.7332 | |
| median | 2182.184 | 2683.142 | 3491.826 | 5073.356 | 2400.206 | 3368.641 | 3883.982 | 2613.315 | 2433.974 | 3405.121 | 3442.941 | 2519.526 | 3046.937 | |
| rank | 1 | 4 | 10 | 13 | 2 | 9 | 12 | 6 | 3 | 11 | 8 | 5 | 7 | |
| C17-F17 | mean | 1871.456 | 2005.135 | 2453.821 | 10,597.65 | 1909.902 | 2475.363 | 2640.065 | 2224.961 | 2019.268 | 2264.054 | 2517.678 | 2212.343 | 2210.214 |
| best | 1831.18 | 1929.821 | 2053.719 | 3574.957 | 1846.274 | 2095.324 | 2481.288 | 1977.931 | 1914.84 | 2076.245 | 2318.989 | 1853.445 | 2079.712 | |
| worst | 1906.218 | 2165.417 | 2812.059 | 31,274.61 | 1967.102 | 2698.859 | 2719.99 | 2613.998 | 2144.187 | 2524.232 | 2753.058 | 2559.711 | 2400.234 | |
| std | 34.6833 | 108.3281 | 340.2979 | 13,785.77 | 50.24343 | 276.5611 | 108.6442 | 275.7001 | 97.66128 | 187.9479 | 216.4953 | 294.7102 | 143.1001 | |
| median | 1874.214 | 1962.652 | 2474.753 | 3770.522 | 1913.116 | 2553.635 | 2679.491 | 2153.958 | 2009.023 | 2227.87 | 2499.333 | 2218.109 | 2180.455 | |
| rank | 1 | 3 | 9 | 13 | 2 | 10 | 12 | 7 | 4 | 8 | 11 | 6 | 5 | |
| C17-F18 | mean | 1884.562 | 90,919.87 | 1,389,568 | 80,080,025 | 1950.484 | 2,428,856 | 8,909,556 | 517,529.6 | 1,541,680 | 3,526,422 | 240,227.7 | 198,781.2 | 5,054,893 |
| best | 1857.253 | 26,791.6 | 299,648 | 52,474,251 | 1905.935 | 122,389.8 | 852,143 | 118,784.1 | 100,638.4 | 1,433,012 | 99,249.04 | 68,546.56 | 1,605,174 | |
| worst | 1941.743 | 266,184.6 | 3,384,215 | 99,570,904 | 1995.318 | 5,934,470 | 21,737,586 | 984,081.8 | 3,883,479 | 6,498,024 | 404,021.8 | 406,261.2 | 7,996,236 | |
| std | 38.65561 | 117,099.7 | 1,452,873 | 20,359,139 | 39.19088 | 2,482,090 | 9,892,121 | 367,838.4 | 1,668,754 | 2,264,944 | 137,125 | 149,305.7 | 3,298,551 | |
| median | 1869.625 | 35,351.63 | 937,204.9 | 84,137,472 | 1950.342 | 1,829,282 | 6,524,247 | 483,626.2 | 1,091,301 | 3,087,327 | 228,820.1 | 160,158.4 | 5,309,081 | |
| rank | 1 | 3 | 7 | 13 | 2 | 9 | 12 | 6 | 8 | 10 | 5 | 4 | 11 | |
| C17-F19 | mean | 1950.499 | 3335.472 | 91,572.27 | 6.82 × 108 | 1933.262 | 1.54 × 109 | 14,619,971 | 1,421,627 | 276,846.2 | 5,881,714 | 160,121 | 14,630.44 | 485,098.8 |
| best | 1940.669 | 2030.43 | 14,294.76 | 4.52 × 108 | 1921.712 | 41,342,458 | 5,450,995 | 72,186 | 73,307.97 | 4,590,769 | 121,887.8 | 8707.597 | 171,700.8 | |
| worst | 1958.422 | 5624.54 | 144,128.7 | 8.89 × 108 | 1939.359 | 5.66 × 109 | 32,121,702 | 2,690,213 | 490,870.3 | 7,719,442 | 215,531.7 | 18,279.15 | 847,776 | |
| std | 7.641626 | 1581.365 | 55,588.55 | 2.04 × 108 | 7.885053 | 2.75 × 109 | 12,527,996 | 1,129,134 | 170,582.7 | 1,476,862 | 44,979.38 | 4145.322 | 295,341.7 | |
| median | 1951.452 | 2843.459 | 103,932.8 | 6.94 × 108 | 1935.989 | 2.35 × 108 | 10,453,594 | 1,462,055 | 271,603.3 | 5,608,322 | 151,532.2 | 15,767.5 | 460,459.2 | |
| rank | 2 | 3 | 5 | 12 | 1 | 13 | 11 | 9 | 7 | 10 | 6 | 4 | 8 | |
| C17-F20 | mean | 2218.661 | 2321.351 | 2605.831 | 3021.328 | 2217.587 | 2692.641 | 3100.685 | 2494.312 | 2542.181 | 2581.204 | 3143.322 | 2630.276 | 2434.181 |
| best | 2172.115 | 2237.079 | 2338.79 | 2931.969 | 2153.46 | 2543.643 | 3041.176 | 2281.39 | 2348.435 | 2429.147 | 2904.297 | 2303.65 | 2279.759 | |
| worst | 2243.554 | 2411.444 | 2769.648 | 3102.604 | 2258.994 | 2862.524 | 3229.713 | 2750.27 | 2743.214 | 2770.632 | 3264.54 | 3049.42 | 2518.498 | |
| std | 31.80584 | 86.94046 | 185.8798 | 72.53707 | 47.02587 | 131.2394 | 87.90274 | 219.2801 | 170.086 | 148.2222 | 167.9671 | 309.2781 | 106.8744 | |
| median | 2229.487 | 2318.44 | 2657.442 | 3025.37 | 2228.948 | 2682.199 | 3065.925 | 2472.794 | 2538.537 | 2562.518 | 3202.225 | 2584.017 | 2469.234 | |
| rank | 2 | 3 | 8 | 11 | 1 | 10 | 12 | 5 | 6 | 7 | 13 | 9 | 4 | |
| C17-F21 | mean | 2403.602 | 2455.2 | 2537.576 | 2671.54 | 2451.798 | 2596.489 | 2624.108 | 2464.941 | 2410.178 | 2548.284 | 2616.671 | 2454.839 | 2547.871 |
| best | 2355.743 | 2413.064 | 2515.265 | 2616.289 | 2381.612 | 2592.025 | 2590.862 | 2410.388 | 2368.967 | 2531.453 | 2609.737 | 2435.622 | 2516.184 | |
| worst | 2519.24 | 2491.044 | 2565.94 | 2732.226 | 2527.027 | 2603.754 | 2654.393 | 2581.813 | 2499.48 | 2569.234 | 2620.676 | 2473.227 | 2568.211 | |
| std | 77.40211 | 32.04248 | 25.48828 | 50.22592 | 66.98331 | 5.380629 | 34.4848 | 80.83535 | 60.28216 | 15.62456 | 5.011353 | 20.69181 | 22.45604 | |
| median | 2369.713 | 2458.347 | 2534.549 | 2668.822 | 2449.276 | 2595.088 | 2625.589 | 2433.781 | 2386.132 | 2546.225 | 2618.136 | 2455.253 | 2553.544 | |
| rank | 1 | 5 | 7 | 13 | 3 | 10 | 12 | 6 | 2 | 9 | 11 | 4 | 8 | |
| C17-F22 | mean | 2300.912 | 3420.821 | 6016.585 | 8171.962 | 2435.215 | 9572.129 | 8317.425 | 4285.503 | 5403.623 | 5171.095 | 7079.976 | 6949.861 | 2764.351 |
| best | 2300.607 | 2826.629 | 2312.315 | 7003.963 | 2423.944 | 9378.809 | 8097.021 | 2307.191 | 2612.314 | 3144.675 | 6045.552 | 5921.042 | 2717.751 | |
| worst | 2301.75 | 4314.511 | 7897.47 | 9708.421 | 2442.782 | 9901.309 | 8511.15 | 6555.56 | 7165.865 | 10,311.14 | 7937.065 | 7465.019 | 2810.387 | |
| std | 0.559452 | 694.6689 | 2514.73 | 1125.176 | 7.982382 | 241.5606 | 169.8963 | 2295.564 | 1953.817 | 3437.178 | 779.0079 | 696.902 | 43.96047 | |
| median | 2300.646 | 3271.073 | 6928.279 | 7987.733 | 2437.066 | 9504.198 | 8330.764 | 4139.63 | 5918.157 | 3614.284 | 7168.643 | 7206.692 | 2764.634 | |
| rank | 1 | 4 | 8 | 11 | 2 | 13 | 12 | 5 | 7 | 6 | 10 | 9 | 3 | |
| C17-F23 | mean | 2730.471 | 3215.293 | 2991.025 | 3298.124 | 2774.497 | 3300.559 | 3153.664 | 2764.772 | 2761.243 | 2948.592 | 3884.844 | 3000.973 | 2999.073 |
| best | 2691.157 | 3096.518 | 2917.382 | 3122.908 | 2725.57 | 3189.956 | 2894.171 | 2719.353 | 2741.353 | 2935.222 | 3783.583 | 2871.538 | 2969.309 | |
| worst | 2806.588 | 3435.044 | 3070.868 | 3564.946 | 2861.898 | 3476.408 | 3302.155 | 2829.515 | 2784.476 | 2959.248 | 4063.831 | 3136.266 | 3021.883 | |
| std | 52.25212 | 154.119 | 62.77169 | 188.2427 | 62.9445 | 122.8799 | 183.8363 | 49.77987 | 21.54624 | 10.06741 | 123.1166 | 135.0474 | 22.61169 | |
| median | 2712.069 | 3164.806 | 2987.924 | 3252.32 | 2755.26 | 3267.937 | 3209.165 | 2755.109 | 2759.571 | 2949.949 | 3845.981 | 2998.045 | 3002.549 | |
| rank | 1 | 10 | 6 | 11 | 4 | 12 | 9 | 3 | 2 | 5 | 13 | 8 | 7 | |
| C17-F24 | mean | 2880.63 | 3259.635 | 3118.144 | 3406.151 | 2907.605 | 3367.598 | 3213.517 | 2920.928 | 2939.198 | 3069.087 | 3490.473 | 3079.172 | 3259.002 |
| best | 2809.71 | 2786.217 | 3088.489 | 3350.229 | 2894.427 | 3255.152 | 3129.533 | 2904.032 | 2880.904 | 3027.837 | 3441.392 | 2972.894 | 3201.354 | |
| worst | 2905.164 | 3458.681 | 3144.198 | 3521.157 | 2932.457 | 3464.58 | 3330.582 | 2949.794 | 3057.925 | 3100.627 | 3538.605 | 3258.899 | 3339.613 | |
| std | 47.28496 | 317.1838 | 24.04771 | 77.69108 | 16.93679 | 96.09487 | 84.67507 | 20.89335 | 83.43905 | 36.60211 | 50.18546 | 132.8847 | 59.21531 | |
| median | 2903.824 | 3396.821 | 3119.945 | 3376.608 | 2901.769 | 3375.33 | 3196.976 | 2914.944 | 2908.981 | 3073.941 | 3490.948 | 3042.448 | 3247.52 | |
| rank | 1 | 10 | 7 | 12 | 2 | 11 | 8 | 3 | 4 | 5 | 13 | 6 | 9 | |
| C17-F25 | mean | 2887.905 | 3057.34 | 2938.705 | 5015.747 | 3023.956 | 3466.492 | 3091.419 | 2918.07 | 3043.638 | 3150.619 | 2979.409 | 2922.536 | 3114.78 |
| best | 2883.986 | 2987.626 | 2901.366 | 4384.512 | 2890.06 | 3332.176 | 3007.826 | 2888.094 | 3016.157 | 3077.278 | 2952.687 | 2897.356 | 3072.749 | |
| worst | 2891.073 | 3119.548 | 2992.388 | 6638.173 | 3089.805 | 3555.045 | 3148.11 | 2971.717 | 3100.885 | 3309.807 | 3001.141 | 2942.863 | 3167.876 | |
| std | 2.933447 | 54.63684 | 40.01622 | 1085.805 | 92.49693 | 95.26176 | 59.59986 | 36.8016 | 39.61029 | 109.4526 | 25.09905 | 20.98515 | 39.36999 | |
| median | 2888.281 | 3061.094 | 2930.532 | 4520.151 | 3057.98 | 3489.374 | 3104.87 | 2906.234 | 3028.756 | 3107.696 | 2981.904 | 2924.962 | 3109.247 | |
| rank | 1 | 8 | 4 | 13 | 6 | 12 | 9 | 2 | 7 | 11 | 5 | 3 | 10 | |
| C17-F26 | mean | 2932.162 | 5792.551 | 7112.147 | 10,557.33 | 2983.243 | 8157.806 | 8582.206 | 5399.407 | 5149.351 | 6657.232 | 8101.595 | 5167.292 | 4370.346 |
| best | 2887.387 | 4244.662 | 6655.78 | 9945.558 | 2900.722 | 7082.87 | 8242.061 | 4798.038 | 4796.37 | 6422.825 | 7075.436 | 3618.219 | 4134.387 | |
| worst | 3041.078 | 7147.491 | 7659.167 | 10,890.32 | 3093.717 | 9406.218 | 8827.586 | 5939.213 | 5750.536 | 6899.911 | 8712.858 | 6951.381 | 4757.879 | |
| std | 72.85753 | 1451.242 | 494.8827 | 426.6739 | 91.42468 | 1081.231 | 249.6577 | 480.6749 | 416.3707 | 201.3114 | 711.6418 | 1720.183 | 269.6611 | |
| median | 2900.091 | 5889.027 | 7066.82 | 10,696.71 | 2969.267 | 8071.068 | 8629.589 | 5430.189 | 5025.249 | 6653.096 | 8309.043 | 5049.785 | 4294.56 | |
| rank | 1 | 7 | 9 | 13 | 2 | 11 | 12 | 6 | 4 | 8 | 10 | 5 | 3 | |
| C17-F27 | mean | 3212.022 | 3534.047 | 3250.925 | 3962.572 | 3298.17 | 3496.265 | 3494.564 | 3236.161 | 3231.383 | 3307.425 | 5546.879 | 3314.279 | 3512.212 |
| best | 3195.721 | 3352.081 | 3233.082 | 3632.976 | 3229.714 | 3407.483 | 3358.285 | 3206.726 | 3216.532 | 3261.276 | 5064.765 | 3233.265 | 3430.828 | |
| worst | 3222.351 | 3740.069 | 3276.898 | 4849.667 | 3327.071 | 3595.241 | 3813.546 | 3291.474 | 3237.716 | 3362.276 | 6389.948 | 3428.025 | 3576.987 | |
| std | 11.44629 | 170.5496 | 18.90387 | 592.3009 | 45.85752 | 89.95278 | 214.1498 | 37.69573 | 9.949078 | 41.58353 | 595.0611 | 83.74264 | 66.5742 | |
| median | 3215.009 | 3522.018 | 3246.861 | 3683.823 | 3317.949 | 3491.168 | 3403.213 | 3223.222 | 3235.643 | 3303.073 | 5366.403 | 3297.913 | 3520.516 | |
| rank | 1 | 11 | 4 | 12 | 5 | 9 | 8 | 3 | 2 | 6 | 13 | 7 | 10 | |
| C17-F28 | mean | 3302.861 | 3546.371 | 3285.617 | 5932.203 | 3221.572 | 4134.473 | 3494.575 | 3246.338 | 3424.764 | 3666.029 | 3691.62 | 3314.008 | 3627.343 |
| best | 3254.533 | 3469.684 | 3267.981 | 5550.003 | 3202.752 | 3948.554 | 3413.911 | 3220.435 | 3327.276 | 3536.347 | 3489.929 | 3218.089 | 3539.319 | |
| worst | 3362.259 | 3604.984 | 3309.976 | 6420.009 | 3252.13 | 4537.352 | 3626.089 | 3280.945 | 3471.122 | 3927.693 | 4071.334 | 3392.695 | 3680.818 | |
| std | 45.60338 | 57.61343 | 20.43417 | 429.9783 | 22.14656 | 274.6438 | 92.90273 | 29.05037 | 67.28895 | 179.3281 | 270.4868 | 85.12066 | 65.47424 | |
| median | 3297.327 | 3555.407 | 3282.255 | 5879.401 | 3215.704 | 4025.993 | 3469.15 | 3241.986 | 3450.329 | 3600.038 | 3602.609 | 3322.625 | 3644.617 | |
| rank | 4 | 8 | 3 | 13 | 1 | 12 | 7 | 2 | 6 | 10 | 11 | 5 | 9 | |
| C17-F29 | mean | 3560.528 | 3889.112 | 4479.882 | 5919.125 | 3675.267 | 5353.658 | 5306.859 | 4004.846 | 4025.698 | 4349.599 | 5280.968 | 4218.421 | 4293.605 |
| best | 3490.151 | 3584.398 | 4313.698 | 4909.763 | 3542.422 | 5046.272 | 4630.521 | 3646.815 | 3755.698 | 4237.691 | 4911.985 | 3808.914 | 4140.599 | |
| worst | 3611.59 | 4163.922 | 4589.025 | 6982.043 | 3823.444 | 5681.6 | 5963.599 | 4220.558 | 4263.946 | 4591.053 | 5740.286 | 4865.097 | 4443.725 | |
| std | 54.88954 | 237.8957 | 118.5045 | 847.9831 | 117.1898 | 292.4008 | 561.9992 | 254.8365 | 247.9412 | 166.1172 | 389.2517 | 452.4459 | 158.5205 | |
| median | 3570.185 | 3904.065 | 4508.403 | 5892.347 | 3667.601 | 5343.38 | 5316.658 | 4076.006 | 4041.574 | 4284.826 | 5235.801 | 4099.837 | 4295.048 | |
| rank | 1 | 3 | 9 | 13 | 2 | 12 | 11 | 4 | 5 | 8 | 10 | 6 | 7 | |
| C17-F30 | mean | 7742.305 | 179,776.5 | 1,269,100 | 3.38 × 109 | 7679.743 | 60,768,716 | 32,463,948 | 3,549,182 | 6,660,655 | 28,705,893 | 2,737,261 | 99,984.65 | 992,091.5 |
| best | 6292.261 | 22,142.69 | 383,760.8 | 2.52 × 109 | 6248.998 | 13,475,637 | 9,172,643 | 1,518,619 | 5,440,686 | 19,256,126 | 1,341,586 | 17,644.38 | 266,268.1 | |
| worst | 9407.668 | 459,312.2 | 2,509,342 | 4.45 × 109 | 9322.427 | 1.18 × 108 | 54,601,906 | 7,489,490 | 8,069,479 | 44,576,334 | 4,164,795 | 290,688.3 | 2,346,103 | |
| std | 1283.647 | 191,970.5 | 921,032.2 | 9.95 × 108 | 1265.365 | 43,813,635 | 23,396,892 | 2,771,717 | 1,213,043 | 11,210,682 | 1,399,201 | 129,358 | 925,161.8 | |
| median | 7634.645 | 118,825.6 | 1,091,648 | 3.27 × 109 | 7573.774 | 55,723,914 | 33,040,622 | 2,594,310 | 6,566,227 | 25,495,556 | 2,721,331 | 45,802.95 | 677,997.4 | |
| rank | 2 | 4 | 6 | 13 | 1 | 12 | 11 | 8 | 9 | 10 | 7 | 3 | 5 | |
| Sum rank | 38 | 174 | 195 | 361 | 64 | 324 | 309 | 141 | 157 | 249 | 244 | 166 | 217 | |
| Mean rank | 1.310345 | 6 | 6.724138 | 12.44828 | 2.206897 | 11.17241 | 10.65517 | 4.862069 | 5.413793 | 8.586207 | 8.413793 | 5.724138 | 7.482759 | |
| Total rank | 1 | 6 | 7 | 13 | 2 | 12 | 11 | 3 | 4 | 10 | 9 | 5 | 8 | |
| GAO | WSO | AVOA | RSA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C17-F1 | mean | 14,553.5 | 2.52 × 1010 | 12,002,919 | 9.79 × 1010 | 8,328,904 | 4.48 × 1010 | 8.24 × 109 | 4,657,064 | 1.08 × 1010 | 2.21 × 1010 | 1.79 × 1010 | 4.29 × 109 | 7.95 × 10 9 |
| best | 11,540.48 | 1.57 × 1010 | 4,081,906 | 8.7 × 1010 | 5,232,940 | 2.5 × 1010 | 4.23 × 109 | 4,298,380 | 4.37 × 109 | 1.9 × 1010 | 1.41 × 1010 | 1.63 × 109 | 4.59 × 10 9 | |
| worst | 18,594.35 | 2.97 × 1010 | 30,750,213 | 1.1 × 1011 | 11,801,662 | 5.49 × 1010 | 1.26 × 1010 | 5,533,840 | 1.52 × 1010 | 3.05 × 1010 | 2.24 × 1010 | 7.79 × 109 | 1.06 × 10 10 | |
| std | 2982.205 | 6.44 × 109 | 12,587,166 | 9.2 × 109 | 2,866,669 | 1.37 × 1010 | 3.45 × 109 | 589,793.4 | 4.81 × 109 | 5.58 × 109 | 3.67 × 109 | 2.59 × 109 | 2.62 × 10 9 | |
| median | 14,039.59 | 2.77 × 1010 | 6,589,779 | 9.76 × 1010 | 8,140,507 | 4.96 × 1010 | 8.08 × 109 | 4,398,018 | 1.19 × 1010 | 1.95 × 1010 | 1.76 × 1010 | 3.87 × 109 | 8.29 × 10 9 | |
| rank | 1 | 11 | 4 | 13 | 3 | 12 | 7 | 2 | 8 | 10 | 9 | 5 | 6 | |
| C17-F3 | mean | 17,143.34 | 105,001.8 | 165,391.3 | 175,765.8 | 17,990.03 | 104,172.2 | 256,160.7 | 47,195.6 | 132,271.4 | 96,821.27 | 198,666.9 | 189,249.9 | 295,551.5 |
| best | 14,095.85 | 82,400.47 | 158,593.6 | 163,034.7 | 14,878.3 | 83,456.61 | 210,096.4 | 38,369.45 | 116,283.4 | 93,036.56 | 180,821 | 150,802.2 | 233,017.7 | |
| worst | 20,804.6 | 125,914.7 | 184,587.1 | 189,487.5 | 21,815.8 | 126,814.1 | 322,045.9 | 57,270.58 | 143,028.9 | 101,964.3 | 206,713.8 | 224,403.1 | 349,331.2 | |
| std | 2926.758 | 18,840.53 | 12,801.09 | 10,869.46 | 3124.825 | 21,210.52 | 48,332.24 | 9608.053 | 12,184.08 | 3778.635 | 12,005.96 | 33,873.53 | 47,753.24 | |
| median | 16,836.45 | 105,845.9 | 159,192.3 | 175,270.5 | 17,633.01 | 103,209.1 | 246,250.2 | 46,571.19 | 134,886.7 | 96,142.11 | 203,566.5 | 190,897.1 | 299,928.5 | |
| rank | 1 | 6 | 8 | 9 | 2 | 5 | 12 | 3 | 7 | 4 | 11 | 10 | 13 | |
| C17-F4 | mean | 555.9812 | 3922.348 | 668.4579 | 24,374.45 | 581.4708 | 8455.619 | 2572.61 | 568.3633 | 1370.46 | 2192.35 | 3087.765 | 1068.314 | 1748.455 |
| best | 533.964 | 2936.023 | 594.6227 | 18,669.14 | 558.7435 | 5004.304 | 1750.866 | 541.0309 | 1262.635 | 1176.683 | 2613.392 | 672.7473 | 1533.777 | |
| worst | 583.575 | 5345.994 | 743.6194 | 26,403.46 | 624.1394 | 12,427.34 | 3482.656 | 620.8195 | 1468.316 | 4872.366 | 3772.885 | 1687.916 | 2035.707 | |
| std | 24.79482 | 1017.416 | 64.95445 | 3805.576 | 30.36838 | 3309.715 | 712.975 | 37.57762 | 86.09834 | 1789.646 | 561.3773 | 475.3013 | 222.7235 | |
| median | 553.193 | 3703.689 | 667.7947 | 26,212.6 | 571.5002 | 8195.416 | 2528.459 | 555.8013 | 1375.445 | 1360.176 | 2982.392 | 956.2969 | 1712.169 | |
| rank | 1 | 11 | 4 | 13 | 3 | 12 | 9 | 2 | 6 | 8 | 10 | 5 | 7 | |
| C17-F5 | mean | 714.1266 | 802.4974 | 901.4393 | 1166.905 | 759.3991 | 1220.453 | 1069.522 | 804.4484 | 760.2189 | 1044.878 | 846.7404 | 815.0165 | 947.1408 |
| best | 681.6816 | 764.8877 | 884.7392 | 1146.007 | 709.5423 | 1156.624 | 1000.118 | 709.3516 | 745.8673 | 1019.009 | 830.3242 | 751.8603 | 890.8249 | |
| worst | 764.4116 | 869.0053 | 924.423 | 1209.405 | 814.5279 | 1274.963 | 1176.858 | 1007.618 | 789.3257 | 1089.369 | 879.0758 | 927.8653 | 977.0538 | |
| std | 38.65027 | 48.52667 | 17.12741 | 28.97798 | 49.22487 | 54.88339 | 81.04347 | 140.6692 | 19.80102 | 30.78979 | 21.95627 | 77.49311 | 40.3683 | |
| median | 705.2067 | 788.0483 | 898.2975 | 1156.103 | 756.7632 | 1225.113 | 1050.556 | 750.412 | 752.8413 | 1035.567 | 838.7808 | 790.1702 | 960.3423 | |
| rank | 1 | 4 | 8 | 12 | 2 | 13 | 11 | 5 | 3 | 10 | 7 | 6 | 9 | |
| C17-F6 | mean | 611.2095 | 657.5897 | 660.8563 | 698.9123 | 638.1769 | 695.1733 | 700.1844 | 638.8012 | 621.6137 | 668.3177 | 663.8223 | 650.4509 | 646.5533 |
| best | 609.7563 | 648.602 | 654.2488 | 696.8387 | 626.523 | 684.2707 | 696.5667 | 629.1829 | 617.123 | 658.1773 | 657.2969 | 645.7214 | 638.6868 | |
| worst | 612.6181 | 671.2048 | 667.3298 | 700.4788 | 649.3564 | 703.0004 | 705.4916 | 651.6013 | 627.9207 | 678.5366 | 669.878 | 658.6062 | 655.6196 | |
| std | 1.225993 | 10.35935 | 5.352443 | 1.667333 | 9.503886 | 8.42664 | 4.266327 | 9.615536 | 4.92571 | 9.30888 | 5.167045 | 5.886562 | 6.951281 | |
| median | 611.2318 | 655.276 | 660.9234 | 699.1658 | 638.4141 | 696.711 | 699.3397 | 637.2102 | 620.7055 | 668.2784 | 664.0572 | 648.7379 | 645.9535 | |
| rank | 1 | 7 | 8 | 12 | 3 | 11 | 13 | 4 | 2 | 10 | 9 | 6 | 5 | |
| C17-F7 | mean | 1025.881 | 1721.176 | 1662.322 | 1979.496 | 1061.397 | 1869.978 | 1952.088 | 1122.436 | 1175.817 | 1555.17 | 1489.926 | 1294.5 | 1340.208 |
| best | 1000.164 | 1616.331 | 1507.457 | 1926.181 | 1041.209 | 1737.332 | 1856.546 | 1041.995 | 1075.823 | 1497.521 | 1409.155 | 1193.467 | 1306.069 | |
| worst | 1057.179 | 1834.234 | 1814.065 | 2015.581 | 1070.832 | 2015.128 | 2040.279 | 1205.173 | 1337.112 | 1655.586 | 1569.725 | 1373.801 | 1369.909 | |
| std | 24.35707 | 112.7002 | 141.5327 | 40.63313 | 13.62912 | 119.6811 | 90.20122 | 66.70626 | 112.9076 | 74.73389 | 70.13841 | 77.66052 | 26.6831 | |
| median | 1023.091 | 1717.069 | 1663.884 | 1988.111 | 1066.772 | 1863.727 | 1955.764 | 1121.288 | 1145.167 | 1533.787 | 1490.412 | 1305.365 | 1342.426 | |
| rank | 1 | 10 | 9 | 13 | 2 | 11 | 12 | 3 | 4 | 8 | 7 | 5 | 6 | |
| C17-F8 | mean | 995.6338 | 1199.155 | 1187.135 | 1475.118 | 1047.464 | 1481.246 | 1287.263 | 1091.472 | 1048.355 | 1328.305 | 1167.883 | 1138.155 | 1266.072 |
| best | 983.0873 | 1157.66 | 1104.657 | 1442.163 | 1029.584 | 1373.77 | 1255.154 | 1019.53 | 978.9894 | 1293.787 | 1142.263 | 1056.075 | 1220.748 | |
| worst | 1013.932 | 1243.697 | 1273.021 | 1518.174 | 1071.654 | 1617.331 | 1339.21 | 1149.662 | 1111.758 | 1373.885 | 1229.819 | 1194.697 | 1319.763 | |
| std | 14.65683 | 42.67117 | 70.45638 | 31.82365 | 20.59496 | 105.9277 | 37.15687 | 54.45485 | 55.44733 | 36.7254 | 41.67991 | 60.67326 | 47.71119 | |
| median | 992.7582 | 1197.632 | 1185.432 | 1470.067 | 1044.309 | 1466.941 | 1277.345 | 1098.349 | 1051.337 | 1322.774 | 1149.726 | 1150.925 | 1261.889 | |
| rank | 1 | 8 | 7 | 12 | 2 | 13 | 10 | 4 | 3 | 11 | 6 | 5 | 9 | |
| C17-F9 | mean | 3508.77 | 28,911.38 | 14,239.23 | 36,756.45 | 4405.262 | 40,698.39 | 27,774.69 | 16,769.14 | 9682.165 | 21,676.54 | 11,727.2 | 10,563.16 | 12,676.64 |
| best | 2346.403 | 23,517.24 | 12,456.48 | 35,478.1 | 2454.814 | 25,476.68 | 20,652.83 | 6137.118 | 4087.611 | 13,214.73 | 9840.69 | 7224.243 | 10,662.33 | |
| worst | 4108.611 | 33,883.7 | 16,745.19 | 38,570.8 | 7193.914 | 49,967.28 | 36,542.78 | 25,502.92 | 19,344.7 | 24,926.32 | 13,118.38 | 15,004.49 | 18,314.94 | |
| std | 802.4975 | 5435.387 | 1862.83 | 1513.347 | 2006.523 | 10,591.15 | 6557.658 | 8003.097 | 6849.259 | 5651.353 | 1499.96 | 3310.715 | 3760.074 | |
| median | 3790.033 | 29,122.29 | 13,877.63 | 36,488.46 | 3986.16 | 43,674.8 | 26,951.58 | 17,718.27 | 7648.173 | 24,282.56 | 11,974.87 | 10,011.96 | 10,864.65 | |
| rank | 1 | 11 | 7 | 12 | 2 | 13 | 10 | 8 | 3 | 9 | 5 | 4 | 6 | |
| C17-F10 | mean | 5767.859 | 8659.802 | 8739.107 | 14,657.63 | 6478.647 | 12,244.83 | 12,459.21 | 8006.238 | 7533.535 | 14,827.86 | 8542.661 | 7895.046 | 12,313.92 |
| best | 5366.673 | 6200.492 | 8098.813 | 13,640.76 | 5496.015 | 11,283.26 | 11,117.82 | 6719.282 | 6798.832 | 14,503.11 | 8163.447 | 6177.5 | 11,437.17 | |
| worst | 6104.604 | 14,286.54 | 9637.659 | 15,377.43 | 7166.545 | 12,768.73 | 13,353.26 | 9065.671 | 7954.246 | 15,217.52 | 9146.476 | 9662.261 | 13,740.61 | |
| std | 335.1443 | 3810.289 | 691.5653 | 853.5516 | 711.7507 | 657.4143 | 1024.224 | 968.6225 | 546.4662 | 334.1279 | 446.1412 | 1429.865 | 1006.377 | |
| median | 5800.079 | 7076.087 | 8609.978 | 14,806.17 | 6626.014 | 12,463.65 | 12,682.88 | 8120 | 7690.53 | 14,795.4 | 8430.361 | 7870.211 | 12,038.94 | |
| rank | 1 | 7 | 8 | 12 | 2 | 9 | 11 | 5 | 3 | 13 | 6 | 4 | 10 | |
| C17-F11 | mean | 1263.481 | 6096.42 | 1626.641 | 20,780.93 | 1282.969 | 11,745.2 | 6389.68 | 1437.742 | 5679.881 | 4963.278 | 16,289.4 | 2583.926 | 24,961.02 |
| best | 1232.308 | 3844.968 | 1430.406 | 19,217.1 | 1246.454 | 5214.658 | 4045.917 | 1275.734 | 3552.577 | 3857.778 | 11,845.87 | 1564.863 | 14,294.87 | |
| worst | 1283.051 | 8972.834 | 1722.341 | 22,088.57 | 1308.7 | 19,864.68 | 10,059.87 | 1576.555 | 8211.372 | 6388.745 | 19,867.07 | 4627.567 | 50,045.37 | |
| std | 23.13329 | 2347.125 | 132.8201 | 1396.216 | 26.16396 | 6685.04 | 2575.006 | 132.8975 | 2117.415 | 1050.716 | 3574.724 | 1389.351 | 16,806.27 | |
| median | 1269.283 | 5783.94 | 1676.908 | 20,909.02 | 1288.361 | 10,950.73 | 5726.466 | 1449.339 | 5477.787 | 4803.294 | 16,722.33 | 2071.638 | 17,751.93 | |
| rank | 1 | 8 | 4 | 12 | 2 | 10 | 9 | 3 | 7 | 6 | 11 | 5 | 13 | |
| C17-F12 | mean | 3,759,630 | 3.08 × 109 | 63,614,775 | 8.18 × 1010 | 15,933,816 | 2.13 × 1010 | 1.83 × 109 | 92,770,078 | 4.76 × 108 | 4.26 × 109 | 2.06 × 109 | 2.03 × 109 | 1.93 × 10 8 |
| best | 3,120,877 | 6.07 × 108 | 25,515,066 | 6.07 × 1010 | 3,269,247 | 1.42 × 1010 | 1.01 × 109 | 66,570,980 | 68,637,499 | 2.05 × 109 | 1.07 × 109 | 1.29 × 108 | 1.54 × 10 8 | |
| worst | 5,026,634 | 6.48 × 109 | 1.03 × 108 | 1.01 × 1011 | 29,463,946 | 2.83 × 1010 | 2.57 × 109 | 1.43 × 108 | 8.17 × 108 | 6.51 × 109 | 2.67 × 109 | 4.68 × 109 | 2.25 × 10 8 | |
| std | 867,286.6 | 2.54 × 109 | 32,204,702 | 1.87 × 1010 | 11,215,199 | 7.09 × 109 | 7.33 × 108 | 33,904,696 | 3.49 × 108 | 1.88 × 109 | 6.94 × 108 | 1.97 × 109 | 35,866,307 | |
| median | 3,445,505 | 2.61 × 109 | 63,038,260 | 8.28 × 1010 | 15,501,035 | 2.14 × 1010 | 1.87 × 109 | 80,957,677 | 5.1 × 108 | 4.24 × 109 | 2.25 × 109 | 1.66 × 109 | 1.98 × 10 8 | |
| rank | 1 | 10 | 3 | 13 | 2 | 12 | 7 | 4 | 6 | 11 | 9 | 8 | 5 | |
| C17-F13 | mean | 20,543.43 | 7.13 × 108 | 141,800.9 | 3.67 × 1010 | 21,237.92 | 7.59 × 109 | 2.11 × 108 | 247,156.6 | 2.47 × 108 | 5.88 × 108 | 11,242,163 | 6.16 × 108 | 26,005,027 |
| best | 15,376.38 | 19,099,120 | 78,023.61 | 2.48 × 1010 | 16,056.18 | 5.03 × 109 | 1.2 × 108 | 194,166.2 | 2.17 × 108 | 3.8 × 108 | 45,145.04 | 26,221.25 | 12,818,531 | |
| worst | 27,661.65 | 1.43 × 109 | 224,553 | 5.03 × 1010 | 28,607.16 | 1.12 × 1010 | 3.77 × 108 | 308,694.8 | 3.16 × 108 | 7.42 × 108 | 32,680,141 | 2.46 × 109 | 54,704,377 | |
| std | 5265.513 | 7.92 × 108 | 65,454.08 | 1.08 × 1010 | 5377.922 | 2.79 × 109 | 1.18 × 108 | 52,336.76 | 46,903,226 | 1.59 × 108 | 15,396,915 | 1.23 × 109 | 19,804,620 | |
| median | 19,567.85 | 7.03 × 108 | 132,313.6 | 3.59 × 1010 | 20,144.16 | 7.08 × 109 | 1.75 × 108 | 242,882.7 | 2.27 × 108 | 6.14 × 108 | 6,121,682 | 149,734 | 18,248,601 | |
| rank | 1 | 11 | 3 | 13 | 2 | 12 | 7 | 4 | 8 | 9 | 5 | 10 | 6 | |
| C17-F14 | mean | 1597.307 | 600,173.8 | 2,218,022 | 34,471,586 | 1678.635 | 5,093,227 | 4,192,458 | 279,639.4 | 1,793,375 | 1,267,223 | 4,946,211 | 240,948.6 | 11,575,392 |
| best | 1562.632 | 185,224.1 | 110,573.9 | 12,465,227 | 1639.592 | 3,093,492 | 1,735,897 | 207,111.7 | 212,073.5 | 812,745.7 | 1,782,005 | 74,420.19 | 4,799,281 | |
| worst | 1617.968 | 1,430,924 | 6,732,015 | 79,830,753 | 1725.082 | 9,688,319 | 7,361,760 | 412,568.6 | 5,453,517 | 2,266,987 | 8,569,881 | 688,466.4 | 14,217,124 | |
| std | 24.00143 | 575,089 | 3,063,340 | 31,173,317 | 35.3101 | 3,084,397 | 2,727,676 | 96,387.31 | 2,463,724 | 679,539.8 | 2,853,620 | 299,315.4 | 4,540,074 | |
| median | 1604.315 | 392,273.7 | 1,014,750 | 22,795,182 | 1674.933 | 3,795,549 | 3,836,088 | 249,438.6 | 753,954.7 | 994,580.2 | 4,716,480 | 100,453.9 | 13,642,580 | |
| rank | 1 | 5 | 8 | 13 | 2 | 11 | 9 | 4 | 7 | 6 | 10 | 3 | 12 | |
| C17-F15 | mean | 2278.122 | 1,918,426 | 56,625.99 | 5.26 × 109 | 2259.208 | 1.83 × 109 | 14,219,521 | 194,386.3 | 1.31 × 108 | 66,651,092 | 2.11 × 108 | 17,821,961 | 12,226,060 |
| best | 2183.166 | 13,016.53 | 35,125.41 | 4.45 × 109 | 2168.222 | 1.08 × 109 | 4,542,309 | 46,119.64 | 54,273.51 | 17,897,687 | 12,105.45 | 8042.893 | 3,671,989 | |
| worst | 2463.577 | 7,144,595 | 86,519.19 | 7.14 × 109 | 2443.118 | 3.61 × 109 | 32,284,842 | 458,767.1 | 4.32 × 108 | 1.36 × 108 | 8.44 × 108 | 71,236,824 | 20,439,957 | |
| std | 126.4823 | 3,491,216 | 21,600.89 | 1.27 × 109 | 125.174 | 1.21 × 109 | 12,437,330 | 192,355 | 2.05 × 108 | 51,513,207 | 4.22 × 108 | 35,609,909 | 9,283,812 | |
| median | 2232.872 | 258,046.4 | 52,429.69 | 4.73 × 109 | 2212.746 | 1.31 × 109 | 10,025,466 | 136,329.3 | 45,952,682 | 56,383,284 | 21,026.03 | 21,487.86 | 12,396,147 | |
| rank | 2 | 5 | 3 | 13 | 1 | 12 | 7 | 4 | 10 | 9 | 11 | 8 | 6 | |
| C17-F16 | mean | 2523.35 | 3142.7 | 4273.055 | 7676.857 | 2524.843 | 5581.054 | 7341.921 | 3652.628 | 3194.303 | 5172.976 | 3615.108 | 3531.027 | 3790.935 |
| best | 2248.739 | 2865.182 | 3720.895 | 6111.503 | 2235.572 | 4317.16 | 6419.835 | 3314.145 | 2513.073 | 4937.946 | 3348.535 | 3133.521 | 3640.193 | |
| worst | 2849.941 | 3306.808 | 4619.853 | 9059.164 | 2831.915 | 6921.292 | 9089.87 | 3852.877 | 3580.118 | 5485.408 | 3817.586 | 4237.175 | 3978.839 | |
| std | 248.4592 | 191.8193 | 386.0529 | 1416.194 | 249.8163 | 1340.965 | 1189.901 | 237.443 | 472.1091 | 246.3174 | 233.5936 | 495.8781 | 140.9372 | |
| median | 2497.361 | 3199.406 | 4375.736 | 7768.381 | 2515.943 | 5542.882 | 6928.989 | 3721.744 | 3342.01 | 5134.274 | 3647.156 | 3376.706 | 3772.355 | |
| rank | 1 | 3 | 9 | 13 | 2 | 11 | 12 | 7 | 4 | 10 | 6 | 5 | 8 | |
| C17-F17 | mean | 2707.987 | 2980.2 | 3569.067 | 12,417.77 | 2739.995 | 8694.875 | 3849.098 | 3174.238 | 2960.83 | 4242.461 | 3788.797 | 3327.726 | 3554.822 |
| best | 2573.454 | 2826.593 | 3286.215 | 8706.209 | 2669.604 | 3961.759 | 3373.148 | 2874.678 | 2707.394 | 3907.595 | 3039.955 | 3129.702 | 2939.71 | |
| worst | 2872.458 | 3175.288 | 4177.956 | 16,710.1 | 2782.582 | 20,149.38 | 4113.558 | 3356.334 | 3450.413 | 4386.915 | 4362.678 | 3628.122 | 3915.836 | |
| std | 123.7582 | 167.3508 | 419.5302 | 3897.022 | 49.62537 | 7728.123 | 326.2007 | 214.7127 | 335.2494 | 225.1485 | 649.6461 | 218.2146 | 425.0624 | |
| median | 2693.018 | 2959.46 | 3406.048 | 12,127.38 | 2753.897 | 5334.178 | 3954.842 | 3232.971 | 2842.756 | 4337.667 | 3876.278 | 3276.54 | 3681.87 | |
| rank | 1 | 4 | 8 | 13 | 2 | 12 | 10 | 5 | 3 | 11 | 9 | 6 | 7 | |
| C17-F18 | mean | 15,216.7 | 1,365,955 | 7,779,299 | 2.14 × 108 | 15,772.3 | 25,039,603 | 63,038,334 | 2,399,810 | 4,407,874 | 6,375,307 | 6,213,809 | 688,185.2 | 9,525,765 |
| best | 6740.69 | 322,064.1 | 1,590,180 | 91,874,841 | 7191.04 | 2,203,537 | 20,713,331 | 647,337.2 | 1,422,857 | 2,612,645 | 2,233,690 | 405,300.8 | 3,454,730 | |
| worst | 29,018.95 | 3,065,480 | 10,900,590 | 3.18 × 108 | 29,848.79 | 58,520,893 | 1.17 × 108 | 4,811,940 | 7,682,387 | 10,961,389 | 13,622,036 | 1,012,622 | 22,724,999 | |
| std | 9963.231 | 1,292,998 | 4,375,760 | 95,362,782 | 10,116.69 | 24,185,228 | 39,852,952 | 1,806,889 | 2,901,609 | 3,444,641 | 5,332,511 | 295,490.3 | 8,953,276 | |
| median | 12,553.59 | 1,038,138 | 9,313,213 | 2.24 × 108 | 13,024.68 | 19,716,992 | 57,291,737 | 2,069,982 | 4,263,127 | 5,963,596 | 4,499,756 | 667,408.8 | 5,961,666 | |
| rank | 1 | 4 | 9 | 13 | 2 | 11 | 12 | 5 | 6 | 8 | 7 | 3 | 10 | |
| C17-F19 | mean | 2293.943 | 5,336,995 | 217,953.8 | 5.72 × 109 | 2277.617 | 1.71 × 109 | 6,512,698 | 3,003,168 | 615,864.9 | 52,611,378 | 339,457.9 | 14,857.85 | 1,227,039 |
| best | 2066.933 | 10,891.04 | 70,004.28 | 3.11 × 109 | 2054.853 | 7,948,977 | 775,698.7 | 387,452.4 | 129,486.9 | 28,462,150 | 167,430.6 | 9629.5 | 432,756.2 | |
| worst | 2609.612 | 21,264,994 | 401,879.8 | 8.28 × 109 | 2595.726 | 4.84 × 109 | 14,711,626 | 6,128,420 | 980,956.3 | 69,545,870 | 512,814.9 | 17,868.24 | 2,255,991 | |
| std | 261.3956 | 10,618,678 | 154,738.8 | 2.17 × 109 | 261.1937 | 2.28 × 109 | 6,365,958 | 2,718,342 | 394,103.7 | 17,554,774 | 151,196.4 | 3865.085 | 866,614.6 | |
| median | 2249.614 | 36,046.9 | 199,965.6 | 5.74 × 109 | 2229.945 | 9.91 × 108 | 5,281,734 | 2,748,399 | 676,508.2 | 56,218,747 | 338,793.1 | 15,966.83 | 1,109,704 | |
| rank | 2 | 9 | 4 | 13 | 1 | 12 | 10 | 8 | 6 | 11 | 5 | 3 | 7 | |
| C17-F20 | mean | 2513.866 | 3018.161 | 3872.479 | 4208.551 | 2653.995 | 3777.941 | 3867.633 | 3270.537 | 3050.774 | 3581.661 | 3631.741 | 3607.874 | 2793.115 |
| best | 2409.529 | 2704.176 | 3404.592 | 3915.663 | 2423.39 | 3344.414 | 3676.826 | 3068.736 | 2867.013 | 3097.769 | 3256.531 | 3122.52 | 2397.439 | |
| worst | 2774.471 | 3568.838 | 4297.382 | 4450.765 | 2826.888 | 4059.381 | 4083.729 | 3457.862 | 3422.019 | 3990.042 | 4149.514 | 4033.223 | 3117.089 | |
| std | 174.2807 | 387.3215 | 451.866 | 222.377 | 182.1288 | 333.4411 | 169.5709 | 187.6622 | 255.2918 | 434.451 | 387.0701 | 393.726 | 305.5244 | |
| median | 2435.732 | 2899.815 | 3893.97 | 4233.888 | 2682.851 | 3853.985 | 3854.989 | 3277.775 | 2957.032 | 3619.417 | 3560.461 | 3637.876 | 2828.967 | |
| rank | 1 | 4 | 12 | 13 | 2 | 10 | 11 | 6 | 5 | 7 | 9 | 8 | 3 | |
| C17-F21 | mean | 2531.346 | 2696.004 | 2776.417 | 3098.527 | 2534.35 | 3032.349 | 3039.543 | 2554.921 | 2511.337 | 2851.206 | 2879.907 | 2627.296 | 2766.011 |
| best | 2463.183 | 2582.783 | 2688.564 | 3029.315 | 2514.342 | 2940.893 | 3024.393 | 2461.154 | 2476.733 | 2807.612 | 2788.54 | 2584.675 | 2734.224 | |
| worst | 2606.947 | 2846.445 | 2883.738 | 3183.214 | 2583.284 | 3134.125 | 3059.281 | 2633.857 | 2563.453 | 2927.856 | 2960.196 | 2651.486 | 2811.403 | |
| std | 60.93002 | 117.389 | 88.55727 | 64.69718 | 32.75536 | 90.8218 | 14.51323 | 86.35629 | 36.99942 | 54.08873 | 71.85458 | 31.25404 | 32.51022 | |
| median | 2527.628 | 2677.395 | 2766.683 | 3090.79 | 2519.886 | 3027.189 | 3037.249 | 2562.336 | 2502.581 | 2834.677 | 2885.445 | 2636.512 | 2759.209 | |
| rank | 2 | 6 | 8 | 13 | 3 | 11 | 12 | 4 | 1 | 9 | 10 | 5 | 7 | |
| C17-F22 | mean | 2317.943 | 10,515.57 | 9803.788 | 16,741.71 | 2454.545 | 14,725.05 | 15,009.33 | 8671.283 | 10,896.57 | 16,462.37 | 11,782.89 | 10,731.79 | 8677.909 |
| best | 2313.226 | 8675.879 | 8893.579 | 15,427.18 | 2415.808 | 13,406.04 | 13,752.53 | 7356.599 | 8490.107 | 15,962.22 | 10,801.92 | 8673.583 | 3773.449 | |
| worst | 2325.262 | 12,098.55 | 10,695.35 | 17,493.49 | 2477.608 | 15,661.92 | 17,232.92 | 10,096.67 | 15,253.11 | 17,147.82 | 12,737.27 | 12,193.1 | 13,745.36 | |
| std | 5.169666 | 1606.074 | 736.9605 | 907.5177 | 27.54961 | 992.7556 | 1638.035 | 1163.704 | 2983.966 | 496.1757 | 803.0463 | 1540.999 | 5393.703 | |
| median | 2316.642 | 10,643.92 | 9813.11 | 17,023.08 | 2462.383 | 14,916.13 | 14,525.93 | 8615.933 | 9921.535 | 16,369.72 | 11,796.17 | 11,030.25 | 8596.412 | |
| rank | 1 | 6 | 5 | 13 | 2 | 10 | 11 | 3 | 8 | 12 | 9 | 7 | 4 | |
| C17-F23 | mean | 2881.727 | 3704.484 | 3392.839 | 3986.698 | 3001.709 | 3953.136 | 3708.9 | 3024.442 | 3027.14 | 3336.887 | 4966.53 | 3421.272 | 3401.637 |
| best | 2862.544 | 3619.689 | 3259.762 | 3827.63 | 2935.197 | 3720.133 | 3372.6 | 3000.34 | 2979.011 | 3299.768 | 4857.063 | 3323.802 | 3353.64 | |
| worst | 2913.196 | 3884.09 | 3547.399 | 4145.13 | 3064.136 | 4185.486 | 4086.312 | 3040.22 | 3075.466 | 3403.308 | 5023.978 | 3480.774 | 3485.028 | |
| std | 23.70954 | 123.6058 | 119.1142 | 130.9662 | 55.49515 | 198.0927 | 295.5549 | 19.24806 | 39.38033 | 45.64418 | 75.0103 | 67.75003 | 60.1368 | |
| median | 2875.584 | 3657.078 | 3382.098 | 3987.017 | 3003.752 | 3953.461 | 3688.345 | 3028.604 | 3027.041 | 3322.235 | 4992.539 | 3440.257 | 3383.94 | |
| rank | 1 | 9 | 6 | 12 | 2 | 11 | 10 | 3 | 4 | 5 | 13 | 8 | 7 | |
| C17-F24 | mean | 3038.787 | 4028.224 | 3679.079 | 4130.017 | 3146.731 | 4133.094 | 3877.877 | 3172.559 | 3222.95 | 3477.013 | 4262.321 | 3738.539 | 3806.884 |
| best | 3027.411 | 3823.858 | 3574.61 | 4017.829 | 3102.63 | 3875.483 | 3746.093 | 3115.712 | 3119.397 | 3454.19 | 4030.677 | 3605.374 | 3716.276 | |
| worst | 3060.731 | 4152.973 | 3759.596 | 4253.614 | 3198.408 | 4287.089 | 4065.552 | 3232.535 | 3367.039 | 3517.98 | 4424.4 | 3876.766 | 3921.35 | |
| std | 15.66003 | 149.4732 | 77.96719 | 111.4572 | 41.67069 | 178.3878 | 134.3584 | 54.22258 | 112.9554 | 29.21587 | 172.8838 | 111.256 | 85.83412 | |
| median | 3033.503 | 4068.032 | 3691.055 | 4124.313 | 3142.943 | 4184.901 | 3849.931 | 3170.995 | 3202.681 | 3467.94 | 4297.103 | 3736.008 | 3794.955 | |
| rank | 1 | 10 | 6 | 11 | 2 | 12 | 9 | 3 | 4 | 5 | 13 | 7 | 8 | |
| C17-F25 | mean | 3104.831 | 4915.11 | 3209.755 | 13,225.84 | 3136.75 | 6281.772 | 4139.484 | 3122.747 | 3999.108 | 4985.944 | 4236.589 | 3220.005 | 4438.616 |
| best | 3044.755 | 3892.863 | 3148.285 | 11,160.31 | 3102.92 | 5338.942 | 3508.061 | 3073.832 | 3882.131 | 4335.129 | 4097.495 | 3108.568 | 4286.427 | |
| worst | 3234.692 | 6364.993 | 3270.78 | 15,046.82 | 3206.335 | 7123.475 | 4551.233 | 3182.13 | 4122.234 | 5844.257 | 4494.352 | 3400.709 | 4641.84 | |
| std | 87.52477 | 1144.015 | 52.82601 | 1623.073 | 47.17018 | 867.0227 | 452.2604 | 53.32415 | 134.017 | 636.2107 | 183.2711 | 126.1991 | 148.101 | |
| median | 3069.938 | 4701.292 | 3209.978 | 13,348.12 | 3118.874 | 6332.336 | 4249.321 | 3117.513 | 3996.034 | 4882.195 | 4177.254 | 3185.372 | 4413.098 | |
| rank | 1 | 10 | 4 | 13 | 3 | 12 | 7 | 2 | 6 | 11 | 8 | 5 | 9 | |
| C17-F26 | mean | 3777.101 | 11,784.36 | 11,856.67 | 16,041.26 | 4830.795 | 14,285.51 | 15,000.12 | 5856.907 | 7468.213 | 9127.18 | 13,003.15 | 7521.003 | 7269.406 |
| best | 3003.992 | 10,212.35 | 11,426.28 | 14,539.68 | 3279.002 | 12,496.3 | 13,779.67 | 5489.546 | 6929.365 | 7084.218 | 12,617.15 | 3631.76 | 6595.043 | |
| worst | 5801.625 | 13,060.54 | 12,428.67 | 17,195.64 | 6671.97 | 15,802.77 | 17,606.04 | 6441.522 | 7971.815 | 10,346.31 | 14,125.17 | 11,719.42 | 8427.224 | |
| std | 1351.612 | 1181.164 | 483.5606 | 1116.16 | 1803.358 | 1363.859 | 1798.803 | 446.8491 | 447.8152 | 1472.329 | 748.1652 | 3669.866 | 858.8363 | |
| median | 3151.393 | 11,932.28 | 11,785.87 | 16,214.85 | 4686.104 | 14,421.48 | 14,307.38 | 5748.281 | 7485.836 | 9539.094 | 12,635.14 | 7366.417 | 7027.678 | |
| rank | 1 | 8 | 9 | 13 | 2 | 11 | 12 | 3 | 5 | 7 | 10 | 6 | 4 | |
| C17-F27 | mean | 3346.281 | 4472.026 | 3786.595 | 5452.493 | 3327.914 | 5182.676 | 4227.945 | 3352.327 | 3611.413 | 3851.884 | 8321.828 | 3939.635 | 4390.701 |
| best | 3271.559 | 4447.754 | 3592.211 | 4995.852 | 3246.939 | 4586.378 | 4036.159 | 3266.144 | 3538.938 | 3636.979 | 8118.6 | 3602.202 | 4114.634 | |
| worst | 3437.758 | 4503.122 | 3971.15 | 6241.117 | 3409.39 | 6827.707 | 4419.18 | 3459.869 | 3763.451 | 4242.572 | 8560.416 | 4205.319 | 4525.522 | |
| std | 75.91211 | 27.94272 | 170.6025 | 550.8051 | 68.06794 | 1097.226 | 205.0116 | 84.48407 | 102.5436 | 269.3932 | 215.9268 | 249.6819 | 193.2365 | |
| median | 3337.904 | 4468.614 | 3791.51 | 5286.501 | 3327.664 | 4658.31 | 4228.22 | 3341.647 | 3571.632 | 3763.992 | 8304.147 | 3975.511 | 4461.325 | |
| rank | 2 | 10 | 5 | 12 | 1 | 11 | 8 | 3 | 4 | 6 | 13 | 7 | 9 | |
| C17-F28 | mean | 3306.815 | 6158.968 | 3569.591 | 10,561.72 | 3346.278 | 7427.443 | 4944.849 | 3307.979 | 4701.016 | 5398.659 | 6125.631 | 3938.473 | 5225.484 |
| best | 3283.8 | 5408.513 | 3476.534 | 10,041.12 | 3295.493 | 5461.916 | 4735.216 | 3275.069 | 4029.702 | 4696.886 | 5596.048 | 3523.454 | 4981.759 | |
| worst | 3327.69 | 6870.392 | 3696.643 | 11,014.54 | 3375.563 | 8220.855 | 5168.117 | 3326.009 | 5536.271 | 6090.742 | 6562.538 | 4583.801 | 5552.983 | |
| std | 19.22675 | 604.3744 | 92.23122 | 410.2028 | 36.42665 | 1318.663 | 177.6043 | 22.52966 | 649.6887 | 667.5129 | 490.3233 | 452.8714 | 282.6891 | |
| median | 3307.886 | 6178.482 | 3552.594 | 10,595.6 | 3357.028 | 8013.501 | 4938.032 | 3315.42 | 4619.046 | 5403.504 | 6171.97 | 3823.319 | 5183.596 | |
| rank | 1 | 11 | 4 | 13 | 3 | 12 | 7 | 2 | 6 | 9 | 10 | 5 | 8 | |
| C17-F29 | mean | 4205.854 | 5355.257 | 5319.407 | 49,098.17 | 4174.684 | 8686.831 | 7487.548 | 4850.099 | 4854.946 | 6606.589 | 7835.099 | 5294.549 | 6323.442 |
| best | 3962.386 | 5001.086 | 4933.961 | 15,947.98 | 3927.712 | 7669.135 | 6357.075 | 4589.776 | 4704.047 | 6391.657 | 7520.297 | 4554.894 | 5749.058 | |
| worst | 4527.838 | 5546.877 | 6107.551 | 118,514.9 | 4502.275 | 10,907.45 | 9208.731 | 5255.592 | 5139.24 | 6864.138 | 8483.466 | 5688.888 | 6721.22 | |
| std | 255.5898 | 243.3059 | 534.441 | 47,222.41 | 261.5826 | 1524.258 | 1215.726 | 285.2666 | 201.9437 | 211.9127 | 438.8483 | 515.1086 | 438.2013 | |
| median | 4166.596 | 5436.532 | 5118.058 | 30,964.87 | 4134.375 | 8085.372 | 7192.193 | 4777.515 | 4788.248 | 6585.281 | 7668.318 | 5467.208 | 6411.745 | |
| rank | 2 | 7 | 6 | 13 | 1 | 12 | 10 | 3 | 4 | 9 | 11 | 5 | 8 | |
| C17-F30 | mean | 1,618,080 | 48,059,983 | 21,703,729 | 5.82 × 109 | 1,780,483 | 1.03 × 109 | 3.21 × 108 | 71,527,639 | 1.65 × 108 | 3.21 × 108 | 2.11 × 108 | 5,128,712 | 68,405,882 |
| best | 1,424,086 | 17,155,339 | 15,119,492 | 4.73 × 109 | 1,414,569 | 1.63 × 108 | 1.89 × 108 | 35,867,005 | 1.3 × 108 | 2.34 × 108 | 1.61 × 108 | 1,827,095 | 51,385,322 | |
| worst | 1,836,627 | 1.01 × 108 | 25,861,408 | 6.83 × 109 | 2,524,633 | 2.59 × 109 | 6.72 × 108 | 1.02 × 108 | 1.91 × 108 | 4.15 × 108 | 3.12 × 108 | 9,012,936 | 1.08 × 10 8 | |
| std | 218,934.4 | 36,779,462 | 5,053,503 | 8.63 × 108 | 521,656.5 | 1.07 × 109 | 2.34 × 108 | 29,861,371 | 26,124,552 | 79,867,440 | 69,575,182 | 3,196,822 | 26,878,690 | |
| median | 1,605,803 | 36,826,199 | 22,917,007 | 5.86 × 109 | 1,591,365 | 6.78 × 108 | 2.12 × 108 | 74,309,997 | 1.69 × 108 | 3.18 × 108 | 1.86 × 108 | 4,837,409 | 56,976,059 | |
| rank | 1 | 5 | 4 | 13 | 2 | 12 | 10 | 7 | 8 | 11 | 9 | 3 | 6 | |
| Sum rank | 34 | 220 | 183 | 363 | 60 | 326 | 285 | 119 | 151 | 255 | 258 | 167 | 218 | |
| Mean rank | 1.172414 | 7.586207 | 6.310345 | 12.51724 | 2.068966 | 11.24138 | 9.827586 | 4.103448 | 5.206897 | 8.793103 | 8.896552 | 5.758621 | 7.517241 | |
| Total rank | 1 | 8 | 6 | 13 | 2 | 12 | 11 | 3 | 4 | 9 | 10 | 5 | 7 | |
| GAO | WSO | AVOA | RSA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C17-F1 | mean | 20,912.44 | 1.22 × 1011 | 7.46 × 109 | 2.51 × 1011 | 3.74 × 108 | 1.34 × 1011 | 6.7 × 1010 | 73,581,256 | 5.68 × 1010 | 9.84 × 1010 | 1.4 × 1011 | 2.75 × 1010 | 6.05 × 10 10 |
| best | 16,541.69 | 1.13 × 1011 | 2.3 × 109 | 2.35 × 1011 | 2.41 × 108 | 1.17 × 1011 | 6.23 × 1010 | 64,783,107 | 3.7 × 1010 | 8.32 × 1010 | 1.32 × 1011 | 1.52 × 1010 | 5.23 × 10 10 | |
| worst | 27,717.39 | 1.4 × 1011 | 1.49 × 1010 | 2.57 × 1011 | 5.14 × 108 | 1.51 × 1011 | 7.38 × 1010 | 92,516,372 | 7.17 × 1010 | 1.15 × 1011 | 1.59 × 1011 | 4.11 × 1010 | 6.66 × 10 10 | |
| std | 4828.014 | 1.26 × 1010 | 5.76 × 109 | 1.06 × 1010 | 1.19 × 108 | 1.37 × 1010 | 4.92 × 109 | 12,778,487 | 1.48 × 1010 | 1.31 × 1010 | 1.3 × 1010 | 1.1 × 1010 | 6.37 × 10 9 | |
| median | 19,695.34 | 1.19 × 1011 | 6.33 × 109 | 2.56 × 1011 | 3.71 × 108 | 1.34 × 1011 | 6.59 × 1010 | 68,512,773 | 5.92 × 1010 | 9.77 × 1010 | 1.34 × 1011 | 2.68 × 1010 | 6.15 × 10 10 | |
| rank | 1 | 10 | 4 | 13 | 3 | 11 | 8 | 2 | 6 | 9 | 12 | 5 | 7 | |
| C17-F3 | mean | 167,218.3 | 311,047.9 | 458,990.6 | 337,914.4 | 171,436.5 | 374,031.9 | 967,631.7 | 518,487.4 | 420,776.6 | 335,622.8 | 364,793.5 | 552,885.3 | 685,800.1 |
| best | 148,279.5 | 293,703.8 | 336,492.7 | 328,256.1 | 154,520.4 | 301,173.3 | 885,141.3 | 412,763.8 | 351,353.7 | 306,622.4 | 351,921.6 | 434,606.2 | 550,559.2 | |
| worst | 180,601 | 322,076.4 | 771,655.5 | 357,719.6 | 201,283.7 | 505,054.8 | 1,131,352 | 670,584.5 | 474,359.5 | 367,271.7 | 373,433.4 | 627,862.4 | 796,742.2 | |
| std | 14,839.17 | 12,529.05 | 209,003.2 | 13,446.05 | 21,330.5 | 90,345.93 | 111,751.1 | 108,653.9 | 51,046.89 | 26,918.59 | 9128.358 | 86,478.11 | 101,484.8 | |
| median | 169,996.3 | 314,205.6 | 363,907 | 332,840.9 | 164,970.9 | 344,949.8 | 927,016.5 | 495,300.6 | 428,696.6 | 334,298.5 | 366,909.6 | 574,536.2 | 697,949.5 | |
| rank | 1 | 3 | 9 | 5 | 2 | 7 | 13 | 10 | 8 | 4 | 6 | 11 | 12 | |
| C17-F4 | mean | 655.7039 | 21,774.05 | 1662.224 | 73,321.34 | 1186.412 | 17,907.78 | 11,191.2 | 739.5621 | 5093.534 | 12,385.77 | 31,842.3 | 4276.123 | 8698.021 |
| best | 595.8195 | 17,433.85 | 1398.495 | 43,521.41 | 1108.667 | 13,665.86 | 9760.209 | 694.4664 | 3321.202 | 9715.491 | 25,588.62 | 1435.661 | 6860.208 | |
| worst | 696.4627 | 29,917.72 | 1851.454 | 94,391.08 | 1306.893 | 22,129.5 | 12,369.16 | 790.3274 | 6945.488 | 15,480.88 | 39,465.68 | 6678.925 | 9846.347 | |
| std | 44.90914 | 5564.829 | 192.679 | 22,193.54 | 94.64766 | 3742.318 | 1075.33 | 47.49333 | 1541.883 | 2413.397 | 5724.487 | 2370.731 | 1284.409 | |
| median | 665.2666 | 19,872.32 | 1699.474 | 77,686.43 | 1165.044 | 17,917.87 | 11,317.72 | 736.7272 | 5053.723 | 12,173.36 | 31,157.44 | 4494.953 | 9042.765 | |
| rank | 1 | 11 | 4 | 13 | 3 | 10 | 8 | 2 | 6 | 9 | 12 | 5 | 7 | |
| C17-F5 | mean | 1166.05 | 1504.914 | 1350.044 | 2009.134 | 1210.08 | 2172.868 | 1906.086 | 1221.411 | 1205.445 | 1820.496 | 1355.463 | 1507.352 | 1723.655 |
| best | 1139.731 | 1380.87 | 1304.366 | 1986.939 | 1179.843 | 2032.825 | 1870.109 | 1129.691 | 1156.931 | 1742.453 | 1278.82 | 1430.764 | 1639.415 | |
| worst | 1218.839 | 1589.623 | 1380.923 | 2020.928 | 1252.769 | 2302.787 | 1925.408 | 1314.041 | 1262.361 | 1892.273 | 1402.39 | 1585.082 | 1847.619 | |
| std | 36.21496 | 88.21671 | 34.10216 | 15.29979 | 32.3499 | 110.4274 | 25.54385 | 87.66381 | 43.43123 | 62.82961 | 57.11354 | 78.18066 | 88.17999 | |
| median | 1152.816 | 1524.582 | 1357.444 | 2014.335 | 1203.855 | 2177.931 | 1914.413 | 1220.955 | 1201.244 | 1823.63 | 1370.32 | 1506.78 | 1703.792 | |
| rank | 1 | 7 | 5 | 12 | 3 | 13 | 11 | 4 | 2 | 10 | 6 | 8 | 9 | |
| C17-F6 | mean | 633.3793 | 669.854 | 666.8515 | 714.5884 | 662.3248 | 728.0069 | 694.2372 | 669.198 | 643.6109 | 689.9683 | 667.5834 | 666.0791 | 665.0116 |
| best | 628.2662 | 661.8741 | 663.6147 | 710.3046 | 653.4113 | 712.535 | 688.9922 | 662.0385 | 636.1507 | 680.4107 | 666.9654 | 660.5087 | 657.8043 | |
| worst | 639.7835 | 676.3993 | 672.4559 | 718.0482 | 666.7799 | 762.8446 | 700.7457 | 676.3073 | 652.1949 | 697.2029 | 668.868 | 669.1201 | 672.3328 | |
| std | 4.822856 | 6.562621 | 3.937282 | 3.511939 | 6.083093 | 23.39071 | 4.905194 | 7.80358 | 7.689992 | 7.061908 | 0.87649 | 3.82012 | 6.884498 | |
| median | 632.7338 | 670.5712 | 665.6676 | 715.0005 | 664.554 | 718.324 | 693.6055 | 669.223 | 643.049 | 691.1298 | 667.2501 | 667.3438 | 664.9546 | |
| rank | 1 | 9 | 6 | 12 | 3 | 13 | 11 | 8 | 2 | 10 | 7 | 5 | 4 | |
| C17-F7 | mean | 1911.916 | 3541.744 | 3243.381 | 3801.276 | 2020.946 | 3797.222 | 3490.289 | 2081.918 | 2095.396 | 3191.277 | 2858.94 | 2791.773 | 2563.793 |
| best | 1816.72 | 3175.644 | 3123.082 | 3776.709 | 1843.88 | 3595.851 | 3387.53 | 1987.152 | 1985.72 | 3087.528 | 2696.081 | 2652.524 | 2490.104 | |
| worst | 1996.955 | 3681.703 | 3366.049 | 3834.327 | 2186.48 | 4075.989 | 3651.572 | 2150.043 | 2257.854 | 3285.241 | 3105.104 | 2969.625 | 2644.502 | |
| std | 73.84701 | 245.1298 | 120.3608 | 24.22757 | 156.5285 | 202.1429 | 117.843 | 76.32504 | 121.5581 | 87.36305 | 177.2088 | 131.4316 | 65.7947 | |
| median | 1916.994 | 3654.815 | 3242.197 | 3797.034 | 2026.713 | 3758.525 | 3461.026 | 2095.239 | 2069.004 | 3196.17 | 2817.288 | 2772.471 | 2560.284 | |
| rank | 1 | 11 | 9 | 13 | 2 | 12 | 10 | 3 | 4 | 8 | 7 | 6 | 5 | |
| C17-F8 | mean | 1479.939 | 1799.874 | 1773.64 | 2533.999 | 1539.319 | 2622.936 | 2272.001 | 1532.856 | 1557.506 | 2176.459 | 1849.688 | 1766.43 | 2092.383 |
| best | 1390.582 | 1630.939 | 1719.477 | 2493.042 | 1470.086 | 2469.493 | 2151.262 | 1404.611 | 1497.673 | 2098.286 | 1770.871 | 1656.793 | 2059.065 | |
| worst | 1576.255 | 1873.937 | 1874.707 | 2623.134 | 1600.872 | 2768.885 | 2436.535 | 1648.465 | 1614.262 | 2245.317 | 1887.851 | 1900.201 | 2137.38 | |
| std | 81.26873 | 114.9677 | 72.14627 | 61.50208 | 67.5484 | 155.8935 | 120.0276 | 99.83087 | 52.78256 | 71.14839 | 53.28624 | 101.1641 | 32.69375 | |
| median | 1476.459 | 1847.311 | 1750.188 | 2509.911 | 1543.158 | 2626.682 | 2250.103 | 1539.175 | 1559.044 | 2181.117 | 1870.014 | 1754.364 | 2086.543 | |
| rank | 1 | 7 | 6 | 12 | 3 | 13 | 11 | 2 | 4 | 10 | 8 | 5 | 9 | |
| C17-F9 | mean | 18,988.95 | 75,301.69 | 27,474.52 | 78,515.61 | 20,581.98 | 119,729.8 | 76,615.32 | 69,359.17 | 51,589.73 | 73,206.16 | 25,144.88 | 31,675.48 | 49,133.87 |
| best | 17,534.05 | 70,403.42 | 24,021.24 | 75,751.77 | 17,157.09 | 78,515.21 | 44,853.75 | 52,525.18 | 37,346.56 | 69,094.37 | 24,224.53 | 28,350.56 | 47,316.16 | |
| worst | 19,864.72 | 82,522.17 | 30,100.94 | 80,276.88 | 22,978.62 | 170,562.3 | 120,610.8 | 82,118.82 | 62,334.65 | 81,821.5 | 26,765.88 | 34,019.72 | 50,386.03 | |
| std | 1014.979 | 5698.842 | 2533.883 | 2044.079 | 2478.55 | 38,430.28 | 31,945.82 | 15,039.91 | 10,826.22 | 5903.298 | 1129.28 | 2717.236 | 1313.108 | |
| median | 19,278.51 | 74,140.59 | 27,887.94 | 79,016.89 | 21,096.12 | 114,920.9 | 70,498.37 | 71,396.33 | 53,338.85 | 70,954.38 | 24,794.55 | 32,165.82 | 49,416.65 | |
| rank | 1 | 10 | 4 | 12 | 2 | 13 | 11 | 8 | 7 | 9 | 3 | 5 | 6 | |
| C17-F10 | mean | 14,359.39 | 19,399.22 | 17,935.55 | 30,430.88 | 15,397.45 | 29,410.51 | 27,898.61 | 15,980.88 | 15,828.8 | 31,963.1 | 17,938.09 | 18,456.5 | 27,359.06 |
| best | 13,588.52 | 17,136.26 | 16,133.09 | 29,343.9 | 13,863.46 | 27,642.05 | 25,792.07 | 15,470.12 | 13,970.59 | 30,839.26 | 17,158.98 | 17,362.09 | 26,489.39 | |
| worst | 15,288.83 | 20,569.25 | 20,986.91 | 30,959.34 | 17,011.82 | 31,013.61 | 29,273.82 | 17,003.14 | 17,570.76 | 32,443.01 | 19,079.19 | 19,693.2 | 28,130.44 | |
| std | 700.8977 | 1553.247 | 2192.594 | 750.2732 | 1304.291 | 1380.703 | 1485.612 | 698.9395 | 1896.195 | 753.3583 | 914.5259 | 1156.665 | 729.5295 | |
| median | 14,280.1 | 19,945.69 | 17,311.1 | 30,710.13 | 15,357.26 | 29,493.18 | 28,264.27 | 15,725.13 | 15,886.93 | 32,285.06 | 17,757.09 | 18,385.36 | 27,408.21 | |
| rank | 1 | 8 | 5 | 12 | 2 | 11 | 10 | 4 | 3 | 13 | 6 | 7 | 9 | |
| C17-F11 | mean | 2283.281 | 82,550.02 | 70,967.33 | 208,606.7 | 5155.297 | 79,645.63 | 196,177.6 | 4901.862 | 64,611.18 | 53,294.21 | 167,260.4 | 56,864.81 | 173,971.6 |
| best | 2174.672 | 64,588.68 | 57,187.83 | 155,577.6 | 3452.397 | 53,901.98 | 138,002.8 | 4238.748 | 45,058.24 | 35,164.28 | 151,438 | 41,683.31 | 118,220.4 | |
| worst | 2372.435 | 109,454.1 | 86,372.24 | 274,283.1 | 9341.941 | 107,434.5 | 324,831.2 | 5676.522 | 89,892.73 | 70,199.98 | 178,425.9 | 81,149.72 | 229,857 | |
| std | 85.50501 | 19,373.98 | 12,757.85 | 50,594.08 | 2813.694 | 28,079.87 | 87,120.08 | 627.6838 | 19,176.61 | 14,322.73 | 12,269.74 | 17,149.44 | 55,041.7 | |
| median | 2293.009 | 78,078.65 | 70,154.63 | 202,283 | 3913.425 | 78,623 | 160,938.1 | 4846.089 | 61,746.87 | 53,906.3 | 169,588.8 | 52,313.1 | 173,904.5 | |
| rank | 1 | 9 | 7 | 13 | 3 | 8 | 12 | 2 | 6 | 4 | 10 | 5 | 11 | |
| C17-F12 | mean | 13,549,934 | 4.59 × 1010 | 6.22 × 108 | 1.7 × 1011 | 2.54 × 108 | 5.69 × 1010 | 1.14 × 1010 | 5.16 × 108 | 1.23 × 1010 | 3.82 × 1010 | 6.69 × 1010 | 1.9 × 1010 | 1.1 × 10 10 |
| best | 11,051,434 | 1.56 × 1010 | 4.81 × 108 | 1.48 × 1011 | 1.19 × 108 | 5.06 × 1010 | 7.91 × 109 | 3.3 × 108 | 3.83 × 109 | 2.95 × 1010 | 5.8 × 1010 | 3.22 × 109 | 7.79 × 10 9 | |
| worst | 17,094,242 | 5.88 × 1010 | 8.18 × 108 | 1.91 × 1011 | 3.27 × 108 | 6.74 × 1010 | 1.74 × 1010 | 6.22 × 108 | 1.97 × 1010 | 4.86 × 1010 | 7.9 × 1010 | 4.81 × 1010 | 1.58 × 10 10 | |
| std | 2,575,896 | 2.03 × 1010 | 1.43 × 108 | 1.9 × 1010 | 92,551,357 | 7.83 × 109 | 4.29 × 109 | 1.3 × 108 | 6.92 × 109 | 7.93 × 109 | 9.52 × 109 | 2 × 1010 | 3.38 × 10 9 | |
| median | 13,027,031 | 5.45 × 1010 | 5.94 × 108 | 1.71 × 1011 | 2.85 × 108 | 5.48 × 1010 | 1.02 × 1010 | 5.56 × 108 | 1.27 × 1010 | 3.74 × 1010 | 6.54 × 1010 | 1.24 × 1010 | 1.02 × 10 10 | |
| rank | 1 | 10 | 4 | 13 | 2 | 11 | 6 | 3 | 7 | 9 | 12 | 8 | 5 | |
| C17-F13 | mean | 36,350.96 | 9.2 × 109 | 61,970.35 | 4.42 × 1010 | 89,467.32 | 1.92 × 1010 | 5.41 × 108 | 442,954.8 | 8.32 × 108 | 3.03 × 109 | 7.97 × 109 | 2.78 × 109 | 2.57 × 10 8 |
| best | 32,150.66 | 4.58 × 109 | 33,152.4 | 3.64 × 1010 | 65,042.21 | 1.75 × 1010 | 5.04 × 108 | 308,678.7 | 5.15 × 108 | 2.32 × 109 | 4.54 × 109 | 1.19 × 108 | 70,258,995 | |
| worst | 43,505.81 | 1.16 × 1010 | 86,223.3 | 5.01 × 1010 | 146,358.2 | 2.2 × 1010 | 6.07 × 108 | 718,468.5 | 1.05 × 109 | 4.29 × 109 | 1.21 × 1010 | 6.47 × 109 | 5.14 × 10 8 | |
| std | 5095.066 | 3.22 × 109 | 22,345.65 | 5.9 × 109 | 38,124.21 | 2.16 × 109 | 46,063,980 | 192,117.4 | 2.25 × 108 | 8.9 × 108 | 3.36 × 109 | 2.68 × 109 | 1.89 × 10 8 | |
| median | 34,873.67 | 1.03 × 1010 | 64,252.85 | 4.51 × 1010 | 73,234.46 | 1.86 × 1010 | 5.27 × 108 | 372,336 | 8.84 × 108 | 2.74 × 109 | 7.64 × 109 | 2.28 × 109 | 2.21 × 10 8 | |
| rank | 1 | 11 | 2 | 13 | 3 | 12 | 6 | 4 | 7 | 9 | 10 | 8 | 5 | |
| C17-F14 | mean | 37,460.72 | 4,489,152 | 4,456,875 | 1.33 × 108 | 37,144.92 | 12,044,625 | 12,300,656 | 1,746,857 | 8,738,866 | 9,298,250 | 11,237,202 | 2,132,081 | 14,691,061 |
| best | 16,361.15 | 1,757,714 | 1,824,839 | 85,227,980 | 16,203.21 | 2,383,941 | 4,250,213 | 436,362.4 | 4,548,999 | 4,212,378 | 7,377,841 | 774,496.8 | 13,230,443 | |
| worst | 75,561.08 | 6,961,340 | 6,473,059 | 1.59 × 108 | 74,945.98 | 23,254,221 | 21,219,928 | 3,559,704 | 17,471,114 | 13,688,403 | 14,581,126 | 4,060,274 | 16,041,918 | |
| std | 26,110.58 | 2,232,142 | 2,151,003 | 33,511,442 | 25,905.58 | 8,976,986 | 7,301,106 | 1,485,338 | 6,023,595 | 4,478,970 | 3,814,456 | 1,471,762 | 1,151,485 | |
| median | 28,960.31 | 4,618,777 | 4,764,802 | 1.44 × 108 | 28,715.24 | 11,270,170 | 11,866,241 | 1,495,681 | 6,467,675 | 9,646,109 | 11,494,920 | 1,846,777 | 14,745,941 | |
| rank | 2 | 6 | 5 | 13 | 1 | 10 | 11 | 3 | 7 | 8 | 9 | 4 | 12 | |
| C17-F15 | mean | 18,882.03 | 98,686,181 | 48,987.56 | 2.29 × 1010 | 57,030.81 | 6.86 × 109 | 1.36 × 108 | 164,097.1 | 4.37 × 108 | 9.37 × 108 | 1.5 × 109 | 2.37 × 108 | 11,419,474 |
| best | 13,638.59 | 3,225,436 | 33,301.29 | 1.34 × 1010 | 31,982.54 | 2.06 × 109 | 87,407,866 | 138,892.2 | 1.87 × 108 | 5.5 × 108 | 9.05 × 108 | 15,041.64 | 9,550,801 | |
| worst | 26,884.85 | 3.12 × 108 | 63,801.66 | 2.79 × 1010 | 83,136.76 | 1.02 × 1010 | 2.33 × 108 | 196,300.4 | 8.23 × 108 | 1.93 × 109 | 1.96 × 109 | 9.46 × 108 | 14,186,872 | |
| std | 5961.071 | 1.46 × 108 | 12,585.04 | 6.49 × 109 | 21,039.18 | 3.58 × 109 | 67,067,445 | 27,529.44 | 2.72 × 108 | 6.66 × 108 | 4.45 × 108 | 4.73 × 108 | 2,084,089 | |
| median | 17,502.33 | 39,800,118 | 49,423.64 | 2.51 × 1010 | 56,501.97 | 7.6 × 109 | 1.13 × 108 | 160,597.8 | 3.68 × 108 | 6.31 × 108 | 1.56 × 109 | 91,930.12 | 10,970,111 | |
| rank | 1 | 6 | 2 | 13 | 3 | 12 | 7 | 4 | 9 | 10 | 11 | 8 | 5 | |
| C17-F16 | mean | 5159.521 | 7911.144 | 7237.618 | 20,529.48 | 5775.412 | 13,231.82 | 17,536.37 | 6208.623 | 6155.142 | 11,501.78 | 11,288.39 | 6462.738 | 10,775.66 |
| best | 4482.443 | 7594.345 | 6297.251 | 18,189.53 | 4964.557 | 11,674.5 | 13,541.34 | 6171.325 | 5459.267 | 10,272.69 | 10,267.51 | 6118.349 | 9633.615 | |
| worst | 5632.458 | 8242.705 | 8100.535 | 25,016.12 | 6480.428 | 15,062.96 | 23,606.65 | 6271.911 | 6685.123 | 13,117.57 | 13,583.71 | 6976.423 | 12,105.7 | |
| std | 548.9745 | 326.0461 | 743.9669 | 3052.189 | 627.8321 | 1402.246 | 4344.409 | 43.90544 | 606.2982 | 1190.737 | 1543.044 | 368.3862 | 1022.479 | |
| median | 5261.591 | 7903.763 | 7276.342 | 19,456.13 | 5828.332 | 13,094.92 | 16,498.74 | 6195.627 | 6238.088 | 11,308.44 | 10,651.17 | 6378.091 | 10,681.67 | |
| rank | 1 | 7 | 6 | 13 | 2 | 11 | 12 | 4 | 3 | 10 | 9 | 5 | 8 | |
| C17-F17 | mean | 4143.881 | 17,256.29 | 6278.188 | 7,660,577 | 4214.135 | 244,517.8 | 11,453.29 | 5751.307 | 4819.8 | 9430.942 | 33,565.25 | 9477.168 | 7289.964 |
| best | 3746.746 | 6565.42 | 5371.806 | 814,252.4 | 3859.68 | 9857.97 | 7790.231 | 5185.425 | 4232.158 | 8686.086 | 15,047.03 | 5453.346 | 7193.519 | |
| worst | 4504.818 | 34,680.9 | 7197.238 | 14,282,162 | 4387.087 | 380,666 | 15,834.67 | 6161.67 | 5523.21 | 10,606.71 | 50,021.65 | 19,192.23 | 7395.844 | |
| std | 313.4527 | 12,940.4 | 753.5212 | 7,595,286 | 239.6748 | 174,764 | 3629.996 | 477.3327 | 646.7451 | 822.6179 | 14,668.01 | 6500.52 | 105.6253 | |
| median | 4161.981 | 13,889.42 | 6271.853 | 7,772,947 | 4304.886 | 293,773.5 | 11,094.13 | 5829.067 | 4761.917 | 9215.487 | 34,596.15 | 6631.55 | 7285.246 | |
| rank | 1 | 10 | 5 | 13 | 2 | 12 | 9 | 4 | 3 | 7 | 11 | 8 | 6 | |
| C17-F18 | mean | 140,921.8 | 3,264,581 | 2,476,386 | 1.01 × 108 | 334,853.4 | 17,184,831 | 12,263,458 | 5,264,912 | 10,835,731 | 18,034,198 | 8,025,842 | 13,669,910 | 10,129,900 |
| best | 137,676.2 | 1,736,452 | 2,182,566 | 68,971,163 | 178,243.2 | 5,271,540 | 12,006,141 | 2,407,412 | 3,654,670 | 13,158,106 | 5,426,248 | 952,614.7 | 7,733,772 | |
| worst | 142,889 | 5,059,186 | 2,906,906 | 1.51 × 108 | 527,595.6 | 42,365,816 | 12,508,264 | 8,765,635 | 17,524,717 | 22,851,226 | 13,174,384 | 36,223,091 | 12,868,662 | |
| std | 2286.571 | 1,383,907 | 339,182.7 | 38,420,398 | 167,720.4 | 17,004,610 | 246,545.2 | 2,622,353 | 7,333,488 | 4,899,214 | 3,491,428 | 16,329,859 | 2,130,627 | |
| median | 141,561 | 3,131,343 | 2,408,037 | 92,865,432 | 316,787.5 | 10,550,984 | 12,269,714 | 4,943,301 | 11,081,769 | 18,063,731 | 6,751,367 | 8,751,967 | 9,958,583 | |
| rank | 1 | 4 | 3 | 13 | 2 | 11 | 9 | 5 | 8 | 12 | 6 | 10 | 7 | |
| C17-F19 | mean | 161,069.6 | 8.42 × 108 | 1,205,021 | 2.31 × 1010 | 169,321.7 | 8.41 × 109 | 1.11 × 108 | 20,443,070 | 66,702,321 | 4.82 × 108 | 4.09 × 108 | 4,904,826 | 17,196,651 |
| best | 38,442.77 | 97,622,306 | 718,063.4 | 2.01 × 1010 | 40,312.61 | 1.21 × 109 | 56,321,277 | 11,725,752 | 13,898,824 | 4.36 × 108 | 1.57 × 108 | 142,122.3 | 13,449,014 | |
| worst | 402,093.3 | 1.63 × 109 | 1,913,021 | 2.63 × 1010 | 411,397 | 1.62 × 1010 | 1.63 × 108 | 26,686,851 | 1.47 × 108 | 5.08 × 108 | 6.21 × 108 | 10,867,115 | 23,529,997 | |
| std | 165,447.5 | 6.67 × 108 | 507,442.8 | 2.86 × 109 | 167,915.7 | 6.13 × 109 | 57,996,119 | 6,580,111 | 57,324,646 | 31,934,561 | 2.08 × 108 | 5,311,723 | 4,425,910 | |
| median | 101,871.1 | 8.2 × 108 | 1,094,500 | 2.29 × 1010 | 112,788.6 | 8.13 × 109 | 1.13 × 108 | 21,679,838 | 52,857,305 | 4.93 × 108 | 4.3 × 108 | 4,305,033 | 15,903,796 | |
| rank | 1 | 11 | 3 | 13 | 2 | 12 | 8 | 6 | 7 | 10 | 9 | 4 | 5 | |
| C17-F20 | mean | 4329.772 | 5183.389 | 6066.485 | 7643.89 | 4432.637 | 7040.717 | 6551.851 | 5158.041 | 7077.601 | 7324.316 | 6241.91 | 5196.925 | 6328.018 |
| best | 3875.227 | 3852.122 | 5777.4 | 7182.534 | 4170.89 | 6256.34 | 6048.655 | 4700.095 | 4372.886 | 6860.291 | 5444.499 | 4783.879 | 5957.546 | |
| worst | 4639.907 | 7866.15 | 6394.717 | 7875.16 | 4595.62 | 7699.216 | 6923.305 | 5389.048 | 8042.899 | 7811.819 | 6908.555 | 6022.863 | 7197.281 | |
| std | 323.251 | 1819.666 | 277.5492 | 321.5951 | 185.1203 | 658.1345 | 389.4126 | 319.7632 | 1804.006 | 486.1558 | 772.4079 | 560.5865 | 583.2411 | |
| median | 4401.977 | 4507.641 | 6046.912 | 7758.933 | 4482.019 | 7103.656 | 6617.722 | 5271.51 | 7947.309 | 7312.577 | 6307.294 | 4990.479 | 6078.622 | |
| rank | 1 | 4 | 6 | 13 | 2 | 10 | 9 | 3 | 11 | 12 | 7 | 5 | 8 | |
| C17-F21 | mean | 2764.742 | 4027.213 | 3664.091 | 4458.728 | 2881.877 | 4335.331 | 4326.582 | 3036.657 | 2992.63 | 3790.589 | 4708.698 | 3666.636 | 3675.619 |
| best | 2699.974 | 3704.178 | 3568.045 | 4347.035 | 2766.476 | 4068.898 | 4124.048 | 2916.202 | 2896.614 | 3678.986 | 4581.198 | 3504.164 | 3582.929 | |
| worst | 2816.339 | 4369.58 | 3764.376 | 4614.097 | 3011.426 | 4510.539 | 4598.794 | 3226.835 | 3070.04 | 3883.529 | 4980.425 | 3849.175 | 3751.677 | |
| std | 48.11086 | 278.4377 | 108.195 | 113.2218 | 101.1698 | 209.0187 | 200.4712 | 133.2488 | 85.81598 | 85.11658 | 185.487 | 143.4907 | 73.69636 | |
| median | 2771.327 | 4017.547 | 3661.971 | 4436.889 | 2874.802 | 4380.944 | 4291.742 | 3001.796 | 3001.933 | 3799.921 | 4636.585 | 3656.602 | 3683.934 | |
| rank | 1 | 9 | 5 | 12 | 2 | 11 | 10 | 4 | 3 | 8 | 13 | 6 | 7 | |
| C17-F22 | mean | 13,298.62 | 21,305.75 | 19,844.61 | 34,680.71 | 15,016.95 | 31,613.32 | 30,881.75 | 18,865.96 | 19,485.72 | 34,416.29 | 21,926.57 | 22,621.27 | 27,306.94 |
| best | 2440.431 | 20,323.85 | 19,177.65 | 34,605.55 | 2499.552 | 31,067.87 | 29,276.12 | 18,173.68 | 18,244.98 | 34,250.53 | 19,895.16 | 20,370.87 | 16,116.15 | |
| worst | 18,623.41 | 22,434.61 | 21,090.76 | 34,718.52 | 20,013.91 | 32,297.65 | 33,319.26 | 19,981.28 | 21,249.71 | 34,868.52 | 23,369.69 | 25,034.51 | 32,184.45 | |
| std | 7377.823 | 876.5613 | 869.2077 | 51.0533 | 8365.608 | 508.4395 | 1796.155 | 858.4155 | 1379.083 | 301.7408 | 1591.5 | 1915.238 | 7562.745 | |
| median | 16,065.31 | 21,232.28 | 19,555.01 | 34,699.38 | 18,777.17 | 31,543.87 | 30,465.81 | 18,654.43 | 19,224.09 | 34,273.06 | 22,220.71 | 22,539.84 | 30,463.59 | |
| rank | 1 | 6 | 5 | 13 | 2 | 11 | 10 | 3 | 4 | 12 | 7 | 8 | 9 | |
| C17-F23 | mean | 3259.665 | 5159.671 | 4303.583 | 5617.314 | 3459.061 | 5770.667 | 5175.464 | 3603.464 | 3674.039 | 4347.467 | 7897.46 | 4725.29 | 4346.781 |
| best | 3226.557 | 4861.07 | 4085.871 | 5421.661 | 3407.754 | 5295.597 | 4895.709 | 3346.847 | 3584.29 | 4256.869 | 7254.263 | 4629.852 | 4136.554 | |
| worst | 3296.342 | 5699.833 | 4502.895 | 5715.713 | 3515.118 | 6042.383 | 5395.633 | 3720.109 | 3785.023 | 4413.904 | 8483.524 | 4814.118 | 4536.905 | |
| std | 32.90116 | 386.3156 | 175.7608 | 135.368 | 51.20413 | 343.2099 | 210.6716 | 176.5002 | 101.0517 | 65.61731 | 525.3169 | 81.32892 | 167.7969 | |
| median | 3257.88 | 5038.891 | 4312.782 | 5665.941 | 3456.686 | 5872.344 | 5205.258 | 3673.45 | 3663.42 | 4359.547 | 7926.026 | 4728.594 | 4356.833 | |
| rank | 1 | 9 | 5 | 11 | 2 | 12 | 10 | 3 | 4 | 7 | 13 | 8 | 6 | |
| C17-F24 | mean | 3846.516 | 7096.235 | 5033.276 | 9584.647 | 3813.223 | 6948.276 | 6335.232 | 4062.592 | 4365.648 | 4951.757 | 10,763.26 | 5983.513 | 5331.613 |
| best | 3726.817 | 6637.348 | 4771.243 | 7955.331 | 3700.374 | 6119.945 | 5877.806 | 3977.801 | 4253.26 | 4854.884 | 10,430.78 | 5485.013 | 4888.407 | |
| worst | 3971.617 | 7846.225 | 5494.416 | 13,585.21 | 3934.351 | 7597.833 | 6803.973 | 4155.626 | 4547.109 | 5135.507 | 11,247.97 | 6457.987 | 5566.537 | |
| std | 124.4288 | 523.1172 | 316.9777 | 2688.925 | 120.7238 | 648.2421 | 447.6772 | 84.17781 | 128.9378 | 128.2864 | 373.6677 | 414.727 | 304.9964 | |
| median | 3843.816 | 6950.683 | 4933.723 | 8399.024 | 3809.084 | 7037.664 | 6329.574 | 4058.471 | 4331.112 | 4908.319 | 10,687.15 | 5995.526 | 5435.753 | |
| rank | 2 | 11 | 6 | 12 | 1 | 10 | 9 | 3 | 4 | 5 | 13 | 8 | 7 | |
| C17-F25 | mean | 3469.147 | 11,520.64 | 4010.435 | 24,401.33 | 3902.052 | 11,610.18 | 8130.608 | 3434.111 | 6741.259 | 10,248.33 | 10,694.92 | 4519.774 | 8918.261 |
| best | 3336.562 | 9524.987 | 3859.072 | 21,905.88 | 3795.043 | 10,384.3 | 6094.109 | 3337.136 | 5476.952 | 9143.045 | 9641.655 | 4026.406 | 8522.142 | |
| worst | 3674.345 | 13,862.05 | 4141.137 | 27,073.78 | 4001.032 | 13,671.79 | 9181.291 | 3482.374 | 8276.049 | 12,322.1 | 11,956.99 | 4767.238 | 9227.662 | |
| std | 151.6605 | 1810.362 | 145.9816 | 2285.452 | 87.68001 | 1426.465 | 1425.184 | 68.04092 | 1159.786 | 1421.174 | 1081.266 | 340.7136 | 293.0999 | |
| median | 3432.84 | 11,347.75 | 4020.765 | 24,312.84 | 3906.067 | 11,192.31 | 8623.515 | 3458.468 | 6606.018 | 9764.085 | 10,590.51 | 4642.725 | 8961.621 | |
| rank | 2 | 11 | 4 | 13 | 3 | 12 | 7 | 1 | 6 | 9 | 10 | 5 | 8 | |
| C17-F26 | mean | 11,776.87 | 32,319.52 | 25,892.01 | 50,965.07 | 12,256.12 | 35,938.6 | 37,175.46 | 13,381.42 | 16,826.64 | 23,075.68 | 35,000.86 | 19,788.26 | 25,645.44 |
| best | 11,355.12 | 29,278.54 | 21,112 | 45,933.69 | 11,587.21 | 33,402.26 | 31,343.9 | 12,486.47 | 14,857.57 | 21,221.76 | 33,204.49 | 18,887.49 | 22,138.29 | |
| worst | 12,047.28 | 35,287.08 | 28,834.86 | 53,243.92 | 12,666.16 | 37,240.48 | 42,580.56 | 13,918.71 | 18,847.41 | 25,247.56 | 36,279.13 | 20,917.45 | 29,733.71 | |
| std | 298.4586 | 2627.895 | 3410.424 | 3447.125 | 509.1323 | 1732.521 | 4886.416 | 654.5382 | 1660.057 | 1677.974 | 1380.682 | 881.7495 | 3999.153 | |
| median | 11,852.55 | 32,356.22 | 26,810.59 | 52,341.34 | 12,385.56 | 36,555.83 | 37,388.69 | 13,560.26 | 16,800.79 | 22,916.7 | 35,259.91 | 19,674.06 | 25,354.89 | |
| rank | 1 | 9 | 8 | 13 | 2 | 11 | 12 | 3 | 4 | 6 | 10 | 5 | 7 | |
| C17-F27 | mean | 3575.611 | 6742.95 | 4375.433 | 11,679.1 | 3675.833 | 6411.141 | 5820.97 | 3703.331 | 4205.741 | 4165.307 | 14,697.54 | 4056.367 | 5266.088 |
| best | 3545.734 | 6081.846 | 4098.366 | 8782.023 | 3592.46 | 4900.306 | 4987.661 | 3563.203 | 4069.706 | 4008.832 | 13,470.22 | 3649.808 | 4973.669 | |
| worst | 3648.183 | 7055.009 | 4747.855 | 15,162.9 | 3770.239 | 7570.592 | 6846.795 | 3795.476 | 4329.609 | 4332.615 | 15,679.32 | 4475.324 | 5397.056 | |
| std | 48.70852 | 449.6358 | 313.9328 | 3294.659 | 72.86347 | 1111.333 | 817.6242 | 111.1698 | 109.3868 | 175.8536 | 998.4654 | 370.4368 | 198.3472 | |
| median | 3554.263 | 6917.473 | 4327.755 | 11,385.73 | 3670.317 | 6586.834 | 5724.713 | 3727.322 | 4211.825 | 4159.891 | 14,820.31 | 4050.168 | 5346.814 | |
| rank | 1 | 11 | 7 | 12 | 2 | 10 | 9 | 3 | 6 | 5 | 13 | 4 | 8 | |
| C17-F28 | mean | 3602.453 | 14,553.69 | 5002.45 | 29,423.48 | 3822.111 | 16,592.32 | 13,193.5 | 3503.023 | 8836.034 | 12,235.73 | 20,761.73 | 7955.561 | 12,025.11 |
| best | 3543.474 | 12,197.62 | 4606.601 | 25,865.71 | 3780.886 | 15,763.65 | 11,910.22 | 3439.876 | 8379.33 | 10,859.02 | 18,468.59 | 5177.514 | 11,155.88 | |
| worst | 3703.404 | 17,079.89 | 5431.228 | 31,600.92 | 3884.097 | 17,453.01 | 14,204.6 | 3559.923 | 9513.755 | 13,945.58 | 23,291.08 | 14,077.41 | 12,859.14 | |
| std | 70.29083 | 2305.749 | 348.1724 | 2544.344 | 49.01329 | 689.9281 | 1102.437 | 49.75649 | 505.5543 | 1309.35 | 2054.307 | 4125.024 | 773.8027 | |
| median | 3581.466 | 14,468.62 | 4985.986 | 30,113.64 | 3811.731 | 16,576.32 | 13,329.6 | 3506.147 | 8725.526 | 12,069.16 | 20,643.62 | 6283.658 | 12,042.7 | |
| rank | 2 | 10 | 4 | 13 | 3 | 11 | 9 | 1 | 6 | 8 | 12 | 5 | 7 | |
| C17-F29 | mean | 7186.205 | 12,015.6 | 9814.17 | 748,982.1 | 7395.086 | 66,078.18 | 18,573.42 | 7827.296 | 8639.945 | 13,867.9 | 24,083.25 | 8587.316 | 12,369.37 |
| best | 6818.963 | 11,515.44 | 9111.304 | 624,851.1 | 7048.406 | 28,968.98 | 17,146.3 | 7510.98 | 8235.103 | 12,396 | 18,510.53 | 7668.281 | 12,005.44 | |
| worst | 7577.929 | 12,378.38 | 10,408.74 | 914,832.3 | 7728.099 | 123,745.8 | 20,612.32 | 8300.293 | 9067.168 | 16,357.95 | 31,591.21 | 9711.056 | 12,680.52 | |
| std | 325.5348 | 384.1453 | 544.8654 | 120,932 | 292.5936 | 42,192.39 | 1496.769 | 380.1452 | 341.9508 | 1721.132 | 6312.584 | 882.8139 | 286.5164 | |
| median | 7173.964 | 12,084.29 | 9868.321 | 728,122.6 | 7401.919 | 55,798.97 | 18,267.52 | 7748.955 | 8628.755 | 13,358.83 | 23,115.64 | 8484.963 | 12,395.76 | |
| rank | 1 | 7 | 6 | 13 | 2 | 12 | 10 | 3 | 5 | 9 | 11 | 4 | 8 | |
| C17-F30 | mean | 3,304,314 | 7.07 × 109 | 47,858,131 | 4.4 × 1010 | 6,031,607 | 1.4 × 1010 | 1.16 × 109 | 1.25 × 108 | 2.67 × 109 | 3.03 × 109 | 1.04 × 1010 | 6.76 × 108 | 5.53 × 10 8 |
| best | 1,736,868 | 4.42 × 109 | 22,468,989 | 3.76 × 1010 | 4,802,998 | 9.63 × 109 | 8.74 × 108 | 84,489,086 | 78,558,419 | 1.3 × 109 | 7.8 × 109 | 10,552,576 | 3.46 × 10 8 | |
| worst | 4,405,575 | 9.95 × 109 | 74,195,320 | 4.81 × 1010 | 6,809,589 | 1.85 × 1010 | 1.82 × 109 | 2.01 × 108 | 7.59 × 109 | 5.85 × 109 | 1.31 × 1010 | 1.75 × 109 | 7.86 × 10 8 | |
| std | 1,122,253 | 2.38 × 109 | 21,902,086 | 4.55 × 109 | 864,695.5 | 3.76 × 109 | 4.52 × 108 | 52,735,484 | 3.38 × 109 | 1.99 × 109 | 2.32 × 109 | 8.38 × 108 | 1.89 × 10 8 | |
| median | 3,537,407 | 6.96 × 109 | 47,384,107 | 4.51 × 1010 | 6,256,920 | 1.39 × 1010 | 9.62 × 108 | 1.06 × 108 | 1.51 × 109 | 2.5 × 109 | 1.03 × 1010 | 4.72 × 108 | 5.41 × 10 8 | |
| rank | 1 | 10 | 3 | 13 | 2 | 12 | 7 | 4 | 8 | 9 | 11 | 6 | 5 | |
| Sum rank | 33 | 247 | 148 | 359 | 66 | 324 | 275 | 109 | 160 | 251 | 274 | 181 | 212 | |
| Mean rank | 1.137931 | 8.517241 | 5.103448 | 12.37931 | 2.275862 | 11.17241 | 9.482759 | 3.758621 | 5.517241 | 8.655172 | 9.448276 | 6.241379 | 7.310345 | |
| Total rank | 1 | 8 | 4 | 13 | 2 | 12 | 11 | 3 | 5 | 9 | 10 | 6 | 7 | |
| GAO | WSO | AVOA | RSA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C19-F1 | mean | 1 | 71,810.88 | 1 | 1 | 1 | 20,217.93 | 11,711,987 | 1,133,810 | 27,216.59 | 68.42838 | 6.21 × 108 | 149,696.8 | 7,924,820 |
| best | 1 | 1162.052 | 1 | 1 | 1 | 2.756454 | 2,455,600 | 376,289.6 | 1.004815 | 1.001003 | 1.49 × 108 | 14,365.34 | 2,790,162 | |
| worst | 1 | 205,671.3 | 1 | 1 | 1 | 80,699.62 | 16,695,679 | 2,287,378 | 94,807.29 | 270.6854 | 1.07 × 109 | 476,077 | 16,698,761 | |
| std | 0 | 92,810.22 | 0 | 0 | 0 | 40,361.5 | 6,381,017 | 842,939.7 | 45,586.06 | 134.9729 | 4.66 × 108 | 218,680.9 | 6,548,692 | |
| median | 1 | 40,205.1 | 1 | 1 | 1 | 84.67389 | 13,848,335 | 935,786 | 7029.039 | 1.013541 | 6.33 × 108 | 54,172.42 | 6,105,179 | |
| rank | 1 | 5 | 1 | 1 | 1 | 3 | 9 | 7 | 4 | 2 | 10 | 6 | 8 | |
| C19-F2 | mean | 1 | 173.085 | 4.697685 | 5.00375 | 3.016487 | 801.2333 | 6143.321 | 564.3356 | 454.8589 | 667.6561 | 27,762.24 | 364.2709 | 858.2781 |
| best | 1 | 98.73351 | 4.308172 | 5 | 2.553251 | 629.09 | 2910.908 | 286.6219 | 210.5741 | 5.569583 | 9861.117 | 227.0451 | 578.5317 | |
| worst | 1 | 267.0959 | 5.005 | 5.005 | 3.5079 | 938.0872 | 9275.1 | 838.9716 | 658.7508 | 1191.552 | 42,469.39 | 545.4075 | 1136.55 | |
| std | 2.07 × 10−10 | 70.52461 | 0.361508 | 0.002502 | 0.391792 | 137.0911 | 2634.042 | 228.0778 | 185.095 | 538.9384 | 15,004.15 | 133.6998 | 290.7565 | |
| median | 1 | 163.2553 | 4.738785 | 5.005 | 3.002399 | 818.8781 | 6193.637 | 565.8743 | 475.0553 | 736.7513 | 29,359.23 | 342.3155 | 859.0152 | |
| rank | 1 | 5 | 3 | 4 | 2 | 10 | 12 | 8 | 7 | 9 | 13 | 6 | 11 | |
| C19-F3 | mean | 1.252026 | 1.893453 | 2.128289 | 8.144879 | 1.464204 | 6.458567 | 6.143913 | 8.967309 | 1.907945 | 4.71987 | 4.00648 | 3.78097 | 5.784606 |
| best | 1.055806 | 1.411199 | 1.410605 | 6.294517 | 1.173223 | 1.7408 | 3.067264 | 7.719486 | 1.208206 | 4.153685 | 2.763422 | 1.409135 | 3.599784 | |
| worst | 1.448438 | 2.377011 | 3.342791 | 9.221102 | 1.756207 | 9.724014 | 9.656947 | 10.71926 | 3.410963 | 5.801678 | 5.917239 | 7.694728 | 7.707829 | |
| std | 0.226445 | 0.555772 | 0.920676 | 1.305179 | 0.242174 | 3.405598 | 2.745714 | 1.499883 | 1.012835 | 0.749746 | 1.386399 | 3.016785 | 1.854326 | |
| median | 1.25193 | 1.8928 | 1.87988 | 8.531949 | 1.463694 | 7.184728 | 5.925721 | 8.715246 | 1.506306 | 4.462058 | 3.672631 | 3.010009 | 5.915405 | |
| rank | 1 | 3 | 5 | 12 | 2 | 11 | 10 | 13 | 4 | 8 | 7 | 6 | 9 | |
| C19-F4 | mean | 8.490857 | 17.43753 | 35.35101 | 74.01385 | 11.45606 | 53.14016 | 59.81028 | 25.57658 | 23.21939 | 35.45653 | 52.03346 | 18.92539 | 22.37215 |
| best | 5.004053 | 13.94927 | 8.968627 | 55.9555 | 7.972665 | 41.50046 | 33.01698 | 22.91293 | 10.11592 | 32.7219 | 39.80328 | 10.94959 | 19.12583 | |
| worst | 9.98565 | 21.89463 | 57.77001 | 94.37194 | 14.94393 | 65.757 | 92.985 | 29.60309 | 38.84724 | 41.06531 | 60.75789 | 36.8552 | 27.50774 | |
| std | 2.373925 | 4.092957 | 20.27293 | 16.5466 | 3.503048 | 11.06681 | 26.38785 | 2.961748 | 13.72705 | 3.919584 | 9.132214 | 12.07601 | 3.595136 | |
| median | 9.486861 | 16.95311 | 37.33271 | 72.86398 | 11.45382 | 52.6516 | 56.61956 | 24.89516 | 21.95719 | 34.01946 | 53.78634 | 13.94839 | 21.42752 | |
| rank | 1 | 3 | 8 | 13 | 2 | 11 | 12 | 7 | 6 | 9 | 10 | 4 | 5 | |
| C19-F5 | mean | 1.040448 | 1.68947 | 1.202223 | 88.34774 | 1.035245 | 29.63456 | 2.041447 | 1.393396 | 1.59657 | 2.936446 | 1.177378 | 1.214415 | 1.727054 |
| best | 1.021119 | 1.211649 | 1.109628 | 66.19828 | 1.008407 | 13.56856 | 1.695794 | 1.240528 | 1.348675 | 2.641299 | 1.155782 | 1.180765 | 1.552317 | |
| worst | 1.058037 | 2.265097 | 1.285169 | 109.1006 | 1.062662 | 62.12907 | 2.361459 | 1.756175 | 1.895775 | 3.143506 | 1.211316 | 1.254888 | 1.843677 | |
| std | 0.016864 | 0.456601 | 0.075539 | 17.55507 | 0.028366 | 22.90052 | 0.280528 | 0.246247 | 0.258672 | 0.224998 | 0.026365 | 0.038036 | 0.125116 | |
| median | 1.041318 | 1.640568 | 1.207046 | 89.04604 | 1.034956 | 21.42031 | 2.054267 | 1.28844 | 1.570914 | 2.980489 | 1.171207 | 1.211003 | 1.756112 | |
| rank | 2 | 8 | 4 | 13 | 1 | 12 | 10 | 6 | 7 | 11 | 3 | 5 | 9 | |
| C19-F6 | mean | 1.070443 | 2.903442 | 7.096602 | 9.950166 | 1.149309 | 7.862816 | 10.69014 | 3.026315 | 3.496531 | 4.579968 | 4.098299 | 3.646271 | 3.230283 |
| best | 1.035309 | 1.803016 | 6.220347 | 9.465644 | 1.074 | 4.400796 | 9.384775 | 1.226604 | 1.337298 | 3.590748 | 1.072484 | 1.533005 | 2.493256 | |
| worst | 1.153231 | 3.607175 | 9.331887 | 10.76195 | 1.238936 | 10.55354 | 11.98097 | 4.368123 | 4.995392 | 5.235327 | 5.658356 | 6.246968 | 4.3958 | |
| std | 0.055523 | 0.795235 | 1.500173 | 0.609953 | 0.070639 | 2.602494 | 1.064884 | 1.374214 | 1.550139 | 0.724406 | 2.146191 | 1.984798 | 0.837016 | |
| median | 1.046616 | 3.101788 | 6.417086 | 9.786536 | 1.14215 | 8.248463 | 10.6974 | 3.255266 | 3.826717 | 4.746899 | 4.831178 | 3.402555 | 3.016039 | |
| rank | 1 | 3 | 10 | 12 | 2 | 11 | 13 | 4 | 6 | 9 | 8 | 7 | 5 | |
| C19-F7 | mean | 269.8869 | 491.5369 | 1083.674 | 1732.261 | 294.3786 | 1407.933 | 1142.598 | 1057.209 | 1178.452 | 1176.09 | 1661.754 | 1152.37 | 708.3514 |
| best | 147.327 | 297.7043 | 804.5591 | 1578.7 | 156.2455 | 1023.022 | 703.3226 | 723.7527 | 1021.721 | 708.6485 | 1504.425 | 658.1489 | 491.0823 | |
| worst | 426.5517 | 759.5538 | 1547.829 | 1817.424 | 451.5611 | 1687.386 | 1794.3 | 1850.827 | 1377.603 | 1523.433 | 1797.54 | 1608.384 | 1094.838 | |
| std | 115.8062 | 207.68 | 353.8715 | 108.7197 | 123.085 | 279.7652 | 463.1718 | 533.431 | 167.8284 | 371.3769 | 133.0367 | 445.3167 | 282.551 | |
| median | 252.8345 | 454.4447 | 991.1533 | 1766.46 | 284.8538 | 1460.662 | 1036.385 | 827.1279 | 1157.242 | 1236.14 | 1672.527 | 1171.473 | 623.7426 | |
| rank | 1 | 3 | 6 | 13 | 2 | 11 | 7 | 5 | 10 | 9 | 12 | 8 | 4 | |
| C19-F8 | mean | 3.020737 | 3.56846 | 4.472057 | 4.821922 | 3.222844 | 4.153506 | 4.853111 | 4.062034 | 3.612028 | 4.304852 | 5.220798 | 4.611625 | 4.53273 |
| best | 1.93757 | 3.019294 | 3.931216 | 4.542727 | 2.751649 | 3.564661 | 4.611607 | 3.565193 | 3.366284 | 4.059899 | 5.124828 | 4.373981 | 4.30402 | |
| worst | 3.832277 | 3.846303 | 4.899725 | 4.990379 | 3.684781 | 4.907803 | 5.087082 | 4.484265 | 4.04011 | 4.874945 | 5.373209 | 4.983297 | 4.673832 | |
| std | 0.81643 | 0.37258 | 0.457621 | 0.199997 | 0.491333 | 0.564 | 0.211666 | 0.435816 | 0.304162 | 0.383203 | 0.120079 | 0.26615 | 0.166595 | |
| median | 3.156551 | 3.704121 | 4.528644 | 4.877291 | 3.227473 | 4.07078 | 4.856877 | 4.09934 | 3.520859 | 4.142282 | 5.192578 | 4.544612 | 4.576533 | |
| rank | 1 | 3 | 8 | 11 | 2 | 6 | 12 | 5 | 4 | 7 | 13 | 10 | 9 | |
| C19-F9 | mean | 1.084898 | 1.176728 | 1.394348 | 3.107928 | 1.107921 | 1.351812 | 1.381376 | 1.17732 | 1.221403 | 1.325084 | 1.212712 | 1.19474 | 1.13892 |
| best | 1.061955 | 1.123308 | 1.078336 | 2.403669 | 1.052251 | 1.199298 | 1.192892 | 1.151336 | 1.1062 | 1.253609 | 1.07988 | 1.090717 | 1.114774 | |
| worst | 1.118152 | 1.243717 | 1.605772 | 3.687815 | 1.177456 | 1.562261 | 1.652451 | 1.204837 | 1.357157 | 1.38638 | 1.303407 | 1.263166 | 1.185336 | |
| std | 0.026145 | 0.054588 | 0.225014 | 0.546669 | 0.054825 | 0.162107 | 0.217617 | 0.024619 | 0.113889 | 0.070005 | 0.098491 | 0.074806 | 0.031898 | |
| median | 1.079743 | 1.169944 | 1.446642 | 3.170114 | 1.100989 | 1.322845 | 1.34008 | 1.176555 | 1.211127 | 1.330173 | 1.23378 | 1.212539 | 1.127786 | |
| rank | 1 | 4 | 12 | 13 | 2 | 10 | 11 | 5 | 8 | 9 | 7 | 6 | 3 | |
| C19-F10 | mean | 18.13078 | 18.03091 | 21.05206 | 21.48397 | 21.0165 | 21.42982 | 21.22793 | 21.04321 | 21.49175 | 21.44677 | 22.69648 | 21.04806 | 21.28325 |
| best | 6.932382 | 7.874518 | 20.99262 | 21.37514 | 21.003 | 21.37636 | 21.06805 | 21.00739 | 21.46041 | 21.39861 | 21.01899 | 20.99969 | 21.12875 | |
| worst | 22.06025 | 21.54158 | 21.19324 | 21.56887 | 21.021 | 21.55954 | 21.61559 | 21.06165 | 21.51818 | 21.52354 | 23.49109 | 21.15059 | 21.41332 | |
| std | 7.47515 | 6.778286 | 0.094957 | 0.080448 | 0.009009 | 0.08687 | 0.259764 | 0.024362 | 0.025405 | 0.054463 | 1.135734 | 0.069157 | 0.122919 | |
| median | 21.76525 | 21.35378 | 21.0112 | 21.49593 | 21.021 | 21.39169 | 21.11404 | 21.0519 | 21.49421 | 21.43248 | 23.13793 | 21.02097 | 21.29547 | |
| rank | 2 | 1 | 6 | 11 | 3 | 9 | 7 | 4 | 12 | 10 | 13 | 5 | 8 | |
| Sum rank | 12 | 38 | 63 | 103 | 19 | 94 | 103 | 64 | 68 | 83 | 96 | 63 | 71 | |
| Mean rank | 1.2 | 3.8 | 6.3 | 10.3 | 1.9 | 9.4 | 10.3 | 6.4 | 6.8 | 8.3 | 9.6 | 6.3 | 7.1 | |
| Total rank | 1 | 3 | 4 | 11 | 2 | 9 | 11 | 5 | 6 | 8 | 10 | 4 | 7 | |
| Compared Algorithm | Objective Function Type | ||||
|---|---|---|---|---|---|
| CEC 2017 | CEC 2019 | ||||
| GAO vs. WSO | 5.4 × 10−15 | 3.18 × 10−21 | 2.07 × 10−21 | 2.29 × 10−21 | 5.91 × 10−6 |
| GAO vs. AVOA | 2.8 × 10−20 | 6.88 × 10−21 | 1.97 × 10−21 | 2.41 × 10−21 | 4.49 × 10−6 |
| GAO vs. RSA | 3.6 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 2.79 × 10−7 |
| GAO vs. MPA | 2.43 × 10−5 | 4.35 × 10−10 | 1.49 × 10−11 | 3.34 × 10−15 | 0.006264 |
| GAO vs. TSA | 7.23 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 1.37 × 10−7 |
| GAO vs. WOA | 9.04 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 1.84 × 10−7 |
| GAO vs. MVO | 8.04 × 10−17 | 5.13 × 10−19 | 5.68 × 10−20 | 6.41 × 10−20 | 4.64 × 10−7 |
| GAO vs. GWO | 1.44 × 10−18 | 9.98 × 10−21 | 5.64 × 10−21 | 9.5 × 10−21 | 1.49 × 10−6 |
| GAO vs. TLBO | 7.06 × 10−20 | 1.97 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 2.28 × 10−7 |
| GAO vs. GSA | 3.02 × 10−20 | 2.87 × 10−21 | 1.97 × 10−21 | 1.97 × 10−21 | 3.57 × 10−8 |
| GAO vs. PSO | 6.25 × 10−20 | 9.98 × 10−21 | 1.72 × 10−20 | 2.24 × 10−21 | 7.06 × 10−7 |
| GAO vs. GA | 3.09 × 10−20 | 1.97 × 10−21 | 2.02 × 10−21 | 1.97 × 10−21 | 1.59 × 10−7 |
| GAO | WSO | AVOA | RSA | MPA | TSA | WOA | MVO | GWO | TLBO | GSA | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11-F1 | mean | 3.300478 | 15.02557 | 25.74562 | 26.00412 | 3.521917 | 20.93273 | 24.34703 | 20.30298 | 13.87947 | 19.79529 | 25.67295 | 19.27164 | 25.88474 |
| best | 4.16 × 10−10 | 11.75673 | 24.83901 | 25.15683 | 4.53 × 10−10 | 12.96597 | 22.0416 | 16.91438 | 1.775842 | 17.00127 | 23.71442 | 8.416087 | 24.27333 | |
| worst | 13.20191 | 19.29177 | 26.94225 | 27.78769 | 14.08767 | 25.02322 | 25.15126 | 24.93986 | 21.48584 | 22.33001 | 27.19836 | 24.58904 | 27.26328 | |
| std | 6.607557 | 3.132729 | 1.052163 | 1.210689 | 7.050878 | 5.524893 | 1.5387 | 3.858004 | 8.592199 | 2.515545 | 1.728391 | 7.344787 | 1.456137 | |
| median | 2.19 × 10−9 | 14.52688 | 25.60061 | 25.53597 | 2.31 × 10−9 | 22.87087 | 25.09763 | 19.67884 | 16.12811 | 19.92494 | 25.88952 | 22.04072 | 26.00117 | |
| rank | 1 | 4 | 11 | 13 | 2 | 8 | 9 | 7 | 3 | 6 | 10 | 5 | 12 | |
| C11-F2 | mean | −26.4809 | −22.3944 | −11.6301 | −8.06028 | −25.3005 | −8.61772 | −13.6102 | −8.31426 | −23.7019 | −9.22187 | −7.19675 | −23.0507 | −11.4007 |
| best | −27.2293 | −22.8813 | −14.0599 | −8.64276 | −26.6172 | −13.6641 | −20.5858 | −10.1138 | −25.4598 | −9.68401 | −8.44895 | −25.5945 | −14.0856 | |
| worst | −25.364 | −21.4054 | −9.06418 | −7.42364 | −24.2799 | −4.97971 | −8.78687 | −6.02627 | −21.5016 | −9.00778 | −6.49843 | −20.5637 | −9.44663 | |
| std | 0.825599 | 0.675642 | 2.045502 | 0.551116 | 1.068355 | 3.956082 | 4.985352 | 2.113823 | 1.696846 | 0.31722 | 0.911664 | 2.056796 | 2.156855 | |
| median | −26.6652 | −22.6454 | −11.6981 | −8.08736 | −25.1525 | −7.91351 | −12.534 | −8.55848 | −23.9231 | −9.09784 | −6.9198 | −23.0223 | −11.0353 | |
| rank | 1 | 5 | 7 | 12 | 2 | 10 | 6 | 11 | 3 | 9 | 13 | 4 | 8 | |
| C11-F4 | mean | −35.3025 | −29.4024 | −17.5227 | −16.7272 | −32.5006 | −27.7957 | −23.1492 | −27.1284 | −32.0504 | −13.2769 | −27.5051 | −7.4195 | −4.2567 |
| best | −35.4432 | −33.8574 | −19.4025 | −19.341 | −34.2508 | −30.6982 | −26.4941 | −31.727 | −34.1547 | −20.0052 | −34.1725 | −10.5338 | −7.32587 | |
| worst | −35.1685 | −27.2841 | −16.1919 | −13.8236 | −31.5536 | −25.9792 | −17.1297 | −24.2157 | −30.4483 | −5.71506 | −19.9298 | −2.61069 | 0 | |
| std | 0.153785 | 3.07155 | 1.378688 | 2.851785 | 1.199952 | 2.140053 | 4.438601 | 3.220723 | 1.563641 | 6.08285 | 6.544209 | 3.393814 | 3.200788 | |
| median | −35.2992 | −28.234 | −17.2482 | −16.8722 | −32.099 | −27.2526 | −24.4866 | −26.2855 | −31.7992 | −13.6936 | −27.9591 | −8.26678 | −4.85046 | |
| rank | 1 | 4 | 9 | 10 | 2 | 5 | 8 | 7 | 3 | 11 | 6 | 12 | 13 | |
| C11-F5 | mean | −28.2978 | −19.3848 | −10.0921 | −10.5136 | −27.3199 | −12.1459 | −18.3796 | −5.08497 | −22.3633 | 0 | −16.3851 | 0 | −0.8672 |
| best | −29.1661 | −23.0059 | −14.7254 | −11.5854 | −28.0821 | −21.209 | −23.0034 | −20.3399 | −26.5965 | 0 | −23.0059 | 0 | −3.46879 | |
| worst | −27.4293 | −16.8457 | −7.09818 | −9.51564 | −26.5001 | 0 | −15.0879 | 0 | −19.5117 | 0 | −8.64304 | 0 | 0 | |
| std | 1.003611 | 2.649821 | 3.386136 | 1.15452 | 0.874335 | 9.192985 | 3.399914 | 10.18012 | 3.19482 | 0 | 5.905717 | 0 | 1.736128 | |
| median | −28.2979 | −18.8438 | −9.27249 | −10.4768 | −27.3487 | −13.6873 | −17.7135 | 0 | −21.6726 | 0 | −16.9457 | 0 | 0 | |
| rank | 1 | 4 | 9 | 8 | 2 | 7 | 5 | 10 | 3 | 12 | 6 | 12 | 11 | |
| C11-F6 | mean | 0.785253 | 1.14754 | 2.024755 | 2.155071 | 0.867687 | 1.452179 | 2.188145 | 1.068278 | 1.208421 | 1.940935 | 1.044281 | 1.257057 | 2.212929 |
| best | 0.665035 | 0.998087 | 1.6614 | 1.83069 | 0.765584 | 1.177085 | 2.075871 | 0.954839 | 0.820258 | 1.889914 | 0.649331 | 0.85164 | 1.95787 | |
| worst | 0.875085 | 1.258533 | 2.187947 | 2.345592 | 1.064378 | 1.650897 | 2.297034 | 1.214887 | 1.950702 | 1.998965 | 1.272956 | 1.715245 | 2.385961 | |
| std | 0.088232 | 0.129965 | 0.247268 | 0.227312 | 0.135582 | 0.206732 | 0.091469 | 0.129917 | 0.523394 | 0.045935 | 0.272997 | 0.354366 | 0.192515 | |
| median | 0.800446 | 1.16677 | 2.124836 | 2.222001 | 0.820394 | 1.490368 | 2.189838 | 1.051694 | 1.031362 | 1.937431 | 1.127418 | 1.230672 | 2.253942 | |
| rank | 1 | 5 | 10 | 11 | 2 | 8 | 12 | 4 | 6 | 9 | 3 | 7 | 13 | |
| C11-F7 | mean | 220 | 220 | 276.5 | 349.25 | 220 | 425.5043 | 291.5 | 224.5 | 229 | 227 | 276.3886 | 826.2645 | 239.25 |
| best | 220 | 220 | 230 | 299 | 220 | 220 | 251 | 220 | 220 | 220 | 231 | 251 | 220 | |
| worst | 220 | 220 | 323 | 404 | 220 | 1042.017 | 351 | 238 | 256 | 238 | 350.5545 | 2184.43 | 259 | |
| std | 0 | 0 | 40.06085 | 43.11181 | 0 | 411.4195 | 45.36272 | 9.009 | 18.018 | 8.726516 | 55.21181 | 913.4908 | 15.96116 | |
| median | 220 | 220 | 276.5 | 347 | 220 | 220 | 282 | 220 | 220 | 225 | 262 | 434.8141 | 239 | |
| rank | 1 | 1 | 7 | 9 | 1 | 10 | 8 | 2 | 4 | 3 | 6 | 11 | 5 | |
| C11-F8 | mean | 9852.127 | 735,450.4 | 1,029,600 | 1,301,689 | 9549.131 | 69,153.55 | 548,774.3 | 93,478.54 | 28,444.15 | 625,190.3 | 955,208.4 | 981,885.4 | 2,206,877 |
| best | 6182.4 | 547,467.2 | 914,559 | 848,186.4 | 6045.388 | 47,218.02 | 446,320.4 | 46,944.39 | 21,243.75 | 506,258.2 | 710,857.7 | 561,536 | 2,183,812 | |
| worst | 12,039.41 | 873,535.9 | 1,112,084 | 1,528,229 | 11,684.98 | 78,837.01 | 612,232.3 | 166,066.1 | 34,209.17 | 713,782.7 | 1,193,111 | 1,351,642 | 2,234,596 | |
| std | 2542.993 | 147,235.4 | 86,895.62 | 308,607.9 | 2436.763 | 14,807.58 | 71,801.99 | 51,002.17 | 5811.795 | 97,974.59 | 198,631 | 328,589.5 | 25,018.57 | |
| median | 10,593.35 | 760,399.2 | 1,045,878 | 1,415,170 | 10,233.08 | 75,279.58 | 568,272.3 | 80,451.8 | 29,161.84 | 640,360.1 | 958,432.4 | 1,007,182 | 2,204,550 | |
| rank | 2 | 8 | 11 | 12 | 1 | 4 | 6 | 5 | 3 | 7 | 9 | 10 | 13 | |
| C11-F9 | mean | −22.2297 | −16.4886 | −8.89083 | −10.1972 | −21.5337 | −11.918 | −10.1325 | −17.3129 | −16.9511 | −10.2886 | −11.6632 | −10.3517 | −9.99235 |
| best | −22.2933 | −18.7915 | −9.07622 | −10.5958 | −21.6259 | −15.7644 | −10.7556 | −21.5793 | −21.4972 | −10.3194 | −11.8653 | −10.3775 | −10.0444 | |
| worst | −22.1512 | −14.5174 | −8.70287 | −9.81793 | −21.3959 | −9.99611 | −9.63545 | −10.3361 | −12.1207 | −10.243 | −11.1938 | −10.2988 | −9.94759 | |
| std | 0.072979 | 2.101764 | 0.195165 | 0.318176 | 0.109809 | 2.63253 | 0.583689 | 5.242781 | 5.152578 | 0.034325 | 0.315282 | 0.036848 | 0.041836 | |
| median | −22.2372 | −16.3228 | −8.89211 | −10.1875 | −21.5565 | −10.9557 | −10.0695 | −18.668 | −17.0932 | −10.296 | −11.7969 | −10.3653 | −9.9887 | |
| rank | 1 | 5 | 13 | 10 | 2 | 6 | 11 | 3 | 4 | 9 | 7 | 8 | 12 | |
| C11-F10 | mean | 275,953.6 | 295,554.2 | 1,728,003 | 10,733,179 | 658,101.1 | 8,232,813 | 1,532,582 | 1,074,459 | 4,504,623 | 5,689,705 | 1,581,079 | 5,704,387 | 6,706,720 |
| best | 111,906.1 | 119,989.6 | 1,671,593 | 10,440,242 | 457,716.5 | 5,796,617 | 1,337,713 | 821,072.7 | 4,262,675 | 5,689,705 | 1,296,552 | 5,689,705 | 6,664,292 | |
| worst | 435,202.3 | 462,364 | 1,774,439 | 10,907,934 | 876,974.8 | 11,926,409 | 1,706,194 | 1,263,682 | 4,637,288 | 5,689,705 | 1,730,846 | 5,723,987 | 6,745,470 | |
| std | 133,433.5 | 141,153.2 | 43,998.11 | 203,866.3 | 219,334.8 | 2,613,703 | 171,410.9 | 198,494.1 | 173,309.1 | 0 | 193,907.3 | 17,440.09 | 40,315.03 | |
| median | 278,353 | 299,931.5 | 1,732,991 | 10,792,271 | 648,856.6 | 7,604,113 | 1,543,210 | 1,106,542 | 4,559,265 | 5,689,705 | 1,648,460 | 5,701,929 | 6,708,560 | |
| rank | 1 | 2 | 7 | 13 | 3 | 12 | 5 | 4 | 8 | 9 | 6 | 10 | 11 | |
| C11-F11 | mean | 1,255,580 | 3,917,084 | 7,200,862 | 15,954,845 | 1,339,465 | 6,290,493 | 6,632,909 | 1,360,726 | 1,564,264 | 15,605,750 | 6,891,201 | 2,353,372 | 15,830,924 |
| best | 1,163,262 | 3,701,366 | 6,994,873 | 14,807,307 | 1,251,074 | 5,759,789 | 6,399,676 | 1,265,380 | 1,294,515 | 14,467,675 | 6,772,346 | 2,135,592 | 15,403,057 | |
| worst | 1,319,053 | 4,098,419 | 7,301,082 | 16,959,124 | 1,419,141 | 7,038,850 | 6,789,678 | 1,434,252 | 1,817,236 | 16,563,952 | 6,988,061 | 2,733,600 | 16,293,068 | |
| std | 65,830.74 | 176,751.4 | 139,435.4 | 883,563.4 | 69,069.69 | 556,954.8 | 167,909.8 | 71,081.87 | 231,779.7 | 890,323.8 | 93,690.64 | 272,693.2 | 385,833 | |
| median | 1,270,002 | 3,934,275 | 7,253,747 | 16,026,475 | 1,343,823 | 6,181,665 | 6,671,142 | 1,371,635 | 1,572,653 | 15,695,687 | 6,902,198 | 2,272,149 | 15,813,785 | |
| rank | 1 | 6 | 10 | 13 | 2 | 7 | 8 | 3 | 4 | 11 | 9 | 5 | 12 | |
| C11-F12 | mean | 15,444.21 | 15,689.16 | 15,454.67 | 16,506.66 | 16,407.44 | 15,508.05 | 15,512.23 | 15,485.82 | 15,505.75 | 16,060.09 | 131,124.1 | 15,519.94 | 18,237.52 |
| best | 15,444.19 | 15,444.23 | 15,451.9 | 15,996.18 | 15,444.19 | 15,481.63 | 15,477.65 | 15,455.13 | 15,478.25 | 15,557.26 | 80,466.2 | 15,498.93 | 15,484.07 | |
| worst | 15,444.23 | 16,387.09 | 15,457.72 | 17,774.94 | 16,970.37 | 15,533.33 | 15,548.93 | 15,509.95 | 15,552.24 | 16,984.35 | 234,290 | 15,531.07 | 25,305.01 | |
| std | 0.020683 | 465.9733 | 2.453554 | 853.3277 | 700.8544 | 24.77537 | 30.85129 | 22.75544 | 32.19287 | 640.2204 | 70,818.17 | 14.34255 | 4739.424 | |
| median | 15,444.21 | 15,462.66 | 15,454.53 | 16,127.77 | 16,607.61 | 15,508.62 | 15,511.18 | 15,489.09 | 15,496.25 | 15,849.38 | 104,870.1 | 15,524.88 | 16,080.5 | |
| rank | 1 | 8 | 2 | 11 | 10 | 5 | 6 | 3 | 4 | 9 | 13 | 7 | 12 | |
| C11-F13 | mean | 18,766.8 | 18,401.87 | 18,913.78 | 276,941.8 | 18,236.95 | 19,424.61 | 19,313 | 19,268.63 | 19,403.55 | 194,506.5 | 19,156.17 | 19,347.18 | 19,047.76 |
| best | 18,634.88 | 18,212.02 | 18,679.04 | 202,857.5 | 18,194.76 | 19,121.09 | 18,855.02 | 18,783.36 | 19,265.81 | 61,049.2 | 18,921.5 | 19,111.92 | 18,922.68 | |
| worst | 18,882.86 | 18,524.11 | 19,086.98 | 400,961 | 18,297.22 | 19,971.19 | 19,580.38 | 19,581.93 | 19,546.94 | 387,895.1 | 19,457.67 | 19,602.18 | 19,231.56 | |
| std | 102.2456 | 134.2627 | 181.9858 | 88,823.39 | 47.91151 | 374.7453 | 317.2627 | 341.1623 | 134.9524 | 145,574.9 | 223.2481 | 265.7884 | 134.1612 | |
| median | 18,774.74 | 18,435.69 | 18,944.54 | 251,974.4 | 18,227.92 | 19,303.08 | 19,408.29 | 19,354.62 | 19,400.72 | 164,540.9 | 19,122.76 | 19,337.31 | 19,018.39 | |
| rank | 3 | 2 | 4 | 13 | 1 | 11 | 8 | 7 | 10 | 12 | 6 | 9 | 5 | |
| C11-F14 | mean | 32,845.08 | 33,006.71 | 239,954.4 | 2,343,498 | 35,130.85 | 35,121.25 | 106,277.4 | 33,151.84 | 33,126.78 | 11,213,596 | 345,205.2 | 33,338.43 | 10,339,440 |
| best | 32,809.43 | 32,844.61 | 61,174.85 | 975,713.9 | 34,595.97 | 33,144.97 | 33,167.07 | 32,986.32 | 32,995.68 | 3,908,323 | 256,209.7 | 33,323.21 | 3,973,087 | |
| worst | 32,880.63 | 33,126.57 | 439,827.3 | 6,129,448 | 35,975.27 | 40,825.27 | 215,083.4 | 33,336.37 | 33,260.65 | 17,145,622 | 392,625.8 | 33,355.63 | 18,906,172 | |
| std | 32.99729 | 135.0197 | 203,624.7 | 2,530,421 | 594.1606 | 3806.85 | 89,156.14 | 145.1283 | 133.9616 | 6,524,456 | 60,919.36 | 14.07213 | 6,314,495 | |
| median | 32,845.14 | 33,027.82 | 229,407.7 | 1,134,415 | 34,976.08 | 33,257.39 | 88,429.47 | 33,142.34 | 33,125.38 | 11,900,220 | 365,992.7 | 33,337.45 | 9,239,251 | |
| rank | 1 | 2 | 9 | 11 | 7 | 6 | 8 | 4 | 3 | 13 | 10 | 5 | 12 | |
| C11-F15 | mean | 133,287.9 | 140,692.8 | 140,076.2 | 2,362,861 | 141,598.2 | 149,095.6 | 146,593 | 141,880.2 | 141,577 | 98,977,989 | 21,150,022 | 94,639,175 | 85,867,595 |
| best | 131,118.5 | 134,258.9 | 137,666.4 | 551,007.8 | 134,966.6 | 146,561.1 | 141,445.7 | 137,935.6 | 136,714 | 88,655,574 | 2,767,679 | 74,104,169 | 33,265,483 | |
| worst | 134,522.7 | 151,586.1 | 142,366.4 | 5,916,825 | 145,841.3 | 152,103.6 | 156,853.3 | 147,252.9 | 149,667.1 | 1.19 × 108 | 42,558,036 | 1.07 × 108 | 1.09 × 108 | |
| std | 1526.05 | 7718.994 | 2597.529 | 2,415,484 | 4710.937 | 2385.079 | 7075.949 | 4394.903 | 6061.095 | 13,890,967 | 16,645,999 | 14,574,652 | 35,688,282 | |
| median | 133,755.2 | 138,463.1 | 140,136 | 1,491,805 | 142,792.5 | 148,858.9 | 144,036.6 | 141,166.2 | 139,963.5 | 94,111,524 | 19,637,186 | 98,813,738 | 1.01 × 108 | |
| rank | 1 | 3 | 2 | 9 | 5 | 8 | 7 | 6 | 4 | 13 | 10 | 12 | 11 | |
| C11-F16 | mean | 1,941,587 | 4,117,826 | 6.39 × 109 | 1.91 × 1010 | 2,040,837 | 9.08 × 108 | 1.14 × 1010 | 2,613,192 | 2,499,625 | 2.23 × 1010 | 1.45 × 1010 | 1.94 × 1010 | 2.1 × 1010 |
| best | 1,931,795 | 1,945,829 | 5.81 × 109 | 1.37 × 1010 | 1,966,761 | 1.5 × 108 | 9.92 × 109 | 2,226,241 | 2,159,827 | 1.83 × 1010 | 1.24 × 1010 | 1.55 × 1010 | 1.76 × 1010 | |
| worst | 1,954,752 | 9,745,854 | 7 × 109 | 2.33 × 1010 | 2,071,974 | 1.41 × 109 | 1.25 × 1010 | 3,051,146 | 3,268,005 | 2.66 × 1010 | 1.89 × 1010 | 2.36 × 1010 | 2.53 × 1010 | |
| std | 10,357.32 | 3,769,921 | 5.24 × 108 | 4.13 × 109 | 49,645.15 | 5.57 × 108 | 1.16 × 109 | 377,328.4 | 520,697.6 | 3.47 × 109 | 3.04 × 109 | 3.31 × 109 | 3.41 × 109 | |
| median | 1,939,901 | 2,389,810 | 6.38 × 109 | 1.96 × 1010 | 2,062,306 | 1.03 × 109 | 1.16 × 1010 | 2,587,691 | 2,285,334 | 2.21 × 1010 | 1.32 × 1010 | 1.93 × 1010 | 2.05 × 1010 | |
| rank | 1 | 5 | 7 | 10 | 2 | 6 | 8 | 4 | 3 | 13 | 9 | 11 | 12 | |
| C11-F17 | mean | 971,895.4 | 1,616,414 | 16,449,493 | 1.45 × 108 | 942,207 | 2,194,127 | 8,381,389 | 1,024,624 | 1,131,755 | 34,761,039 | 9,159,466 | 1.79 × 108 | 1.25 × 108 |
| best | 966,588.8 | 1,094,971 | 9,228,474 | 1 × 108 | 939,995.7 | 1,628,158 | 2,842,721 | 958,818.7 | 977,032.3 | 27,241,740 | 942,142.4 | 1.57 × 108 | 1.22 × 108 | |
| worst | 977,835.8 | 2,285,712 | 29,396,167 | 1.66 × 108 | 947,316 | 2,469,335 | 17,189,839 | 1,193,542 | 1,328,731 | 37,388,284 | 20,419,966 | 2.05 × 108 | 1.27 × 108 | |
| std | 6043.012 | 494,783.1 | 9,399,624 | 30,732,120 | 3441.709 | 385,943.9 | 6,235,833 | 113,169.6 | 170,025 | 5,019,190 | 8,622,080 | 23,693,281 | 1,843,552 | |
| median | 971,578.6 | 1,542,486 | 13,586,665 | 1.57 × 108 | 940,758.1 | 2,339,508 | 6,746,499 | 973,067.3 | 1,110,628 | 37,207,066 | 7,637,878 | 1.78 × 108 | 1.25 × 108 | |
| rank | 2 | 5 | 9 | 12 | 1 | 6 | 7 | 3 | 4 | 10 | 8 | 13 | 11 | |
| C11-F18 | mean | 1,015,441 | 2,590,116 | 16,582,334 | 1.42 × 108 | 988,564.9 | 2,966,643 | 7,039,845 | 1,550,619 | 1,435,166 | 35,274,115 | 17,309,844 | 1.72 × 108 | 1.25 × 108 |
| best | 970,440.6 | 1,954,981 | 14,730,898 | 1.23 × 108 | 943,556.8 | 2,458,931 | 4,995,010 | 1,347,378 | 1,246,367 | 28,101,008 | 15,122,456 | 1.6 × 108 | 1.21 × 108 | |
| worst | 1,082,763 | 3,891,235 | 20,548,870 | 1.79 × 108 | 1,060,958 | 3,238,732 | 9,466,270 | 1,926,756 | 1,590,758 | 46,848,216 | 18,652,552 | 1.84 × 108 | 1.28 × 108 | |
| std | 52,663 | 880,283.7 | 2,680,868 | 26,129,675 | 54,245.33 | 363,495.4 | 2,012,868 | 259,593.2 | 174,182.5 | 8,801,161 | 1,578,438 | 12,279,513 | 3,177,603 | |
| median | 1,004,281 | 2,257,125 | 15,524,785 | 1.34 × 108 | 974,872.4 | 3,084,455 | 6,849,050 | 1,464,171 | 1,451,771 | 33,073,619 | 17,732,185 | 1.72 × 108 | 1.26 × 108 | |
| rank | 2 | 5 | 8 | 12 | 1 | 6 | 7 | 4 | 3 | 10 | 9 | 13 | 11 | |
| C11-F19 | mean | 974,847.4 | 3,058,450 | 14,619,890 | 1.54 × 108 | 981,440.7 | 2,527,801 | 7,589,122 | 965,971 | 1,036,557 | 30,666,064 | 12,400,485 | 1.92 × 108 | 1.29 × 108 |
| best | 944,022.2 | 1,019,342 | 12,702,812 | 1.34 × 108 | 945,830.8 | 2,410,961 | 2,746,274 | 951,663.6 | 960,231.2 | 28,071,917 | 11,125,050 | 1.72 × 108 | 1.26 × 108 | |
| worst | 1,014,915 | 8,406,301 | 16,683,672 | 1.83 × 108 | 1,019,498 | 2,730,807 | 13,705,947 | 1,001,277 | 1,185,908 | 36,835,950 | 15,782,650 | 2.21 × 108 | 1.31 × 108 | |
| std | 36,191.37 | 3,584,352 | 1,653,942 | 20,589,549 | 39,571.94 | 152,159.2 | 4,553,151 | 23,629.47 | 101,531.9 | 4,176,821 | 2,261,768 | 21,032,934 | 2,385,169 | |
| median | 970,226.3 | 1,404,078 | 14,546,539 | 1.49 × 108 | 980,217.1 | 2,484,719 | 6,952,133 | 955,471.6 | 1,000,045 | 28,878,195 | 11,347,120 | 1.88 × 108 | 1.3 × 108 | |
| rank | 2 | 6 | 9 | 12 | 3 | 5 | 7 | 1 | 4 | 10 | 8 | 13 | 11 | |
| C11-F20 | mean | 10.49163 | 18.43484 | 37.38995 | 91.01355 | 11.21275 | 29.05794 | 40.96432 | 29.92222 | 25.24142 | 129.9098 | 44.83753 | 121 | 95.16216 |
| best | 8.851506 | 17.10456 | 35.08192 | 66.45898 | 9.358565 | 19.49597 | 28.1708 | 22.61783 | 24.07106 | 106.0516 | 31.58387 | 109.7915 | 78.9184 | |
| worst | 13.71088 | 20.77307 | 38.49468 | 115.651 | 14.72046 | 37.54154 | 56.17231 | 36.91662 | 26.50252 | 168.6126 | 53.55251 | 130.3309 | 126.8521 | |
| std | 2.187018 | 1.638565 | 1.604061 | 21.75983 | 2.3932 | 7.98459 | 14.64249 | 5.883188 | 0.997189 | 26.96817 | 9.367526 | 10.30455 | 21.87485 | |
| median | 9.702059 | 17.93087 | 37.9916 | 90.97211 | 10.386 | 29.59713 | 39.75708 | 30.07722 | 25.19605 | 122.4875 | 47.10687 | 121.9389 | 87.43907 | |
| rank | 1 | 3 | 7 | 10 | 2 | 5 | 8 | 6 | 4 | 13 | 9 | 12 | 11 | |
| C11-F21 | mean | 13.73264 | 27.48089 | 47.41507 | 74.30445 | 14.63561 | 34.45979 | 38.14793 | 32.33235 | 23.10522 | 99.56062 | 59.11908 | 114.8943 | 114.5445 |
| best | 12.11314 | 25.26953 | 41.00099 | 52.03457 | 12.85559 | 30.74852 | 36.12422 | 26.44499 | 21.55421 | 67.47136 | 47.68592 | 110.8849 | 84.39572 | |
| worst | 17.85657 | 32.64845 | 56.32061 | 85.38791 | 18.951 | 36.50066 | 41.20724 | 38.10353 | 25.6474 | 131.7346 | 70.84651 | 119.2162 | 147.2729 | |
| std | 2.759916 | 3.47892 | 7.092501 | 15.12056 | 2.890697 | 2.552249 | 2.1656 | 6.458469 | 1.934922 | 28.15673 | 9.498156 | 3.70323 | 27.02112 | |
| median | 12.48042 | 26.00279 | 46.16933 | 79.89766 | 13.36792 | 35.295 | 37.63014 | 32.39043 | 22.60963 | 99.51824 | 58.97195 | 114.7381 | 113.2546 | |
| rank | 1 | 4 | 8 | 10 | 2 | 6 | 7 | 5 | 3 | 11 | 9 | 13 | 12 | |
| C11-F22 | mean | 3.300478 | 15.02557 | 25.74562 | 26.00412 | 3.521917 | 20.93273 | 24.34703 | 20.30298 | 13.87947 | 19.79529 | 25.67295 | 19.27164 | 25.88474 |
| best | 4.16 × 10−10 | 11.75673 | 24.83901 | 25.15683 | 4.53 × 10−10 | 12.96597 | 22.0416 | 16.91438 | 1.775842 | 17.00127 | 23.71442 | 8.416087 | 24.27333 | |
| worst | 13.20191 | 19.29177 | 26.94225 | 27.78769 | 14.08767 | 25.02322 | 25.15126 | 24.93986 | 21.48584 | 22.33001 | 27.19836 | 24.58904 | 27.26328 | |
| std | 6.607557 | 3.132729 | 1.052163 | 1.210689 | 7.050878 | 5.524893 | 1.5387 | 3.858004 | 8.592199 | 2.515545 | 1.728391 | 7.344787 | 1.456137 | |
| median | 2.19 × 10−9 | 14.52688 | 25.60061 | 25.53597 | 2.31 × 10−9 | 22.87087 | 25.09763 | 19.67884 | 16.12811 | 19.92494 | 25.88952 | 22.04072 | 26.00117 | |
| rank | 1 | 4 | 11 | 13 | 2 | 8 | 9 | 7 | 3 | 6 | 10 | 5 | 12 | |
| Sum rank | 27 | 88 | 160 | 222 | 54 | 142 | 152 | 100 | 84 | 201 | 167 | 193 | 219 | |
| Mean rank | 1.285714 | 4.190476 | 7.619048 | 10.57143 | 2.571429 | 6.761905 | 7.238095 | 4.761905 | 4 | 9.571429 | 7.952381 | 9.190476 | 10.42857 | |
| Total rank | 1 | 4 | 8 | 13 | 2 | 6 | 7 | 5 | 3 | 11 | 9 | 10 | 12 | |
| Wilcoxon: p-value | 4.8 × 10−12 | 8.49 × 10−15 | 1.71 × 10−15 | 0.001914 | 5.36 × 10−15 | 5.76 × 10−15 | 1.75 × 10−11 | 2.11 × 10−12 | 3.66 × 10−15 | 8.8 × 10−15 | 1.71 × 10−15 | 2.5 × 10−15 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghani, M.; Trojovský, P.; Malik, O.P. Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 121. https://doi.org/10.3390/biomimetics8010121
Dehghani M, Trojovský P, Malik OP. Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics. 2023; 8(1):121. https://doi.org/10.3390/biomimetics8010121
Chicago/Turabian StyleDehghani, Mohammad, Pavel Trojovský, and Om Parkash Malik. 2023. "Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems" Biomimetics 8, no. 1: 121. https://doi.org/10.3390/biomimetics8010121
APA StyleDehghani, M., Trojovský, P., & Malik, O. P. (2023). Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics, 8(1), 121. https://doi.org/10.3390/biomimetics8010121






