Living Plants Ecosystem Sensing: A Quantum Bridge between Thermodynamics and Bioelectricity
Abstract
1. Introduction
2. Materials and Methods
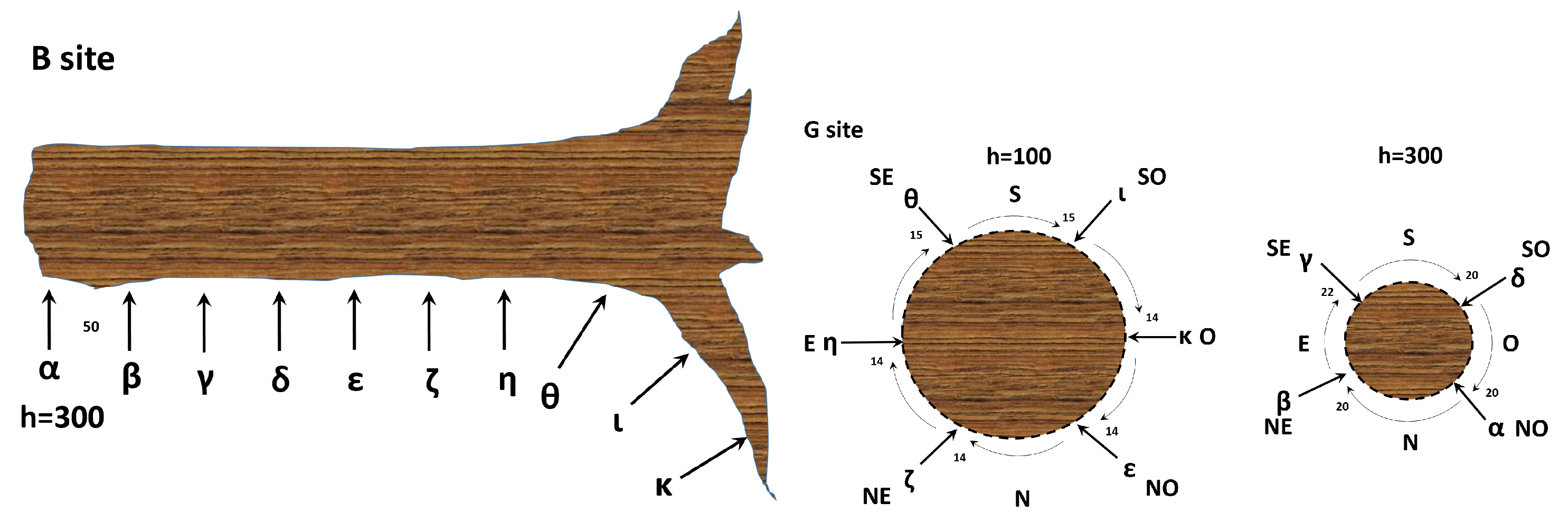
2.1. Experimental Setup
2.2. Numerical Analysis
- (1)
- The Shannon entropy () is a measure of the uncertainty of a discrete random variable. Given a random variable s with n elements, , and its probability distribution , the Shannon entropy can be expressed mathematically as in Equation (1).
- (2)
- (3)
- The Tsallis entropy (), a generalization of the standard Boltzmann–Gibbs entropy, represents a non-extensive entropy measure [42]. The mathematical expression of this entropy is represented by Equation (3), in which q and k denote the degree of non-extensivity and a positive constant, respectively. Our empirical study implements a setting of and .
- (4)
- The space filling () is defined as the ratio of non-zero elements in the signal s to the total length of the signal.
- (5)
- The Expressiveness () is determined as the ratio of the Shannon entropy () to the space filling (). This metric provides an indication of the “economy of diversity”.
- (6)
- The diversity index () quantitatively assesses the number of unique activities of interest present in the acquired signal and considers phylogenetic relationships between these activities, including aspects, such as the richness, divergence, and evenness. Its mathematical formulation is given by Equation (4), where we set the parameter q to 3.
- (7)
- The Simpson diversity () is a measure of the concentration of individuals classified into types and can be calculated as . The range of is between 0 and 1, with 1 indicating infinite diversity, and 0 representing no diversity.
- (8)
- The Lempel–Ziv complexity () is utilised as a measure of temporal signal diversity, with a focus on its compressibility. The calculation of was performed using the Kolmogorov complexity algorithm [43]. This metric has been found to be valuable in providing a scalar measurement for estimating the bandwidth of random processes and quantifying the harmonic variability in quasi-periodic signals.
- (9)
- The perturbation complexity index (PCI) () is determined by the normalisation of the Lempel–Ziv complexity of the spatiotemporal pattern of the signal, relative to its Shannon entropy ().
- (10)
- The Kolmogorov complexity () is a metric that evaluates the information content of a signal. It quantifies the minimum length of a binary code required to describe the signal, assuming an optimal encoding, and can be expressed mathematically as per Equation (5).where is the output of the binary program when executed on a fixed reference universal Turing machine, and is the length of the binary program .
- (11)
- The fractal dimension () quantifies the self-similarity of a signal across multiple scales. In accordance with the notion that signals exhibiting more irregular or chaotic patterns are expected to exhibit a higher fractal dimension than signals featuring more regular or predictable patterns, in this study, the fractal dimension of a signal was calculated using the Higuchi method [44]. This method is based on the fractal dimension formula for a curve as represented by . Here, the parameter d represents the step size used in signal sampling, and represents the natural logarithm.
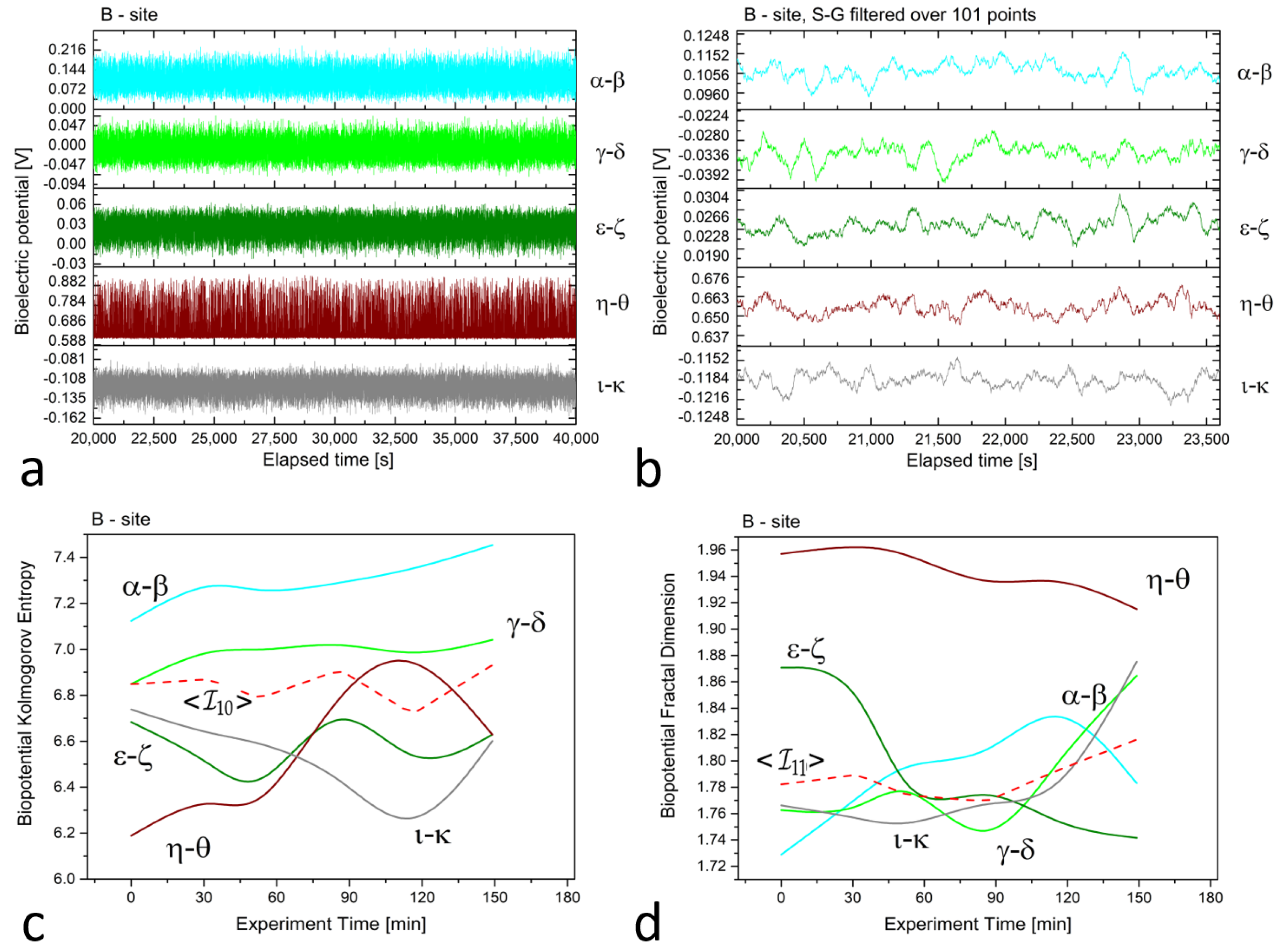
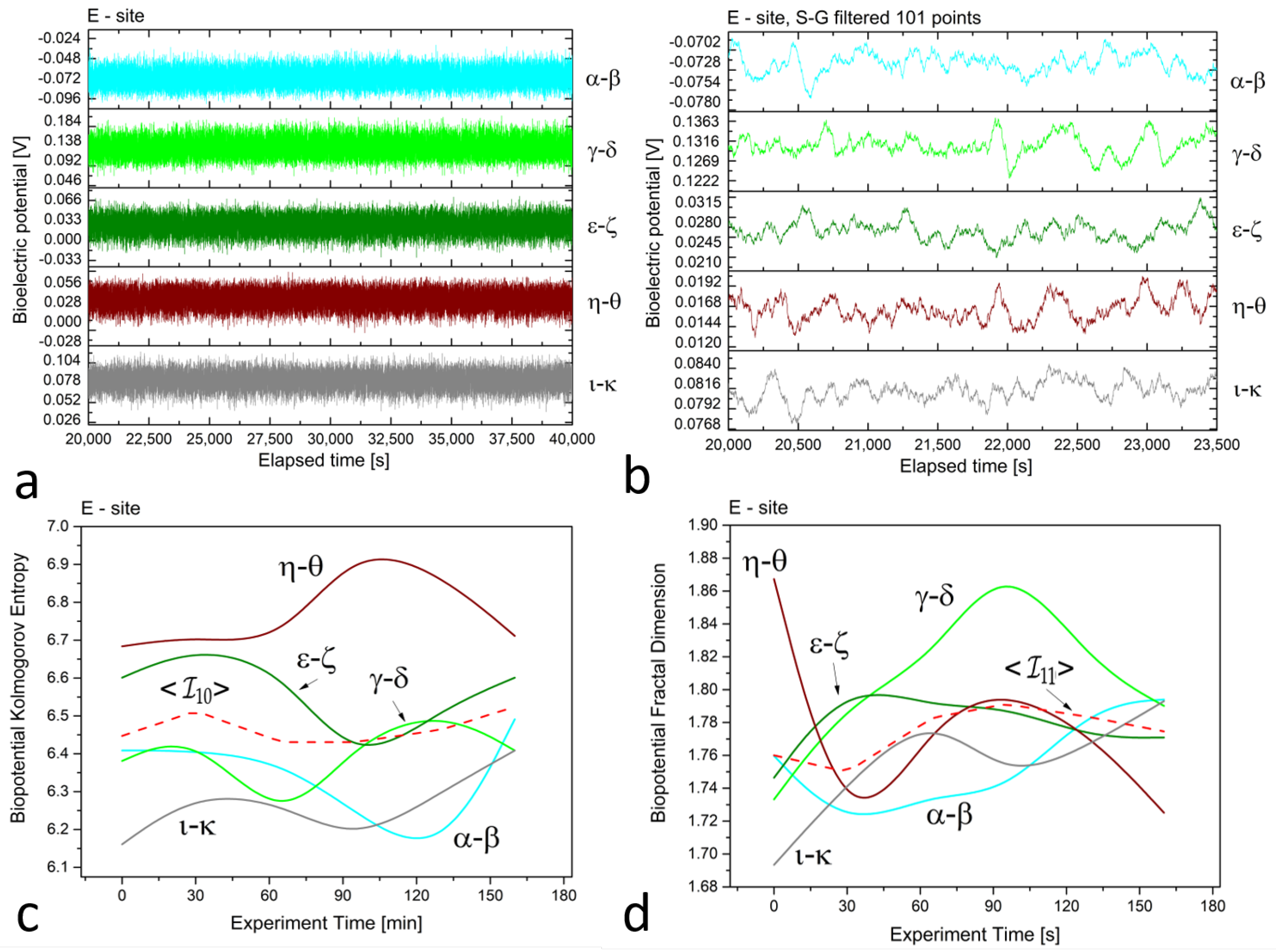
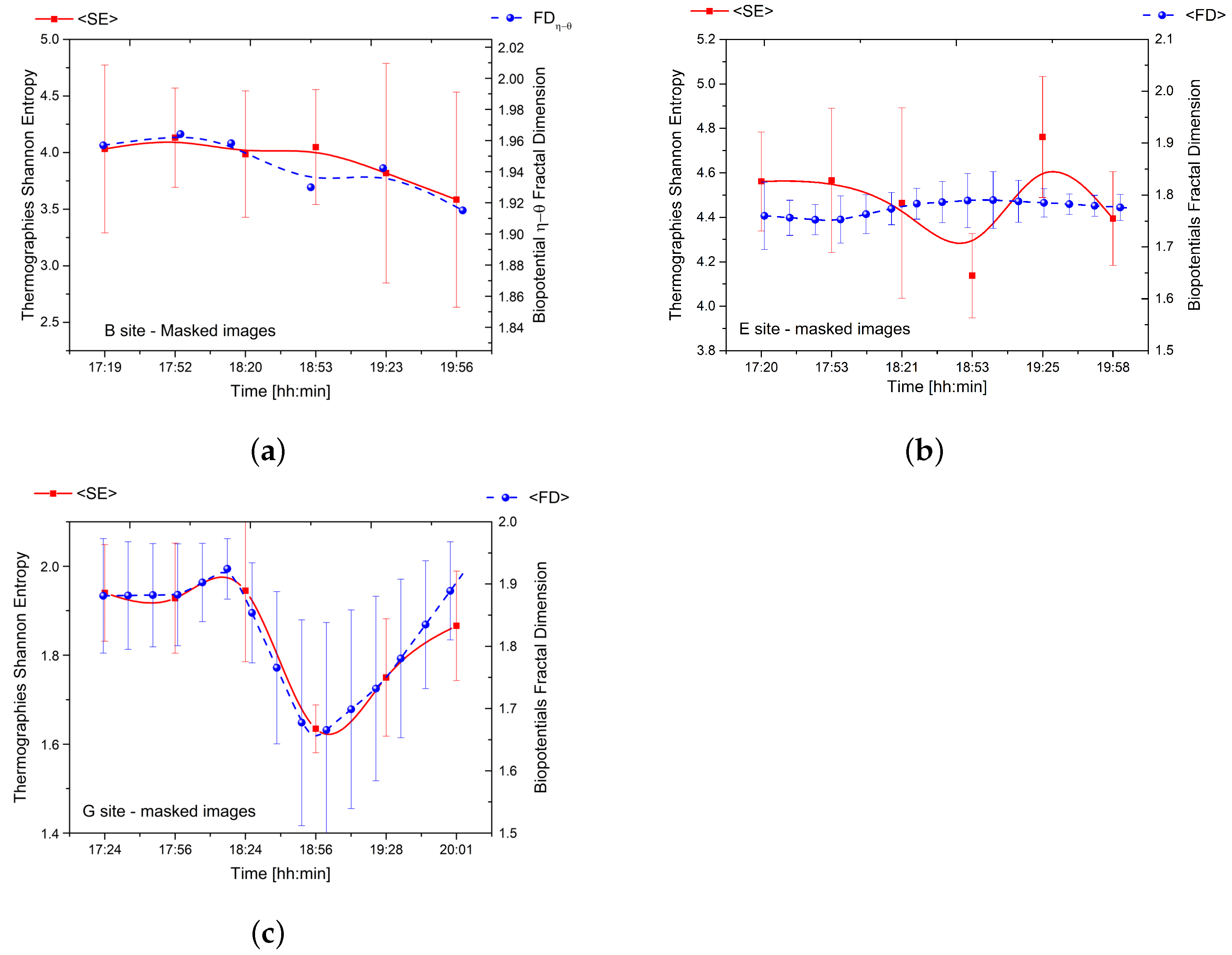
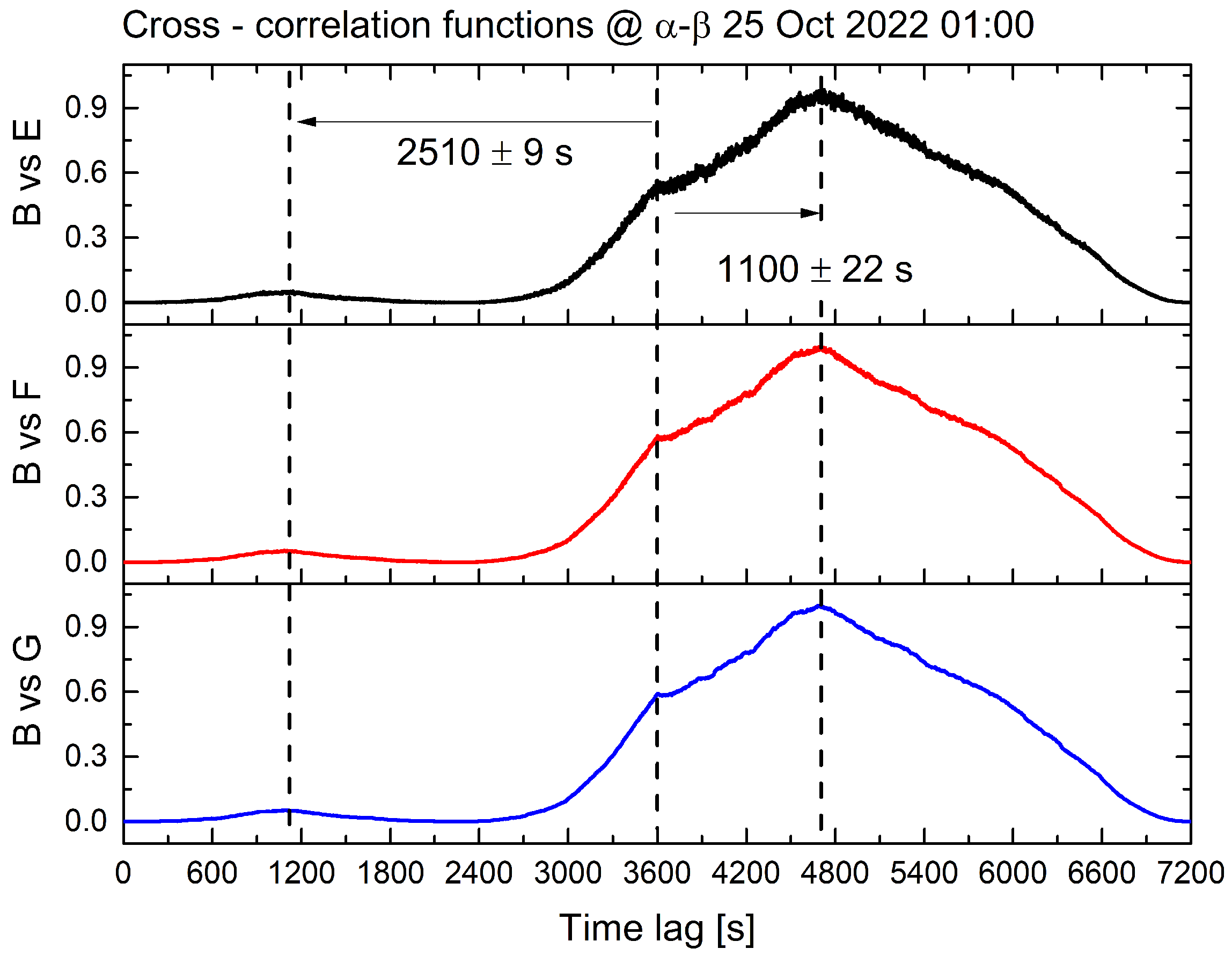
3. Results
4. Theoretical Modelling
4.1. On the Molecular Dynamics Underlying the Observed Electrical Activity
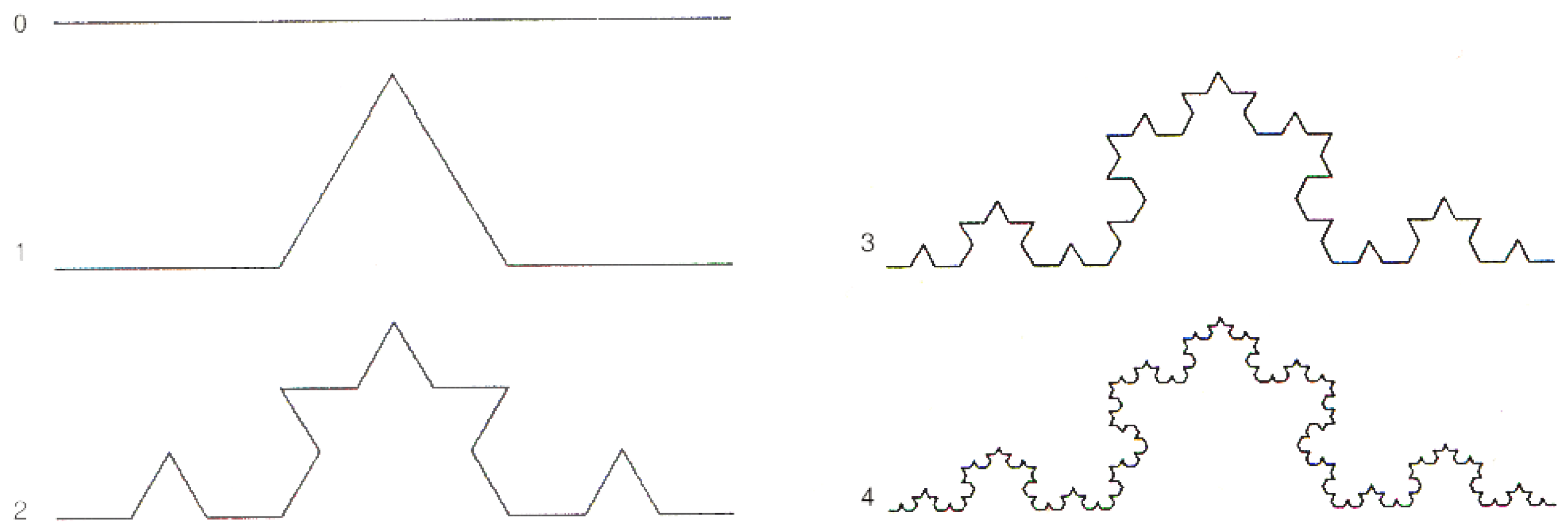
4.2. Thermal Effects, Free Energy, Entropy, and Fractal Self-Similarity
4.3. Entanglement and Collective Dynamical Effects
5. Conclusions and Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Dipole-Wave-Quanta Condensation and Bioelectric Potential
Appendix A.2. Entropy and the Arrow of Time
Appendix A.3. Fractal Self-Similarity and Coherent States
References
- Trewavas, A. Plant intelligence: Mindless mastery. Nature 2002, 415, 841. [Google Scholar] [CrossRef] [PubMed]
- Trewavas, A. Green plants as intelligent organisms. Trends Plant Sci. 2005, 10, 413–419. [Google Scholar] [CrossRef] [PubMed]
- Karpiński, S.; Szechyńska-Hebda, M. Secret life of plants: From memory to intelligence. Plant Signal. Behav. 2010, 5, 1391–1394. [Google Scholar] [CrossRef] [PubMed]
- Trewavas, A. Intelligence, cognition, and language of green plants. Front. Psychol. 2016, 7, 588. [Google Scholar] [CrossRef]
- Trewavas, T. Plant intelligence: An overview. BioScience 2016, 66, 542–551. [Google Scholar] [CrossRef]
- Brenner, E.D.; Stahlberg, R.; Mancuso, S.; Vivanco, J.; Baluška, F.; Van Volkenburgh, E. Plant neurobiology: An integrated view of plant signaling. Trends Plant Sci. 2006, 11, 413–419. [Google Scholar] [CrossRef]
- Leyser, O. The control of shoot branching: An example of plant information processing. Plant Cell Environ. 2009, 32, 694–703. [Google Scholar] [CrossRef]
- Garzón, P.C.; Keijzer, F. Cognition in plants. In Plant-Environment Interactions; Springer: Berlin/Heidelberg, Germany, 2009; pp. 247–266. [Google Scholar]
- Bassel, G.W. Information Processing and Distributed Computation in Plant Organs. Trends Plant Sci. 2018, 23, 994–1005. [Google Scholar] [CrossRef]
- Baluška, F.; Mancuso, S. Plant neurobiology: From sensory biology, via plant communication, to social plant behavior. Cogn. Process. 2009, 10, 3–7. [Google Scholar] [CrossRef]
- Baluska, F.; Mancuso, S. Plants and animals: Convergent evolution in action? In Plant-Environment Interactions; Springer: Berlin/Heidelberg, Germany, 2009; pp. 285–301. [Google Scholar]
- Mescher, M.C.; De Moraes, C.M. Role of plant sensory perception in plant–animal interactions. J. Exp. Bot. 2014, 66, 425–433. [Google Scholar] [CrossRef]
- Baluška, F.; Levin, M. On having no head: Cognition throughout biological systems. Front. Psychol. 2016, 7, 902. [Google Scholar] [CrossRef] [PubMed]
- Calvo, P.; Baluška, F.; Sims, A. “Feature Detection” vs. “Predictive Coding” Models of Plant Behavior. Front. Psychol. 2016, 7, 1505. [Google Scholar] [CrossRef] [PubMed]
- Baluška, F.; Lev-Yadun, S.; Mancuso, S. Swarm intelligence in plant roots. Trends Ecol. Evol. 2010, 25, 682–683. [Google Scholar] [CrossRef] [PubMed]
- Trebacz, K.; Dziubinska, H.; Krol, E. Electrical signals in long-distance communication in plants. In Communication in Plants; Springer: Berlin/Heidelberg, Germany, 2006; pp. 277–290. [Google Scholar]
- Fromm, J.; Lautner, S. Electrical signals and their physiological significance in plants. Plant Cell Environ. 2007, 30, 249–257. [Google Scholar] [CrossRef]
- Zimmermann, M.R.; Mithöfer, A. Electrical long-distance signaling in plants. In Long-Distance Systemic Signaling and Communication in Plants; Springer: Berlin/Heidelberg, Germany, 2013; pp. 291–308. [Google Scholar]
- Pickard, B.G. Spontaneous electrical activity in shoots of Ipomoea, Pisum and Xanthium. Planta 1971, 102, 91–113. [Google Scholar] [CrossRef]
- Simons, P. The role of electricity in plant movements. New Phytol. 1981, 87, 11–37. [Google Scholar] [CrossRef]
- Fromm, J. Control of phloem unloading by action potentials in Mimosa. Physiol. Plant. 1991, 83, 529–533. [Google Scholar] [CrossRef]
- Sibaoka, T. Rapid plant movements triggered by action potentials. Bot. Mag. Shokubutsu-Gaku 1991, 104, 73–95. [Google Scholar] [CrossRef]
- Volkov, A.G.; Foster, J.C.; Ashby, T.A.; Walker, R.K.; Johnson, J.A.; Markin, V.S. Mimosa pudica: Electrical and mechanical stimulation of plant movements. Plant Cell Environ. 2010, 33, 163–173. [Google Scholar] [CrossRef]
- Minorsky, P. Temperature sensing by plants: A review and hypothesis. Plant Cell Environ. 1989, 12, 119–135. [Google Scholar] [CrossRef]
- Volkov, A.G. Green plants: Electrochemical interfaces. J. Electroanal. Chem. 2000, 483, 150–156. [Google Scholar] [CrossRef]
- Roblin, G. Analysis of the variation potential induced by wounding in plants. Plant Cell Physiol. 1985, 26, 455–461. [Google Scholar] [CrossRef]
- Pickard, B.G. Action potentials in higher plants. Bot. Rev. 1973, 39, 172–201. [Google Scholar] [CrossRef]
- Brodribb, T.J. Xylem hydraulic physiology: The functional backbone of terrestrial plant productivity. Plant Sci. 2009, 177, 245–251. [Google Scholar] [CrossRef]
- Zimmermann, M.R.; Mithöfer, A.; Will, T.; Felle, H.H.; Furch, A.C. Herbivore-triggered electrophysiological reactions: Candidates for systemic signals in higher plants and the challenge of their identification. Plant Physiol. 2016, 170, 2407–2419. [Google Scholar] [CrossRef]
- Holbrook, N.M.; Zwieniecki, M.A. Vascular Transport in Plants; Elsevier: Cambridge, MA, USA, 2011. [Google Scholar]
- Namdari, F.; Bahador, N. Modeling trees internal tissue for estimating electrical leakage current. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1663–1674. [Google Scholar] [CrossRef]
- Chiolerio, A.; Dehshibi, M.; Vitiello, G.; Adamatzky, A. Molecular Collective Response and Dynamical Symmetry Properties in Biopotentials of Superior Plants: Experimental Observations and Quantum Field Theory Modeling. Symmetry 2022, 14, 1792. [Google Scholar] [CrossRef]
- Tattoni, C.; Ciolli, M.; Ferretti, F.; Cantiani, M.G. Monitoring spatial and temporal pattern of Paneveggio forest (northern Italy) from 1859 to 2006. IForest-Biogeosci. For. 2010, 3, 72. [Google Scholar] [CrossRef]
- Auricchio, L.; Cook, E.; Pacini, G. (Eds.) ‘Fatto di Fiemme’: Stradivari’s violins and the musical trees of the Paneveggio. In Invaluable Trees: Cultures of Nature; Voltaire Foundation: Oxford, UK, 2012. [Google Scholar]
- Burckle, L.; Grissino-Mayer, H.D. Stradivari, violins, tree rings, and the Maunder Minimum: A hypothesis. Dendrochronologia 2003, 21, 41–45. [Google Scholar] [CrossRef]
- Cherubini, P. Tree-ring dating of musical instruments. Science 2021, 373, 1434–1436. [Google Scholar] [CrossRef]
- Dehshibi, M.M.; Adamatzky, A. Electrical activity of fungi: Spikes detection and complexity analysis. Biosystems 2021, 203, 104373. [Google Scholar] [CrossRef]
- Dehshibi, M.M.; Chiolerio, A.; Nikolaidou, A.; Mayne, R.; Gandia, A.; Ashtari-Majlan, M.; Adamatzky, A. Stimulating Fungi Pleurotus ostreatus with Hydrocortisone. ACS Biomater. Sci. Eng. 2021, 7, 3718–3726. [Google Scholar] [CrossRef] [PubMed]
- Chiolerio, A.; Dehshibi, M.M.; Manfredi, D.; Adamatzky, A. Living wearables: Bacterial reactive glove. Biosystems 2022, 218, 104691. [Google Scholar] [CrossRef] [PubMed]
- Dehshibi, M.M.; Olugbade, T.; Diaz-de Maria, F.; Bianchi-Berthouze, N.; Tajadura-Jiménez, A. Pain level and pain-related behaviour classification using GRU-based sparsely-connected RNNs. arXiv 2022, arXiv:2212.14806. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, Statistical Laboratory of the University of California, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kaspar, F.; Schuster, H. Easily calculable measure for the complexity of spatiotemporal patterns. Phys. Rev. A 1987, 36, 842. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Itzykson, C.; Zuber, J. Electromagnetic Field and Spontaneous Symmetry Breaking in Biological Matter; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Umezawa, H.; Matsumoto, H.; Tachiki, M. Thermo Field Dynamics and Condensed States; North-Holland: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Umezawa, H. Advanced Field Theory: Micro, Macro, and Thermal Physics; AIP: New York, NY, USA, 1993. [Google Scholar]
- Blasone, M.; Jizba, P.; Vitiello, G. Quantum Field Theory and Its Macroscopic Manifestations; Imperial College Press: London, UK, 2011. [Google Scholar]
- Matsumoto, H.; Umezawa, H.; Vitiello, G.; Wyly, J. Spontaneous breakdown of a non-Abelian symmetry. Phys. Rev. 1974, D9, 2806–2813. [Google Scholar] [CrossRef]
- Shah, M.; Umezawa, H.; Vitiello, G. Relation among spin operators and magnons. Phys. Rev. 1974, B10, 4724–4726. [Google Scholar] [CrossRef]
- Matsumoto, H.; Papastamatiou, N.J.; Umezawa, H.; Vitiello, G. Dynamical rearrangement in Anderson-Higgs-Kibble mechanism. Nucl. Phys. B 1975, 97, 61–89. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. A quantum field theoretical approach to the collective behaviour of biological systems. Nucl. Phys. B 1985, 251, 375–400. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. Electromagnetic field and spontaneous symmetry breaking in biological matter. Nucl. Phys. B 1986, 275, 185–199. [Google Scholar] [CrossRef]
- Matsumoto, H.; Papastamatiou, N.J.; Umezawa, H. The boson transformation and the vortex solutions. Nucl. Phys. B 1975, 97, 90–124. [Google Scholar] [CrossRef]
- Fermi, E. Termodinamica; Boringhieri: Torino, Italy, 1958. [Google Scholar]
- Landau, L.; Lifshitz, E.M. Statistical Physics; Pergamon Press: Oxford, UK, 1958. [Google Scholar]
- Vitiello, G. Fractals, coherent states and self-similarity induced noncommutative geometry. Phys. Lett. A 2012, 376, 2527–2532. [Google Scholar] [CrossRef]
- Vitiello, G. On the isomorphism between dissipative systems, fractal self-similarity and electrodynamics. Toward an integrated vision of nature. Systems 2014, 2, 203–216. [Google Scholar] [CrossRef]
- Celeghini, E.; Rasetti, M.; Vitiello, G. Quantum Dissipation. Ann. Phys. 1992, 215, 156–170. [Google Scholar] [CrossRef]
- Perelomov, A. Generalized Coherent States and Their Applications; Springer: Berlin, Germany, 1986. [Google Scholar]
- Hilborn, R. Chaos and Nonlinear Dynamics; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Sabbadini, S.; Vitiello, G. Entanglement and phase-mediated correlations in quantum field theory. Application to brain-mind states. Appl. Sci. 2019, 9, 3203. [Google Scholar] [CrossRef]
- Vitiello, G. Fractals, metamorphoses and symmetries in quantum field theory. EPJ Web Conf. 2022, 263, 01008. [Google Scholar] [CrossRef]
- Vitiello, G. Symmetries and Metamorphoses. Symmetry 2020, 12, 907. [Google Scholar] [CrossRef]
- Gerry, C.; Knight, P. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Lechelon, M.; Meriguet, Y.; Gori, M.; Ruffenach, S.; Nardecchia, I.; Floriani, E.; Coquillat, D.; Teppe, F.; Mailfert, S.; Marguet, D.; et al. Experimental evidence for long-distance electrodynamic intermolecular forces. Sci. Adv. 2022, 8, eabl5855. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S. (Eds.) Fractals in Science; Springer: Berlin, Germany, 1995. [Google Scholar]
- Peitgen, H.; Jurgens, H.; Saupe, D. Chaos and Fractals. New Frontiers of Science; Springer: Berlin, Germany, 1986. [Google Scholar]
- Bak, P.; Creutz, M. Fractals and self-organized criticality. In Fractals in Science; Bunde, A., Havlin, S., Eds.; Springer: Berlin, Germany, 1995. [Google Scholar]
- Klauder, J.; Skagerstam, B. Coherent States; World Scientific: Singapore, 1985. [Google Scholar]
- Celeghini, E.; Rasetti, M.; Vitiello, G. On squeezing and quantum groups. Phys. Rev. Lett. 1991, 66, 2056–2059. [Google Scholar] [CrossRef] [PubMed]
- Celeghini, E.; De Martino, S.; De Siena, S.; Rasetti, M.; Vitiello, G. Quantum groups, coherent states, squeezing and lattice quantum mechanics. Ann. Phys. 1995, 241, 50–67. [Google Scholar] [CrossRef]
- Biedenharn, L.; Lohe, M. An extension of the Borel-Weil construction to the quantum group Uq(n). Comm. Math. Phys. 1992, 146, 483–504. [Google Scholar] [CrossRef]
- Yuen, H. Two photon coherent states of the radiation field. Phys. Rev. A 1976, 13, 2226–2243. [Google Scholar] [CrossRef]

| Date | Time | Average Air Temperature [°C] | Average Lag Time [s] | Average Speed [m/s] |
|---|---|---|---|---|
| 24 October 2022 | 19:00 | 8.1 | 0.5 | 32 |
| 25 October 2022 | 01:00 | 6.9 | 1539 | 0.01 |
| 25 October 2022 | 07:00 | 5.0 | 0 | ∞ |
| 25 October 2022 | 13:00 | 9.3 | 0.5 | 32 |
| 25 October 2022 | 19:00 | 6.4 | 2.67 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiolerio, A.; Vitiello, G.; Dehshibi, M.M.; Adamatzky, A. Living Plants Ecosystem Sensing: A Quantum Bridge between Thermodynamics and Bioelectricity. Biomimetics 2023, 8, 122. https://doi.org/10.3390/biomimetics8010122
Chiolerio A, Vitiello G, Dehshibi MM, Adamatzky A. Living Plants Ecosystem Sensing: A Quantum Bridge between Thermodynamics and Bioelectricity. Biomimetics. 2023; 8(1):122. https://doi.org/10.3390/biomimetics8010122
Chicago/Turabian StyleChiolerio, Alessandro, Giuseppe Vitiello, Mohammad Mahdi Dehshibi, and Andrew Adamatzky. 2023. "Living Plants Ecosystem Sensing: A Quantum Bridge between Thermodynamics and Bioelectricity" Biomimetics 8, no. 1: 122. https://doi.org/10.3390/biomimetics8010122
APA StyleChiolerio, A., Vitiello, G., Dehshibi, M. M., & Adamatzky, A. (2023). Living Plants Ecosystem Sensing: A Quantum Bridge between Thermodynamics and Bioelectricity. Biomimetics, 8(1), 122. https://doi.org/10.3390/biomimetics8010122









