An Improved Chimp-Inspired Optimization Algorithm for Large-Scale Spherical Vehicle Routing Problem with Time Windows
Abstract
1. Introduction
2. Related Work
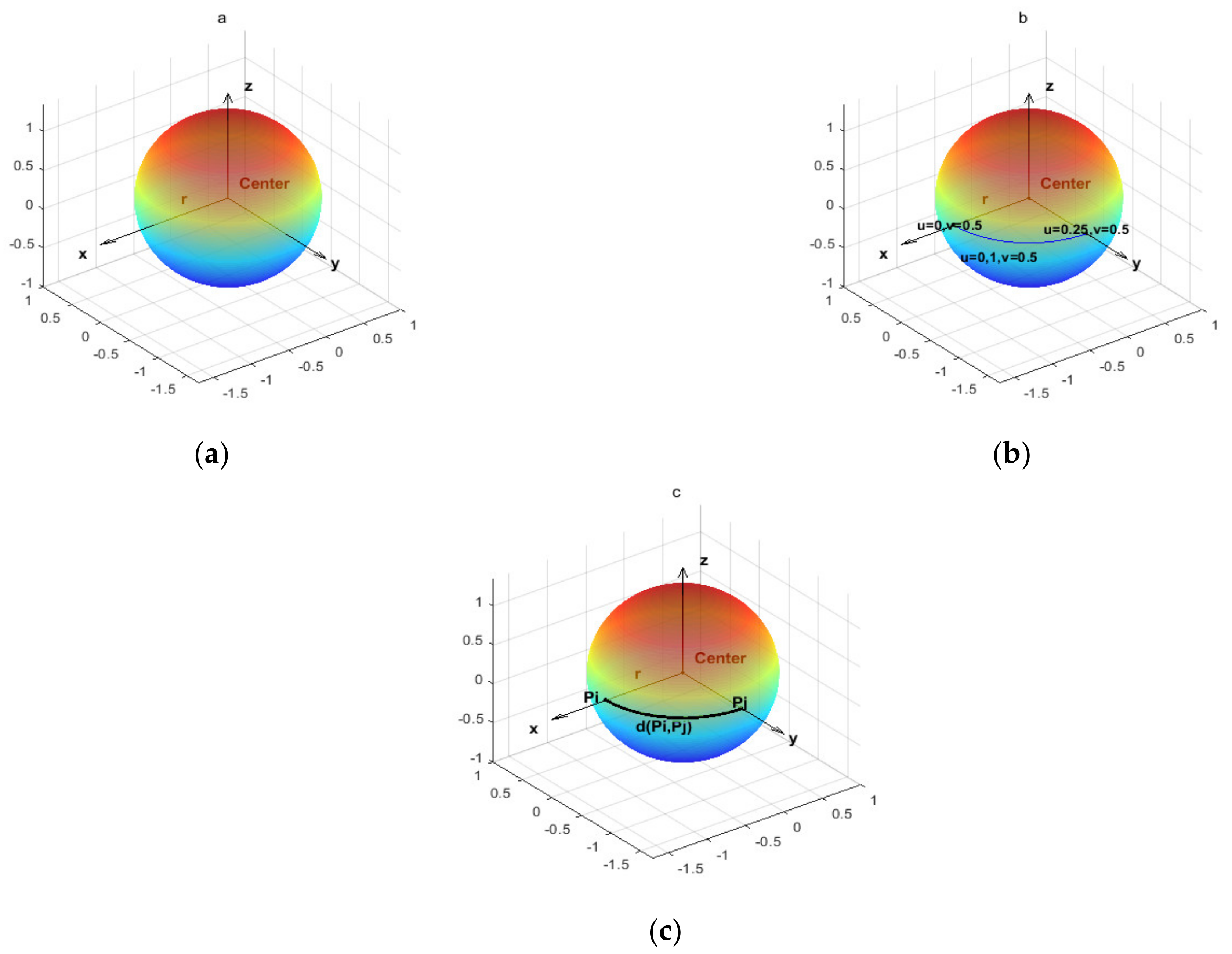
2.1. Geometric Definition of Sphere
2.2. Definition of Points on the Sphere
2.3. Geodesics between Two Points on the Sphere
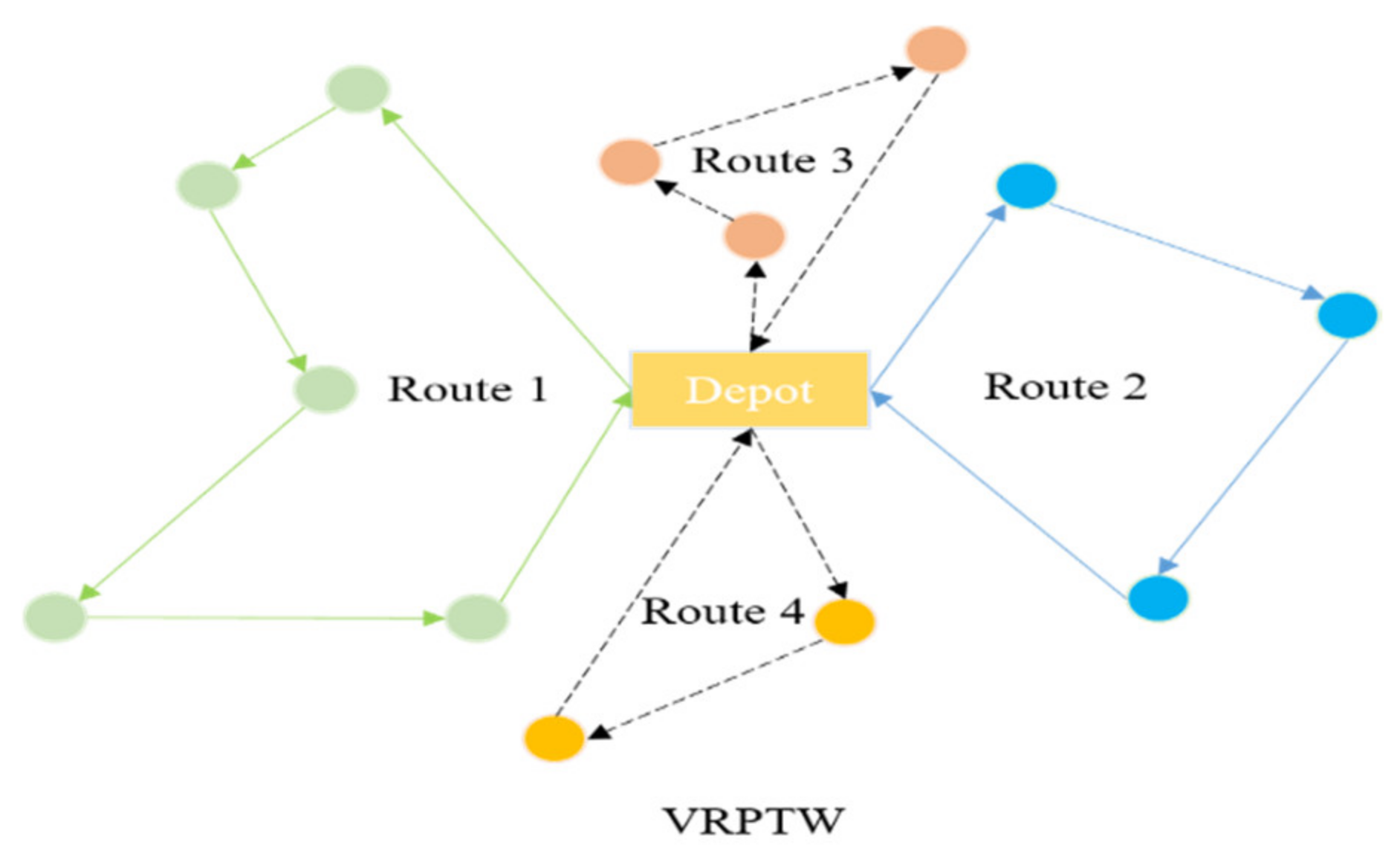
3. Mathematical Model of Spherical VRPTW
3.1. VRPTW on a 2D Plane
3.2. Three-Dimensional Spherical VRPTW Model
4. The Proposed Algorithm (MG-ChOA) for the Spherical VRPTW
4.1. The Chimp Optimization Algorithm (ChOA)
| Algorithm 1: The pseudo code of ChOA |
| 1. Initialize the population (i = 1,…, N). |
| 2. Set f, a, c, m = chaotic_value, and u is a random number in [0, 1]. |
| 3. Calculate individuals’ fitnesses. |
| 4. Select four leaders. |
| 5. while Iter < Max_iter |
| 6. for each individual |
| 7. Update f, a, c, m based on Equations (23)–(25). |
| 8. end for |
| 9. for each agent |
| 10. if (u < 0.5) |
| 11. if (|a| < 1) |
| 12. Update its position based on Equations (26)–(28). |
| 13. else if (|a| > 1) |
| 14. Select a random individual. |
| 15. end if |
| 16. else if (u > 0.5) |
| 17. Update its position based on a chaotic_value. |
| 18. end if |
| 19. end for |
| 20. Calculate individuals’ fitnesses and select four leaders. |
| 21. t = t + 1. |
| 22. end while |
| 23. Obtain the best solution. |
4.2. The Proposed MG-ChOA for the Spherical VRPTW
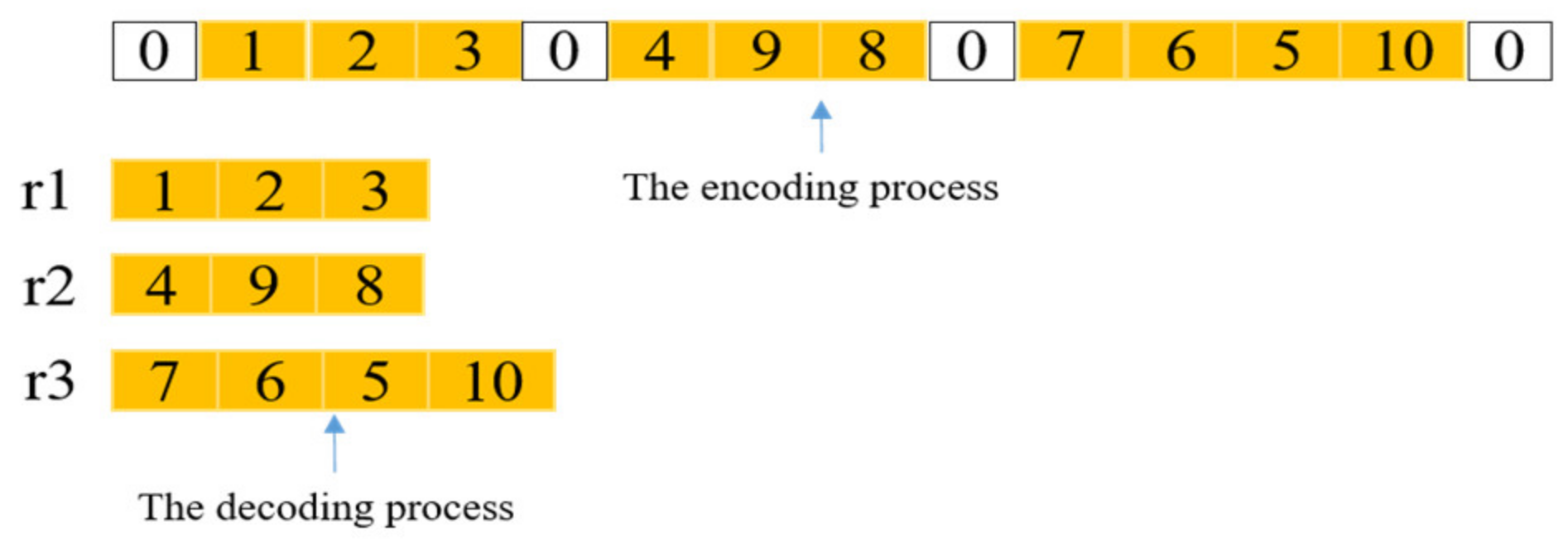
4.2.1. Encoding and Decoding of the Spherical VRPTW
4.2.2. Initializing Population Using the Quantum Coding
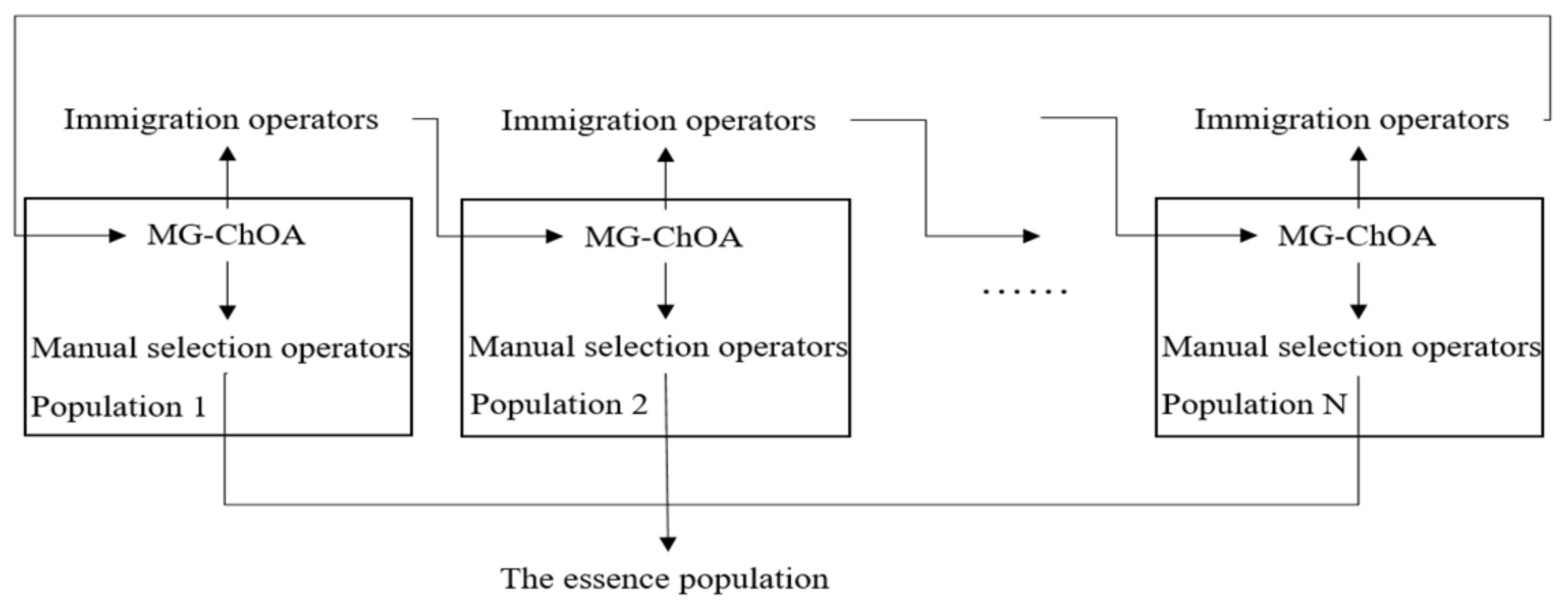
4.2.3. The Multiple-Population Strategy for MG-ChOA
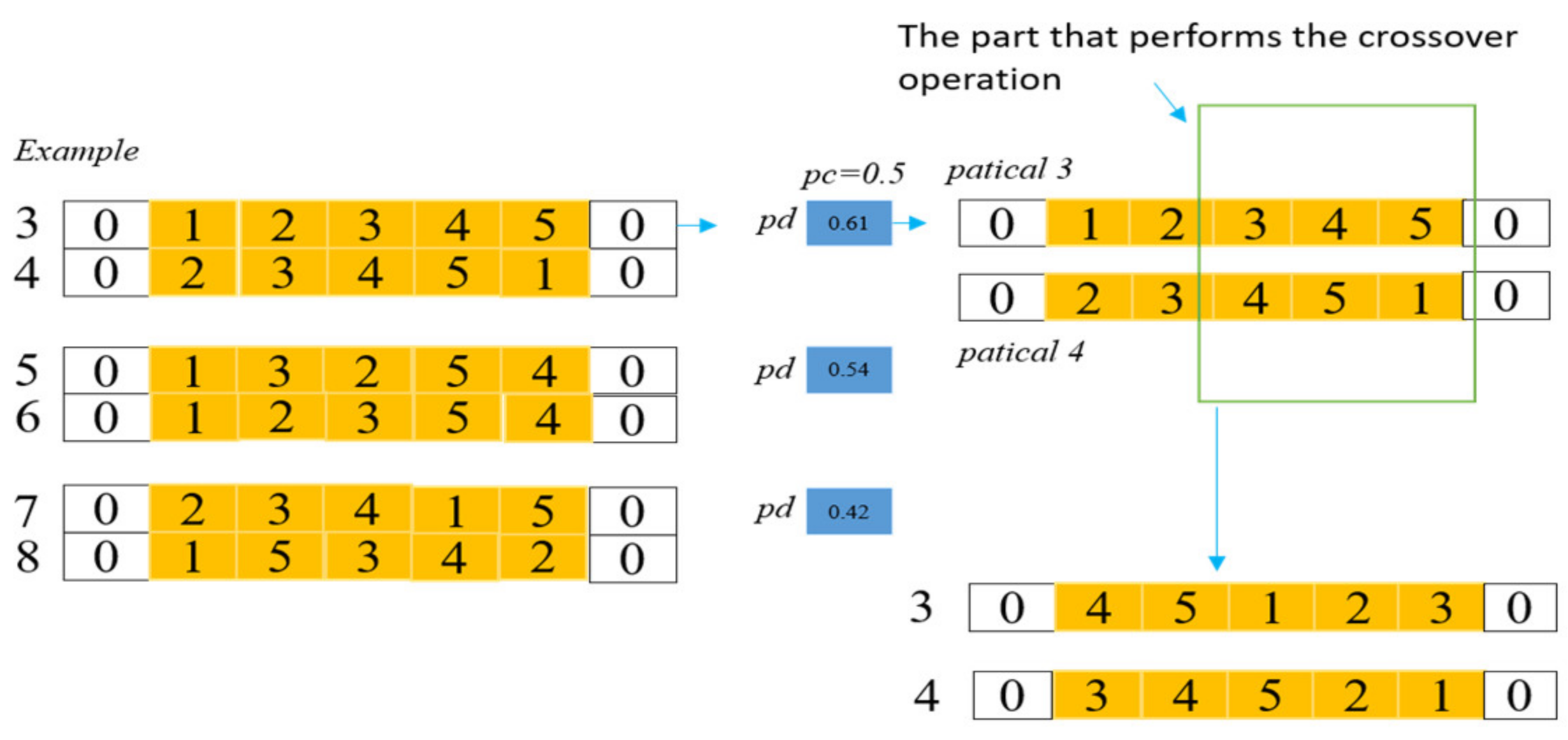
4.2.4. Genetic Operators
4.2.5. Local Search Strategy
4.2.6. Computational Complexity Analysis
| Algorithm 2: The pseudo code of the proposed MG-ChOA algorithm |
| 1. Initialize f, a, c, m, the probability of crossover and mutation. |
| 2. Initialize multiple quantum populations, (i = 1,…, N). |
| 3. while Iter < Max_iter |
| 4. Calculate the fitness of each population and obtain the essence population. |
| 5. Select the top four solutions from the essence population as leaders. |
| 6. Update each population by ChOA, and obtain new populations. |
| 7. Perform the selection, recombination, mutation, and local search strategy to obtain the offspring. |
| 8. Update f, a, c, m based on Equations (23)–(25). |
| 9. end while |
| 10. Obtain the optimal individual and accomplish data saving. |
5. Experimental Results and Discussion
5.1. Experimental Setup
5.2. Performance Comparison of Algorithms for Two-Dimensional Datasets
5.3. Performance Comparison of Algorithms for Low-Dimensional Instances
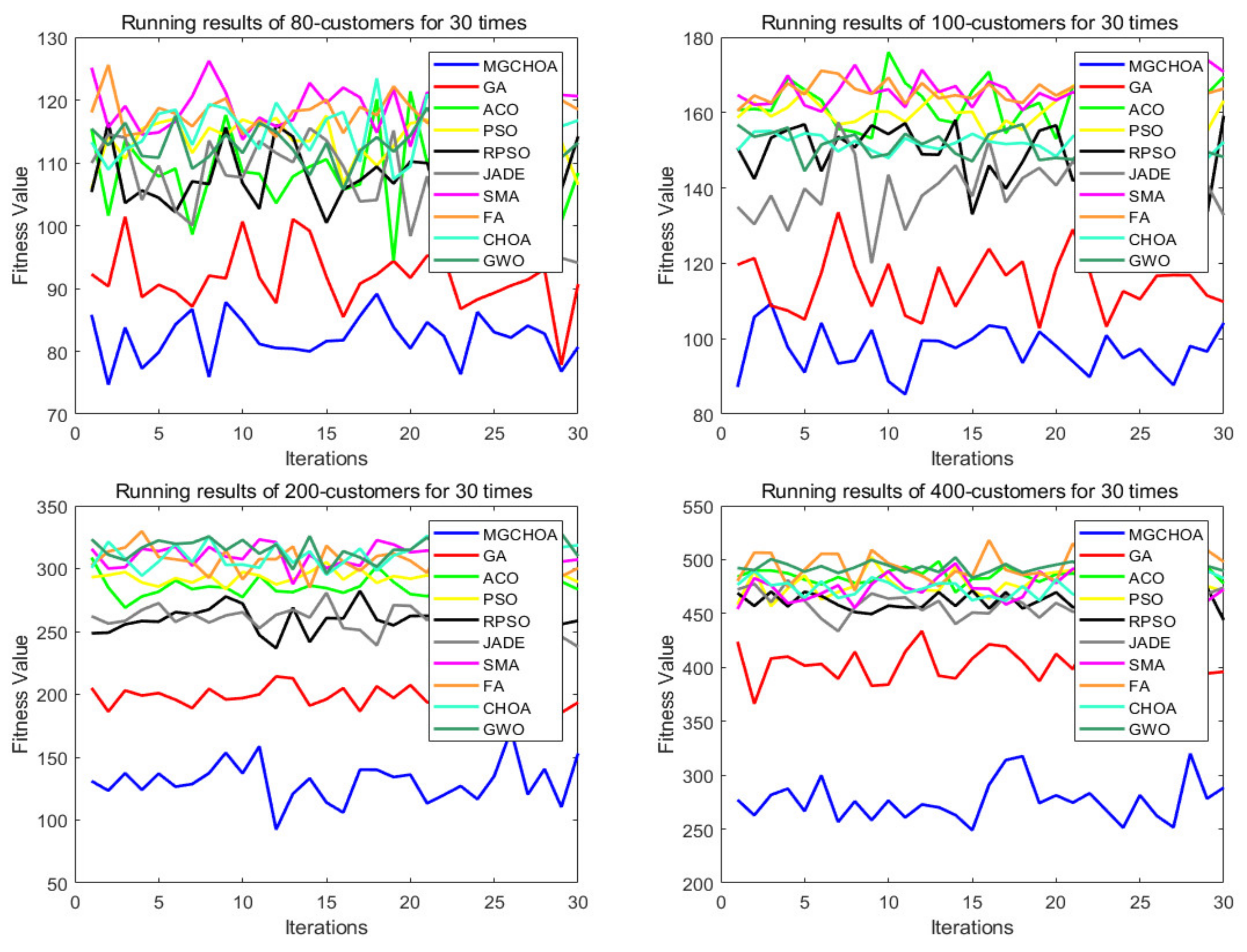
5.4. Performance Comparison of Algorithms for High-Dimensional Instances

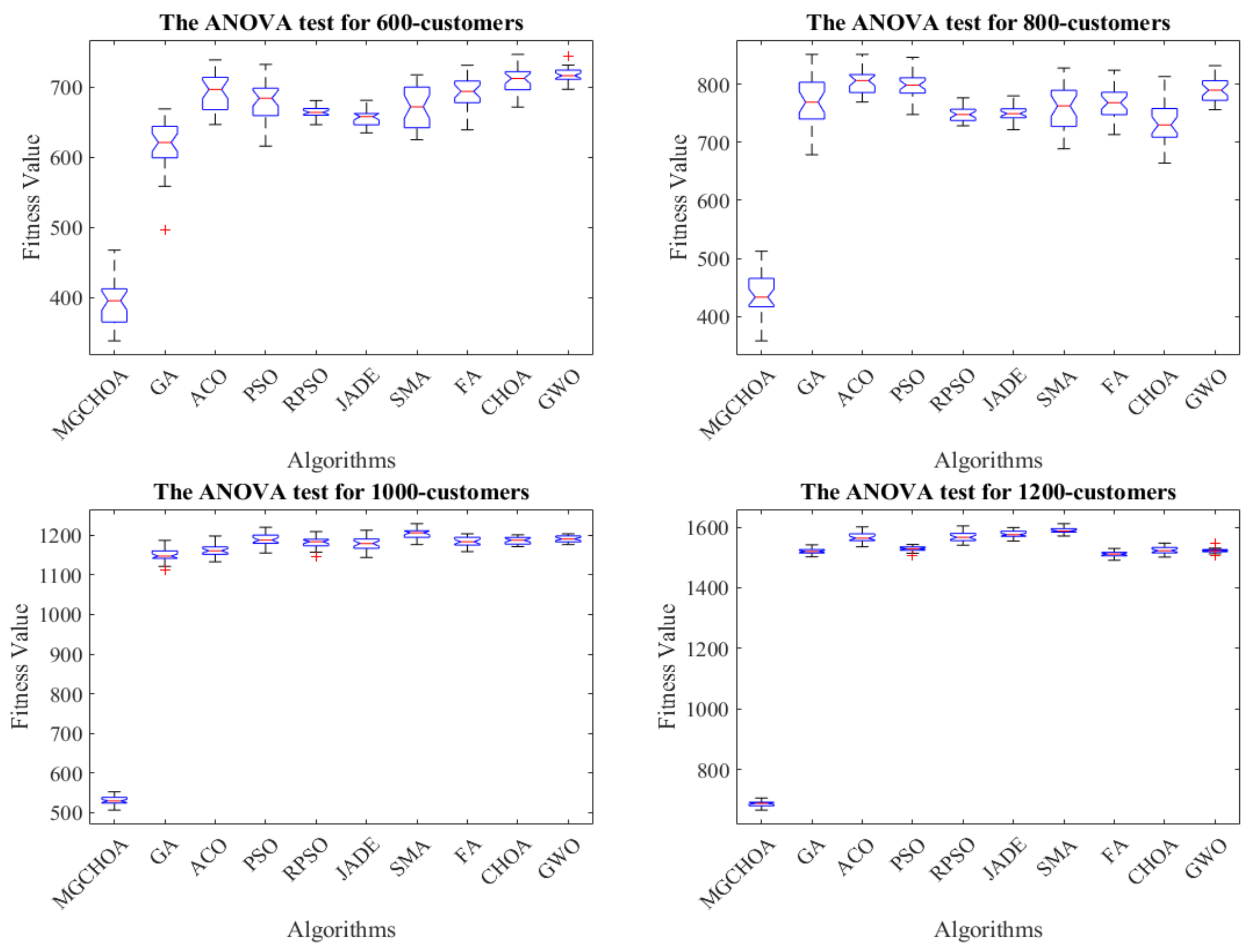
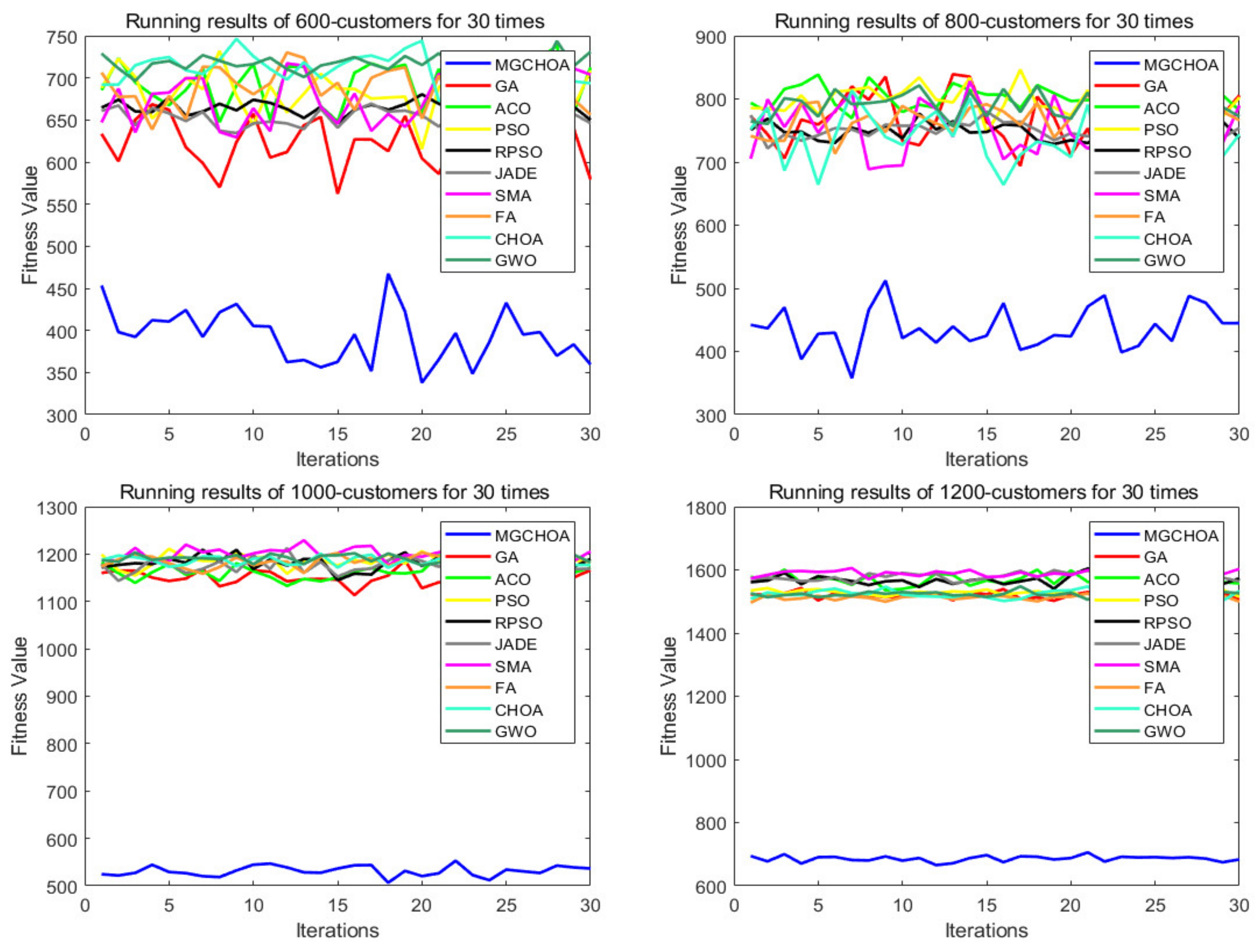
5.5. Performance Limit Test of MG-ChOA
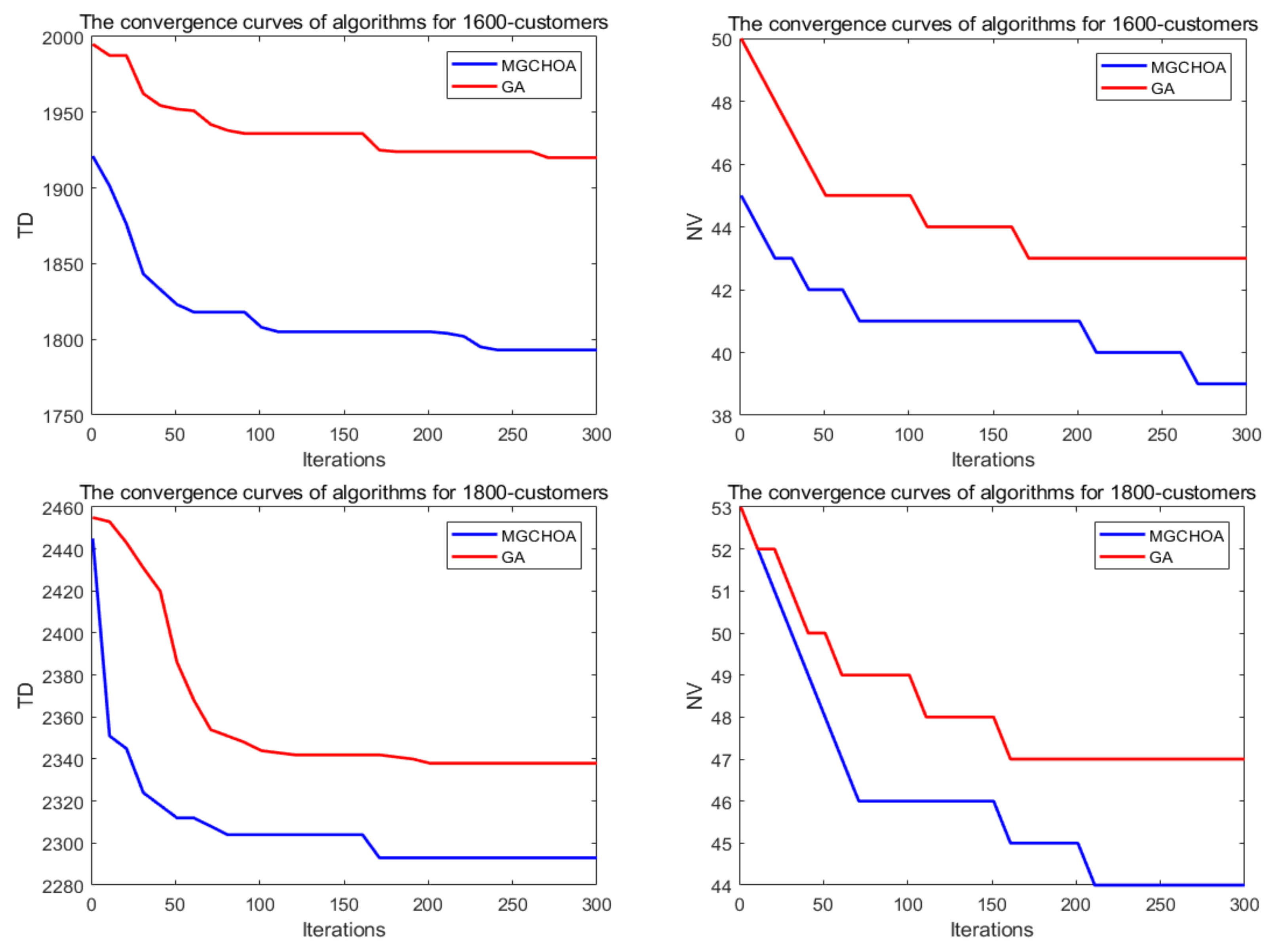
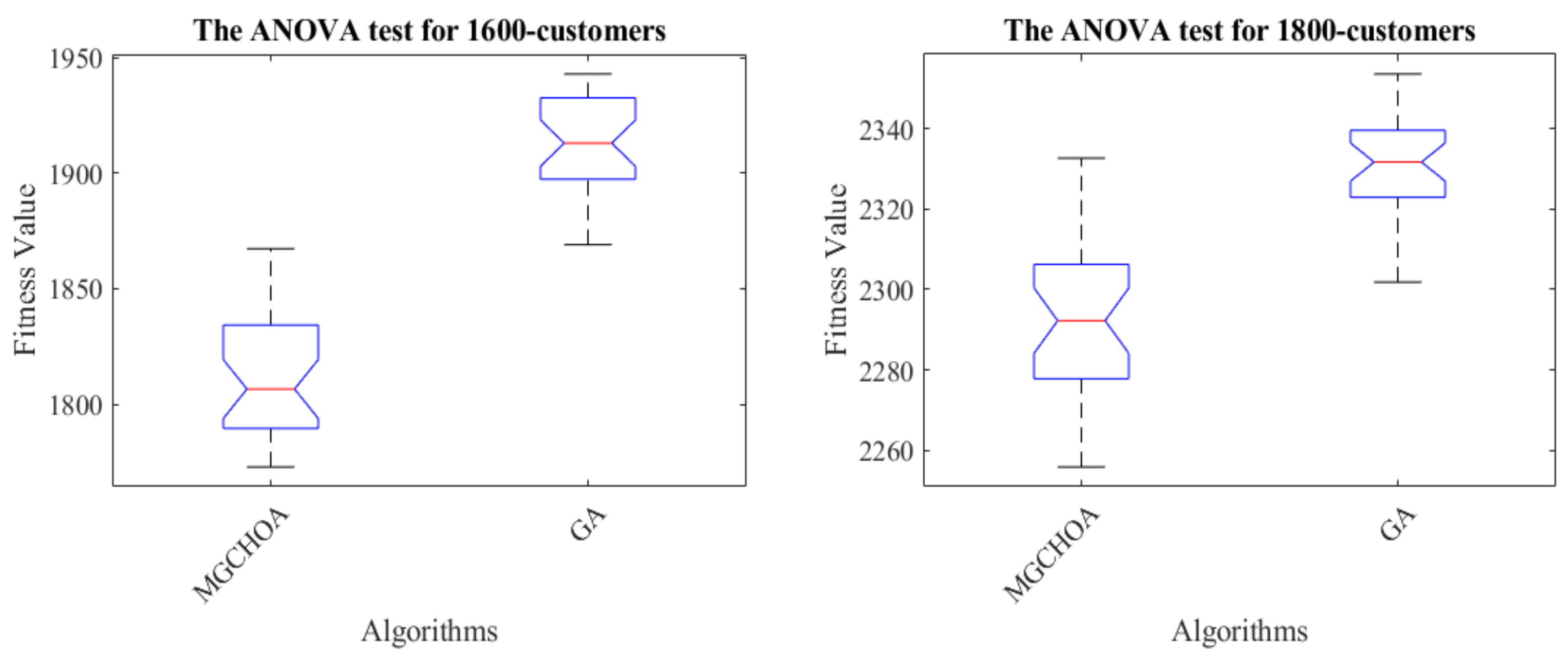
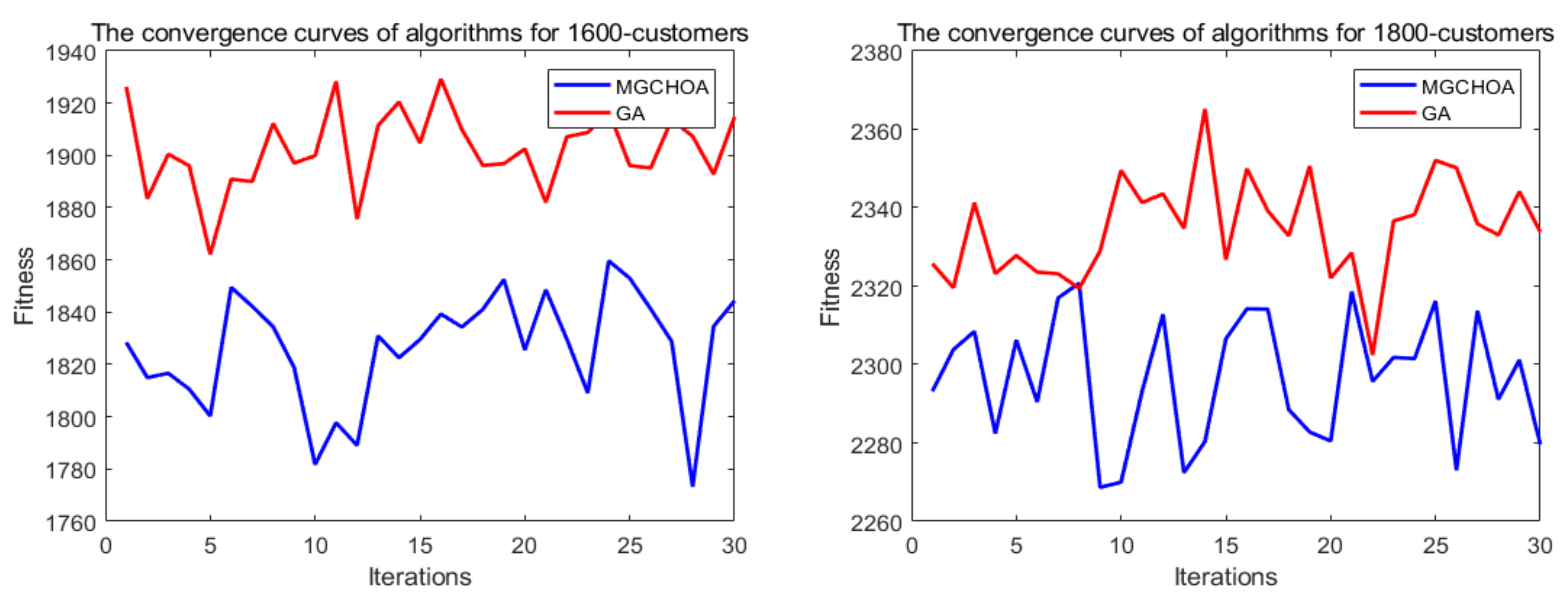
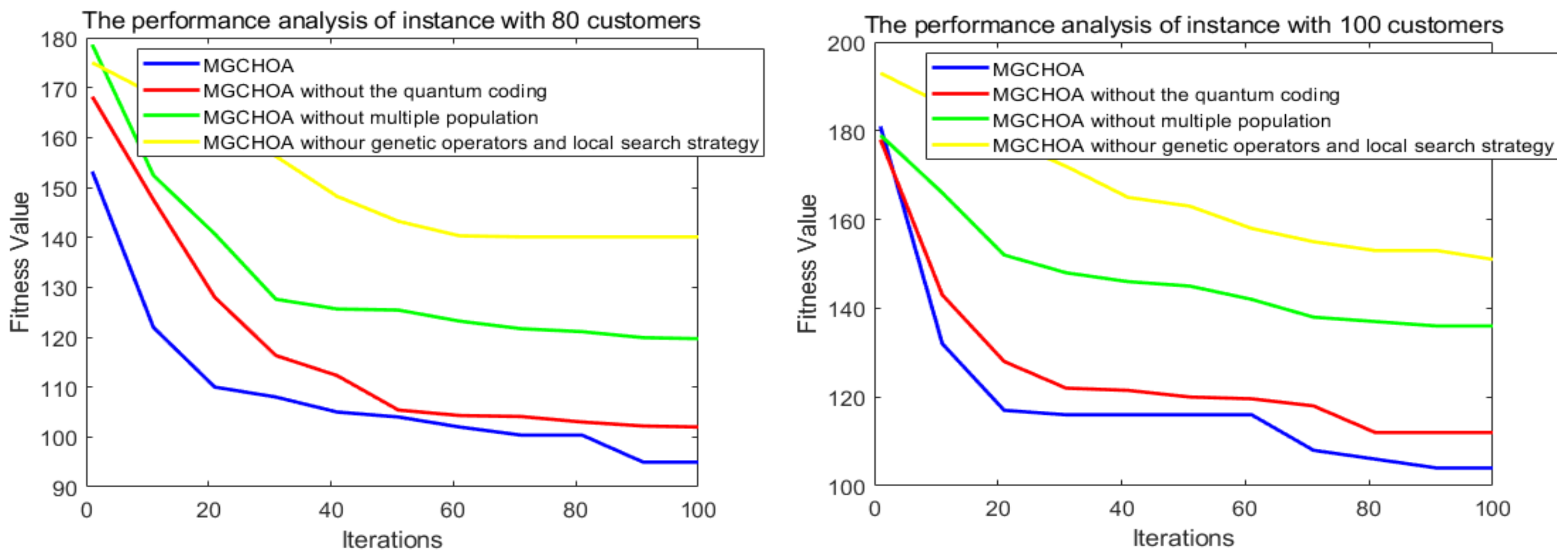
5.6. Performance Analysis of Different Strategies
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. (Eds.) The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Yu, Y.; Wang, S.; Wang, J.; Huang, M. A branch-and-price algorithm for the heterogeneous fleet green vehicle routing problem with time windows. Transp. Res. Part B Methodol. 2019, 122, 511–527. [Google Scholar] [CrossRef]
- Xu, Z.; Elomri, A.; Pokharel, S.; Mutlu, F. A model for capacitated green vehicle routing problem with the time-varying vehicle speed and soft time windows. Comput. Ind. Eng. 2019, 137, 106011. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, L.; Lim, A. An evolutionary local search for the capacitated vehicle routing problem minimizing fuel consumption under three-dimensional loading constraints. Transp. Res. Part B Methodol. 2015, 82, 20–35. [Google Scholar] [CrossRef]
- Duan, F.; He, X. Multiple depots incomplete open vehicle routing problem based on carbon tax. In Bio-Inspired Computing-Theories and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 98–107. [Google Scholar]
- Ghannadpour, S.F.; Zarrabi, A. Multi-objective heterogeneous vehicle routing and scheduling problem with energy minimizing. Swarm Evol. Comput. 2019, 44, 728–747. [Google Scholar] [CrossRef]
- Li, H.; Yuan, J.; Lv, T.; Chang, X. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems considering carbon dioxide emissions. Transp. Res. Part D Transp. Environ. 2016, 49, 231–245. [Google Scholar] [CrossRef]
- Pessoa, A.; Sadykov, R.; Uchoa, E.; Vanderbeck, F. A generic exact solver for vehicle routing and related problems. Math. Program. 2020, 183, 483–523. [Google Scholar] [CrossRef]
- Xiao, Y.; Konak, A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 146–166. [Google Scholar] [CrossRef]
- Çimen, M.; Soysal, M. Time-dependent green vehicle routing problem with stochastic vehicle speeds: An approximate dynamic programming algorithm. Transp. Res. Part D Transp. Environ. 2017, 54, 82–98. [Google Scholar] [CrossRef]
- Behnke, M.; Kirschstein, T. The impact of path selection on GHG emissions in city logistics. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 320–336. [Google Scholar] [CrossRef]
- Da Costa, P.R.D.O.; Mauceri, S.; Carroll, P.; Pallonetto, F. A genetic algorithm for a green vehicle routing problem. Electron. Notes Discret. Math. 2018, 64, 65–74. [Google Scholar] [CrossRef]
- Das, A.; Mathieu, C. A quasipolynomial time approximation scheme for Euclidean capacitated vehicle routing. Algorithmica 2015, 73, 115–142. [Google Scholar] [CrossRef]
- Khachay, M.; Ogorodnikov, Y.; Khachay, D. Efficient approximation of the metric CVRP in spaces of fixed doubling dimension. J. Glob. Optim. 2021, 80, 679–710. [Google Scholar] [CrossRef]
- Back, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Webster, B.; Bernhard, P.J. A Local Search Optimization Algorithm Based on Natural Principles of Gravitation; Scholarship Repository at Florida Tech: Melbourne, FL, USA, 2003. [Google Scholar]
- Beni, G.; Wang, J. Swarm Intelligence in Cellular Robotic Systems. In Robots and Biological Systems: Towards a New Bionics; Springer: Berlin/Heidelberg, Germany, 1993; pp. 703–712. [Google Scholar]
- Storn, R. Differential Evolution Research—Trends and Open Questions. In Advances in Differential Evolution; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–31. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, UK, 1992. [Google Scholar]
- Simon, D. Biogeography-Based Optimization. IEEE Trans Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inform. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inform. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp Optimization Algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A Mayfly Optimization Algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2019, 191, 105190. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A Nature-Inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A Novel Nature-Inspired Algorithm for Optimization: Squirrel Search Algorithm. Swarm Evol. Comput. 2018, 44, 148–175. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel Meta-Heuristic Bald eagle Search Optimisation Algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Mafarja, I.M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comp. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Singh, A. An Artificial Bee colony Algorithm for the Leaf-Constrained Minimum Spanning Tree Problem. Appl. Soft Comput. 2009, 9, 625–631. [Google Scholar] [CrossRef]
- Neumann, F.; Witt, C. Ant colony Optimization and the Minimum Spanning Tree Problem. Theor. Comp. Sci. 2007, 411, 2406–2413. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. In International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, Y.; Tang, Z.; Luo, Q. Artificial Electric Field Algorithm with Inertia and Repulsion for Spherical Minimum Spanning Tree. Appl. Intell. 2022, 52, 195–214. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 1, 1097–1105. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Cully, A.; Togelius, J. AlphaStar: An evolutionary computation perspective. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 314–315. [Google Scholar]
- Tian, Y.; Zhang, K.; Li, J.; Lin, X.; Yang, B. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Juhn, Y.; Liu, H. Artificial intelligence approaches using natural language processing to advance EHR-based clinical research. J. Allergy Clin. Immunol. 2020, 145, 463–469. [Google Scholar] [CrossRef]
- Trappey, A.J.C.; Trappey, C.V.; Wu, J.L.; Wang, J.W.C. Intelligent compilation opatent summaries using machine learning and natural language processing techniques. Adv. Eng. Inform. 2020, 43, 101027. [Google Scholar] [CrossRef]
- Dmitriev, E.A.; Myasnikov, V.V. Possibility estimation of 3D scene reconstruction from multiple images. In Proceedings of the International Conference on Information Technology and Nanotechnology, Samara, Russia, 23–27 May 2022; pp. 293–296. [Google Scholar]
- Gkioxari, G.; Malik, J.; Johnson, J. Mesh R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 9785–9795. [Google Scholar]
- Sayers, W.; Savić, D.R.A.G.A.N.; Kapelan, Z.; Kellagher, R. Artificial intelligence techniques for flood risk management in urban environments. Procedia Eng. 2014, 70, 1505–1512. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savić, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the art for genetic algorithms and beyond in water resources planning and management. J. Water Resour. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Paul, P.V.; Moganarangan, N.; Kumar, S.S.; Raju, R.; Vengattaraman, T.; Dhavachelvan, P. Performance analyses over population seeding techniques of the permutation-coded genetic algorithm: An empirical study based on traveling salesman problems. Appl. Soft Comput. 2015, 32, 383–402. [Google Scholar] [CrossRef]
- Islam, M.L.; Shatabda, S.; Rashid, M.A.; Khan, M.G.M.; Rahman, M.S. Protein structure prediction from inaccurate and sparse NMR data using an enhanced genetic algorithm. Comput. Biol. Chem. 2019, 79, 6–15. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. Handb. Metaheuristics 2010, 146, 227–263. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecno di Milano, Milan, Italy, 1992. [Google Scholar]
- Solano-Charris, E.; Prins, C.; Santos, A.C. Local search based metaheuristics for the robust vehicle routing problem with discrete scenarios. Appl. Soft Comput. 2015, 32, 518–531. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Fan, J.; Xu, M.; Liu, Y.; Wang, H. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. J. Clean. Prod. 2019, 232, 12–29. [Google Scholar] [CrossRef]
- Chen, G.; Wu, X.; Li, J.; Guo, H. Green vehicle routing and scheduling optimization of ship steel distribution center based on improved intelligent water drop algorithms. Math. Probl. Eng. 2020, 2020, 9839634. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Y.; Xue, W.; Li, J. Vehicle routing problem with fuel consumption and carbon emission. Int. J. Prod. Econ. 2015, 170, 234–242. [Google Scholar] [CrossRef]
- Zulvia, F.E.; Kuo, R.J.; Nugroho, D.Y. A many-objective gradient evolution algorithm for solving a green vehicle routing problem with time windows and time dependency for perishable products. J. Clean. Prod. 2020, 242, 118428. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, Y.; Zhou, G.; Deng, W.; Luo, Q. Bioinspired Bare Bones Mayfly Algorithm for Large-Scale Spherical Minimum Spanning Tree. Front. Bioeng. Biotechnol. 2022, 10, 830037. [Google Scholar] [CrossRef]
- Si, T.; Patra, D.K.; Mondal, S.; Mukherjee, P. Breast DCE-MRI segmentation for lesion detection using Chimp Optimization Algorithm. Expert Syst. Appl. 2022, 204, 117481. [Google Scholar] [CrossRef]
- Sharma, A.; Nanda, S.J. A multi-objective chimp optimization algorithm for seismicity de-clustering. Appl. Soft Comput. 2022, 121, 108742. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Y.; Yuan, H.; Khishe, M.; Mohammadi, M. Nodes clustering and multi-hop routing protocol optimization using hybrid chimp optimization and hunger games search algorithms for sustainable energy efficient underwater wireless sensor networks. Sustain. Comput. Inform. Syst. 2022, 35, 100731. [Google Scholar] [CrossRef]
- Hu, G.; Dou, W.; Wang, X.; Abbas, M. An enhanced chimp optimization algorithm for optimal degree reduction of Said–Ball curves. Math. Comput. Simul. 2022, 197, 207–252. [Google Scholar] [CrossRef]
- Chen, F.; Yang, C.; Khishe, M. Diagnose Parkinson’s disease and cleft lip and palate using deep convolutional neural networks evolved by IP-based chimp optimization algorithm. Biomed. Signal Process. Control 2022, 77, 103688. [Google Scholar] [CrossRef]
- Du, N.; Zhou, Y.; Deng, W.; Luo, Q. Improved chimp optimization algorithm for three-dimensional path planning problem. Multimed. Tools Appl. 2022, 81, 1–26. [Google Scholar] [CrossRef]
- Du, N.; Luo, Q.; Du, Y.; Zhou, Y. Color Image Enhancement: A Metaheuristic Chimp Optimization Algorithm. Neural Process. Lett. 2022, 54, 1–40. [Google Scholar] [CrossRef]
- Hearn, D.D.; Pauline Baker, M. Computer Graphics with Open GL; Publishing House of Electronics Industry: Beijing, China, 2004; p. 672. [Google Scholar]
- Eldem, H.; Ülker, E. The Application of Ant colony Optimization in the Solution of 3D Traveling Salesman Problem on a Sphere. Eng. Sci. Technol. Int. J. 2017, 20, 1242–1248. [Google Scholar] [CrossRef]
- Uğur, A.; Korukoğlu, S.; Ali, Ç.; Cinsdikici, M. Genetic Algorithm Based Solution for Tsp on a Sphere. Math. Comput. Appl. 2009, 14, 219–228. [Google Scholar] [CrossRef]
- Lomnitz, C. On the Distribution of Distances between Random Points on a Sphere. Bull. Seismol. Soc. America 1995, 85, 951–953. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Borowska, B. An improved particle swarm optimization algorithm with repair procedure. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2017; pp. 1–16. [Google Scholar]
- Su, J.L.; Wang, H. An improved adaptive differential evolution algorithm for single unmanned aerial vehicle multitasking. Def. Technol. 2021, 17, 1967–1975. [Google Scholar] [CrossRef]
- Chen, G.; Shen, Y.; Zhang, Y.; Zhang, W.; Wang, D.; He, B. 2D multi-area coverage path planning using L-SHADE in simulated ocean survey. Appl. Soft Comput. 2021, 112, 107754. [Google Scholar] [CrossRef]
- Borowska, B. Learning Competitive Swarm Optimization. Entropy 2022, 24, 283. [Google Scholar] [CrossRef]
- Tong, X.; Yuan, B.; Li, B. Model complex control CMA-ES. Swarm Evol. Comput. 2019, 50, 100558. [Google Scholar] [CrossRef]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference; Springer: Berlin/Heidelberg, Germany, 2011; pp. 977–979. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A Practical Tutorial on the Use of Nonparametric Statistical Tests as a Methodology for Comparing Evolutionary and Swarm Intelligence Algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Zimmerman, D.W.; Zumbo, B.D. Relative power of the Wilcoxon test, the Friedman test, and repeated-measures ANOVA on ranks. J. Exp. Educ. 1993, 62, 75–86. [Google Scholar] [CrossRef]


| Number of customer nodes | |
| Set of customers as {0,1,…N}, where 0 is the depot | |
| Set of vehicles, = {1,…,K} | |
| Number of vehicles | |
| Index of vehicles () | |
| Distance between nodes i and j | |
| Travel time between nodes i and j | |
| Earliest arrival time at node i | |
| Latest arrival time at node i | |
| Service time of node i | |
| Demand of customer i | |
| Capacity of vehicle k | |
| Arrival time of vehicle k to i | |
| Waiting time at customer i |
| Algorithms | Authors | Parameters |
|---|---|---|
| MG-ChOA | This paper | P = 2, m was calculated by Gaussian mapping, pc = 0.9, pm = 0.1, and the number of customers deleted in the local search strategy was 15% of the total |
| GA | Holland [20] | pc = 0.8, pm = 0.8 |
| ACO | This paper | The pheromone was set to 4, heuristic information was 5, waiting time was 2, time window width was 3, parameter controlling ant movement was 0.5, evaporation rate of pheromone was 0.85, and the constant affecting pheromone updating was 5 |
| PSO | Kennedy et al. [32] | The inertia weight was 0.2, global learning coefficient was 1, and the self-learning coefficient was 0.7 |
| RPSO | Borowska [72] | The inertia weight was 0.6, acceleration constants were c1 = c2 = 1.7, and the number of particles with the worst fitness p was set as 3. |
| JADE | Borowska [73] | Parameters of the algorithm changed adaptively |
| SMA | Li et al. [79] | The parameter controlling foraging was 0.03 |
| FA | Yang [35] | The basic value of the attraction coefficient was 0.8, the mutation coefficient was 0.8, and the light absorption coefficient was 0.8 |
| ChOA | Khishe et al. [25] | Parameters of the algorithm changed adaptively |
| GWO | Mirjalili et al. [37] | Parameters of the algorithm changed adaptively |
| Datasets | Best Known | MG-ChOA | %Difference in TD | |||
|---|---|---|---|---|---|---|
| NV | Authors | TD | NV | TD | ||
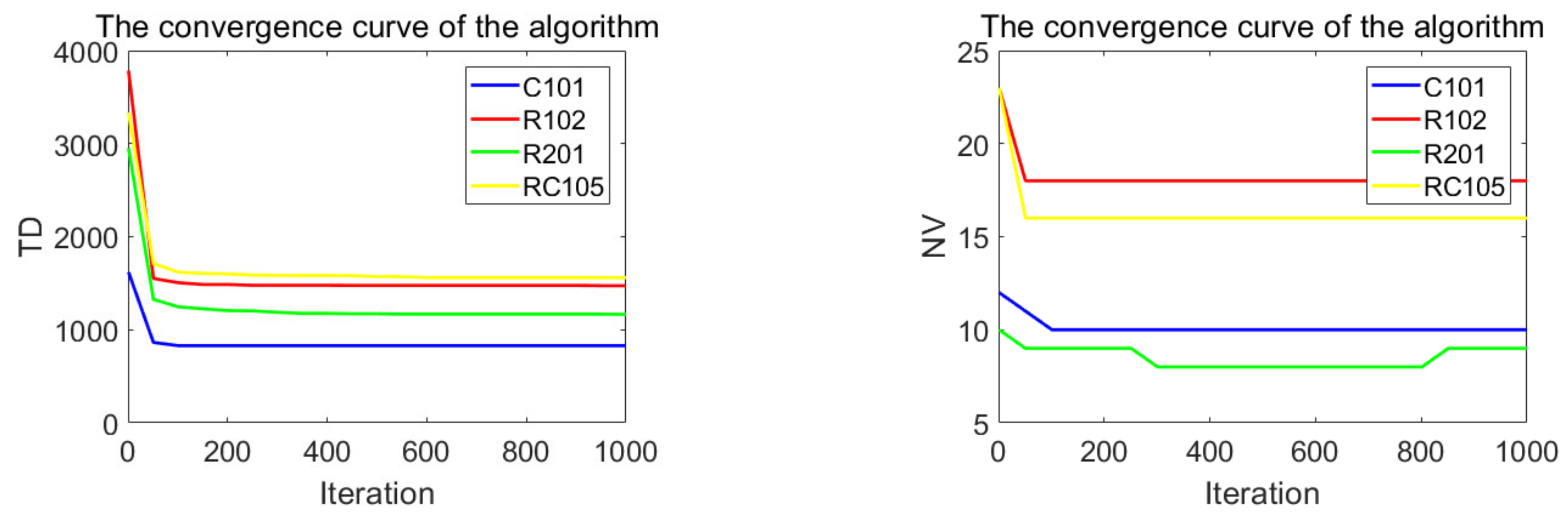
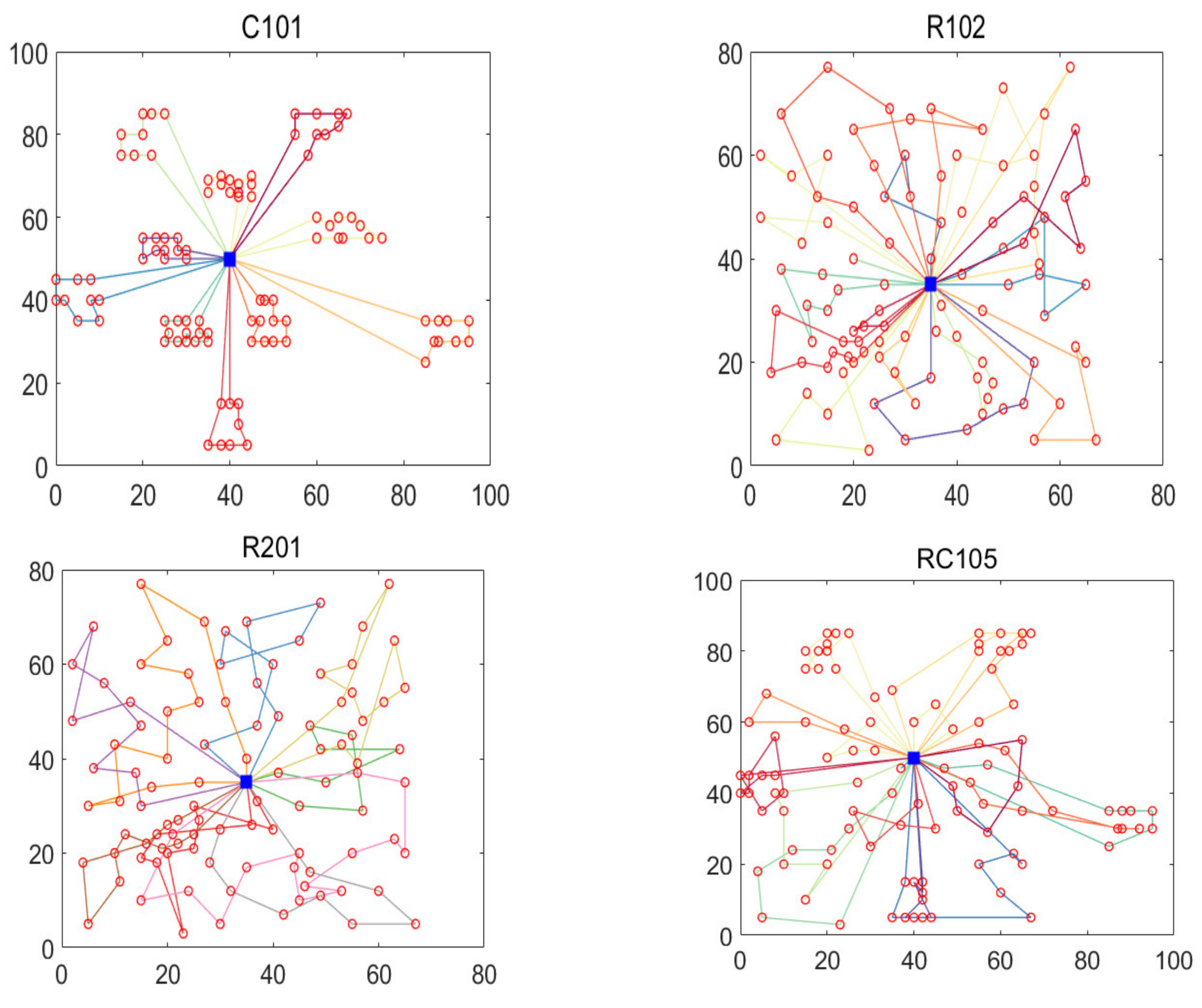
| C101 | Rochat | 10 | 828.94 | 10 | 828.94 | 0.00 |
| R102 | Rochat | 17 | 1486.12 | 18 | 1473.62 | −0.84 |
| R201 | Homberger | 4 | 1252.37 | 9 | 1165.10 | −7.49 |
| RC105 | Berger | 13 | 1629.44 | 8 | 1234.1 | −3.20 |
| Instances | Algorithms | Best | Worst | Mean | Std | Rank |
|---|---|---|---|---|---|---|
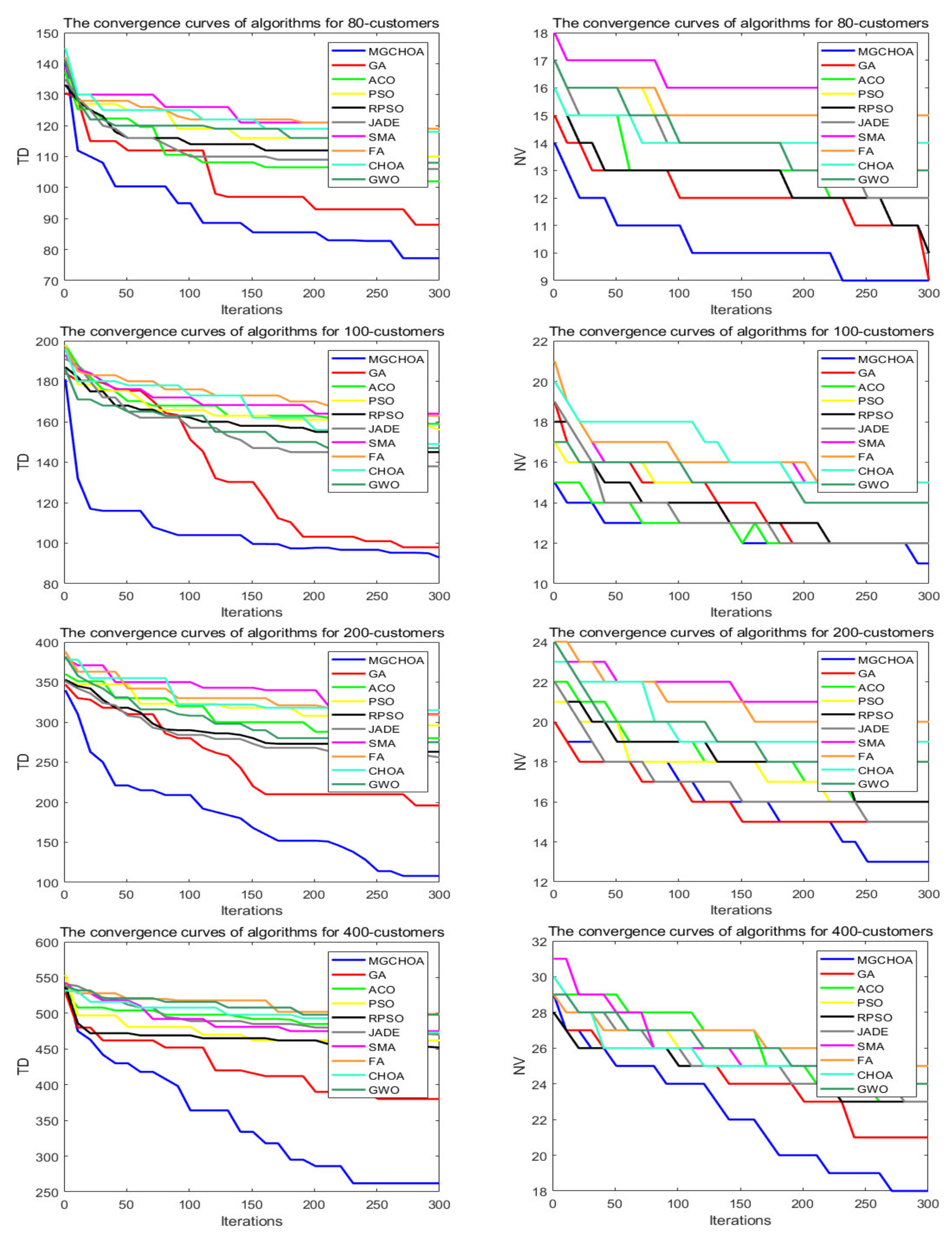
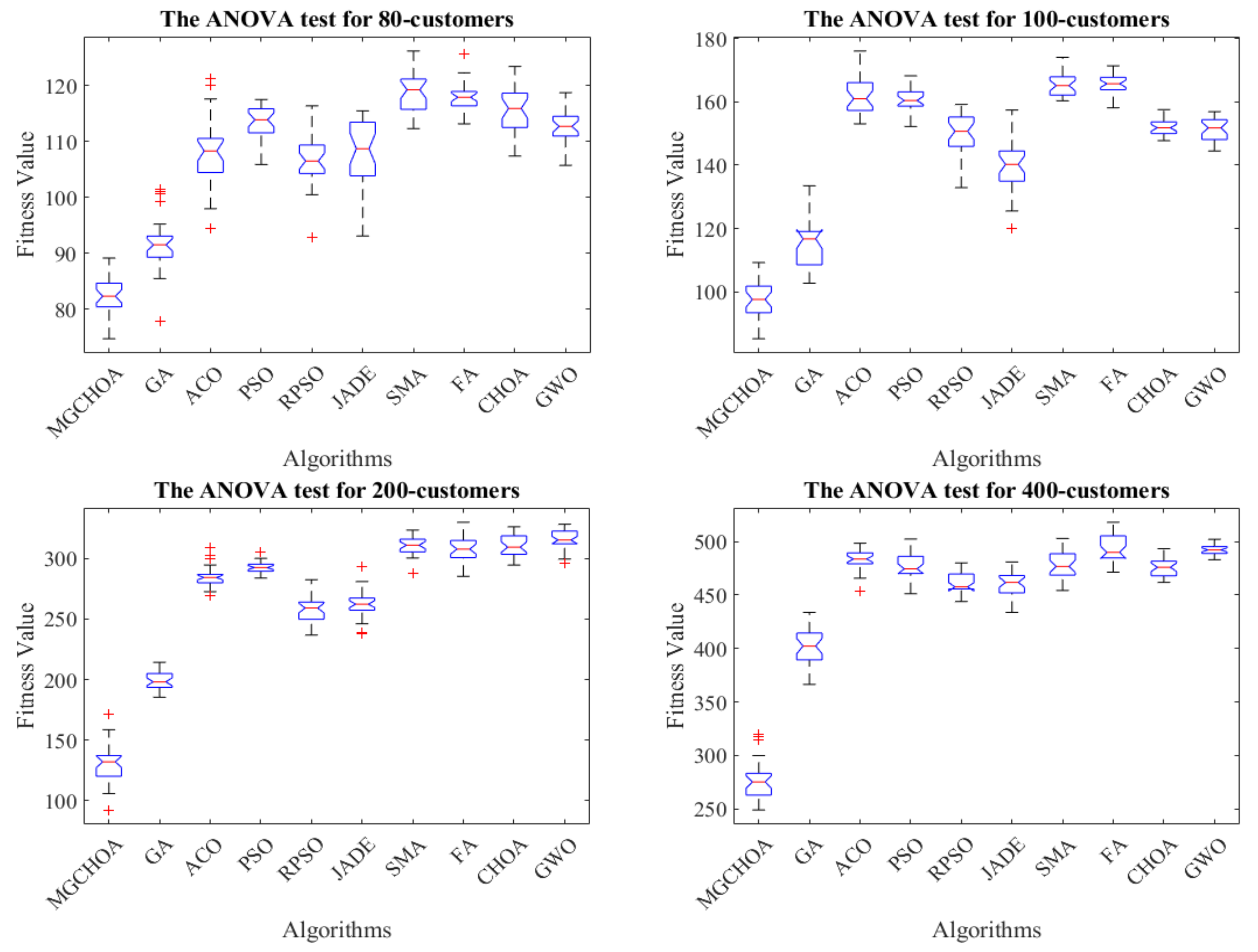
| 80 | MG-ChOA | 74.6915 | 89.1348 | 82.1517 | 3.5346 | 1 |
| GA | 77.8541 | 101.4105 | 91.6031 | 4.7625 | 2 | |
| ACO | 94.4498 | 121.3766 | 107.9738 | 6.2796 | 7 | |
| PSO | 105.8825 | 117.5272 | 113.3724 | 3.1874 | 6 | |
| RPSO | 92.8541 | 116.4105 | 106.8345 | 4.9541 | 3 | |
| JADE | 93.0822 | 115.5015 | 107.3124 | 6.6533 | 5 | |
| SMA | 112.3210 | 126.2165 | 118.7991 | 3.4966 | 10 | |
| FA | 113.1794 | 125.5953 | 117.9425 | 2.7192 | 8 | |
| ChOA | 107.4037 | 123.4656 | 115.5410 | 3.8180 | 9 | |
| GWO | 105.7460 | 118.7477 | 112.6344 | 3.0227 | 4 | |
| 100 | MG-ChOA | 85.2594 | 109.3002 | 97.0352 | 5.8962 | 1 |
| GA | 102.7593 | 133.5235 | 114.7344 | 7.3826 | 2 | |
| ACO | 153.0400 | 176.0259 | 162.3654 | 5.7970 | 9 | |
| PSO | 152.1939 | 168.1939 | 160.8924 | 3.6269 | 7 | |
| RPSO | 132.9432 | 159.1628 | 149.4894 | 6.7970 | 6 | |
| JADE | 120.0249 | 157.4222 | 139.4843 | 8.3004 | 5 | |
| SMA | 160.3001 | 174.0341 | 165.4979 | 3.8072 | 10 | |
| FA | 158.1066 | 171.3606 | 165.7973 | 2.9858 | 8 | |
| ChOA | 147.7598 | 157.5543 | 151.6967 | 2.5188 | 4 | |
| GWO | 144.5013 | 156.8961 | 151.5078 | 3.4927 | 3 | |
| 200 | MG-ChOA | 92.4894 | 171.5740 | 130.6591 | 16.0142 | 2 |
| GA | 185.4160 | 214.2204 | 199.0548 | 7.6380 | 1 | |
| ACO | 269.0036 | 308.7602 | 284.6381 | 8.3779 | 5 | |
| PSO | 283.7265 | 305.1323 | 292.6501 | 4.4139 | 4 | |
| RPSO | 236.7104 | 282.2716 | 258.7564 | 10.2254 | 3 | |
| JADE | 237.7484 | 293.4480 | 261.7672 | 10.8409 | 6 | |
| SMA | 287.7402 | 323.2023 | 309.9585 | 7.7234 | 7 | |
| FA | 285.0593 | 329.6599 | 307.5770 | 9.8884 | 8 | |
| ChOA | 294.4387 | 326.0060 | 310.2144 | 8.7833 | 9 | |
| GWO | 296.0258 | 328.0148 | 315.6643 | 7.8676 | 10 | |
| 400 | MG-ChOA | 248.9622 | 319.9879 | 276.4939 | 18.1938 | 1 |
| GA | 366.3048 | 433.7308 | 401.4895 | 16.6535 | 3 | |
| ACO | 454.0676 | 498.4261 | 482.8094 | 9.0784 | 6 | |
| PSO | 451.2690 | 502.3332 | 476.5840 | 12.6521 | 7 | |
| RPSO | 443.9548 | 480.0339 | 461.6864 | 8.34601 | 2 | |
| JADE | 433.6780 | 480.9550 | 460.5177 | 10.7607 | 4 | |
| SMA | 454.1847 | 502.8520 | 477.1359 | 12.5691 | 9 | |
| FA | 471.2963 | 518.0317 | 492.6073 | 12.2617 | 10 | |
| ChOA | 461.8166 | 493.2990 | 475.5718 | 9.2174 | 5 | |
| GWO | 483.0315 | 502.0965 | 492.3936 | 4.2985 | 8 |
| Instances | GA | ACO | PSO | RPSO | JADE | SMA | FA | ChOA | GWO |
|---|---|---|---|---|---|---|---|---|---|
| 80 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| 100 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| 200 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| 400 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| Instances | Algorithms | Best | Worst | Mean | Std | Rank |
|---|---|---|---|---|---|---|
| 600 | MG-ChOA | 337.9706 | 467.3819 | 393.3942 | 31.1964 | 1 |
| GA | 496.1133 | 668.4894 | 615.0010 | 37.3412 | 4 | |
| ACO | 646.3231 | 738.3302 | 692.2071 | 26.8871 | 8 | |
| PSO | 615.6234 | 732.0994 | 679.0999 | 25.8592 | 5 | |
| RPSO | 646.1737 | 680.3887 | 663.5755 | 8.2341 | 2 | |
| JADE | 634.4642 | 680.8589 | 654.7950 | 11.2532 | 3 | |
| SMA | 624.6327 | 717.2041 | 670.4092 | 28.6820 | 6 | |
| FA | 638.7109 | 730.8624 | 689.8933 | 23.4781 | 7 | |
| ChOA | 671.0393 | 746.3261 | 709.2050 | 18.7072 | 10 | |
| GWO | 696.4319 | 743.7724 | 716.6254 | 9.9470 | 9 | |
| 800 | MG-ChOA | 357.7428 | 512.2769 | 436.7981 | 32.8699 | 1 |
| GA | 678.5272 | 851.5621 | 769.3450 | 44.8163 | 8 | |
| ACO | 769.4406 | 851.4780 | 804.6975 | 19.5546 | 10 | |
| PSO | 747.8239 | 846.6075 | 797.8163 | 21.5773 | 9 | |
| RPSO | 728.5422 | 776.7191 | 748.1957 | 12.2668 | 2 | |
| JADE | 721.68571 | 780.1052 | 750.1521 | 12.0138 | 3 | |
| SMA | 688.8120 | 827.9618 | 757.8355 | 39.4238 | 6 | |
| FA | 713.2352 | 824.3031 | 767.2942 | 24.4921 | 5 | |
| ChOA | 664.0851 | 813.3595 | 733.6243 | 37.8625 | 4 | |
| GWO | 756.3863 | 832.1562 | 791.0453 | 19.8800 | 7 | |
| 1000 | MG-ChOA | 506.5729 | 552.8227 | 531.1736 | 10.5891 | 1 |
| GA | 1113.3512 | 1186.7736 | 1148.6414 | 14.9046 | 2 | |
| ACO | 1132.8896 | 1197.7980 | 1161.3229 | 13.9392 | 3 | |
| PSO | 1154.9312 | 1219.9879 | 1188.6006 | 15.3536 | 9 | |
| RPSO | 1145.0236 | 1209.0242 | 1182.4126 | 15.3321 | 6 | |
| JADE | 1143.6047 | 1212.5595 | 1177.5565 | 15.4292 | 8 | |
| SMA | 1176.3676 | 1229.0331 | 1203.5824 | 12.5634 | 10 | |
| FA | 1158.5719 | 1203.2321 | 1183.8478 | 11.3573 | 5 | |
| ChOA | 1171.0874 | 1200.9404 | 1185.5053 | 9.2586 | 4 | |
| GWO | 1176.2921 | 1203.2903 | 1190.6301 | 8.3314 | 7 | |
| 1200 | MG-ChOA | 665.4418 | 705.5305 | 685.8351 | 9.0505 | 1 |
| GA | 1502.4781 | 1542.2096 | 1519.9860 | 9.4525 | 3 | |
| ACO | 1535.6057 | 1601.0904 | 1567.2093 | 16.7193 | 7 | |
| PSO | 1505.9321 | 1543.2443 | 1528.1268 | 9.0864 | 5 | |
| RPSO | 1540.4621 | 1604.3669 | 1568.7338 | 14.3821 | 9 | |
| JADE | 1554.5170 | 1598.9232 | 1577.1516 | 11.8324 | 8 | |
| SMA | 1570.9568 | 1611.9386 | 1589.1695 | 9.2840 | 10 | |
| FA | 1490.7260 | 1530.2589 | 1510.9637 | 8.8396 | 2 | |
| ChOA | 1501.5574 | 1547.4414 | 1523.5250 | 11.8448 | 6 | |
| GWO | 1505.9274 | 1547.6684 | 1522.6388 | 7.6334 | 4 |
| Instances | GA | ACO | PSO | RPSO | JADE | SMA | FA | ChOA | GWO |
|---|---|---|---|---|---|---|---|---|---|
| 600 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| 800 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| 1000 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| 1200 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| Instances | Algorithms | Best | Worst | Mean | Std | Rank |
|---|---|---|---|---|---|---|
| 1600 | MG-ChOA | 1772.9074 | 1867.3117 | 1811.1547 | 25.8704 | 1 |
| GA | 1869.0448 | 1942.9288 | 1913.8718 | 19.4836 | 2 | |
| 1800 | MG-ChOA | 2255.8563 | 2332.6466 | 2291.6476 | 20.7723 | 1 |
| GA | 2301.8192 | 2353.5944 | 2330.8980 | 13.3407 | 2 |
| Instances | GA |
|---|---|
| 1600 | 1.73 × 10−6 |
| 1800 | 1.73 × 10−6 |
| Instances | P = 1 | P = 2 | P = 3 | P = 5 | P = 6 | P = 7 | P = 8 |
|---|---|---|---|---|---|---|---|
| 80 | 82.4214 | 74.6215 | 83.5353 | 83.3345 | 84.6859 | 86.2861 | 85.4101 |
| 200 | 124.7481 | 92.1894 | 128.2701 | 137.8198 | 153.1216 | 158.3709 | 171.8740 |
| 600 | 351.8525 | 337.4706 | 364.4159 | 392.7295 | 410.9527 | 421.8533 | 453.388 |
| 800 | 402.7831 | 387.2349 | 424.9258 | 443.1142 | 465.9428 | 477.8761 | 512.2769 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Zhou, Y.; Huang, H.; Luo, Q. An Improved Chimp-Inspired Optimization Algorithm for Large-Scale Spherical Vehicle Routing Problem with Time Windows. Biomimetics 2022, 7, 241. https://doi.org/10.3390/biomimetics7040241
Xiang Y, Zhou Y, Huang H, Luo Q. An Improved Chimp-Inspired Optimization Algorithm for Large-Scale Spherical Vehicle Routing Problem with Time Windows. Biomimetics. 2022; 7(4):241. https://doi.org/10.3390/biomimetics7040241
Chicago/Turabian StyleXiang, Yifei, Yongquan Zhou, Huajuan Huang, and Qifang Luo. 2022. "An Improved Chimp-Inspired Optimization Algorithm for Large-Scale Spherical Vehicle Routing Problem with Time Windows" Biomimetics 7, no. 4: 241. https://doi.org/10.3390/biomimetics7040241
APA StyleXiang, Y., Zhou, Y., Huang, H., & Luo, Q. (2022). An Improved Chimp-Inspired Optimization Algorithm for Large-Scale Spherical Vehicle Routing Problem with Time Windows. Biomimetics, 7(4), 241. https://doi.org/10.3390/biomimetics7040241




