Research on Logistics Distribution Center Location Based on Hybrid Beetle Antennae Search and Rain Algorithm
Abstract
1. Introduction
2. Logistics Distribution Center Location Model
- The logistics distribution center needs to satisfy the demand of all the locations.
- Each demand location has and can only be supplied by one logistics distribution center.
- The product of and is the smallest, where is the demand of each location and is the distance to the nearest distribution center.
- Other costs are not considered in this paper.
3. The Hybrid BRA
3.1. The Original BAS Algorithm
- Step 1: Build a search model that describes a random direction of the beetle’s search,where is a random function and is the dimension of solution space.
- Step 2: Create the space coordinates of beetle’s left and right antennae,where and indicate the position of the left and right antennae of the longicorn beetle on the iteration, respectively; indicates the position of the centroid of the longicorn beetle on the iteration; and indicates the distance between the left and right antennae.
- Step 3: The fitness function is used to judge the intensity of food smell received by the left and right antennae, that is, the values of and . denotes the fitness function.
- Step 4: Update the position of the longhorn beetle based on Equation (9),where denotes the step size factor at the iteration and is a symbolic function.
- Step 5: Determine whether the current solution meets the stop condition. If this condition is satisfied, stop the execution. Otherwise, jump to Step 2 and execute the loop.
3.2. The Original RA
- Step 1: A random number of raindrops are produced in dark clouds, as shown in Equation (10):where is a random number with uniform distribution. and are the upper and lower limits of the solution space, respectively.
- Step 2: The raindrop falls on the ground and splits into many small raindrops, as shown in Equation (11):where is the position of the split little raindrop. is a group of uniformly distributed -dimensional random numbers. represents the coverage radius of a raindrop that splits into small raindrops. and represent the maximum and minimum values of , respectively.
- Step 3: These split small raindrops are recombined into large raindrops based on Equation (12):where represents the number of the split small raindrops.
- Step 4: The weight of the raindrops is calculate and the position of the current individual is updated according to the range of , as shown in Equation (13):where and are random numbers that conform to the normal distribution; is the contraction factor of the current raindrop ; and are the upper and lower limits of , respectively; is the search factor of the optimal raindrop ; and and are the upper and lower limits of , respectively. and decrease linearly.
- Step 5: The best raindrop is selected, it is determined whether the end condition is satisfied. If it is satisfied, the execution is stopped. Otherwise, the loop is executed after jumping to Step 2.
3.3. The Hybrid BRA Procedure
- In the BAS algorithm, the search direction of the beetle is determined by the fitness values of the left and right antennae. In the RA, the individual with approaches the optimal position of the current generation as the number of iterations increases. From Equation (13), it can be seen that the search direction of is random. In order to better guide the search direction of , the search direction strategy of the BAS algorithm is introduced into the RA. It can be supposed that represents the position of one beetle’s antennae and is the position of another beetle’s antennae; therefore, the search direction of can be determined by the position relation between and , that is , and the position update formula of individuals of weight can be improved as follows:
- In the RA, from Equation (13), it can be seen that the individuals with and are discarded, and the same number of individuals are generated randomly in the solution space. The discarded solutions are the ones with a poor position or a lack of diversity near . The generated new solutions are randomly dispersed in the solution space which essentially increases the global search ability of the algorithm. Through the improvement of Equation (14), the global search ability of the individual with is enhanced a lot. Therefore, in this paper, the individuals with and are used to improve the local search ability. The same number of new solutions are randomly generated near and the search direction is introduced, and the position update equation is improved as follows:where is the maximum radius raindrops near the lowest position and can be modified by the user based on actual needs.
4. Experimental Studies on Benchmark Functions
4.1. Benchmark Functions
4.2. Parameter Setting
- : , , ;
- : , , ;
- : , , , ;
- : , , ;
- : , , , , , , ;
- : , , , , .
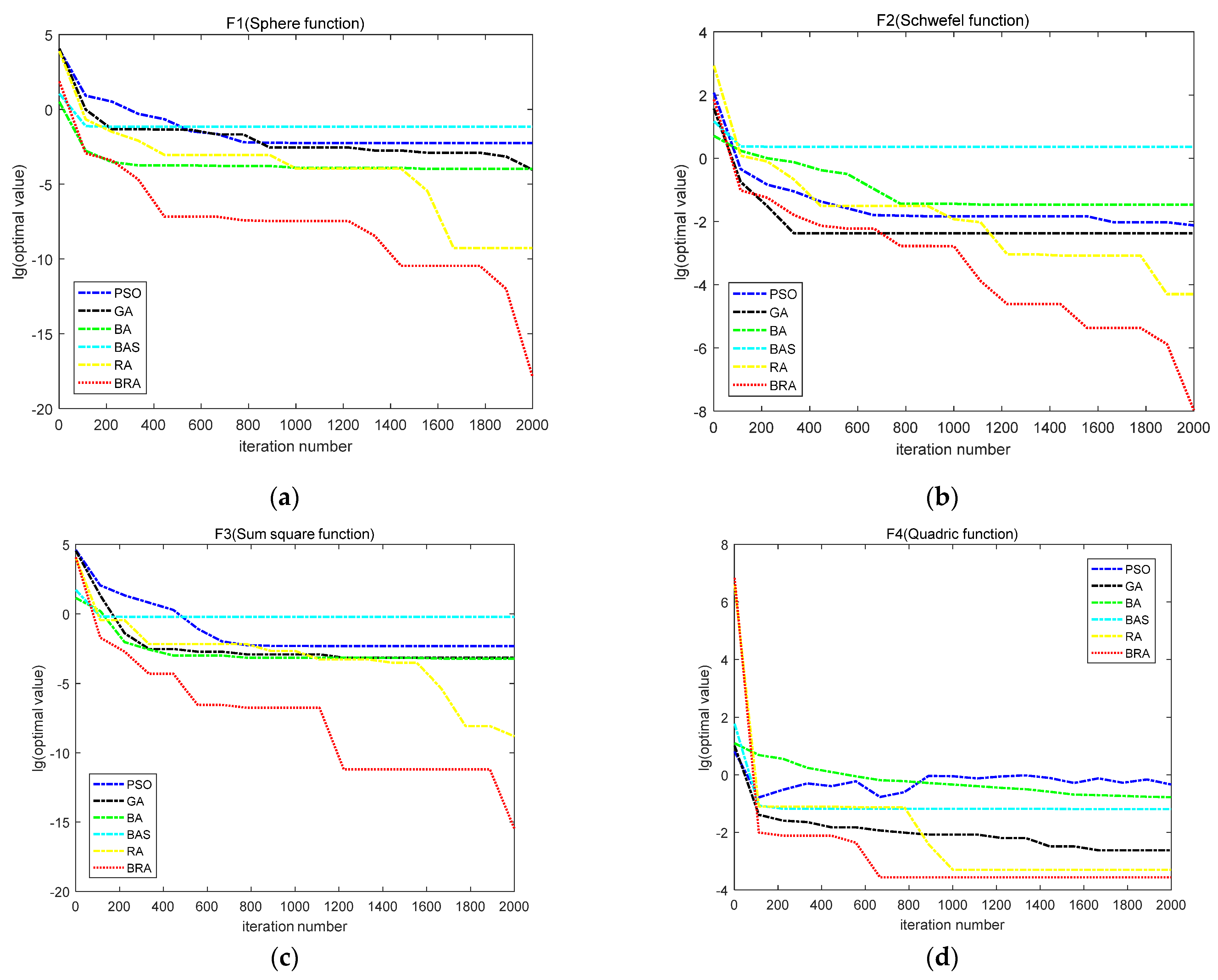
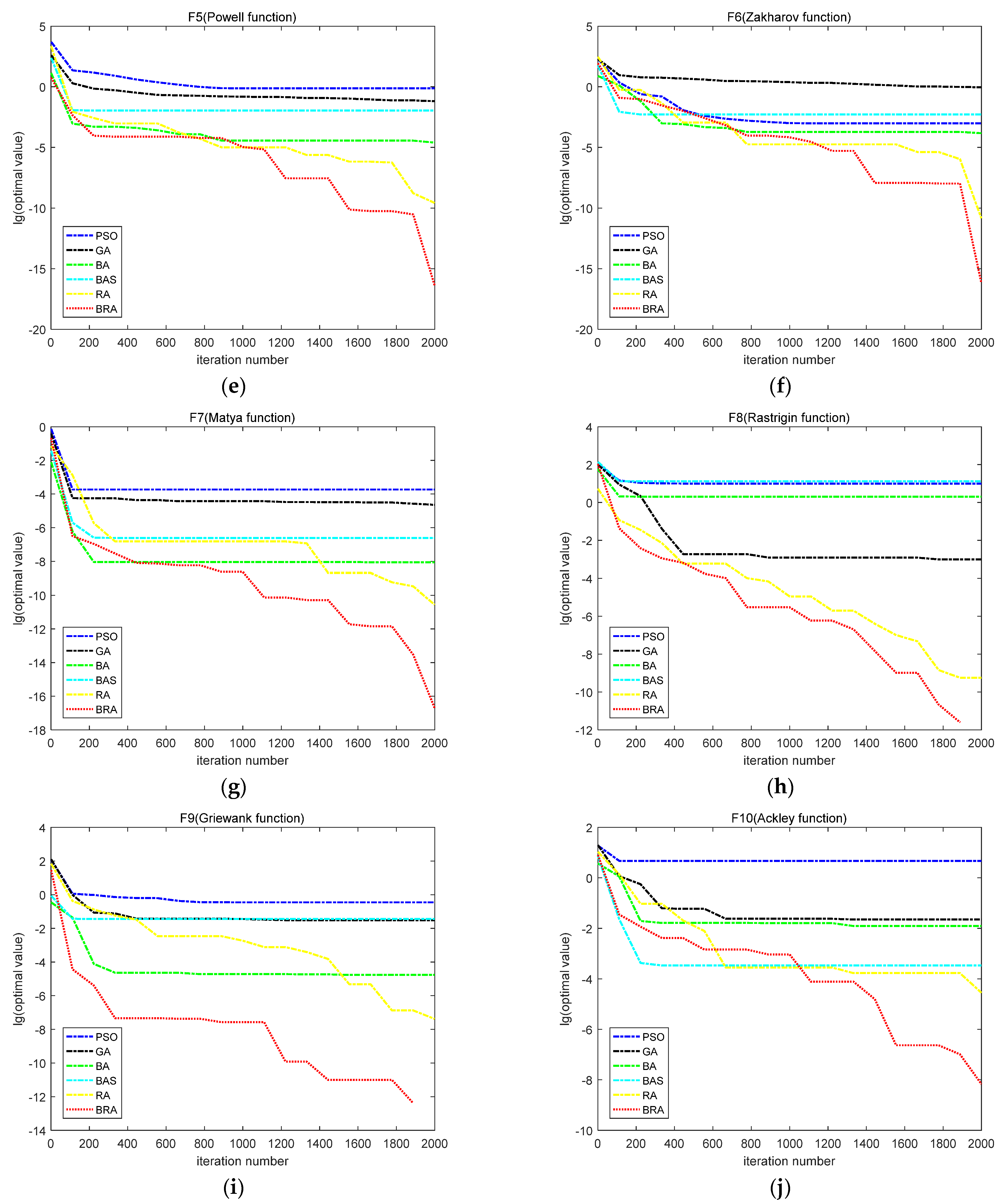
4.3. Numerical Results and Analysis
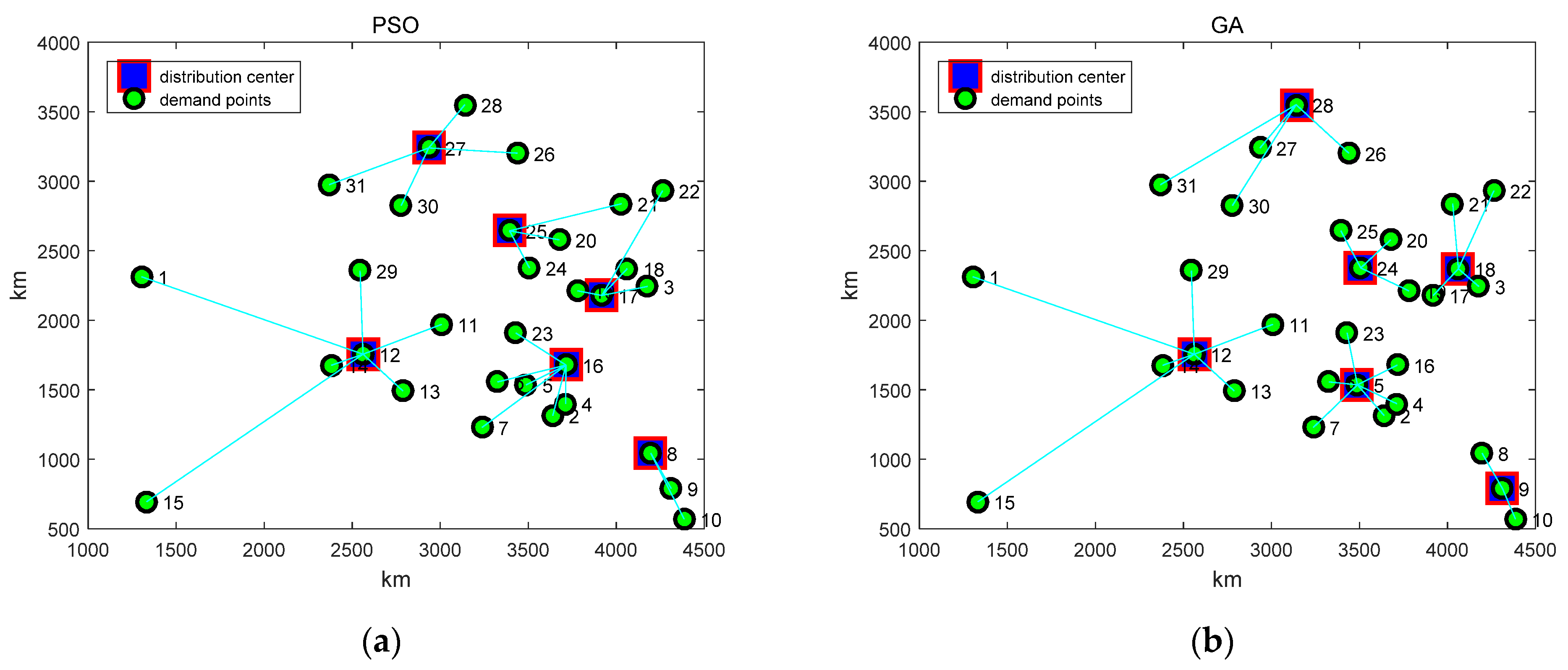
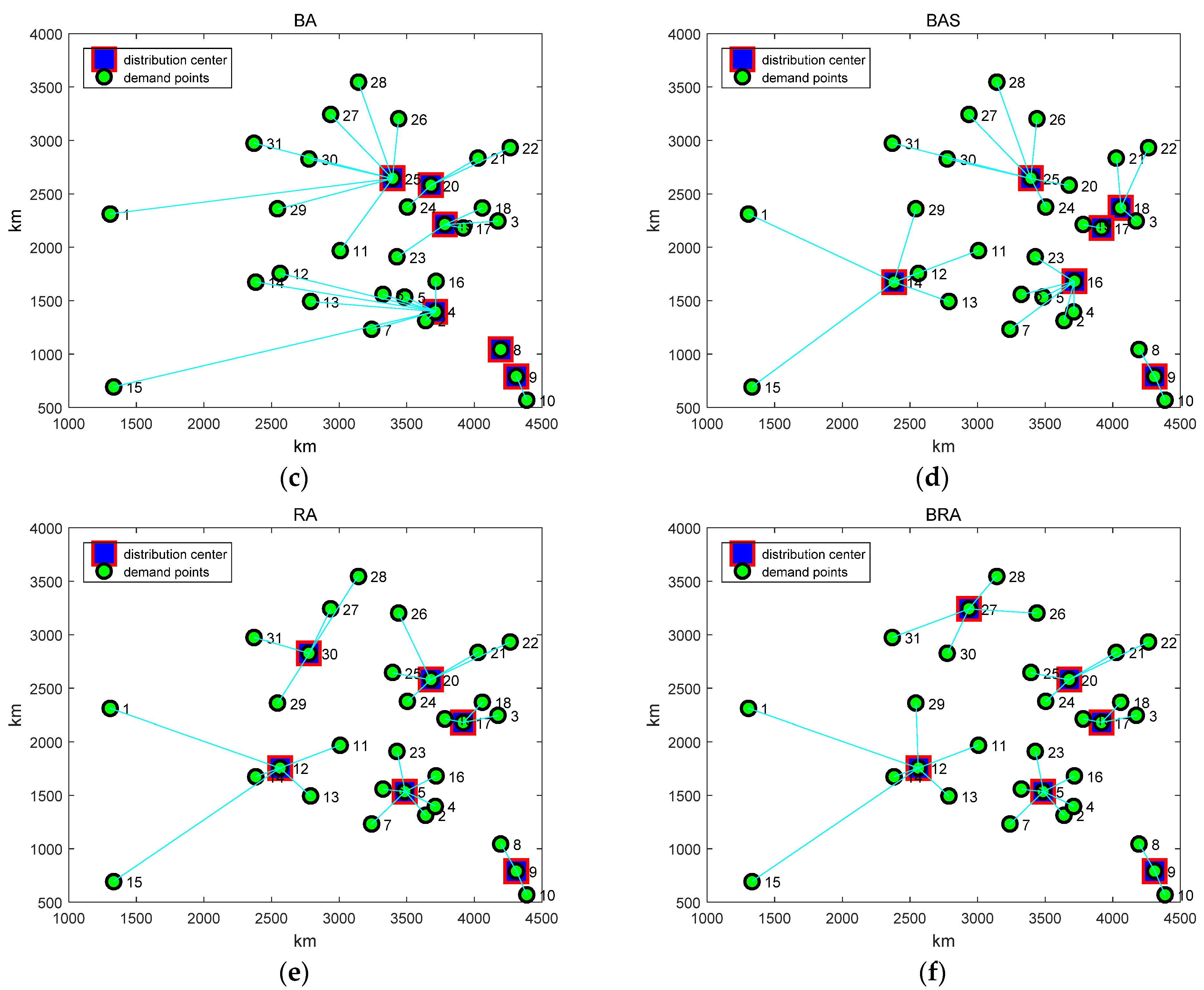
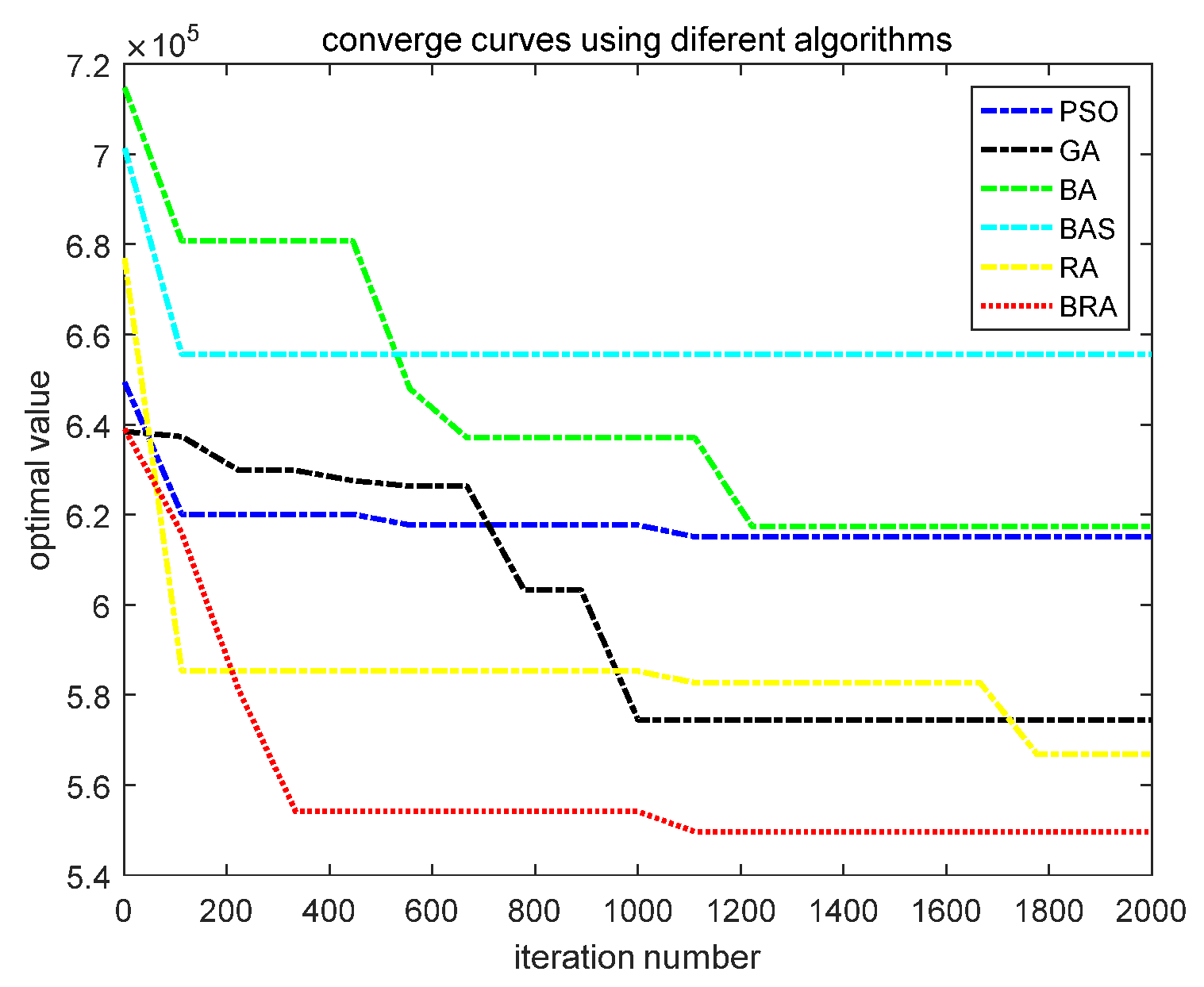
5. Application Studies on Logistics Distribution Centers’ Location
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, C.; Goh, M.; Zhao, Y.; Zheng, J. Location selection of city Logistics centers under sustainability. Transp. Res. Part D Transp. Environ. 2015, 36, 29–44. [Google Scholar] [CrossRef]
- Chi, R.; Su, Y.X.; Qu, Z.J.; Chi, X.X. A hybridization of cuckoo search and differential evolution for the logistics distribution center location problem. Math. Probl. Eng. 2019, 2019, 7051248. [Google Scholar] [CrossRef]
- Lee, P.T.W.; Hu, Z.H.; Lee, S.J.; Feng, X.H.; Notteboom, T. Strategic locations for logistics distribution centers along the Belt and Road: Explorative analysis and research agenda. Transp. Policy 2022, 116, 24–47. [Google Scholar] [CrossRef]
- Liu, P.D.; Li, Y. Multiattribute decision method for comprehensive logistics distribution center location selection based on 2-dimensional linguistic information. Inf. Sci. 2020, 538, 209–244. [Google Scholar] [CrossRef]
- Sun, H.J.; Gao, Z.Y.; Wu, J.J. A bi-level programming model and solution algorithm for the location of logistics distribution centers. Appl. Math. Model. 2008, 32, 610–616. [Google Scholar] [CrossRef]
- Bongartz, I.; Calamai, P.H.; Conn, A.R. A projection method for lp norm location-allocation problems. Math. Program. 1994, 66, 283–312. [Google Scholar] [CrossRef]
- Liu, S.J.; Wang, Z.; Miao, R.; Xu, J.; Huang, H. Research of location selection of distribution center for service based on gravity method. Appl. Mech. Mater. 2013, 433, 2419–2423. [Google Scholar] [CrossRef]
- Taniguchi, E.; Noritake, M.; Yamada, T. Optimal size and location planning of public logistics terminals. Transp. Res. Part E: Logist. Transp. Rev. 1999, 35, 207–222. [Google Scholar] [CrossRef]
- Christensen, T.R.L.; Andreas, K. A fast exact method for the capacitated facility location problem with differentiable convex production costs. Eur. J. Oper. Res. 2021, 292, 855–868. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Chen, N.; She, N.; Li, K. Location optimization of a competitive distribution center for urban cold chain logistics in terms of low-carbon emissions. Comput. Ind. Eng. 2021, 154, 107120. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.L.; Xu, M.Z.; Liu, Y. Two-echelon logistics distribution region partitioning problem based on a hybrid particle swarm optimization–genetic algorithm. Expert Syst. Appl. 2015, 42, 5019–5031. [Google Scholar] [CrossRef]
- Cui, H.X.; Qiu, J.L.; Cao, J.D.; Guo, M. Route optimization in township logistics distribution considering customer satisfaction based on adaptive genetic algorithm. Math. Comput. Simul. 2022, 204, 28–42. [Google Scholar] [CrossRef]
- Enrique, D.; José, M. A neural model for the p-median problem. Comput. Oper. Res. 2008, 35, 404–416. [Google Scholar]
- Thongdee, T.; Pitakaso, R. Differential evolution algorithms solving a multi-objective, source and stage location-allocation problem. Ind. Eng. Manag. Syst. 2015, 14, 11–21. [Google Scholar] [CrossRef]
- Jha, A.; Somani, K.; Tiwari, M.K.; Chan, F.T.S.; Fernandes, K.J. Minimizing transportation cost of a joint inventory location model using modified adaptive differential evolution algorithm. Int. J. Adv. Manuf. Technol. 2012, 60, 329–341. [Google Scholar] [CrossRef]
- Wang, L.; Qu, H.; Chen, T.; Yan, F.P. An Effective Hybrid Self-Adapting Deferential Evolution Algorithm for the Joint Replenishment and Location-Inventory Problem in A Tree Level Supply Level Supply Chain. Sci. World J. 2013, 2013, 270249. [Google Scholar] [CrossRef]
- Hua, X.; Hu, X.; Yuan, W.W. Research optimization on logistics distribution center location based on adaptive particle swarm algorithm. Optik 2016, 127, 8443–8450. [Google Scholar] [CrossRef]
- Qi, C.M. Application of Improved Discrete Particle Swarm Optimization in Logistics Distribution Routing Problem. Procedia Eng. 2011, 15, 3673–3677. [Google Scholar] [CrossRef]
- Liu, H.J. Research on cloud computing adaptive task scheduling based on ant colony algorithm. Optik 2016, 258, 168677. [Google Scholar] [CrossRef]
- Teschemacher, U.; Reinhart, G. Ant Colony Optimization Algorithms to Enable Dynamic Milkrun Logistics. Procedia CIRP 2017, 63, 762–767. [Google Scholar] [CrossRef]
- Li, S.; Jiang, X.Y. BAS: Beetle Antennae Search Algorithm for Optimization Problems. arXiv 2017, 10, 1–3. [Google Scholar]
- Xie, S.; Chu, X.M.; Zheng, M.; Liu, C.G. Ship predictive collision avoidance method based on an improved beetle antennae search algorithm. Ocean Eng. 2019, 192, 106542. [Google Scholar] [CrossRef]
- Khan, A.H.; Cao, X.W.; Xu, B.; Li, S. Beetle Antennae Search: Using Biomimetic Foraging Behaviour of Beetles to Fool a Well-Trained Neuro-Intelligent System. Biomimetics 2022, 7, 84. [Google Scholar] [CrossRef] [PubMed]
- Li, X.Q.; Jiang, H.K.; Niu, M.G.; Wang, R.X. An enhanced selective ensemble deep learning method for rolling bearing fault diagnosis with beetle antennae search algorithm. Mech. Syst. Signal Process. 2020, 142, 106752. [Google Scholar] [CrossRef]
- Qian, J.; Wang, P.; Pu, C.G.; Peng, X.L.; Chen, G.G. Application of modified beetle antennae search algorithm and BP power flow prediction model on multi-objective optimal active power dispatch. Appl. Soft Comput. 2021, 113, 108027. [Google Scholar] [CrossRef]
- Chi, R.; Chi, X.X. Rain Algorithm: A new metaheuristic method for optimization problems. engrXiv 2022, 7, 2460. [Google Scholar]
- Shi, F.; Wang, H.; Yu, L.; Hu, F. 30 Cases Analysis of IntelligentAlgorithm Based on Matlab, 2nd ed.; Beihang University Press: Beijing, China, 2011; pp. 118–128. [Google Scholar]
- Hedar, A.R.; Fukushima, M. Tabu search directed by direct search methods for nonlinear global optimization. Eur. J. Oper. Res. 2006, 170, 329–349. [Google Scholar] [CrossRef]
- Wang, L.; Zou, F.; Hei, X. A hybridization of teaching-learning-based optimization and differential evolution for chaotic time series prediction. Neural Comput. Appl. 2014, 9, 1407–1422. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. Stud. Comput. Intell. 2010, 284, 65–74. [Google Scholar]

| No. | Name | Formula | D | Range | Optima |
|---|---|---|---|---|---|
| F1 | Sphere | 10 | [−100, 100] | 0 | |
| F2 | Schwefel 2.22 | 10 | [−10, 10] | 0 | |
| F3 | Sum square | 10 | [−10, 10] | 0 | |
| F4 | Quadric | 10 | [−1.28, 1.28] | 0 | |
| F5 | Powell | 24 | [−4, 5] | 0 | |
| F6 | Zakharov | 10 | [−5, 10] | 0 | |
| F7 | Matyas | 10 | [−5, 10] | 0 | |
| F8 | Rastrigin | 10 | [−5.12, 5.12] | 0 | |
| F9 | Griewank | 10 | [−600, 600] | 0 | |
| F10 | Ackley | 10 | [−32, 32] | 0 |
| Function Criteria | F1 Sphere | F2 Schwefel 2.2.2 | ||||||
| Best | Worst | Mean | Std | Best | Worst | Mean | Std | |
| PSO | 5.14 × 10−6 | 1.23 × 10−2 | 1.50 × 10−3 | 2.20 × 10−3 | 4.50 × 10−3 | 1.206 × 10−1 | 2.87 × 10−2 | 2.52 × 10−2 |
| GA | 9.64 × 10−5 | 9.20 × 10−3 | 1.40 × 10−3 | 1.60 × 10−3 | 3.32 × 10−4 | 1.11 × 10−2 | 2.70 × 10−3 | 2.30 × 10−3 |
| BA | 6.38 × 10−5 | 1.87 × 10−4 | 1.18 × 10−4 | 3.91 × 10−5 | 2.53 × 10−2 | 3.43 × 10−2 | 2.91 × 10−2 | 3.43 × 10−3 |
| BAS | 6.79 × 10−2 | 4.69 × 10−1 | 3.16 × 10−1 | 1.49 × 10−1 | 6.39 × 10−1 | 2.84 | 1.47 | 7.11 × 10−1 |
| RA | 2.08 × 10−8 | 2.44 ×10−10 | 3.57 × 10−9 | 6.55 × 10−9 | 2.28 × 10−5 | 6.75 × 10−7 | 6.55 × 10−6 | 6.26 × 10−6 |
| BRA | 4.50 × 10−20 | 2.10 × 10−17 | 6.65 ×10−18 | 6.82 × 10−18 | 3.63 × 10−10 | 7.07 × 10−9 | 1.99 × 10−9 | 2.27 × 10−9 |
| Function Criteria | F3 Sum square | F4 Quadric | ||||||
| Best | Worst | Mean | Std | Best | Worst | Mean | Std | |
| PSO | 1.00 × 10−4 | 1.86 × 10−1 | 2.02 × 10−2 | 3.53 × 10−2 | 6.70 × 10−3 | 4.27 × 10−2 | 2.48 × 10−2 | 8.60 × 10−3 |
| GA | 1.58 × 10−5 | 4.80 × 10−2 | 7.20 × 10−3 | 1.09 × 10−2 | 9.00 × 10−4 | 5.60 × 10−3 | 2.80 × 10−3 | 1.10 × 10−3 |
| BA | 3.74 × 10−4 | 7.21 × 10−4 | 5.41 × 10−4 | 1.12 × 10−4 | 9.15 × 10−2 | 3.21 × 10−1 | 1.74 × 10−1 | 6.56 × 10−2 |
| BAS | 6.07 × 10−1 | 1.19 × 101 | 5.99 | 5.39 | 6.35 × 10−2 | 8.72 | 1.86 | 3.07 |
| RA | 1.04 ×10−10 | 1.49 × 10−7 | 2.43 × 10−8 | 4.60 × 10−8 | 1.38 × 10−3 | 2.87 × 10−5 | 4.22 × 10−4 | 3.97 × 10−4 |
| BRA | 1.60 × 10−19 | 1.71 × 10−17 | 6.15 × 10−18 | 5.35 × 10−18 | 6.35 × 10−6 | 5.27 × 10−4 | 1.23 × 10−4 | 1.60 × 10−4 |
| Function Criteria | F5 Powell | F6 Zakharov | ||||||
| Best | Worst | Mean | Std | Best | Worst | Mean | Std | |
| PSO | 2.28 × 10−1 | 1.56 × 102 | 5.21 | 21.9 | 1.94 × 10−5 | 33.7 | 6.74 × 10−1 | 4.76 |
| GA | 4.80 × 10−3 | 7.83 × 10−2 | 4.18 × 10−2 | 2.02 × 10−2 | 9.48 × 10−2 | 1.91 | 6.35 × 10−1 | 4.38 × 10−1 |
| BA | 1.89 × 10−5 | 1.38 × 10−4 | 5.40 × 10−5 | 3.53 × 10−5 | 1.38 × 10−4 | 3.16 × 10−4 | 2.11 × 10−4 | 6.25 × 10−5 |
| BAS | 4.01 × 10−3 | 2.42 × 10−1 | 5.98 × 10−2 | 1.02 × 10−1 | 1.77 × 10−3 | 1.19 | 4.78 × 10−1 | 5.87 × 10−1 |
| RA | 2.02 ×10−13 | 1.44 × 10−9 | 4.19 ×10−10 | 5.06 ×10−10 | 1.45 ×10−11 | 2.52 × 10−8 | 6.19 × 10−9 | 9.51 × 10−9 |
| BRA | 2.38 × 10−20 | 9.40 × 10−17 | 3.24 × 10−17 | 3.39 × 10−17 | 1.37 × 10−17 | 2.12× 10−15 | 6.06× 10−16 | 7.47 × 10 −16 |
| Function Criteria | F7 Matyas | F8 Rastrigin | ||||||
| Best | Worst | Mean | Std | Best | Worst | Mean | Std | |
| PSO | 1.67 × 10−2 | 9.61 | 6.70 | 2.08 | 1.67 × 10−2 | 9.61 | 6.70 | 2.08 |
| GA | 1.13 × 10−6 | 5.50 × 10−3 | 7.29 × 10−4 | 9.82 × 10−4 | 1.13 × 10−6 | 5.50 × 10−3 | 7.29 × 10−4 | 9.82 × 10−4 |
| BA | 2.01 | 9.97 | 6.78 | 3.09 | 2.01 | 9.97 | 6.78 | 3.09 |
| BAS | 1.71 × 10−9 | 3.35 × 10−5 | 7.14 × 10−6 | 1.48 × 10−5 | 1.19 × 101 | 4.01 × 101 | 2.39 × 101 | 8.36 |
| RA | 2.28 ×10−17 | 2.60 ×10−11 | 4.74 ×10−12 | 8.74 ×10−12 | 1.10 ×10−12 | 1.60 × 10−9 | 5.09 × 10−10 | 5.99 ×10−10 |
| BRA | 1.14 × 10−20 | 1.81 × 10−17 | 3.65 × 10−18 | 5.87 × 10−18 | 0 | 0 | 0 | 0 |
| Function Criteria | F9 Griewank | F10 Ackley | ||||||
| Best | Worst | Mean | Std | Best | Worst | Mean | Std | |
| PSO | 3.82 × 10−2 | 3.91 × 10−1 | 1.54 × 10−1 | 8.49 × 10−2 | 2.69 | 4.72 | 3.43 | 6.01 × 10−1 |
| GA | 4.74 × 10−4 | 1.09 × 10−1 | 4.93 × 10−2 | 2.54 × 10−2 | 1.43 × 10−3 | 2.24 × 10−2 | 1.01 × 10−2 | 6.01 × 10−3 |
| BA | 8.72 × 10−6 | 1.71 × 10−5 | 1.25 × 10−5 | 3.12 × 10−6 | 1.24 × 10−2 | 3.02 | 1.93 | 8.64 × 10−1 |
| BAS | 3.29 × 10−2 | 2.31 × 10−1 | 1.26 × 10−1 | 8.58 × 10−2 | 3.39 × 10−4 | 2.93 × 10−2 | 2.28 × 10−3 | 1.53 × 10−3 |
| RA | 6.21 ×10−11 | 2.64 × 10−7 | 4.52 × 10−8 | 9.22 × 10−8 | 1.94 × 10−7 | 4.50 × 10−5 | 1.77 × 10−5 | 1.44 × 10−5 |
| BRA | 0 | 0 | 0 | 0 | 3.56 × 10−11 | 6.91 × 10−9 | 1.90 × 10−9 | 1.99 ×10−9 |
| i | (Ui, Vi) | ci | i | (Ui, Vi) | ci | i | (Ui, Vi) | ci |
|---|---|---|---|---|---|---|---|---|
| 1 | (1304, 2312) | 20 | 12 | (2562, 1756) | 40 | 23 | (3429, 1908) | 80 |
| 2 | (3639, 1315) | 90 | 13 | (2788, 1491) | 40 | 24 | (3507, 2376) | 70 |
| 3 | (4177, 2244) | 90 | 14 | (2381, 1676) | 40 | 25 | (3394, 2643) | 80 |
| 4 | (3712, 1399) | 60 | 15 | (1332, 695) | 20 | 26 | (3439, 3201) | 40 |
| 5 | (3488, 1535) | 70 | 16 | (3715, 1678) | 80 | 27 | (2935, 3240) | 40 |
| 6 | (3326, 1556) | 70 | 17 | (3918, 2179) | 90 | 28 | (3140, 3550) | 60 |
| 7 | (3238, 1229) | 40 | 18 | (4061, 2370) | 70 | 29 | (2545, 2357) | 70 |
| 8 | (4196, 1044) | 90 | 19 | (3780, 2212) | 100 | 30 | (2778, 2826) | 50 |
| 9 | (4312, 790) | 90 | 20 | (3676, 2578) | 50 | 31 | (2370, 2975) | 30 |
| 10 | (4386, 570) | 70 | 21 | (4029, 2838) | 50 | |||
| 11 | (3007, 1970) | 60 | 22 | (4263, 2934) | 50 |
| Algorithms | Optimal Distribution Center (j) | Cost | |||||
|---|---|---|---|---|---|---|---|
| j1 | j2 | j3 | j4 | j5 | j6 | ||
| PSO | 27 | 16 | 25 | 17 | 8 | 12 | 6.15 × 105 |
| GA | 30 | 20 | 9 | 14 | 17 | 5 | 5.74 × 105 |
| BA | 19 | 9 | 25 | 20 | 8 | 4 | 6.08 × 105 |
| BAS | 16 | 25 | 9 | 18 | 14 | 17 | 6.56 × 105 |
| RA | 5 | 30 | 9 | 20 | 12 | 17 | 5.67 × 105 |
| BRA | 5 | 27 | 9 | 20 | 12 | 17 | 5.54 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Z.; Chi, X.; Chi, R. Research on Logistics Distribution Center Location Based on Hybrid Beetle Antennae Search and Rain Algorithm. Biomimetics 2022, 7, 194. https://doi.org/10.3390/biomimetics7040194
Mei Z, Chi X, Chi R. Research on Logistics Distribution Center Location Based on Hybrid Beetle Antennae Search and Rain Algorithm. Biomimetics. 2022; 7(4):194. https://doi.org/10.3390/biomimetics7040194
Chicago/Turabian StyleMei, Zhimin, Xuexin Chi, and Rui Chi. 2022. "Research on Logistics Distribution Center Location Based on Hybrid Beetle Antennae Search and Rain Algorithm" Biomimetics 7, no. 4: 194. https://doi.org/10.3390/biomimetics7040194
APA StyleMei, Z., Chi, X., & Chi, R. (2022). Research on Logistics Distribution Center Location Based on Hybrid Beetle Antennae Search and Rain Algorithm. Biomimetics, 7(4), 194. https://doi.org/10.3390/biomimetics7040194









