Investigation on the Anisotropic Wetting Properties of Water Droplets on Bio-Inspired Groove Structures Fabricated by 3D Printing and Surface Modifications
Abstract
1. Introduction
2. Materials and Methods
2.1. Dart-Shaped Structure Design
2.2. Experiments
2.2.1. Preparation of Dart-Shaped Pattern
2.2.2. Structural and Morphological Characterization
2.2.3. Surface Modification
2.2.4. Observation of Wetting Behavior
3. Results
3.1. Surface Characterization
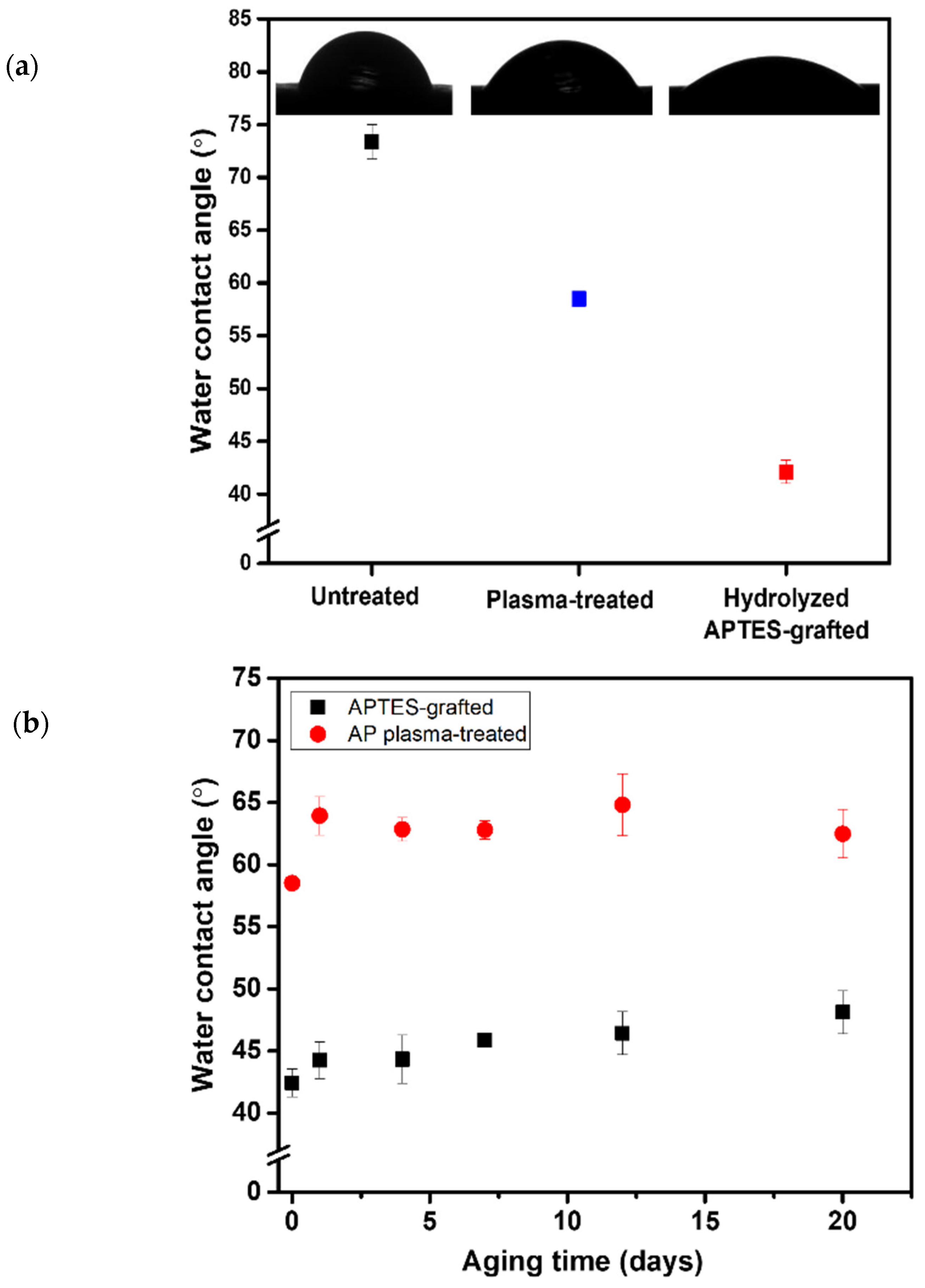
3.1.1. Static Contact Angle Measurement
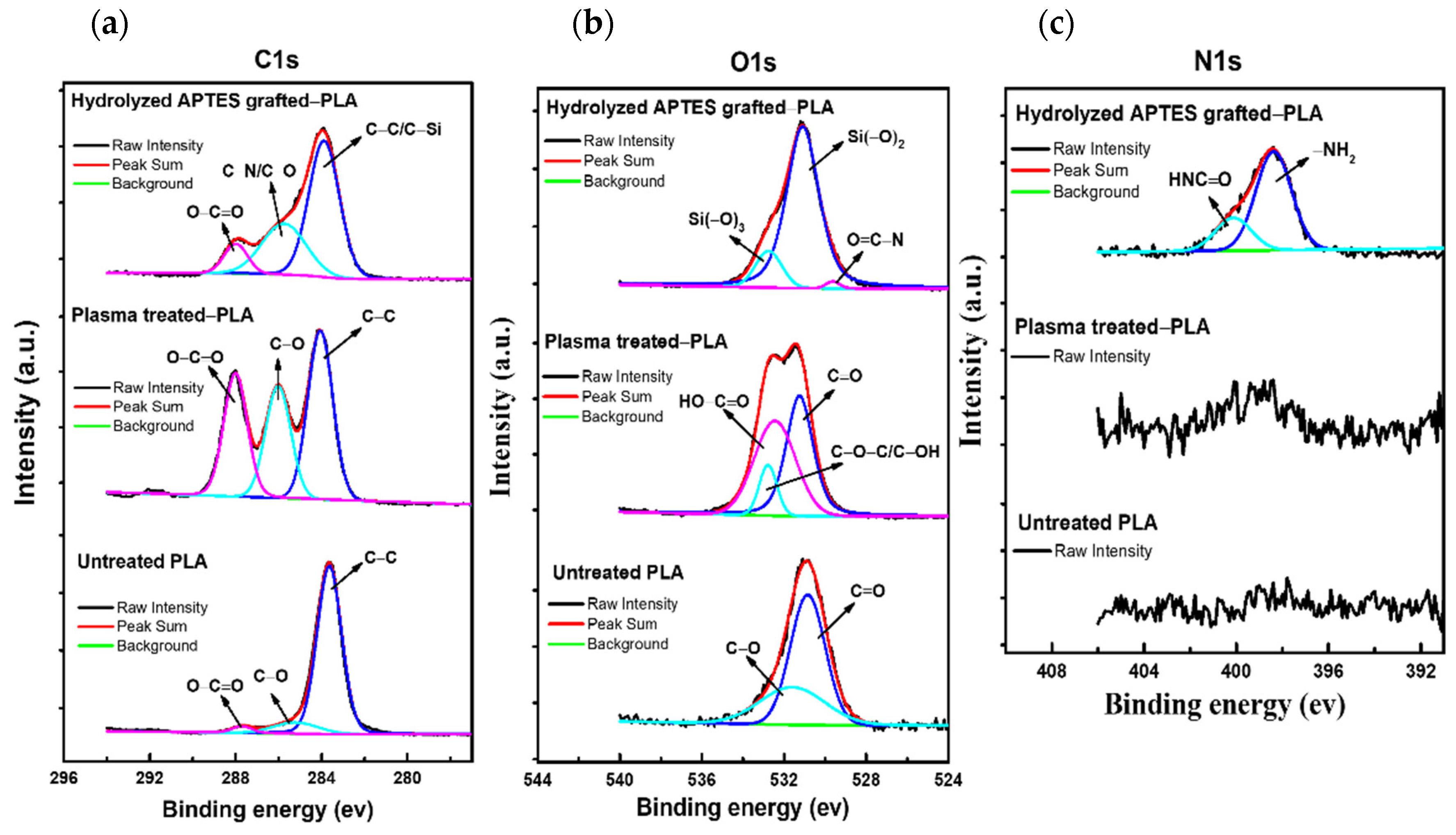
3.1.2. Chemical Composition Analysis
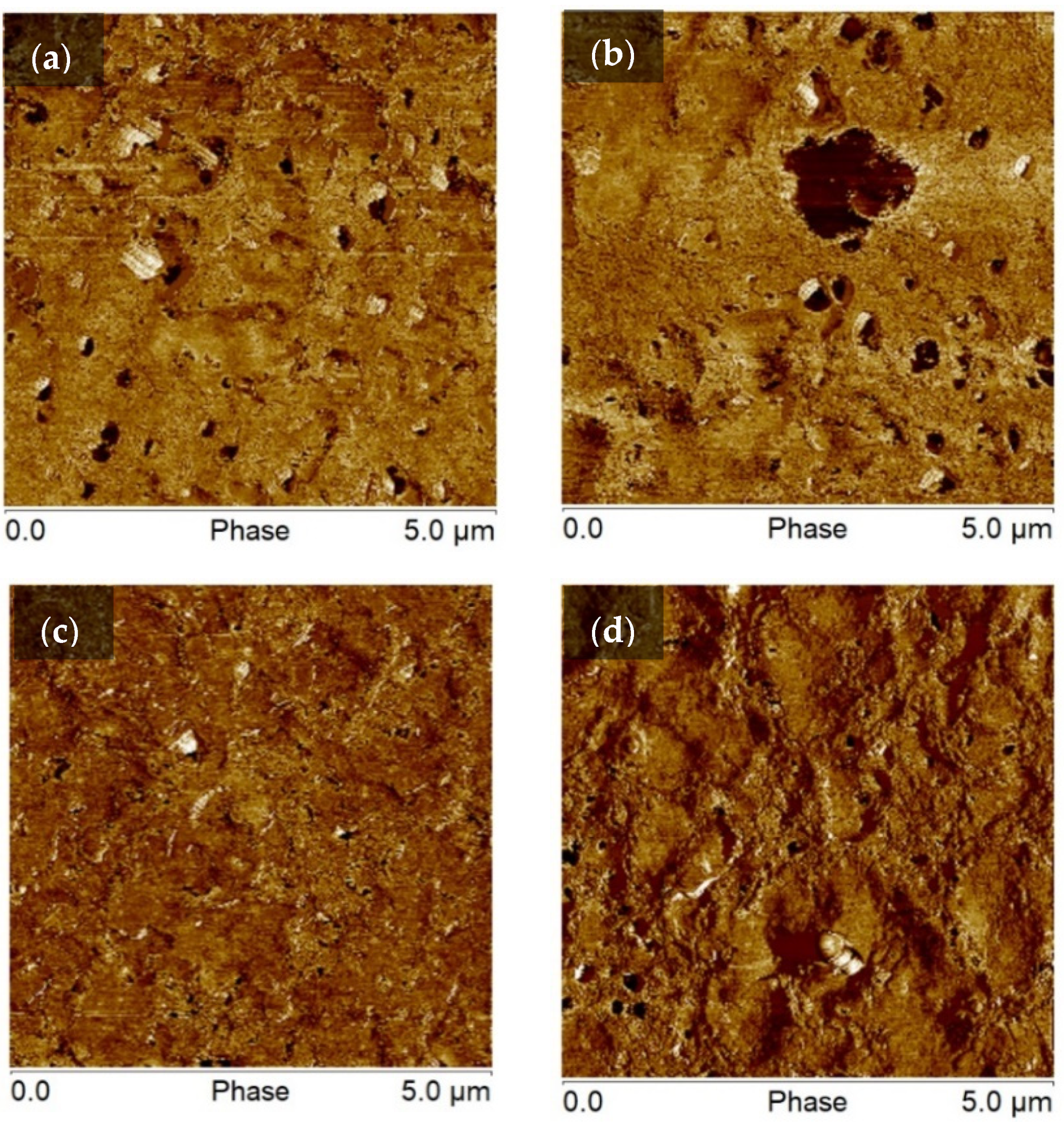
3.1.3. Surface Morphology Characterization
3.2. Dynamic Wetting Behavior on 3D-Printed Dart-Shaped Pattern Array
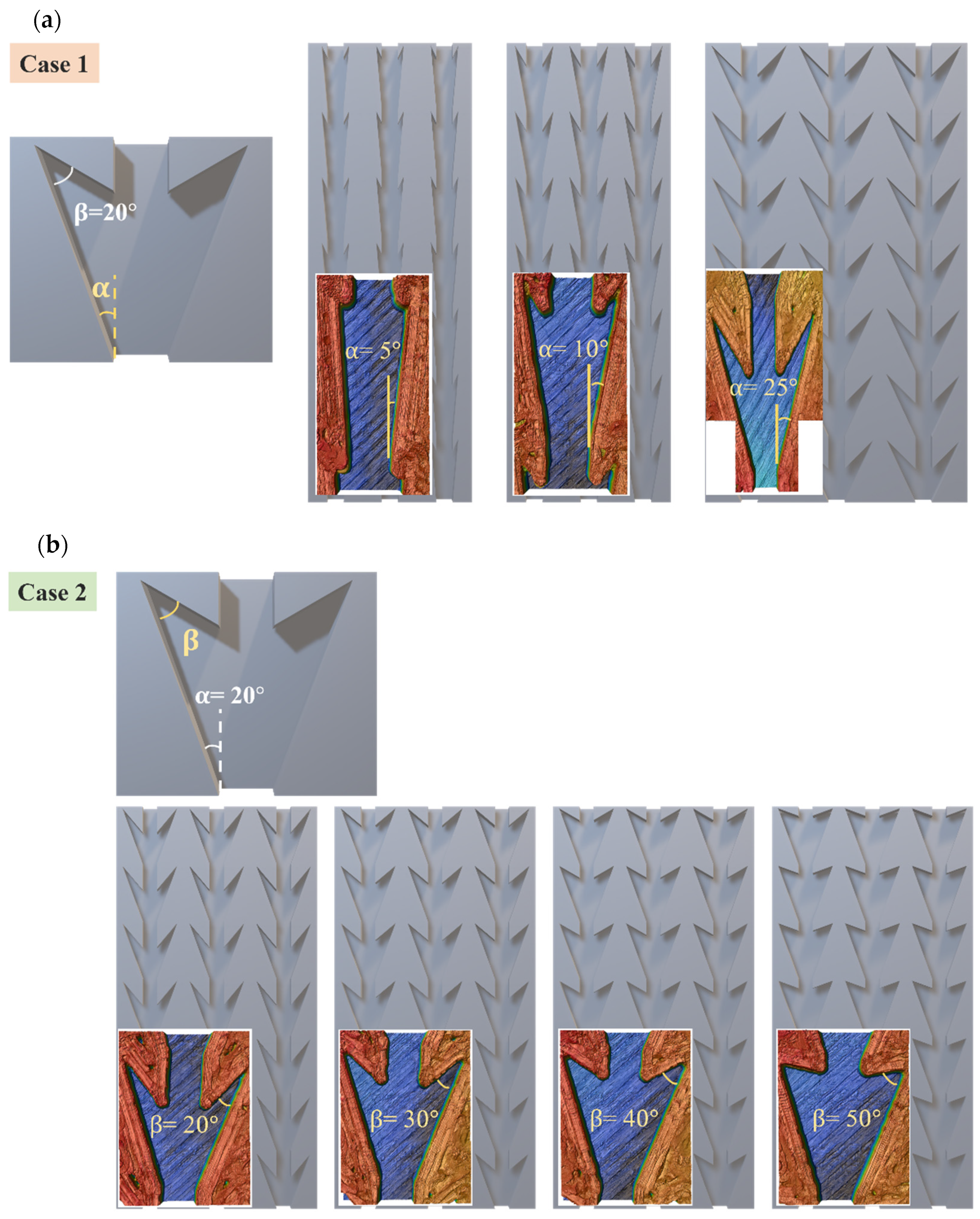
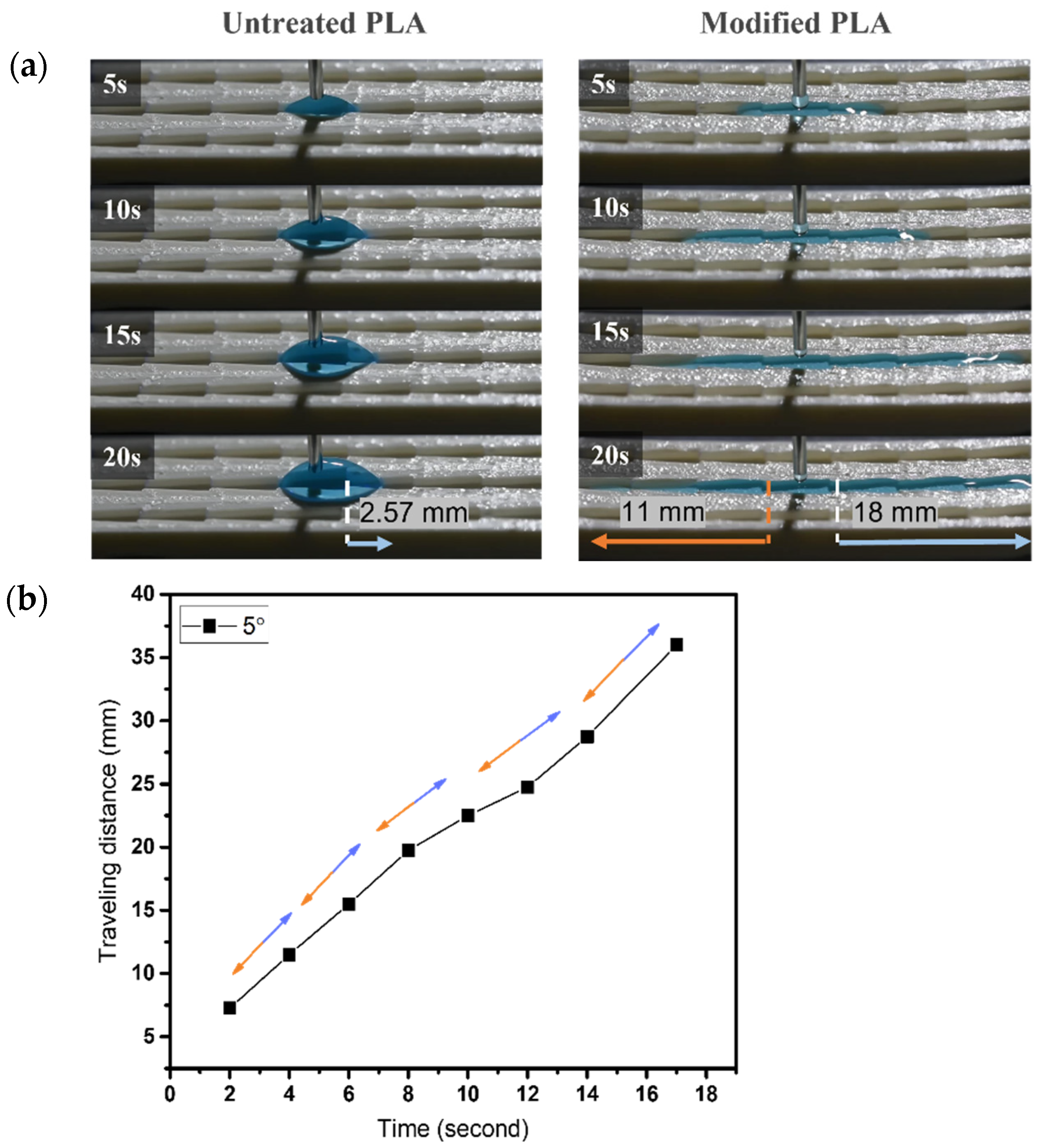
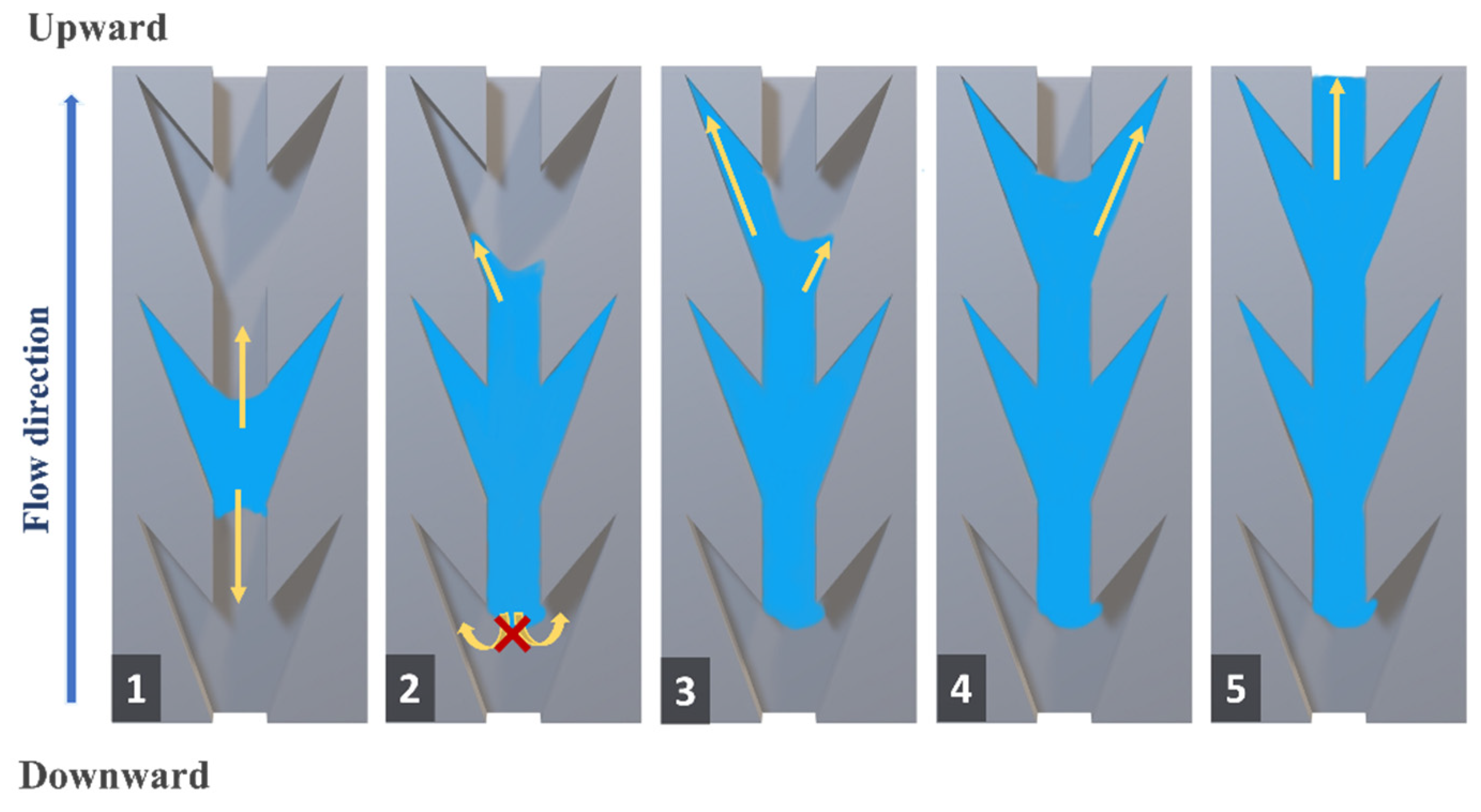
3.2.1. Dynamic Wetting Behavior of Case 1
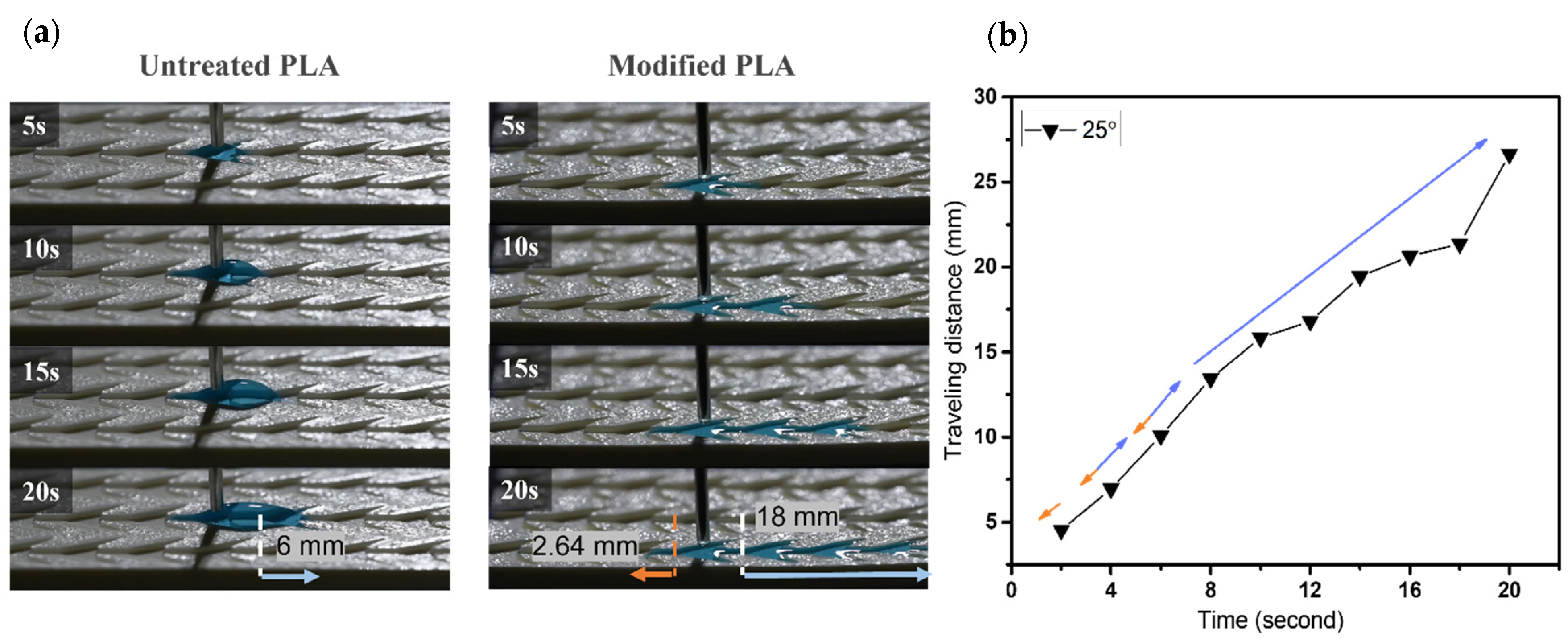
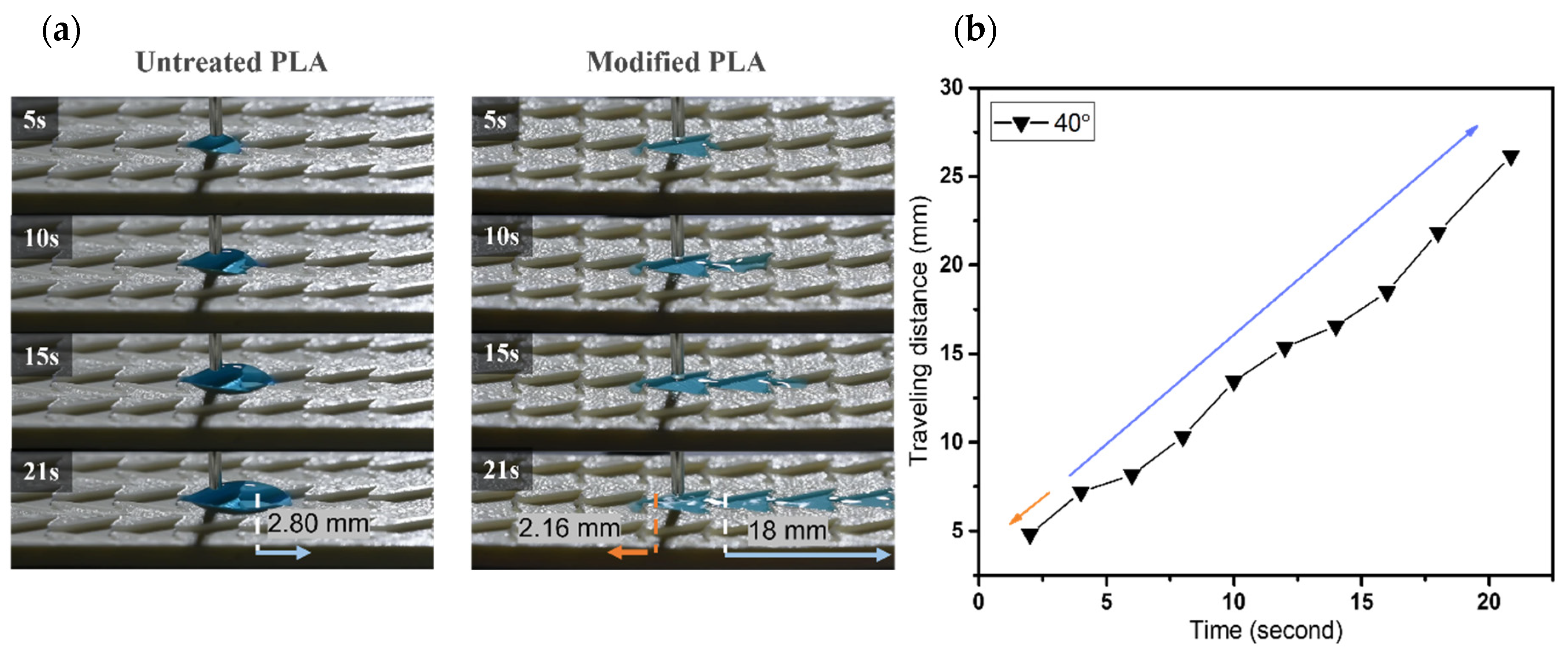
3.2.2. Dynamic Wetting Behavior of Case 2
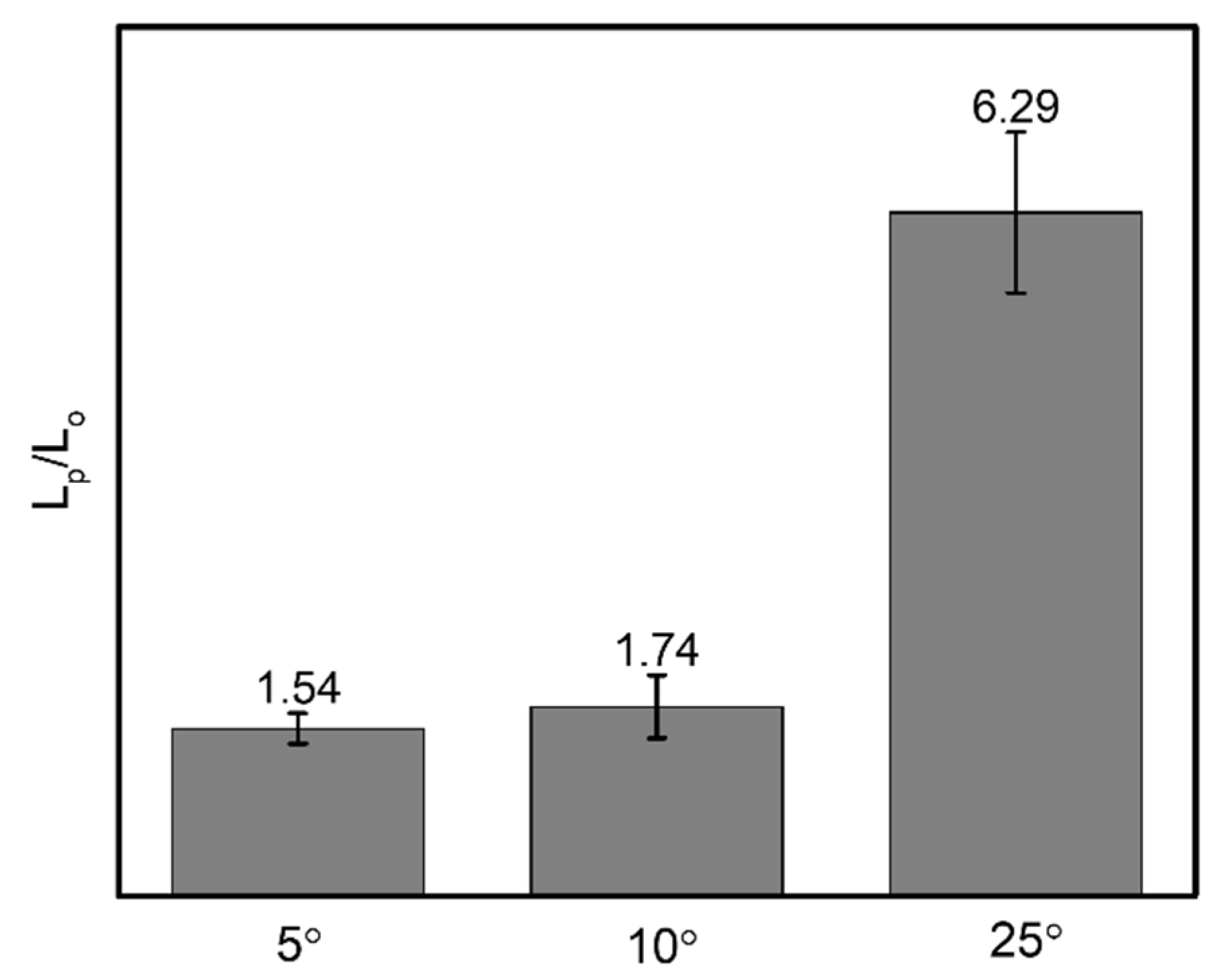
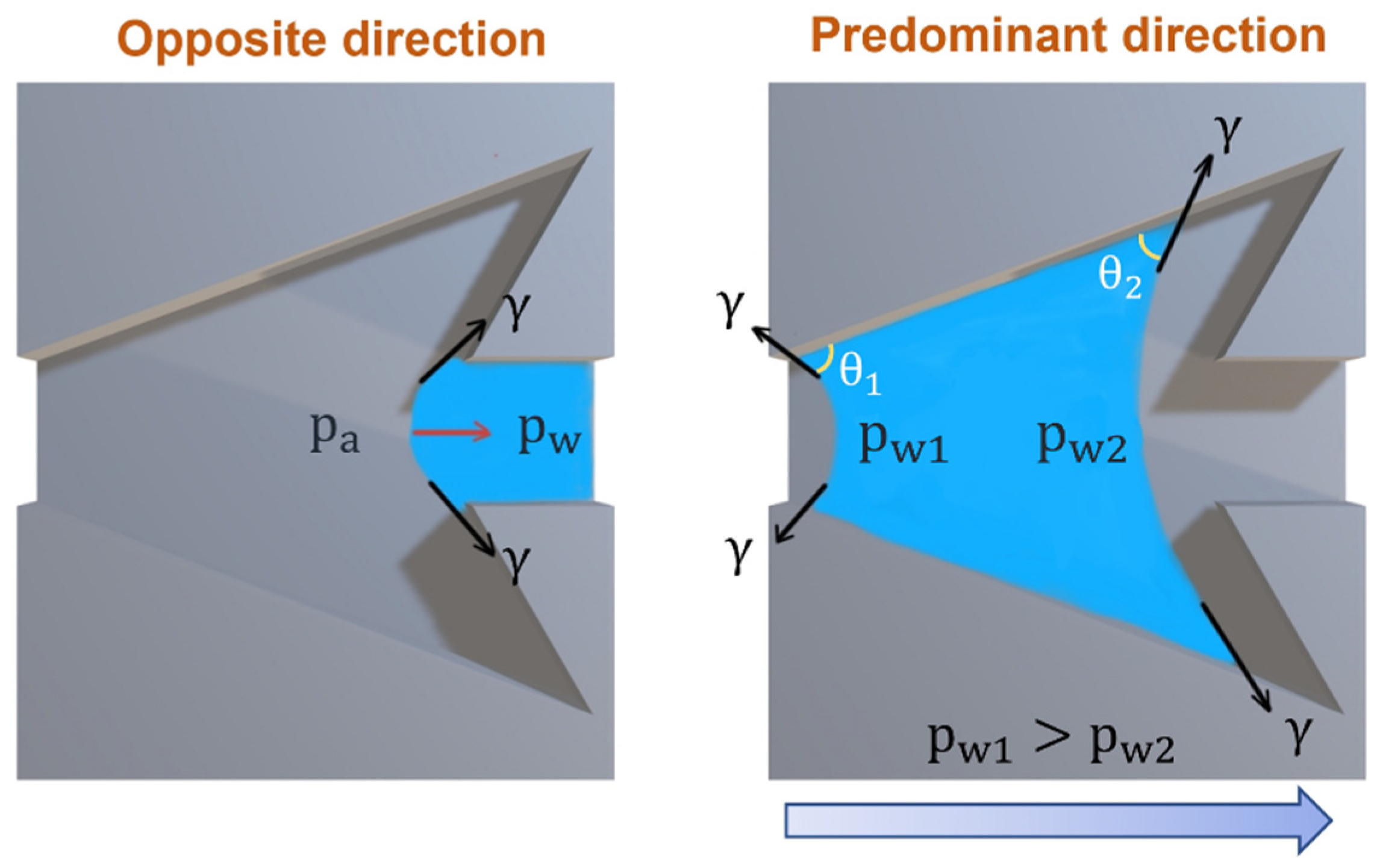
3.2.3. Wetting Behavior of Dart-Shaped Groove
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gau, H.; Herminghaus, S.; Lenz, P.; Lipowsky, R. Liquid morphologies on structured surfaces: From microchannels to microchips. Science 1999, 283, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Hancock, M.J.; Sekeroglu, K.; Demirel, M.C. Bioinspired directional surfaces for adhesion wetting and transport. Adv. Funct. Mater. 2012, 22, 2223–2234. [Google Scholar] [CrossRef]
- Ueda, E.; Levkin, P.A. Emerging applications of superhydrophilic-superhydrophobic. Adv. Mater. 2013, 25, 1234–1247. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.; Song, Y.; Jiang, L. Applications of bio-inspired special wettable surfaces. Adv. Mater. 2011, 23, 719–734. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Andrew, M.; Li, J.; Yeomans, J.M.; Wang, Z. Symmetry breaking in drop bouncing on curved surfaces. Nat. Commun. 2015, 6, 10034. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Jiang, L.; Li, J. Bio-inspired design of multiscale structures for function integration. Nano Today 2011, 6, 155–175. [Google Scholar] [CrossRef]
- Zheng, Y.; Bai, H.; Huang, Z.; Tian, X.; Nie, F.Q.; Zhao, Y.; Zhai, J.; Jiang, L. Directional water collection on wetted spider silk. Nature 2010, 463, 640–643. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, P.; Zhang, L.; Liu, H.; Jiang, Y.; Zhang, D.; Han, Z.; Jiang, L. Continuous directional water transport on the peristome surface of Nepenthes alata. Nature 2016, 532, 85–89. [Google Scholar] [CrossRef]
- Li, C.; Li, N.; Zhang, X.; Dong, Z.; Chen, H.; Jiang, L. Uni-directional transportation on peristome-mimetic surfaces for completely wetting liquids. Angew. Chem. Int. Ed. 2016, 55, 14988–14992. [Google Scholar] [CrossRef]
- Wong, T.S.; Kang, S.H.; Tang, S.K.; Smythe, E.J.; Hatton, B.D.; Grinthal, A.; Aizenberg, J. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 2011, 477, 443–447. [Google Scholar] [CrossRef]
- Barthlott, W.; Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Gao, X.; Yan, X.; Yao, X.; Xu, L.; Zhang, K.; Zhang, J.; Yang, B.; Jiang, L. The dry-style antifogging properties of mosquito compound eyes and artificial analogues prepared by soft lithography. Adv. Mater. 2007, 19, 2213–2217. [Google Scholar] [CrossRef]
- Epstein, A.K.; Pokroy, B.; Seminara, A.; Aizenberg, J. Bacterial biofilm shows persistent resistance to liquid wetting and gas penetration. Proc. Natl. Acad. Sci. USA 2011, 108, 995–1000. [Google Scholar] [CrossRef]
- Quéré, D. Non-sticking drops. Rep. Prog. Phys. 2005, 68, 2495. [Google Scholar] [CrossRef]
- Autumn, K.; Liang, Y.A.; Hsieh, S.T.; Zesch, W.; Chan, W.P.; Kenny, T.W.; Fearing, R.; Full, R.J. Adhesive force of a single gecko foot-hair. Nature 2000, 405, 681–685. [Google Scholar] [CrossRef] [PubMed]
- Autumn, K.; Sitti, M.; Liang, Y.A.; Peattie, A.M.; Hansen, W.R.; Sponberg, S.; Kenny, T.W.; Fearing, R.; Israelachvili, J.N.; Full, R.J. Evidence for van der Waals adhesion in gecko setae. Proc. Natl. Acad. Sci. USA 2002, 99, 12252–12256. [Google Scholar] [CrossRef]
- Shahsavan, H.; Salili, S.M.; Jákli, A.; Zhao, B. Smart muscle-driven self-cleaning of biomimetic microstructures from liquid crystal elastomers. Adv. Mater. 2015, 27, 6828–6833. [Google Scholar] [CrossRef]
- Parker, A.R.; Lawrence, C.R. Water capture by a desert beetle. Nature 2001, 414, 33–34. [Google Scholar] [CrossRef]
- Brown, P.S.; Bhushan, B. Bioinspired materials for water supply and management: Water collection, water purification and separation of water from oil. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20160135. [Google Scholar] [CrossRef]
- Park, K.C.; Kim, P.; Grinthal, A.; He, N.; Fox, D.; Weaver, J.C.; Aizenberg, J. Condensation on slippery asymmetric bumps. Nature 2016, 531, 78–82. [Google Scholar] [CrossRef]
- Gao, C.; Wang, L.; Lin, Y.; Li, J.; Liu, Y.; Li, X.; Feng, S.; Zheng, Y. Droplets manipulated on photothermal organogel surfaces. Adv. Funct. Mater. 2018, 28, 1803072. [Google Scholar] [CrossRef]
- Shi, D.; Chen, Y.; Chen, X.; Chen, X.; Gao, J.; He, Y.; Wong, C.P. Ladderlike tapered pillars enabling spontaneous and consecutive liquid transport. ACS Appl. Mater. Interfaces 2018, 10, 34735–34743. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhu, K.; Cao, B.; Zhang, Z.; Wu, B.; Liang, L.; Chai, G.; Liu, A. Smart design of wettability-patterned gradients on substrate-independent coated surfaces to control unidirectional spreading of droplets. Soft Matter 2017, 13, 2995–3002. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, S.; Jiang, L. Nature-inspired superwettability systems. Nat. Rev. Mater. 2017, 2, 17036. [Google Scholar] [CrossRef]
- Dou, X.; Li, S.; Liu, J. Zero curvature-surface driven small objects. Appl. Phys. Lett. 2017, 111, 081602. [Google Scholar] [CrossRef]
- Dai, Q.; Ji, Y.; Chong, Z.; Huang, W.; Wang, X. Manipulating thermocapillary migration via superoleophobic surfaces with wedge shaped superoleophilic grooves. J. Colloid Interface Sci. 2019, 557, 837–844. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.; Shang, W.; Feng, S.; Zhu, S.; Xing, Y.; Li, D.; Hou, Y.; Zheng, Y. Controlled droplet transport to target on a high adhesion surface with multi-gradients. Sci. Rep. 2017, 7, 45687. [Google Scholar] [CrossRef]
- Bhushan, B.; Feng, W. Water collection and transport in bioinspired nested triangular patterns. Trans. R. Soc. A 2020, 378, 20190441. [Google Scholar] [CrossRef]
- Ershov, S.; Khelifa, F.; Lemaur, V.; Cornil, J.; Cossement, D.; Habibi, Y.; Dubois, P.; Snyders, R. Free radical generation and concentration in a plasma polymer: The effect of aromaticity. ACS Appl. Mater. Interfaces 2014, 6, 12395–12405. [Google Scholar] [CrossRef]
- Geng, H.; Bai, H.; Fan, Y.; Wang, S.; Ba, T.; Yu, C.; Cao, M.; Jiang, L. Unidirectional water delivery on a superhydrophilic surface with two-dimensional asymmetrical wettability barriers. Mater. Horiz. 2018, 5, 303–308. [Google Scholar] [CrossRef]
- Luo, C.; Heng, X.; Xiang, M. Behavior of a liquid drop between two nonparallel plates. Langmuir 2014, 30, 8373–8380. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mai, N.P.U.; Chen, P.-Y. Investigation on the Anisotropic Wetting Properties of Water Droplets on Bio-Inspired Groove Structures Fabricated by 3D Printing and Surface Modifications. Biomimetics 2022, 7, 174. https://doi.org/10.3390/biomimetics7040174
Mai NPU, Chen P-Y. Investigation on the Anisotropic Wetting Properties of Water Droplets on Bio-Inspired Groove Structures Fabricated by 3D Printing and Surface Modifications. Biomimetics. 2022; 7(4):174. https://doi.org/10.3390/biomimetics7040174
Chicago/Turabian StyleMai, Ngoc Phuong Uyen, and Po-Yu Chen. 2022. "Investigation on the Anisotropic Wetting Properties of Water Droplets on Bio-Inspired Groove Structures Fabricated by 3D Printing and Surface Modifications" Biomimetics 7, no. 4: 174. https://doi.org/10.3390/biomimetics7040174
APA StyleMai, N. P. U., & Chen, P.-Y. (2022). Investigation on the Anisotropic Wetting Properties of Water Droplets on Bio-Inspired Groove Structures Fabricated by 3D Printing and Surface Modifications. Biomimetics, 7(4), 174. https://doi.org/10.3390/biomimetics7040174






