Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures
Abstract
1. Introduction
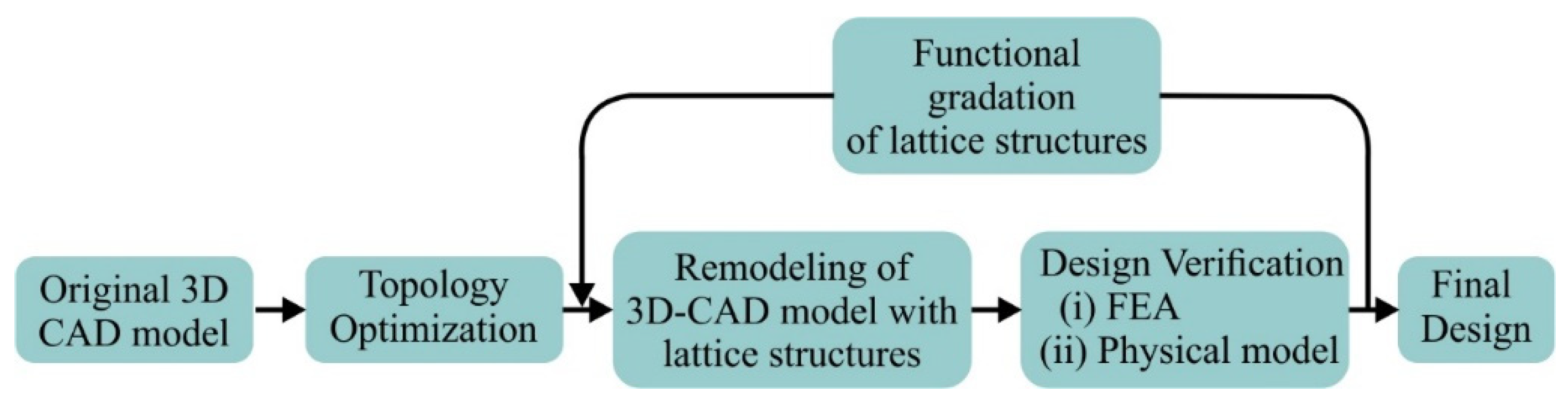
2. Materials and Methods
2.1. Design of Hip Implant
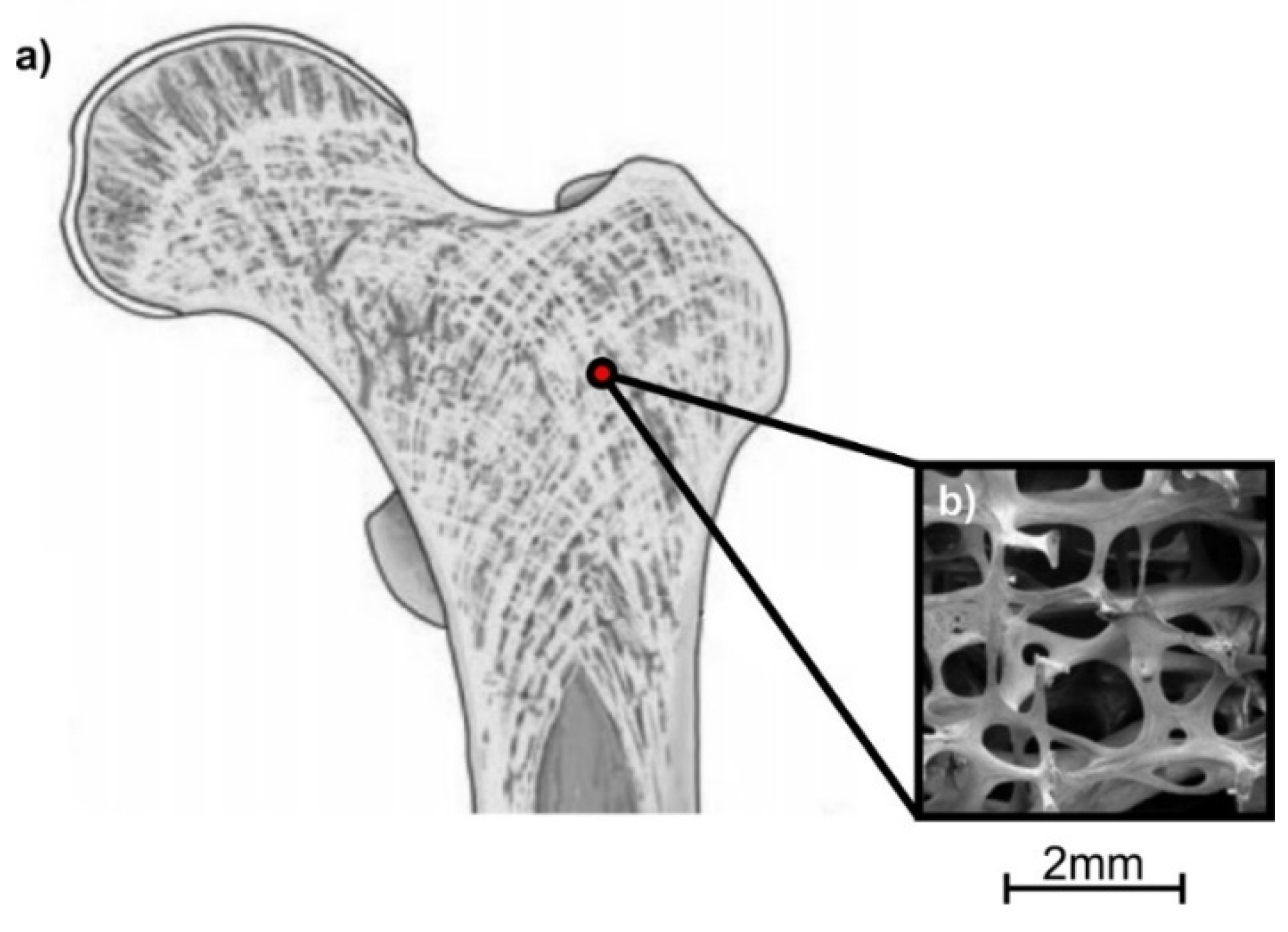
2.2. Lattice Structure Configuration
2.3. Finite Element Analysis
3. Results and Discussion
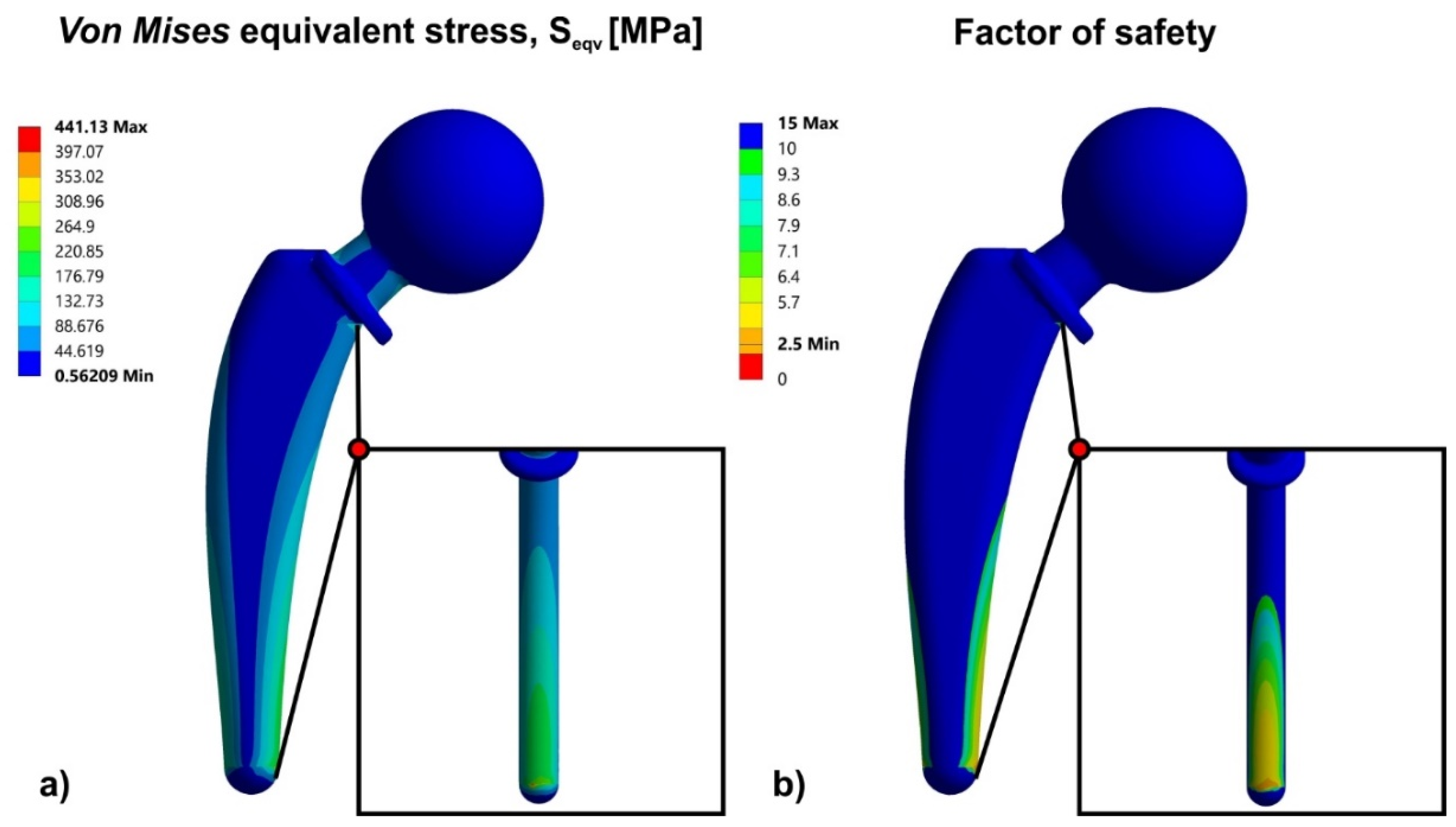
3.1. Finite Element Analysis for Solid Hip Implant
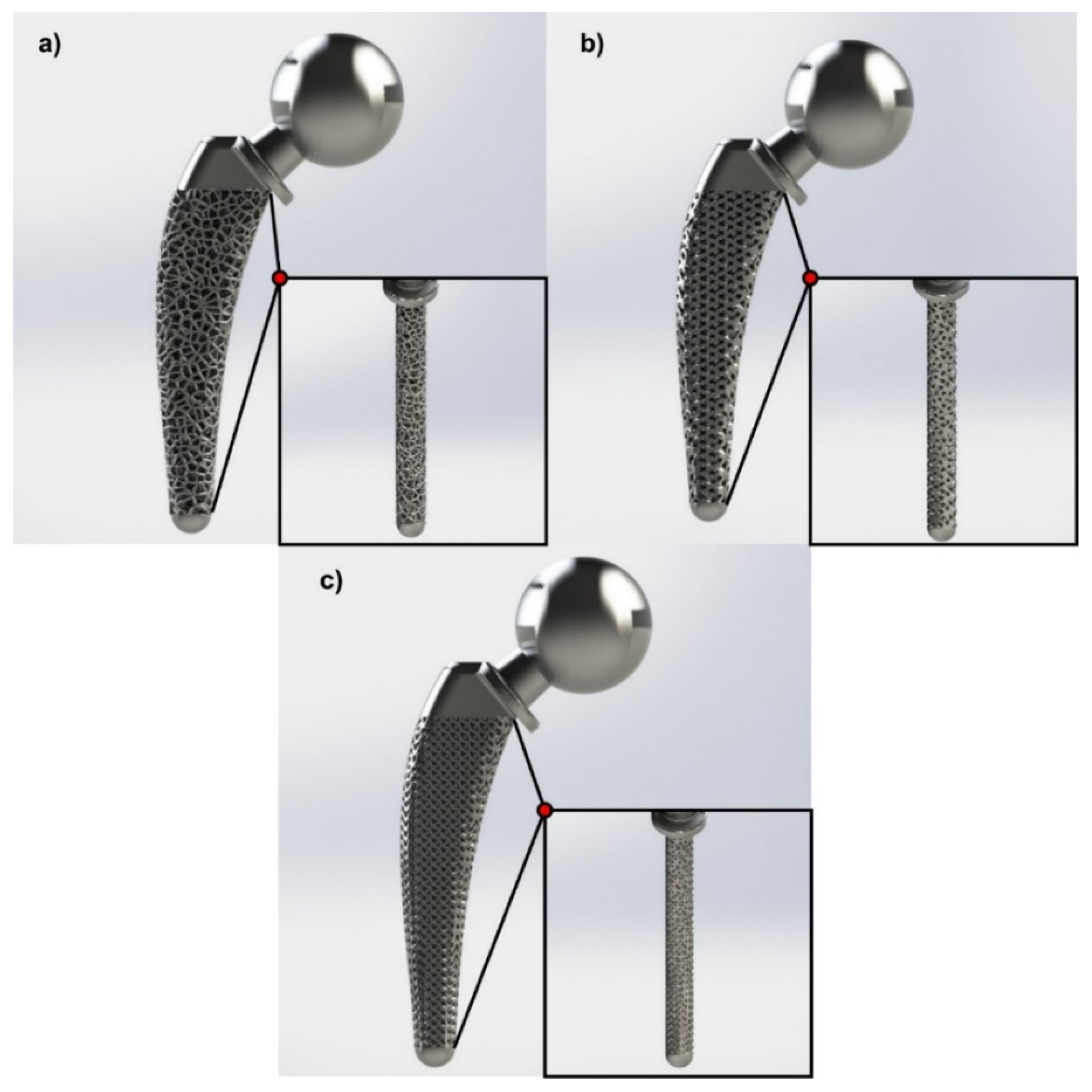
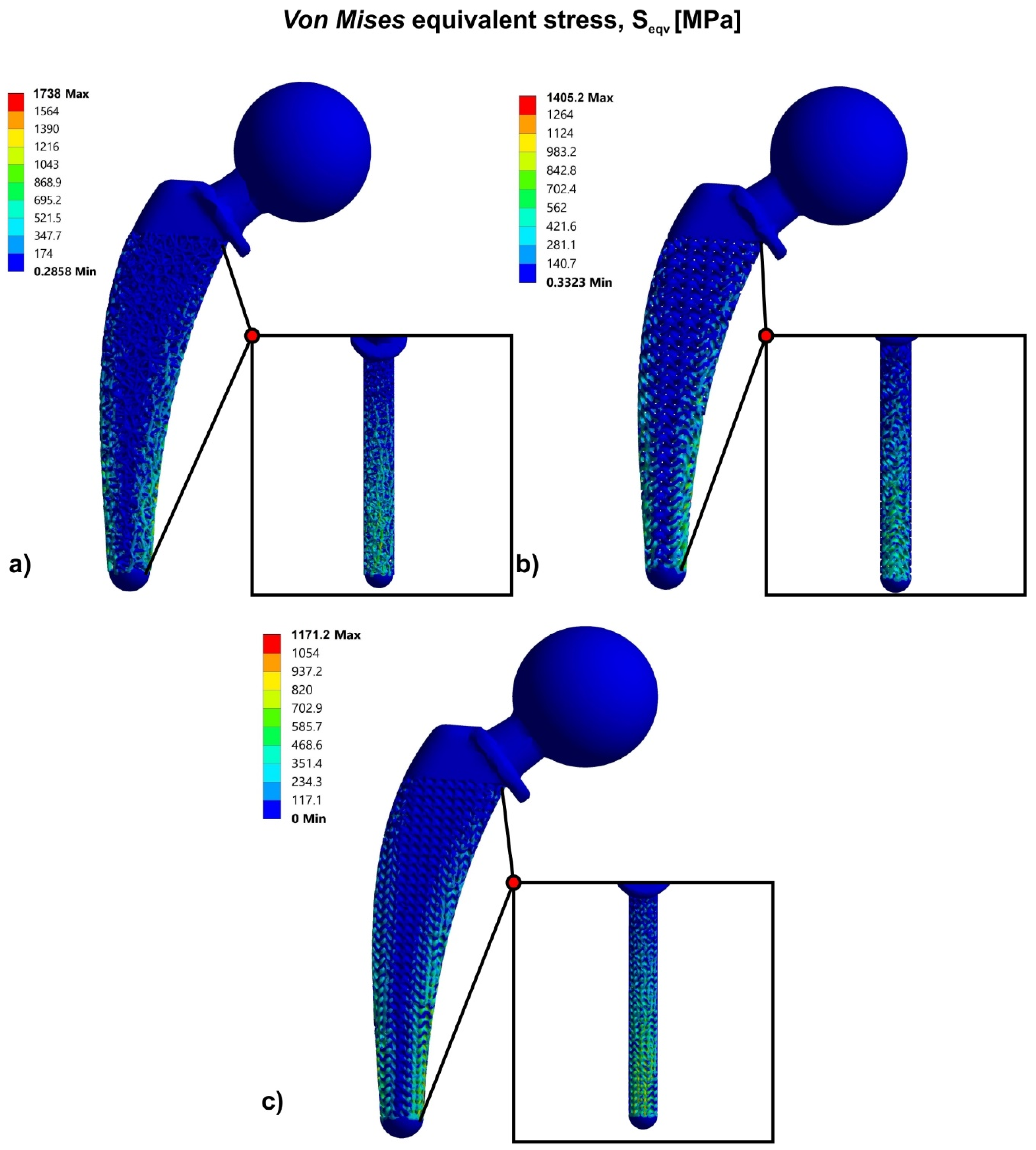
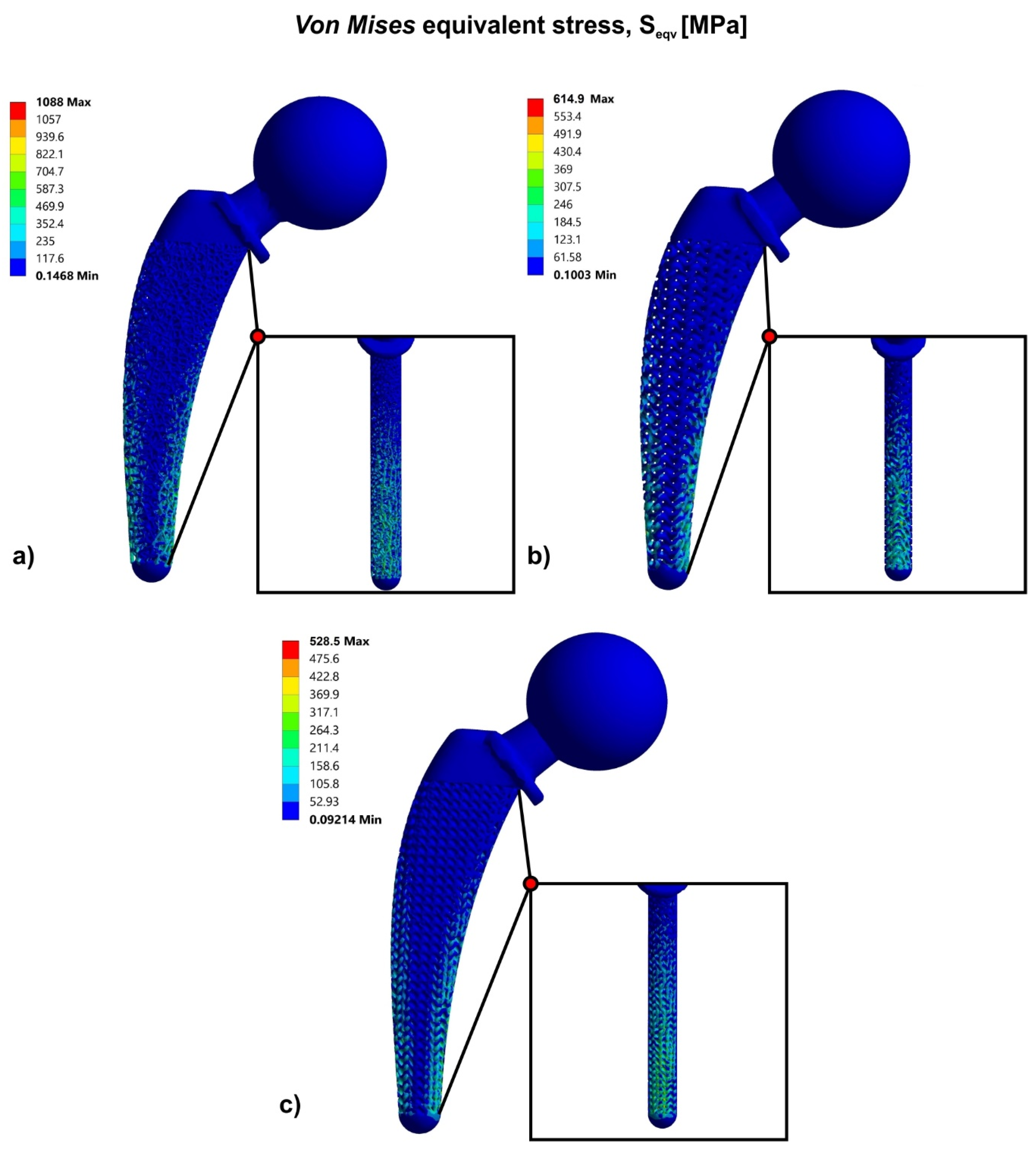
3.2. Topology Optimization through Lattice Structures
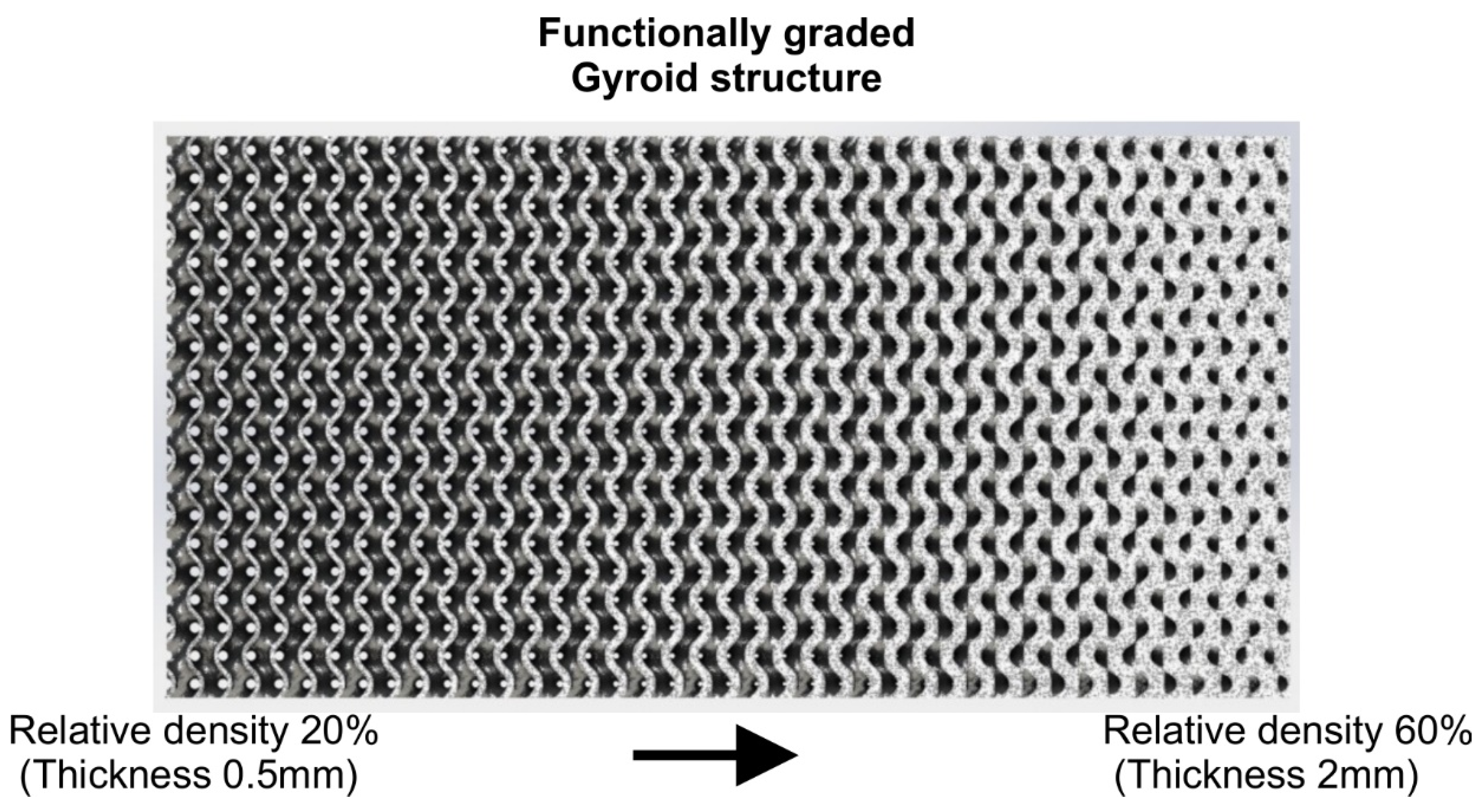
3.3. Functional Gradation of Lattice Structures
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2010. [Google Scholar]
- Frazier, W.E. Digital Manufacturing of Metallic Components: Vision and Roadmap. In Solid Free Form Fabrication Proceedings; University of Texas at Austin: Austin, TX, USA, 2010. [Google Scholar]
- Karavasili, C.; Tsongas, K.; Andreadis, I.I.; Andriotis, E.G.; Papachristou, E.T.; Papi, R.M.; Tzetzis, D.; Fatouros, D.G. Physico-mechanical and finite element analysis evaluation of 3D printable alginate-methylcellulose inks for wound healing applications. Carbohydr. Polym. 2020, 247, 116666. [Google Scholar] [CrossRef]
- Xenikakis, I.; Tzimtzimis, M.; Tsongas, K.; Andreadis, D.; Demiri, E.; Tzetzis, D.; Fatouros, D. Fabrication and finite element analysis of stereolithographic 3D printed microneedles for transdermal delivery of model dyes across human skin in vitro. Eur. J. Pharm. Sci. 2019, 137, 104976. [Google Scholar] [CrossRef]
- Mansour, M.; Tsongas, K.; Tzetzis, D. Measurement of the mechanical and dynamic properties of 3D printed polylactic acid reinforced with graphene. Polym.-Plast. Technol. Eng. 2019, 58, 1234–1244. [Google Scholar] [CrossRef]
- Mansour, M.; Tsongas, K.; Tzetzis, D.; Antoniadis, A. Mechanical and dynamic behavior of fused filament fabrication 3D printed polyethylene terephthalate glycol reinforced with carbon fibers. Polym.-Plast. Technol. Eng. 2018, 57, 1715–1725. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin, Germany; New York, NY, USA, 2003. [Google Scholar]
- Ehrgott, M. Multicriteria Optimization; Springer: Berlin, Germany, 2005. [Google Scholar]
- Rosen, D.W. Research supporting principles for design for additive manufacturing. J. Virtual Phys. Prototyp. 2014, 9, 225–232. [Google Scholar] [CrossRef]
- Larsen, S.D.; Sigmund, O.; Groen, J.P. Optimal truss and frame design from projected homogenization-based topology optimization. J. Struct. Multidiscip. Optim. 2018, 57, 1461–1474. [Google Scholar] [CrossRef]
- Gebisa, A.W.; Lemu, H.G. A case study on topology optimized design for additive Manufacturing. IOP Conf. Ser. Mater. Sci. Eng. 2017, 276, 12026. [Google Scholar] [CrossRef]
- Li, C.; Kim, I.Y.; Jeswiet, J. Conceptual and detailed design of an automotive engine cradle by using topology, shape, and size optimization. J. Struct. Multidiscip. Optim. 2015, 51, 547–564. [Google Scholar] [CrossRef]
- González-Henríquez, C.M.; Sarabia-Vallejos, M.A.; Rodriguez-Hernandez, J. Polymers for additive manufacturing and 4D-printing: Materials, methodologies, and biomedical applications. J. Polym. Sci. 2019, 94, 57–116. [Google Scholar] [CrossRef]
- Heinl, P.; Müller, L.; Körner, C.; Singer, R.F.; Müller, F.A. Cellular Ti–6Al–4V structures with interconnected macro porosity for bone implants fabricated by selective electron beam melting. J. Acta Biomater. 2008, 4, 1536–1544. [Google Scholar] [CrossRef] [PubMed]
- Dias, M.R.; Guedes, J.M.; Flanagan, C.L.; Hollister, S.J.; Fernandes, P.R. Optimization of scaffold design for bone tissue engineering: A computational and experimental study. J. Med. Eng. Phys. 2014, 36, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Mansour, M.T.; Tsongas, K.; Tzetzis, D.; Antoniadis, A. The in-plane compression performance of hierarchical honeycomb additive manufactured structures. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012015. [Google Scholar] [CrossRef]
- Helou, M.; Kara, S. Design, analysis and manufacturing of lattice structures: An overview. Int. J. Comput. Integr. Manuf. 2018, 31, 243–261. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Al-Ketan, O.; Al-Rub, R.K.A. Multifunctional mechanical-metamaterials based on triply periodic minimal surface lattices: A review. J. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Al-Rub, R.K.A. Topology-Mechanical Property Relationship of 3D Printed Strut, Skeletal, and Sheet Based Periodic Metallic Cellular Materials. J. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Mahmoud, D.; Elbestawi, M.A. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopaedic Implants: A Review. J. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar]
- Gabbrielli, R.; Turner, I.G.; Bowen, C.R.; Wang, H.; Johnston, S.; Rosen, D.; Cheng, A.; Humayun, A.; Cohen, D.J.; Boyan, B.D. Design of a graded cellular structure for an acetabular hip replacement component. In Proceedings of the Seventeenth Solid Freeform Fabrication Symposium, Austin, TX, USA, 14–16 August 2006. [Google Scholar]
- España, F.A.; Balla, V.K.; Bose, S.; Bandyopadhyay, A. Design and fabrication of CoCrMo alloy based novel structures for load bearing implants using laser engineered net shaping. J. Mater. Sci. Eng. C 2010, 30, 50–57. [Google Scholar] [CrossRef]
- Hazlehurst, K.B.; Wang, C.J.; Stanford, M. The potential application of a Cobalt Chrome Molybdenum femoral stem with functionally graded orthotropic structures manufactured using Laser Melting technologies. J. Med. Hypotheses 2013, 81, 1096–1099. [Google Scholar] [CrossRef]
- Limmahakhun, S.; Oloyede, A.; Chantarapanich, N. Alternative designs of load—Sharing cobalt chromium graded femoral stems. J. Mater. Today Commun. 2017, 12, 1–10. [Google Scholar] [CrossRef]
- Quevedo González, F.J. Computational Design of Functionally Graded Hip Implants by Means of Additively Manufactured Porous Materials. Ph.D. Thesis, École de Technologie Supérieure, Montreal, QC, Canada, 2016. [Google Scholar]
- Fantini, M.; Curto, M.; De Crescenzio, F. A method to design biomimetic scaffolds for bone tissue engineering based on Voronoi lattices. J. Virtual Phys. Prototyp. 2016, 11, 77–90. [Google Scholar] [CrossRef]
- Liang, H.; Yang, Y.; Xie, D.; Li, L.; Mao, N.; Wang, C.; Tian, Z.; Jiang, Q.; Shen, L. Trabecular-like Ti-6Al-4V scaffolds for orthopedic: Fabrication by selective laser melting and in vitro biocompatibility. J. Mater. Sci. Technol. 2019, 35, 1284–1297. [Google Scholar] [CrossRef]
- Standard Specification for Total Hip Joint Prosthesis and Hip Endoprosthesis Bearing Surfaces Made of Metallic, Ceramic, and Polymeric Materials; ASTM F2033-12; ASTM International: West Conshohocken, PA, USA, 2012.
- Charnley, J.; Kamangar, A.; Longfield, M.D. The optimum size of prosthetic heads in relation to wear of plastic sockets in total replacement of the hip. J. Med. Biol. Eng. 1969, 7, 31–39. [Google Scholar] [CrossRef]
- McKee, G.K. Development in total hip joint replacement. Lond. Inst. Mech. Eng. 1967, 85–89. [Google Scholar]
- Müller, M.E. Total hip prosthesis. J. Clin. Orthop. Relat. Res. 1970, 11, 46–68. [Google Scholar]
- Hybbinette, C.H. Long-term Results of Wear of Plastic Hip Prostheses. Arch. Orthop. Trauma. Surg. 1985, 104, 28–30. [Google Scholar] [CrossRef] [PubMed]
- El-Shiekh, H.; El-Din, F. Finite Element Simulation of Hip Joint Replacement under Static and Dynamic Loading. Ph.D. Thesis, School of Mechanical and Manufacturing Engineering, Dublin City University, Dublin, Ireland, 2002. [Google Scholar]
- Okabe, A.; Boots, B.; Sugihara, K. Spatial Tessellations–Concepts and Applications of Voronoi Diagrams; Wiley: Chichester, UK, 1992. [Google Scholar]
- Scheinpflug, J.; Pfeiffenberger, M.; Damerau, A.; Schwarz, F.; Textor, M.; Lang, A.; Schulze, F. Journey into Bone Models: A Review. Genes 2018, 9, 247. [Google Scholar] [CrossRef] [PubMed]
- Sieberath, A.; Della Bella, E.; Ferreira, A.M.; Gentile, P.; Eglin, D.; Dalgarno, K. A Comparison of Osteoblast and Osteoclast In Vitro Co-Culture Models and Their Translation for Preclinical Drug Testing Applications. Int. J. Mol. Sci. 2020, 21, 912. [Google Scholar] [CrossRef] [PubMed]
- Pelanconi, M.; Ortona, A. Nature-Inspired, Ultra-Lightweight Structures with Gyroid Cores Produced by Additive Manufacturing and Reinforced by Unidirectional Carbon Fiber Ribs. J. Mater. 2019, 12, 4134. [Google Scholar] [CrossRef]
- Pulsifer, D.P.; Lakhtakia, A. Background and survey of bio replication techniques. Bioinspiration Biomim. 2011, 6, 031001. [Google Scholar] [CrossRef]
- Galusha, J.W.; Richey, L.R.; Gardner, J.S.; Cha, J.N.; Bartl, M.H. Discovery of a diamond-based photonic crystal structure in beetle scales. Phys. Rev. E 2008, 77, 2–5. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rezgui, R.; Rowshan, R.; Du, H.; Fang, N.X.; Abu Al-Rub, R.K. Micro-architected Stretching-Dominated Mechanical Metamaterials with Minimal Surface Topologies. J. Adv. Eng. Mater. 2018, 20, 1800029. [Google Scholar] [CrossRef]
- Vector Clip Art of Black and White Butterfly with Wide Spread Wings. Available online: https://freesvg.org/vector-clip-art-of-black-and-white-butterfly-with-wide-spread-wings (accessed on 10 September 2020).
- Alwattar, T.A.; Mian, A. Developing an Equivalent Solid Material Model for BCC Lattice Cell Structures Involving Vertical and Horizontal Struts. J. Compos. Sci. 2020, 4, 74. [Google Scholar] [CrossRef]
- Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.; Shi, Y.; Yang, S. Continuous graded Gyroid cellular structures fabricated by selective laser melting: Design, manufacturing and mechanical properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
- Khan, M.A.; Prasad, N.R.; Krishnan, S.N.; Raja, S.K.; Jappes, J.T.W.; Duraiselvam, M. Laser-treated austenitic steel and Nickel alloy for human implants. J. Mater. Manuf. Process. 2017, 32, 1635–1641. [Google Scholar] [CrossRef]
- Standard Specification for Wrought Cobalt-20Chromium-15Tungsten-10Nickel Alloy for Surgical Implant Applications (UNS R30605); ASTM F90-14; ASTM International: West Conshohocken, PA, USA, 2014.
- Ducheyne, P.; Hastings, G.W. Functional behavior of orthopedic biomaterials, Volume II: Fundamentals. CRC Ser. Struct. Prop. Relatsh. Biomater. 1984, 2, 21. [Google Scholar]
- McLeish, R.D.; Charnley, J. Abduction forces in the one-legged stance. J. Biomech. 1970, 3, 191–209. [Google Scholar] [CrossRef]
- Bergmann, G.; Graichen, F.; Rohlmann, A. Hip joint loading during walking and running, measured in two patients. J. Biomech. 1993, 26, 969–990. [Google Scholar] [CrossRef]
- Colic, K.; Sedmak, A.; Grbovic, A.; Tatic, U.; Sedmak, S.; Djordjevic, B. Finite element modeling of hip implant static loading. Procedia Eng. 2016, 149, 257–262. [Google Scholar] [CrossRef]
- Thomas, C.D.L.; Feik, S.A.; Clement, J.G. Regional variation of intracortical porosity in the midshaft of the human femur: Age and sex differences. J. Anat. 2005, 206, 115–125. [Google Scholar] [CrossRef]
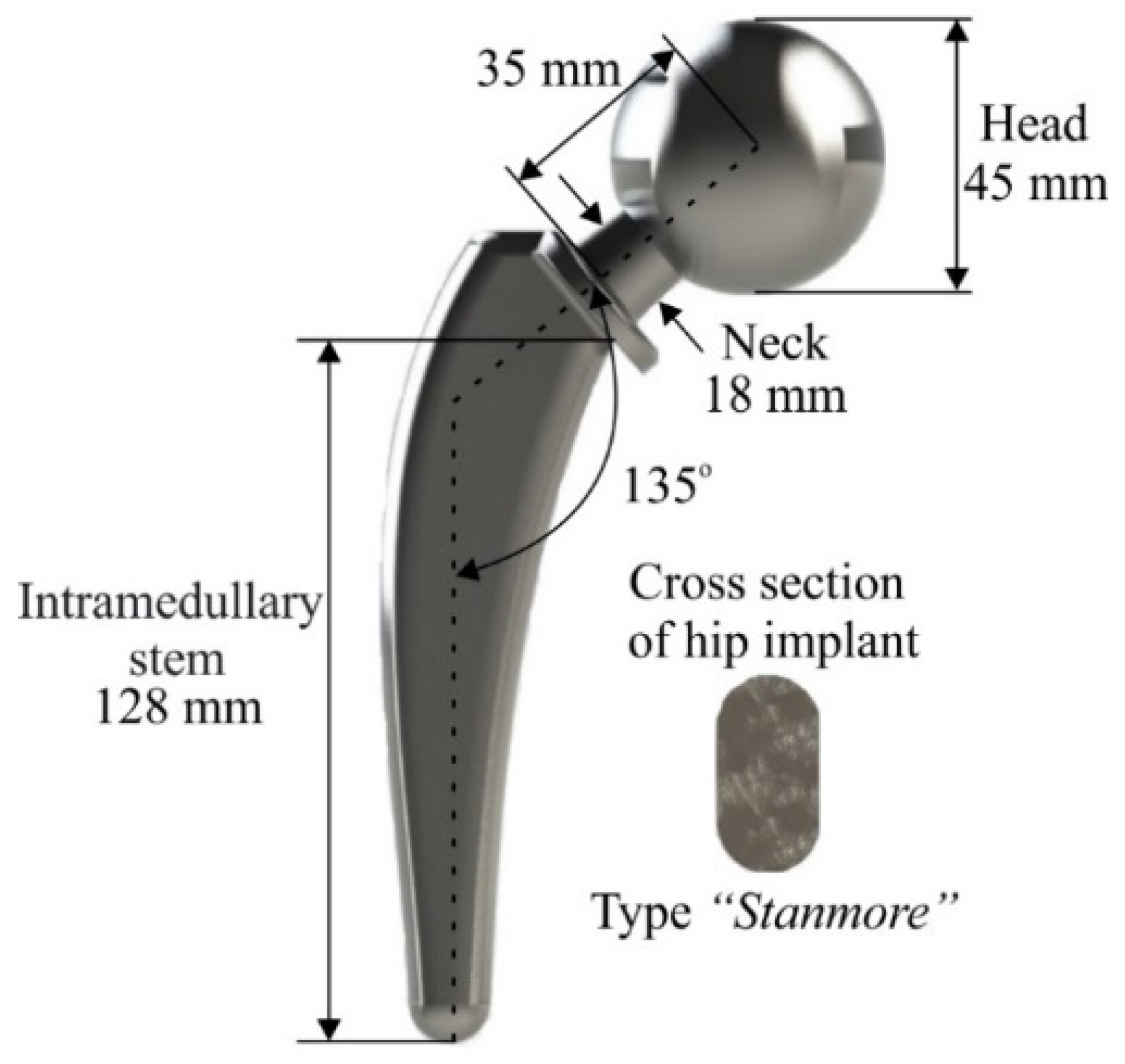
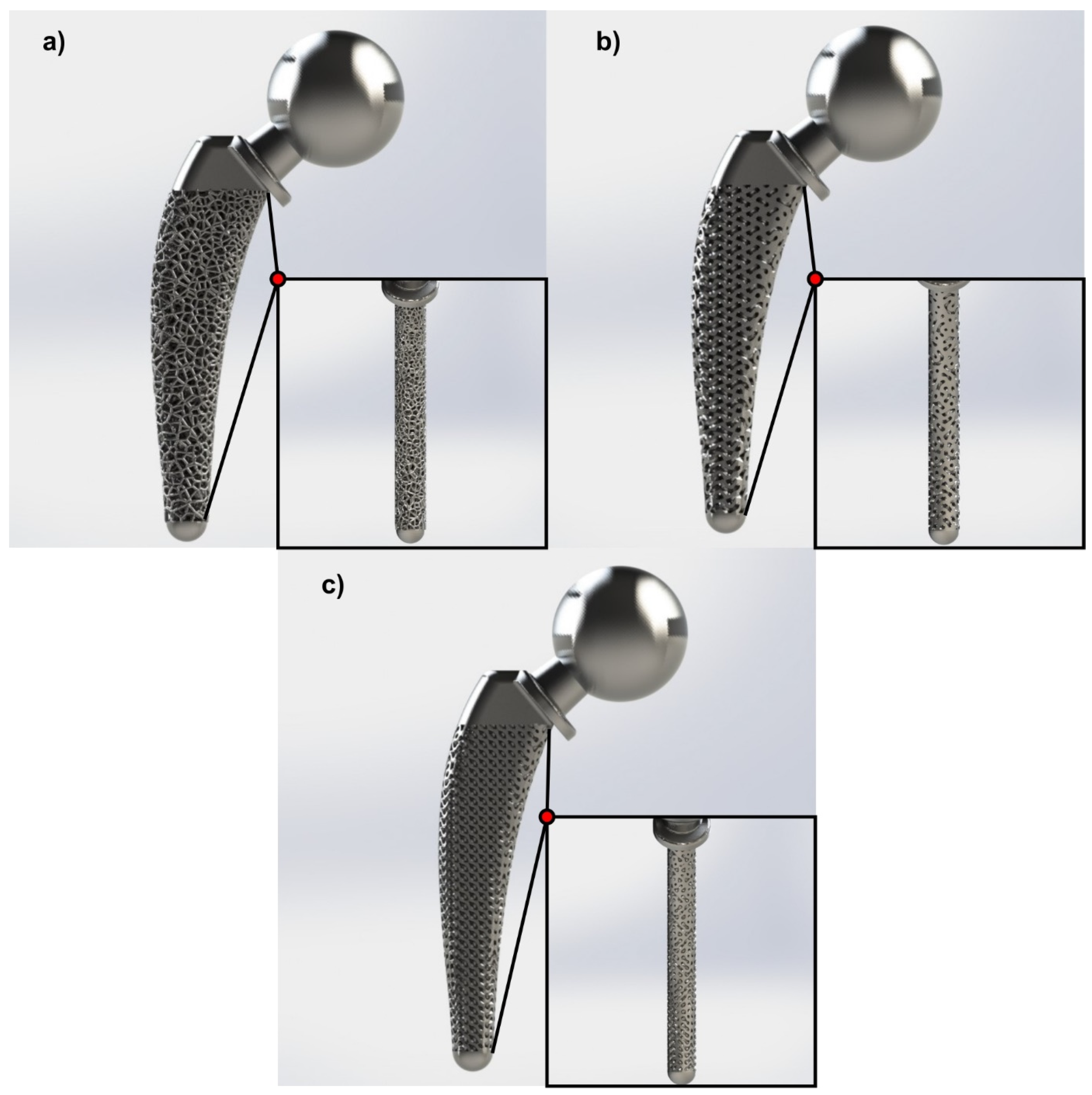
| Design Parameters | Typical Values |
|---|---|
| Length of intramedullary stem | 120 mm–180 mm |
| Length of neck | 10 mm–40 mm |
| Head diameter | 22 mm–45 mm |
| Neck diameter | 13 mm–30 mm |
| Angle of head placement | 135°–145° |
| Chemical Requirements | |||||||
|---|---|---|---|---|---|---|---|
| Ni | Fe | Mo | Mn | Si | Cr | C | |
| Min (%) | 50 | Balance | 2.8 | 0.35 | 0.35 | 17 | 0.08 |
| Max (%) | 55 | 3.3 | 21 | ||||
| Mechanical Properties | Typical Values |
|---|---|
| Density | 8.19 g/cm3 |
| Elastic Modulus | 200 GPa |
| Poisson Ratio | 0.29 |
| Yield Strength | 1100 MPa |
| Ultimate Yield Strength | 1375 MPa |
| Type of Movement | Max. Load (% Weight) | Max. Force on Hip Joint |
|---|---|---|
| Slow walking | 282 | 2075 N |
| Climbing upstairs | 356 | 2620 N |
| Climbing downstairs | 387 | 2850 N |
| Tripping | 720 | 5300 N |
| Lattice Structure | Factor of Safety (FOS) | Ultimate Factor of Safety (FOSUlt) |
|---|---|---|
| Voronoi | 0.63 | 0.79 |
| Gyroid | 0.78 | 0.98 |
| Schwarz Diamond | 0.94 | 1.17 |
| Hip Implant Versions | Factor of Safety (FOS) | Ult. Factor of Safety (FOSUlt) | Weight (g) |
|---|---|---|---|
| Solid | 2.5 | 3.12 | 975 |
| Topology optimized | |||
| Voronoi | 0.63 | 0.79 | 600 |
| Gyroid | 0.78 | 0.98 | |
| Schwarz Diamond | 0.94 | 1.17 | |
| Topology optimized and functionally graded | |||
| Voronoi | 1.01 | 1.26 | 600 |
| Gyroid | 1.79 | 2.24 | |
| Schwarz Diamond | 2.08 | 2.6 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures. Biomimetics 2020, 5, 44. https://doi.org/10.3390/biomimetics5030044
Kladovasilakis N, Tsongas K, Tzetzis D. Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures. Biomimetics. 2020; 5(3):44. https://doi.org/10.3390/biomimetics5030044
Chicago/Turabian StyleKladovasilakis, Nikolaos, Konstantinos Tsongas, and Dimitrios Tzetzis. 2020. "Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures" Biomimetics 5, no. 3: 44. https://doi.org/10.3390/biomimetics5030044
APA StyleKladovasilakis, N., Tsongas, K., & Tzetzis, D. (2020). Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures. Biomimetics, 5(3), 44. https://doi.org/10.3390/biomimetics5030044







