1. Introduction
The term plankton refers to the body of passively floating or weakly motile organisms in a natural water body and is chiefly made up of phytoplankton, zooplankton, bacteria, and viruses, as well as the larvae of many marine invertebrates and fish that inhabit open water. The availability of plankton directly affects the health and existence of fish, shellfish, and larger animals [
1,
2]. Furthermore, some plankton form blooms, which can lead to increased fouling rates, marine animal mortalities, low dissolved oxygen, and food web disruption [
3,
4]. Whether plankton are performing a positive or negative role in the food chain, the underlying mechanisms of their movement are poorly understood [
5]. Both physical and biological mechanisms affect the movement of planktonic organisms [
6,
7,
8,
9], and the dispersal of aquatic organisms can be mostly active, mostly passive, or a mixture of the two [
10,
11,
12].
Mathematical models of plankton movement typically assume that the organisms either: (1) go passively with the flow (similar to tracer particles) [
13,
14]; or (2) have an additional random motion that can be added to the background flow velocity [
15,
16] to represent turbulence or small, directed movements. Robust and predictive models of plankton movement are difficult to obtain given their small size (<1 mm) in comparison to the relatively large size of their environments (on the order of meters to thousands of kilometers). Furthermore, it is well known that environmental cues and local structures in the flow environment can drastically alter plankton distributions [
17,
18], but the incorporation of these high-order effects into mathematical models has been limited [
19]. For example, larval and other planktonic organisms can bias their distributions using environmental cues such as light, chemical gradients, gravity, and shear [
20,
21]. To better understand and predict the movement of plankton, we need to understand how flow and other environmental signals interact with zooplankton behavior to influence their distributions. This will likely involve: (1) determining the level of granularity needed to represent flow fields, such as whether or not smaller scale obstacles such as macrophytes need to be incorporated into flow models; (2) developing computational methods for incorporating zooplankton movement and behavior; and (3) using these methods to determine plankton distributions.
Of particular relevance to this case study is the role that submerged macrophytes play in altering plankton movement at the centimeter scale. Macrophytes provide organisms with shelter from flows across multiple scales, from emergent mangroves on the scale of meters that provide shelter against storm flows greater than 10 m/s to submerged sea grass on the order of centimeters that grow in estuaries and bays with slow flows on the order of 1–10 mm/s [
22]. Accurate modeling of flow in vegetative structures (e.g., wetland environments or plant canopies) is necessary to assess the ability of these natural environments to mitigate the effects of storm surge, serve as hosts for biological species, and alter the dispersal patterns of larva [
22,
23,
24,
25]. A complete understanding of the fluid behavior within and around these regions is vital when assessing the ability of the vegetated structure to meet predefined goals for their use or consequences associated with their presence in a given environment.
The physical behavior of the flow is altered as fluid passes through the vegetated region since the structure creates resistance, impeding the flow. The presence of vegetation in a flow domain serves to decrease momentum (or inertial effects) of the fluid, increase disturbance to the flow, and possibly change the flow from laminar to turbulent. Vegetative structures also potentially increase the ability of microorganisms to survive within these habitats by preventing wash out. The overall effect of the vegetation on the flow differs depending on several factors, including the density of the bed structure [
22,
24,
26], the height of the plant canopy [
24,
25], and the heterogeneity of the vegetation within the structure [
22,
23]. There may also be a significant change in flow behavior above the canopy or vegetated structure, as the physics of the flow in these transition regions are defined, in part, by the resistance to flow offered by the flexible vegetation. These resistance elements create a shear effect on the fluid that encourages the development of vortices. Defining the transition region in these cases may present challenges, as turbulent shear flow also exists in the regions closest to the top of the canopy [
25]. Ideally, appropriate models for flow through these systems would consider the distinct multiphysics and multiscale features of the environment. These include descriptions at the blade-scale needed to model the local environments of microorganisms to the macroscale models needed to describe large-scale canopy flows [
22].
Simplified analytical models and computational fluid dynamics have previously been used to understand how larger scale vegetation shelters organisms and prevents erosion in strong flows [
22,
27,
28,
29]. Similarly, smaller scale plants have an important fluid dynamic role by altering local fluid dynamics, sheltering organisms at the microscale, and altering mixing dynamics in the benthos [
30,
31,
32]. At the canopy scale, a standard approach for modeling fluid momentum within a vegetated region decomposes both the velocity and pressure using time-averaged components and associated deviations [
22,
33,
34,
35]. At the smaller scale, detailed spatial and temporal aspects of the flow can be quantified using measurements taken in a flume or by using computational fluid dynamics [
36,
37,
38]. In this paper, we focus our attention on the role of centimeter scale submerged macrophytes in altering flow environments on the order of 1–10 cm/s and the subsequent movement of plankton. We focus on biophysical processes at this scale given its tractability as a first step in developing appropriate flow and agent-based models. We note that the agent-based code developed here can be readily applied across a much wider range of scales if an approximation of the flow field is available as an input.
We use
Artemia spp., a genus of saltwater plankton commonly known as brine shrimp, to experimentally quantify how the presence, height, and density of simplified macrophytes alter their distributions in flow. Brine shrimp, also known as sea monkeys, serve as an excellent model organism given their availability and ease of culturing [
39]. Experimentally derived “diffusion” coefficients describing the random active movements of newly hatched nauplii have been determined previously by Kohler et al. [
39]. This organismal system can also be used to develop behavioral models such as movement towards light or a concentration gradient. Behavioral models can then be incorporated into flow models to determine the impact of behavior on distributions and dispersal rates. As a first attempt to mathematically describe and experimentally quantify the movement of plankton in sheltering structures, we injected newly hatched nauplii into physical models of macrophyte beds that have been immersed in a flow tank. The concentrations of brine shrimp were tracked over time in two regions downstream of the physical model. The flows within and around the physical model were determined numerically and validated experimentally using particle image velocimetry.
As we resolved the fluid dynamic models of individual plankton and their basic locomotory characteristics, we then used these results to specify agent-based models in order to explore emergent patterns or behaviors in the population as a whole. Agent-based models (or individual-based models) are models in which individuals are described as autonomous entities which can then interact with each other and/or their environment. They have adaptive behavior which can include continual adjustments to changes in their environment, the presence and behavior of other agents, or to their own internal states [
40]. These models are typically stochastic in nature and are particularly well suited to the task of exploring how simple, single-organism dynamics can give rise to population-level, aggregate phenomena. For this case study, we developed an agent-based model that assumes the brine shrimp move at the local fluid velocity and with some additional random motion representing active swimming. The distributions of brine shrimp over time predicted by the agent-based model are then reported.
The use of this modeling framework and associated software released with this paper extends well beyond the case study considered here. Agent-based models enjoy widespread use across a variety of ecological contexts with varying levels of complexity (e.g., [
41,
42,
43,
44] or see [
45] for a long list of citations). However, from a mathematical perspective, parsimony is critical in forming an agent-based model that can inform theory. When properly formulated in the context of lab or field observations, they can be powerful tools for forging a connection between key individual-level behaviors and macroscopic group properties [
46,
47]. This understanding can then be used to form robust mathematical characterizations of population movement.
While a variety of software packages exist that provide comprehensive simulation environments for agent-based modeling [
48], they tend to be for high-level, general use, and are not well suited to the specific challenges of incorporating fluid–structure interaction data for swimmers in continuous 2D or 3D environments.
Planktos is an object-oriented modeling environment capable of interfacing with 2D or 3D flow data. Custom agent behavior and response to flow gradients can be tested and visualized both quickly and easily, with 1D analytical flow fields available internally for environmental comparison.
Planktos is documented for additional use by other researchers and has been made permanently available as open source software on GitHub.
2. Methods
Here, we provide a brief overview of the experimental and theoretical frameworks used to describe the movement of zooplankton in a complex flow environment. Newly hatched Artemia nauplii were injected into physical models of macrophyte beds in a flow tank. The distributions of nauplii over time were tracked at two locations downstream of the physical model. The flow fields were reproduced using computational fluid dynamics and validated experimentally. Agent-based models were used to describe the distributions of nauplii as they were advected with the fluid and moved with an additional random motion that models active swimming. The macrophyte density and height were varied for both the experiments and the simulations.
2.1. Relevant Dimensionless Numbers
There are a few dimensionless numbers that are useful when analyzing the movement of plankton. The Reynolds number
is defined as
where
is the density of the fluid,
is the dynamic viscosity,
U is a characteristic velocity (such as the swimming speed),
L is a characteristic length (such as the body length), and
is the kinematic fluid viscosity. The Reynolds number can be thought of as the ratio of inertial forces to viscous forces acting in the fluid flow. An example of biological flows where
1 can be seen in the case of fish swimming, while the movement of bacteria by flagella occurs at
1. Low
flows such as those experienced by bacteria are reversible, which means that if you drive motion with a boundary then move that boundary back through the same path, the fluid will return to its initial state [
49]. During ontogeny,
Artemia grow across a range of body sizes from hundreds of microns to 1 cm. Newly hatched larva, or nauplii, swim with their two antennae in a motion that is similar to a breaststroke near a Reynolds number of 1, whereas adults row with a series of swimming appendages near a Reynolds number of 40 [
50,
51]. In this study, we used nauplii that were within a few days of hatching such that they swim near
.
Another useful dimensionless number is the velocity ratio,
, that describes the ability of an organism to swim against a flow and is useful when considering the relative importance of active and passive transport and determining which models of dispersal are appropriate [
19]. This ratio is given as
where
is the organism’s swimming velocity and
gives the vertical and horizontal velocity components of the background flow, respectively. For larval planktonic organisms,
and
are typically on the order of one or less. For larger and/or adult organisms, the interaction between active locomotion and physical transport become more complex. For low values of
, passive drifting is the predominant mechanism of dispersal, and organisms are swept along with the background flow. For intermediate and high values of
, self-propulsion becomes significant and behavior can greatly influence movement and resulting dispersal patterns. For
Artemia, the velocity ratio,
, varies from 0.001 to 100, which is calculated using swimming speeds that vary from about 1–10 mm/s with background flow speeds that range 1–1000 mm/s. These parameters represent conditions ranging from stagnant regions of salt lakes to typical flows plankton would experience in the ocean. In the experiments described here,
ranged from about 0.02 to 10, motivating our agent-based model that considers both advection and diffusion.
2.2. Macrophyte Models
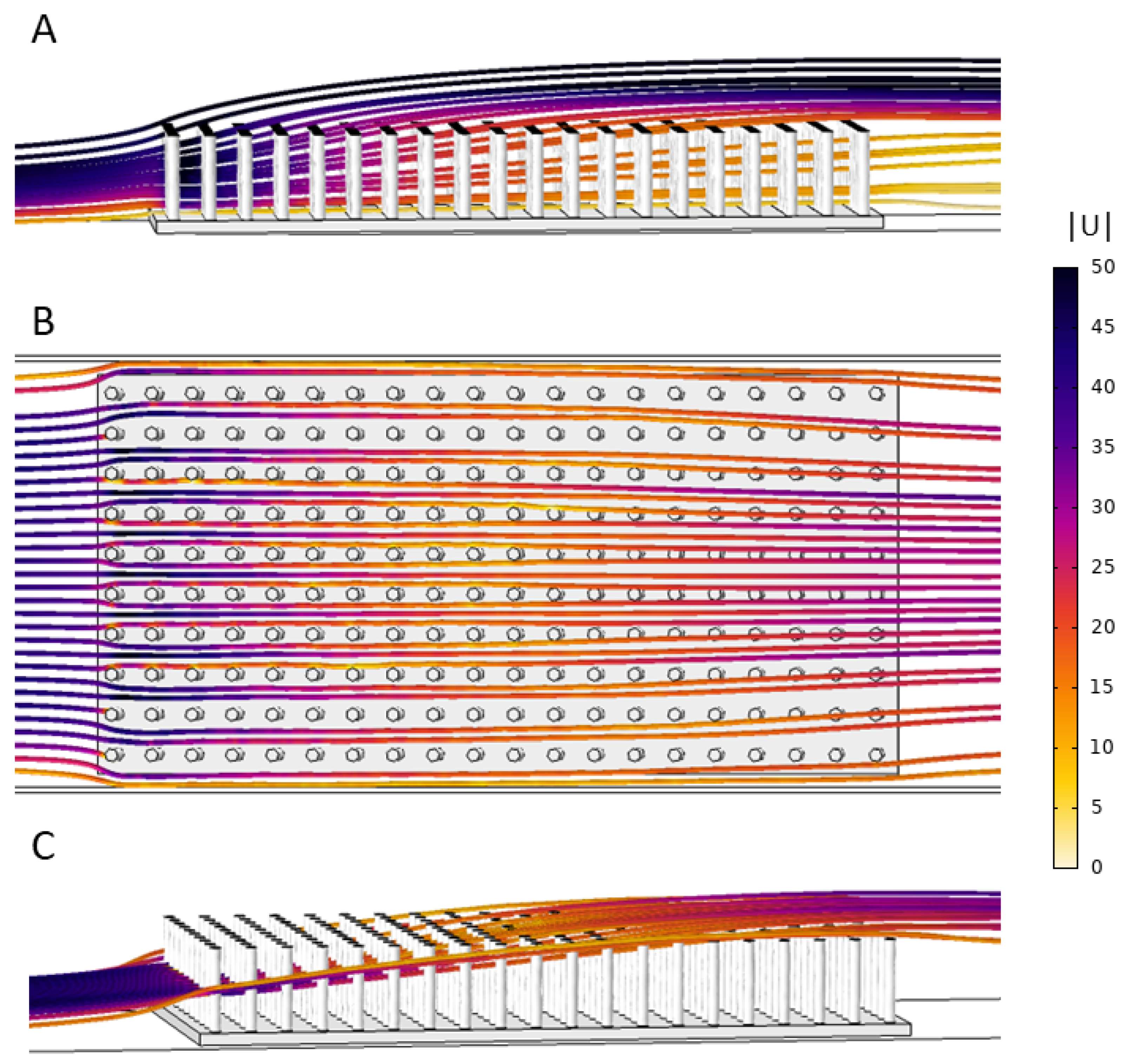
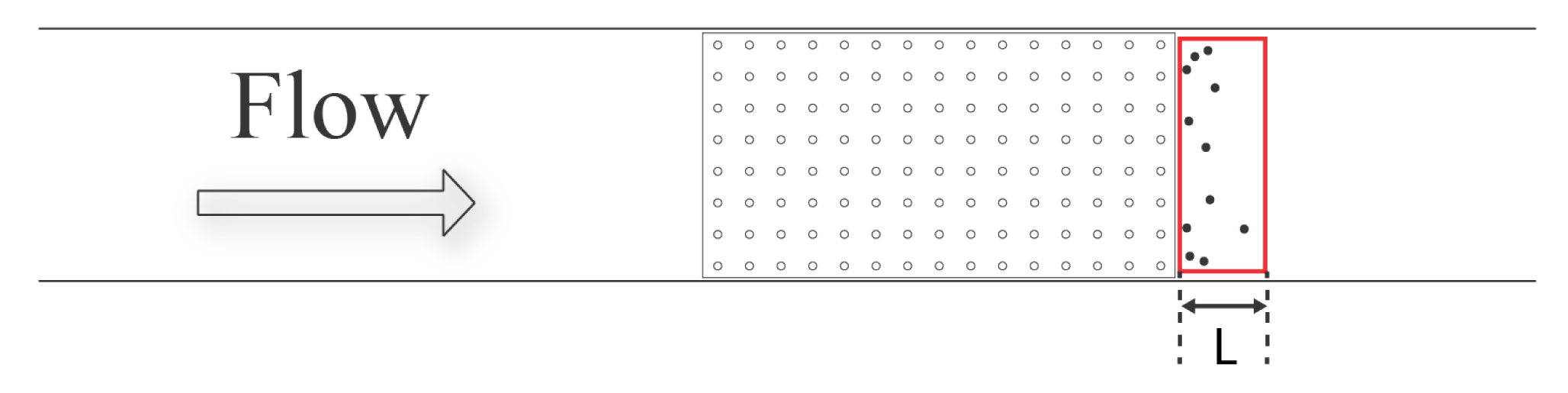
Submerged macrophyte beds were approximated as rigid cylinders arranged in a regular grid and 3D printed for flow tank experiments. For all models, the base consisted of a 7.5 cm × 15 cm × 0.25 cm rectangular prism, bonded to rigid cylinders that were 0.25 cm in diameter. To vary the density of the macrophyte bed, models were created that contained evenly spaced cylinders in 8 × 15, 10 × 20, and 15 × 30 arrangements. Note that the longest dimension was in the direction of flow. In addition, models of each density were constructed with uniform cylinder heights of 1, 2, or 3 cm for a total of nine models. The models were designed as one component in Autodesk Fusion 360 and saved in stl format. Using stl files, models were 3D printed on uPrint SE Plus, using ABS as build material, at the UNC Makerspace. The models used for particle image velocimetry were lightly spray painted black.
2.3. Flow Tank Set Up
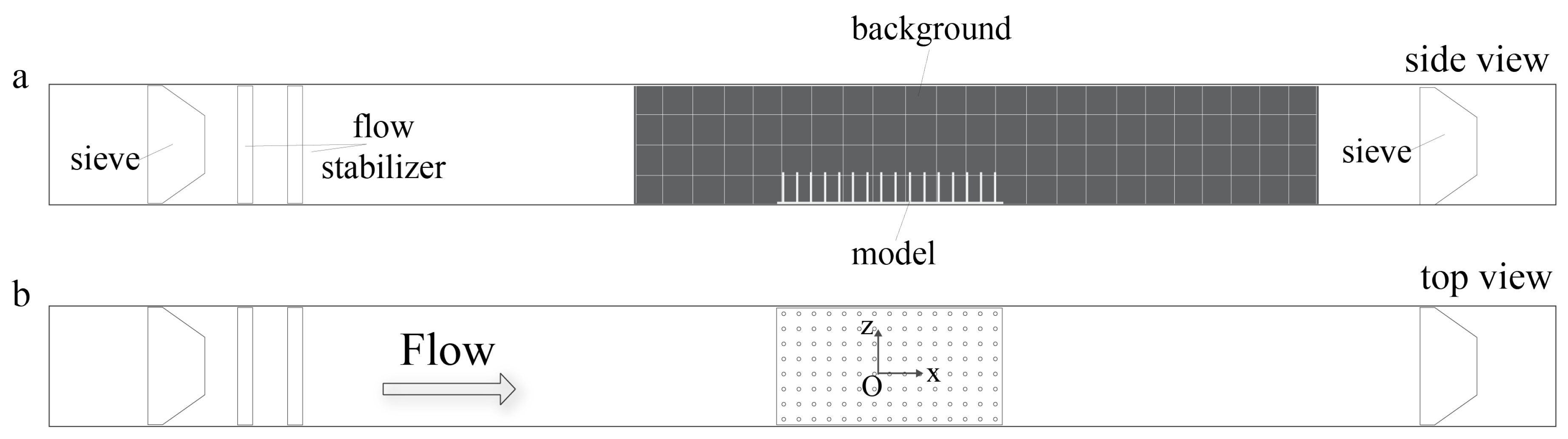
For the flow experiments, the physical models of submerged macrophyte beds were placed at the center of the bottom of an optically accessible 8 cm × 8 cm × 100 cm plexiglass flow tank that was custom built based upon Vogel and LaBarbera [
52] (see
Figure 1). The models were held in place using marine putty as if submerged and rooted. Two
Artemia sieves were placed at far upstream and downstream from the model in order to prevent feeding the injected organisms back into the system. The dimensions of the sieves were 8.64 cm × 7.87 cm × 4.45 cm with 180 micron mesh size. A black background with thickness less than a millimeter was placed in the flow tank to enhance the contrast between the
Artemia nauplii and the background. The background included a grid with 2 cm × 2 cm squares to facilitate tracking. Constant flow was generated by a propeller attached to a variable speed motor, and the flow within the empty channel had a maximum average velocity of 4.4 cm/s. The flow tank was filled with seawater of 35 ppt salinity, and the height of the water was kept at 7.5 cm to prevent overflowing when the propeller was in action.
2.4. Measurements of Flow
The temperature of the salt water in the flow tank was about 20 C such that its density was assumed to be = 1025 kg/m with a dynamic viscosity = 0.00108 Ns/m. A parabolic profile was used to set the inflow conditions for the computations, and the volumetric flow rate was matched to that measured experimentally for the case of no model. This resulted in a maximum inflow velocity of 0.0444 m/s. Setting the characteristic velocity to this maximum value, U = 0.0444 m/s, one can calculate at the scale of the individual cylinders and at the scale of the macrophyte bed. Using a characteristic length equal to the height of the cylinders, h = 0.01–0.03 m, the bed-based ranged from 421–1264. Using the diameter of the cylinders, D = 0.0025 m, the cylinder-based was about 105. This range of is reasonable for using direct numerical simulation of the Navier–Stokes equations to obtain the flows around and over the macrophyte beds.
2.4.1. Particle Image Velocimetry
The fluid velocities within the flow tank were obtained using 2D particle image velocimetry (PIV) and used for validation of the numerical simulations. PIV is a non-intrusive technique used to obtain instantaneous and spatially resolved information on a flow field by recording the single or multiple exposed images of passive tracer particles suspended in the fluid. In general, a monochromatic coherent light source is used to illuminate these small seeding particles, and the positions of the particles are recorded at set time intervals. The displacement
of a single particle or group of particles is deduced from correlation-based post processing of these images. A map of the velocity of motion of the tracers in the flow field can thus be obtained using
. For more information on this technique, please refer to Raffel et al. [
53] and Willert and Gharib [
54].
In this work, the laser sheet was generated by a 1 W Nd:YAG, Diode Pumped Solid State Laser (DPSS) laser manufactured by LaVision GmbH, which emits light at a wavelength of 532 nm with a maximum modulation of 10 kHz. The laser beam was converted into a planar sheet approximately 3 mm thick using a set of focusing optics. Uniform seeding of the fluid was accomplished by inserting 10 micron glass hollow spheres (LaVision GmbH) into the flow tank and mixing to achieve a near homogeneous distribution prior to each experiment. A Photron FASTCAM SA3 high-speed camera with Tokina Macro 100 F2.8 D lens attached was used for capturing images with a 1024 × 1024 resolution at 500 Hz for 1 s. The spatial resolution was 0.017 mm per pixel. All frames were pre-processed in order to remove glares and unwanted brightness in images. To do this, local minimum of series were subtracted from each frame. Then, the cylinder array and regions outside the flow were masked before analyzing images in Davis 8.0 (LaVision). Velocity vectors were calculated using cross-correlation, multi-pass iterations with 2 passes. The size of the interrogation windows was set to 64 × 64 and 32 × 32 pixels with 50% overlap, respectively. The resulting flow fields were post-processed using a non-linear filter to remove faulty vectors. Finally, the velocity fields of the entire image set were averaged to get the average velocity profiles.
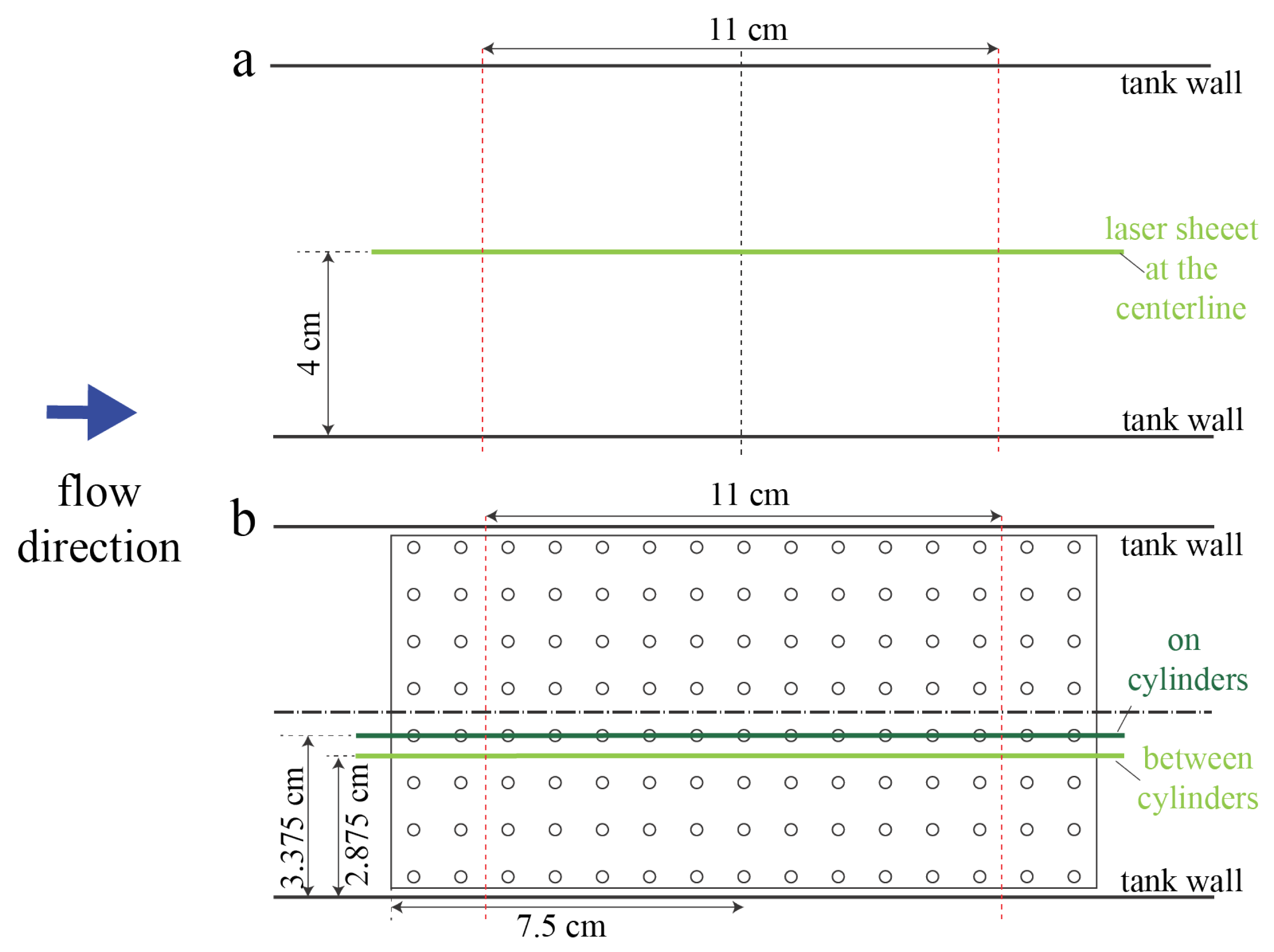
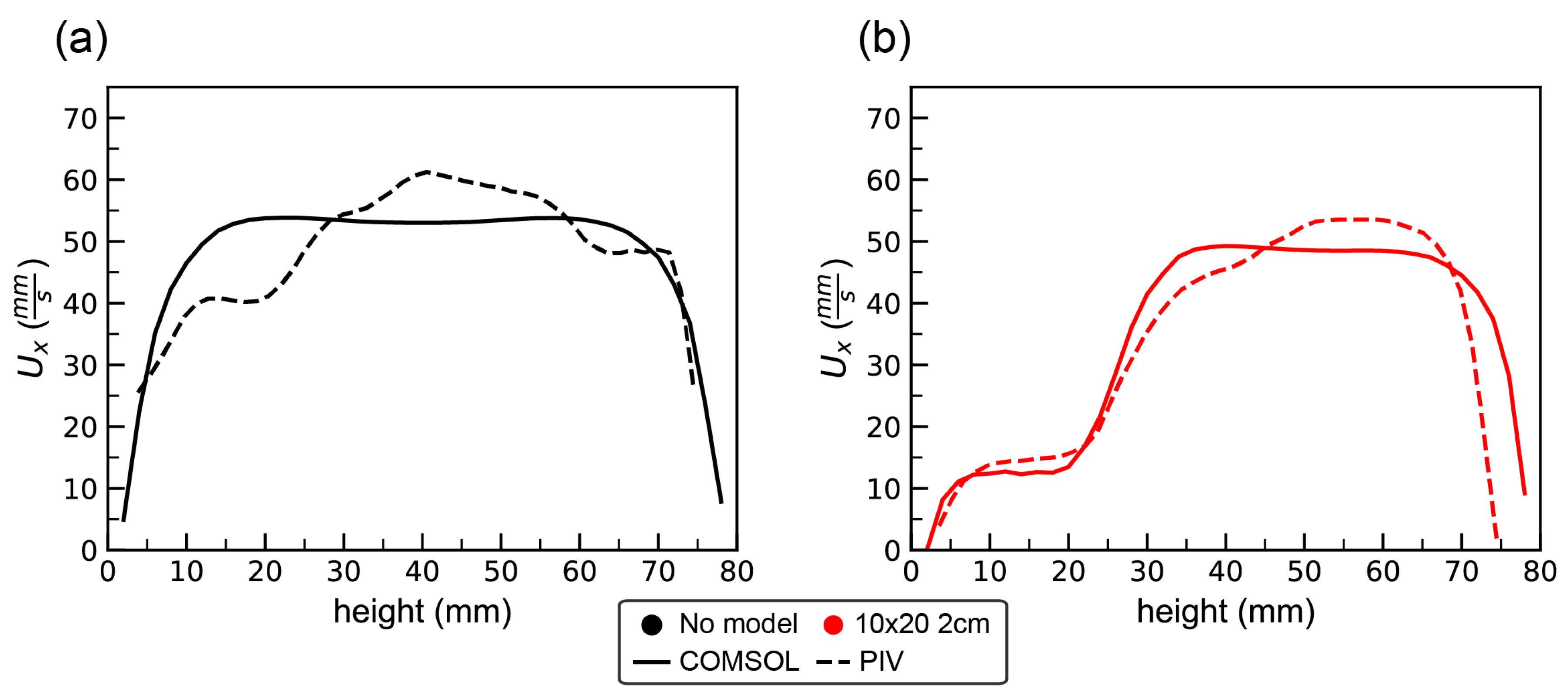
For validation of numerical simulations, PIV measurements were taken in an empty tank and in the tank with the 10 × 20 2-cm macrophyte model. Flow velocities within two different planes tangential to the flow were measured. The first plane passed between the middle two cylinders rows. The second plane passed through the center of the cylinders in the middle of the model.
Figure 2 shows the position of laser sheet for these two scenarios.
Note that it was difficult to resolve the flow field within the model due to the narrow gap between cylinders and the fact that the model is optically inaccessible. However, PIV measurements still produced sufficiently detailed information about the flow field for comparison with numerical simulations since we compared the regions that were optically accessible.
2.4.2. Computational Fluid Dynamics
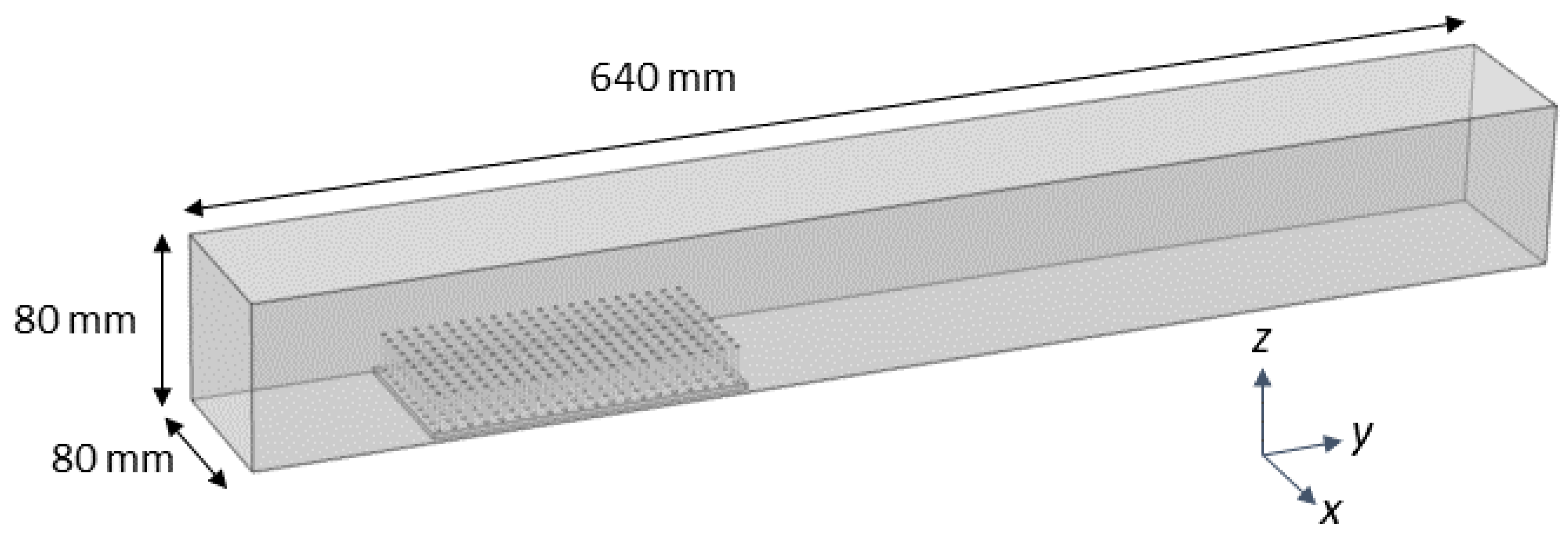
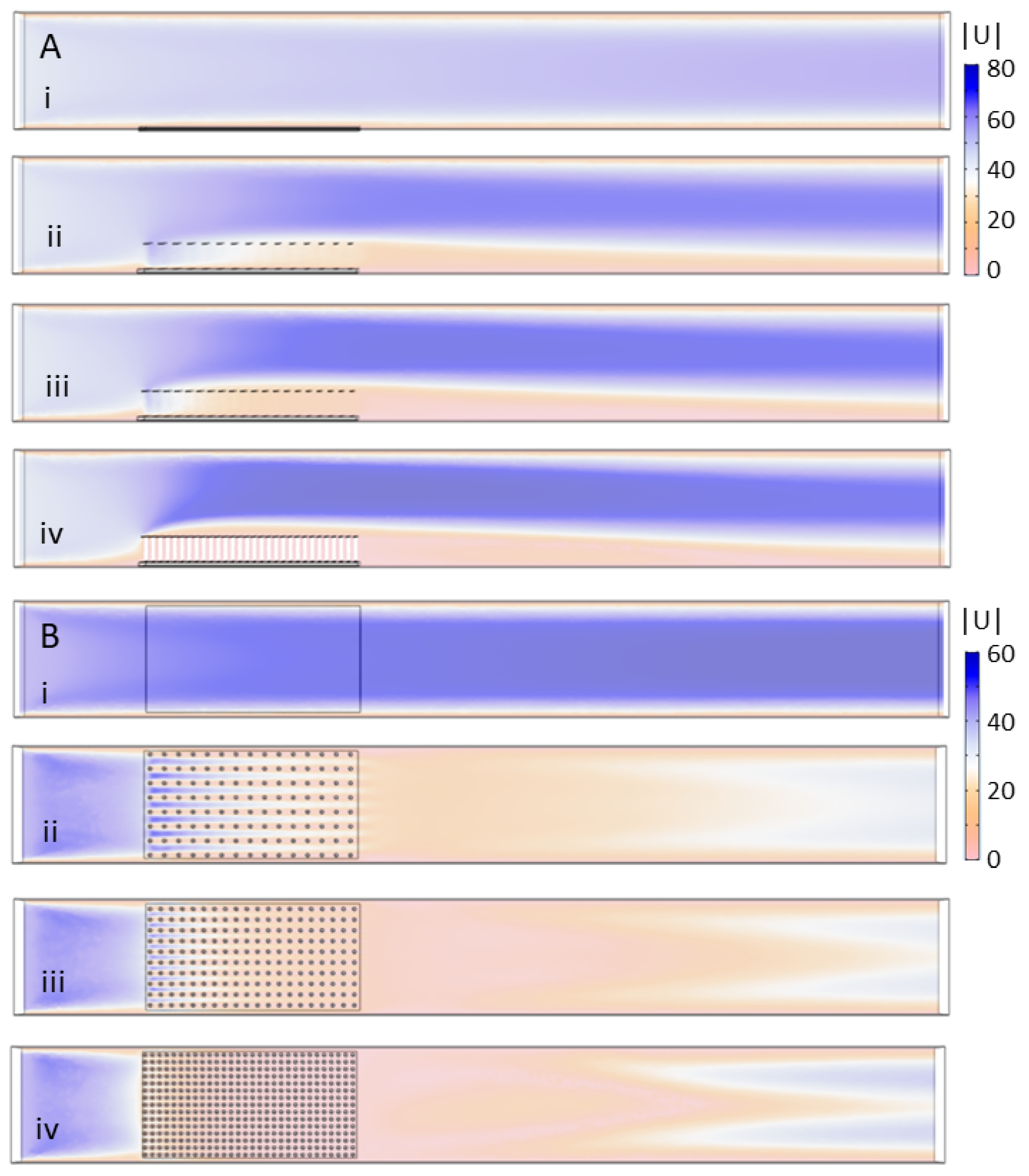
COMSOL Multiphysics 4.5 was used to mesh the fluid domain and solve the steady Navier-Stokes equations. The single-phase laminar flow physics solver was used to perform a stationary study (e.g.,
. The fluid domain had dimensions of 80 mm × 320 mm × 80 mm, similar to the actual flow tank. The density and dynamic viscosity of the fluid was set to
= 1025 kg/m
with a dynamic viscosity
= 0.00108, within the range of typical seawater. The entrance of the domain was given an inlet boundary condition of parabolic flow with a maximum velocity of 44.4 mm/s in the center of the domain, unless otherwise noted. The back wall was given a zero pressure outlet condition. All other walls used a no-slip boundary condition. A free tetrahedral mesh of normal resolution calibrated for fluid dynamics was used to discretize the fluid domain (see
Figure 3).
The same .stl files used for 3D printing were used for the COMSOL simulations. These models were positioned at the bottom of the computational flow tank and in the middle of the domain. The steady Navier–Stokes equations were solved in the rectangular domain with the model region subtracted. No slip conditions were employed on the model boundaries and sides of the domain. Note that, for the simulations without a model, the plate without cylinders was positioned in the bottom of the tank.
2.5. Dispersal Experiments
The concentration of plankton under steady background flow in the presence and absence of macrophyte models was recorded at spatial locations downstream of the models. Experiments were repeated three times for each model (including the no model case), for a total of 30 experiments. The video recordings were processed to quantify dispersal patterns as a function of macrophyte density and height. For each scenario, the numbers of plankton measured in each experiment were added together to obtain a combined distribution.
2.5.1. Preparation of Artemia Larvae
One gram of Artemia cysts (Grade A Brine Shrimp Eggs, Brine Shrimp Direct) was hatched in 1 L of seawater with a concentration of 35 ppt. After 48 h, nauplii were separated from empty shells by filtering the hatching water using a 180-micron Artemia sieve. The nauplii were transferred into a 2-L beaker filled with fresh seawater at 35 ppt. Note that the filtering process did not completely separate empty shells, and negligible amounts of shells and unhatched eggs were present in the final mixture.
2.5.2. Injection of Brine Shrimp into the Flow Tank
Before each experiment, 0.5 L of salt water with Artemia was filtered and concentrated into a 40-mL solution. As a result of the concentration process, organisms were introduced into the flow as a dense patch with minimal flow disturbance. After each experiment, unused Artemia were returned into the 2-L beaker and given sufficient time (≈10 min) to recover. This procedure was put in place to ensure that the nauplii were active during the experiments.
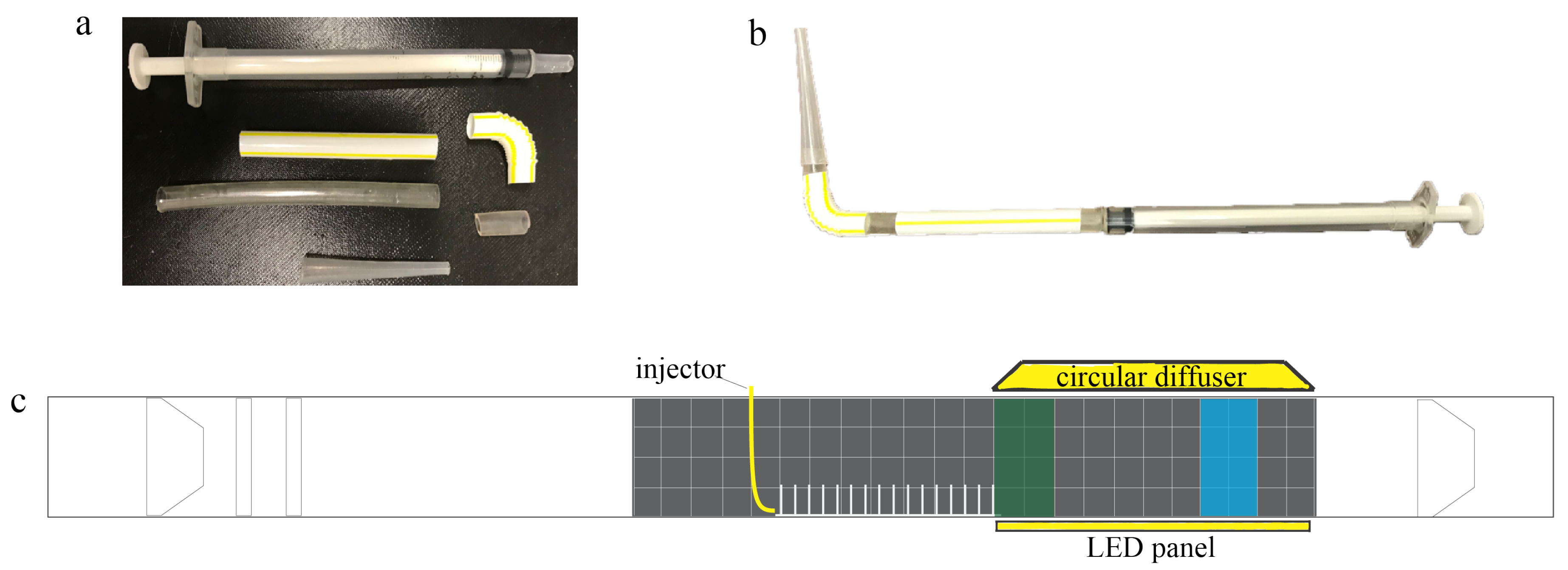
Larvae were placed in the flow tank using a 1 mL injector with a modified tip, as shown in
Figure 4a,b. The injector was designed to minimize flow disturbance when submerged in the tank. Before each injection, 0.1 mL of air was pipetted before taking up 0.2 mL of the nauplii and salt water. This initial bubble was used to signal when the injection was complete. Finally, 0.1 mL of air was pipetted to serve as a seal to prevent the early release of nauplii into the flow. Between each experiment, the mouth of the injector was gently washed with salt water to remove any remaining larvae or eggs. All injections were performed at the center of the flow tank in the region directly upstream of the model and above the base plate, as shown in
Figure 4c. The average injection speed was 33.31 mm/s with 11.89 mm/s standard deviation and 32.97 mm/s median for 30 trials.
2.5.3. Recording Dispersal of Plankton
Brine shrimp nauplii were recorded using three Sony Alpha 6300 cameras with 16–50 mm stock lenses. One camera was used to record the injection of larvae and their initial movement through the macrophyte model. The concentration of brine shrimp directly downstream of the macrophyte model was recorded using the remaining two cameras. One camera was placed immediately after the model to record the nauplii within a region named the “green zone”, and the other camera was placed 15 cm downstream of the model, and this region was named the “blue zone”. Each zone consists of eight 2 cm × 2 cm cells, making each zone 4 cm (W) × 8 cm (H). All recordings were taken at 30 fps with 4K resolution. The shutter speed was set to 1/640 s.
To resolve individual brine shrimp in a relatively large volume of fluid, significant attention was given to lighting. One Flashpoint FPLCL1144R LED Circular Diffuser and one Fositan TL-336AS LED Video Light with custom diffuser were used to evenly illuminate the volume of water in the flow tank. The circular diffuser was set to maximum intensity and placed above the flow tank right after the model. The Fositan LED panel was also set to maximum intensity and placed below the flow tank. A plain white piece of paper was used to cover the Fositan LED panel to act as a diffuser.
2.5.4. Processing Recordings
Recordings from the camera positioned upstream of the macrophyte model were used to determine the injection velocity of the brine shrimp solution. In this case, it was assumed that the brine shrimp act as passive tracers that move at the local fluid velocity. The recordings from the cameras placed downstream were then used to determine the number of nauplii over time in the green and blue zones. Videos were played frame by frame using Quicktime Player 7.0. Each zone consisted of eight 2 cm × 2 cm squares. The organisms in each square were counted at 0.5 s intervals and recorded into an Excel spreadsheet for further processing. To improve the precision of counting the nauplii, a screenshot of the region of interest was taken and each organism was marked as it was counted using Adobe Photoshop CC (Adobe Photoshop CC Version 20.0.6, Adobe Creative Cloud).
The number of brine shrimp in each zone and for each increment in time for the three experiments were combined for comparisons between model cases and the agent-based simulations. All experimental results were plotted in MATLAB [
55].
2.6. Agent-Based Modeling (ABM) Framework: Planktos
For this project, we make use of an in-house, open source, agent-based framework called
Planktos [
56] that is capable of exploring emergent patterns of organisms in complex flow regimes based on individual-level behavioral rules. Agent-based models (or individual-based models) are models in which individuals are described as autonomous entities which can then interact with each other and/or their environment. In this setting, simulated organisms can have adaptive behavior which can include continual adjustments in response to changes in their environment, the presence and behavior of other agents, or to their own internal states [
40].
For this preliminary study, brine shrimp were assumed to move via a random walk such that their effective diffusivity was comparable to experimental data from Kohler et al. [
39] and their mean drift corresponded to the local flow velocity. Numerically speaking, this means that the location of each individual agent (brine shrimp) was independently updated at each time step using the time-invariant flow field simulated in COMSOL (for a given model geometry) and a three-dimensional normal distribution as given in the equation
with
given to be the 3 × 3 covariance matrix with the variance as derived from Kohler et al. [
39] along the diagonal and zeros elsewhere, and
the fluid velocity at
, found by linearly interpolating the numerical flow field grid specified in COMSOL. In the case that agents crossed a domain boundary corresponding to the tank wall or the surface of the fluid, they were placed on the boundary by translating back to the nearest point on the edge of the domain. If agents crossed the upstream or downstream boundary of the domain, they were considered to have left the experimental environment and were no longer tracked in any way for the remainder of the simulation. In this first study, individuals did not interact with each other and they did not modify the flow field.
While various software packages exist that provide comprehensive simulation environments for agent-based modeling [
48], they tend to be for high-level, general use and are not well suited to the specific challenges of incorporating fluid–structure interaction data for swimmers in continuous 2D or 3D environments.
Planktos is an object-oriented modeling environment written in Python and specifically built for interfacing with numerical 2D or 3D flow data, including time-varying flows (although this feature was not used in this study). Custom agent behavior and response to flow gradients can be tested and visualized both quickly and easily, with 1D analytical flow fields available internally for environmental comparison [
56].
Some of the capabilities of Planktos that we specifically used in our study of Artemia include:
VTK-based import of 2D or 3D time-dependent fluid flow data and flow interpolation between grid points
Fluid flow tiling with periodic boundary conditions to expand the domain
Selection of boundary conditions for agents
2D and 3D plotting of agent movement, including summary statistics and density histograms
2.7. Agent-Based Simulation and Experimental Results
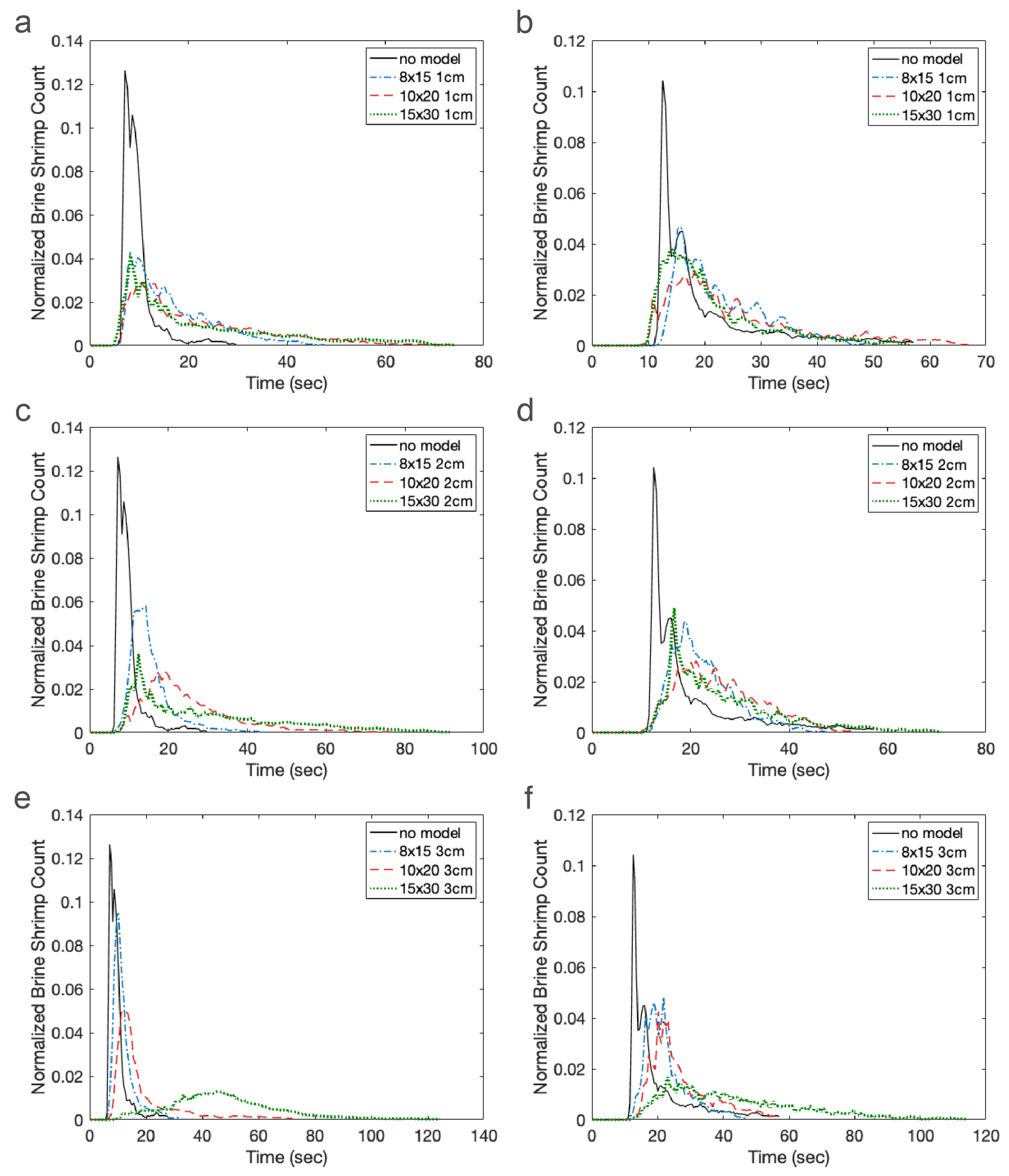
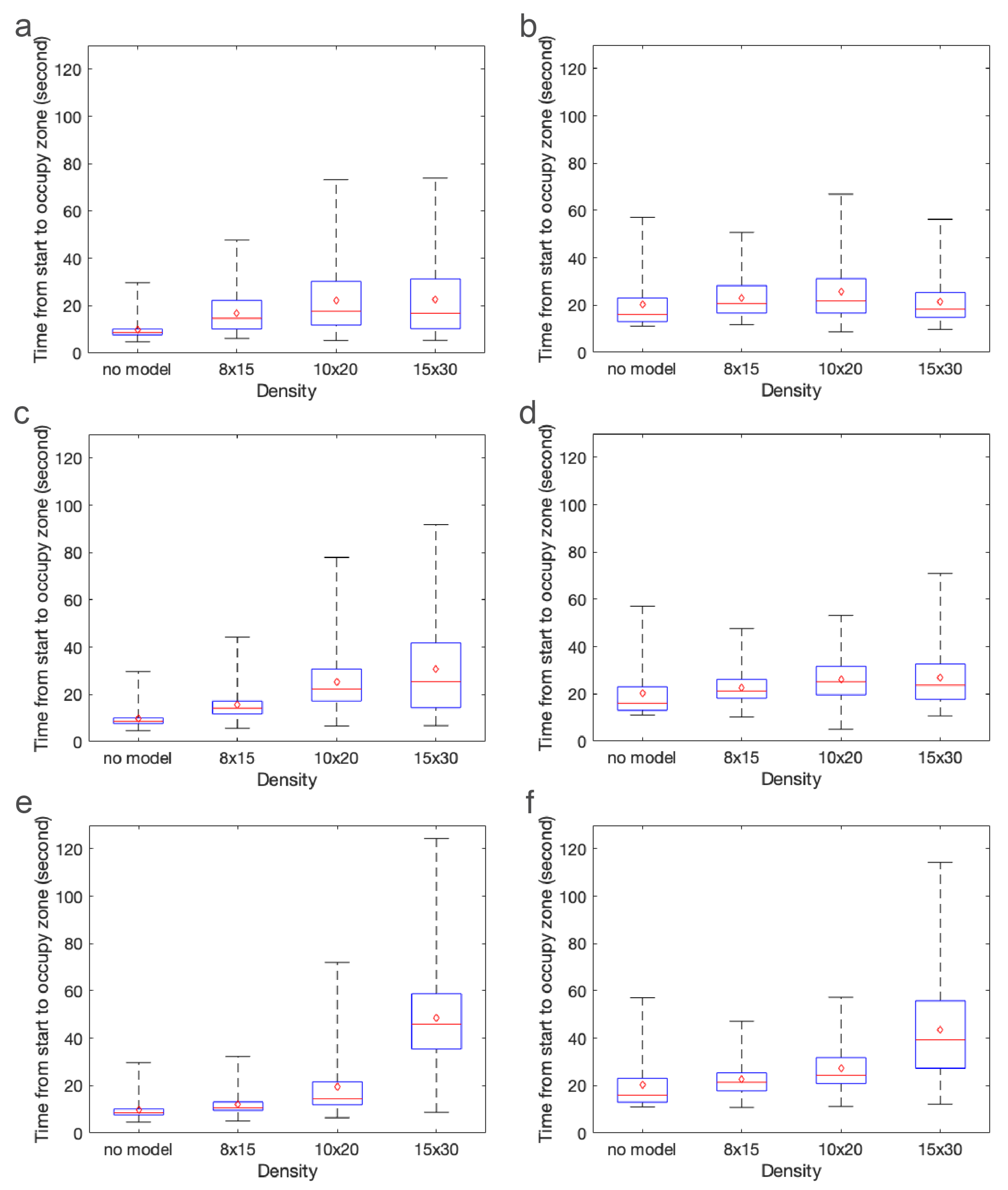
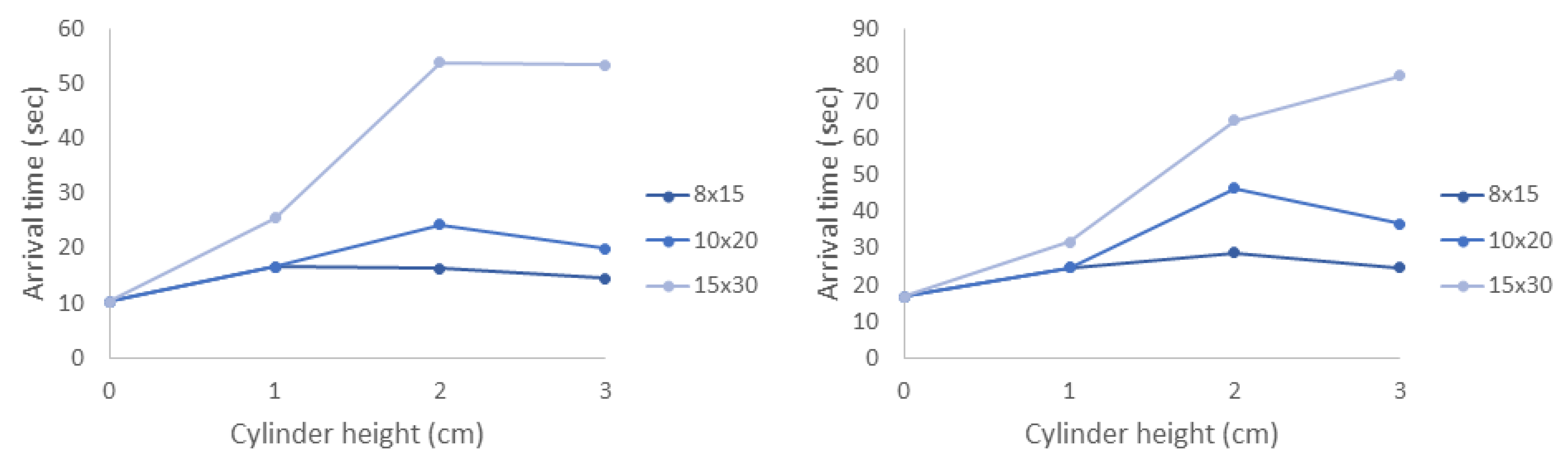
There are several challenges with directly comparing the experimental results with the agent-based simulations. It is difficult to track individual Artemia nauplii (≈1 mm) as they move through a relatively large 3D volume of fluid (≈4000 cm). We could not track individuals throughout the duration of the experiment, but we could count the number of nauplii present in each zone in 0.5 s intervals. On the other hand, we could easily track individuals in the agent-based simulations. Because we knew the location of each individual at any time, we could calculate the exact times that each individual arrived in the green and blue zones (the arrival times). In the experiments, we could only report how many individuals were present in the zone at each time, and these individuals could remain in the zone for several time increments. Furthermore, the amount of time individuals spent in the zone was proportional to the density of cylinders in the macrophyte models, as this slowed the local flow velocities. We report arrival times for the agent-based simulations and the number of nauplii in each zone at each time increment for the experiments. Despite the differences in the data we could obtain from simulations and experiments, both metrics do reveal similar trends.
There are also some differences in parameter values describing the experiment and used in the simulations. For example, we do not know the number of brine shrimp injected into the flow tank experiments, which likely varied to some degree between experiments. For consistency, the agent-based simulations included 10,000 agents in each simulation. We estimate that each experiment included a couple thousand brine shrimp. We also do not know the effective diffusivity of the brine shrimp in each experiment. The nauplii were approximately 48 h post fertilization, but there was some variation in incubation time and activity due to the time of day and treatment of the brine shrimp. In the agent-based simulations, we always used the same diffusivity reported by Kohler et al., but, for newly hatched nauplii, potentially of a different species and ordered from a different supplier. Finally, there were some variations in the volumetric flow rate of the experiments. The control dial was always set to the same setting, but the presence of models as well as their height and density changed the resistance to flow and the resulting flow speed. In the simulations, the peak inflow velocity was always set to 44 mm/s. For these reasons, we do not directly compare experiments and simulations, but look for similar trends in dispersal patterns.
4. Discussion
In this paper, we develop an open source agent-based code for simulating plankton movement in complex flow fields. This framework was applied to a relatively simple case of brine shrimp moving through an idealized model of a macrophyte bed at the scale of tens of centimeters. Using this simple test case, we found that: (1) arrival times are largely affected by the density of the macrophyte model; (2) the effect of macrophyte height on arrival times is not straightforward; and (3) downstream arrival times are a non-monotonic function of the effective diffusivity of the agents. Predictive models of the dispersal of plankton whose trajectories are significantly determined by both the local fluid flow and their own behavior are important for many conservation applications. For example, high fidelity dispersal models of invasive species such as some bivalves [
58,
59], starfish [
60,
61] and copepods, for example,
Oithona davisae [
58], could focus removal efforts and inform the timing and location of the release of biocontrol agents. Models of the dispersal of the biocontrol agents themselves could allow more effective release of these organisms. In terms of the role of macrophytes and other protective structures in sheltering plankton, predictive models could inform the best placement and geometry of artificial reefs and could identify key locations where vegetation and reefs should be protected.
Work to leverage existing and further develop state-of-the-art numerical methods and mathematical analyses to reveal how organism swimming performance, behavior, and environment conditions alter dispersal and subsequent distributions of plankton have applications to multiple areas of biological oceanography and conservation. Using theoretically and experimentally determined estimates of thrust and mathematical models of behavior (including preferred dispersal conditions), scientists could predict and validate dispersal distributions across a variety of landscapes. Significant consideration needs to be given to the mathematical challenges in describing the dispersal of tiny organisms, including: (i) modeling techniques to connect dynamics at various spatial and temporal scales; (ii) data collection protocols and data accessibility; (iii) agent-based models that incorporate animal behavior and swimming trajectories; and (iv) code generation that is well-documented and generally applicable for both education and research. The primary goal of this study was to document such an approach for a model organism in an idealized setting.
The results of this paper clearly show that both the average time to arrive in each zone and the variance depend strongly on the density of the macrophytes. This is primarily due to the strong nonlinear effect that cylinder density has on local flow speed as well as the region of flow that is sheltered downstream of the model. Cylinder height has a weaker effect on arrival times, likely due to the fact that the brine shrimp are injected near the bottom of the tank where differences in flow speeds are negligible. One exception to this is that the densest and tallest model greatly increased the time that brine shrimp arrived or appeared in the zones in both the experiments and the simulations. This is likely due to the large, sheltered region downstream of the model.
These results clearly demonstrate that the density of macrophytes, natural and artificial reefs, and other structures has a strong effect on plankton retention time. Since there is a strong nonlinear transition where such structures act as either nearly impermeable regions or porous layers with significant leakiness [
36,
62], it is critical that sheltering structures be above this leaky-to-solid threshold. Furthermore, dense, tall structures may create slow flow regions downstream that could also shelter plankton.
Our results also suggest areas for future research. Our numerical simulations of the flow fields ignored unsteady effects that could either increase the spatial variance of the brine shrimp due to fluctuations in the velocity field or condense the spatial distribution given the effect of separatrices in the flow. It was also assumed that the brine shrimp move in a way that is well described by an unbiased random walk. It is known that nauplii use phototaxis and may avoid regions of strong flow or high shear. Any bias in the movement to swim together or apart would also alter their distributions. These higher-order effects underscore the need for more complex models that consider both behavior and temporally varying flow fields.
We introduced an open source, agent-based framework called Planktos to quantify emergent spatial and temporal patterns of plankton and other small organisms in complex flows based on individual-level behavioral rules. The unique feature of this open source platform is that the movement of agents is easily coupled to flow. This feature makes the software particularly suitable for modeling the movement of marine, aquatic, and aerial plankton across the scales of centimeters to tens of meters. Accordingly, the code should find immediate use in applications focused on resolving the movement of plankton within complex flow fields such as water flow through macrophyte beds and reefs. Massive agents may also be easily introduced to consider the dispersal of aerial plankton (small insects, spiders, etc.) due to winds through a crop field or forest patch.