The Ground Effect in Anguilliform Swimming
Abstract
1. Introduction
2. Materials and Methods
2.1. Fish Body Kinematics and Non-Dimensional Parameters
2.2. The Numerical Method
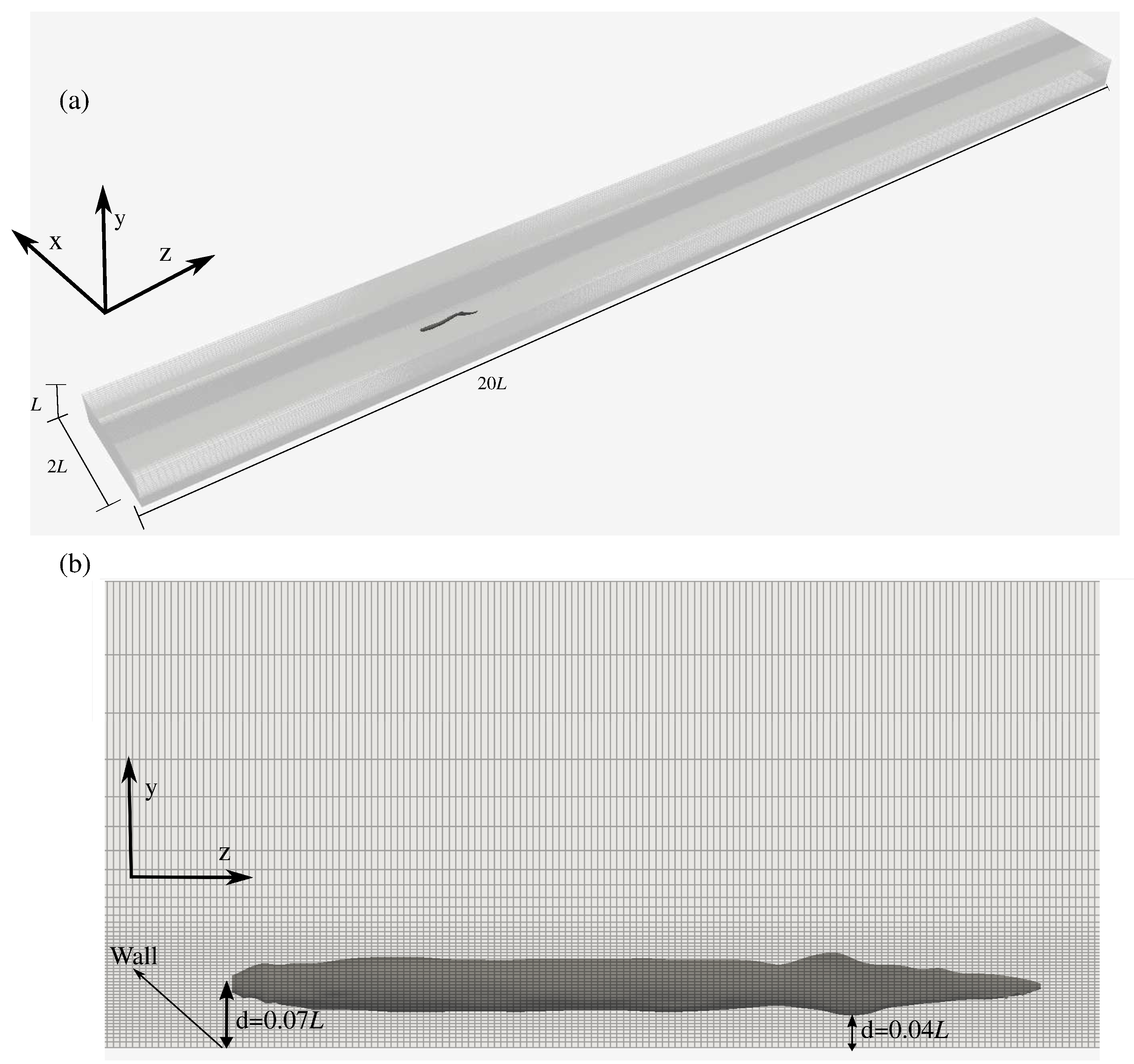
2.3. Computational Details
2.4. Calculation of Hydrodynamic Forces and Swimming Efficiency
3. Results and Discussion
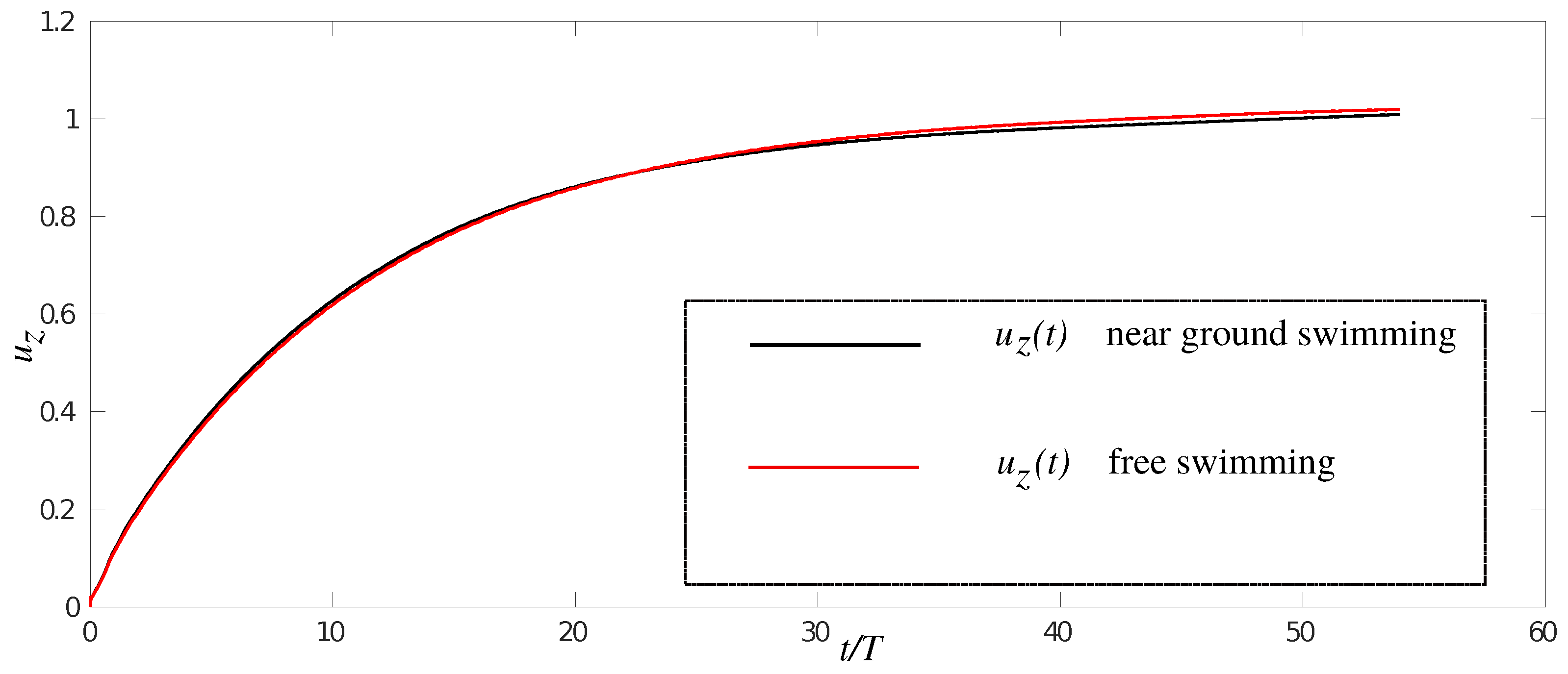
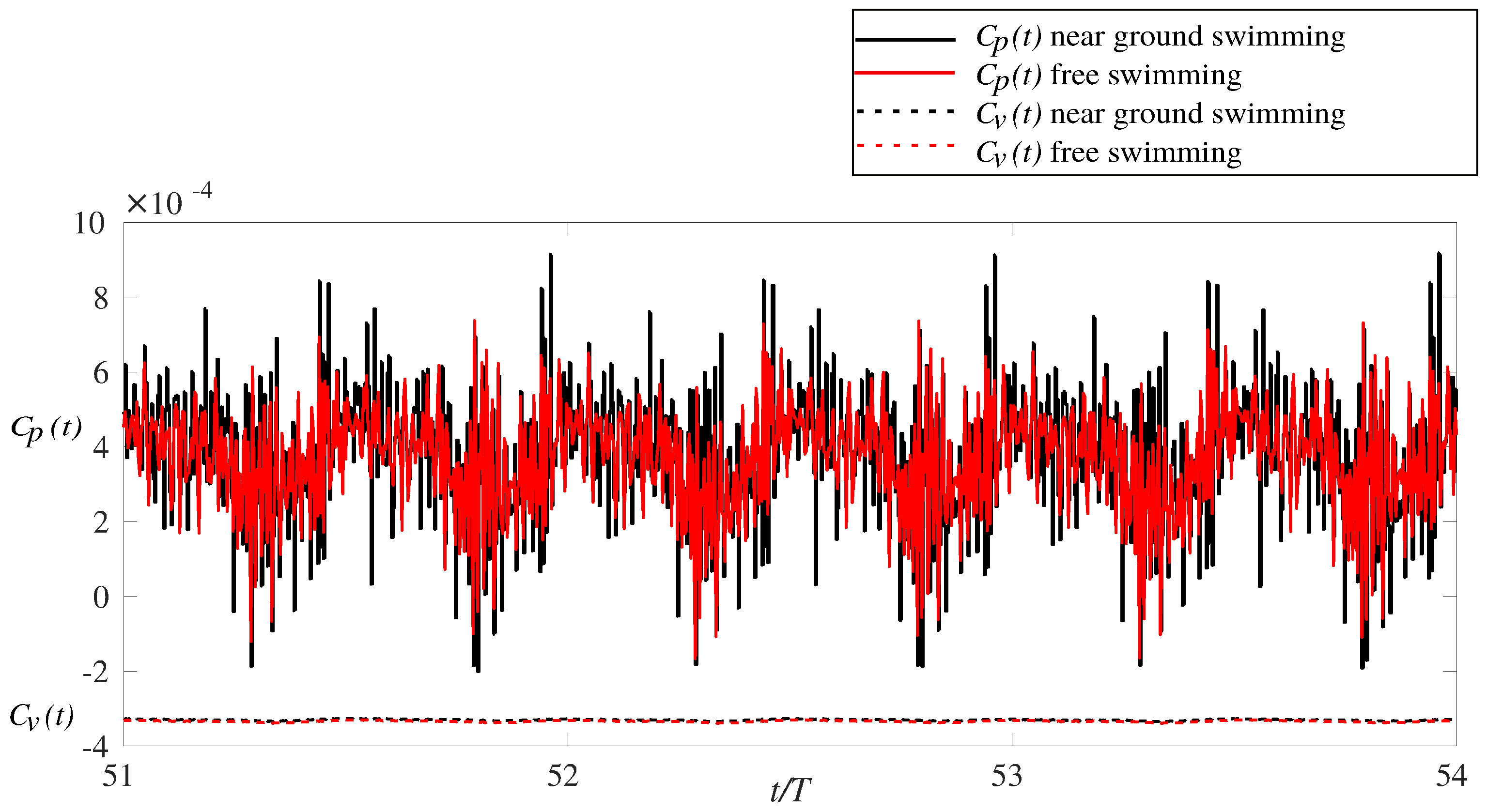
3.1. Effects of Ground Swimming Performance
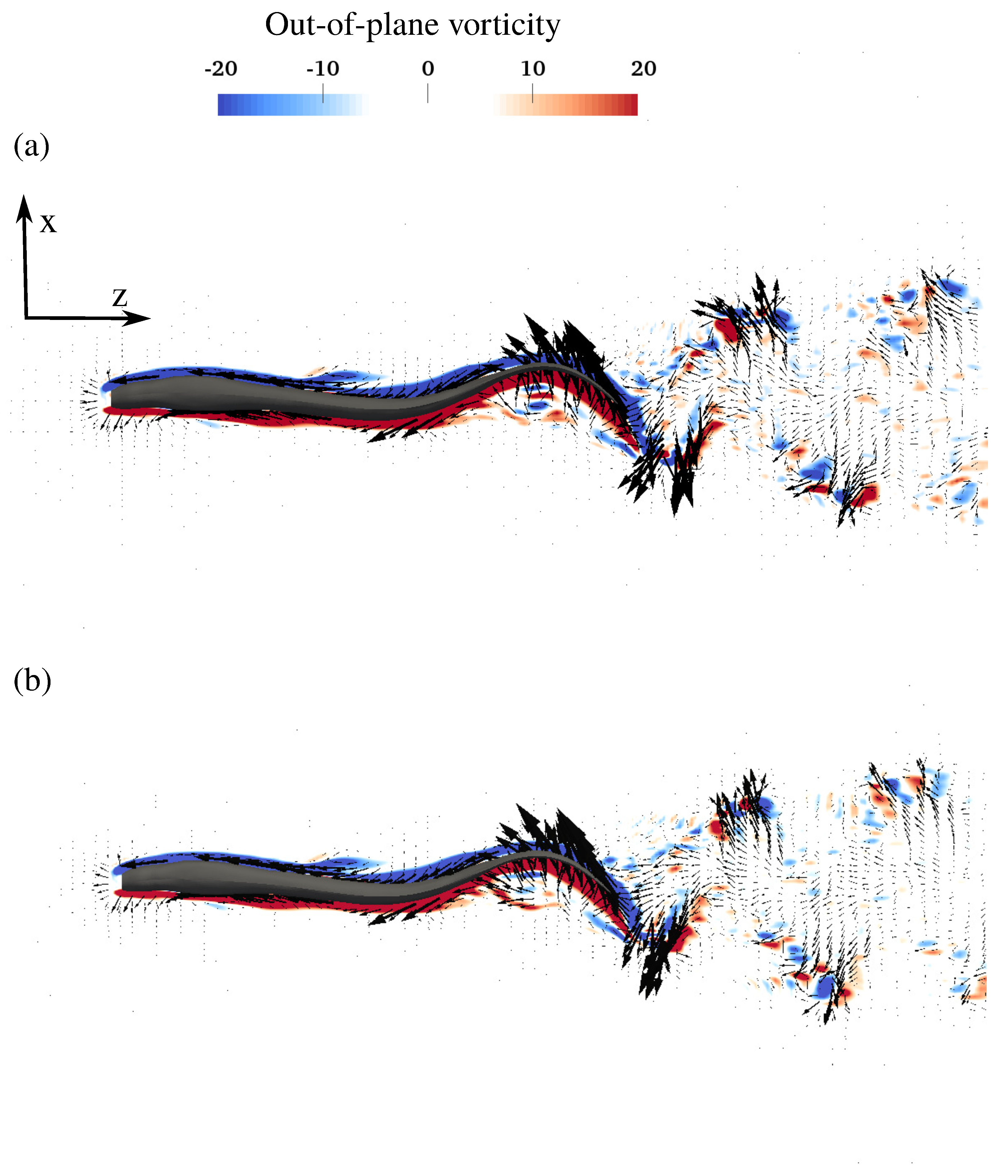
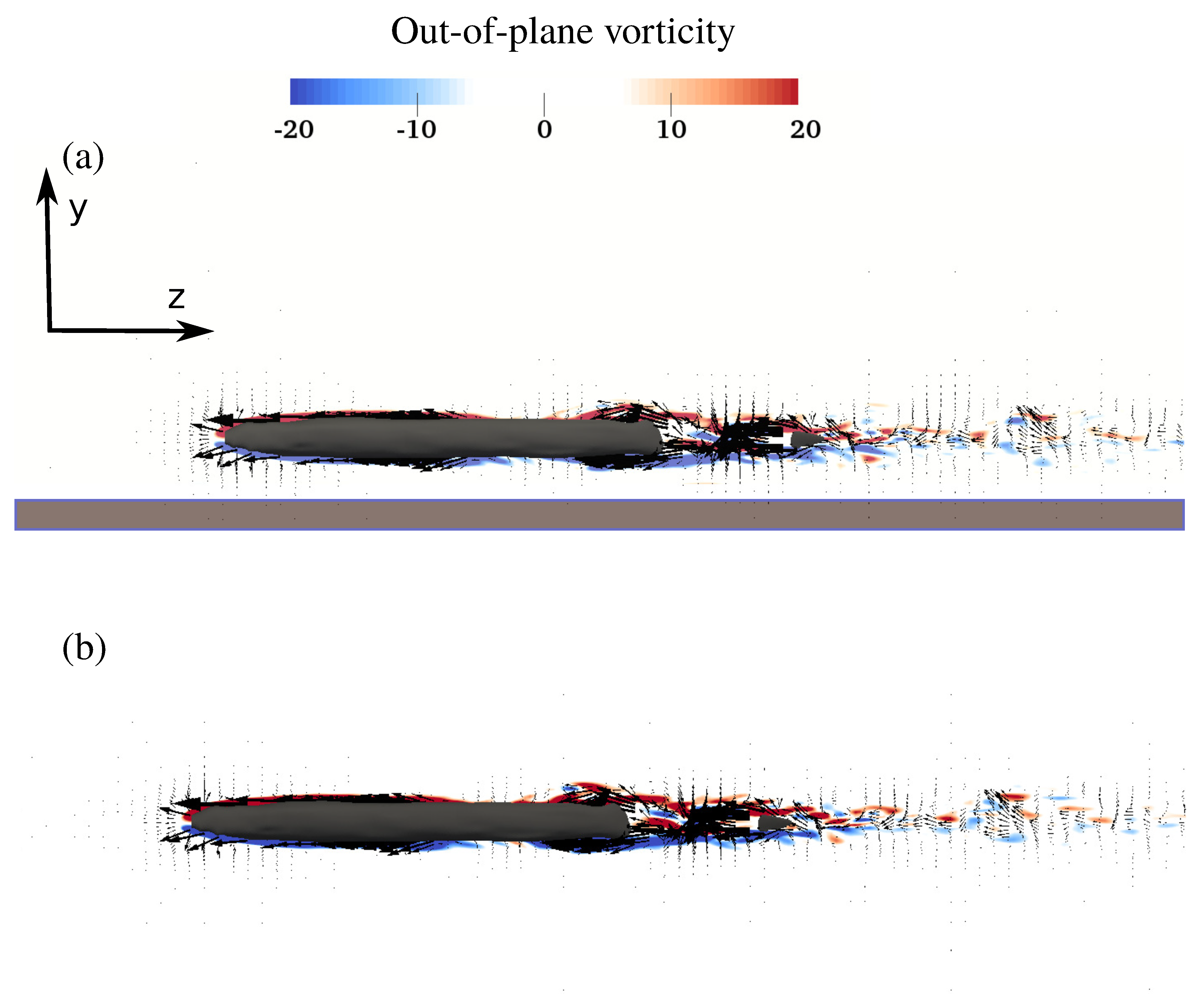
3.2. Flow Field
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| a | amplitude envelope of lateral motion |
| maximum amplitude | |
| A | maximum lateral excursion of the tail over a cycle |
| force coefficient | |
| pressure force coefficient | |
| mean axial force coefficient | |
| viscous force coefficient | |
| D | drag |
| f | tail-beat frequency |
| F | force exerted on the fish body by the flow |
| h | lateral excursion of the body |
| velocity of the lateral undulations | |
| k | wave number of the body undulations |
| L | fish length |
| PIV | particle image velocimetry |
| mean power loss | |
| Reynolds number | |
| Strouhal number | |
| t | time |
| T | thrust |
| mean thrust force | |
| U | swimming speed |
| V | speed of the backward undulatory body wave |
| z | axial flow direction measured along the fish axis from the tip of the fish’s snout |
| slip velocity | |
| Froude propulsive efficiency | |
| wavelength | |
| kinematic viscosity of water | |
| fluid density | |
| tail-beat period | |
| viscous stress | |
| angular frequency |
References
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming: I. Wake structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef]
- Blevins, E.; Lauder, G.V. Swimming near the substrate: A simple robotic model of stingray locomotion. Bioinspir. Biomimetics 2013, 8, 016005. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Tighe, K. Freshwater eels. Family Anguillidae. In Fishes of the Gulf of Maine; Smithsonian Institution Press: Washington, DC, USA, 2002; pp. 92–95. [Google Scholar]
- Blake, R. Mechanics of gliding in birds with special reference to the influence of the ground effect. J. Biomech. 1983, 16, 649–654. [Google Scholar] [CrossRef]
- Webb, P.W. The effect of solid and porous channel walls on steady swimming of steelhead trout Oncorhynchus mykiss. J. Exp. Biol. 1993, 178, 97–108. [Google Scholar]
- Webb, P.W. Kinematics of plaice, Pleuronectes platessa, and cod, Gadus morhua, swimming near the bottom. J. Exp. Biol. 2002, 205, 2125–2134. [Google Scholar] [PubMed]
- Nowroozi, B.N.; Strother, J.A.; Horton, J.M.; Summers, A.P.; Brainerd, E.L. Whole-body lift and ground effect during pectoral fin locomotion in the northern spearnose poacher (Agonopsis vulsa). Zoology 2009, 112, 393–402. [Google Scholar] [CrossRef]
- Park, S.G.; Kim, B.; Sung, H.J. Hydrodynamics of a self-propelled flexible fin near the ground. Phys. Fluids 2017, 29, 051902. [Google Scholar] [CrossRef]
- Gao, T.; Lu, X.Y. Insect normal hovering flight in ground effect. Phys. Fluids 2008, 20, 087101. [Google Scholar] [CrossRef]
- Quinn, D.B.; Lauder, G.V.; Smits, A.J. Flexible propulsors in ground effect. Bioinspir. Biomimetics 2014, 9, 036008. [Google Scholar] [CrossRef]
- Fernández Prats, R. Hydrodynamics of Pitching Foils: Flexibility and Ground Effects. Ph.D. Thesis, Universitat Rovira i Virgili, Tarragona, Spain, 2015. [Google Scholar]
- Mivehchi, A.; Dahl, J.; Licht, S. Heaving and pitching oscillating foil propulsion in ground effect. J. Fluids Struct. 2016, 63, 174–187. [Google Scholar] [CrossRef]
- Dai, L.; He, G.; Zhang, X. Self-propelled swimming of a flexible plunging foil near a solid wall. Bioinspir. Biomimetics 2016, 11, 046005. [Google Scholar] [CrossRef] [PubMed]
- Perkins, M.; Elles, D.; Badlissi, G.; Mivehchi, A.; Dahl, J.; Licht, S. Rolling and pitching oscillating foil propulsion in ground effect. Bioinspir. Biomimetics 2017, 13, 016003. [Google Scholar] [CrossRef] [PubMed]
- Kurt, M.; Cochran-Carney, J.; Zhong, Q.; Mivehchi, A.; Quinn, D.B.; Moored, K.W. Swimming freely near the ground leads to flow-mediated equilibrium altitudes. J. Fluid Mech. 2019, 875, R1-14. [Google Scholar] [CrossRef]
- Gray, J. Studies in animal locomotion: I. The movement of fish with special reference to the eel. J. Exp. Biol. 1933, 10, 88–104. [Google Scholar]
- Vorus, W.S.; Taravella, B.M. Anguilliform fish propulsion of highest hydrodynamic efficiency. J. Mar. Sci. Appl. 2011, 10, 163. [Google Scholar] [CrossRef]
- Müller, U.K.; van den Boogaart, J.G.; van Leeuwen, J.L. Flow patterns of larval fish: undulatory swimming in the intermediate flow regime. J. Exp. Biol. 2008, 211, 196–205. [Google Scholar] [CrossRef]
- Devarakonda, N.S. Hydrodynamics of an Anguilliform Swimming Motion Using Morison’s Equation. Master’s Thesis, The University of New Orleans, New Orleans, LA, USA, 2018. [Google Scholar]
- Lighthill, M.J. Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1971, 179, 125–138. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Triantafyllou, G.; Yue, D. Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Hultmark, M.; Leftwich, M.; Smits, A.J. Flowfield measurements in the wake of a robotic lamprey. Exp. Fluids 2007, 43, 683–690. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. On the role of form and kinematics on the hydrodynamics of self-propelled body/caudal fin swimming. J. Exp. Biol. 2010, 213, 89–107. [Google Scholar] [CrossRef]
- Borazjani, I.; Ge, L.; Sotiropoulos, F. Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. J. Comput. Phys. 2008, 227, 7587–7620. [Google Scholar] [CrossRef] [PubMed]
- Bottom II, R.; Borazjani, I.; Blevins, E.; Lauder, G. Hydrodynamics of swimming in stingrays: numerical simulations and the role of the leading-edge vortex. J. Fluid Mech. 2016, 788, 407–443. [Google Scholar] [CrossRef]
- Daghooghi, M.; Borazjani, I. The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomimetics 2015, 10, 056018. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Sotiropoulos, F. A numerical method for solving the 3D unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 2007, 225, 1782–1809. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; Siam: Philadelphia, PA, USA, 2003; Volume 82. [Google Scholar]
- Balay, S.; Buschelman, K.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; Smith, B.F.; Zhang, H. PETSc Web Page 2001. Available online: http://www.mcs.anl.gov/petsc (accessed on 12 February 2016).
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Borazjani, I. Reducing flow separation of an inclined plate via travelling waves. J. Fluid Mech. 2019, 880, 831–863. [Google Scholar] [CrossRef]
- Akbarzadeh, A.M.; Borazjani, I. Large eddy simulations of a turbulent channel flow with a deforming wall undergoing high steepness traveling waves. Phys. Fluids 2019, 31, 125107. [Google Scholar] [CrossRef]
- Borazjani, I.; Daghooghi, M. The fish tail motion forms an attached leading edge vortex. Proc. R. Soc. B 2013, 280, 2012–2071. [Google Scholar] [CrossRef]
- Borazjani, I.; Akbarzadeh, A. Large Eddy Simulations of Flows with Moving Boundaries: In Modeling and Simulation of Turbulent Mixing and Reaction; Springer: Singapore, 2020; pp. 201–225. [Google Scholar]
- Akbarzadeh, A.; Borazjani, I. A numerical study on controlling flow separation via surface morphing in the form of backward traveling waves. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3589. [Google Scholar]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of anguilliform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2009, 212, 576–592. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef]
- Borazjani, I. Numerical Simulations of Fluid-Structure Interaction Problems in Biological Flows; University of Minnesota: Minneapolis, MN, USA, 2008. [Google Scholar]
- Hunt, J.C.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows; CTR-S88; Center for Turbulence Research Report; Stanford Univ.: Stanford, CA, USA, 1988; p. 193. [Google Scholar]
- Shen, L.; Zhang, X.; Yue, D.K.; Triantafyllou, M.S. Turbulent flow over a flexible wall undergoing a streamwise travelling wave motion. J. Fluid Mech. 2003, 484, 197–221. [Google Scholar] [CrossRef]
- Müller, U.; Van Den Heuvel, B.; Stamhuis, E.; Videler, J. Fish foot prints: morphology and energetics of the wake behind a continuously swimming mullet (Chelon labrosus Risso). J. Exp. Biol. 1997, 200, 2893–2906. [Google Scholar]
- Sackton, T.B.; Lazzaro, B.P.; Schlenke, T.A.; Evans, J.D.; Hultmark, D.; Clark, A.G. Dynamic evolution of the innate immune system in Drosophila. Nat. Genet. 2007, 39, 1461. [Google Scholar] [CrossRef] [PubMed]
- Schlichting, H.; Gersten, K.; Krause, E.; Oertel, H.; Mayes, K. Boundary-Layer Theory; Springer: New York, NY, USA, 1968; Volume 7. [Google Scholar]
- Aleyev, Y.G. Nekton; Dr W: The Hague, The Netherlands, 1977. [Google Scholar]
- Donatelli, C.M.; Summers, A.P.; Tytell, E.D. Long-axis twisting during locomotion of elongate fishes. J. Exp. Biol. 2017, 220, 3632–3640. [Google Scholar] [CrossRef]

| Swimming Conditions | |||
|---|---|---|---|
| Near ground swimming | 19.92% | ||
| Free swimming | 20.73% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogunka, U.E.; Daghooghi, M.; Akbarzadeh, A.M.; Borazjani, I. The Ground Effect in Anguilliform Swimming. Biomimetics 2020, 5, 9. https://doi.org/10.3390/biomimetics5010009
Ogunka UE, Daghooghi M, Akbarzadeh AM, Borazjani I. The Ground Effect in Anguilliform Swimming. Biomimetics. 2020; 5(1):9. https://doi.org/10.3390/biomimetics5010009
Chicago/Turabian StyleOgunka, Uchenna E., Mohsen Daghooghi, Amir M. Akbarzadeh, and Iman Borazjani. 2020. "The Ground Effect in Anguilliform Swimming" Biomimetics 5, no. 1: 9. https://doi.org/10.3390/biomimetics5010009
APA StyleOgunka, U. E., Daghooghi, M., Akbarzadeh, A. M., & Borazjani, I. (2020). The Ground Effect in Anguilliform Swimming. Biomimetics, 5(1), 9. https://doi.org/10.3390/biomimetics5010009






