Hydrodynamics of Vortex Generation during Bell Contraction by the Hydromedusa Eutonina indicans (Romanes, 1876)
Abstract
1. Introduction
2. Materials and Methods
3. Results
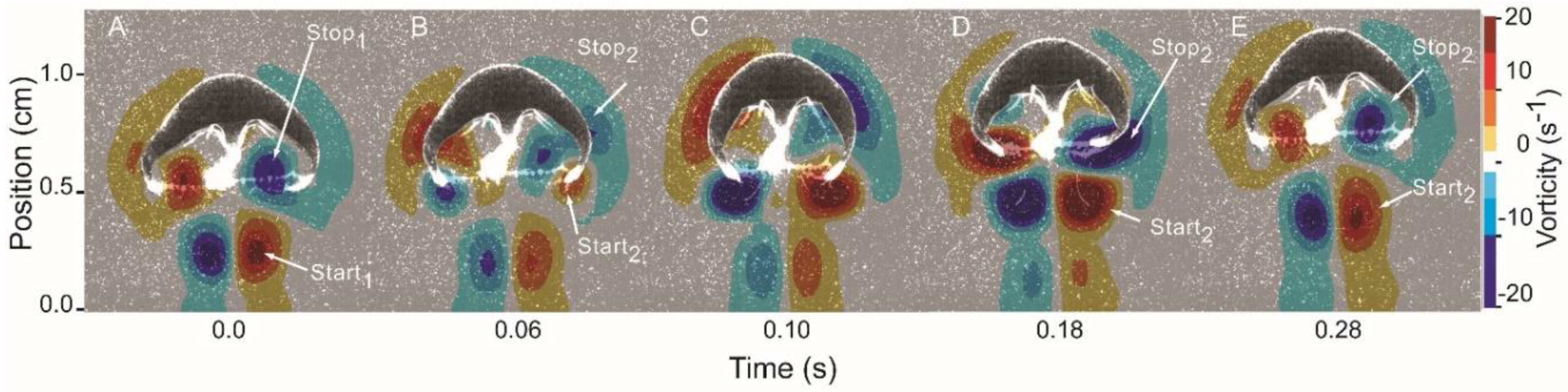
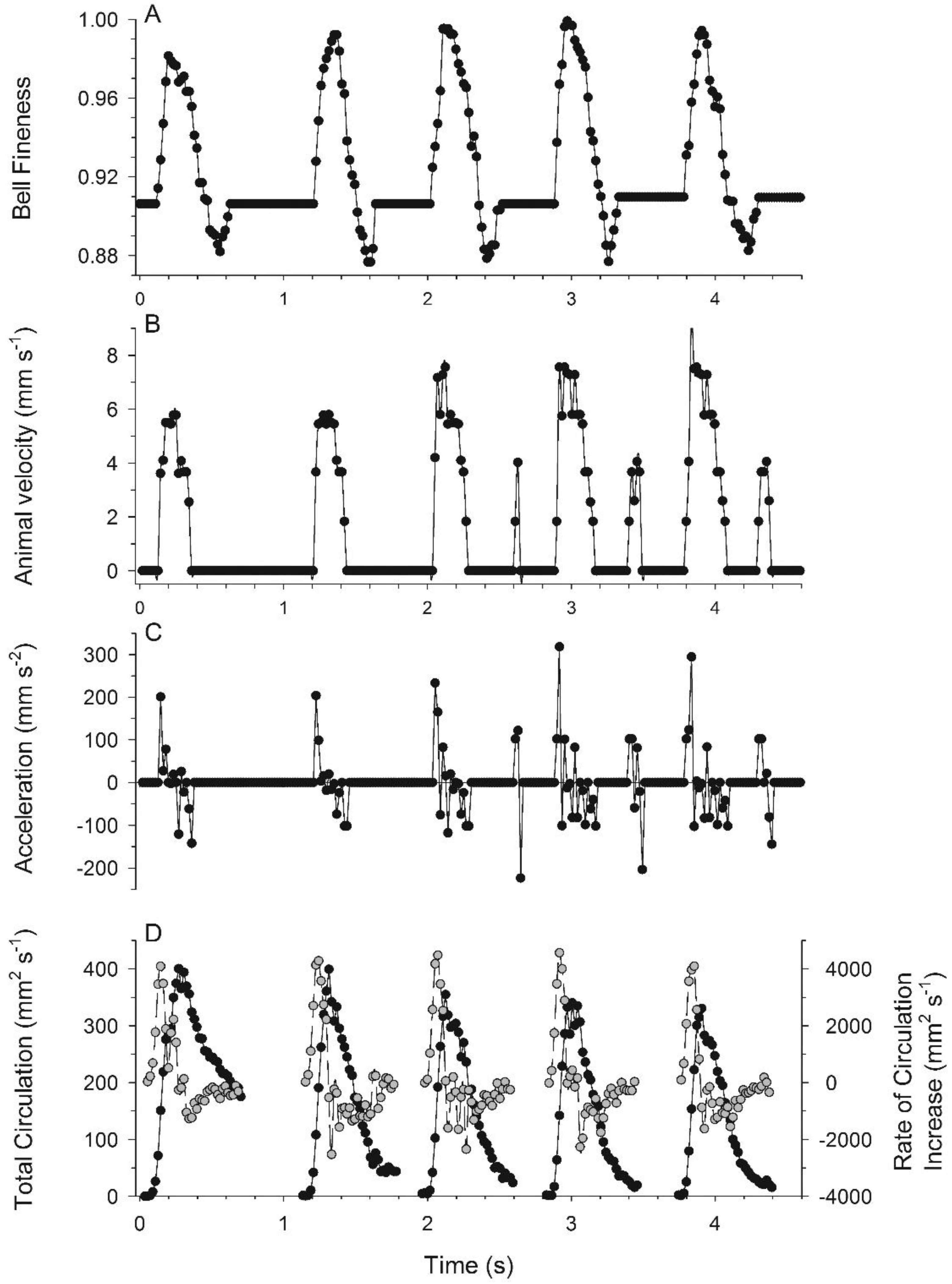
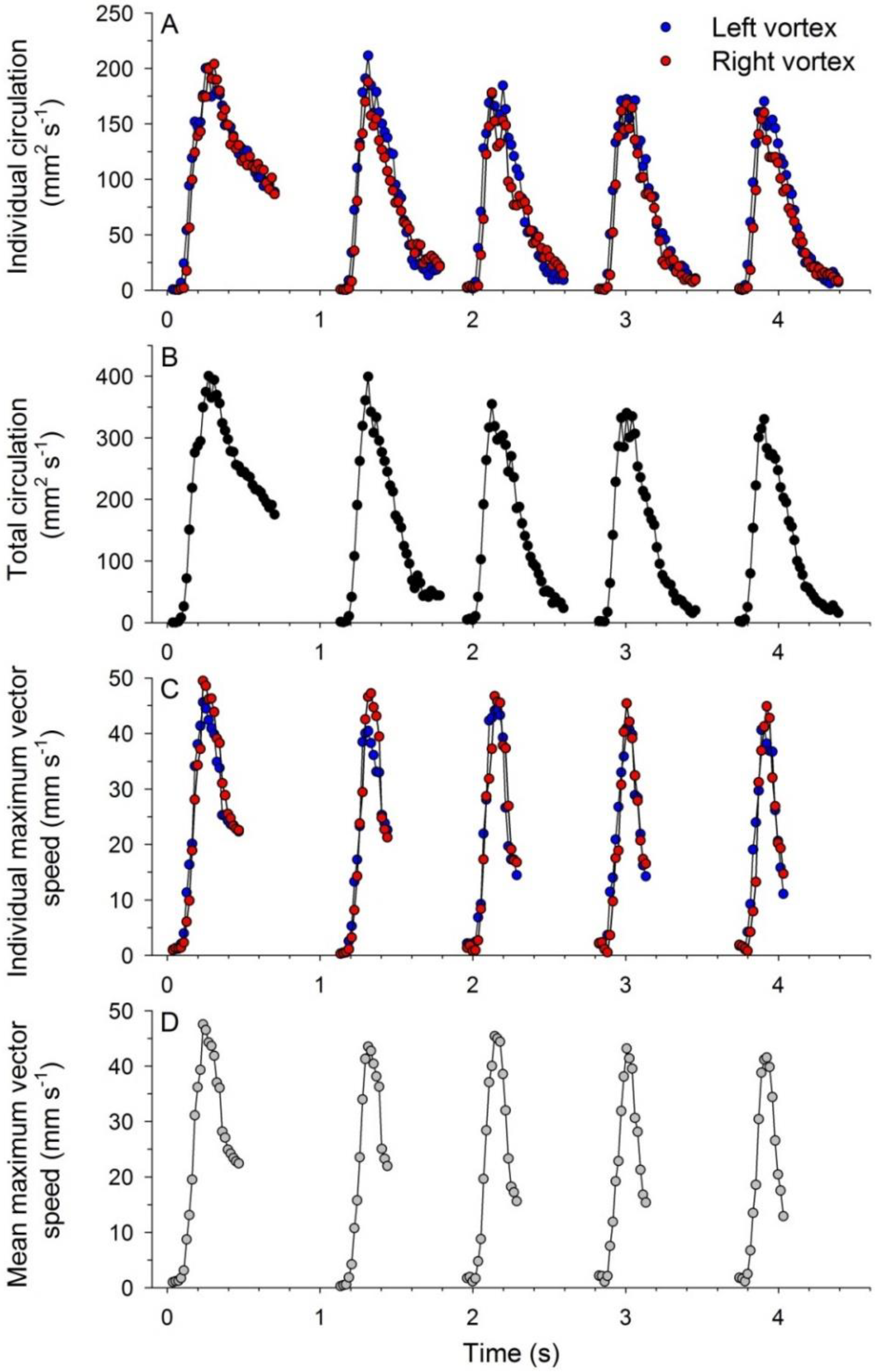
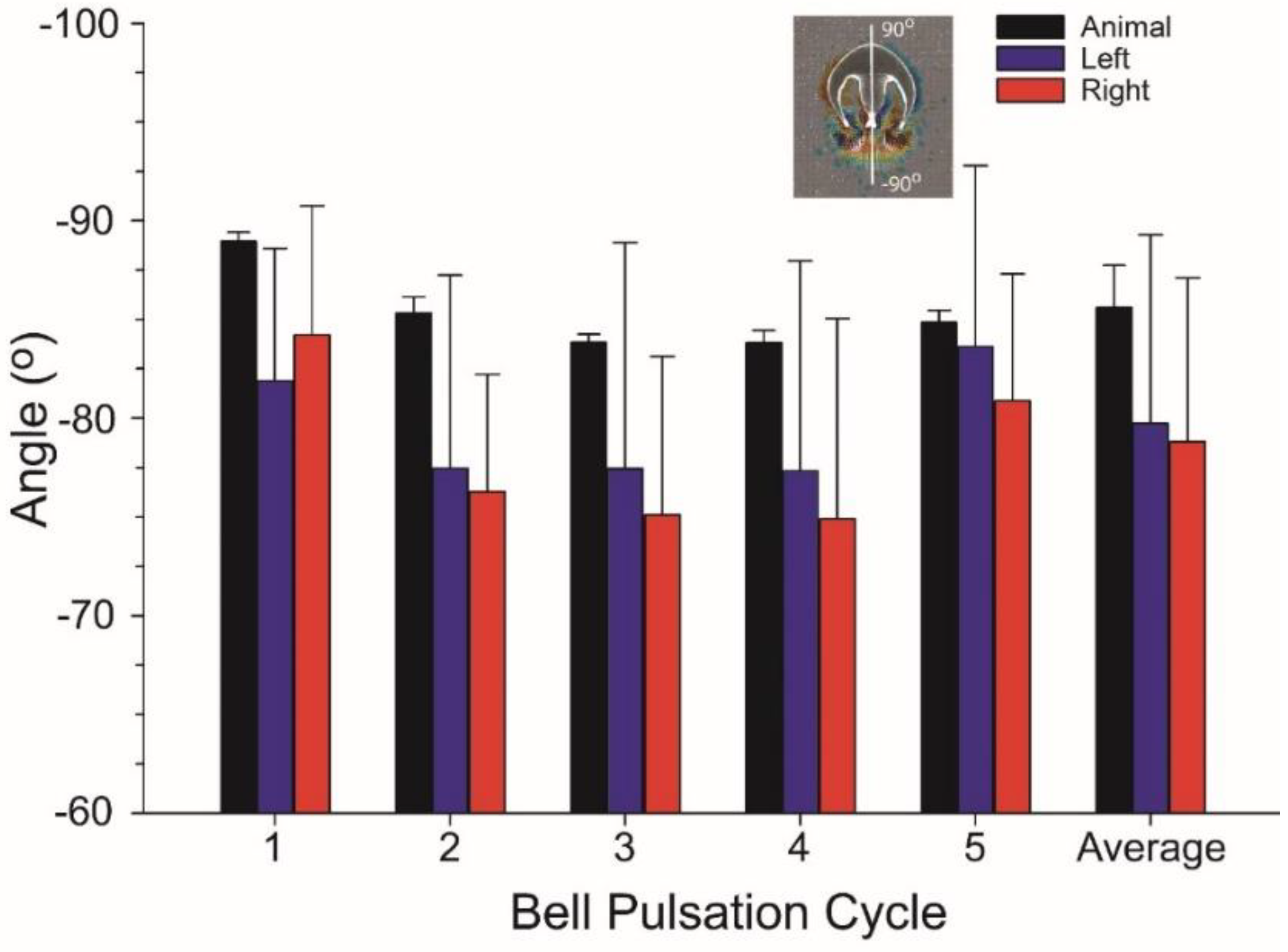
3.1. Body Kinematics and Vortex Development
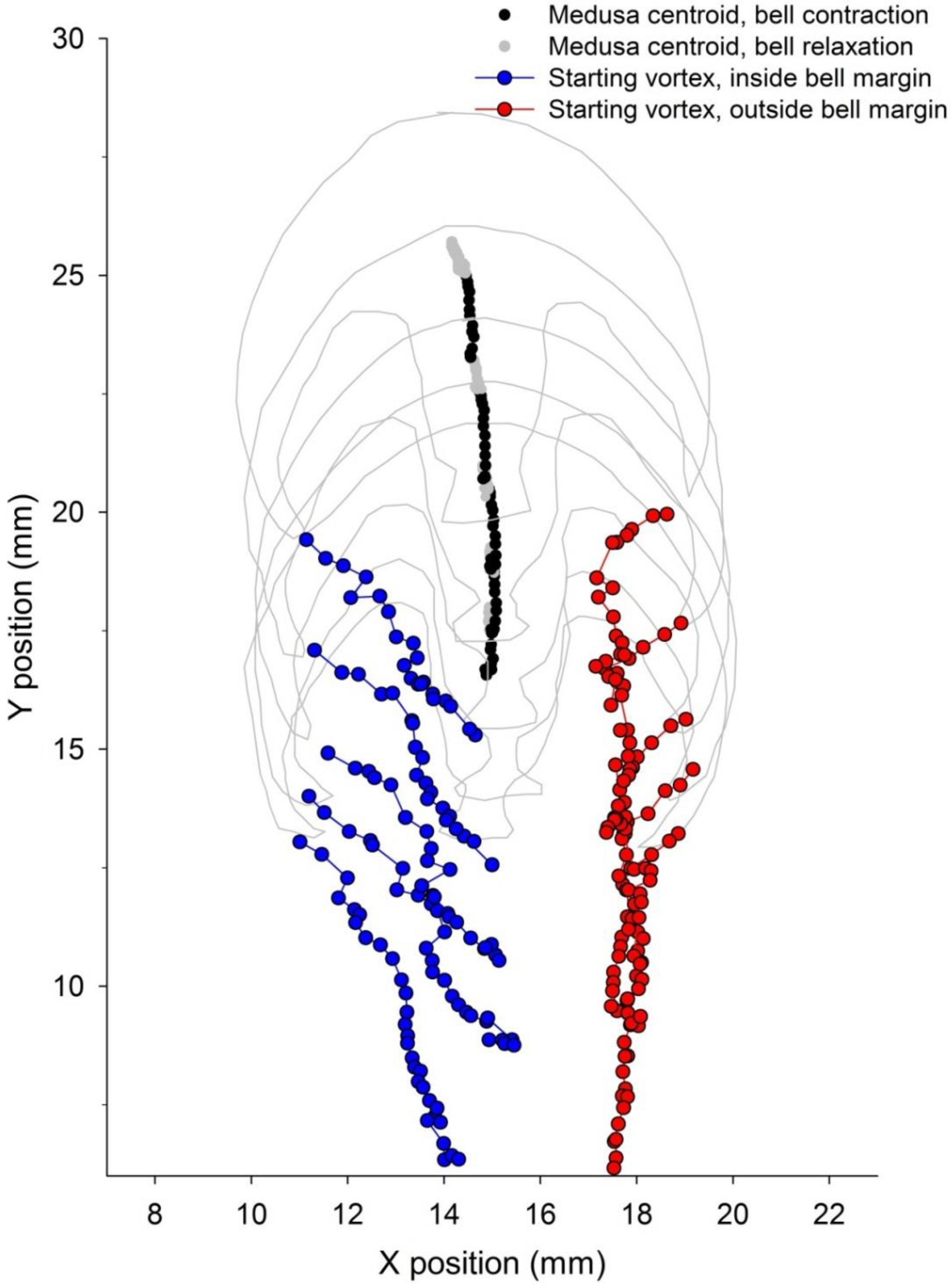
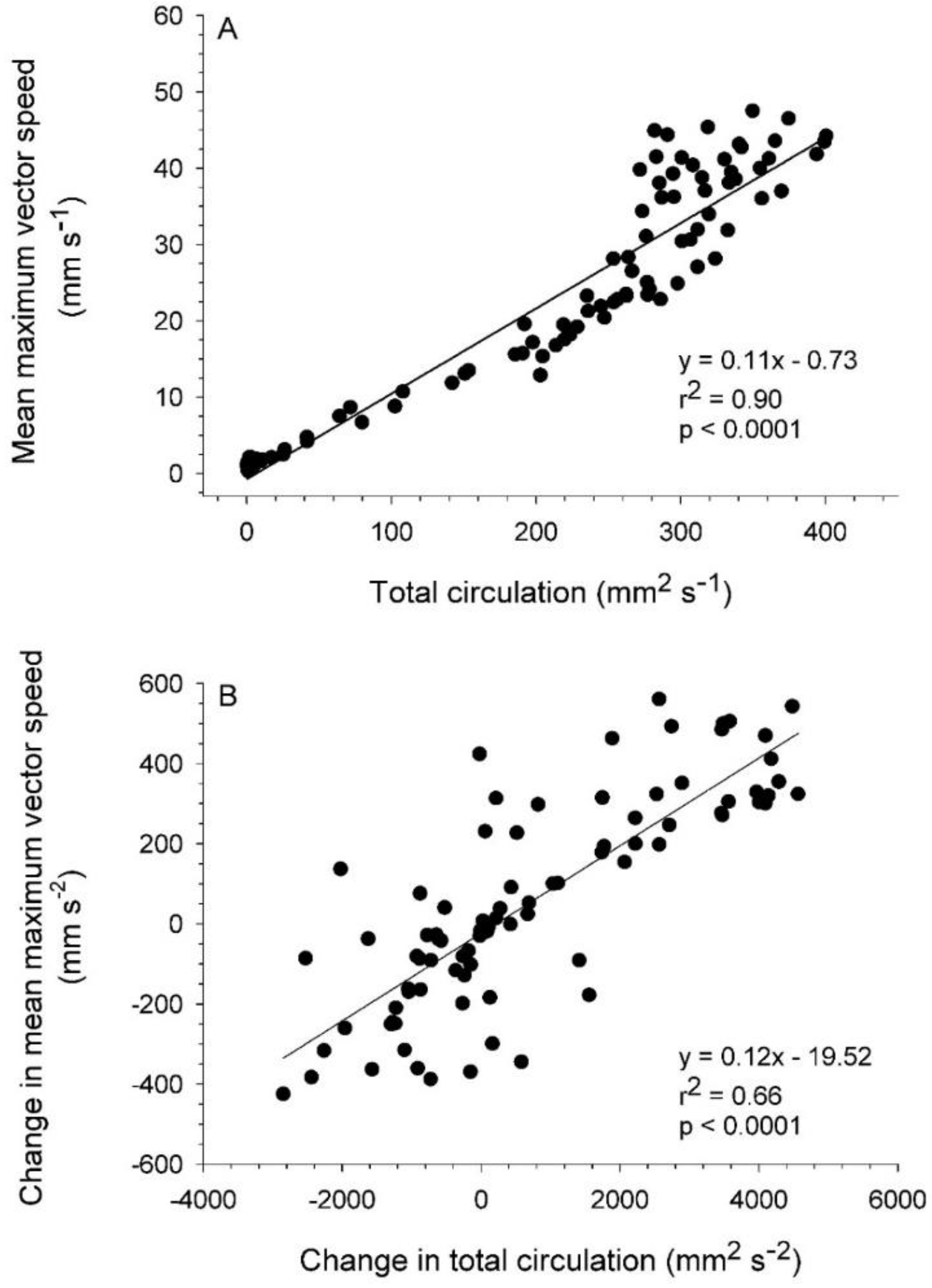
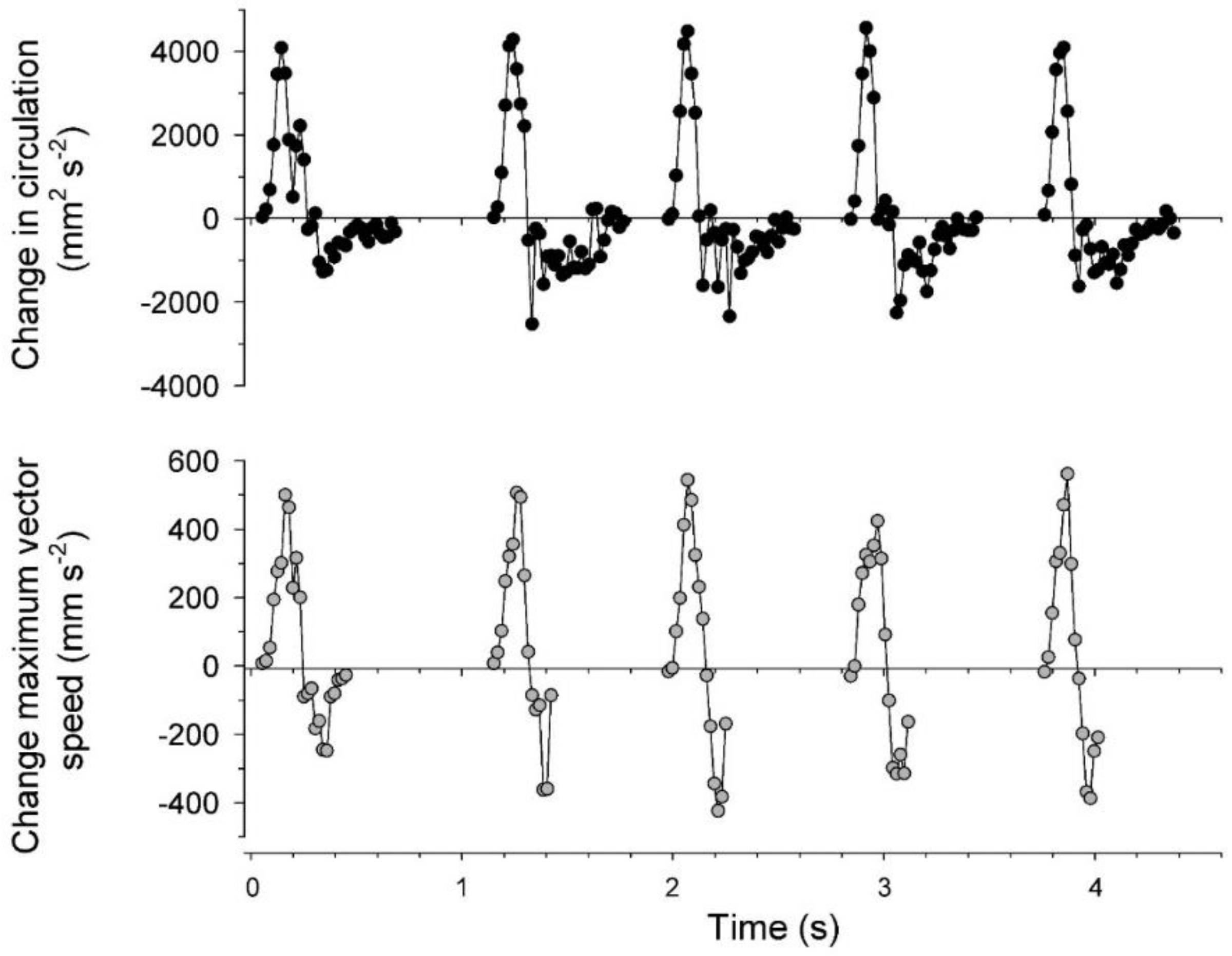
3.2. Vortex Interactions, Momentum Transfer, and Body Motion
4. Discussion
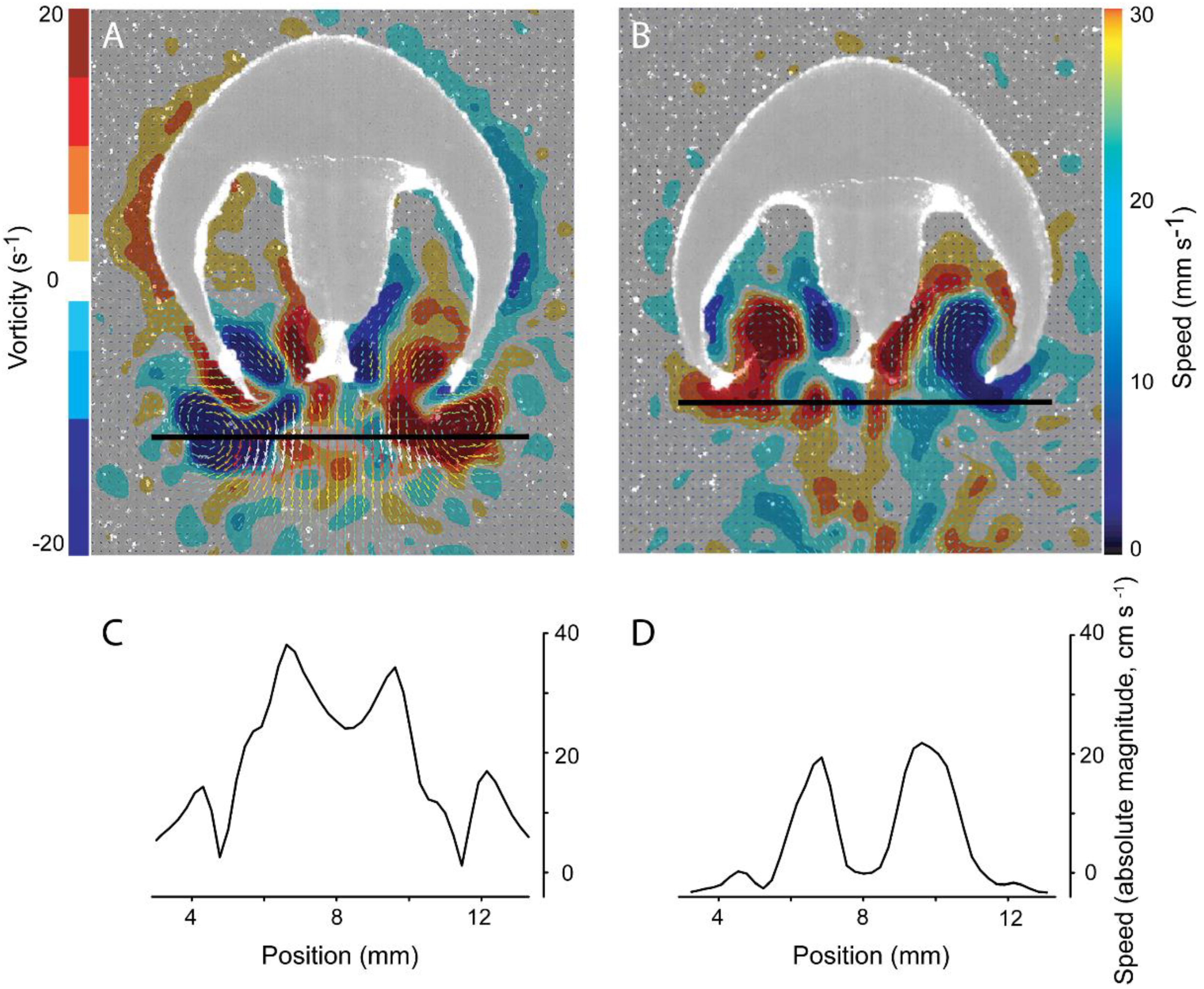
4.1. Evaluation of Thrust Estimation Methods
4.2. Mechanical Basis of Jet Thrust Production
Author Contributions
Funding
Conflicts of Interest
References
- Dunn, C.W.; Hejnol, A.; Matus, D.Q.; Pang, K.; Browne, W.E.; Smith, S.A.; Seaver, E.; Rouse, G.W.; Obst, M.; Edgecombe, G.D.; et al. Broad phylogenomic sampling improves resolution of the animal tree of life. Nature 2008, 452, 745–749. [Google Scholar] [CrossRef] [PubMed]
- Whelan, N.V.; Kocot, K.M.; Moroz, L.L.; Halanych, K.M. Error, signal, and the placement of Ctenophora sister to all other animals. Proc. Natl. Acad. Sci. USA 2015, 112, 5773–5778. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, P.; Halgedahl, S.L.; Hendricks, J.R.; Jarrard, R.D.; Marques, A.C.; Collins, A.G.; Lieberman, B.S. Exceptionally preserved jellyfishes from the Middle Cambrian. PLoS ONE 2007, 2, e1121. [Google Scholar] [CrossRef] [PubMed]
- Daniel, T.L. Mechanics and energetics of medusan jet propulsion. Can. J. Zool. 1983, 61, 1406–1420. [Google Scholar] [CrossRef]
- Colin, S.P.; Costello, J.H. Morphology, swimming performance, and propulsive mode of six co-occurring hydromedusae. J. Exp. Biol. 2002, 205, 427–437. [Google Scholar] [PubMed]
- Dabiri, J.O.; Colin, S.P.; Costello, J.H.; Gharib, M. Flow patterns generated by oblate medusan jellyfish: Field measurements and laboratory analyses. J. Exp. Biol. 2005, 208, 1257–1265. [Google Scholar] [CrossRef] [PubMed]
- Costello, J.H.; Colin, S.P.; Dabiri, J.O. The medusan morphospace: Phylogenetic constraints, biomechanical solutions and ecological consequences. Invertebr. Biol. 2008, 127, 265–290. [Google Scholar] [CrossRef]
- Colin, S.P.; Costello, J.H.; Dabiri, J.O.; Villanueva, A.; Blottman, J.B.; Gemmell, B.J.; Priya, S. Biomimetic and live medusae reveal the mechanistic advantages of a flexible bell margin. PLoS ONE 2012, 7, e48909. [Google Scholar] [CrossRef] [PubMed]
- Hoover, A.P.; Griffith, B.E.; Miller, L.A. Quantifying performance in the medusan mechanospace with an actively swimming three-dimensional jellyfish model. J. Fluid Mech. 2017, 813, 1112–1155. [Google Scholar] [CrossRef]
- Triantafyllou, G.S.; Triantafyllou, M.S.; Grosenbaugh, M.A. Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Lauder, G.V.; Tytell, E.D. Hydrodynamics of undulatory propulsion. In Fish Biomechanics; Shadwick, R.E., Lauder, G.V., Eds.; Academic Press: San Diego, CA, USA, 2006; pp. 425–468. [Google Scholar]
- Rayner, J.M.V. Vortex theory of animal flight. J. Exp. Biol. 1979, 91, 697–796. [Google Scholar]
- Hedenstrom, A.; Johansson, L.C.; Wolf, M.; von Busse, R.; Winter, Y.; Spedding, G.R. Bat flight generates complex aerodynamic tracks. Science 2007, 316, 894–897. [Google Scholar] [CrossRef] [PubMed]
- Dabiri, J.O.; Colin, S.P.; Katija, K.; Costello, J.H. A wake-based correlate of swimming performance and foraging behavior in seven co-occurring jellyfish species. J. Exp. Biol. 2010, 213, 1217–1225. [Google Scholar] [CrossRef] [PubMed]
- Colin, S.P.; Costello, J.H.; Katija, K.; Seymour, J.; Kiefer, K. Propulsion and maneuvering in cubomedusae: Mechanisms and utility. PLoS ONE 2013, 8, e56393. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming. I. Wake structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef] [PubMed]
- Stanaway, S.K.; Shariff, K.; Hussain, F. Head-on collision of viscous vortex rings. In Proceedings of the 1988 Summer Program, Mountain View, CA, USA, 1 December 1988. [Google Scholar]
- Lim, T.T.; Nickels, T.B. Instability and reconnection in the head-on collision of two vortex rings. Science 1992, 357, 225–227. [Google Scholar] [CrossRef]
- Ahlborn, B.; Chapman, S.; Stafford, R.; Blake, R.W.; Harper, D. Experimental simulation of the thrust phases of fast-start swimming of fish. J. Exp. Biol. 1997, 200, 2301–2312. [Google Scholar] [PubMed]
- Ahlborn, B.; Harper, D.; Blake, R.; Ahlborn, D.; Cam, M. Fish without footprints. J. Theor. Biol. 1991, 148, 521–533. [Google Scholar] [CrossRef]
- Wolfgang, M.J.; Anderson, J.M.; Grosenbaugh, M.A.; Yue, D.K.P.; Triantafyllou, M.S. Near-body flow dynamics in swimming fish. J. Exp. Biol. 1999, 202, 2303–2327. [Google Scholar] [PubMed]
- Li, G.; Müller, U.K.; van Leeuwen, J.L.; Liu, H. Body dynamics and hydrodynamics of swimming fish larvae: A computational study. J. Exp. Biol. 2012, 215, 4015–4033. [Google Scholar] [CrossRef] [PubMed]
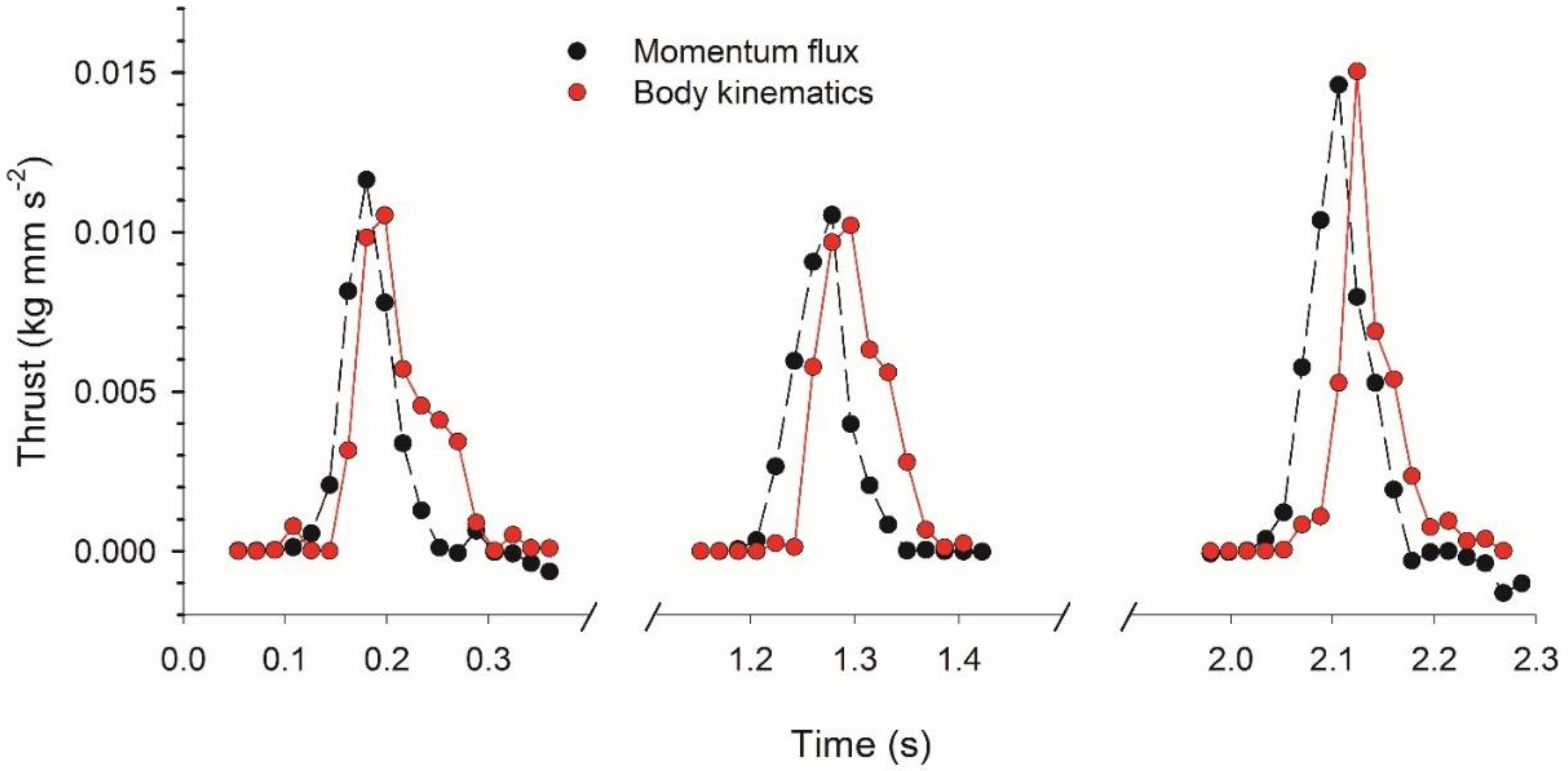
| Cycle | 1 | 2 | 3 | Average |
|---|---|---|---|---|
| Peak Force (kg mm s−2) | 0.0116 | 0.0105 | 0.0146 | 0.0122 |
| Impulse (kg mm s−1) | 0.0021 | 0.0019 | 0.0026 | 0.0022 |
| Predicted Velocity (mm s−1) | 3.7 | 3.3 | 4.6 | 3.9 |
| Observed Velocity (mm s−1) | 3.8 | 4.1 | 4.8 | 4.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costello, J.H.; Colin, S.P.; Gemmell, B.J.; Dabiri, J.O. Hydrodynamics of Vortex Generation during Bell Contraction by the Hydromedusa Eutonina indicans (Romanes, 1876). Biomimetics 2019, 4, 44. https://doi.org/10.3390/biomimetics4030044
Costello JH, Colin SP, Gemmell BJ, Dabiri JO. Hydrodynamics of Vortex Generation during Bell Contraction by the Hydromedusa Eutonina indicans (Romanes, 1876). Biomimetics. 2019; 4(3):44. https://doi.org/10.3390/biomimetics4030044
Chicago/Turabian StyleCostello, John H., Sean P. Colin, Brad J. Gemmell, and John O. Dabiri. 2019. "Hydrodynamics of Vortex Generation during Bell Contraction by the Hydromedusa Eutonina indicans (Romanes, 1876)" Biomimetics 4, no. 3: 44. https://doi.org/10.3390/biomimetics4030044
APA StyleCostello, J. H., Colin, S. P., Gemmell, B. J., & Dabiri, J. O. (2019). Hydrodynamics of Vortex Generation during Bell Contraction by the Hydromedusa Eutonina indicans (Romanes, 1876). Biomimetics, 4(3), 44. https://doi.org/10.3390/biomimetics4030044




