Fiber Embroidery of Self-Sensing Soft Actuators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Spiral Pattern Design for Embroidered Actuators
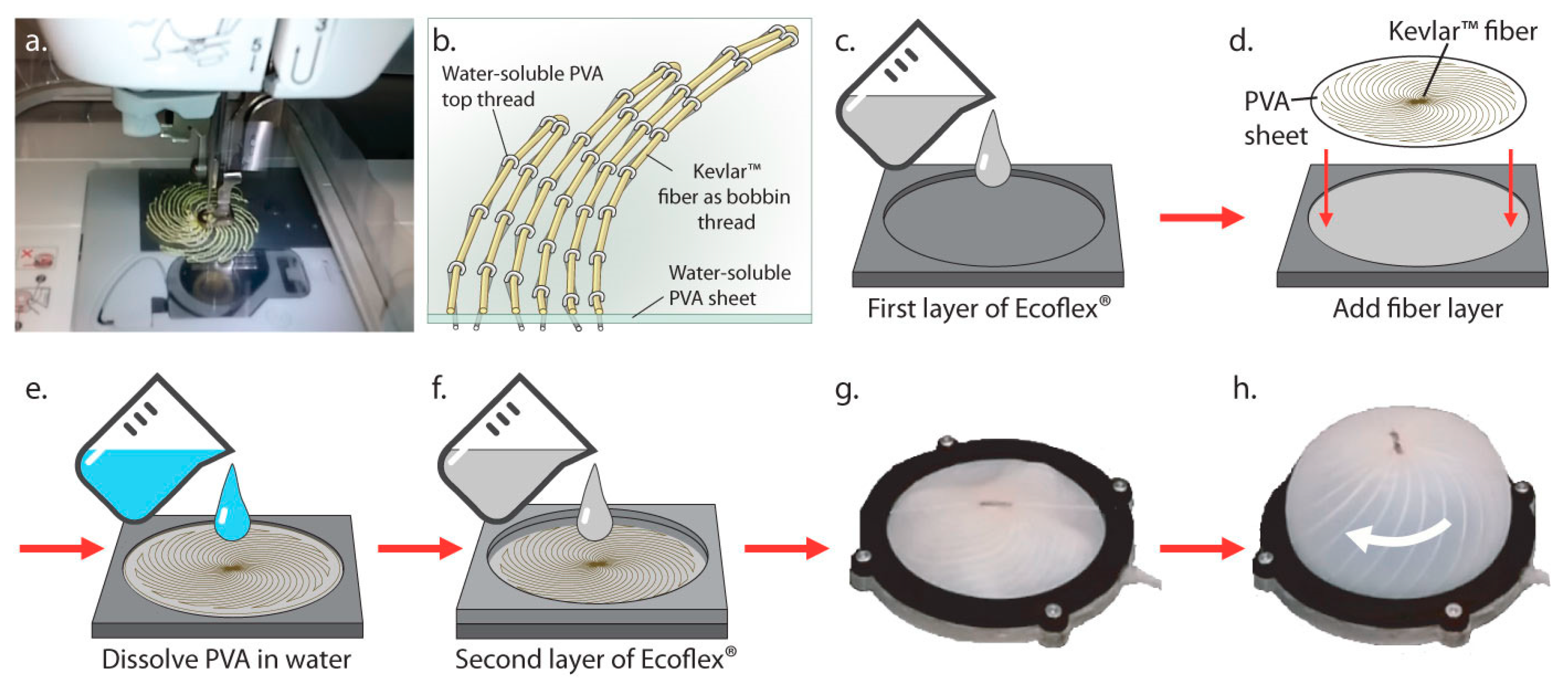
2.2. Membrane Fabrication
2.3. Testing Methods
2.3.1. Measuring Inflation of Soft Actuators
2.3.2. Rotational Motion Measurements
2.3.3. Shape Characterization
2.3.4. Torque Measurements
2.3.5. Fiber Optic Lamination and Testing
3. Actuator Model
3.1. Energy Balance
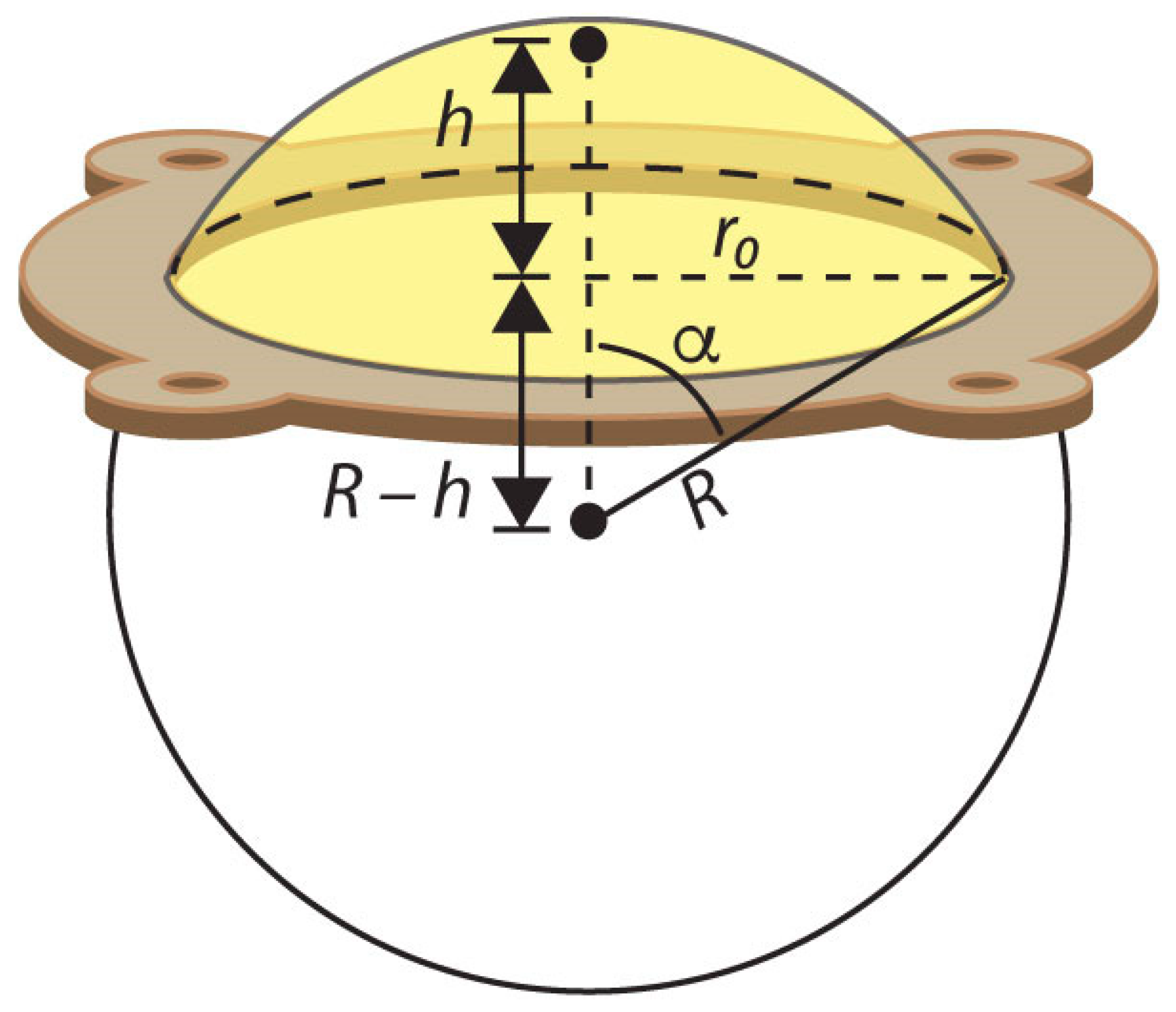
3.2. Spherical Cap Approximation
3.3. Spiral Mapping onto Spherical Cap
3.4. Values for Coefficients
3.4.1. Strain Energy
3.4.2. Shear Energy
4. Results and Discussion
4.1. Rotation Angle vs. Pressure
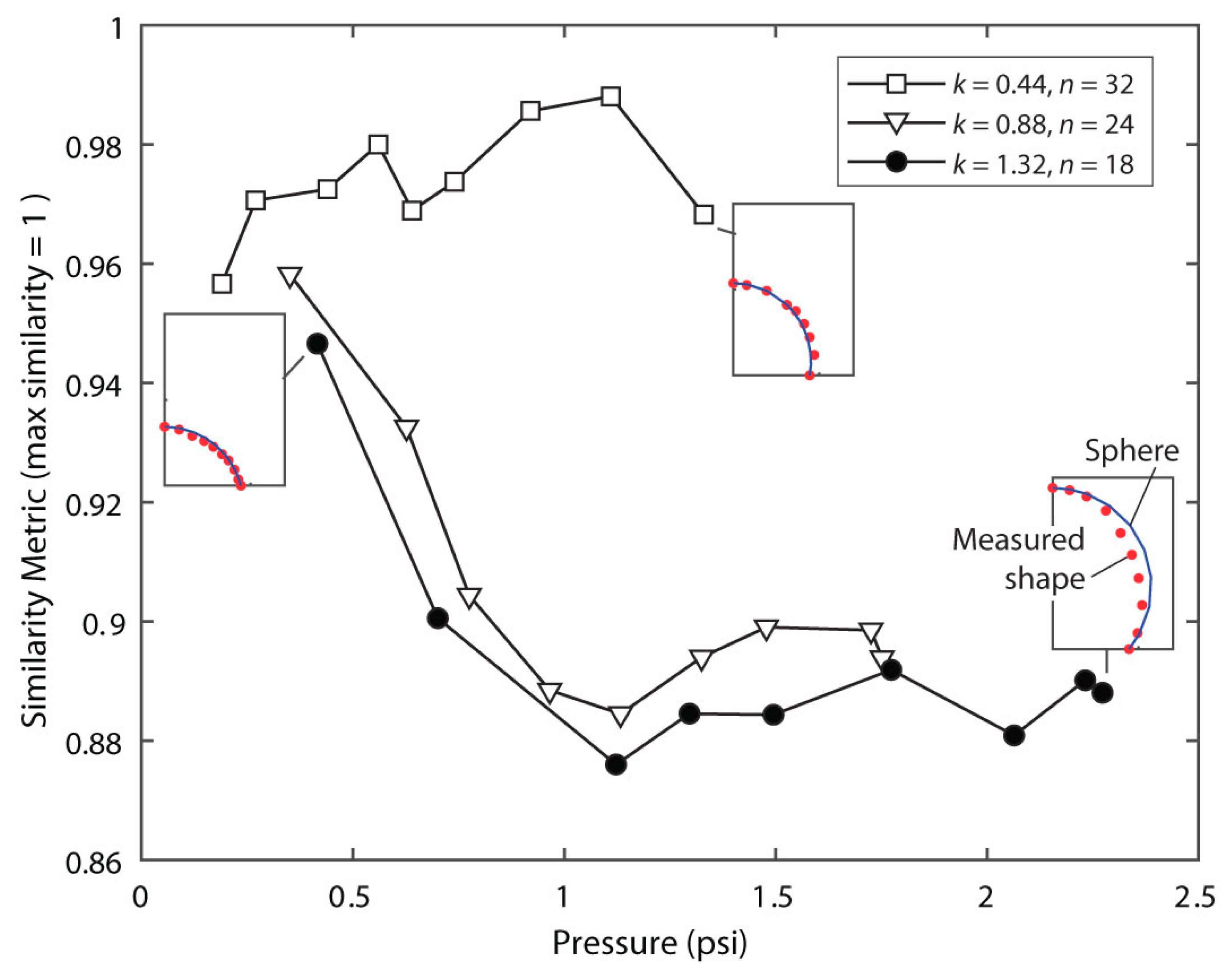
4.2. Actuator Shape Compared with Spherical Cap Model
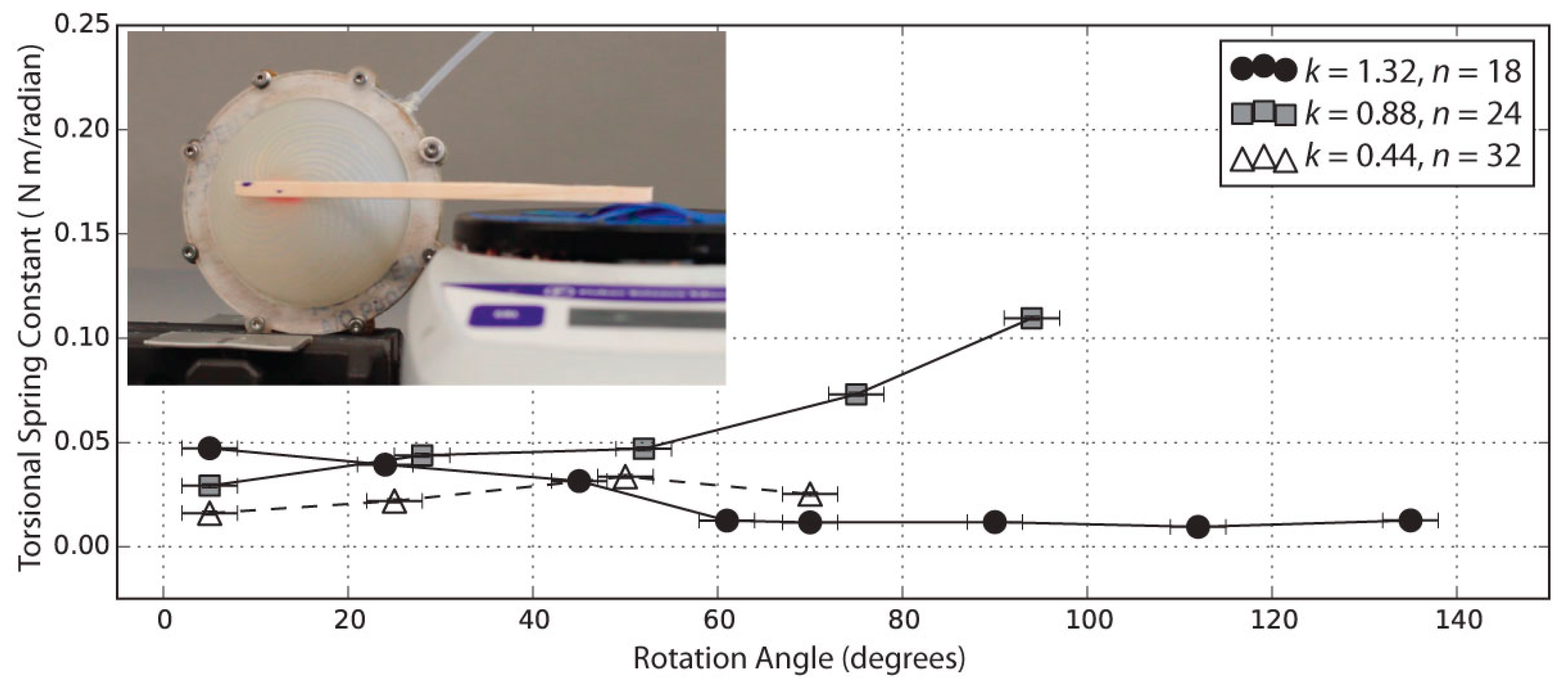
4.3. Torque Exerted by the Actuator
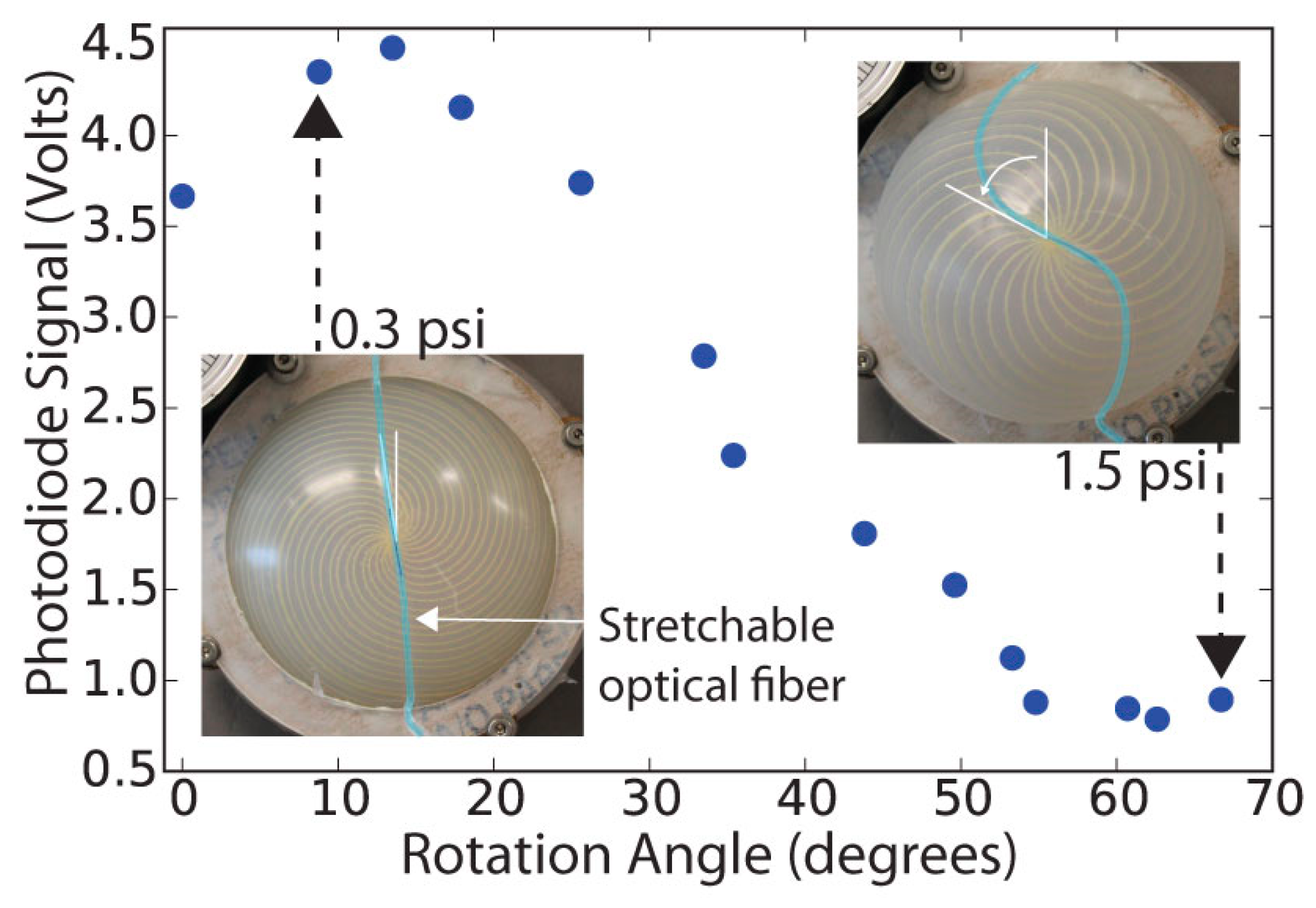
4.4. Optical Detection of Actuator State
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Leeuwen, J.L.; De Groot, J.H.; Kier, W.M. Evolutionary mechanics of protrusible tentacles and tongues. Neth. J. Zool. 2000, 50, 113–119. [Google Scholar] [CrossRef]
- Van Leeuwen, J.L.; Kier, W.M. Functional design of tentacles in squid: Linking sarcomere ultrastructure to gross morphological dynamics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1997, 352, 551–571. [Google Scholar] [CrossRef]
- Kier, W.; Leeuwen, J. A kinematic analysis of tentacle extension in the squid Loligo pealei. J. Exp. Biol. 1997, 200, 41–53. [Google Scholar] [PubMed]
- Yang, D.; Mosadegh, B.; Ainla, A.; Lee, B.; Khashai, F.; Suo, Z.; Bertoldi, K.; Whitesides, G.M. Buckling of elastomeric beams enables actuation of soft machines. Adv. Mater. 2015, 27, 6323–6327. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Niiyama, R.; Ou, J.; Follmer, S.; Della Silva, C.; Ishii, H. PneUI: Pneumatically Actuated Soft Composite Materials for Shape Changing Interfaces. In Proceedings of the 26th annual ACM symposium on User interface software and technology, St. Andrews, UK, 8–11 October 2013; pp. 13–22. [Google Scholar]
- Ainla, A.; Verma, M.S.; Yang, D.; Whitesides, G.M. Soft, rotating pneumatic actuator. Soft Robot. 2017, 4, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Stilli, A.; Grattarola, L.; Wurdemann, H.A.; Althoefer, K. Variable Stiffness Link (VSL): Toward Inherently Safe Robotic Manipulators. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4971–4976. [Google Scholar]
- Stilli, A.; Wurdemann, H.A.; Althoefer, K. A novel concept for safe, stiffness-controllable robot links. Soft Robot. 2017, 4, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Voisembert, S.; Riwan, A.; Mechbal, N.; Barraco, A. A Novel Inflatable Robot with Constant and Continuous Volume. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 5843–5848. [Google Scholar]
- Liang, X.; Yap, H.K.; Guo, J.; Yeow, R.C.H.; Sun, Y.; Chui, C.K. Design and Characterization of a Novel FabricBased Robotic Arm for Future Wearable Robot Application. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 367–372. [Google Scholar]
- Tondu, B. Modelling of the McKibben artificial muscle: A review. J. Intell. Mater. Syst. Struct. 2012, 23, 223–253. [Google Scholar] [CrossRef]
- Roche, E.T.; Wohlfarth, R.; Overvelde, J.T.B.; Vasilyev, N.V.; Pigula, F.A.; Mooney, D.J.; Bertoldi, K.; Walsh, C.J. A bioinspired soft actuated material. Adv. Mater. 2014, 26, 1200–1206. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Polygerinos, P.; Overvelde, J.T.B.; Galloway, K.C.; Bertoldi, K.; Walsh, C.J. Interaction forces of soft fiber reinforced bending actuators. IEEE/ASME Trans. Mechatron. 2016, 22, 717–727. [Google Scholar] [CrossRef]
- Connolly, F.; Polygerinos, P.; Walsh, C.J.; Bertoldi, K. Mechanical programming of soft actuators by varying fiber angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maziz, A.; Concas, A.; Khaldi, A.; Stålhand, J.; Persson, N.; Jager, E.W.H. Knitting and weaving artificial muscles. Sci. Adv. 2017, 3, e1600327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pikul, J.H.; Li, S.; Bai, H.; Hanlon, R.T.; Cohen, I.; Shepherd, R.F. Stretchable surfaces with programmable 3D texture morphing for synthetic camouflaging skins. Science 2017, 358, 210–214. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Yin, J. Design of multifunctional soft doming actuator for soft machines. Adv. Mater. Technol. 2018, 3, 1800069. [Google Scholar] [CrossRef]
- Feng, C.; Li, Q.; Zeng, Y.; Su, X.; Yu, H. 2D to 3D convertible terahertz chiral metamaterial with integrated pneumatic actuator. Opt. Express 2018, 26, 14421–14432. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, R.; Ochoa, M.; Yu, W.; Ziaie, B. A sewing-enabled stitch-and-transfer method for robust, ultra-stretchable, conductive interconnects. J. Micromech. Microeng. 2014, 24, 095018. [Google Scholar] [CrossRef]
- Harnett, C.K.; Zhao, H.; Shepherd, R.F. Stretchable optical fibers: Threads for strain-sensitive textiles. Adv. Mat. Technol. 2017, 2, 1700087. [Google Scholar] [CrossRef]
- Goulbourne, N.C.; Mockensturm, E.M.; Frecker, M.I. Electro-elastomers: Large deformation analysis of silicone membranes. Int. J. Solids Struct. 2007, 44, 2609–2626. [Google Scholar] [CrossRef]
- Feng, W.W. On axisymmetrical deformations of nonlinear membranes. J. Appl. Mech. 1970, 37, 1002–1011. [Google Scholar]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Kulkarni, P. Centrifugal Forming and Mechanical Properties of Silicone-Based Elastomers for Soft Robotic Actuators. Master’s Thesis, Rutgers University Graduate School, New Brunswick, NJ, USA, 2015; p. 26. [Google Scholar]
- Kim, D.H.; Lu, N.; Ghaffari, R.; Kim, Y.-S.; Lee, S.P.; Xu, L.; Wu, J.; Kim, R.H.; Song, J.; Liu, Z.; et al. Materials for multifunctional balloon catheters with capabilities in cardiac electrophysiological mapping and ablation therapy. Nat. Mater. 2011, 10, 316–323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thill, C.L.; Etches, J.; Bond, I.; Potter, K.; Weaver, P. Morphing skins. Aeronaut. J. 2008, 112, 117–139. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Zhang, Y.; Liu, B.; Rubinstein, S.M.; Bertoldi, K. Kirigami skins make a simple soft actuator crawl. Sci. Robot. 2018, 3, eaar7555. [Google Scholar] [CrossRef]
- Smith, M.L.; Yanega, G.M.; Ruina, A. Elastic instability model of rapid beak closure in hummingbirds. J. Theor. Biol. 2011, 282, 41–51. [Google Scholar] [CrossRef] [PubMed]

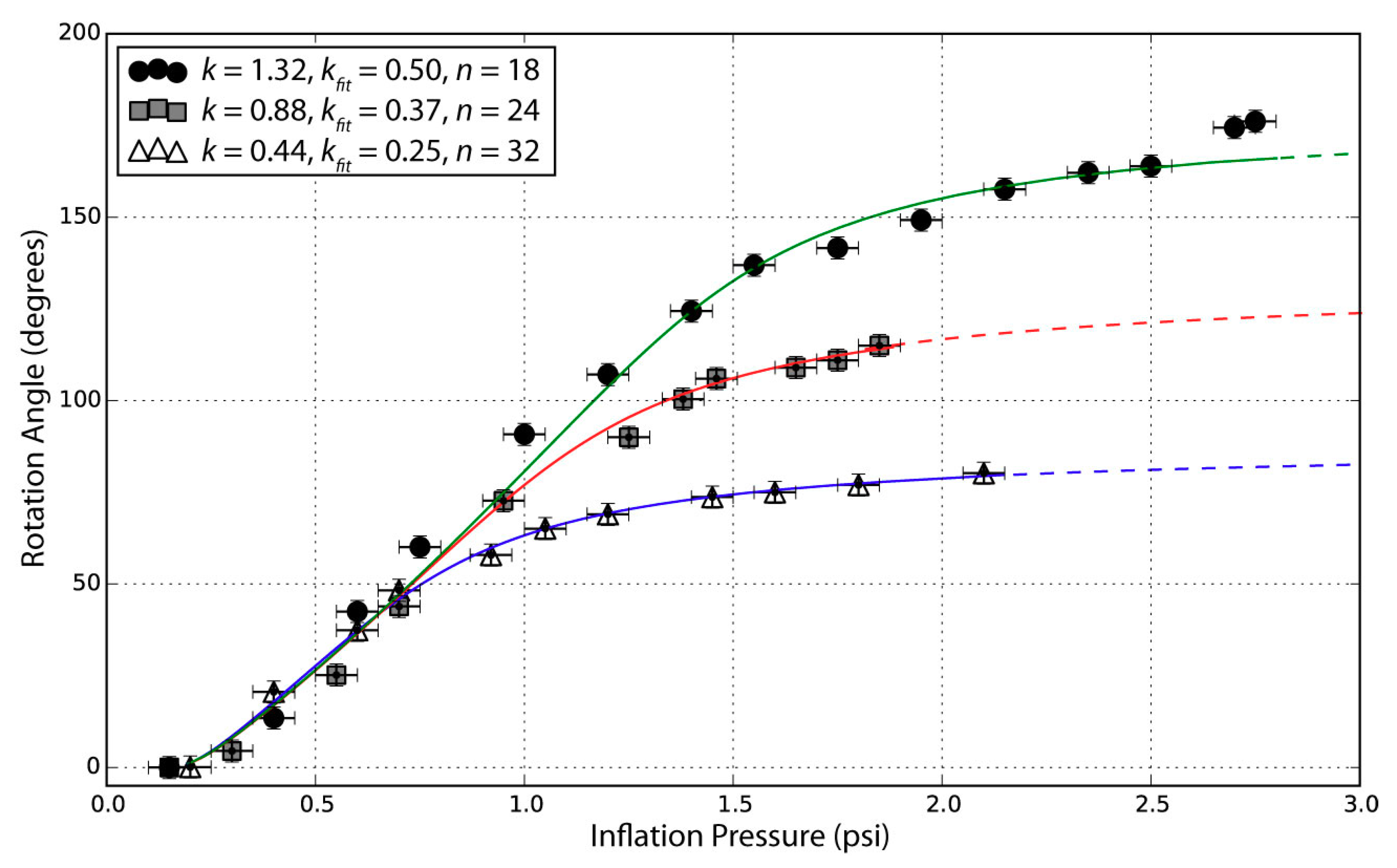
| k | n | Maximum Observed Rotation Angle (Degrees) | Pressure at Maximum Rotation (psi) |
|---|---|---|---|
| 0.44 | 32 | 80 | 2.1 |
| 0.88 | 24 | 115 | 1.85 |
| 1.32 | 18 | 176 | 2.75 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceron, S.; Cohen, I.; Shepherd, R.F.; Pikul, J.H.; Harnett, C. Fiber Embroidery of Self-Sensing Soft Actuators. Biomimetics 2018, 3, 24. https://doi.org/10.3390/biomimetics3030024
Ceron S, Cohen I, Shepherd RF, Pikul JH, Harnett C. Fiber Embroidery of Self-Sensing Soft Actuators. Biomimetics. 2018; 3(3):24. https://doi.org/10.3390/biomimetics3030024
Chicago/Turabian StyleCeron, Steven, Itai Cohen, Robert F. Shepherd, James H. Pikul, and Cindy Harnett. 2018. "Fiber Embroidery of Self-Sensing Soft Actuators" Biomimetics 3, no. 3: 24. https://doi.org/10.3390/biomimetics3030024
APA StyleCeron, S., Cohen, I., Shepherd, R. F., Pikul, J. H., & Harnett, C. (2018). Fiber Embroidery of Self-Sensing Soft Actuators. Biomimetics, 3(3), 24. https://doi.org/10.3390/biomimetics3030024






