Multi-Strategy Honey Badger Algorithm for Global Optimization
Abstract
1. Introduction
2. Fundamentals of Honey Badger Algorithm
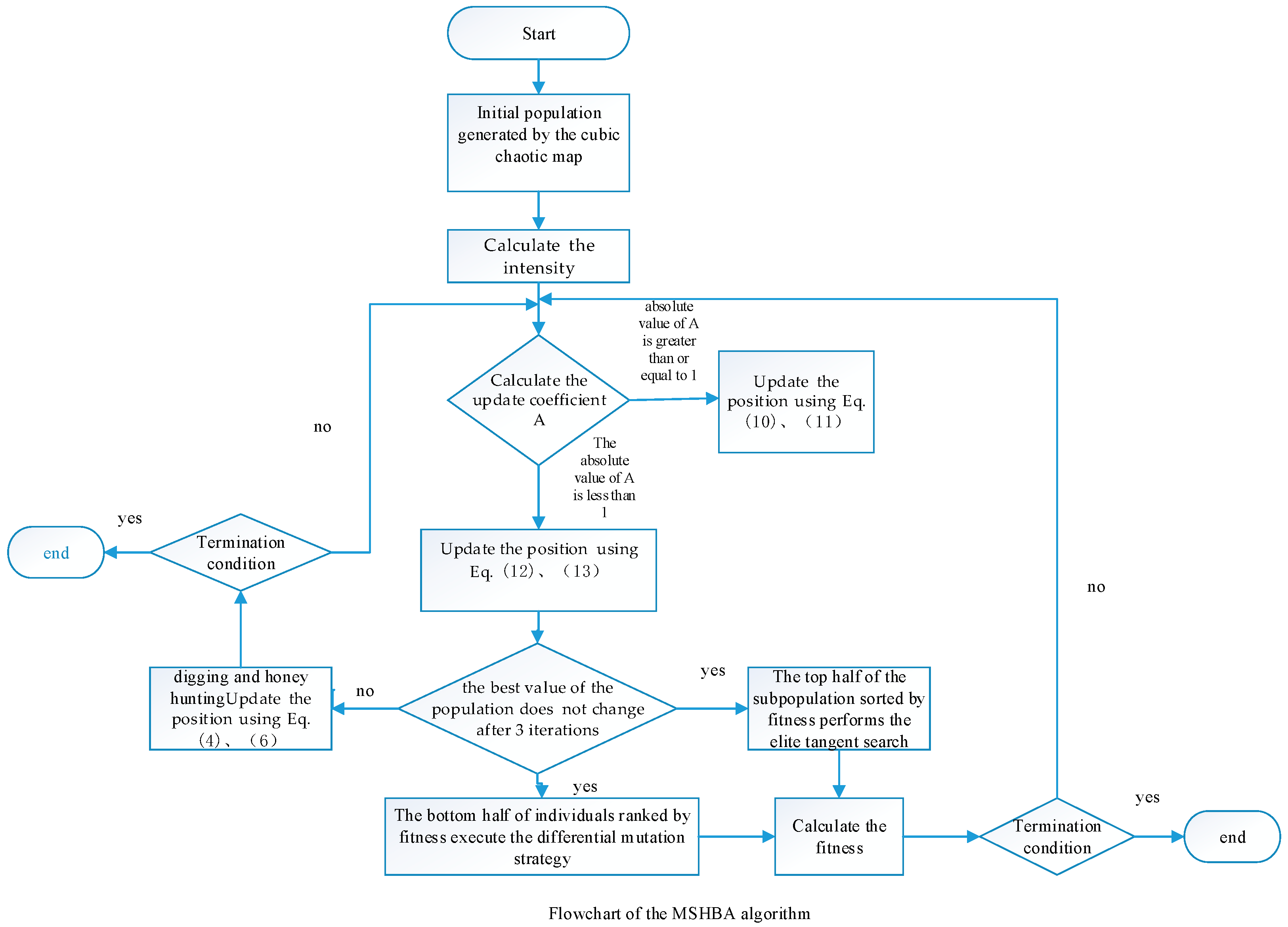
3. Multi-Strategy Honey Badger Algorithm
3.1. Cubic Chaotic Mapping
3.2. Introduction of Random Value Perturbation Strategy for Honey Badger Algorithm
3.3. Population Remains the Best Value Unchanged After Three Iterations, Elite Tangent Search and Differential Variation Strategy Are Executed
3.3.1. Migration Strategy of Elite Subpopulation
3.3.2. Exploration of Subpopulation Evolution Strategies
| Algorithm 1 Pseudo Code of MSHBA |
| Set parameters , . Initialize population using Equations (7) and (8) while do Update the decreasing factor using (3). for i = 1 to N do Calculate the intensity using Equation (2). Calculate using Equation (9). if Update the position using Equations (10) and (11). else Update the position using Equations (5) and (6). end. If the best value of the population does not change after 3 iterations The first half of the subpopulation performs the elite tangent search strategy. Update the position using Equations (12) and (13). The second half of the subpopulation performs the differential mutation strategy. Update the position using Equation (14). else digging and honey hunting Update the position using Equations (4) and (6) end If stop criteria satisfied. Output the optimal solution. else return Calculate using Equation (9). end |
4. Experimental Results and Discussion
4.1. Parameter Settings
4.2. Benchmark Testing Functions
4.3. Comparison of MSHBA Algorithm with Other Algorithms
4.4. MSHBA and Other Algorithms’ Rank-Sum Test
4.5. MSHBA and Other Algorithms of Boxplot
4.6. MSHBA for Test Function of Fitness Change Curve
5. MSHBA for Solving Classical Engineering Problems
5.1. Weight Minimization of a Speed Reducer (WMSR) [51]
5.2. Tension/Compression Spring Design (TCSD) [52]
5.3. Pressure Vessel Design (PVD) [52]
5.4. Welded Beam Design (WBD) [52]
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Houssein, E.H.; Helmy, B.E.-D.; Rezk, H.; Nassef, A.M. An enhanced archimedes optimization algorithm based on local escaping operator and orthogonal learning for PEM fuel cell parameter identification. Eng. Appl. Artif. Intell. 2021, 103, 104309. [Google Scholar] [CrossRef]
- Houssein, E.H.; Mahdy, M.A.; Fathy, A.; Rezk, H. A modified marine predator algorithm based on opposition based learning for tracking the global MPP of shaded PV system. Expert Syst. Appl. 2021, 183, 115253. [Google Scholar] [CrossRef]
- James, C. Introduction to Stochastics Search and Optimization; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Parejo, J.A.; Ruiz-Cortés, A.; Lozano, S.; Fernandez, P. Metaheuristic optimization frameworks: A survey and benchmarking. Soft Comput. 2012, 16, 527–561. [Google Scholar] [CrossRef]
- Hassan, M.H.; Houssein, E.H.; Mahdy, M.A.; Kamel, S. An improved manta ray foraging optimizer for cost-effective emission dispatch problems. Eng. Appl. Artif. Intell. 2021, 100, 104–155. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Houssein, E.H.; Hassanien, A.E.; Taha, A.; Hassanien, E. Maximizing lifetime of large-scale wireless sensor networks using multi-objective whale optimization algorithm. Telecommun. Syst. 2019, 72, 243–259. [Google Scholar] [CrossRef]
- Houssein, E.H.; Helmy, B.E.-D.; Oliva, D.; Elngar, A.A.; Shaban, H. A novel black widow optimization algorithm for multilevel thresholding image segmentation. Expert Syst. Appl. 2021, 167, 114159. [Google Scholar] [CrossRef]
- Hussain, K.; Neggaz, N.; Zhu, W.; Houssein, E.H. An efficient hybrid sine-cosine harris hawks optimization for low and high-dimensional feature selection. Expert Syst. Appl. 2021, 176, 114778. [Google Scholar] [CrossRef]
- Neggaz, N.; Houssein, E.H.; Hussain, K. An efficient henry gas solubility optimization for feature selection. Expert Syst. Appl. 2020, 152, 113364. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Kilany, M.; Houssein, E.H.; AlQaheri, H. Intelligent human emotion recognition based on elephant herding optimization tuned support vector regression. Biomed. Signal Process. Control 2018, 45, 182–191. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. A modified henry gas solubility optimization for solving motif discovery problem. Neural Comput. Appl. 2019, 32, 10759–10771. [Google Scholar] [CrossRef]
- Sadollah, A.; Sayyaadi, H.; Yadav, A. A dynamic metaheuristic optimization model inspired by biological nervous systems: Neural network algorithm. Appl. Soft Comput. 2018, 71, 747–782. [Google Scholar] [CrossRef]
- Qin, F.; Zain, A.M.; Zhou, K.-Q. Harmony search algorithm and related variants: A systematic review. Swarm Evol. Comput. 2022, 74, 101126. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Geem, Z.W. A Comprehensive Survey of the Harmony Search Algorithm in Clustering Applications. Appl. Sci. 2020, 10, 3827. [Google Scholar] [CrossRef]
- Rajeev, S.; Krishnamoorthy, C.S. Discrete optimization of structures using genetic algorithms. J. Struct. Eng. 1992, 118, 1233–1250. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Houssein, E.H.; Rezk, H.; Fathy, A.; Mahdy, M.A.; Nassef, A.M. A modified adaptive guided differential evolution algorithm applied to engineering applications. Eng. Appl. Artif. Intell. 2022, 113, 104920. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Priya, R.D.; Sivaraj, R.; Anitha, N.; Devisurya, V. Tri-staged feature selection in multi-class heterogeneous datasets using memetic algorithm and cuckoo search optimization. Expert Syst. Appl. 2022, 209, 118286. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization-Artificial ants as a computational intelligence technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Zhao, D.; Lei, L.; Yu, F.; Heidari, A.A.; Wang, M.; Oliva, D.; Muhammad, K.; Chen, H. Ant colony optimization with horizontal and vertical crossover search: Fundamental visions for multi-threshold image segmentation. Expert. Syst. Appl. 2021, 167, 114122. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Ma, M.; Wu, J.; Shi, Y.; Yue, L.; Yang, C.; Chen, X. Chaotic Random Opposition-Based Learning and Cauchy Mutation Improved Moth-Flame Optimization Algorithm for Intelligent Route Planning of Multiple UAVs. IEEE Access 2022, 10, 49385–49397. [Google Scholar] [CrossRef]
- Yu, X.; Wu, X. Ensemble grey wolf Optimizer and its application for image segmentation. Expert Syst. Appl. 2022, 209, 118267. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. Artificialgorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Ali, A.A.; Shaban, H. An efficient multi-objective gorilla troops optimizer for minimizing energy consumption of large-scale wireless sensor networks. Expert Syst. Appl. 2023, 212, 118827. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Beşkirli, M. A novel Invasive Weed Optimization with levy flight for optimization problems: The case of forecasting energy demand. Energy Rep. 2022, 8 (Suppl. S1), 1102–1111. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, L.; Lin, Y.; Hei, X.; Yu, G.; Lu, X. An efficient multi-objective artificial raindrop algorithm and its application to dynamic optimization problems in chemical processes. Appl. Soft Comput. 2017, 58, 354–377. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hosney, M.E.; Mohamed, W.M.; Ali, A.A.; Younis, E.M.G. Fuzzy-based hunger games search algorithm for global optimization and feature selection using medical data. Neural Comput. Appl. 2022, 35, 5251–5275. [Google Scholar] [CrossRef]
- Houssein, E.H.; Oliva, D.; Çelik, E.; Emam, M.M.; Ghoniem, R.M. Boosted sooty tern optimization algorithm for global optimization and feature selection. Expert Syst. Appl. 2023, 113, 119015. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X.; Wei, G. An enhanced black widow optimization algorithm for feature selection. Knowl.-Based Syst. 2022, 235, 107638. [Google Scholar] [CrossRef]
- Abualigah, L.; Almotairi, K.H.; Elaziz, M.A. Multilevel thresholding image segmentation using meta-heuristic optimization algorithms: Comparative analysis, open challenges and new trends. Appl. Intell. 2022, 53, 11654–11704. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hussain, K.; Abualigah, L.; Elaziz, M.A.; Alomoush, W.; Dhiman, G.; Djenouri, Y.; Cuevas, E. An improved opposition-based marine predators algorithm for global optimization and multilevel thresholding image segmentation. Knowl.-Based Syst. 2021, 229, 107348. [Google Scholar] [CrossRef]
- Sharma, P.; Dinkar, S.K. A Linearly Adaptive Sine–Cosine Algorithm with Application in Deep Neural Network for Feature Optimization in Arrhythmia Classification using ECG Signals. Knowl. Based Syst. 2022, 242, 108411. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, X.; Fang, G.; Xu, Y.-P. Many-objective optimization with improved shuffled frog leaping algorithm for inter-basin water transfers. Adv. Water Resour. 2020, 138, 103531. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Panigrahi, B.K. A hybridization of an improved particle swarm optimization and gravitational search algorithm for multi-robot path planning. Swarm Evol. Comput. 2016, 28, 14–28. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, N.; Wang, X.; Li, M. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst. Appl. 2022, 215, 119327. [Google Scholar] [CrossRef]
- Gao, D.; Wang, G.-G.; Pedrycz, W. Solving fuzzy job-shop scheduling problem using DE algorithm improved by a selection mechanism. IEEE Trans. Fuzzy Syst. 2020, 28, 3265–3275. [Google Scholar] [CrossRef]
- Dong, Z.R.; Bian, X.Y.; Zhao, S. Ship pipe route design using improved multi-objective ant colony optimization. Ocean. Eng. 2022, 258, 111789. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J.; Li, M.; Hussien, A.G.; Abbas, M. EJS: Multi-strategy enhanced jellyfish search algorithm for engineering applications. Mathematics 2023, 11, 851. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Yazdani, M.; Jolai, F. Lion optimization algorithm (LOA): A nature-inspired metaheuristic algorithm. J. Comput. Des. Eng. 2016, 3, 24–36. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Lochert, C.; Scheuermann, B.; Mauve, M. A Survey on congestion control for mobile ad-hoc networks. Wiley Wirel. Commun. Mob. Comput. 2007, 7, 655–676. [Google Scholar] [CrossRef]
- Zheng, J.F.; Zhan, H.W.; Huang, W.; Zhang, H.; Wu, Z.X. Development of Levy Flight and Its Application in Intelligent Optimization Algorithm. Comput. Sci. 2021, 48, 190–206. [Google Scholar]
- Pant, M.; Thangaraj, R.; Singh, V. Optimization of mechanical design problems using improved differential evolution algorithm. Int. J. Recent Trends Eng. 2009, 1, 21. [Google Scholar]
- He, X.; Zhou, Y. Enhancing the performance of differential evolution with covariance matrix self-adaptation. Appl. Soft Comput. 2018, 64, 227–243. [Google Scholar] [CrossRef]
- Yahi, A.; Bekkouche, T.; Daachi, M.E.H.; Diffellah, N. A color image encryption scheme based on 1D cubic map. Optik 2022, 249, 168290. [Google Scholar] [CrossRef]
- He, S.; Xia, X. Random perturbation subsampling for rank regression with massive data. Stat. Sci. 2024, 35, 13–28. [Google Scholar] [CrossRef]
- Ting, H.; Yong, C.; Peng, C. Improved Honey Badger Algorithm Based on Elite Tangent Search and Differential Mutation with Applications in Fault Diagnosis. Processes 2025, 13, 256. [Google Scholar] [CrossRef]


































| No. | Functions | ||
|---|---|---|---|
| Unimodal Functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 3 | Shifted and Rotated Zakharov Function | 300 | |
| Simple Multimodal Functions | 4 | Shifted and Rotated Rosenbrock’s Function | 400 |
| 5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| 6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| 7 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 9 | Shifted and Rotated Levy Function | 900 | |
| 10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid Functions | 11 | Hybrid Function 1 (N = 3) | 1100 |
| 12 | Hybrid Function 2 (N = 3) | 1200 | |
| 13 | Hybrid Function 3 (N = 3) | 1300 | |
| 14 | Hybrid Function 4 (N = 4) | 1400 | |
| 15 | Hybrid Function 5 (N = 4) | 1500 | |
| 16 | Hybrid Function 6 (N = 4) | 1600 | |
| 17 | Hybrid Function 6 (N = 5) | 1700 | |
| 18 | Hybrid Function 6 (N = 5) | 1800 | |
| 19 | Hybrid Function 6 (N = 5) | 1900 | |
| 20 | Hybrid Function 6 (N = 6) | 2000 | |
| Composition Functions | 21 | Composition Function 1 (N = 3) | 2100 |
| 22 | Composition Function 2 (N = 3) | 2200 | |
| 23 | Composition Function 3 (N = 4) | 2300 | |
| 24 | Composition Function 4 (N = 4) | 2400 | |
| 25 | Composition Function 5 (N = 5) | 2500 | |
| 26 | Composition Function 6 (N = 5) | 2600 | |
| 27 | Composition Function 7 (N = 6) | 2700 | |
| 28 | Composition Function 8 (N = 6) | 2800 | |
| 29 | Composition Function 9 (N = 3) | 2900 | |
| 30 | Composition Function 10 (N = 3) | 3000 | |
| Search Range: [−100, 100]D | |||
| Algorithm | Parameters |
|---|---|
| COA | coati number = 30 |
| = 500 | |
| HHO | harris hawk number = 30 |
| = 500 | |
| DBO | dung beetle number = 30 |
| = 500 | |
| OOA | osprey number = 30 |
| = 500 | |
| HBA | honey badger number = 30 |
| = 500, | |
| MSHBA | honey badger number = 30 |
| = 500, |
| Function | Index | MSHBA | HBA | COA | DBO | OOA | HHO |
|---|---|---|---|---|---|---|---|
| F1 | min | 36,332.21327 | 75,683.73185 | 44,680,368,018 | 24,217,484,929 | 42,002,907,856 | 100,012,066.4 |
| F1 | std | 16,173,366.95 | 168,770,925.9 | 7,033,529,135 | 4,766,539,484 | 8,294,013,405 | 345,955,374.9 |
| F1 | avg | 4,000,756.794 | 33,619,961.06 | 59,731,161,880 | 32,021,958,760 | 56,223,524,199 | 439,575,119.5 |
| F1 | median | 601,797.5757 | 675,483.5145 | 59,521,568,792 | 31,651,854,438 | 55,292,058,030 | 359,305,702.1 |
| F1 | worse | 89,307,263.31 | 925,953,472.7 | 70,695,016,541 | 45,351,521,182 | 69,887,934,634 | 1,665,291,319 |
| F3 | min | 8168.289781 | 19,637.28281 | 79,071.67443 | 66,751.90092 | 73,028.09308 | 29,344.23558 |
| F3 | std | 4174.231446 | 7984.245853 | 5087.478975 | 7426.879035 | 8097.010339 | 7765.054029 |
| F3 | avg | 15,583.03135 | 39,438.34153 | 90,069.39714 | 83,047.78088 | 92,758.2175 | 56,224.97662 |
| F3 | median | 15,452.63833 | 39,285.10263 | 91,008.4233 | 84,055.46423 | 92,718.38541 | 57,878.3185 |
| F3 | worse | 25,626.58143 | 53,569.16705 | 102,566.6383 | 97,344.63217 | 106,866.2551 | 65,724.612 |
| Function | Index | MSHBA | HBA | COA | DBO | OOA | HHO |
|---|---|---|---|---|---|---|---|
| F4 | min | 471.2650759 | 429.8653134 | 8676.540438 | 2280.188398 | 8831.397677 | 575.0612356 |
| F4 | std | 25.33961218 | 43.35479888 | 3016.503386 | 2310.15102 | 2999.807664 | 92.66355947 |
| F4 | avg | 515.5658011 | 520.6357708 | 15,449.90137 | 7926.726708 | 15,696.97266 | 696.2467487 |
| F4 | median | 515.2685906 | 517.3036816 | 15,432.69729 | 7380.836144 | 16,168.57155 | 686.963974 |
| F4 | worse | 577.3558248 | 655.374618 | 20,979.75537 | 13,948.7729 | 21,098.8796 | 988.4041393 |
| F5 | min | 539.0543882 | 579.7459582 | 876.9745056 | 800.7163328 | 867.1474351 | 728.1264447 |
| F5 | std | 18.20793472 | 29.64264405 | 25.76207594 | 25.19753215 | 29.87765232 | 31.15405432 |
| F5 | avg | 574.301356 | 632.031401 | 924.9641367 | 847.6968692 | 932.0657073 | 771.1397853 |
| F5 | median | 572.9181152 | 627.5478741 | 924.0502838 | 847.4039296 | 940.4132239 | 761.3208434 |
| F5 | worse | 604.1481834 | 682.386896 | 973.0416522 | 898.4303847 | 973.4967331 | 838.8982555 |
| F6 | min | 601.0876771 | 611.1461317 | 665.2970351 | 662.3393043 | 672.4335121 | 651.8707445 |
| F6 | std | 1.781596467 | 8.878423374 | 7.281224277 | 5.15257125 | 7.909286248 | 6.135355419 |
| F6 | avg | 603.6710611 | 624.3606534 | 689.514728 | 672.996196 | 686.6871553 | 668.0205421 |
| F6 | median | 603.3518742 | 622.8009585 | 690.0552519 | 673.1831749 | 686.0670717 | 669.1685594 |
| F6 | worse | 609.0684128 | 643.7839895 | 701.1380974 | 688.384032 | 700.7970491 | 678.3770071 |
| F7 | min | 768.6980104 | 833.5550622 | 1293.006629 | 1152.28046 | 1315.449088 | 1094.740061 |
| F7 | std | 28.66807361 | 52.49891689 | 52.54483794 | 49.95929834 | 51.01027465 | 70.4876899 |
| F7 | avg | 830.1325411 | 918.1773428 | 1415.336924 | 1235.876865 | 1424.787752 | 1296.86546 |
| F7 | median | 825.2929227 | 910.1463155 | 1423.410195 | 1241.328018 | 1431.421863 | 1299.322915 |
| F7 | worse | 890.7828372 | 1077.243893 | 1490.873207 | 1366.684645 | 1521.818079 | 1446.083503 |
| F8 | min | 831.0104332 | 858.9079183 | 1095.554037 | 999.9313048 | 1100.350225 | 893.4379959 |
| F8 | std | 19.90774063 | 23.66975249 | 29.29692127 | 28.47589637 | 25.34583604 | 29.25608386 |
| F8 | avg | 870.4349257 | 911.7121488 | 1149.864364 | 1068.882781 | 1142.133401 | 978.6668202 |
| F8 | median | 869.1223147 | 914.0218159 | 1160.078501 | 1071.807161 | 1142.377033 | 981.8118432 |
| F8 | worse | 919.1643449 | 944.7739496 | 1205.976809 | 1129.482433 | 1198.86356 | 1051.396815 |
| F9 | min | 959.6080177 | 1423.433841 | 6152.58414 | 5931.118374 | 7591.509447 | 6594.499632 |
| F9 | std | 395.2917037 | 1300.922409 | 1812.590238 | 1337.351272 | 1321.566109 | 1082.513028 |
| F9 | avg | 1378.269659 | 3472.94881 | 10,986.97698 | 8787.753614 | 10,324.26437 | 8567.879885 |
| F9 | median | 1309.063502 | 3491.843097 | 11,539.11699 | 8729.923302 | 10,502.01987 | 8495.984721 |
| F9 | worse | 2725.432474 | 7361.937422 | 13,698.38918 | 11,540.95279 | 12,481.84783 | 11,199.1604 |
| F10 | min | 4458.587604 | 3460.782787 | 7955.326892 | 5450.488897 | 7973.199151 | 4769.375371 |
| F10 | std | 1173.509975 | 797.6259678 | 404.9918699 | 853.6256714 | 387.2710695 | 702.6015629 |
| F10 | avg | 6400.185464 | 5481.735706 | 8748.598856 | 8428.448871 | 8846.051736 | 6105.540435 |
| F10 | median | 6220.904127 | 5403.067257 | 8732.714625 | 8671.413401 | 8974.089012 | 6014.950217 |
| F10 | worse | 9396.640306 | 6946.520619 | 9410.282349 | 9321.163997 | 9490.914007 | 7373.924473 |
| Function | Index | MSHBA | HBA | COA | DBO | OOA | HHO |
|---|---|---|---|---|---|---|---|
| F11 | min | 1151.199156 | 1216.423405 | 6495.47519 | 3090.359845 | 5484.64063 | 1373.055653 |
| F11 | std | 57.83557438 | 75.42573148 | 1587.626307 | 1310.326628 | 2394.807543 | 244.8888555 |
| F11 | avg | 1262.325404 | 1330.453477 | 8809.916041 | 5676.5758 | 9412.856873 | 1623.867058 |
| F11 | median | 1260.735078 | 1309.604659 | 8710.004238 | 5763.694408 | 9777.235861 | 1560.535589 |
| F11 | worse | 1423.229704 | 1503.400433 | 11763.67689 | 8596.097835 | 13,794.18423 | 2627.061678 |
| F12 | min | 74,900.73363 | 54,677.46578 | 8,004,724,178 | 789,307,016.7 | 8,182,408,482 | 13,090,571.92 |
| F12 | std | 1,345,797.802 | 1,313,184.577 | 3,913,546,223 | 2,659,696,551 | 3,045,040,816 | 52,989,396.93 |
| F12 | avg | 1,099,451.974 | 1,568,902.392 | 14,865,255,255 | 6,982,785,082 | 13,644,525,715 | 84,803,095.81 |
| F12 | median | 442,557.8368 | 1,176,808.69 | 15,136,388,350 | 7,476,784,291 | 13,123,772,480 | 68,615,743.72 |
| F12 | worse | 5,792,037.187 | 4,574,308.946 | 20,744,229,988 | 11,789,738,550 | 20,395,893,476 | 210,539,888.9 |
| F13 | min | 4539.3718 | 6150.165678 | 1,489,333,852 | 397,260,539 | 1,817,805,403 | 286,183.994 |
| F13 | std | 25,110.96118 | 824,912.7205 | 4,505,373,761 | 2,632,621,263 | 5,200,050,627 | 813,240.6509 |
| F13 | avg | 32,644.09 | 208,033.3399 | 10,597,566,249 | 3,442,195,466 | 9,670,358,613 | 1,066,786.477 |
| F13 | median | 19,401.24954 | 45,344.86841 | 10,172,352,017 | 3,644,524,954 | 8,417,691,801 | 836,432.0973 |
| F13 | worse | 72,977.0981 | 4,566,519.743 | 24,141,559,320 | 10,745,888,750 | 20,809,917,388 | 4,074,357.755 |
| F14 | min | 1711.831641 | 3326.949485 | 112,724.0795 | 38,819.47772 | 231,396.1531 | 47,760.74738 |
| F14 | std | 5936.700152 | 32,243.53052 | 2,155,628.537 | 825,536.1505 | 9,825,484.425 | 885,781.4279 |
| F14 | avg | 6989.518107 | 33,974.40606 | 2,191,192.564 | 798,810.2527 | 7,100,756.591 | 873,504.5218 |
| F14 | median | 4602.076785 | 19,658.03254 | 1,616,476.92 | 627,218.5244 | 3,353,309.042 | 514,502.6535 |
| F14 | worse | 28,745.95484 | 123,532.4077 | 11,557,981.02 | 3,576,983.465 | 45,832,920.4 | 3,472,437.752 |
| F15 | min | 2250.446281 | 2959.719795 | 5,121,496.847 | 280,652.7269 | 55,165,095.95 | 24,165.02678 |
| F15 | std | 13,856.94895 | 23,486.89054 | 471,974,341.2 | 36,434,849.5 | 561,614,606.5 | 49,771.67436 |
| F15 | avg | 13,675.28316 | 18,354.87093 | 611,253,276.5 | 12,629,448.73 | 690,445,609.7 | 118,023.198 |
| F15 | median | 5277.728094 | 11,497.20992 | 470,200,572.1 | 3,714,150.257 | 456,713,103.9 | 117,371.5719 |
| F15 | worse | 43,960.42823 | 121,903.6222 | 1,550,944,089 | 203,183,415 | 2,071,388,517 | 253,191.8004 |
| F16 | min | 2012.847914 | 2080.678415 | 4374.877498 | 3423.942514 | 4651.21137 | 3055.309339 |
| F16 | std | 216.1472784 | 286.7054735 | 897.7786711 | 365.8196407 | 1070.803158 | 473.6407211 |
| F16 | avg | 2386.539097 | 2605.07065 | 5770.466952 | 4112.25227 | 5881.963404 | 3731.242326 |
| F16 | median | 2421.91985 | 2585.41721 | 5780.02071 | 4072.127174 | 5587.376156 | 3654.007111 |
| F16 | worse | 2859.637434 | 3122.262691 | 7372.069495 | 4816.439998 | 8935.997457 | 5239.164841 |
| F17 | min | 1742.372139 | 1852.49437 | 2180.186923 | 2443.362849 | 2652.781695 | 2163.695568 |
| F17 | std | 173.9290205 | 224.6373734 | 2928.131984 | 270.8783634 | 5932.261031 | 297.7302024 |
| F17 | avg | 2070.236317 | 2392.484763 | 4779.393382 | 2881.051447 | 6107.295908 | 2808.588621 |
| F17 | median | 2043.869238 | 2408.685995 | 3782.066417 | 2864.486819 | 4961.477045 | 2848.983717 |
| F17 | worse | 2393.895527 | 2833.384685 | 17,991.16568 | 3314.360198 | 34,438.94604 | 3373.572517 |
| F18 | min | 20,702.75367 | 31,131.69771 | 3,827,698.722 | 753,574.3712 | 705,790.5116 | 126,809.6891 |
| F18 | std | 216,050.8949 | 2,160,010.371 | 38,061,181.03 | 5,430,566.948 | 66,536,117.46 | 5,914,002.752 |
| F18 | avg | 229,876.8588 | 729,865.1567 | 42,928,859.6 | 6,213,346.655 | 59,235,659.85 | 3,859,932.405 |
| F18 | median | 163,273.2064 | 238,578.3376 | 31,545,216.57 | 5,021,293.509 | 38,632,192.56 | 1,369,412.165 |
| F18 | worse | 944,167.6911 | 12,062,231.49 | 162,754,395.1 | 24,131,433.9 | 239,549,282.8 | 22,515,593.58 |
| F19 | min | 2101.48023 | 2313.362816 | 15,734,537.68 | 24,800,002.02 | 16,199,347.56 | 106,105.1687 |
| F19 | std | 14,150.43313 | 19,935.19608 | 535,984,424.3 | 146,049,396 | 400,151,587.5 | 1,256,830.774 |
| F19 | avg | 12,701.80058 | 18,755.67073 | 550,228,302.6 | 188,822,826.3 | 583,411,721.3 | 1,485,477.19 |
| F19 | median | 6789.886063 | 6281.857242 | 473,418,261.1 | 162,652,180.2 | 538,321,091.8 | 1,268,606.797 |
| F19 | worse | 54,393.0664 | 56,697.17763 | 2,215,792,102 | 813,804,423 | 1,523,573,922 | 6,134,312.848 |
| F20 | min | 2184.836364 | 2190.038131 | 2669.009695 | 2474.725265 | 2737.773396 | 2498.676162 |
| F20 | std | 322.9574545 | 255.6539361 | 202.9663686 | 186.1973247 | 160.9241292 | 214.2404172 |
| F20 | avg | 2734.554772 | 2629.882676 | 3035.771044 | 2818.567668 | 3022.743016 | 2840.438917 |
| F20 | median | 2734.954573 | 2613.020621 | 3052.304652 | 2857.109462 | 3007.500388 | 2863.102686 |
| F20 | worse | 3375.434061 | 3284.237114 | 3347.476599 | 3183.688842 | 3397.753491 | 3187.744902 |
| Function | Index | MSHBA | HBA | COA | DBO | OOA | HHO |
|---|---|---|---|---|---|---|---|
| F21 | min | 2328.374724 | 2361.606655 | 2674.255547 | 2298.81606 | 2645.305901 | 2474.986844 |
| F21 | std | 21.54562477 | 38.07026351 | 50.71681329 | 100.6468838 | 52.20327744 | 45.93516289 |
| F21 | avg | 2361.621356 | 2416.934175 | 2756.923906 | 2567.787301 | 2724.265894 | 2571.424771 |
| F21 | median | 2357.666469 | 2406.345148 | 2746.03419 | 2589.163152 | 2712.186617 | 2576.02751 |
| F21 | worse | 2414.891953 | 2522.446549 | 2874.9941 | 2686.106601 | 2824.396175 | 2680.325844 |
| F22 | min | 2303.011291 | 2303.803668 | 7394.126495 | 4952.563534 | 6418.441063 | 2476.604061 |
| F22 | std | 2744.984439 | 2699.275571 | 931.1823853 | 896.2348088 | 942.4142636 | 1299.944318 |
| F22 | avg | 5774.571329 | 4396.5146 | 9541.698929 | 6635.578235 | 9424.101049 | 7201.58516 |
| F22 | median | 6346.938172 | 2320.466744 | 9879.163007 | 6547.412031 | 9661.900511 | 7380.529293 |
| F22 | worse | 10,872.12746 | 10,131.19902 | 10,808.01632 | 9530.784605 | 10,457.53553 | 9091.500067 |
| F23 | min | 2692.701686 | 2716.74975 | 3341.941897 | 3011.274542 | 3417.293907 | 2931.615137 |
| F23 | std | 28.03445356 | 108.1414638 | 129.6919588 | 93.6055587 | 176.4835198 | 125.9967206 |
| F23 | avg | 2725.141462 | 2838.0616 | 3582.434161 | 3151.875958 | 3711.998019 | 3224.611813 |
| F23 | median | 2720.602588 | 2815.566227 | 3615.876905 | 3150.723736 | 3725.884802 | 3241.020759 |
| F23 | worse | 2799.636423 | 3335.541587 | 3865.707013 | 3410.174895 | 4027.514463 | 3500.775722 |
| F24 | min | 2854.03441 | 2898.570428 | 3426.104423 | 3221.32036 | 3653.231463 | 3239.149426 |
| F24 | std | 22.94711896 | 182.4346651 | 168.4636008 | 96.51085244 | 238.7841852 | 143.9425178 |
| F24 | avg | 2895.846485 | 3068.665229 | 3811.681441 | 3378.431225 | 4082.877526 | 3486.40142 |
| F24 | median | 2894.773175 | 2992.307582 | 3803.227557 | 3388.283471 | 4042.760674 | 3511.12618 |
| F24 | worse | 2936.830332 | 3561.44684 | 4170.948434 | 3584.009764 | 4569.061377 | 3869.309011 |
| F25 | min | 2888.0339 | 2889.844867 | 4161.153332 | 3749.612239 | 4145.77482 | 2954.389479 |
| F25 | std | 21.77833403 | 19.55326434 | 471.1370306 | 294.308607 | 546.961207 | 31.74155552 |
| F25 | avg | 2916.041587 | 2920.008898 | 5155.440152 | 4240.862875 | 5036.006864 | 3011.140246 |
| F25 | median | 2913.782999 | 2921.419063 | 5091.019266 | 4245.502821 | 4923.789288 | 3011.853877 |
| F25 | worse | 2977.465659 | 2956.292902 | 6111.927067 | 4807.583137 | 6440.720825 | 3090.130785 |
| F26 | min | 3868.10695 | 2822.411128 | 9865.2935 | 6691.216754 | 9515.474664 | 4212.221834 |
| F26 | std | 261.0555857 | 1040.547875 | 864.1190973 | 788.4414258 | 1171.659009 | 1197.068098 |
| F26 | avg | 4412.029682 | 5011.391515 | 11,468.69385 | 8328.356632 | 11,584.74908 | 8015.494868 |
| F26 | median | 4401.137387 | 5037.256627 | 11,510.98905 | 8549.826893 | 11,562.82741 | 8317.378243 |
| F26 | worse | 4954.540489 | 6919.703493 | 13,334.83768 | 9603.896656 | 14,288.20873 | 9897.642704 |
| F27 | min | 3203.596686 | 3217.64719 | 3764.298723 | 3397.702045 | 3735.00574 | 3276.890401 |
| F27 | std | 375.1604378 | 173.3180073 | 501.2971062 | 150.2258588 | 534.7853183 | 205.0072178 |
| F27 | avg | 3418.462613 | 3342.389701 | 4493.857869 | 3669.40638 | 4841.336833 | 3535.701627 |
| F27 | median | 3304.911169 | 3307.459554 | 4424.195815 | 3657.460642 | 4843.963482 | 3487.872732 |
| F27 | worse | 4809.336071 | 4068.668299 | 5725.68992 | 3956.127687 | 6093.658352 | 4273.873259 |
| F28 | min | 3207.537647 | 3215.539111 | 6219.829655 | 4759.858161 | 6276.802658 | 3347.569615 |
| F28 | std | 964.1069312 | 35.93018009 | 596.6879353 | 380.8594573 | 614.0424277 | 68.96732179 |
| F28 | avg | 3619.889274 | 3282.614929 | 7422.944436 | 5542.163689 | 7385.34041 | 3474.906644 |
| F28 | median | 3273.387211 | 3286.34706 | 7541.352154 | 5660.78289 | 7489.362639 | 3461.763521 |
| F28 | worse | 6912.590173 | 3382.611969 | 8724.415482 | 6185.494938 | 8414.745851 | 3666.251144 |
| F29 | min | 3494.322658 | 3467.102238 | 5827.179913 | 4377.03191 | 5186.816056 | 4153.204096 |
| F29 | std | 390.6260893 | 287.9024078 | 1235.80597 | 360.3593788 | 1843.805616 | 395.5045007 |
| F29 | avg | 4024.048157 | 4096.387997 | 7398.869217 | 5018.876752 | 8150.940429 | 5056.387627 |
| F29 | median | 3975.567817 | 4111.554342 | 7068.020938 | 4970.159496 | 7617.972569 | 5160.819057 |
| F29 | worse | 4891.942631 | 4820.404623 | 11,120.62393 | 5660.56642 | 12,418.38164 | 5796.888337 |
| F30 | min | 6596.26567 | 7878.446768 | 568,099,420.9 | 22,276,646.83 | 262,230,934.4 | 2,198,313.919 |
| F30 | std | 6851.453476 | 88,005.28982 | 903,137,928.5 | 289,290,425.3 | 1,130,305,003 | 9,307,191.494 |
| F30 | avg | 17,546.12975 | 72,406.14781 | 1,713,122,036 | 214,934,810.1 | 1,920,168,273 | 11,292,240.97 |
| F30 | median | 16,024.00032 | 30,456.11583 | 1,407,603,022 | 143,764,437.1 | 1,586,940,284 | 10,002,707.62 |
| F30 | worse | 42,228.44695 | 386,843.3297 | 4,408,681,625 | 1,646,995,834 | 4,855,238,130 | 41,377,423.53 |
| Function | HBA | COA | DBO | OOA | HHO |
|---|---|---|---|---|---|
| F1 | 0.662734758 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F3 | 4.97517 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F4 | 0.589451169 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.68973 × 10−11 |
| F5 | 1.07018 × 10−9 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F6 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F7 | 1.85673 × 10−9 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F8 | 9.83289 × 10−8 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 4.97517 × 10−11 |
| F9 | 3.15889 × 10−10 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F10 | 0.001679756 | 8.48477 × 10−9 | 2.19589 × 10−7 | 5.96731 × 10−9 | 0.539510317 |
| F11 | 0.000268057 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 4.97517 × 10−11 |
| F12 | 0.072445596 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F13 | 0.027086318 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F14 | 9.06321 × 10−8 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F15 | 0.129670225 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 1.09367 × 10−10 |
| F16 | 0.003033948 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F17 | 1.02773 × 10−6 | 7.38908 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 1.46431 × 10−10 |
| F18 | 0.065671258 | 3.01986 × 10−11 | 4.07716 × 10−11 | 3.68973 × 10−11 | 3.19674 × 10−9 |
| F19 | 0.239849991 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F20 | 0.180899533 | 0.000253058 | 0.162375022 | 0.00033679 | 0.122352926 |
| F21 | 7.77255 × 10−9 | 3.01986 × 10−11 | 1.54652 × 10−9 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F22 | 0.185766856 | 5.0922 × 10−8 | 0.529782491 | 1.35943 × 10−7 | 0.023243447 |
| F23 | 1.41098 × 10−9 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F24 | 1.41098 × 10−9 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| F25 | 0.340288465 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 4.97517 × 10−11 |
| F26 | 0.000268057 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 4.19968 × 10−10 |
| F27 | 0.641423523 | 1.69472 × 10−9 | 7.69496 × 10−8 | 4.19968 × 10−10 | 4.63897 × 10−5 |
| F28 | 0.8766349 | 8.99341 × 10−11 | 2.60151 × 10−8 | 8.99341 × 10−11 | 1.72903 × 10−6 |
| F29 | 0.206205487 | 3.01986 × 10−11 | 9.7555 × 10−10 | 3.01986 × 10−11 | 1.41098 × 10−9 |
| F30 | 2.95898 × 10−5 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 |
| Engineering 1 | Index | MSHBA | COA | DBO | OOA | HHO | HBA |
|---|---|---|---|---|---|---|---|
| F1 | min | 2994.424466 | 2994.424466 | 2994.424467 | 3005.476722 | 2994.424466 | 2994.424466 |
| F1 | std | 2.84848056 | 65.16978689 | 45.09751196 | 5.028371006 | 2.368455165 | 2.54734021 |
| F1 | avg | 2995.358009 | 3056.1574 | 3034.296393 | 3012.829612 | 2995.046823 | 2995.376420 |
| F1 | median | 2994.424466 | 3038.368266 | 3033.701596 | 3011.346302 | 2994.424466 | 2994.424466 |
| F1 | worse | 3003.75982 | 3188.264544 | 3188.264544 | 3025.967663 | 3003.75982 | 3002.57892 |
| Engineering 2 | Index | MSHBA | COA | DBO | OOA | HHO | HBA |
|---|---|---|---|---|---|---|---|
| F2 | min | 0.01266534 | 0.012676941 | 0.012669641 | 0.012669581 | 0.012667402 | 0.01266421 |
| F2 | std | 0.00127634 | 0.00217847 | 0.000982581 | 0.000156243 | 0.001532633 | 0.001254356 |
| F2 | avg | 0.013211802 | 0.014403461 | 0.013158595 | 0.012834463 | 0.013415017 | 0.013321041 |
| F2 | median | 0.012719054 | 0.01312391 | 0.012843473 | 0.012763832 | 0.012719054 | 0.012718236 |
| F2 | worse | 0.017773158 | 0.018026697 | 0.017773158 | 0.013347791 | 0.017773158 | 0.017764532 |
| Engineering 3 | Index | MSHBA | COA | DBO | OOA | HHO | HBA |
|---|---|---|---|---|---|---|---|
| F3 | min | 6059.714335 | 6059.71435 | 6059.714552 | 6060.37146 | 6059.714335 | 6061.823546 |
| F3 | std | 512.5757289 | 579.9510833 | 316.2129992 | 374.7160367 | 540.7771321 | 524.34210589 |
| F3 | avg | 6513.097363 | 6594.239536 | 6451.562474 | 6238.452261 | 6688.493798 | 6534.0238912 |
| F3 | median | 6370.779717 | 6338.958449 | 6410.086778 | 6065.4648 | 6728.854785 | 6380.2384513 |
| F3 | worse | 7544.492518 | 7544.492518 | 7332.843509 | 7425.013265 | 7544.492518 | 7678.5642312 |
| Engineering 3 | Index | MSHBA | COA | DBO | OOA | HHO | HBA |
|---|---|---|---|---|---|---|---|
| F3 | min | 1.670217919 | 1.672242773 | 1.670218795 | 1.6717035 | 1.670218056 | 1.670217919 |
| F3 | std | 0.142683524 | 0.113967612 | 0.084676517 | 0.002774216 | 0.239656288 | 0.142683524 |
| F3 | avg | 1.787526474 | 1.789799218 | 1.71024892 | 1.67635062 | 1.81837122 | 1.787526474 |
| F3 | median | 1.72404532 | 1.771026028 | 1.670359559 | 1.676323843 | 1.724064807 | 1.72404532 |
| F3 | worse | 2.183640071 | 2.282913448 | 1.979411719 | 1.682554819 | 2.679760746 | 2.183640071 |
| Algorithm | X1 | X2 | X3 | X4 | X5 | X6 | X7 |
|---|---|---|---|---|---|---|---|
| MSHBA | 3.5 | 0.7 | 17 | 7.3 | 7.71532 | 3.35054 | 5.28665 |
| COA | 3.5 | 0.7 | 17 | 7.3 | 7.71532 | 3.35054 | 5.28665 |
| DBO | 3.5 | 0.7 | 17 | 7.3 | 7.71532 | 3.35054 | 5.28665 |
| OOA | 3.5 | 0.7 | 17 | 7.37735 | 7.93909 | 3.35091 | 5.28803 |
| HHO | 3.5 | 0.7 | 17 | 7.3 | 7.71532 | 3.35054 | 5.28665 |
| HBA | 3.5 | 0.7 | 17 | 7.3 | 7.71532 | 3.35054 | 5.28665 |
| Algorithm | X1 | X2 | X3 |
|---|---|---|---|
| MSHBA | 0.05 | 0.317425 | 14.0278 |
| COA | 0.0526386 | 0.379993 | 10.0444 |
| DBO | 0.0514621 | 0.351283 | 11.6148 |
| OOA | 0.0505182 | 0.329028 | 13.1295 |
| HHO | 0.0519519 | 0.363074 | 10.9258 |
| HBA | 0.05 | 0.317425 | 14.0278 |
| Algorithm | X1 | X2 | X3 | X4 |
|---|---|---|---|---|
| MSHBA | 12.84797 | 6.88227 | 42.09382 | 176.89271 |
| COA | 12.58581 | 7.04886 | 41.63912 | 182.41281 |
| DBO | 13.20307 | 6.57646 | 40.66877 | 195.19762 |
| OOA | 15.07952 | 7.73834 | 48.57513 | 110.06771 |
| HHO | 14.88946 | 8.10283 | 48.57513 | 110.06775 |
| HBA | 13.43681 | 6.95521 | 42.08866 | 177.10523 |
| Algorithm | X1 | X2 | X3 | X4 |
|---|---|---|---|---|
| MSHBA | 0.19883 | 3.33741 | 9.19213 | 0.19883 |
| COA | 0.19795 | 3.36312 | 9.19134 | 0.19891 |
| DBO | 0.19775 | 3.35981 | 9.19012 | 0.19914 |
| OOA | 0.19563 | 3.48621 | 9.20923 | 0.19947 |
| HHO | 0.19932 | 3.44251 | 9.15293 | 0.20123 |
| HBA | 0.19673 | 3.37823 | 9.19134 | 0.19883 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Huang, H. Multi-Strategy Honey Badger Algorithm for Global Optimization. Biomimetics 2025, 10, 581. https://doi.org/10.3390/biomimetics10090581
Guo D, Huang H. Multi-Strategy Honey Badger Algorithm for Global Optimization. Biomimetics. 2025; 10(9):581. https://doi.org/10.3390/biomimetics10090581
Chicago/Turabian StyleGuo, Delong, and Huajuan Huang. 2025. "Multi-Strategy Honey Badger Algorithm for Global Optimization" Biomimetics 10, no. 9: 581. https://doi.org/10.3390/biomimetics10090581
APA StyleGuo, D., & Huang, H. (2025). Multi-Strategy Honey Badger Algorithm for Global Optimization. Biomimetics, 10(9), 581. https://doi.org/10.3390/biomimetics10090581




