Abstract
In this paper, a biologically congruent parallel mechanism (PM) inspired by the masticatory system of human beings has been proposed to recreate complete chewing behaviours in three-dimensional space. The mechanism is featured by direct constraints from the base (DCFB) to its end effector at two higher kinematic pairs (HKPs), which greatly raise its topological complexity. Meanwhile, friction effects occur at HKPs and actuators, causing wear and then reducing motion accuracy. Regarding these, an inverse dynamic model that can raise the computational efficiency and the modelling fidelity is proposed, being prepared to be applied to realise accurate real-time motion and/or force control. In it, Euler parameters are employed to express the motions of the constrained end effector, and Newton–Euler’s law is applied, which can conveniently incorporate friction effects at both HKPs and actuators into the dynamic model. Numerical results show that the time consumption of the model using Euler parameters is only approximately 23% of that of the model using Euler angles, and friction effects significantly increase the model’s nonlinearity. Further, from the comparison between the models of the target PM and its counterpart free of DCFB, these constraints sharply raise the modelling complexity in terms of the transformation between Euler parameters and Euler angles in the end effector and the computational cost of inverse dynamics.
1. Introduction
Mastication is a complex process in , where the foods are chewed to smaller and softer boluses that can be swallowed safely [1]. The food industry has a strong curiosity in this process, since exploring the human-food interaction is beneficial for evaluating food texture properties so as to develop favourable, healthy, and appealing food products. Currently, machines used to assess food textures in vitro only simply compress the test foods in one dimension, which is far away from the real complicated chewing motions of human beings in . Recruiting healthy volunteers is associated with long-time consumption and high expenditure, and the results are not objective. Thereby, robotic devices that can accurately replicate complete masticatory behaviours in terms of chewing forces and motions in are greatly needed. With their assistance, newly developed food samples can be chewed in a human-like manner, then food textures can be analysed reliably and efficiently. To this end, it is very natural to design a robotic mechanism by mimicking the muscle-skeleton biostructure of the masticatory system: its end effector is the moving mandible, the base is the fixed maxilla, and six revolute-spherical-spherical (RSS) parallel linkages working synchronously are the major chewing muscles, namely, the temporalis, the masseter, and the pterygoid [2]. The underlined letter R indicates it is the active joint. Left and right direct constraints from the base (DCFB) to the end effector form two higher kinematic pairs (HKPs), playing the role of the crucial temporomandibular joints (TMJs). As a result, from the viewpoint of mechanism, the designed prototype is a spatial parallel mechanism (PM) receiving DCFB to the end effector. These constraints evidently render this mechanism different from others, since PMs in general do not have this sort of constraints. They increase the topological complexity, bringing two parasitic motions and two redundant actuations simultaneously [2]. It is fundamental to stress that theoretically, two kinematic chains in the mechanism can be taken out to reduce its topological complexity; then it would have no actuation redundancy. Nonetheless, the biological features of the chewing system in terms of the roles of primary chewing muscles and TMJs cannot be explored adequately via this simpler mechanism, and the potential engineering applications could be limited. Hence, the bio-inspired mechanism under study is designed as faithfully as we can.
Due to the closed-loops, PMs are superior to their serial counterparts in terms of larger load carrying capacity [3], better motion accuracy [4,5], and lower moving inertias [6,7], even if their singularity problems are more complex and the workspace is smaller. Thus, they can exert these strengths in the domains where their desirable features are greatly needed [8,9], e.g., machine tools [10,11,12,13,14], fast pick-and-place manipulators [15], haptic devices [16], pointing devices [17], and physical human-robot interaction [18,19].
Before the designed mechanism is employed to evaluate newly developed foods in the food industry, there are two concerns about its practical applications. The first is that, due to the DCFB, parasitic motion variables are strongly coupled by translational and rotational degrees of freedom (DOFs). They have complicated trigonometric functions as in Equation (5) of [20], where XYZ Euler angles were used to characterise rotations of the end effector. These complex and lengthy equations considerably increase the computational time in dynamic models, being not in favour of real-time model-based controller design. Thus, more efficient alternatives to Euler angles are sought to reduce the computational cost. In the literature, Euler parameters, i.e., unit quaternions, deeply attract our interest. From the Euler theorem, the orientation of a rigid body can be defined by its rotation around an axis by an angle of rotation θ at any instant of time [21]. Thereby, these parameters are stated as
where u is the unit vector around which the rotation of the body occurs, and its three elements are the projections along the orthogonal axes of the inertia frame. Although four parameters are used to describe rotations in , indicating they are not completely independent and that one constraint equation is needed; this cumbersome feature is more than compensated for by their desirable merits as:
- 1.
- Any orientation of a body in can be defined satisfactorily since there are no inherent singularity problems.
- 2.
- Kinematic equations associated with them have purely algebraic operators and are free of trigonometric functions, as with Euler angles, being computationally more efficient. As a result, they are easy to implement in a computer program in simpler and more compact manners.
Regarding these, they are adopted to describe the motions of the end effector of the mechanism under study to enhance the computational efficiency. From the literature, Euler parameters have been widely applied in many arenas due to their advantages. For instance, a general Euler parameter-based dynamic model was built by the Lagrange formulation for mechanical systems [22]. Many useful and interesting identities between Euler parameters and their derivatives were presented in [21], based on which the dynamic model can be more compact and efficient [23]. An attitude regulator for an arbitrary rigid body was designed with these parameters in [24], leading to a linear feedback law, where neither linearisation nor simplification assumptions such as small angular rates or attitude error angles were made. This presentation avoids nonlinear equations of motion (EOMs) and a nonlinear feedback law associated with Cayley–Rodrigues parameters. Euler parameters were utilised to model the end effector rotation errors in resolved rate and acceleration control of serial manipulators in [25]. The formulation considerably simplifies the stability analysis of orientation error equations. In [26], their utilisation in a spherical joint avoided the introduction of three virtual orthogonal revolute joints with zero length of intermediate links in the general manner, which raised the sizes of associated matrices in the EOMs and finally the computational burden. The dynamic modelling of a spatial RSSR serial mechanism showed that the CPU time has a 10% improvement over the virtual revolute joints method, and less computer memory is required. To address the photogrammetric problem, a closed-form solution was provided in [27], where unit quaternions were used to simplify the derivation of the solution.
As far as their applications in PMs are concerned, in [28], based on the number of constant zero components of Euler parameters, they were classified into 15 cases, and their kinematic interpretation was presented. Then, the orientation of the end effector of a 3-DOF 3-RER PM with orthogonal platforms was represented using Euler parameters effectively. Letters R and E denote revolute joint and planar joint, respectively. In [29], the above-mentioned 15 cases of classification were used again, then Euler parameters were employed together with Euler angles, algebraic geometry, and axodes to effectively identify and compare distinct continuous motion characteristics of three 2-DOF pointing mechanisms, i.e., a gimbal structure, a 1-RR&2-RRR spherical PM, and an Omni-Wrist III. A systematic classification of a 3-RER PM based on the type/number of operation modes varying with link parameters was presented in [30]. Euler parameters are found to be very useful for identifying the motion characteristics of the end effector.
Apart from the computational cost, the second concern in the designed mechanism is that, in practical experiments of its prototype, at the direct constraints from the base to the end effector, wear appears due to friction effects, further introducing clearances and reducing motion accuracy. Additionally, friction exists in the brushes, rotors, and bearings inside the actuators, but it is not desirable to disassemble them frequently to lubricate those parts. In this regard, for the sake of reliable and accurate manipulations of the robotic device in practice, the friction is worth being considered in the inverse dynamic model to analyse its effects.
In terms of friction effects in PMs, from the literature, a Lagrange-based approach was proposed to analyse the forward dynamics of a 3-PRS PM in [24], where the LuGre friction effects are modelled at active prismatic joints. Letters P and S denote a prismatic joint and a spherical joint, respectively. On this basis, the influence on the motion accuracy was analysed. EOMs of forward dynamics with a closed form were formatted by the Udwadia–Kalaba approach for a planar 2RRR/RR PM with actuation redundancy in [31]. In [32], the friction effects were expressed by the Stribeck model in the artificial hip joint, thrust ball bearing, and linear module of 2(3PUS+S) PM. The letter U denotes a universal joint. Their parameters were identified by a least-squares method, and their negative effects were compensated for through a feedforward compensation method. An explicit dynamic model with joint friction was established for a 4-UPS PM, which was incorporated into a 5-DOF hybrid polishing robot [14]. The Newton–Euler method was utilised to build the model, and friction effects were modelled by the Coulomb-viscous friction model. To build an accurate dynamic model of a hybrid spray-painting robot in [33], the Stribeck friction model was used to express friction effects in all active joints. The coefficients were identified, and these effects were compensated for in the inverse dynamic model. A nonlinear friction model, which can capture viscous, Coulomb, and Stribeck effects, was developed for the 2RRR/RR PM in [34]. The comparison of the control performance between this model and the Coulomb-viscous friction model showed that the trajectory tracking accuracy was improved significantly in the former.
From the literature review, the practical applications of Euler parameters can be found extensively, and their theoretical study has reached an in-depth level. However, their application in PMs, especially those with various constraints from lower kinematic pairs and HKPs like the one under study, has not been reported yet. In terms of friction effects, they are considered only in a few publications about the dynamics of PMs. In the target PM, to reduce the computational demands of inverse dynamics and the negative effects from friction, an Euler parameter-based inverse dynamic model with friction effects at HKPs and actuators is built in this paper. The two novelties are summarised as:
- 1.
- Euler parameters are employed to describe the motions of the constrained end effector in the target PM, sharply reducing the computational expenditure of the model.
- 2.
- Friction effects are accounted for at HKPs and active revolute joints, arriving at a nonlinear but more accurate inverse dynamic model.
The paper is organised as follows: in Section 2, the mechanism under study is described in detail. The motions of the end effector are studied using Euler parameters in Section 3. In Section 4, the inverse dynamic model with friction effects is built by Newton–Euler’s law. Numerical computations are presented in Section 5 to find the transformation between Euler parameters and Euler angles, the dynamic performances of the mechanism under study, and the influence of constraints at HKPs on kinematics and dynamics. Finally, some conclusions are given in Section 6.
2. The Robotic Mechanism
The scheme of the target PM constrained at two HKPs is illustrated in Figure 1. The fixed maxilla to which the inertia frame {S} is assigned is not shown in the figure for a clear exhibition of moving bodies. The movable lower jaw, namely, the end effector, is connected to the base by six independent kinematic linkages. Frame {S} owns a horizontal XS-YS plane perpendicular to the vertical ZS axis. At the mass centre OM of the end effector, a body-fixed frame {M} is set. Frames {S} and {M} are completely coincident when the mechanism is at the home position, i.e., the upper and lower jaws are occlusal. The position coordinates of OM in {S} denote the translations of the end effector, and its orientations with respect to the inertia frame are computed by Euler parameters. In the chains, the crank GiSi (i = 1,…,6) is actuated by a revolute joint centred at Gi, and the coupler SiMi connects the crank and the end effector at its two ends Si and Mi, respectively, using spherical joints. A frame {Ci} is attached to Gi to express the rotation of the ith actuator. In it, the axis is from Gi to Si, the axis runs through the rotational axis of the actuator, and the axis completes the frame, obeying the right-hand rule. A frame {Ni} is attached to the mass centre Ei of the coupler to describe its motions in {S}. The axis points from Si to Mi, the axis is parallel to the cross product of two unit vectors defined along the and XS axes, and the axis is defined by the right-hand rule. Note that only one actuator frame {C5} and one coupler frame {N5} are drawn as illustrative examples in the diagram for the sake of clarity.

Figure 1.
A schematic view of the mechanism under study: ① and ② are condylar balls, and ③ and ④ are articular surfaces of TMJs.
From a close observation of Figure 1, one can see that the point-contact HKPs mimicking TMJs between left and right condylar balls and condylar surfaces are only schematic, since the former can only receive unilateral constraints from the latter. Hence, in the prototype, due to motion errors in engineering practice, condylar balls are separated from articular surfaces easily. Thus, the nature of the mechanism is changed. In these regards, the HKP-related mechanical parts in engineering practice are shown in Figure 2 with the computer-aided design (CAD) model of the prototype. The condylar ball slips along a condylar socket that has a width equal to its diameter. Thereby, the point-contact HKPs during the arbitrary motions of the end effector can always exist. By this design, the motion of the condyle ball centre Ti (i = L, R) is always constrained onto a surface, which is offset from the upper and lower surfaces of the socket by the ball radius. Thereupon, it is clear that the end effector is actuated by six chains and constrained by the base at two HKPs simultaneously.
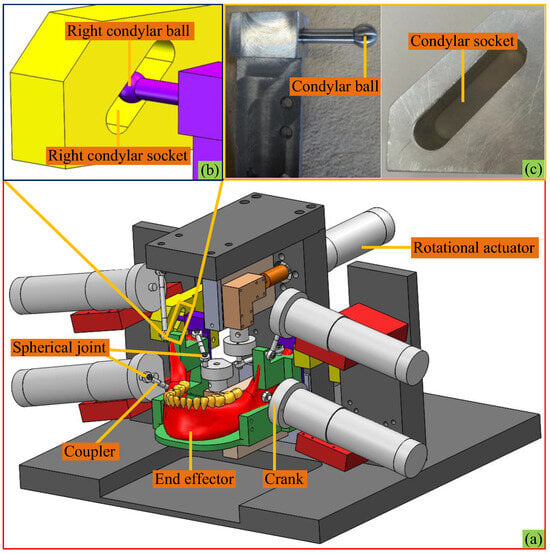
Figure 2.
The mechanism under study: (a) CAD model, (b) HKP at the right side, (c) HKP-related mechanical parts.
3. Kinematics
The kinematics of the end effector using Euler parameters is analysed in this section so as to be utilised adequately in the dynamics in Section 4.
3.1. Constrained Motions of the End Effector
The influence of DCFB on the end effector is first derived. In the inertia frame {S}, the mathematical functions of the planar surfaces where the condylar ball centres Ti (i = L, R) are situated
where are the coordinates of the left and right planes along the YS axis, respectively.
The coordinates of Ti (i = L, R) in {S} are
where denotes the position coordinates of the mass centre OM in {S}, is the position vector of Ti in {M}, which is constant, and rotates frame {S} to frame {M} using Euler parameters θ and is expressed in a quadratic form
where ,, I3 is the 3 × 3 identity matrix, and is the 3 × 3 cross-product matrix spanned by . Critically, fulfils the normality constraint condition
Therefore, the four quantities in are not all independent.
Substituting Equations (3) and (4) into Equation (2) produces the geometric constraint equation at two HKPs as
where is the ith (i = 1,3) row of . Owing to the left-right symmetry of and in {M}, a summation and a subtraction of the two equations in Equation (6) sidewise yield
where denotes the ith element of . Thus, under DCFB, Z and are parasitic motion variables, rather than DOFs of the 6RSS PM free of these constraints. Specifically, Z is constituted by both a linear DOF X and Euler parameters contained in , while is only composed of the other three elements in . Hence, the four entries in are further coupled on the basis of Equation (5).
Equation (7) has purely algebraic functions but no trigonometric functions. By comparison, the parasitic motion variable Z in Equation (6) of [20] has the same expression as that in Equation (7), but the rotation matrix in it is full of trigonometric functions.
The seven coordinates describing the motion of the end effector are grouped as
In view of the three scalar equations in Equations (5) and (7), the mechanism has four DOFs, which is also in accordance with the result from the Kutzbach–Grübler criterion [35]. Remember the six actuations are invariant; thus, redundant actuations in the mechanism are essentially caused by DCFB onto the end effector, which is completely different from the two primary accesses in [36].
After identifying the parasitic motions, five independent coordinates of are used to express the four DOFs and grouped in a 5 × 1 vector as
Note that it is not four coordinates of that are used to express the DOFs of the mechanism. Two reasons account for this choice. Firstly, putting θ3 in Equation (7) into the quadratic constraint in Equation (5) can produce a complicated expression of θi (i = 0,1,2), which is not in favour of the computational cost. Secondly, via the optimisation in Section 5.1, all variables in can be conveniently obtained numerically.
Henceforth, to characterise an instantaneous configuration of the end effector, Equation (8), or Equations (5), (7), and (9) ad hoc are needed. In other words, the mechanism performs motions in six directions with five independent coordinates, two parasitic motion variables, and one normality constraint condition.
The 7 × 5 Jacobian matrix MJ between and as
Differentiating this equation produces
The twist of the end effector can be computed as
where is the translational velocity of OM, is the rotational velocity, and
On this basis, the first time-rate of the twist is easily derived as
It is noted that though there are some common figures, equations, and texts between this paper and [20], they are in Section 2 and Section 3.1, serving as the foundation of this paper, since the focus of this paper is on the use of Euler parameters and the friction effects, and these two aspects do not exist in [20]. Finally, the dynamic models in this manuscript and [20] are built by Newton–Euler’s law and the energy-based methods, respectively. Therefore, these replications are not critical.
3.2. Crank GiSi
The crank only rotates around the fixed axis of frame {Ci}; however, it is not easy to express its rotations using Euler parameters where . The reason is as follows: from the geometric relationship, one can derive
in which is the rotation matrix of GiSi in {S} at the initial configuration of the mechanism, is the rotation matrix about the axis
and where is the length of . On the one hand, as depicted in Figure 1, one can find
then squaring the two sides of Equation (17) and rewriting the results produce
On the other hand, one can find
Since the crank GiSi can only rotate around the axis, the four elements in are
where cis the angular displacement of the ith active revolute joint around the axis. In this manner, putting Equations (15), (16), and (19), and in Equation (20) into Equation (18) gives rise to a scalar equation
where is the scalar on the right-hand side of Equation (18). However, it can be shown from Equation (21) that it is hard to compute and simultaneously, since in general, nine numerical values of a 3 × 3 rotation matrix are all needed, as drawn from the conclusion after reviewing the various sorts of methods in [37]. However, if and in Equation (20) are substituted into (21), can be derived using the procedure in Section 2 of [2]. In fact, substituting Equation (20) into Equation (16) easily produces
which is actually the rotation matrix by the Euler angle around the axis. In these regards, the kinematics of the ith actuator including its displacement, velocity, and acceleration is still derived as that in Section 2 of [2] and Section 3.2 of [20] using .
3.3. Coupler SiMi
The motions of the coupler SiMi (i = 1,…,6) are also needed for its rigid-body dynamics. On the one hand, the coordinate vector of SiMi is computed as
where is the rotation matrix of SiMi in {S} at the initial configuration of the mechanism; is the length of SiMi, and is the rotation matrix since the configuration using Euler parameters
where
On the other hand, geometrically, SiMi can also be computed from the differences of the coordinate vector of Mi and Si as
where and is the constant coordinate vector of Mi in {M}, is the constant position vector of Gi since it is fixed in {S}, and is derived using Equations (15) and (22). When computing , numerical values of the right-hand side of Equation (25) are all available, i.e., the motions of the end effector and the crank have been derived before. Combining Equations (23)–(25), one can find
whose left-hand side is actually the first column of from Equation (24), and is the known 3 × 1 vector at the right-hand side of Equation (25). By taking the normality constraint equation
into consideration, there are in total four unknowns and four nonlinear scalar equations which can be solved numerically, being neither simple nor straightforward. However, the mechanism is featured by the end effector constrained by the base directly. As such, the rotations of the couplers by virtue of Euler parameters will be left for future work. In summary, in the kinematics of the mechanism, Euler parameters are only utilised in the end effector, while Euler angles in the kinematic chains, as in [2] and [20], are still employed to describe their rotations.
4. Dynamic Model
Before the dynamic model is established, two reasonable assumptions about friction effects are made: 1. The two HKPs are easily subject to wear and tear due to friction forces. Thereby, from the viewpoint of practical applications, these forces are incorporated into the dynamic model to make it more accurate. Meanwhile, in the prototype, revolute joints are actuated by DC servo motors, and it is hard to lubricate the inner bodies, such as brushes, rotors, or bearings. Henceforth, friction torques in these joints are also modelled. 2. Frictional moments exist in twelve passive spherical joints; however, the size of the ball in the socket is very small, so these moments are not large. Additionally, friction effects in passive spherical joints of PMs have been studied in [14] already. To avoid a tedious deviation in the dynamic model and highlight the unique HKPs, all spherical joints are assumed friction-free.
Friction effects are tightly related to constraint forces at joints, which are difficult to find using energy-based dynamic methods, such as the Lagrangian formulation or Hamilton’s equations. Additionally, in view of the intrinsic dependence of Euler parameters, Lagrange multipliers are needed if Lagrange equations are used to build the model. They would greatly increase the number of coordinates in the model. Consequently, the methods in [21,38] are not adopted, and the dynamic model of the entire mechanism is built using the classical Newton–Euler’s law. A great deal of friction models have been reviewed in [39], which are classified into static and dynamic types. In view of the complex topology of the target mechanism, the classical Coulomb and viscous friction model, which belongs to the static type, is applied.
4.1. End Effector
The free-body diagram of the end effector is shown in Figure 3. The forces acting on the end effector include constraint forces at spherical joints Mi, its gravity at OM in which mEE is the mass and is the gravitational acceleration vector, the reacted chewing force FB at point B of a left lower molar, and constraint forces and friction forces acting at Ti from the surfaces of condylar sockets. can be computed as
where is along the orthogonal direction of the planar surface specified in Equation (2), and is the component of along the ZS axis. The friction force at HKPs under the Coulomb and viscous friction model is
where and are Coulomb and viscous coefficients, respectively, is the absolute value of , and is the two-norm sum of the linear velocity at Ti. As a result, friction forces at HKPs are not only a function of but also the dynamics of the entire mechanism. The schematic diagram of the constraint forces from condylar sockets and the friction forces at the condylar ball from the sagittal view is displayed in Figure 4. One can see that is perpendicular to the surface on which Ti is constrained, and is on this planar surface. can be decomposed into two components, which are along the ZS and XS axes, respectively.
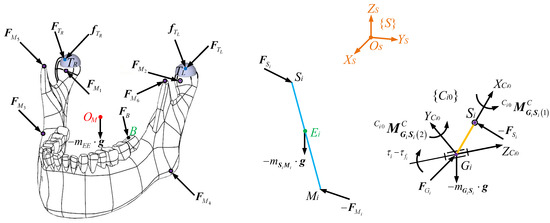
Figure 3.
Free-body diagram of the end effector, the ith (i = 1,…,6) coupler, and the ith crank.
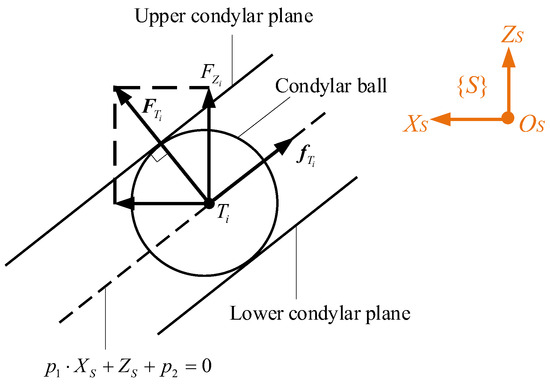
Figure 4.
Schematic diagram of the constraint forces from condylar sockets and the friction forces at the condylar ball.
Note that since at all time instants of the tracked trajectory in Section 5, is nonzero, then the case is not considered in the following. By the Newton–Euler formulation, the EOMs of the lower jaw are
where
In Equation (31), and are cross-product matrices spanned by and , respectively, is the reacted wrench on the end effector by FB. mEE is the mass of the end effector, is the inertia matrix of the end effector updated as a function of its orientations in {S}, and is the inertia tensor of the end effector with respect to {M}.
Putting Equations (28) and (29) into Equation (30) gives rise to a compact form as
where
and is the Kronecker product.
4.2. Coupler SiMi
The free-body diagram of the ith coupler is given in Figure 3. Via the Newton–Euler’s law, for the ith coupler, one can format
where is the constraint forces at Si acting at SiMi, is the mass, and is the linear acceleration of Ei, and are the angular velocity and acceleration, respectively, is the inertia tensor with respect to Ei and built in {S}, and is the inertia tensor with respect to Ei and built in {Ni}. Combining the two equations in Equation (33) yields
where .
Among the three scalar equations in Equation (34), arbitrarily only two are independent; the last two are chosen for the following computation. Thus, for the six couplers, one can write
where , and the subscripts (2:3,:) and (2:3) denote the last two rows of and the last two entries of , respectively. Meanwhile, repeating the first equation in Equation (33) six times for the six couplers produces
where
These equations will be incorporated into those for the end effector and crank to build the dynamic model of the entire mechanism.
4.3. Crank GiSi
To find frictional torques at active revolute joints at Gi, the constraint force is to be derived. The free-body diagram of the ith crank is shown in Figure 3. Firstly, because the crank owns a cylinder shape, and it only rotates around the central line, which is along the axis of frame {Ci}, its force equilibrium in {S} produces
where is the mass and its mass centre locates at the axis. can be expressed in frame {Ci0} as
to minimise computational overhead, where frame {Ci0} denotes frame {Ci} when the angular displacement of the ith crank is zero. As such, for the six revolute joints, a compact form of all constraint forces at Gi can be written as
The Euler’s law is used to write the rotational EOM of the ith crank in {Ci0} as
where is the 2 × 1 vector containing two constraint moments around the and axes of {Ci0}, and are the actuating torque and the frictional torque in the ith actuator, respectively, is the angular acceleration, and is the rotational inertia of the ith crank. Thereby, around the direction of actuations, i.e., from the third line of Equation (40), one can list
where is the cross-product matrix of and means the third line. By the Coulomb and viscous friction model, is computed as
where Ri is the friction arm of the ith actuator, and are the Coulomb and viscous coefficients, respectively, and sgn(·) is the sign function. Additionally, can be written as
Putting it into Equation (40) produces
where . As a result, for the six cranks, one can derive
where
In addition, from the first two lines of Equation (40), one can write
where is the first two lines of .
4.4. Entire Mechanism
Combining the EOMs of the end effector in Equation (32) and the six couplers in Equation (35) generates
Then, can be computed as
where
Thus, with Equation (36), all constraint forces at S1~S6 can be computed as
where . Finally, putting Equation (49) into Equation (45) produces the explicit dynamic model of the entire mechanism with friction effects at HKPs and revolute joints as
where
are known matrices if the motions of the mechanism are given. There are six equations and eight unknowns in and in this model, indicating that actuating torques and friction effects should be optimally computed. Furthermore, a closer observation of Equation (50) can lead to the following remarks:
- 1.
- Even if a simple Coulomb and viscous friction model, which is classified as a static one in [39] is employed, friction effects at HKPs significantly enhance the nonlinearity of the dynamic model in terms of explicitly, and they implicitly influence frictional torques , since is the function of as shown in Equations (39), (42), and (49). Regarding these, friction effects at HKPs and revolute joints are strongly coupled, and actuating torques are influenced by them.
- 2.
- If all friction effects are neglected, Equation (50) degrades to the form of
4.5. Optimal Goals to Distribute Actuating Torques
Because the inverse dynamic model of the mechanism under study is underdetermined with six nonlinear equations and eight unknowns, actuating torques can be optimally distributed to meet different dynamic performances. In this optimisation problem, the eight unknowns are the optimal variables, and physical constraints include:
Constraint forces cannot exceed the axial and radial loading capacities of the chosen actuator in the prototype;
The output power of the actuator is below its maximum power capacity;
The inverse dynamic model, Equation (50), is the nonlinear equality constraint.
Based on the physical application of the mechanism, three optimal goals are individually set to produce different performances.
As far as the initial guess under the three optimal goals is concerned, at t = 0, and are used as the initial guess, and the obtained values of and FZ are used as the initial guess of the optimisation scheme at the next time instant. This loop is repeated for each time interval until the end of the timeline.
4.5.1. Minimal Actuating Torques
This goal can be mathematically defined as
where is the two-norm sum of . The physical meaning of this goal is to minimize the output torque from the actuator, in favour of motor sizing in the design stage of the mechatronics system. In fact, this goal is often achieved in PMs with redundant actuations by virtue of the Moore–Penrose pseudo-inverse matrix to directly compute , as in [40,41,42,43]. However, in Equation (50), and have different units, and the nonlinear term exists. Henceforth, a more complex optimisation algorithm is needed to numerically compute and simultaneously.
4.5.2. Minimal Constraint Forces at S1~S6
As shown from Equations (38) and (46), directly influences constraint wrenches at Gi. Because the chewing behaviours of human beings to be mimicked by the designed mechanism are approximately periodic, large constraint wrenches at Gi bring large vibrations and impulses to the base and neighbouring devices. As such, a second goal is set as
which can minimize the constraint forces at Si and then reduce these abovementioned negative effects.
4.5.3. Minimal Constraint Forces at HKPs
A large constraint force at a HKP tends to cause large friction and then wear and tear easily occurs in the condylar ball and the condylar socket. Regarding this, a third goal is defined as
which can minimise the constraint forces at HKPs; thus, wear and clearance caused by friction effects can be minimised.
Finally, the sequential quadratic programming (SQP) method is characterised by fast convergence, and nonlinear constraints, as mentioned above, can be easily incorporated. Thus, this method is to be employed to optimally compute the dynamic model.
It is noted that what we are concerned about is whether the designed mechanism can vividly reproduce the chewing behaviours of human subjects; thus, this robotic device can be applied in the food industry to evaluate the newly developed food properties as mentioned in Section 1. Secondly, the mechanism is actually a simplified model of the human chewing system, which has more muscles than those in the designed mechanism. In these regards, how the muscles in the human masticatory system work synchronously under the control of the central neural system is left to the oral biologists to discover.
5. Numerical Computations and Discussions
The coordinates of Gi and Si (i = 1,…,6) in frame {S}, and Mi in frame {M} are summarised in Table 1, and the geometrical and inertia parameters of the mechanism are summarised in Table 2.

Table 1.
Coordinates of Gi and Si (i = 1,…,6) in frame {S}, and Mi in frame {M} (unit: mm).

Table 2.
Mechanical parameters of the mechanism.
5.1. Computation of and
To study the dynamic model numerically, the mechanism is commanded to follow a lower incisor path of a healthy volunteer in . To track the trajectory with respect to displacement, only three scalar equations can be formatted as
where contains three position coordinates of the incisor point I in frame {M}, and is the position vector of this point in {S}, whose numerical values are exhibited in the first subplot of Figure 5. The letters D, V, and A in labels of the three subplots in the first column denote displacement, velocity, and acceleration, respectively. In Equation (55), there are only three equations but five unknowns in , i.e., theoretically, there are infinite solutions. Nonetheless, it is not easy to numerically resolve this set of nonlinear equations. From the literature, the algorithm in [44] enlightened us: to identify the solution to a transcendental equation in that paper, the equation is not computed numerically. The researchers’ logic is that the values of the unknown variables that can make the absolute value of the transcendental equation as small as possible are the solutions. By virtue of this idea, to find one feasible solution of , a single-aim optimisation problem is constructed as
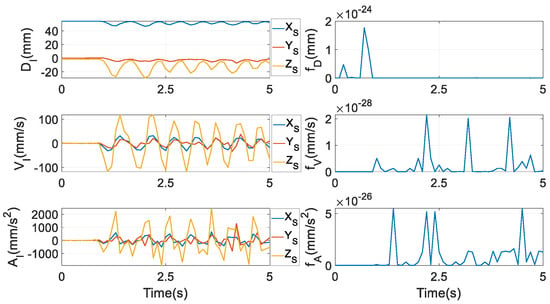
Figure 5.
An incisor trajectory of a healthy human subject and the tracking errors.
Constraints: Equations (5) and (7)
Method: SQP
The physical meaning of the aim is to track the predefined incisor trajectory with the smallest tracking error in terms of displacement. The ranges of X and Y are determined by the length and width of the socket that holds the condylar ball in the prototype, respectively.
After is obtained, can be computed by Equation (7). At t = 0, is used as initial guess, and the obtained values of are used as the initial guess of the optimisation scheme at the next time instant. The loop is repeated for each time interval until the end of the timeline.
Correspondingly, in tracking the velocity of this trajectory, cannot be uniquely determined, since, likewise, there are five unknowns in but only three equations, as
where MI is the 3 × 5 Jacobian matrix between the coordinates of the incisor point I and , and is the 3 × 1 velocity vector of the incisor trajectory, whose numerical values are given in the second subplot of the first column of Figure 5. From Equation (5), constraint equations from the velocity and the acceleration levels can be attained by differentiating it with respect to time once and twice, respectively
Thus, to reach one feasible solution of , a second optimisation problem is set as
Constraints: Equations (10) and (58)
Method: SQP
where numerical values of in MI are fed from those computed by Equation (56). The physical meaning of this aim is to track the predefined incisor trajectory with the smallest tracking error in terms of velocity. At t = 0, is used asan initial guess, and the obtained values of are used as the initial guesses of the optimisation scheme at the next time instant. The loop is repeated for each time interval until the end of the timeline.
Finally, to compute , only three scalar equations can be written as
where is the predefined 3 × 1 acceleration vector of the incisor point I, whose numerical values are shown in the third subplot of the first column of Figure 5, and is the first time-rate of . Identically, to reach a feasible solution of , a third optimisation problem is set as
Constraints: Equations (11) and (59)
Method: SQP
where numerical values of in MI and are fed from those computed in Equations (56) and (60). The physical meaning of this aim is to track the predefined incisor trajectory with the smallest tracking error in terms of acceleration. After this, and can be computed from Equation (10) and Equation (11), respectively. At t = 0, is used as initial guess, and the obtained values of are used as the initial guess of the optimisation scheme at the next time instant. The loop is repeated for each time interval until the end of the timeline.
By these three optimisation procedures, the numerical values of fD, fV, and fA are obtained as in the second column of Figure 5, being very tiny. Thus, the predefined incisor trajectory is reckoned to be tightly followed in terms of displacement, velocity, and acceleration. Correspondingly, all are shown in the first seven subfigures of Figure 6, where D, V, and A mean displacement, velocity, and acceleration, respectively, and the subscripts T and R indicate translation and rotation, respectively. Unambiguously, the motion range of the parasitic motion variable Z is far larger than that of X and Y, and the magnitudes of and are also far larger than their counterparts. This discovery is very different from [45], where parasitic motions are required to be as small as possible. Additionally, the magnitudes of θ1 and θ3 are nearly equivalent, due to the coefficient in front of θ1 in the formula of θ3 from Equation (7) being almost equal 1. and are computed by Equations (12) and (14), and they are given in the last two subfigures.
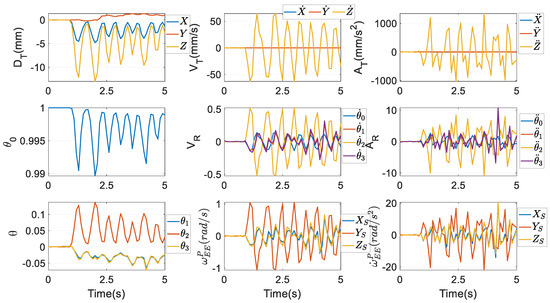
Figure 6.
Motions of the end effector by .
.
Note that by following the predefined incisor trajectory, the denominator of θ3 as in Equation (7), is nonzero. Perhaps in the entire workspace of the mechanism, there are some configurations where the denominator of θ3 is zero; then θ3 cannot be computed from Equation (7), and probably some other coordinates in the four Euler parameters would be switched as parasitic motion variables. It is worth a deeper investigation in the future work.
5.2. Transformation Between Euler Parameters and Euler Angles
A critical reason to employ Euler parameters to describe the constrained motions of the end effector is to reduce the computational cost, as stated in Section 1. To this end, for a fair comparison, the end effector must undergo identical motions as expressed by Euler parameters if some other sets of parameters are employed, such as Euler angles. However, this cannot be realised in the target PM due to DCFB. The reason is as follows.
Firstly, when Euler angles are used to describe the rotation of the end effector, the parameters describing its configuration are grouped in a 6 × 1 vector as in Equation (3) of [20]
where XA, YA, and ZA are the coordinates of OM in the inertia frame {S}, and α, β, and γ are the XYZ Euler angles. A superscript A is added to indicate parameters expressing translations are used together with Euler angles. Then, the four DOFs are grouped in a 4 × 1 vector as
For the parasitic motions, ZA owns a completely identical expression as Z in Equation (7); however, the rotation matrix in it is expressed by Euler angles. The parasitic Euler angle in Equation (5) of [20] is repeated here as
where s(·) and c(·) indicate sin(·) and cos(·), respectively.
Thereby, by virtue of Euler angles, these parasitic motions are full of trigonometric functions. Note that two translational DOFs along the Xs and Ys axes of {S} exist in both and . As such, to derive the passage from Euler parameters to Euler angles, one can easily define
where is the rotation matrix calculated by α, β, and γ. Then, an identical posture of the end effector in terms of both the translation of OM and the orientation of the end effector can be achieved by Euler parameters and Euler angles. The three Euler angles can be computed by
where rij (i, j = 1,…,3) means the element at the ith row and jth column of the rotation matrix in Equation (4).
However, one identical twist of the end effector is not easy to be reached by these two sets of parameters. Apart from Equation (12), the twist using can also be written in the form of
where is the 6 × 4 twist-shaping matrix and is the first time-rate of .
If tEE from Equations (12) and (68) is equivalent, we can find
where I2 is the 2 × 2 identity matrix, and O2 are the 2 × 3 and 2 × 2 zero matrix, respectively, M1b2 is the 4 × 5 submatrix of M1b containing its third to the sixth rows, and MA2 is the 4 × 4 submatrix of MA containing its third to the sixth rows. Thus, from the first two rows of Equation (69), we can find
In fact, this can also be attained from the first two equations of Equation (66). Afterwards, from the last four rows, we can obtain
where and . It derives that
If the twist of the end effector tEE is predefined from , i.e., Equation (12), then we need to compute and from Equation (72); however, the four rows of are generally independent. Thus, it is an overdetermined set of linear equations. It is not easy to find the solutions to and . Likewise, if tEE is predefined from , i.e., Equation (68), then we need to compute ~ from Equation (72), and generally the four rows of M1b22 are independent. Thus, it is not easy to find the solutions to ~ neither.
Following the same logic, a first time-rate of the twist using Euler parameters cannot be equivalently expressed by Euler angles, and vice versa. This phenomenon is clearly caused by DCFB which produce parasitic motions and then reduce the number of DOFs. In summary, an identical configuration can be reached by Euler parameters and Euler angles, whilst these two sets of parameters can reach neither an identical twist nor its first time-rate.
In this regard, the optimisation procedure in Section 5.1 is implemented again to obtain , which are independent of the procedures to compute . Then, from Section 3 of [20], and can be computed as given in Figure 7, and can be further attained by differentiating . These values are used in the dynamic model to make a relatively fair comparison, to find which set of parameters is more computationally efficient.
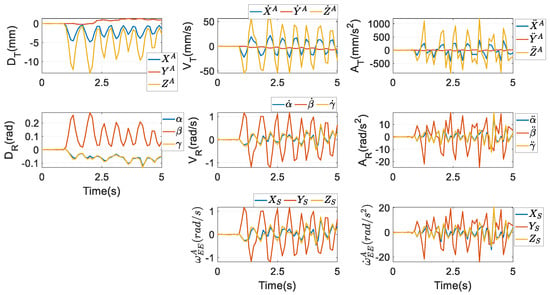
Figure 7.
Motions of the end effector by .
From Figure 6 and Figure 7, their first subplots are equivalent, as stated after Equation (66). However, as far as the first time-rate of the coordinates of the mass centre OM is concerned, from the second subplot, differences between and , and those between and are much more apparent. The same conclusions can also be made in terms of the second time-rate of the coordinates of OM, as shown in the third subplot. From the subplots about rotations, though the profiles of θ1~θ3 are very close to those of α, β, and γ, their amplitudes are clearly not equivalent. Through the optimisation scheme in Equation (56), the coefficient in front of θ1 in the formula of θ3 from Equation (7) almost equals 1. Besides, the analogous optimisation scheme also renders the value of γ almost equivalent to that of α through Equation (64).
The profiles of the rotational velocity computed via Euler parameters at the bottom row of Figure 6 are similar to those of the rotational velocity computed via Euler angles at the bottom row of Figure 7. Actually, their numerical values are different at every time instant, however. The same conclusion can be reached by the rotational acceleration. The differences between and are displayed in the first subplot of Figure 8, while in the second one, the differences between and are presented.
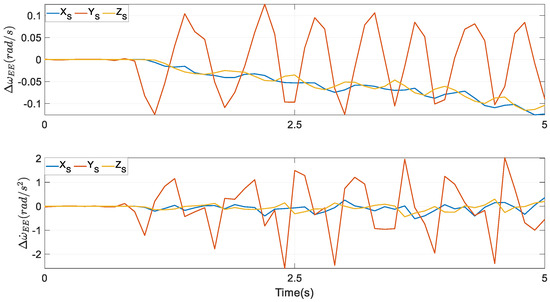
Figure 8.
Angular velocity and angular acceleration differences were computed from Euler parameters and Euler angles in the end effector of the target mechanism.
5.3. Dynamic Performances
Corresponding to the three optimal goals in Section 4.5, the following performance indices are set to justify the optimisation problem:
where N is the number of sampling instants along the timeline, is the two-norm sum of the specific vector at the ith instant. The physical meanings of F1~F3 are to compute the mean values of the two-norm sum of the actuating torques, the constraint forces at HKPs along the ZS axis, and the constraint forces at Si (i = 1,…,6), respectively, along the timeline. They correspond to the three optimal goals in Section 4.5 sequentially.
Additionally, some other indices are set to see their strong correlations with F2 and F3
where . The physical meanings of F4~F7 are to compute the mean values of the two-norm sum of the friction torques at active revolute joints, the constraint moments at Gi (i = 1,…,6), the sum of the friction forces at two HKPs, and the constraint forces at Gi (i = 1,…,6), respectively, along the timeline. Evidently, from the derivation of the dynamic model in Section 4.1, Section 4.2, Section 4.3 and Section 4.4, F4~F6 and F7 are tightly related to F2 and F3, respectively. By setting these performance indices, the correctness of the computations can be verified.
In general, true friction coefficients in the friction model are identified in practice to compensate for their effects; in this paper, their values are assumed to show the friction effects, however. Their practical identification will be performed in the future. For the Coulomb and viscous friction model, all the coefficients are set as
An experimentally measured reacted chewing force in {S} on peanuts by an orally healthy male volunteer on his molars, as in Figure 9, acts on the lower left molar at point B. The magnitude in the vertical direction in the inertia frame is far larger than its components along the XS and YS axes in every stroke, indicating that larger bite forces in this direction are needed to chew the peanuts.
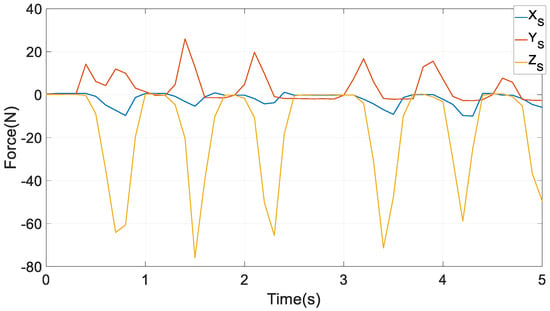
Figure 9.
Reaction forces from chewing on peanuts to the molar in {S} [20].
Under the first aim in Equation (52), actuating torques , friction torques , constraint forces FZ, and friction forces at Ti are given in Figure 10. All these variables are following an identical rhythm. Evidently, there is a certain degree of symmetry between and , and (i = 1,3,5), respectively. At most of the time instants, and are negative and positive, respectively, indicating that the right and left condylar balls are receiving constraint forces from the upper and lower surfaces of the two condylar sockets, respectively. That is because a reacted bite force FB is acting at a left molar, tending to rotate the end effector around the positive direction of the XS axis. Additionally, has larger peaks than , then friction peaks at TR are accordingly larger than those at TL.
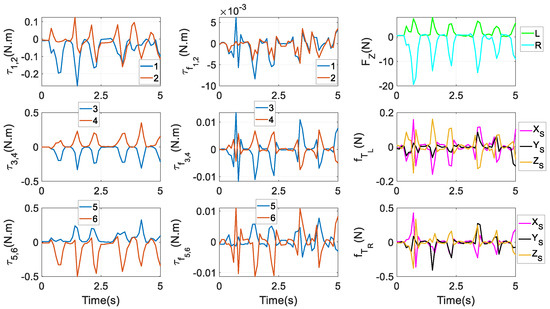
Figure 10.
Actuating torques and friction torques at active revolute joints, and constraint forces and friction forces at HKPs under the first optimal goal in Equation (52).
The proportions between friction effects and actuating torques in each actuator are computed as
where is the ith entry of , and is the 6 × 1 friction torque vector accounting for friction effects at both HKPs and actuators with respect to the output shafts of actuators.
Numerical results under the three optimal goals are displayed in the three columns of Figure 11, respectively. Under the first aim, the proportion in the second actuator can even reach up to over 6000% at t = 1 s. The largest proportion in the fourth actuator is over 100% at t = 0, and at t = 2.7 s, the largest proportion in the fifth actuator is approximately 60%. Under the second aim, one can also find that at t = 0.1 s and 3.8 s, the proportion in the fourth actuator is over 350%, and at t = 2.9 s, 3.7 s, and 4.4 s, the proportion in the fifth actuator is between 50% and 100%. Finally, under the third aim, at t = 4.6 s, the proportion in the fourth actuator is over 100%. This shows that the friction has negative effects that cannot be ignored in the motion accuracy, and lubrications are needed to reduce wear at HKPs and revolute joints. Additionally, the proportions vary significantly across different optimal goals for torque distributions. Under the third goal, in the first and second actuators, the proportions are limited between , being very consistent.
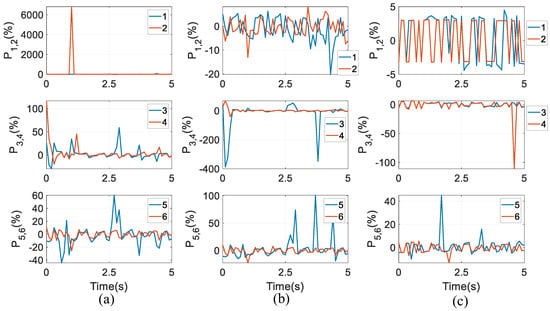
Figure 11.
Proportions between friction effects and actuating torques under three optimal goals: (a) the first goal, (b) the second goal, and (c) the third goal.
Constraint forces at Si (i = 1,…,6) are given in Figure 12. It is interesting to notice that at S1, the components along the XS and YS axes are nearly equivalent, whilst at S2, the component along the YS axis has the highest peak. At S3 and S4, the component along the XS axis experiences the largest magnitude, while at S5 and S6, the component along the ZS axis has the largest magnitude. In Equation (37), from to constraint forces at Gi, only one term is needed; while in the prototype, the crank is not heavy. As a result, the graphical exhibitions of and do not have a significant difference. The figure of is not provided to save pages. Constraint moments at Gi around and axes are given in Figure 13. By comparing it with the first column of Figure 10, apparently, the magnitude of constraint moments is much smaller than that of actuating torques. Under the second and third optimal goals, the profiles of actuating torques and friction torques at revolute joints, constraint forces and friction forces at Ti (i = L, R), constraint forces at Si (i = 1,…,6), and constraint moments at Gi are similar to their counterparts as in Figure 8, Figure 9, Figure 10 and Figure 11. Thus, they are not depicted as saving pages.
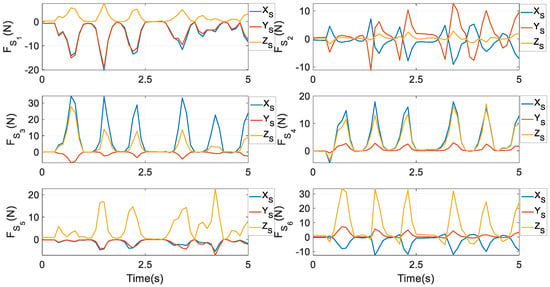
Figure 12.
Constraint forces under the first optimal goal in Equation (52).
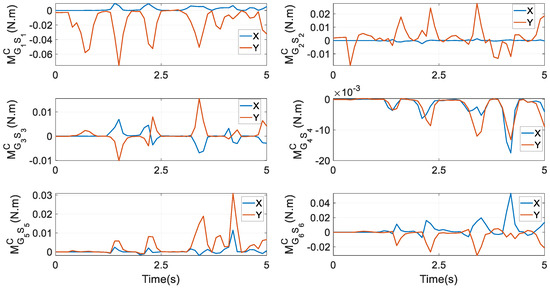
Figure 13.
Constraint moments at Gi (i = 1,…,6) under the first optimal goal in Equation (52).
To make a comparison of dynamic performances under different optimal goals, numerical values of the proposed indices in Equations (73) and (74) are given in Table 3. The performance indices are always the smallest under the corresponding optimal goals, as remarked in bold, meaning the correctness of the optimisation issues in Section 4.5. Specifically, under G3, F3 is almost zero, so friction forces there can be sharply reduced, and a longer period of utilisation of HKP-related mechanical parts can be permitted. Additionally, due to the correlation between F2 and F4~F6, the smallest F2 under G2 also gives rise to the smallest F4~F6. Owing to the strong correlation between F3 and F7, the smallest F3 under G3 also produces the smallest F7. These numerical results prove the correctness of the computation. The inverse dynamic model using also reaches the identical remarks as above-mentioned, which can be found in the second row of Table 3.

Table 3.
Dynamic performance indices in the target mechanism and the 6RSS PM.
The procedures are formatted in Matlab installed on a personal computer with an Intel (R) Xeon (R) W-2235 CPU@3.80 GHz and 32 GB of RAM. The computational time of the target PM using and under three different optimal goals is given in the first two clusters of Figure 14. The dynamic model using Euler parameters to express motions of the end effector is much less time-consuming, which is only approximately 23% of that using Euler angles. Hence, the computational demands can be considerably alleviated by Euler parameters; then real-time control is possible. It apparently proves that in and parasitic motion variables, the algebraic functions are more efficient than the trigonometric functions, generating a faster dynamic model. Additionally, the computational cost under the third optimal goal is a little heavier than that under the other two goals in the target PM.
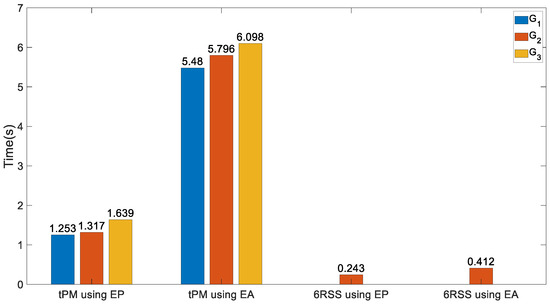
Figure 14.
Computational time of the mechanism under study from three optimal goals and its counterpart without DCFB.
5.4. The 6RSS PM
A schematic diagram of the 6RSS PM is displayed in Figure 15. From the comparison between it and Figure 1, one can see that clearly the 6RSS PM can be obtained by deleting the DCFB from the end effector, while other items are invariant.
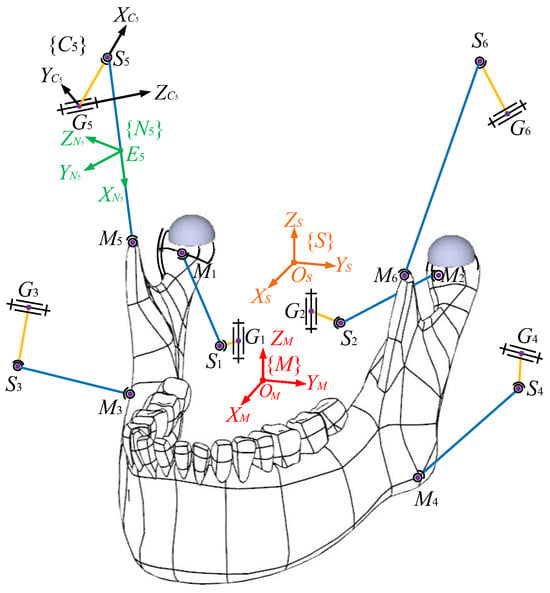
Figure 15.
Schematic diagram of the 6RSS PM.
As stated in Section 5.2, due to DCFB in the target mechanism, an identical twist and its first time-rate of the end effector cannot be achieved by and , since DCFB eliminates DOFs and produces parasitic motions. However, in the 6RSS PM with three translational DOFs and three rotational DOFs, both the angular velocity and acceleration of its end effector using Euler parameters can be easily converted to those using Euler angles, and vice versa. The reason is as follows: The two sets of parameters to describe the configuration of the end effector are
where x, y, and z are translational DOFs along the three axes in frame {S}, e is Euler parameters, and , , and are three XYZ Euler angles. Since its translations at position, velocity, and acceleration levels are completely independent of these two sets of parameters describing rotations, in the following, only the rotation at its three levels is analysed using Euler parameters and Euler angles. The angular velocity of the end effector using these two sets of parameters is expressed as
and
respectively, where
When the rotation is defined by e, the three Euler angles can be computed as
where sij (i, j = 1,…,3) means the element at the ith row and jth column of the rotation matrix defined by e. According to Equations (77) and (78), when it yields
where is directly inverted if it is not singular. Specifically, when
i.e., , is singular, corresponding to the so-called gimbal lock inherent to Euler angles. However, this configuration can be circumvented in the trajectory planning. Specifically, when tracking the incisor trajectory in Figure 5, it is not reached, fortunately. Further, the angular acceleration by Euler parameters and Euler angles is
and
respectively. Thus, the second time-rate of can be computed as
when .
On the contrary, if the rotation is defined by Euler angles , one can have the values of e from Equations (47)–(50) of [46]
where tij (i, j = 1,…,3) means the element at the ith row and jth column of the rotation matrix defined by . Because the four quantities in e are not all independent, from Equation (77), one can further write
where and means the first time-rate of e. Thus, all the three terms in can be computed as
when is invertible. The reason to choose e0 in the denominator in is that in the workspace of the 6RSS PM, e0 is nonzero. Furthermore, when , from Equation (86), one can find
Then, from
all four terms in and are available numerically. Based on this derivation, for the end effector of the 6RSS PM, two sets of rotational parameters can be available to realise identical rotations at position, velocity, and acceleration levels.
In this regard, by giving the numerical values of of the target PM directly to of the 6RSS PM, can be computed using the procedure in this section, and the end effector of the 6RSS PM can perform identical motions as those of the end effector of the target PM, as shown in Figure 6, to make a fairer and more convenient comparison in computational demands between dynamic models of these two PMs. The inverse dynamic model of the 6RSS PM can be established following the procedure in Section 4; henceforth, it is not provided again. Note that because this mechanism has six actuations and six DOFs, its actuating torques have a closed-form solution without the optimisations in Section 4.5. On this basis, its dynamic performance is shown in the last two lines of Table 1, where the indices are completely identical. More precisely, the differences and difference ratios of actuating torques are given in Figure 16, where
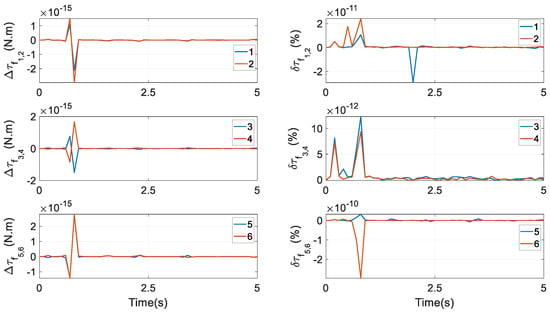
Figure 16.
Differences and difference ratios of actuating torques of the 6RSS PM using Euler parameters and Euler angles.
and are the output torque by the ith actuator and calculated from the model using Euler parameters and Euler angles, respectively. These differences are very minor, indicating that under one identical motion expressed by these two sets of parameters, actuations are invariant. An identical exhibition can also be observed in friction torques at revolute joints. For the sake of brevity, their graph is not provided.
The computational time of the dynamic model of the 6RSS PM using Euler parameters is only approximately 60% of that using Euler angles, as shown in Figure 14, which again denotes that Euler parameters are more efficient than Euler angles. From the comparison between the mechanism under study and the 6RSS PM in Figure 14, DCFB significantly raises the modelling burden in kinematics and dynamics. Furthermore, one interesting discovery in Table 1 is, for the target PM under the third goal, i.e., Equation (54), all indices are close to those of the 6RSS PM, the constraint forces at HKPs being nearly zero, as if in the mechanism under study there were no DCFB to the end effector. Henceforth, the optimisation procedures play an important role in attaining it.
6. Conclusions
In this paper, the rotation of the end effector of a PM constrained directly by the base at two HKPs was expressed via Euler parameters, and the inverse dynamic model was built with friction effects at HKPs and active revolute joints using Newton–Euler’s law. Five conclusions can be drawn as follows:
- 1.
- The computational demand in the dynamic model with Euler parameters is only approximately 23% of that using Euler angles. Likewise, great computational savings can be achieved in the 6RSS PM. Thus, Euler parameters are an elegant alternative to Euler angles in releasing the nonlinearity and reducing the computational cost.
- 2.
- Euler parameters can be converted smoothly to Euler angles to realise identical configurations of the end effector of the PM under study. However, neither its twist nor the first time-rate of the twist can be set equivalent to these two sets of parameters. On the contrary, rotations of the end effector in the 6RSS PM can be set identically at the levels of angular displacement, velocity, and acceleration using Euler parameters and Euler angles. It is the DCFB that introduces these difficulties.
- 3.
- Friction effects at HKPs and revolute joints are strongly coupled via constraint forces at lower kinematic pairs as intermediate variables, and they significantly raise the nonlinearity of the dynamic model.
- 4.
- From the comparison between the mechanism under study and the 6RSS PM, even if DCFB is applied to the end effector, it considerably increases the computational demands in the former, actuating torques can be optimised to achieve different dynamic performances under different optimal goals. Performance indices that have strong relations with those under the predefined goals also reach their optimal values. By contrast, the inverse dynamic model of the 6RSS PM has a unique closed-form solution once its motions are predefined.
- 5.
- In the target PM, the computational cost under the third optimal goal is a little heavier than that under the other two goals, but this goal can facilitate a longer utilisation time of HKP-related mechanical parts. Under this goal, the performance indices of the target PM are almost equivalent to those of the 6RSS PM.
The dynamic model of the target mechanism using Euler parameters under the third goal will be incorporated into a motion controller design in experiments in our future work. Friction effects at HKPs and active joints will be identified offline and compensated for to raise the control accuracy.
Author Contributions
Conceptualization, C.C.; methodology, C.C. and Y.L.; software, Y.L.; validation, Y.L.; investigation, C.C.; resources, X.Y.; data curation, C.C.; writing—original draft preparation, C.C.; writing—review and editing, Y.L.; supervision, X.Y.; project administration, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The study is supported by a grant from the Natural Science Foundation of Shaanxi Province under Grant No. 2025JC-YBMS-507-8.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available from the corresponding author under a reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, W.; Bronlund, J. Mastication Robots: Biological Inspiration to Implementation; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Cheng, C.; Xu, W.; Shang, J. Kinematics, stiffness and natural frequency of a redundantly actuated masticatory robot constrained by two point-contact higher kinematic pairs. In IEEE/RSJ International Conference on Intelligent Robots and Systems; IEEE: Hamgburg, Germany, 2015; pp. 963–970. [Google Scholar]
- Chen, C.; Liao, T. Trajectory planning of parallel kinematic manipulators for the maximum dynamic load-carrying capacity. Meccanica 2016, 51, 1653–1674. [Google Scholar] [CrossRef]
- Chen, G.; Wang, H.; Lin, Z. A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance. Mech. Mach. Theory 2013, 64, 1–17. [Google Scholar] [CrossRef]
- Han, J.; Wang, P.; Dong, F.; Zhao, X.; Chen, S. Optimal design of adaptive robust control for a planar two-DOF redundantly actuated parallel robot. Nonlinear Dyn. 2021, 105, 2341–2362. [Google Scholar] [CrossRef]
- Corbel, D.; Gouttefarde, M.; Company, O.; Pierrot, F. Actuation Redundancy as a Way to Improve the Acceleration Capabilities of 3T and 3T1R Pick-and-Place Parallel Manipulators. J. Mech. Robot. 2010, 2, 041002. [Google Scholar] [CrossRef]
- Wang, L.; Wang, D.; Wu, J. Dynamic performance analysis of parallel manipulators based on two-inertia-system. Mech. Mach. Theory 2019, 137, 237–253. [Google Scholar] [CrossRef]
- Merlet, J. Parallel Robots; Springer Science & Business Media: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Zou, Q.; Zhang, Y.; Shi, Y.; Zhang, S.; Zhang, Y. Mechanical Design and Analysis of a Novel Symmetrical 2T1R Parallel Robot. Electronics 2025, 14, 1596. [Google Scholar] [CrossRef]
- Russo, M.; Zhang, D.; Liu, X.; Xie, Z. A review of parallel kinematic machine tools: Design, modeling, and applications. Int. J. Mach. Tools Manuf. 2024, 196, 104118. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J. Parallel Kinematics: Type, Kinematics, and Optimal Design; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zou, Q.; Shi, Y.; Zhang, S.; Zhang, H.; Li, L.; Huang, G.; Zhang, D. Design and Performance Analysis of a Novel Group of Translational Parallel Robots for a Three-Axis Grinding Machine. Electronics 2025, 14, 427. [Google Scholar] [CrossRef]
- Jia, Y.; Chen, X.; Zhang, L.; Ning, C. Dynamic characteristics and reliability analysis of parallel mechanism with clearance joints and parameter uncertainties. Meccanica 2023, 58, 813–842. [Google Scholar] [CrossRef]
- Guo, F.; Cheng, G.; Pang, Y. Explicit dynamic modeling with joint friction and coupling analysis of a 5-DOF hybrid polishing robot. Mech. Mach. Theory 2022, 167, 104509. [Google Scholar] [CrossRef]
- Liao, B.; Lou, Y.; Li, Z.; Shi, J.; Chen, X. Design and analysis of a novel parallel manipulator for pick-and-place applications. Meccanica 2016, 51, 1595–1606. [Google Scholar] [CrossRef]
- Leonardis, D.; Santamato, G.; Gabardi, M.; Solazzi, M.; Frisoli, A. A parallel-elastic actuation approach for wide bandwidth fingertip haptic devices. Meccanica 2022, 57, 739–749. [Google Scholar] [CrossRef]
- Di Gregorio, R.; Callegari, M.; Battistelli, M. Real-time algorithm based on two extra sensors for monitoring platform’s orientation of underactuated parallel wrists. Meccanica 2016, 51, 1535–1545. [Google Scholar] [CrossRef]
- Wen, K.; Nguyen, T.; Harton, D.; Laliberté, T.; Gosselin, C. A backdrivable kinematically redundant (6 + 3)-degree-of-freedom hybrid parallel robot for intuitive sensorless physical human–robot interaction. IEEE Trans. Robot. 2021, 37, 1222–1238. [Google Scholar] [CrossRef]
- Lapierre, M.; Gosselin, C. A Parallel SCARA Robot With Low-Impedance Backdrivability and a Remotely Operated Gripper With Unlimited Rotation. IEEE Robot. Autom. Lett. 2024, 9, 3980–3987. [Google Scholar] [CrossRef]
- Cheng, C.; Yuan, X.; Chen, Y.; Dang, Y. Rigid-body inverse dynamics of a spatial redundantly actuated parallel mechanism constrained by two point contact higher kinematic pairs. Mech. Ind. 2023, 24, 28. [Google Scholar] [CrossRef]
- Nikravesh, P.; Wehage, R.; Kwon, O. Euler Parameters in Computational Kinematics and Dynamics. Part 1 J. Mech. Transm. Autom. Des. 1985, 107, 358–365. [Google Scholar] [CrossRef]
- Nikravesh, P.; Chung, I. Application of Euler Parameters to the Dynamic Analysis of Three-Dimensional Constrained Mechanical Systems. J. Mech. Des. 1982, 104, 785–791. [Google Scholar] [CrossRef]
- Nikravesh, P.; Kwon, O.; Wehage, R. Euler Parameters in Computational Kinematics and Dynamics. Part 2 J. Mech. Transm. Autom. Des. 1985, 107, 366–369. [Google Scholar] [CrossRef]
- Yuan, W.; Tsai, M. A novel approach for forward dynamic analysis of 3-PRS parallel manipulator with consideration of friction effect. Robot. Comput.-Integr. Manuf. 2014, 30, 315–325. [Google Scholar] [CrossRef]
- Yuan, J. Closed-loop manipulator control using quaternion feedback. IEEE J. Robot. Autom. 1988, 4, 434–440. [Google Scholar] [CrossRef]
- Rahmani, H.; Saha, S.; Rao, P. An improved dynamic modeling of a multibody system with spherical joints. Multibody Syst. Dyn. 2009, 21, 325–345. [Google Scholar] [CrossRef]
- Horn, B. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Kong, X. Reconfiguration analysis of a 3-DOF parallel mechanism using Euler parameter quaternions and algebraic geometry method. Mech. Mach. Theory 2014, 74, 188–201. [Google Scholar] [CrossRef]
- Yu, J.; Jin, Z.; Kong, X. Identification and Comparison for Continuous Motion Characteristics of Three Two-Degree-of-Freedom Pointing Mechanisms. J. Mech. Robot. 2017, 9, 051015. [Google Scholar] [CrossRef]
- Kong, X. Classification of a 3-RER Parallel Manipulator Based on the Type and Number of Operation Modes. J. Mech. Robot. 2021, 13, 021013. [Google Scholar] [CrossRef]
- Hui, J.; Pan, M.; Zhao, R.; Luo, L.; Wu, L. The closed-form motion equation of redundant actuation parallel robot with joint friction: An application of the Udwadia-Kalaba approach. Nonlinear Dyn. 2018, 93, 689–703. [Google Scholar] [CrossRef]
- Shan, X.; Cheng, G. Structural error and friction compensation control of a 2(3PUS + S) parallel manipulator. Mech. Mach. Theory 2018, 124, 92–103. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.; Wang, L.; Yu, Z. Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot. Comput.-Integr. Manuf. 2020, 63, 101923. [Google Scholar] [CrossRef]
- Shang, W.; Cong, S.; Zhang, Y. Nonlinear friction compensation of a 2-DOF planar parallel manipulator. Mechatronics 2008, 18, 340–346. [Google Scholar] [CrossRef]
- Gogu, G. Mobility of mechanisms: A critical review. Mech. Mach. Theory 2005, 40, 1068–1097. [Google Scholar] [CrossRef]
- Gosselin, C.; Schreiber, T. Redundancy in Parallel Mechanisms: A Review. Appl. Mech. Rev. 2018, 70, 010802. [Google Scholar] [CrossRef]
- Sarabandi, S.; Thomas, F. A Survey on the Computation of Quaternions From Rotation Matrices. J. Mech. Robot. 2019, 11, 021006. [Google Scholar] [CrossRef]
- Udwadia, F.; Schutte, A. An Alternative Derivation of the Quaternion Equations of Motion for Rigid-Body Rotational Dynamics. J. Appl. Mech. 2010, 77, 044505. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Claro, J.C.P.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Liu, X.; Yao, J.; Li, Q.; Zhao, Y. Coordination dynamics and model-based neural network synchronous controls for redundantly full-actuated parallel manipulator. Mech. Mach. Theory 2022, 160, 104284. [Google Scholar] [CrossRef]
- Liu, S.; Peng, G.; Gao, H. Dynamic modeling and terminal sliding mode control of a 3-DOF redundantly actuated parallel platform. Mechatronics 2019, 60, 26–33. [Google Scholar] [CrossRef]
- Yan, P.; Huang, H.; Li, B.; Zhou, D. A 5-DOF redundantly actuated parallel mechanism for large tilting five-face machining. Mech. Mach. Theory 2022, 172, 104785. [Google Scholar] [CrossRef]
- Liu, Z.; Tao, R.; Fan, J.; Wang, Z.; Jing, F.; Tan, M. Kinematics, dynamics, and load distribution analysis of a 4-PPPS redundantly actuated parallel manipulator. Mech. Mach. Theory 2022, 167, 104494. [Google Scholar] [CrossRef]
- Bestle, D.; Abbas, L.; Rui, X. Recursive eigenvalue search algorithm for transfer matrix method of linear flexible multibody systems. Multibody Syst. Dyn. 2013, 32, 429–444. [Google Scholar] [CrossRef]
- Carretero, J.; Podhorodeski, R.; Nahon, M.; Gosselin, C. Kinematic Analysis and Optimization of a New Three Degree-of-Freedom Spatial Parallel Manipulator. J. Mech. Des. 1999, 122, 17–24. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson, Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).