Next Article in Journal
Comprehensive Stiffness Modeling and Evaluation of an Orthopedic Surgical Robot for Enhanced Cutting Operation Performance
Previous Article in Journal
Three Strategies Enhance the Bionic Coati Optimization Algorithm for Global Optimization and Feature Selection Problems
Previous Article in Special Issue
Investigation of Droplet Spreading and Rebound Dynamics on Superhydrophobic Surfaces Using Machine Learning
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomimetics
Volume 10
Issue 6
10.3390/biomimetics10060382
biomimetics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Surfactant on Bubble Formation on Superhydrophobic Surface in Quasi-Static Regime

by
Hangjian Ling
*,
John Ready
and
Daniel O’Coin
Department of Mechanical Engineering, University of Massachusetts Dartmouth, Dartmouth, MA 02747, USA
*
Author to whom correspondence should be addressed.
Biomimetics 2025, 10(6), 382; https://doi.org/10.3390/biomimetics10060382
Submission received: 6 May 2025 / Revised: 21 May 2025 / Accepted: 5 June 2025 / Published: 7 June 2025
(This article belongs to the Special Issue Bioinspired Superhydrophobic Surfaces: Challenges, Solutions and Applications)
Browse Figures
Review Reports Versions Notes

Abstract

We experimentally studied the effect of a surfactant on bubble formation on a superhydrophobic surface (SHS). The bubble was created by injecting gas through an orifice on the SHS at a constant flow rate in the quasi-static regime. The surfactant, 1-pentanol, was mixed with water at concentration C ranging from 0 to 0.08 mol/L, corresponding to surface tension σ ranging from 72 to 43 mN/m. We found that as C increased, the bubble detachment volume (Vd) and maximum bubble base radius (Rdmax) decreased. For a low surfactant concentration, the static contact angle θ0 remained nearly constant, and Vd and Rdmax decreased due to lower surface tensions, following the scaling laws Rdmax~σ1/2 and Vd~σ3/2. The bubble shapes at different concentrations were self-similar. The bubble height, bubble base radius, radius at the bubble apex, and neck radius all scaled with the capillary length. For high surfactant concentrations, however, θ0 was greatly reduced, and Vd and Rdmax decreased due to the combined effects of reduced θ0 and smaller σ. Lastly, we found that the surfactant had a negligible impact on the forces acting on the bubble, except for reducing their magnitudes, and had little effect on the dynamics of bubble pinch-off, except for reducing the time and length scales. Overall, our results provide a better understanding of bubble formation on complex surfaces in complex liquids.

1. Introduction

Recently, superhydrophobic surfaces (SHSs), inspired by lotus leaves and animal skins, have been proven to be a new approach to control bubble formation [1,2,3,4,5] and bubble movement [6]. An SHS exhibits a large static contact angle of θ0 > 150° due to a combination of surface roughness and hydrophobic chemistry [7]. Due to the large θ0, the SHS facilitates the formation of larger bubbles than do hydrophilic and hydrophobic surfaces. SHSs have found a wide range of applications, from reducing drag in turbulent flows [8,9,10,11] to enhancing boiling heat transfer [1,2] and preventing engineered surfaces from undergoing biofouling [12] and icing [13]. Most of these applications take advantage of the presence of the gas layer on SHSs. Understanding bubble formation on SHSs could potentially provide new solutions to sustain the gas layer on the surface and thus benefit the broader applications of SHSs. Furthermore, controlling bubble formation in liquid solutions is crucial for many other industrial and biomedical applications, including pool boiling heat transfer [14], surface cleaning [15], chemical processing [16], mineral particle recovery [17], and drug delivery [18].
Bubble formation due to gas injection through a nozzle or orifice has been extensively investigated [19,20]. The detached bubble volume (Vd) is affected by many parameters, including the liquid properties [21,22,23,24,25], surface tension [26], gravity [27], surface wettability [28,29,30], orifice configuration [31,32,33], and gas flow rate [34,35]. Depending on the gas flow rate Q, the bubble formation can be separated into two regimes [36]: the quasi-static regime for small Q and the dynamic regime for large Q. In the quasi-static regime, the main forces acting on the bubble are due to surface tension and hydrostatic pressure, and Vd is independent of the gas flow rate [36]. In the dynamic regime, the forces due to the momentums of liquid and gas cannot be ignored, and Vd increases with the gas flow rate [37]. Depending on the surface wettability, bubble formation follows two modes [38]: the pinning mode for well-wetting surfaces (i.e., hydrophilic) and the de-pinning mode for poorly wetting surfaces (i.e., hydrophobic). In the pinning mode, the bubble base remains pinned at the rim of the orifice, whereas in the de-pinning mode, the bubble base expands beyond the orifice rim, leading to a larger Vd [39,40]. Furthermore, for hydrophobic surfaces, with increasing static contact angle θ0, the bubble base radius increases, resulting in a larger Vd [38].
Bubble formation on SHSs has received growing interest recently. A few researchers [41,42,43,44] investigated the effect of the size of the SHS region on bubble formation under a quasi-static regime. They found that with increasing size of the SHS, the bubble formation transitions from the pinning mode, where the bubble base is pinned at the rim of the SHS, to the de-pinning mode, where the bubble base moves along the SHS. Breveleri et al. [45] studied the bubble formation on an SHS fabricated on a porous material and found an increase in the bubble size with increasing pressure difference across the porous surface. Recently, O’Coin and Ling [46] examined the effect of the gas flow rate on bubble formation on an SHS under the quasi-static regime, and they found an increase in Vd with increasing gas flow rate.
However, the effect of surfactants on bubble formation on SHSs has not been studied, despite the fact that surfactants are widely present in natural environments and are used in many engineering systems. Surfactants typically adsorb at the gas–liquid interface due to their amphiphilic properties and are well-known for reducing the surface tension. The effect of surfactants on bubble formation at the nozzle and orifice has been extensively studied [47,48,49,50,51,52,53,54,55]. It is generally agreed that at low gas flow rates, a small amount of surfactant greatly reduces the detached bubble size due to the reduction of surface tension [52,54]. However, at high gas flow rates, due to the reduced time scale of bubble formation, the surfactants do not have sufficient time to reach the equilibrium concentration at the bubble surface. As a result, at high gas flow rates, the detached bubble size in surfactant solution is close to that in pure water [52]. In addition to reducing surface tension, surfactants have been shown to reduce the static contact angle of SHSs [56,57]. Therefore, surfactants may significantly alter bubble formation on SHSs due to the changes in the surface tension and static contact angle.
The goal of this experimental study is to investigate, for the first time, the effect of surfactants on bubble formation on SHSs. We use 1-pentanol as the surfactant model and focus on bubble formation at a low gas flow rate. The time scale of bubble formation is much longer than the time needed for the surfactant to reach the equilibrium concentration, rendering the effect of dynamic surface tension negligible. We apply high-speed imaging to capture the bubble shape, measure the bubble geometrical parameters by processing the recorded images, and calculate the forces acting on the bubble. We show that for low surfactant concentrations, the static contact angle θ0 remains nearly constant, the bubble shapes at different concentrations are self-similar, and the bubble size scales with the capillary length. However, for high surfactant concentrations, θ0 is greatly reduced, and the bubble size decreases due to the combination effect of smaller θ0 and smaller σ. We also discuss the effect of 1-pentanol on the dynamics of bubble pinch-off and the forces acting on the bubble.

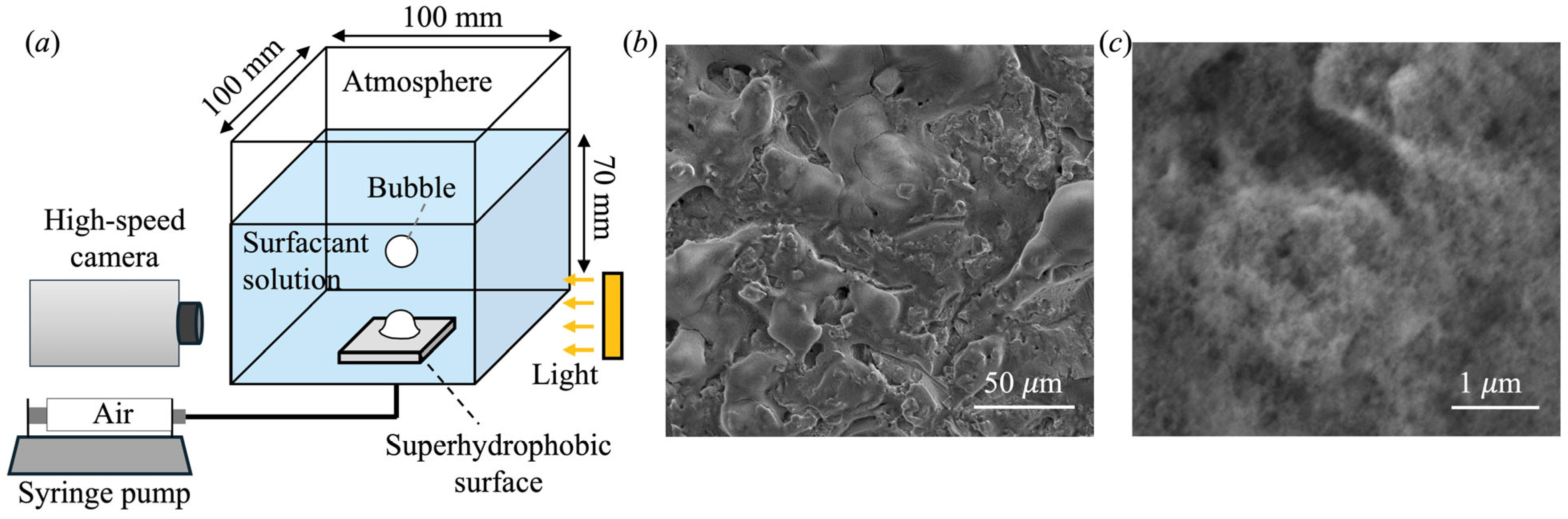
2. Materials and Methods

The experimental setup for measuring bubble formation in the surfactant solution is shown in Figure 1a. This setup was also employed in our previous studies [44,46]. A transparent acrylic tank with inner dimensions of 100 mm by 100 mm was filled with the surfactant solution (density ρL = 997 kg/m3) to a height of 70 mm. A superhydrophobic surface (SHS) with dimensions of 50 mm by 50 mm was installed at the bottom of the tank. The SHS was fabricated by sandblasting an aluminum surface with an abrasive medium of grit size 60 (particle mesh size 35 to 100), followed by spray-coating the textured surface with hydrophobic nanoparticles (SOFT99 Corp, La Habra, CA, USA, Glaco Mirror Coat Zero). The aluminum surface was cleaned in an ultrasonic bath before and after the sandblasting. Figure 1b,c show the surface texture of the SHS obtained by scanning electron microscopy. Clearly, the SHS exhibited a combination of micro- and nano-scale surface roughness. When submerged in water, the SHS maintained a Cassie–Baxter state and trapped a thin layer of air. The experiments were performed at room temperature of T = 25 °C.
The surfactant solution was prepared by mixing 1-pentanol (Sigma-Aldrich, St. Louis, MO, USA, #398268, >99%, CAS #71-41-0) with deionized (DI) water. We selected 1-pentanol as the surfactant model due to its well-characterized kinetics of dynamic adsorption [58,59]. The concentration of 1-pentanol in the solution, denoted by C, ranged from 0 to 0.08 mol/L, where C = 0 corresponded to pure water. Due to the low concentration used, the addition of surfactant to water caused no significant changes in physical properties, except for the surface tension. The equilibrium surface tension between the air and the 1-pentanol solution, denoted by σ, was measured using the pendant droplet method [60]. The pendant drop method was calibrated by measuring the surface tension of pure water. For each concentration, the measurement was repeated at least five times, and the uncertainty was less than 2 mN/m. The surface tension for pure water was found to be 72 mN/m, which agreed well with the typically reported value. Figure 2a shows the measured σ as a function of C. The results showed good agreement with the Szyszkowski model [61], expressed as
σ = σ0 − ℛT/ω ln(1 + kC)
where σ0 denotes the surface tension of pure water, ℛ is the ideal gas constant, T is the temperature, ω is the limiting partial molar area of the solute at the surface, and k is the solute adsorption coefficient. For 1-pentanol [61], ω = 1.48 × 105 m2/mol and k = 66 L/mol. Furthermore, we estimated the time scale τe for reaching the equilibrium interfacial surfactant concentration based on the following model [62]:
τe ~ (kaC/Γ∞ + kd)−1
where ka is the adsorption kinematic coefficient, kd is the desorption kinematic coefficient, and Γ∞ is the maximum interfacial surfactant concentration. For 1-pentanol solutions with different concentrations, ka, kd, and Γ∞ are constants [58,59]: ka = 3.00 × 10−3 cm/s, kd = 1.10 × 102 s−1, and Γ∞ = 5.90 × 10−10 mol/cm2. According to this model, for the current range concentration, τe < 0.006 s, which is more than two orders of magnitude smaller than the time scale of the bubbling period (~1 s). Therefore, we can safely assume that the surfactant concentration at the bubble surface reaches equilibrium during the bubble formation.
Figure 2b shows the static contact angle θ0 of the SHS as a function of C. The static contact angle was measured by the sessile-drop-fitting method with a small droplet (~5 μL) seated on the surface [63]. With increasing C from 0 to 0.05 mol/L, there was only a slight decrease in the static contact angle from 159 ± 2° to 155 ± 2°. However, with a further increase in the concentration to C = 0.08 mol/L, θ0 decreased significantly to 131 ± 2°, consistent with the observation by Mohammadi et al. [56]. This decrease in the static contact angle is likely due to the adsorption of surfactant on the SHS and the resulting reduction in interfacial energy between the liquid and solid. Previous studies [38] have also shown that for bubble formation on a hydrophobic surface (θ0 > 90°), the detached bubble volume increases with increasing θ0. Therefore, as will be shown later, for low concentrations C < 0.05 mol/L, where the change in θ0 is small, the detached bubble volume is mainly affected due to the change in surface tension. However, at high concentrations C = 0.08 mol/L, since θ0 is greatly reduced, the detached bubble volume decreases because of a combined effect of reduced surface tension and reduced θ0.
The bubble was created on the SHS by injecting air (density ρG = 1.2 kg/m3) through a 0.5 mm diameter orifice located at the center of the SHS at a constant gas flow rate. The size of the orifice was consistent with that used in the literature by Rubio-Rubio et al. [41] and Qiao et al. [43], who also investigated bubble formation on superhydrophobic surfaces. We expect that for superhydrophobic surfaces with large static contact angles (>150°), the orifice size has a negligible impact on the detached bubble size. However, for small static contact angles (<150°), the orifice size may influence bubble formation as shown by Heidarian et al. [28]. The effect of the orifice size on bubble formation is left for future investigation. A syringe pump (Model #NE-1010 SyringeONE, by New Era Pump System Inc., Farmingdale, NY, USA) was used to supply gas. To ensure a constant flow rate, the air passed through a long needle (152 mm in length, inner diameter 0.61 mm) before reaching the orifice. The bubble formation was recorded by a high-speed camera (PCO.dimax S4, Howell, MI, USA, pixel size 11 µm, 2016 × 2016 pixels) at a frame rate of 1000 frames per second. The spatial resolution of the imaging system was 34 µm/pixel. A collimated light (Thorlabs, model #QTH10, power 50 mW) was used for illumination. The data was recorded after a series of bubbles had formed and detached from the surface. The light was switched on briefly and did not change the temperature of the solution. The size of the bubble was much smaller than that of the tank. We expected that the side walls of the tank would have a negligible impact on bubble formation. The bubble formation was in the single-bubbling regime, and previously formed bubbles had minimal influence on the observed one. All experiments were performed at room temperature of 25 ± 1 °C. The acrylic tank was rinsed with deionized water at least three times prior to the experiments to ensure the purity of the surfactant solution.
Table 1 summarizes the main experimental parameters, including the 1-pentanol concentration (C), surface tension (σ), and static contact angle (θ0). The key experimental results, including the maximum bubble base radius (Rbmax) and bubble detached volume (Vd), are also provided in the table. Rbmax can be analogized to the nozzle radius for a bubble detached from a nozzle. We calculated the critical gas flow rate for the transition from the quasi-static regime to the dynamic regime as follows [36]: Qcr = π (16/3g2)1/6 (σRbmax/ρL)5/6, where g = 9.78 m2/s is the gravitational acceleration. In the current study, the gas flow rate was Q < 30 mL/min, corresponding to Q/Qcr < 0.07. The Weber number We=ρLQ2/πσRbmax3 (ratio of gas momentum to surface tension) did not exceed 2 × 10−3. At this small flow rate, the bubble formation was in the quasi-static regime, and Q had little influence on the detached bubble volume [46]. The capillary length scale, defined as lσ = (σ/ρLg)0.5, is also provided in Table 1.

3. Results and Discussion

Figure 3 shows the time evolution of bubble shapes for five different 1-pentanol concentrations: C = 0, 0.01, 0.02, 0.05, and 0.08 mol/L. With increasing C, the bubble size, along with the detached volume, gradually decreased. For all cases, the bubble formation progressed through two stages: an initial expansion stage and a final necking stage. During the expansion stage (0 < t < 0.99T0), the bubble grew in both the horizontal and vertical directions due to the gas injection. The bubble was in the quasi-static condition due to the balance between the surface tension and hydrostatic pressure. However, during the necking stage (0.99T0 < t < T0), the bubble reached its maximum equilibrium volume and could no longer maintain the quasi-static condition. Instead, the bubble shape changed dramatically under the impact of surface tension and buoyancy. The necking process can be characterized by the formation of a neck near the bubble base and a rapid reduction in the neck radius. The necking stage occupied a very small portion of the whole bubbling period. In all cases, due to the constant gas flow rate, the bubble volume increased linearly with time.
Figure 4a shows the maximum bubble base radius (Rbmax) as a function of C. Clearly, with increasing C, Rbmax reduced due to the reduced surface tension. A similar trend was observed for a hydrophobic surface made of Teflon by Mirsandi et al. [29]. Figure 4b shows the bubble detached volume (Vd) as a function of C. For comparison, the Tate volume [64] VT = 2πRbmaxσ/(ρL − ρG)g, derived based on the balance between the surface tension force and buoyancy force, was also plotted. Note that the effect of the contact angle in the expression of the Tate volume was ignored. Clearly, the trend that Vd decreased with increasing C was captured by VT. This agreement suggests that a reduction in Vd results from two factors: the decrease in σ and the decrease in Rbmax.
Figure 4c and d show Rbmax/lσ and Vd/lσ3 as a function of C, respectively. Interestingly, for low concentrations C < 0.05 mol/L, Rbmax/lσ and Vd/lσ3 were nearly constant, suggesting that the capillary length was a proper length scale for normalization. Therefore, we derived the scaling laws for Rbmax and Vd in terms of surface tension as follows:
Rbmax ~ lσ ~ σ1/2
Vd ~ lσ3 ~ σ3/2
To confirm the proposed scaling relations, Figure 5a and b present Rbmax and Vd as a function of σ, respectively. Clearly, for C < 0.05 mol/L, the two scaling laws had good agreement with the measurements. However, for the highest concentration C = 0.08 mol/L, both Rbmax and Vd were much smaller than the prediction based on the scaling laws. This is attributed to the fact that, at the highest concentration, the static contact angle was significantly reduced, leading to a further decrease in Rbmax and Vd. In general, the detached bubble size depends on both the static contact angle [38] and surface tension. We expect that the scaling laws shown in Equations (3) and (4) hold for low surfactant concentrations, where the static contact angle is not significantly modified and only the surface tension is reduced due to the presence of surfactants.
Figure 6 shows the evolutions of the bubble geometrical parameters, including the bubble height H, bubble base radius Rb, and radius at the bubble apex Ra, as a function of bubble volume V for four different 1-pentanol concentrations: C = 0, 0.02, 0.05, and 0.08 mol/L. In Figure 6a–c, results are shown in the dimensional form. In Figure 6d–f, results are shown in the dimensionless form, where lσ was chosen as the characterized length scale for normalization. Since the volume was linearly proportional to time, the curves had the same trends when plotted as a function of time. To measure these geometrical parameters, we employed an image processing method described in our previous work [44]. The procedure mainly involved a binarization of the image based on an intensity threshold to segment the region belonging to the bubble. V was calculated by accumulating the cross-sectional area at each height level from the bottom to the top of the bubble. Ra was determined by fitting the bubble apex with a circle of radius Ra. The uncertainty for determining the boundary of the bubble was less than 1 pixel or 34 µm.
As shown in Figure 6, the curves had similar trends regardless of the value of C. During the bubble growing period, with increasing volume, H increased linearly with V, Ra gradually decreased, and Rb experienced an initial increase due to bubble expansion along the horizontal surface and then became nearly constant. During the necking period, with increasing volume, all geometrical parameters changed dramatically, including a sudden increase in H and Ra and a sudden decrease in Rb due to the retraction of the contact line along the surface. With increasing C, all the geometrical parameters decreased due to the reductions in the surface tension and static contact angle. Interestingly, as shown in Figure 6d–f, showing the results in the dimensionless form, for low 1-pentanol concentrations C < 0.05 mol/L, the curves collapsed. This result implies that, for low concentrations C < 0.05 mol/L, the bubble shapes were self-similar. The capillary length was an appropriate scale for normalization, and the surfactant did not affect the kinematics of bubble formation, except for reducing the length scale. For the highest concentration C = 0.08 mol/L, the normalized curves did not overlap with others. This deviation is likely due to the significantly lower static contact angle compared to the other cases.
Figure 7 shows the evolution of the contact angle (θb) at the bubble base as a function of bubble volume for four different 1-pentanol concentrations. θb was measured by applying second-order polynomial fitting to the bubble shape near the contact point with the solid surface. Clearly, for C < 0.05 mol/L, as the bubble volume increased and as the bubble base expanded along the horizontal surface, θb was nearly a constant, consistent with the observation by Rubio-Rubio et al. [41]. Furthermore, with increasing C, the trend in θb was consistent with the trend in θ0. For low 1-pentanol concentrations C < 0.05 mol/L, the effect of C on θb was small. For the highest 1-pentanol concentration C = 0.08 mol/L, θb was much smaller than it was in other cases.
Figure 8a shows the evolution of the bubble shape just before detachment (or pinch-off) for C = 0. The time to bubble pinch-off was defined as τ, with τ = 0 as the time of pinch-off. A neck formed near the base of the bubble at τ~20 ms. Approaching the pinch-off, the neck radius decreased at an accelerated rate. We measured the minimum neck radius and defined it as Rn. Figure 8b shows the time evolutions of Rn for four different values of C. For all cases, as expected, Rn decreased to 0 as τ approached 0. Moreover, with increasing C, in agreement with the smaller bubble size, Rn decreased. However, as shown in Figure 8c, after the normalization of Rn by Rbmax and τ by the capillary–inertia time scale τn = (ρLRbmax 3/σ)0.5, all the profiles collapsed nicely and roughly agreed with the trends observed for the pinch-off of a bubble from a nozzle [65]. All profiles exhibited a power-law relation, Rn ~ τn0.57, where the exponent 0.57 is consistent with values reported in the literature [65,66,67,68] for the pinch-off of a bubble from a nozzle. This result suggests that the necking process was primarily driven by liquid inertia [66] and that the surface tension had a negligible impact on the dynamics of necking, except for reducing the length and time scales.
Finally, following our previous work [44], we performed a force balance analysis for the bubble. In the current study, since the gas flow rate was low and the bubble formation was in the quasi-static regime, the dynamic forces due to the momentums and viscosities of gas and liquid were negligible. We mainly calculated three static forces acting on the bubble: (1) the pressure force FP = (2σ/Ra + ρGgH)πRb2 mainly caused by the surface tension at the bubble apex; (2) the surface tension force FS= −2πRbσsinθb applied at the rim of the bubble base; and (3) the buoyancy force FB = (ρL − ρG)gV − ρLgHπRb2 due to the imbalance in the hydrostatic pressure applied on the bubble surface. Note that FP is in the upward direction since the pressure in the bubble is higher than that in the liquid due to surface tension, and FB is in the downward direction since the hydrostatic pressure applied on the bubble is in the downward direction.
Figure 9a and b show the three forces (FP, FS, and FB) as well as their summation FP + FB + FS as a function of bubble volume for two 1-pentanol concentrations: C = 0 and 0.08 mol/L. The forces were normalized by the buoyancy force (ρL − ρG)gVd, which corresponded to the detached bubble volume. Clearly, regardless of the value of C, the growth of the bubble was governed by similar forces: one lifting force FP and two retaining forces FS and FB. The three forces were roughly in balance (FP + FB + FS was close to 0). As the bubble volume increased, the magnitudes of FP and FB increased linearly with the volume, while FS quickly reached a nearly constant value. This result confirms that the dynamic forces due to the momentums of the injected gas and the surrounding liquid were negligible. Furthermore, this result suggests that the surface tension and static contact angle had little impact on the dynamics of bubble formation, except for reducing the magnitude of the forces.

4. Conclusions

In summary, we experimentally investigated the effect of 1-pentanol on bubble formation on a superhydrophobic surface (SHS) in the quasi-static regime. To quantify the bubble formation, we measured various geometrical parameters, including the bubble height, bubble base radius, radius at the bubble apex, contact angle, neck radius, and detached volume. We also calculated the forces acting on the bubble based on these geometrical parameters. Our key findings are summarized below:
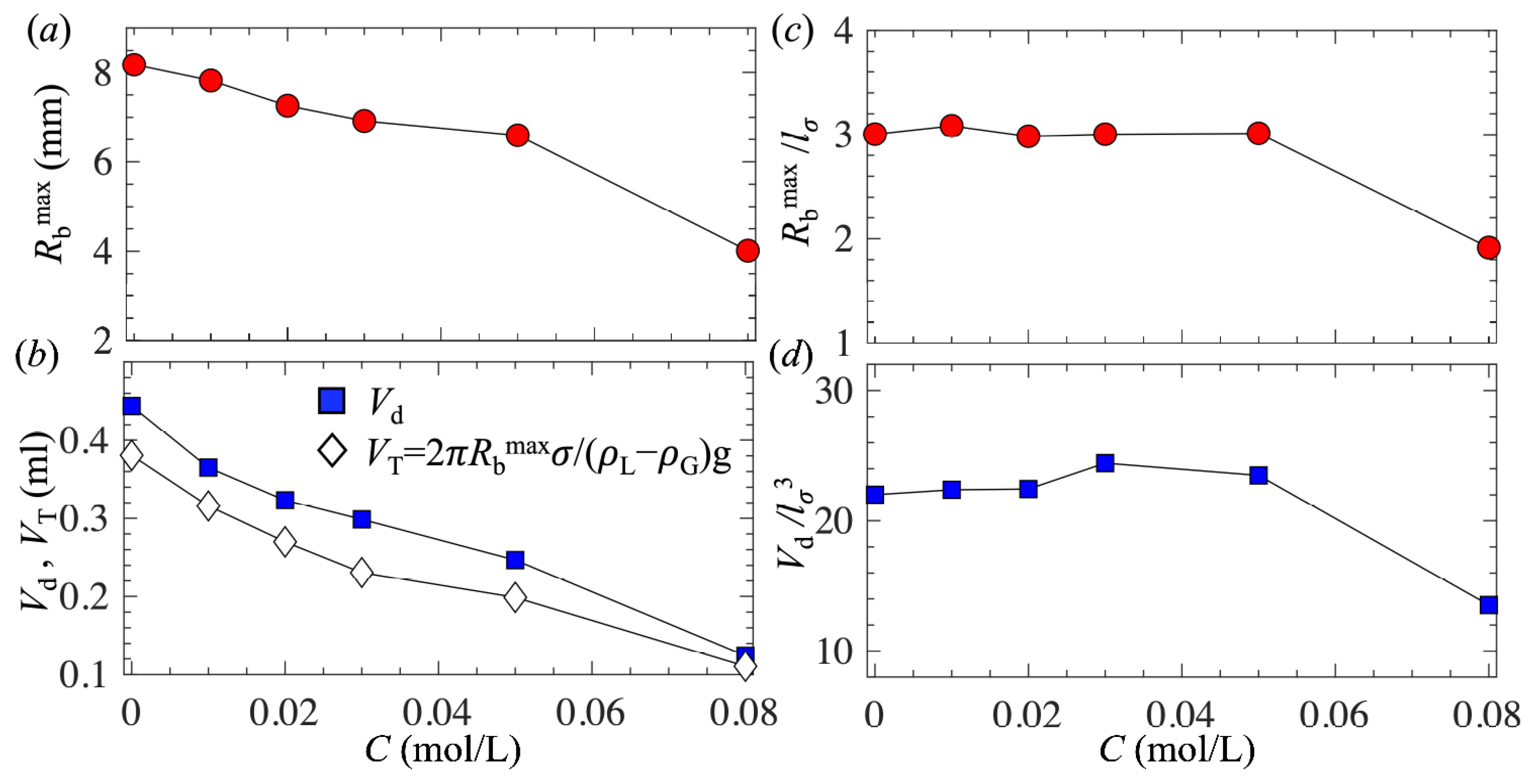
  • As the surfactant concentration increased, all bubble geometrical parameters, including the bubble detached size, decreased.
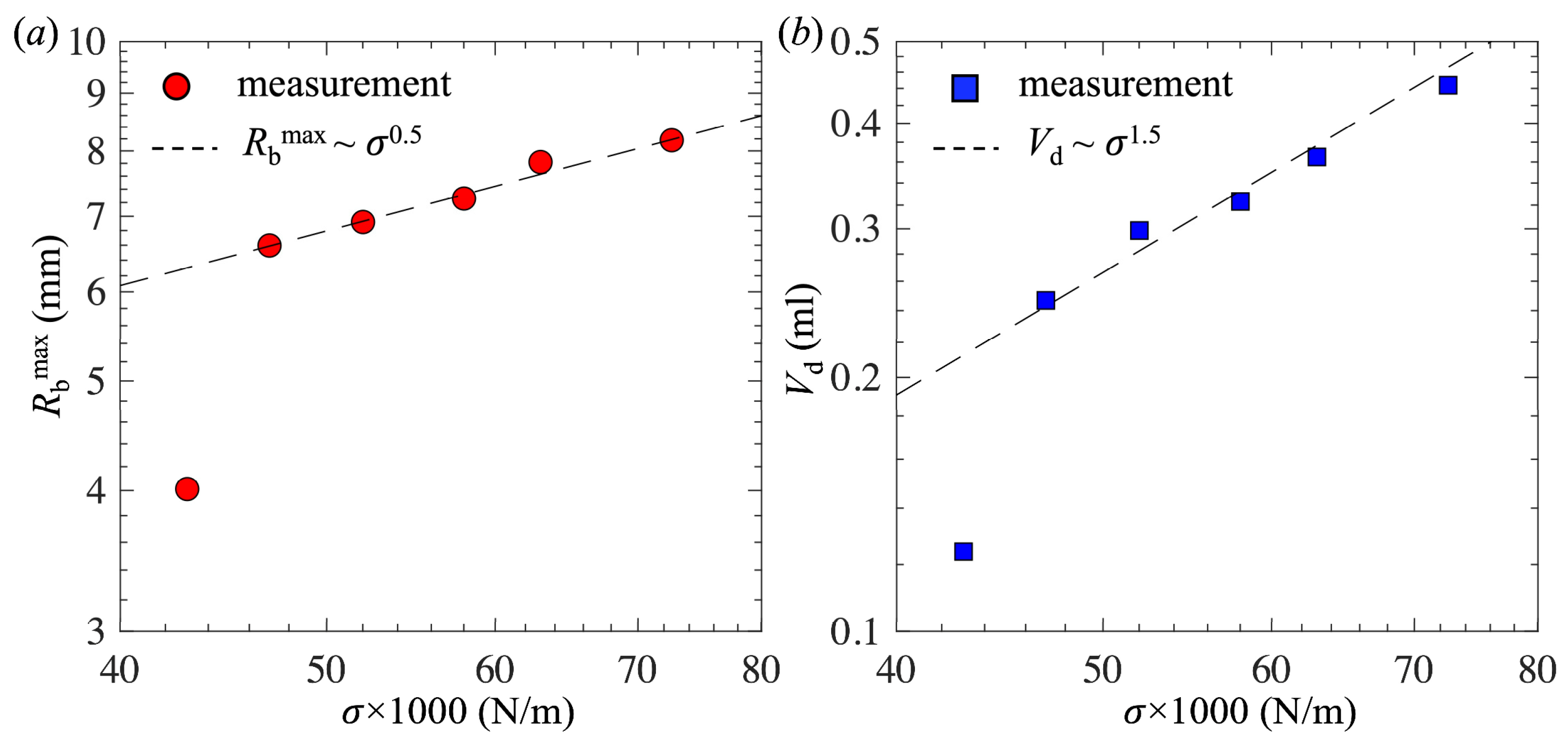
  • For low surfactant concentrations, θ0 remained nearly constant, bubble shapes at different concentrations were self-similar, and Rdmax and Vd decreased following the scaling laws Rdmax~σ1/2 and Vd~σ3/2, respectively.
  • For high surfactant concentrations, θ0 was greatly reduced, and Rdmax and Vd decreased due to the combined effects of reduced surface tension and a lower static contact angle.
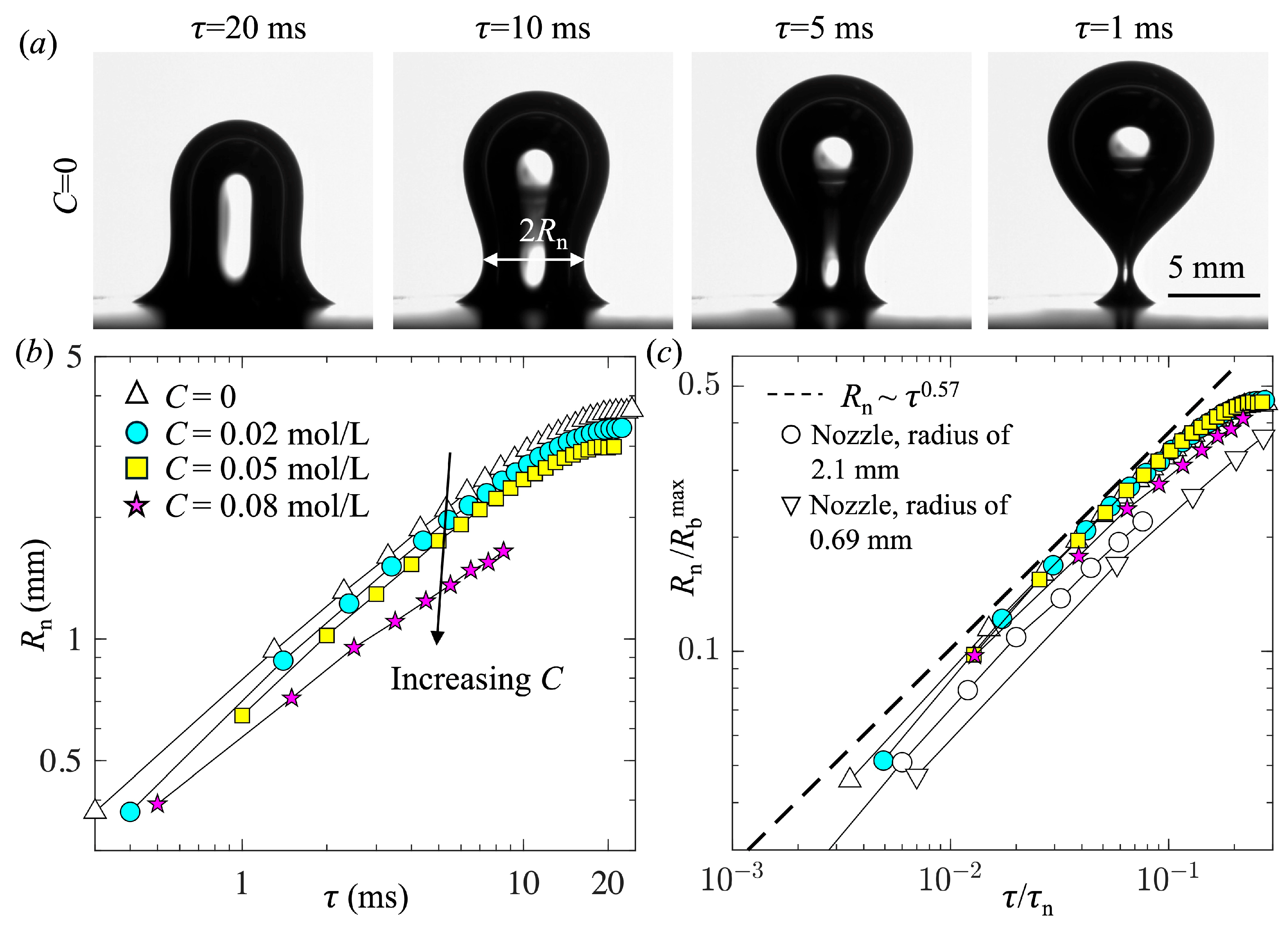
  • The surfactant had little impact on the dynamics of bubble pinch-off, except for reducing the time and length scales. The minimum neck radius followed a power-law relation, Rn~τ0.57, similar to that observed for bubble pinch-off from a nozzle.
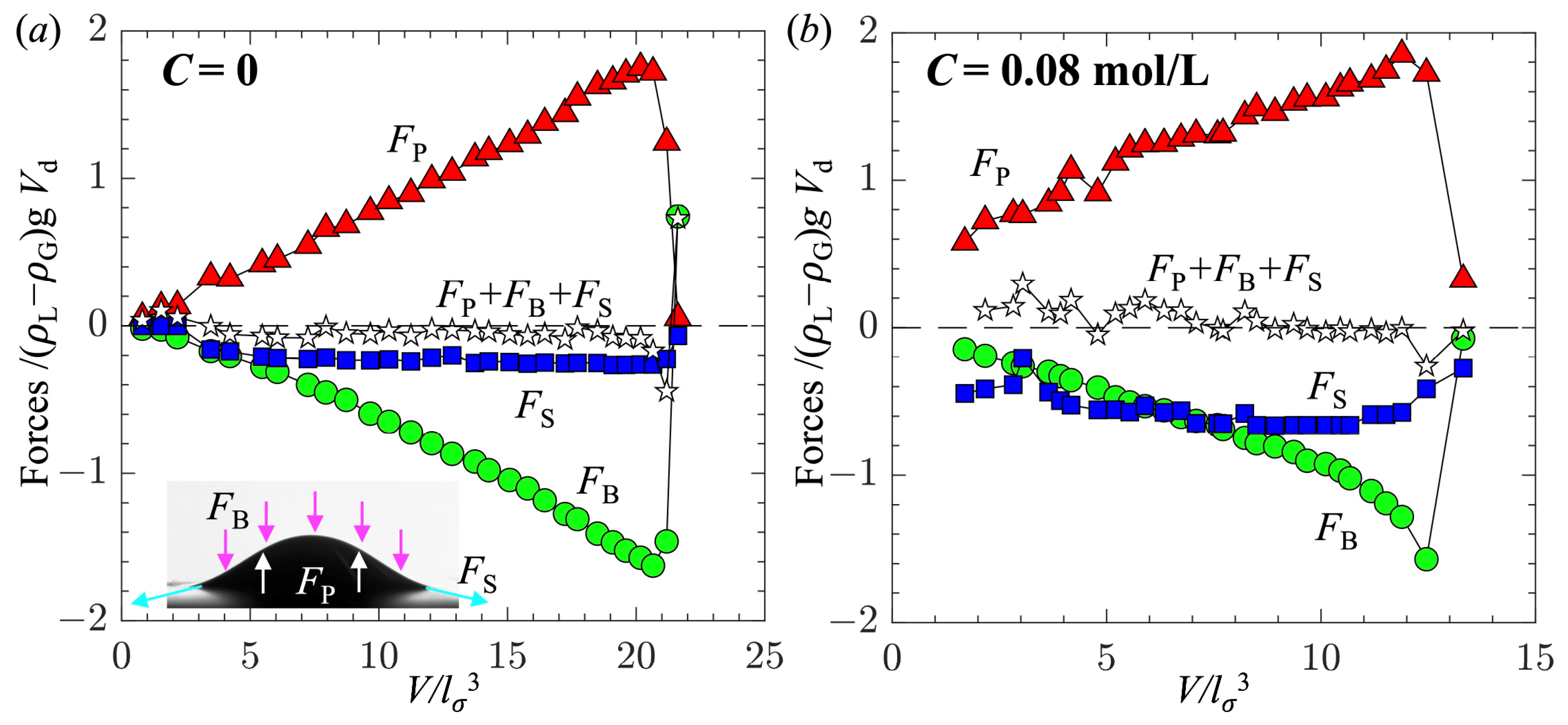
  • The surfactant had negligible impact on the forces acting on the bubble, except for reducing their magnitudes. The growth of the bubble was governed by a balance between surface tension and hydrostatic pressure.
Overall, our results provide deeper insights into bubble formation on complex surfaces in complex solutions. However, our study was limited to one type of surfactant (nonionic 1-pentanol), one type of SHS, and the quasi-static regime. Future studies should investigate the effects of surfactant types (anionic, cationic, and nonionic), textural geometries of the SHS, and gas flow rates on bubble formation. Regardless of the surfactant type or surface treatment, we can conclude from our results that the surfactant affects bubble formation through two main mechanisms: (1) reducing surface tension due to surfactant adsorption at the gas–liquid interface and (2) reducing the static contact angle due to surfactant adsorption at the solid–liquid interface. Both effects depend on the surfactant concentration and lead to a reduction in the detached bubble size. The scaling law shown in Figure 5 holds at low surfactant concentrations, where the static contact angle is not significantly modified. Furthermore, we expect that decreasing the solid fraction of the SHS, which increases the static contact angle (according to the Cassie–Baxter model), leads to an increase in the detached bubble size. As the gas flow rate increases to the dynamic regime, the effect of the surfactant on bubble formation may weaken, as the surfactant may not have sufficient time to reach the equilibrium concentration at the gas–liquid interface.

Author Contributions

Conceptualization, H.L.; methodology, H.L.; formal analysis, H.L.; investigation, H.L., J.R. and D.O.; resources, H.L.; data curation, J.R. and D.O.; writing—original draft preparation, H.L.; writing—review and editing, H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Science Foundation grant number 2041479 and 2339606, the University of Massachusetts OTCV Technology Development Fund, and the University of Massachusetts Dartmouth Internal Seed Fund.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.

Acknowledgments

We thank Paul Sousa for assistance in fabricating the experimental setup.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Searle, M.; Emerson, P.; Crockett, J.; Maynes, D. Influence of microstructure geometry on pool boiling at superhydrophobic surfaces. Int. J. Heat Mass Transf. 2018, 127, 772–783. [Google Scholar] [CrossRef]
  2. Betz, A.R.; Jenkins, J.; Kim, C.-J.; Attinger, D. Boiling heat transfer on superhydrophilic, superhydrophobic, and superbiphilic surfaces. Int. J. Heat Mass Transf. 2013, 57, 733–741. [Google Scholar] [CrossRef]
  3. Lim, C.S.; Di Sia, G.; Hung, Y.M. Extraordinry enhancement of nucleate pool boiling on intrinsically biphilic graphene nanostructured surfaces. Appl. Therm. Eng. 2023, 218, 119354. [Google Scholar] [CrossRef]
  4. Huynh, S.H.; Zahidi, A.A.A.; Muradoglu, M.; Cheong, B.H.P.; Ng, T.W. Plastron-Mediated Growth of Captive Bubbles on Superhydrophobic Surfaces. Langmuir 2015, 31, 6695–6703. [Google Scholar] [CrossRef]
  5. Chen, C.; Huang, Z.; Shi, L.A.; Jiao, Y.; Zhu, S.; Li, J.; Hu, Y.; Chu, J.; Wu, D.; Jiang, L. Remote Photothermal Actuation of Underwater Bubble toward Arbitrary Direction on Planar Slippery Fe3O4-Doped Surfaces. Adv. Funct. Mater. 2019, 29, 1904766. [Google Scholar] [CrossRef]
  6. Jiao, Y.; Li, C.; Wu, S.; Hu, Y.; Li, J.; Yang, L.; Wu, D.; Chu, J. Switchable Underwater Bubble Wettability on Laser-Induced Titanium Multiscale Micro-/Nanostructures by Vertically Crossed Scanning. ACS Appl. Mater. Interfaces 2018, 10, 16867–16873. [Google Scholar] [CrossRef] [PubMed]
  7. Mohammadshahi, S.; Breveleri, J.; Ling, H. Fabrication and characterization of super-hydrophobic surfaces based on sandpapers and nano-particle coatings. Colloids Surf. A Physicochem. Eng. Asp. 2023, 666, 131358. [Google Scholar] [CrossRef]
  8. Mohammadshahi, S.; O’Coin, D.; Ling, H. Impact of sandpaper grit size on drag reduction and plastron stability of super-hydrophobic surface in turbulent flows. Phys. Fluids 2024, 36, 025139. [Google Scholar] [CrossRef]
  9. Cheng, X.; Wang, X.; Jiang, N. Experimental investigation on the modified coherent structures in the turbulent boundary layer by superhydrophobic surface. Phys. Fluids 2025, 37, 035195. [Google Scholar] [CrossRef]
  10. Ling, H.; Srinivasan, S.; Golovin, K.; McKinley, G.H.; Tuteja, A.; Katz, J. High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 2016, 801, 670–703. [Google Scholar] [CrossRef]
  11. Wang, Z.; Liu, X.; Ji, J.; Tao, T.; Zhang, T.; Xu, J.; Jiao, Y.; Liu, K. Underwater Drag Reduction and Buoyancy Enhancement on Biomimetic Antiabrasive Superhydrophobic Coatings. ACS Appl. Mater. Interfaces 2021, 13, 48270–48280. [Google Scholar] [CrossRef] [PubMed]
  12. Elius, M.; Richard, S.; Boyle, K.; Chang, W.S.; Moisander, P.H.; Ling, H. Impact of gas bubbles on bacterial adhesion on super-hydrophobic aluminum surfaces. Res. Surf. Interfaces 2024, 15, 100211. [Google Scholar] [CrossRef]
  13. Zhang, C.; Pei, K.; Zhao, J.; Zhou, Y.; Zhang, S.; Han, X.; Guo, Z. Hierarchical dandelion-like superhydrophobic surfaces with excellent stability and photothermal performance for efficient anti-/deicing. Chem. Eng. J. 2025, 510, 161582. [Google Scholar] [CrossRef]
  14. Guan, S.Y.; Zhang, Z.H.; Wu, R.; Gu, X.K.; Zhao, C.Y. Pool boiling inside micro-nano composite pores: Thermofluids behaviors and heat transfer enhancement. Appl. Phys. Lett. 2024, 124, 093508. [Google Scholar] [CrossRef]
  15. Corbett, C.; Wang, Q.; Smith, W.; Liu, W.; Walmsley, A.D. Cleaning effects due to shape oscillation of bubbles over a rigid boundary. Phys. Fluids 2023, 35, 123335. [Google Scholar] [CrossRef]
  16. Cheng, H.B.; Lu, Y.W. Applications of textured surfaces on bubble trapping and degassing for microfluidic devices. Microfluid. Nanofluidics 2014, 17, 855–862. [Google Scholar] [CrossRef]
  17. Zeng, L.; Lu, J.; Tryggvason, G. A numerical study of the capture of hydrophobic particles by a buoyant bubble. Phys. Fluids 2025, 37, 013343. [Google Scholar] [CrossRef]
  18. Roovers, S.; Segers, T.; Lajoinie, G.; Deprez, J.; Versluis, M.; De Smedt, S.C.; Lentacker, I. The Role of Ultrasound-Driven Microbubble Dynamics in Drug Delivery: From Microbubble Fundamentals to Clinical Translation. Langmuir 2019, 35, 10173–10191. [Google Scholar] [CrossRef]
  19. Kulkarni, A.A.; Joshi, J.B. Bubble Formation and Bubble Rise Velocity in Gas−Liquid Systems: A Review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
  20. Li, S.; Xiao, H.; Wang, Z.; Zhang, H.; Chen, A.; Huang, Q.; Yang, C. Theoretical model for predicting bubble formation from submerged orifices. Chem. Eng. J. 2024, 496, 153893. [Google Scholar] [CrossRef]
  21. Terasaka, K.; Tsuge, H. Bubble formation at a single orifice in non-Newtonian liquids. Chem. Eng. Sci. 1991, 46, 85–93. [Google Scholar] [CrossRef]
  22. Vafaei, S.; Wen, D. Spreading of triple line and dynamics of bubble growth inside nanoparticle dispersions on top of a substrate plate. J. Colloid. Interface Sci. 2011, 362, 285–291. [Google Scholar] [CrossRef] [PubMed]
  23. Vafaei, S.; Wen, D. Effect of Gold Nanoparticles on the Dynamics of Gas Bubbles. Langmuir 2010, 26, 6902–6907. [Google Scholar] [CrossRef] [PubMed]
  24. Ji, B.; Yang, Z.; Feng, J. Oil-coated bubble formation from submerged coaxial orifices. Phys. Rev. Fluids 2021, 6, 33602. [Google Scholar] [CrossRef]
  25. Zhou, Y.; Ji, B.; Zhao, C.; Bo, H. Bubble formation from a submerged orifice in a thin liquid layer: Detachment and bursting. Phys. Fluids 2021, 33, 013305. [Google Scholar] [CrossRef]
  26. Jia, M.; Pang, M. Influence of wettability and surface tension on bubble formation from a needle. Asia-Pac. J. Chem. Eng. 2025, 20, e3169. [Google Scholar] [CrossRef]
  27. Zhang, Q.; Mo, D.; Moon, S.; Janowitz, J.; Ringle, D.; Mays, D.; Diddle, A.; Rexroat, J.; Lee, E.; Luo, T. Bubble nucleation and growth on microstructured surfaces under microgravity. Npj Microgravity 2024, 10, 13. [Google Scholar] [CrossRef]
  28. Heidarian, A.; Sun, B.; Soria, J. Effects of nozzle size and surface hydrophobicity on microbubble generation. Phys. Fluids 2025, 37, 012012. [Google Scholar] [CrossRef]
  29. Mirsandi, H.; Smit, W.J.; Kong, G.; Baltussen, M.W.; Peters, E.A.J.F.; Kuipers, J.A.M. Influence of wetting conditions on bubble formation from a submerged orifice. Exp. Fluids 2020, 61, 83. [Google Scholar] [CrossRef]
  30. Corchero, G.; Medina, A.; Higuera, F.J. Effect of wetting conditions and flow rate on bubble formation at orifices submerged in water. Colloids Surf. A Physicochem. Eng. Asp. 2006, 290, 41–49. [Google Scholar] [CrossRef]
  31. Xie, J.; Zhu, X.; Liao, Q.; Wang, H.; Ding, Y.-D. Dynamics of bubble formation and detachment from an immersed micro-orifice on a plate. Int. J. Heat Mass Transf. 2012, 55, 3205–3213. [Google Scholar] [CrossRef]
  32. Mohseni, E.; Jose Kalayathine, J.; Reinecke, S.F.; Hampel, U. Dynamics of bubble formation at micro-orifices under constant gas flow conditions. Int. J. Multiph. Flow 2020, 132, 103407. [Google Scholar] [CrossRef]
  33. Hanafizadeh, P.; Sattari, A.; Hosseini-Doost, S.E.; Nouri, A.G.; Ashjaee, M. Effect of orifice shape on bubble formation mechanism. Meccanica 2018, 53, 2461–2483. [Google Scholar] [CrossRef]
  34. Qu, C.; Yu, Y.; Zhang, J. Experimental study of bubbling regimes on submerged micro-orifices. Int. J. Heat Mass Transf. 2017, 111, 17–28. [Google Scholar] [CrossRef]
  35. Zhang, J.; Yu, Y.; Qu, C.; Zhang, Y. Experimental study and numerical simulation of periodic bubble formation at submerged micron-sized nozzles with constant gas flow rate. Chem. Eng. Sci. 2017, 168, 1–10. [Google Scholar] [CrossRef]
  36. Oguz, H.N.; Prosperetti, A. Dynamics of bubble growth and detachment from a needle. J. Fluid Mech. 1993, 257, 111–145. [Google Scholar] [CrossRef]
  37. Ma, J.; Li, J.; Zhou, P.; Song, Y.; Chai, L.; Zhou, C.Q. A viewpoint on the dynamics of bubble formation from a submerged nozzle. Eur. J. Mech.-B/Fluids 2019, 78, 276–283. [Google Scholar] [CrossRef]
  38. Gerlach, D.; Biswas, G.; Durst, F.; Kolobaric, V. Quasi-static bubble formation on submerged orifices. Int. J. Heat Mass Transf. 2005, 48, 425–438. [Google Scholar] [CrossRef]
  39. Hecht, K.J.; Velagala, S.; Easo, D.A.; Saleem, M.A.; Krause, U. Influence of Wettability on Bubble Formation from Submerged Orifices. Ind. Eng. Chem. Res. 2020, 59, 4071–4078. [Google Scholar] [CrossRef]
  40. Gnyloskurenko, S.; Byakova, A.; Nakamura, T.; Raychenko, O. Influence of wettability on bubble formation in liquid. J. Mater. Sci. 2005, 40, 2437–2441. [Google Scholar] [CrossRef]
  41. Rubio-Rubio, M.; Bolaños-Jiménez, R.; Martínez-Bazán, C.; Muñoz-Hervás, J.C.; Sevilla, A. Superhydrophobic substrates allow the generation of giant quasi-static bubbles. J. Fluid Mech. 2021, 912, A25. [Google Scholar] [CrossRef]
  42. Pereira, J.; Cautela, R.; Moita, A.; Moreira, A. Effect of the Size of the Superhydrophobic Regions of Biphilic Surfaces on the Bubble Dynamics. Symmetry 2023, 15, 949. [Google Scholar] [CrossRef]
  43. Qiao, S.; Cai, C.; Chen, W.; Pan, C.; Liu, Y. Control of the shape of bubble growth on underwater substrates with different sizes of superhydrophobic circles. Phys. Fluids 2022, 34, 067110. [Google Scholar] [CrossRef]
  44. O’Coin, D.; Ling, H. Dynamics of bubble formation on superhydrophobic surface under a constant gas flow rate at quasi-static regime. Phys. Fluids 2024, 36, 083303. [Google Scholar] [CrossRef]
  45. Breveleri, J.; Mohammadshahi, S.; Dunigan, T.; Ling, H. Plastron restoration for underwater superhydrophobic surface by porous material and gas injection. Colloids Surf. A Physicochem. Eng. Asp. 2023, 676, 132319. [Google Scholar] [CrossRef]
  46. O’Coin, D.; Ling, H. Effect of gas flow rate on bubble formation on superhydrophobic surface. Droplet 2025, 4, e148. [Google Scholar] [CrossRef]
  47. Xu, Q.; Nakajima, M.; Ichikawa, S.; Nakamura, N.; Roy, P.; Okadome, H.; Shiina, T. Effects of surfactant and electrolyte concentrations on bubble formation and stabilization. J. Colloid Interface Sci. 2009, 332, 208–214. [Google Scholar] [CrossRef]
  48. Loubière, K.; Hébrard, G. Influence of liquid surface tension (surfactants) on bubble formation at rigid and flexible orifices. Chem. Eng. Process. Process Intensif. 2004, 43, 1361–1369. [Google Scholar] [CrossRef]
  49. Kukizaki, M.; Baba, Y. Effect of surfactant type on microbubble formation behavior using Shirasu porous glass (SPG) membranes. Colloids Surf. A Physicochem. Eng. Asp. 2008, 326, 129–137. [Google Scholar] [CrossRef]
  50. Zhang, X.; Uddin, M.d.H.; Yang, H.; Toikka, G.; Ducker, W.; Maeda, N. Effects of Surfactants on the Formation and the Stability of Interfacial Nanobubbles. Langmuir 2012, 28, 10471–10477. [Google Scholar] [CrossRef]
  51. Hsu, S.-H.; Lee, W.-H.; Yang, Y.-M.; Chang, C.-H.; Maa, J.-R. Bubble Formation at an Orifice in Surfactant Solutions under Constant-Flow Conditions. Ind. Eng. Chem. Res. 2000, 39, 1473–1479. [Google Scholar] [CrossRef]
  52. Babu, R.; Das, M.K. Effects of surface-active agents on bubble growth and detachment from submerged orifice. Chem. Eng. Sci. 2018, 179, 172–184. [Google Scholar] [CrossRef]
  53. Yang, Y.-M.; Yeh, S.-J.; Hsiung, C.-K.; Chien, C.-L.; Chang, C.-H.; Maa, J.-R. Bubble Formation in Catanionic Surfactant Solutions under Constant-Flow Conditions. J. Chem. Eng. Jpn. 2001, 34, 563–567. [Google Scholar] [CrossRef]
  54. Kurimoto, R.; Yasuda, T.; Minagawa, H. Effects of surfactant on quasi-static bubble growth from an orifice. Chem. Eng. Process. Process Intensif. 2016, 104, 154–159. [Google Scholar] [CrossRef]
  55. King, L.; Sadhal, S.S. Effect of surfactants on the growth and departure of bubbles from solid surfaces. Heat Mass Transf. 2014, 50, 373–382. [Google Scholar] [CrossRef]
  56. Mohammadi, R.; Wassink, J.; Amirfazli, A. Effect of Surfactants on Wetting of Super-Hydrophobic Surfaces. Langmuir 2004, 20, 9657–9662. [Google Scholar] [CrossRef] [PubMed]
  57. Chang, F.-M.; Sheng, Y.-J.; Chen, H.; Tsao, H.-K. From superhydrophobic to superhydrophilic surfaces tuned by surfactant solutions. Appl. Phys. Lett. 2007, 91, 094108. [Google Scholar] [CrossRef]
  58. Fainerman, V.B. Dynamic Surface Tension and kinetics of Adsorption in Solutions of Normal Alcohls. Kolloid. Z. 1982, 44, 598–603. [Google Scholar]
  59. Takagi, S.; Uda, T.; Watanabe, Y.; Matsumoto, Y. Behavior of a Rising Bubble in Water with Surfactant Dissolution: 1st Report, Steady Behavior. Trans. Jpn. Soc. Mech. Eng. Ser. B 2003, 69, 2192–2199. [Google Scholar] [CrossRef]
  60. Daerr, A.; Mogne, A. Pendent_Drop: An ImageJ Plugin to Measure the Surface Tension from an Image of a Pendent Drop. J. Open Res. Softw. 2016, 4, 3. [Google Scholar] [CrossRef]
  61. Hey, M.J.; Kippax, P.G. Surface tensions of mixed aqueous solutions of tert-butanol and n-pentanol. Colloids Surf. A Physicochem. Eng. Asp. 2005, 262, 198–203. [Google Scholar] [CrossRef]
  62. Tagawa, Y.; Takagi, S.; Matsumoto, Y. Surfactant effect on path instability of a rising bubble. J. Fluid Mech. 2014, 738, 124–142. [Google Scholar] [CrossRef]
  63. Hung, Y.-L.; Chang, Y.-Y.; Wang, M.-J.; Lin, S.-Y. A simple method for measuring the superhydrophobic contact angle with high accuracy. Rev. Sci. Instrum. 2010, 81, 065105. [Google Scholar] [CrossRef] [PubMed]
  64. Tate, T. On the magnitude of a drop of liquid formed under different circumstances. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1864, 27, 176–180. [Google Scholar] [CrossRef]
  65. Thoroddsen, S.T.; Etoh, T.G.; Takehara, K. Experiments on bubble pinch-off. Phys. Fluids 2007, 19, 042101. [Google Scholar] [CrossRef]
  66. Burton, J.C.; Waldrep, R.; Taborek, P. Scaling and Instabilities in Bubble Pinch-Off. Phys. Rev. Lett. 2005, 94, 184502. [Google Scholar] [CrossRef]
  67. Keim, N.C.; Møller, P.; Zhang, W.W.; Nagel, S.R. Breakup of Air Bubbles in Water: Memory and Breakdown of Cylindrical Symmetry. Phys. Rev. Lett. 2006, 97, 144503. [Google Scholar] [CrossRef]
  68. Quan, S.; Hua, J. Numerical studies of bubble necking in viscous liquids. Phys. Rev. E 2008, 77, 66303. [Google Scholar] [CrossRef]
Biomimetics 10 00382 g001
Figure 1. (a) Schematic drawing of experimental setup for measuring bubble formation on superhydrophobic surface; (b,c) SEM images of superhydrophobic surface.
Figure 1. (a) Schematic drawing of experimental setup for measuring bubble formation on superhydrophobic surface; (b,c) SEM images of superhydrophobic surface.
Biomimetics 10 00382 g001
Biomimetics 10 00382 g002
Figure 2. (a) Surface tension as a function of the 1-pentanol concentration and (b) the static contact angle of the superhydrophobic surface as a function of the 1-pentanol concentration. The dashed line in (a) is the Szyszkowski model [61]. The inserted image in (b) is a water droplet seated on the SHS.
Figure 2. (a) Surface tension as a function of the 1-pentanol concentration and (b) the static contact angle of the superhydrophobic surface as a function of the 1-pentanol concentration. The dashed line in (a) is the Szyszkowski model [61]. The inserted image in (b) is a water droplet seated on the SHS.
Biomimetics 10 00382 g002
Biomimetics 10 00382 g003
Figure 3. The time evolution of bubble shapes for five different 1-pentanol concentrations ranging from 0 to 0.08 mol/L. Time t = 0 is defined as the time of detachment of the previous bubble, and T0 is the bubbling period.
Figure 3. The time evolution of bubble shapes for five different 1-pentanol concentrations ranging from 0 to 0.08 mol/L. Time t = 0 is defined as the time of detachment of the previous bubble, and T0 is the bubbling period.
Biomimetics 10 00382 g003
Biomimetics 10 00382 g004
Figure 4. (a,c) The maximum bubble base radius as a function of the 1-pentanol concentration, and (b,d) the detached bubble volume as a function of the 1-pentanol concentration. In (c) and (d), Rbmax and Vd are normalized by lσ and lσ3, respectively, where lσ = (σ/ρLg)0.5 is the capillary length.
Figure 4. (a,c) The maximum bubble base radius as a function of the 1-pentanol concentration, and (b,d) the detached bubble volume as a function of the 1-pentanol concentration. In (c) and (d), Rbmax and Vd are normalized by lσ and lσ3, respectively, where lσ = (σ/ρLg)0.5 is the capillary length.
Biomimetics 10 00382 g004
Biomimetics 10 00382 g005
Figure 5. (a) The bubble maximum base radius and (b) bubble detached volume as a function of surface tension. Both axes are shown in log scale. The dashed lines are fitted to the experimental data in the large surface tension range.
Figure 5. (a) The bubble maximum base radius and (b) bubble detached volume as a function of surface tension. Both axes are shown in log scale. The dashed lines are fitted to the experimental data in the large surface tension range.
Biomimetics 10 00382 g005
Biomimetics 10 00382 g006
Figure 6. (a,d) Bubble height, (b,e) bubble base radius, and (c,f) bubble radius at the apex as a function of bubble volume. In (d–f), the length and volume are normalized by lσ and lσ3, respectively.
Figure 6. (a,d) Bubble height, (b,e) bubble base radius, and (c,f) bubble radius at the apex as a function of bubble volume. In (d–f), the length and volume are normalized by lσ and lσ3, respectively.
Biomimetics 10 00382 g006
Biomimetics 10 00382 g007
Figure 7. Evolution of contact angle at bubble base as function of bubble volume.
Figure 7. Evolution of contact angle at bubble base as function of bubble volume.
Biomimetics 10 00382 g007
Biomimetics 10 00382 g008
Figure 8. (a) The evolution of the bubble shape during the necking period for C = 0 and (b,c) variations in the minimum neck radius as a function of time to pinch-off. In (c), the length and time are normalized by Rbmax and the capillary–inertia time scale, respectively. The results for bubble pinch-off from a nozzle obtained by Thoroddsen et al. [65] are also shown in (c). The dashed line shows the best power-law fitting the current data.
Figure 8. (a) The evolution of the bubble shape during the necking period for C = 0 and (b,c) variations in the minimum neck radius as a function of time to pinch-off. In (c), the length and time are normalized by Rbmax and the capillary–inertia time scale, respectively. The results for bubble pinch-off from a nozzle obtained by Thoroddsen et al. [65] are also shown in (c). The dashed line shows the best power-law fitting the current data.
Biomimetics 10 00382 g008
Biomimetics 10 00382 g009
Figure 9. Variations in forces, including the pressure force FP, buoyancy force FB, surface tension force FS, and their summation FP + FB + FS, for (a) C = 0 and (b) C = 0.08 mol/L, as a function of bubble volume. The forces are normalized by (ρL − ρG)gVd and the volume is normalized by lσ3. The inserted image in (a) illustrated the forces applied on the bubble.
Figure 9. Variations in forces, including the pressure force FP, buoyancy force FB, surface tension force FS, and their summation FP + FB + FS, for (a) C = 0 and (b) C = 0.08 mol/L, as a function of bubble volume. The forces are normalized by (ρL − ρG)gVd and the volume is normalized by lσ3. The inserted image in (a) illustrated the forces applied on the bubble.
Biomimetics 10 00382 g009
Table 1. The main experimental parameters and experimental results in the current study.
Table 1. The main experimental parameters and experimental results in the current study.
C (mol/L)σ (mN/m)θ0 (°)Rbmax (mm)Vd (mL)lσ (mm)
0721598.20.442.7
0.01631597.80.372.5
0.02581587.30.322.4
0.03521566.90.302.3
0.05471556.60.252.2
0.08431314.00.122.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ling, H.; Ready, J.; O’Coin, D. Effect of Surfactant on Bubble Formation on Superhydrophobic Surface in Quasi-Static Regime. Biomimetics 2025, 10, 382. https://doi.org/10.3390/biomimetics10060382

AMA Style

Ling H, Ready J, O’Coin D. Effect of Surfactant on Bubble Formation on Superhydrophobic Surface in Quasi-Static Regime. Biomimetics. 2025; 10(6):382. https://doi.org/10.3390/biomimetics10060382

Chicago/Turabian Style

Ling, Hangjian, John Ready, and Daniel O’Coin. 2025. "Effect of Surfactant on Bubble Formation on Superhydrophobic Surface in Quasi-Static Regime" Biomimetics 10, no. 6: 382. https://doi.org/10.3390/biomimetics10060382

APA Style

Ling, H., Ready, J., & O’Coin, D. (2025). Effect of Surfactant on Bubble Formation on Superhydrophobic Surface in Quasi-Static Regime. Biomimetics, 10(6), 382. https://doi.org/10.3390/biomimetics10060382

Article Metrics

Back to TopTop