Comprehensive Stiffness Modeling and Evaluation of an Orthopedic Surgical Robot for Enhanced Cutting Operation Performance
Abstract
1. Introduction
2. Stiffness Modeling of Cutting Systems for Orthopedic Surgical Robots
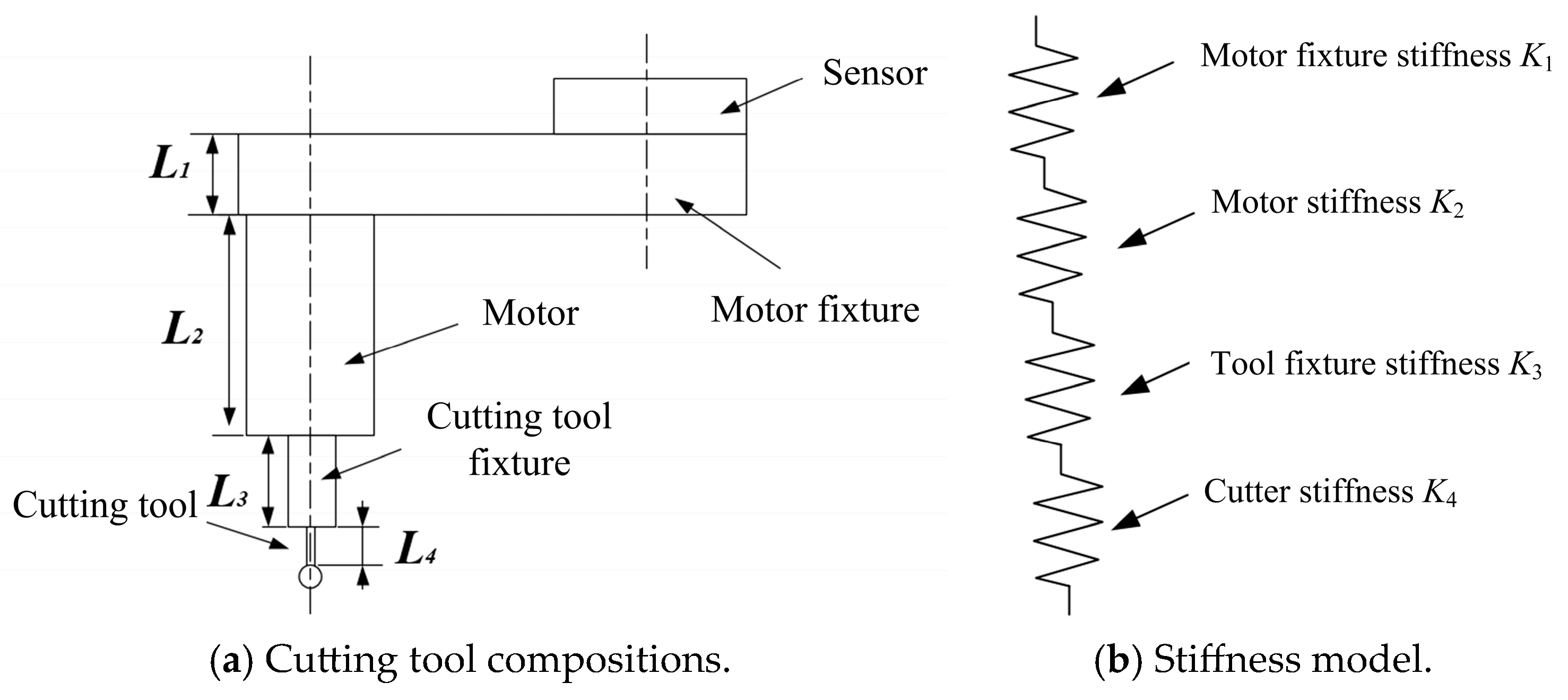
2.1. Stiffness of Cutting Tool and Sensor
2.2. Robot End Stiffness
2.3. Robot Joint Stiffness
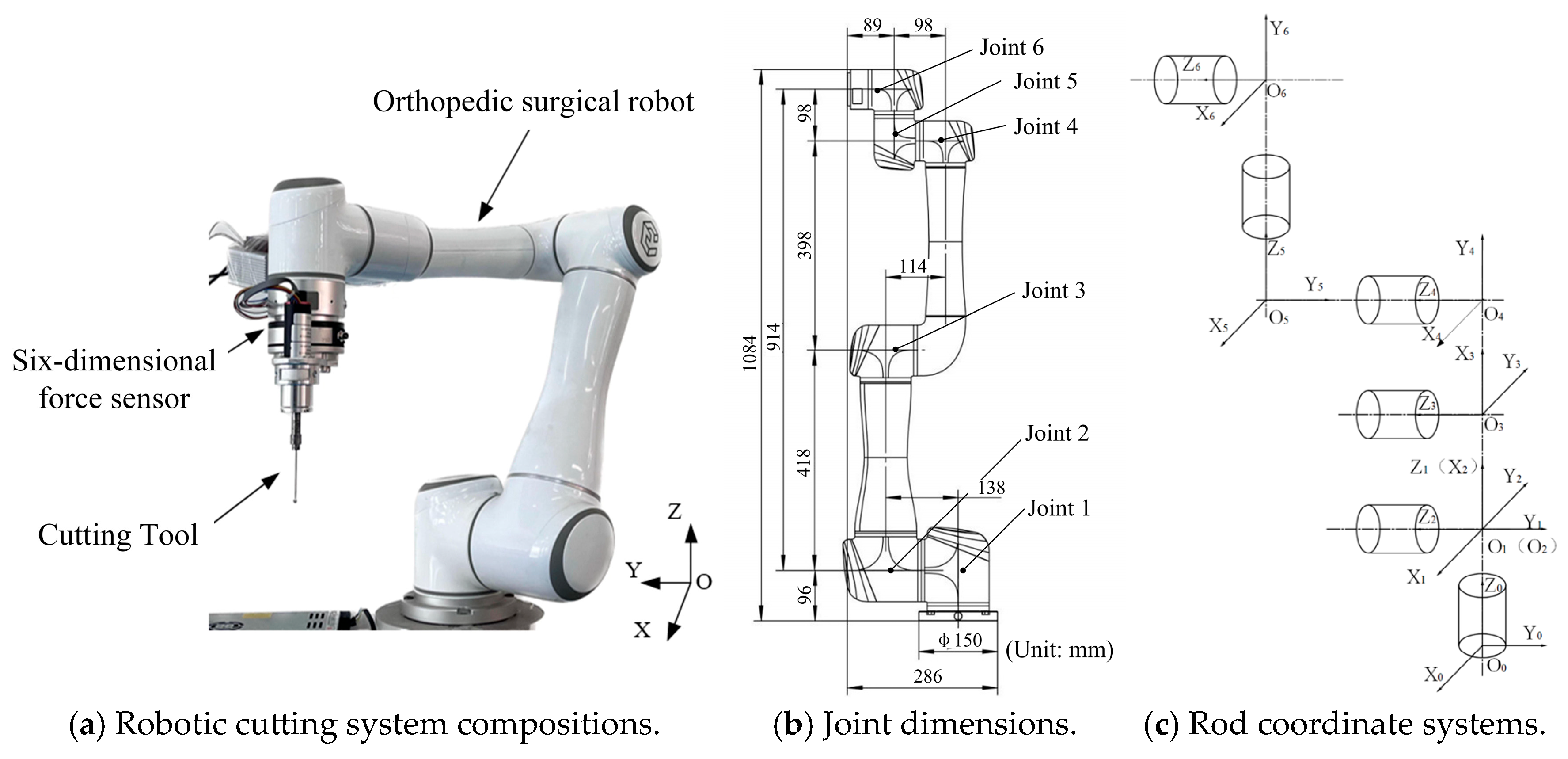
3. Joint Stiffness Identification of Orthopedic Surgical Robot
3.1. Robot Joint Stiffness Identification Experiment
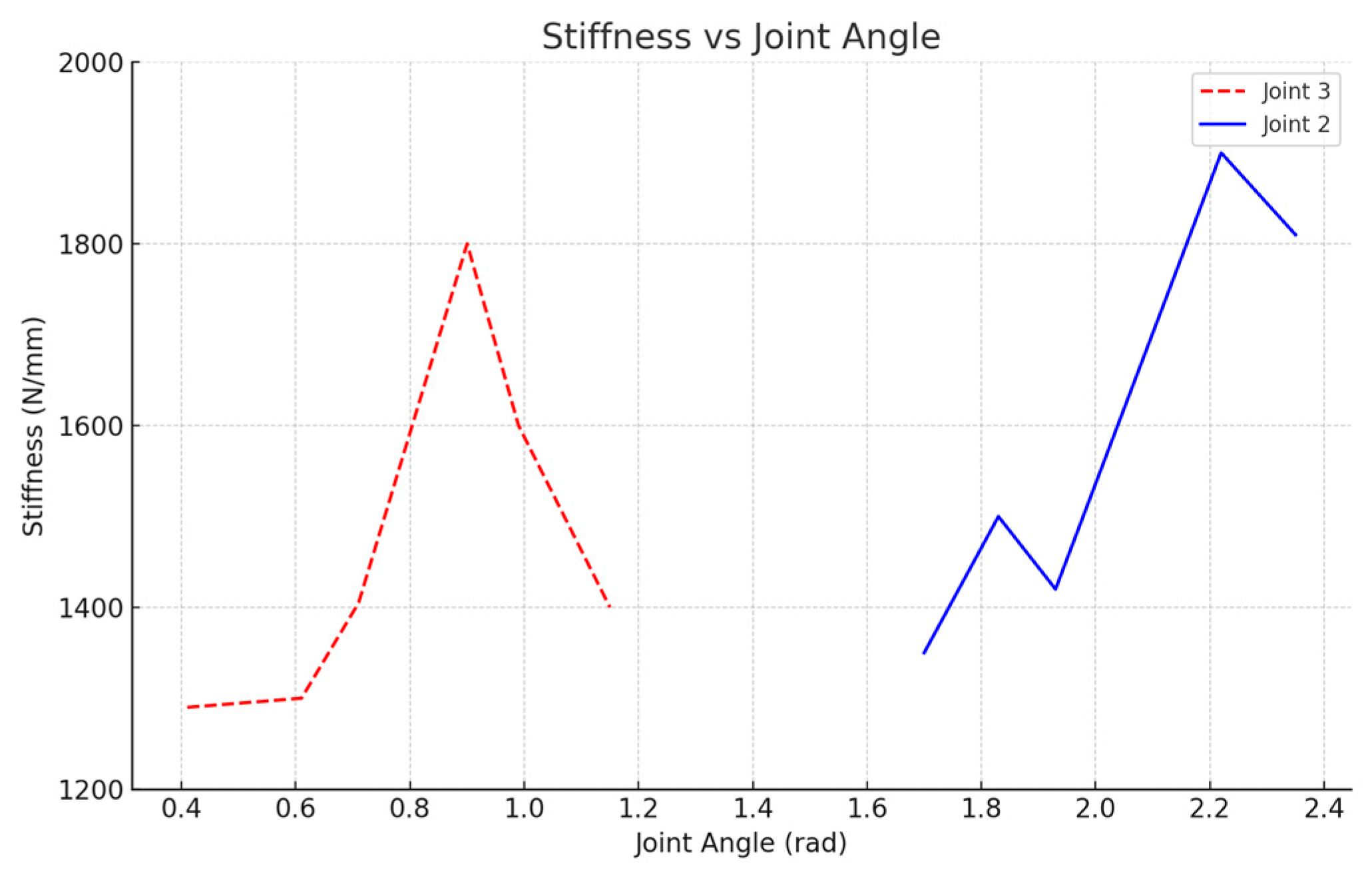
3.2. Joint Stiffness Identification Results
4. Operation Stiffness Simulation During Orthopedic Surgery Robot Cutting
4.1. Preparation for Operation Stiffness Simulation
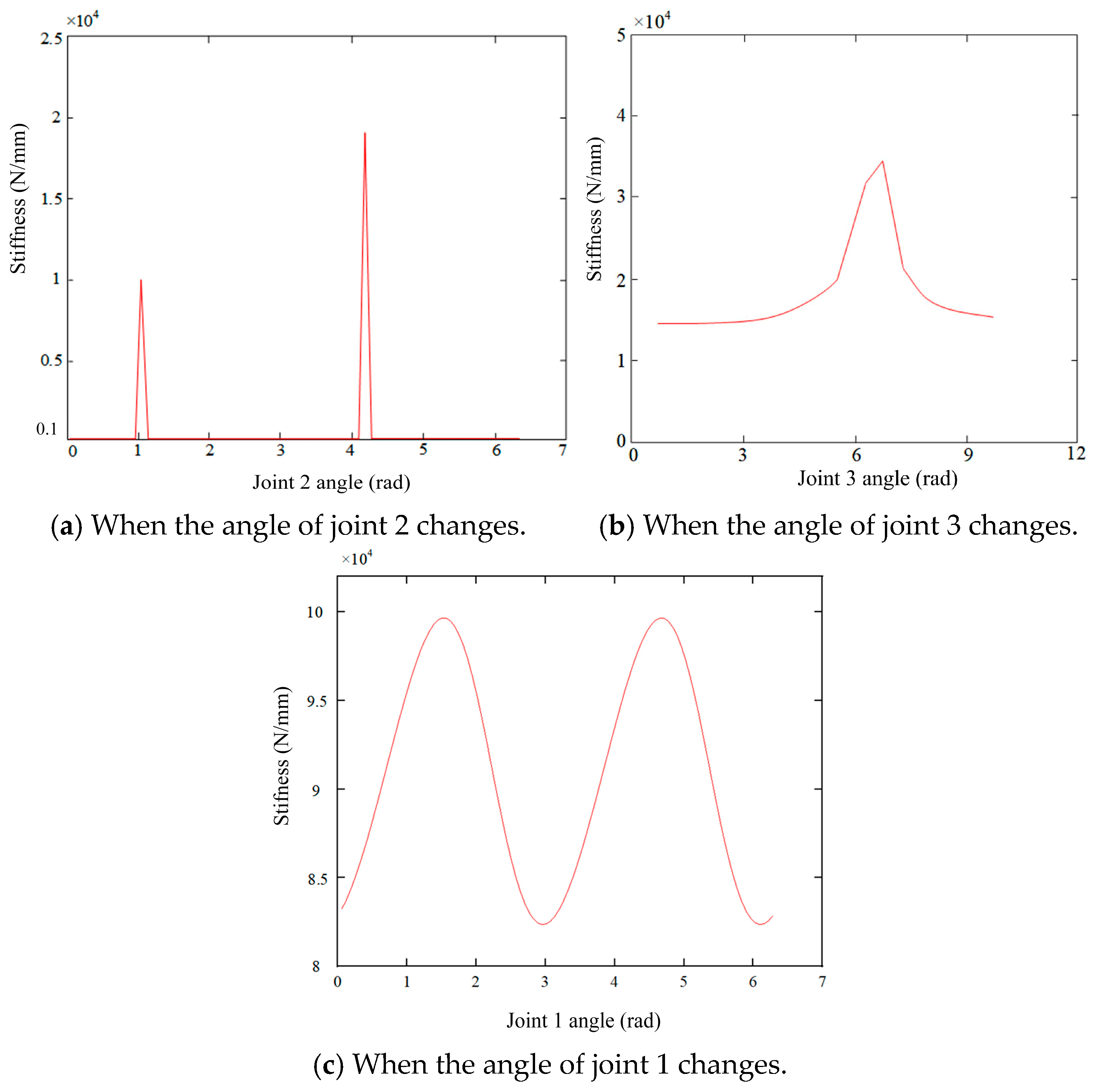
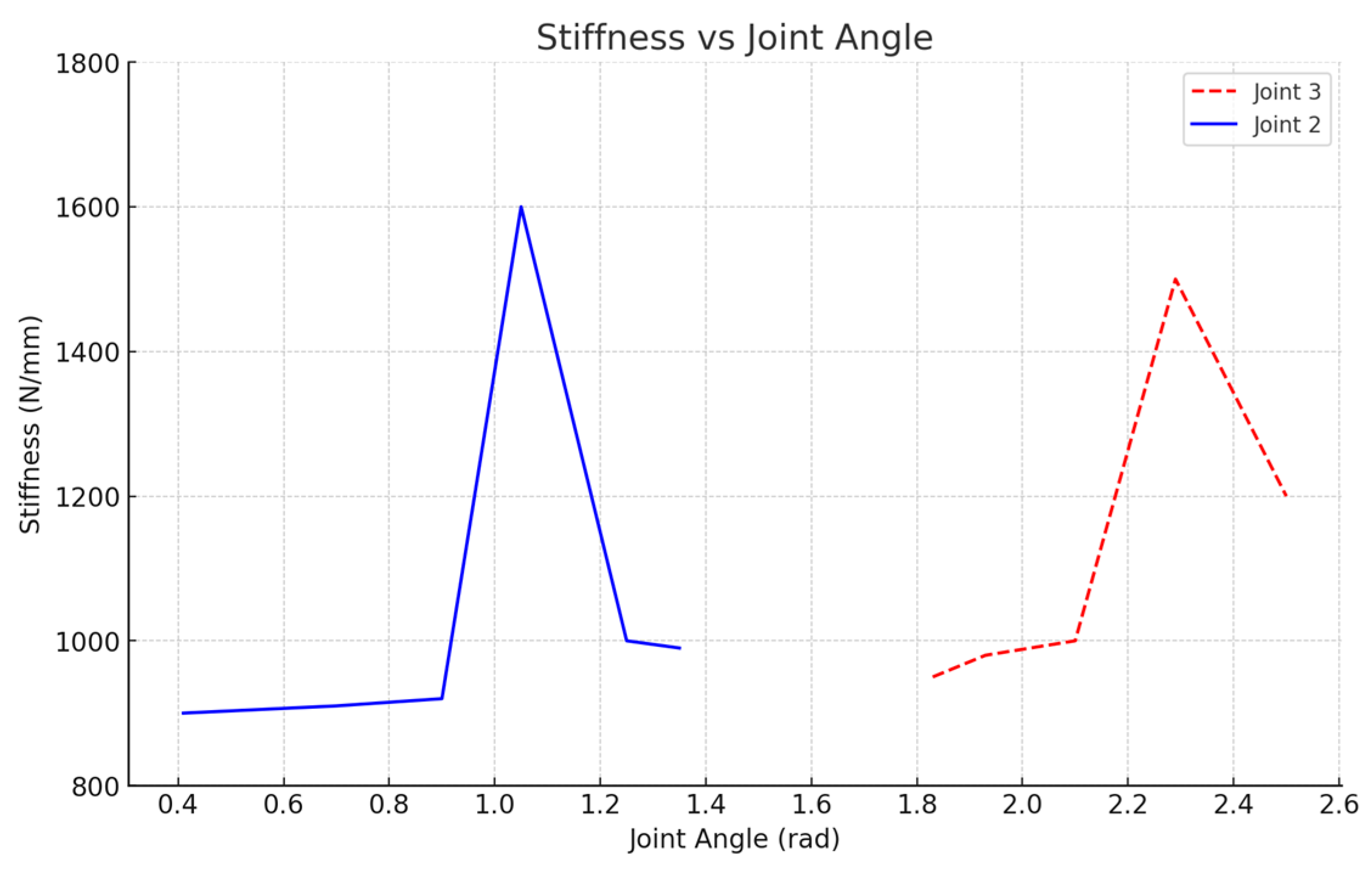
4.2. Analysis of the Variation in Stiffness in X-Axis Direction at the End of the Robot
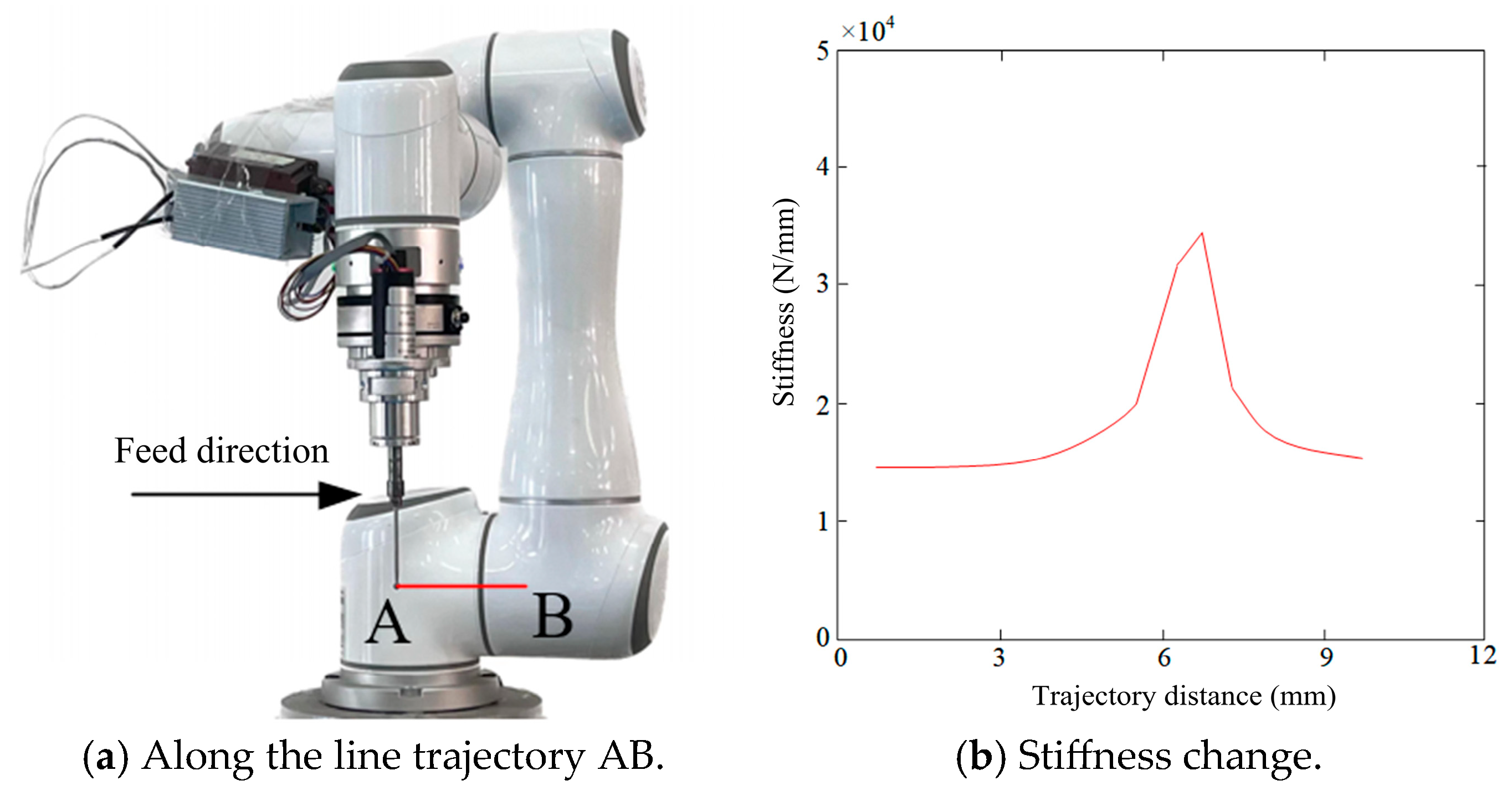
4.3. Analysis of Robot End-Effector Stiffness Variation Along Linear Trajectories
4.4. Stiffness Change in Robot End in Z-Axis Direction
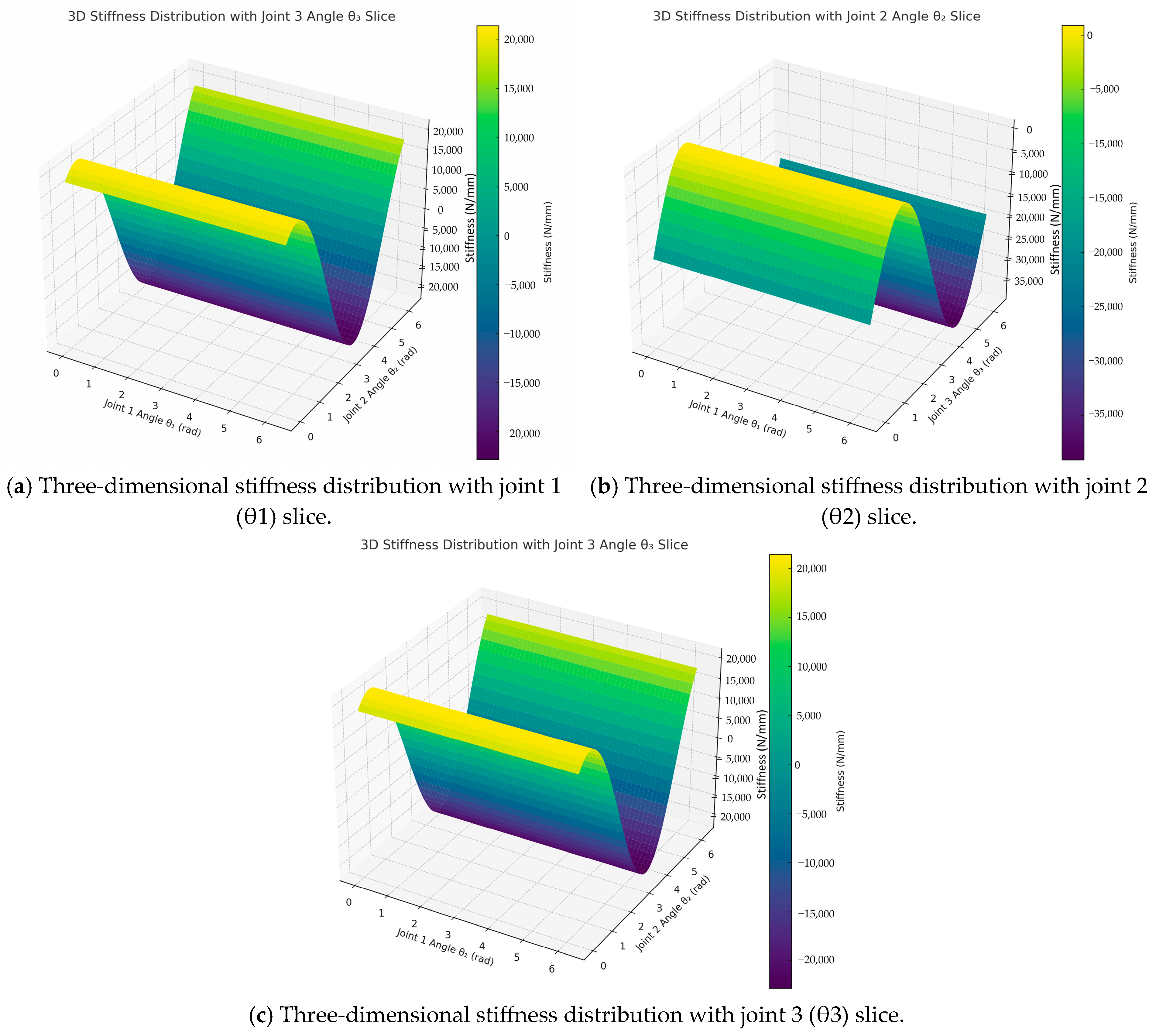
4.5. Mapping Method of Stiffness Distribution in the Robot Workspace
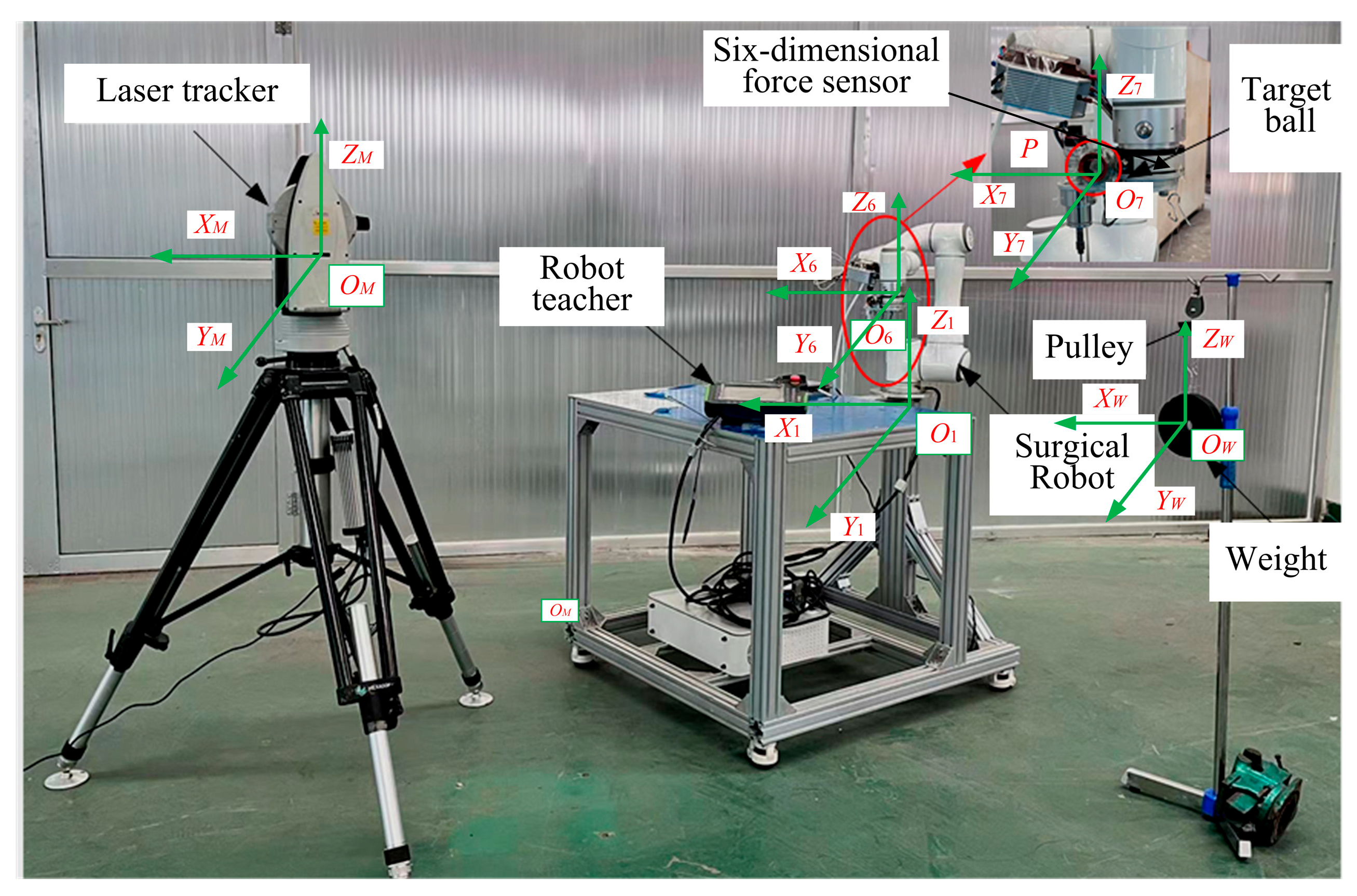
5. Stiffness Measurement Experiments of Orthopedic Surgical Robot
5.1. Experimental Methodology
5.2. Stiffness Behavior in the X-Axis Direction
5.3. Stiffness Behavior in the Z-Axis Direction:
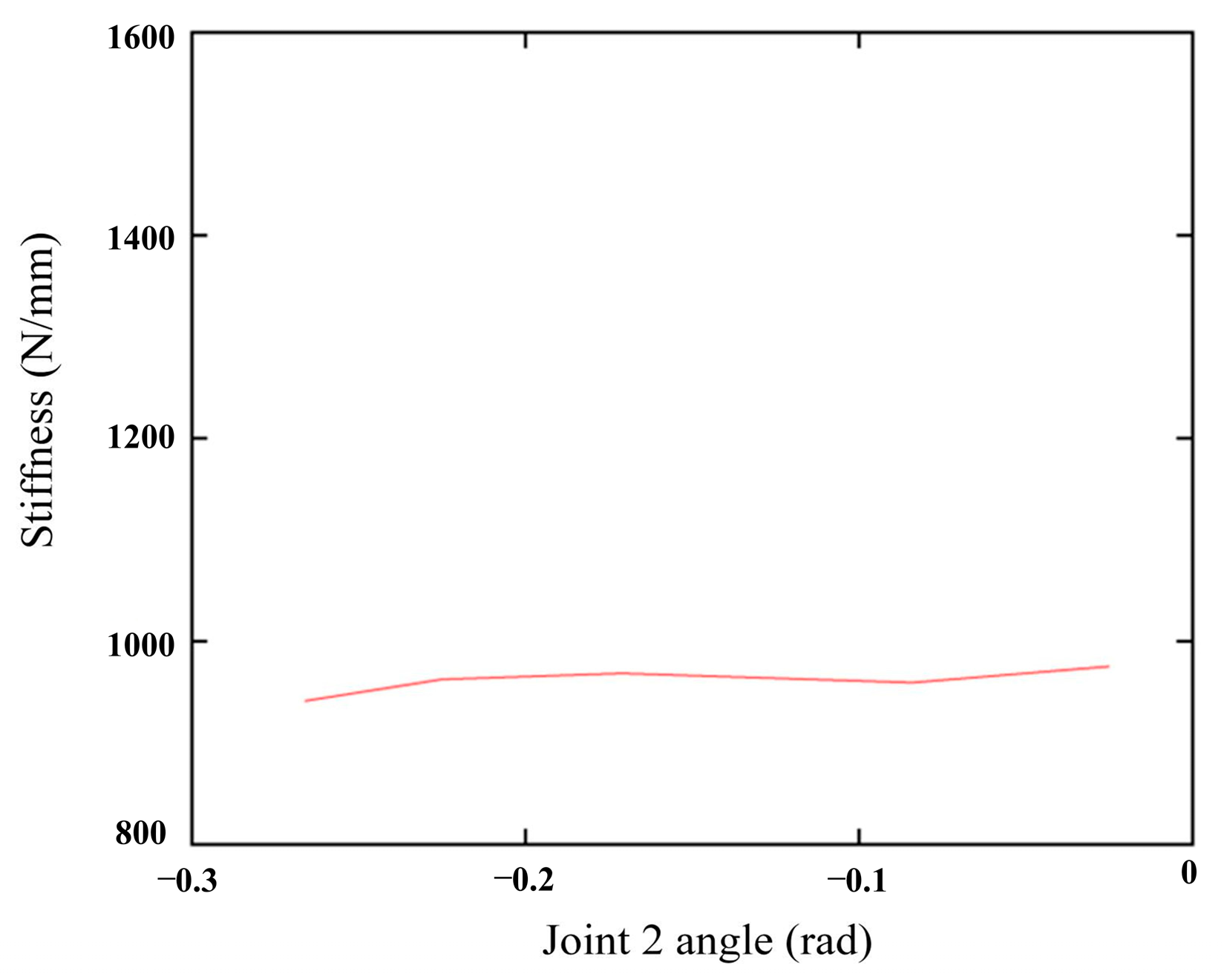
5.4. Smooth Changes in the X-Axis Stiffness
6. Validation of the Integrated Stiffness Model in Real Surgical Bone Cutting Operations
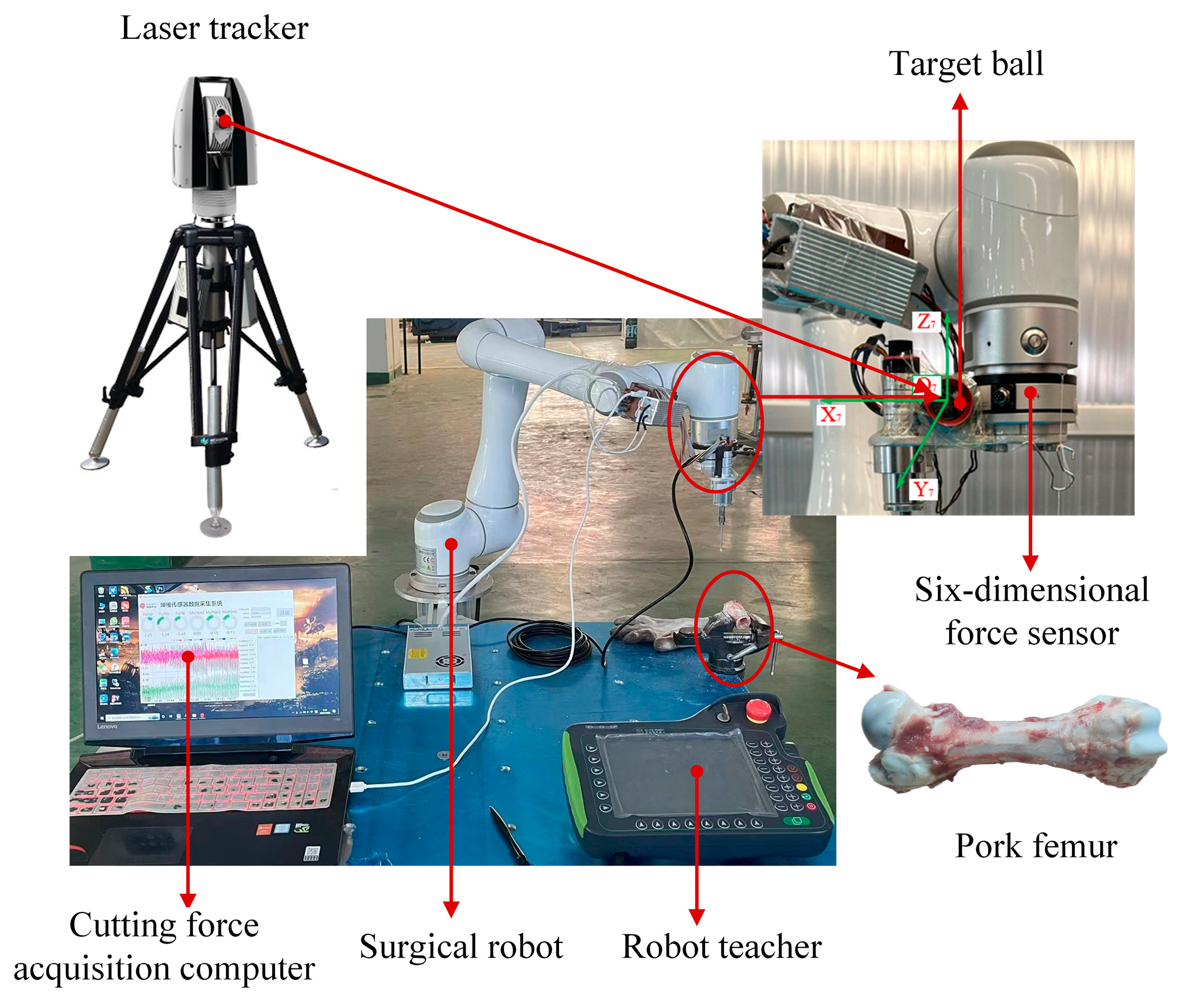
6.1. Construction of Bone Cutting Experimental Platform and Model Validation
6.2. Experimental Method and Data Collection Process
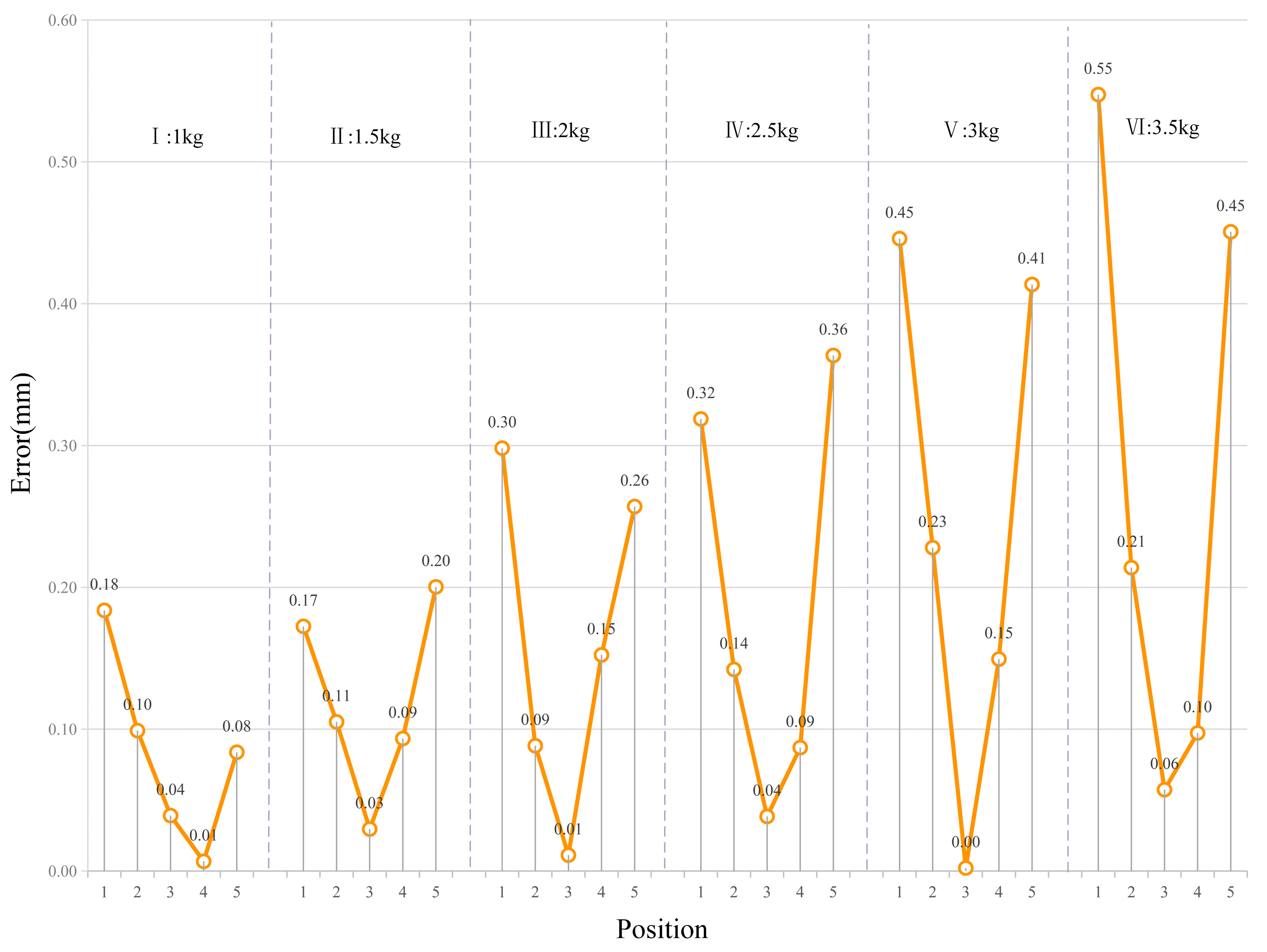
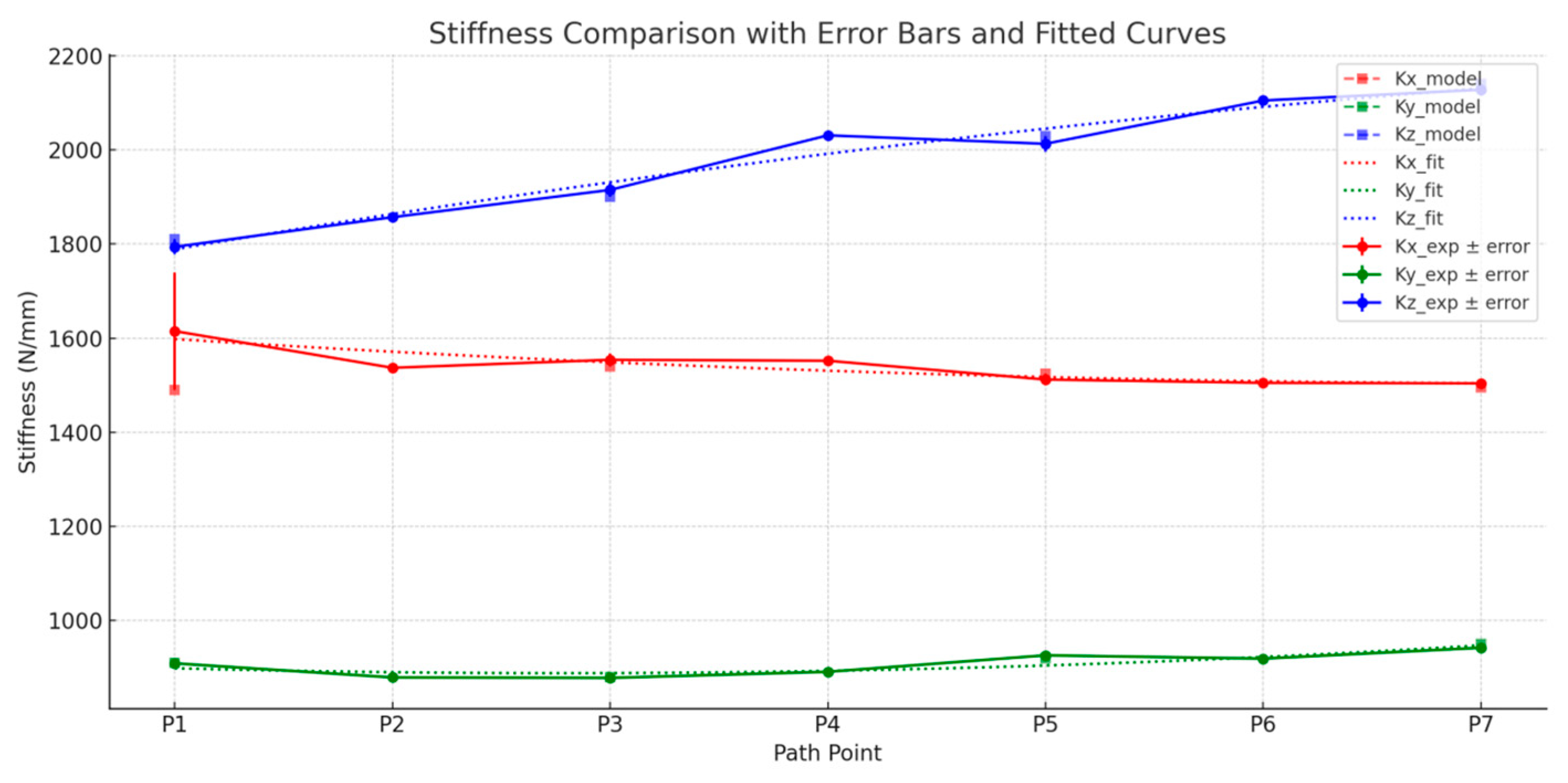
6.3. Stiffness Prediction and Error Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Z.; Tian, H.; Han, X.; Wu, J.; Zhang, W.; Li, C.; Qiu, L.; Duan, X.; Tian, W. A respiratory motion prediction method based on LSTM-AE with attention mechanism for spine surgery. Cyborg Bionic Syst. 2024, 5, 0063. [Google Scholar] [CrossRef] [PubMed]
- Bahadori, S.; Williams, J.M.; Collard, S.; Swain, I. Can a purposeful walk intervention with a distance goal using an activity monitor improve individuals’ daily activity and function post total hip replacement surgery. A randomized pilot trial. Cyborg Bionic Syst. 2023, 4, 0069. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Yu, Y.; He, F. Research on reliability of mode coupling chatter of orthopedic surgery robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 8609–8620. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Q.; Yang, Z.; Jiang, Y.; Xu, J. A state-of-the-art review on robotic milling of complex parts with high efficiency and precision. Robot. Comput.-Integr. Manuf. 2023, 79, 102436. [Google Scholar] [CrossRef]
- Kumar, R. Biomechanical considerations in osteoporotic fracture fixation. Indian J. Orthop. 2025, 59, 256–270. [Google Scholar] [CrossRef]
- Le, H.M.; Do, T.N.; Cao, L.; Phee, S.J. Towards active variable stiffness manipulators for surgical robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1766–1771. [Google Scholar] [CrossRef]
- Luceri, F.; Tamini, J.; Ferrua, P.; Ricci, D.; Batailler, C.; Lustig, S.; Peretti, G.M. Total knee arthroplasty after distal femoral osteotomy: A systematic review and current concepts. SICOT-J 2020, 6, 35. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Tang, X.; Chen, C.; Peng, F.; Yan, R.; Zhou, L.; Li, Z.; Wu, J. High precision and efficiency robotic milling of complex parts: Challenges, approaches, and trends. Chin. J. Aeronaut. 2022, 35, 22–46. [Google Scholar] [CrossRef]
- Cohen, J.S.; Gu, A.; Lopez, N.S.; Park, M.S.; Fehring, K.A.; Sculco, P.K. Efficacy of revision surgery for the treatment of stiffness after total knee arthroplasty: A systematic review. J. Arthroplast. 2018, 33, 3049–3055. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Wang, Q.H.; Xie, H.L.; Li, J.R.; Hua, P. Optimization of robot posture and workpiece setup in robotic milling with stiffness threshold. IEEE/ASME Trans. Mechatron. 2021, 27, 582–593. [Google Scholar] [CrossRef]
- Tokgoz, E.; Levitt, S.; Sosa, D.; Carola, N.A.; Patel, V. Robotics applications in total knee arthroplasty. In Total Knee Arthroplasty: A Review of Medical and Biomedical Engineering and Science Concepts; Springer: Cham, Switzerland, 2023; pp. 155–174. [Google Scholar] [CrossRef]
- Yang, S.H.; Xiao, F.R.; Lai, D.M.; Wei, C.K.; Tsuang, F.Y. A dynamic interbody cage improves bone formation in anterior cervical surgery: A porcine biomechanical study. Clin. Orthop. Relat. Res. 2021, 479, 2547–2558. [Google Scholar] [CrossRef]
- Zhu, J.; Guo, Y.; Zhang, Y.; Chen, N. A Review of the Application of Thermal Analysis in the Development of Bone Tissue Repair Materials. Int. J. Thermophys. 2023, 44, 124. [Google Scholar] [CrossRef]
- Dai, X.; Wu, D.; Xu, K.; Ming, P.; Cao, S.; Yu, L. Viscoelastic Mechanics: From Pathology and Cell Fate to Tissue Regeneration Biomaterial Development. ACS Appl. Mater. Interfaces 2025, 17, 8751–8770. [Google Scholar] [CrossRef] [PubMed]
- Celikag, H.; Sims, N.D.; Ozturk, E. Cartesian Stiffness Optimization for Serial Arm Robots. Procedia CIRP 2018, 77, 566–569. [Google Scholar] [CrossRef]
- Rezaei, A.; Akbarzadeh, A.; Akbarzadeh-T, M.R. An investigation on stiffness of a 3-PSP spatial parallel mechanism with flexible moving platform using invariant form. Mech. Mach. Theory 2012, 51, 195–216. [Google Scholar] [CrossRef]
- Shanmugasundar, G.; Sivaramakrishnan, R.; Meganathan, S.; Balasubramani, S. Structural optimization of a five degrees of freedom (T-3R-T) robot manipulator using finite element analysis. Mater. Today Proc. 2019, 16, 1325–1332. [Google Scholar] [CrossRef]
- Corradini, C.; Fauroux, J.C.; Krut, S. Evaluation of a 4-degree of freedom parallel manipulator stiffness. In Proceedings of the 11th World Congress in Mechanisms and Machine Science, Tianjin, China, 18–21 August 2003; pp. 1857–1861. [Google Scholar]
- Trochimczuk, R.; Łukaszewicz, A.; Mikołajczyk, T.; Aggogeri Borboni, A. Finite element method stiffness analysis of a novel telemanipulator for minimally invasive surgery. Simulation 2019, 95, 1015–1025. [Google Scholar] [CrossRef]
- Avilés, R.; Ajuria, M.G.; Hormaza, M.V.; Hernández, A. A procedure based on finite elements for the solution of nonlinear problems in the kinematic analysis of mechanisms. Finite Elem. Anal. Des. 1996, 22, 305–327. [Google Scholar] [CrossRef]
- Klimchik, A.; Pashkevich, A.; Chablat, D. Fundamentals of manipulator stiffness modeling using matrix structural analysis. Mech. Mach. Theory 2018, 133, 365–394. [Google Scholar] [CrossRef]
- Soares, G.D.L., Jr.; Carvalho, J.C.M.; Gonçalves, R.S. Stiffness analysis of multibody systems using matrix structural analysis—MSA. Robotica 2016, 34, 2368–2385. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.C.; Chen, Q.H. Analytical elastostatic stiffness modeling of parallel manipulators considering the compliance of the link and joint. Appl. Math. Model. 2020, 78, 322–349. [Google Scholar] [CrossRef]
- Li, Q.C.; Xu, L.M.; Chen, Q.H.; Chai, X.X. Analytical Elastostatic Stiffness Modeling of Overconstrained Parallel Manipulators Using Geometric Algebra and Strain Energy. J. Mech. Robot. 2021, 11, 031007. [Google Scholar] [CrossRef]
- Cao, W.A.; Yang, D.H.; Ding, H.F. A method for stiffness analysis of over-constrained parallel robotic mechanisms with Scara motion. Robot. Comput. Integr. Manuf. 2018, 49, 426–435. [Google Scholar] [CrossRef]
- Zhang, D.; Gosselin, C.M. Kinetostatic modeling of N-DOF parallel mechanisms with a passive constraining leg and prismatic actuators. J. Mech. Des. 2001, 123, 375–381. [Google Scholar] [CrossRef]
- Pashkevich, A.; Chablat, D.; Wenger, P. Stiffness analysis of overconstrained parallel manipulators. Mech. Mach. Theory 2009, 44, 966–982. [Google Scholar] [CrossRef]
- Salisbury, J.K. Active stiffness control of a manipulator in cartesian coordinates. In Proceedings of the 1980 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980; pp. 95–100. [Google Scholar]
- Gosselin, C. Stiffness mapping for parallel manipulators. IEEE Trans. Robot. Autom. 1990, 6, 377–382. [Google Scholar] [CrossRef]
- Hoevenaars, A.G.; Lambert, P.; Herder, J.L. Experimental Validation of Jacobian-Based Stiffness Analysis Method for Parallel Manipulators with Nonredundant Legs. J. Mech. Robot. 2016, 8, 341–352. [Google Scholar] [CrossRef]
- Huang, C.; Hung, W.H.; Kao, I. New conservative stiffness mapping for the Stewart-Gough platform. IEEE Int. Conf. Robot. Autom. ICRA 2022, 1, 823–828. [Google Scholar]
- Sheng, D.; Qing, N.; Zhang, L.; Yu, H.D.; Wang, H. Static Stiffness Analysis of Exechon Parallel Manipulator Based on Screw Theory. In Proceedings of the 6th Asian Conference on Multibody Dynamics (ACMD), Shanghai, China, 26–30 August 2012; pp. 1–7. [Google Scholar]
- Pashkevich, A.; Klimchik, A.; Chablat, D. Enhanced stiffness modeling of manipulators with passive joints. Mech. Mach. Theory. 2011, 46, 662–679. [Google Scholar] [CrossRef]
- Lin, J.; Li, Y.; Xie, Y.; Hu, J.; Min, J. Joint stiffness identification of industrial serial robots using 3D digital image correlation techniques. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 536–551. [Google Scholar] [CrossRef]
- Slamani, M.; Nubiola, A.; Bonev, I. Assessment of the positioning performance of an industrial robot. Ind. Robot. Int. J. Robot. Res. Appl. 2021, 39, 57–68. [Google Scholar] [CrossRef]
- Dumas, C.; Caro, S.; Cherif, M.; Garnier, S.; Furet, B. Joint stiffness identification of industrial serial robots. Robotica 2012, 30, 649–659. [Google Scholar] [CrossRef]
- Kamali, K.; Bonev, I.A. Optimal experiment design for elasto-geometrical calibration of industrial robots. IEEE/ASME Trans. Mechatron. 2019, 24, 2733–2744. [Google Scholar] [CrossRef]
- Nubiola, A.; Slamani, M.; Joubair, A.; Bonev, I.A. Comparison of two calibration methods for a small industrial robot based on an optical CMM and a laser tracker. Robotica 2014, 32, 447–466. [Google Scholar] [CrossRef]
- Bottin, M.; Cocuzza, S.; Comand, N.; Doria, A. Modeling and Identification of an Industrial Robot with a Selective Modal Approach. Appl. Sci. 2020, 10, 4619. [Google Scholar] [CrossRef]
- Hovland, G.E.; Berglund, E.; Hanssen, S. Identification of coupled elastic dynamics using inverse eigenvalue theory. In Proceedings of the 32nd ISR (International Symposium on Robotics), Seoul, Republic of Korea, 19–21 April 2001; Volume 19, p. 21. [Google Scholar]
- Zanchettin, A.M.; Lacevic, B. Safe and minimum-time path-following problem for collaborative industrial robots. J. Manuf. Syst. 2022, 65, 686–693. [Google Scholar] [CrossRef]
- Kamali, K.; Joubair, A.; Bonev, I.A.; Bigras, P. Elasto-geometrical calibration of an industrial robot under multidirectional external loads using a laser tracker. In Proceedings of the 2016 IEEE International Conference on Robotics Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 4320–4327. [Google Scholar]


| Positions | θ1 (°) | θ2 (°) | θ3 (°) | θ4 (°) | θ5 (°) | θ6 (°) | |
|---|---|---|---|---|---|---|---|
| 1 | −3.33 | −102.37 | 110.19 | 260.95 | 89.31 | 221.98 | 0.356 |
| 2 | 66.38 | −93.95 | 105.13 | 258.52 | 91.25 | 286.33 | 0.345 |
| 3 | 37.88 | −82.08 | 94.36 | 255.22 | 91.26 | 259.74 | 0.378 |
| 4 | 13.75 | −77.53 | 91.53 | 252.95 | 91.98 | 234.03 | 0.423 |
| 5 | 54.60 | −79.96 | 89.42 | 259.31 | 88.94 | 272.86 | 0.521 |
| Positions | (/mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I: 1 kg | II: 1.5 kg | |||||||||||
| 1 | 4.12 | 5.13 | −7.73 | 0.03 | 0.03 | 0.22 | 8.66 | 6.12 | −10.61 | 0.01 | 0.08 | 0.33 |
| 2 | 5.11 | 4.22 | −7.48 | 0.05 | 0.07 | 0.24 | 9.56 | 6.55 | −9.52 | 0.01 | 0.02 | 0.34 |
| 3 | 6.23 | 5.32 | −5.73 | 0.01 | 0.05 | 0.30 | 10.02 | 5.33 | −9.81 | 0.02 | 0.11 | 0.45 |
| 4 | 7.32 | 4.55 | −5.07 | 0.02 | 0.06 | 0.32 | 11.13 | 6.32 | −7.82 | 0.03 | 0.10 | 0.48 |
| 5 | 8.56 | 3.12 | −4.12 | 0.01 | 0.06 | 0.29 | 12.54 | 7.35 | −3.70 | 0.01 | 0.07 | 0.42 |
| III: 2 kg | IV: 2.5 kg | |||||||||||
| 1 | 13.77 | 10.21 | −10.3 | 0.03 | 0.12 | 0.43 | 20.23 | 12.22 | −8.15 | 0.07 | 0.02 | 0.53 |
| 2 | 14.65 | 9.36 | −9.89 | 0.01 | 0.04 | 0.53 | 21.24 | 10.26 | −8.28 | 0.03 | 0.08 | 0.57 |
| 3 | 15.75 | 8.44 | −8.98 | 0.04 | 0.12 | 0.58 | 22.42 | 8.55 | −7.02 | 0.04 | 0.15 | 0.72 |
| 4 | 16.26 | 8.22 | −8.23 | 0.11 | 0.18 | 0.62 | 23.33 | 7.65 | −4.71 | 0.05 | 0.16 | 0.76 |
| 5 | 18.33 | 7.28 | −3.32 | 0.01 | 0.11 | 0.55 | 24.01 | 6.22 | −3.14 | 0.05 | 0.15 | 0.68 |
| V: 3 kg | VI: 3.5 kg | |||||||||||
| 1 | 25.12 | 10.35 | −12.72 | 0.02 | 0.11 | 0.63 | 30.12 | 12.11 | −13.08 | 0.01 | 0.08 | 0.77 |
| 2 | 26.43 | 9.51 | −10.54 | 0.01 | 0.07 | 0.66 | 31.23 | 11.15 | −11.19 | 0.04 | 0.10 | 0.77 |
| 3 | 27.46 | 8.36 | −8.72 | 0.05 | 0.18 | 0.85 | 32.36 | 10.28 | −8.49 | 0.09 | 0.24 | 1.03 |
| 4 | 28.62 | 6.38 | −6.34 | 0.08 | 0.20 | 0.92 | 33.31 | 8.61 | −6.42 | 0.06 | 0.21 | 1.06 |
| 5 | 29.12 | 5.27 | −4.92 | 0.06 | 0.21 | 0.81 | 33.78 | 7.64 | −5.05 | 0.04 | 0.21 | 0.97 |
| Joints Stiffness | kq1 | kq2 | kq3 | kq4 | kq5 | kq6 |
|---|---|---|---|---|---|---|
| Stiffness value (Nm/rad) | 4.68 × 105 | 5.56 × 105 | 4.57 × 105 | 2.75 × 105 | 9.55 × 104 | 8.36 × 104 |
| Positions | (/mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I: 1 kg | II: 1.5 kg | |||||||||||
| 1 | 4.12 | 5.13 | −7.73 | 0.23 | 0.15 | 0.30 | 8.66 | 6.12 | −10.61 | 0.28 | 0.01 | 0.34 |
| 2 | 5.11 | 4.22 | −7.48 | 0.19 | −0.08 | 0.29 | 9.56 | 6.55 | −9.52 | 0.20 | −0.07 | 0.34 |
| 3 | 6.23 | 5.32 | −5.73 | 0.18 | 0.01 | 0.29 | 10.02 | 5.33 | −9.81 | 0.45 | 0.29 | 0.33 |
| 4 | 7.32 | 4.55 | −5.07 | 0.21 | 0.05 | 0.26 | 11.13 | 6.32 | −7.82 | 0.28 | 0.01 | 0.34 |
| 5 | 8.56 | 3.12 | −4.12 | 0.28 | 0.01 | 0.25 | 12.54 | 7.35 | −3.70 | 0.20 | −0.07 | 0.34 |
| III: 2 kg | IV: 2.5 kg | |||||||||||
| 1 | 13.77 | 10.21 | −10.3 | 0.46 | 0.30 | 0.50 | 20.23 | 12.22 | −8.15 | 0.58 | 0.38 | 0.50 |
| 2 | 14.65 | 9.36 | −9.89 | 0.39 | 0.02 | 0.48 | 21.24 | 10.26 | −8.28 | 0.49 | 0.03 | 0.52 |
| 3 | 15.75 | 8.44 | −8.98 | 0.37 | 0.01 | 0.48 | 22.42 | 8.55 | −7.02 | 0.46 | 0.01 | 0.52 |
| 4 | 16.26 | 8.22 | −8.23 | 0.26 | −0.12 | 0.41 | 23.33 | 7.65 | −4.71 | 0.33 | −0.14 | 0.59 |
| 5 | 18.33 | 7.28 | −3.32 | 0.60 | 0.38 | 0.41 | 24.01 | 6.22 | −3.14 | 0.75 | 0.48 | 0.58 |
| V: 3 kg | VI: 3.5 kg | |||||||||||
| 1 | 25.12 | 10.35 | −12.72 | 0.70 | 0.46 | 0.70 | 30.12 | 12.11 | −13.08 | 0.81 | 0.53 | 0.89 |
| 2 | 26.43 | 9.51 | −10.54 | 0.59 | 0.04 | 0.67 | 31.23 | 11.15 | −11.19 | 0.69 | 0.04 | 0.71 |
| 3 | 27.46 | 8.36 | −8.72 | 0.55 | 0.01 | 0.68 | 32.36 | 10.28 | −8.49 | 0.65 | 0.0 | 0.91 |
| 4 | 28.62 | 6.38 | −6.34 | 0.39 | −0.17 | 0.67 | 33.31 | 8.61 | −6.42 | 0.46 | −0.20 | 0.85 |
| 5 | 29.12 | 5.27 | −4.92 | 0.90 | 0.57 | 0.66 | 33.78 | 7.64 | −5.05 | 1.05 | 0.67 | 0.73 |
| (mm) | (mm) | (rad) | (rad) | |
|---|---|---|---|---|
| 1 | 96 | 0 | ||
| 2 | 0 | 418 | 0 | |
| 3 | 0 | 398 | 0 | |
| 4 | 114 | 0 | ||
| 5 | 98 | 0 | ||
| 6 | 89 | 0 | 0 |
| Joint Angles | |||
|---|---|---|---|
| Change range (rad) |
| Position Points | (rad) | (rad) | (rad) | (rad) | (rad) | (rad) | (N/mm) | (N/mm) | (N/mm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.047 | 0.408 | 1.902 | 4.660 | 1.571 | 3.141 | 889 | 905 | 1370 |
| 2 | 1.047 | 0.696 | 1.902 | 4.660 | 1.570 | 3.140 | 900 | 949 | 1637 |
| 3 | 1.046 | 0.883 | 1.901 | 4.661 | 1.571 | 3.141 | 926 | 1038 | 1521 |
| 4 | 1.047 | 1.058 | 1.902 | 4.660 | 1.570 | 3.140 | 1568 | 910 | 1589 |
| 5 | 1.047 | 1.245 | 1.901 | 4.659 | 1.569 | 3.141 | 980 | 911 | 1300 |
| 6 | 1.047 | 1.332 | 1.902 | 4.660 | 1.570 | 3.142 | 960 | 932 | 1570 |
| 7 | 1.046 | 2.094 | 1.832 | 4.433 | 1.571 | 3.141 | 935 | 950 | 1500 |
| 8 | 1.047 | 2.093 | 1.919 | 4.432 | 1.570 | 3.140 | 968 | 1042 | 1486 |
| 9 | 1.045 | 2.094 | 2.107 | 4.433 | 1.571 | 3.141 | 997 | 958 | 1554 |
| 10 | 1.047 | 2.095 | 2.268 | 4.431 | 1.570 | 3.140 | 1500 | 1024 | 1561 |
| 11 | 1.046 | 2.095 | 2.347 | 4.433 | 1.571 | 3.141 | 1389 | 1053 | 1370 |
| 12 | 1.045 | 2.094 | 2.489 | 4.430 | 1.570 | 3.142 | 1206 | 795 | 1486 |
| 13 | 1.047 | 1.715 | 1.901 | 4.660 | 1.571 | 3.140 | 1138 | 635 | 1335 |
| 14 | 1.047 | 1.832 | 1.902 | 4.661 | 1.572 | 3.142 | 1030 | 851 | 1500 |
| 15 | 1.047 | 1.919 | 1.901 | 4.660 | 1.571 | 3.141 | 1055 | 631 | 1426 |
| 16 | 1.046 | 2.224 | 1.902 | 4.661 | 1.570 | 3.142 | 1046 | 760 | 1924 |
| 17 | 1.047 | 2.281 | 1.903 | 4.660 | 1.571 | 3.143 | 810 | 765 | 1877 |
| 18 | 1.047 | 2.368 | 1.903 | 4.662 | 1.572 | 3.141 | 800 | 751 | 1816 |
| 19 | 0.872 | 1.658 | 0.432 | 4.537 | 1.745 | 3.490 | 797 | 742 | 1276 |
| 20 | 0.871 | 1.657 | 0.619 | 4.536 | 1.744 | 3.491 | 808 | 646 | 1300 |
| 21 | 0.872 | 1.658 | 0.707 | 4.537 | 1.744 | 3.491 | 1138 | 615 | 1430 |
| 22 | 0.871 | 1.658 | 0.891 | 4.537 | 1.745 | 3.490 | 1030 | 625 | 1800 |
| 23 | 0.870 | 1.656 | 0.968 | 4.538 | 1.746 | 3.491 | 936 | 756 | 1610 |
| 24 | 0.872 | 1.656 | 1.132 | 4.536 | 1.745 | 3.490 | 1127 | 797 | 1420 |
| 25 | 1.813 | −0.025 | 0.654 | 0.015 | −2.355 | −3.411 | 1020 | 949 | 1589 |
| 26 | 1.878 | −0.171 | 0.545 | 0.019 | −2.310 | −3.502 | 968 | 1038 | 1864 |
| 27 | 1.956 | −0.266 | 0.630 | 0.021 | −2.301 | −3.801 | 941 | 910 | 1808 |
| 28 | 2.182 | −0.084 | 0.501 | 0.022 | −2.354 | −3.587 | 959 | 911 | 1391 |
| 29 | 2.180 | −0.225 | 0.311 | 0.024 | −2.130 | −3.802 | 975 | 932 | 1570 |
| Pose Points | Fx (N) | Δx (mm) | Fy (N) | Δy (mm) | Fz (N) | Δz (mm) | Kx_exp (N/mm) | Ky_exp (N/mm) | Kz_exp (N/mm) |
|---|---|---|---|---|---|---|---|---|---|
| P1 | 4.2 | 0.0026 | 2.0 | 0.0022 | 6.1 | 0.0034 | 1615 | 909 | 1794 |
| P2 | 6.3 | 0.0041 | 2.9 | 0.0033 | 9.1 | 0.0049 | 1537 | 879 | 1857 |
| P3 | 8.7 | 0.0056 | 3.6 | 0.0041 | 11.3 | 0.0059 | 1554 | 878 | 1915 |
| P4 | 10.4 | 0.0067 | 4.1 | 0.0046 | 13.2 | 0.0065 | 1552 | 891 | 2031 |
| P5 | 13.0 | 0.0086 | 5.0 | 0.0054 | 15.9 | 0.0079 | 1512 | 926 | 2013 |
| P6 | 15.2 | 0.0101 | 5.7 | 0.0062 | 18.1 | 0.0086 | 1505 | 919 | 2105 |
| P7 | 17.3 | 0.0115 | 6.5 | 0.0069 | 20.0 | 0.0094 | 1504 | 942 | 2128 |
| Pose Points | Kx_model (N/mm) | Kx_exp (N/mm) | (%) | Ky_model (N/mm) | Ky_exp (N/mm) | (%) | Kz_model (N/mm) | Kz_exp (N/mm) | (%) |
|---|---|---|---|---|---|---|---|---|---|
| P1 | 1490 | 1615 | 7.74 | 910 | 909 | 0.11 | 1810 | 1794 | 0.88 |
| P3 | 1540 | 1554 | 0.90 | 880 | 878 | 0.23 | 1900 | 1915 | 0.79 |
| P5 | 1525 | 1512 | 0.85 | 920 | 926 | 0.65 | 2030 | 2013 | 0.84 |
| P7 | 1495 | 1504 | 0.60 | 950 | 942 | 0.84 | 2140 | 2128 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Zhang, M.; Tan, J.; Chen, Z.; Chen, G. Comprehensive Stiffness Modeling and Evaluation of an Orthopedic Surgical Robot for Enhanced Cutting Operation Performance. Biomimetics 2025, 10, 383. https://doi.org/10.3390/biomimetics10060383
Tian H, Zhang M, Tan J, Chen Z, Chen G. Comprehensive Stiffness Modeling and Evaluation of an Orthopedic Surgical Robot for Enhanced Cutting Operation Performance. Biomimetics. 2025; 10(6):383. https://doi.org/10.3390/biomimetics10060383
Chicago/Turabian StyleTian, Heqiang, Mengke Zhang, Jiezhong Tan, Zhuo Chen, and Guangqing Chen. 2025. "Comprehensive Stiffness Modeling and Evaluation of an Orthopedic Surgical Robot for Enhanced Cutting Operation Performance" Biomimetics 10, no. 6: 383. https://doi.org/10.3390/biomimetics10060383
APA StyleTian, H., Zhang, M., Tan, J., Chen, Z., & Chen, G. (2025). Comprehensive Stiffness Modeling and Evaluation of an Orthopedic Surgical Robot for Enhanced Cutting Operation Performance. Biomimetics, 10(6), 383. https://doi.org/10.3390/biomimetics10060383






