An Improved Northern Goshawk Optimization Algorithm for Mural Image Segmentation
Abstract
1. Introduction
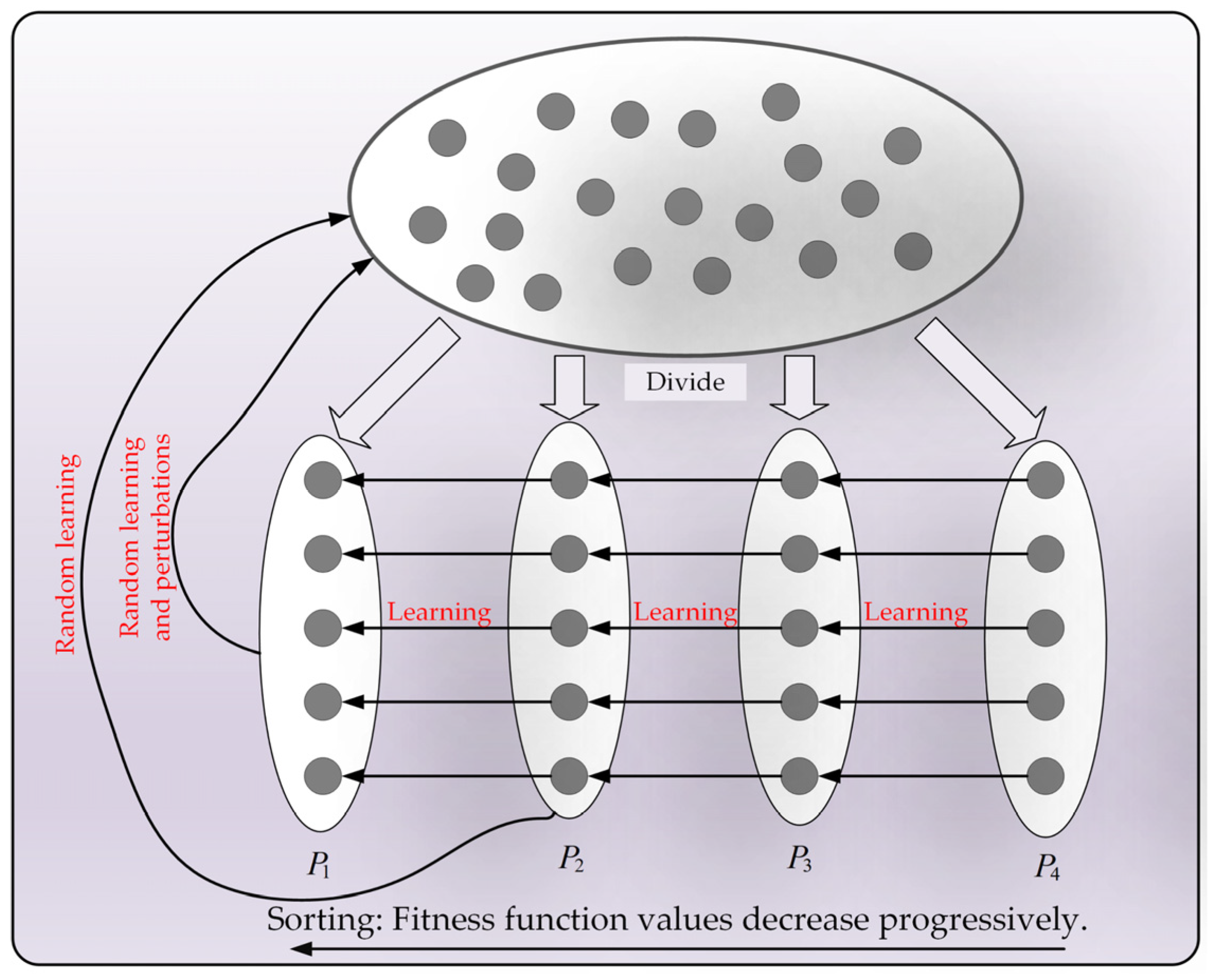
- The off-center learning strategy was integrated by incorporating the fitness function values of individuals, specifically by guiding the population with off-center individuals, effectively enhancing the algorithm’s global search capability.
- The partitioned learning strategy was included by integrating fitness function values, and by applying diverse learning methods to the population, better balance between the exploration and development phases was achieved, thereby improving the algorithm’s ability to escape from local suboptimal solutions.
- The Bernstein-weighted learning strategy was applied by leveraging the weighted properties of second-order Bernstein polynomials, and by guiding the population with weighted individuals, the algorithm’s development performance was effectively improved.
- Building upon the NGO algorithm, an enhanced NGO algorithm named OPBNGO was proposed by integrating the aforementioned three learning strategies.
- The OPBNGO algorithm was employed to solve multi-threshold segmentation problems on eight mural images, achieving remarkable results in terms of fitness function values, PSNR, SSIM, and FSIM metrics, thereby confirming that the OPBNGO algorithm is a promising image segmentation method.
2. Mathematical Model of Northern Goshawk Optimization
2.1. Population Initialization
2.2. Exploration Phase
2.3. Exploitation Phase
2.4. Implementation of the NGO Algorithm
| Algorithm 1: Pseudo code for NGO algorithm |
| Input: Population size (), Dimension of the optimization problem (), Upper bound of the optimization problem () and lower bound (), Maximum number of iterations (). Output: Global best solution ().
|
3. Mathematical Model of Improved Northern Goshawk Optimization
3.1. Off-Center Learning Strategy
3.2. Partitioned Learning Strategy
3.3. Bernstein-Weighted Learning Strategy
3.4. Implementation of the OPBNGO Algorithm
| Algorithm 2: Pseudo code for OPBNGO algorithm |
| Input: Population size (), Dimension of the optimization problem (), Upper bound of the optimization problem () and lower bound (), Maximum number of iterations (). Output: Global best solution ().
|
3.5. Time Complexity of the OPBNGO Algorithm
4. Results and Discussion on Mural Image Segmentation
4.1. Concept of Otsu Thresholding Technique
4.2. Experimental Results Analysis of Mural Image Segmentation
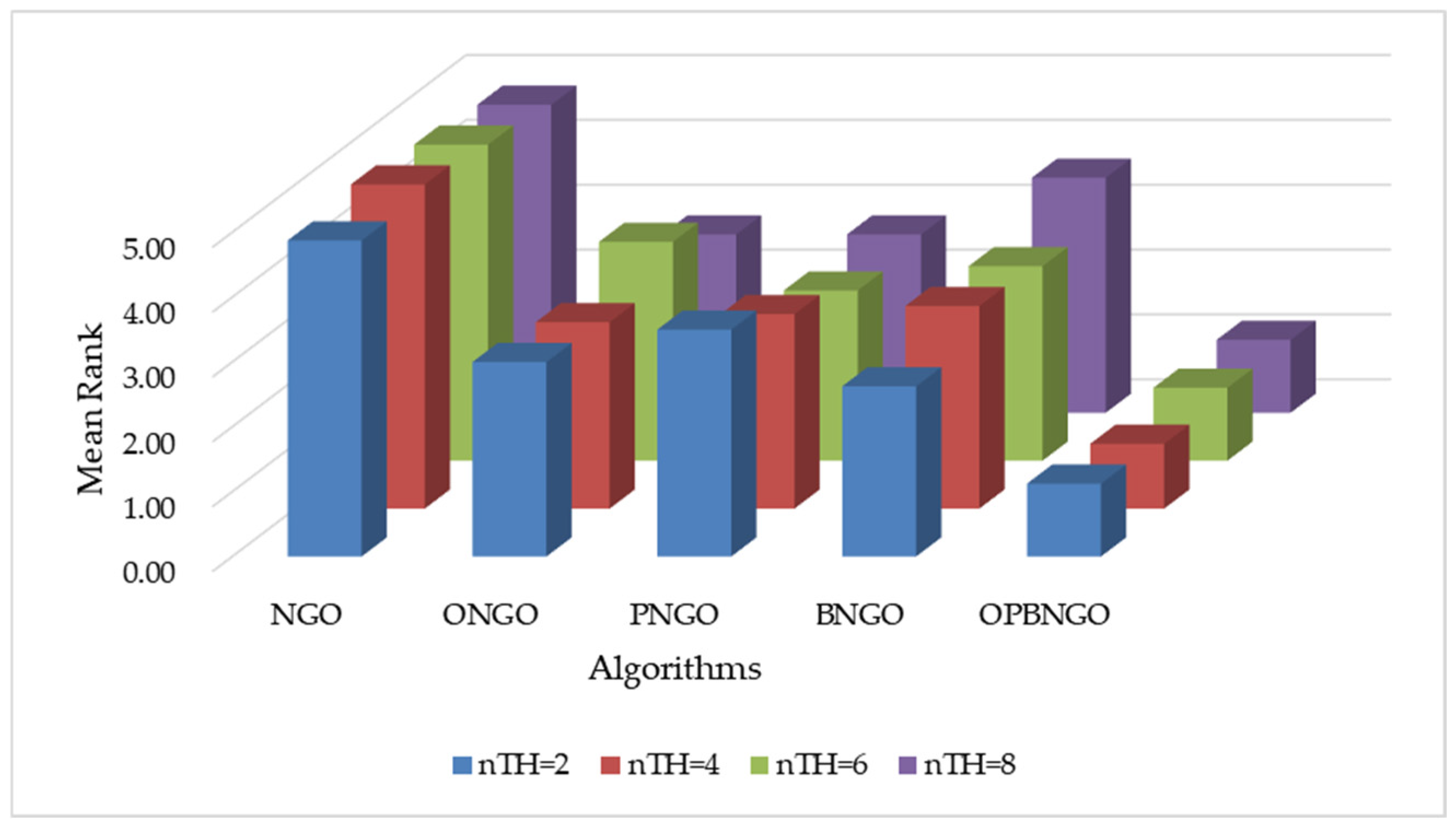
4.2.1. Strategy Effectiveness Analysis of Mural Image Segmentation
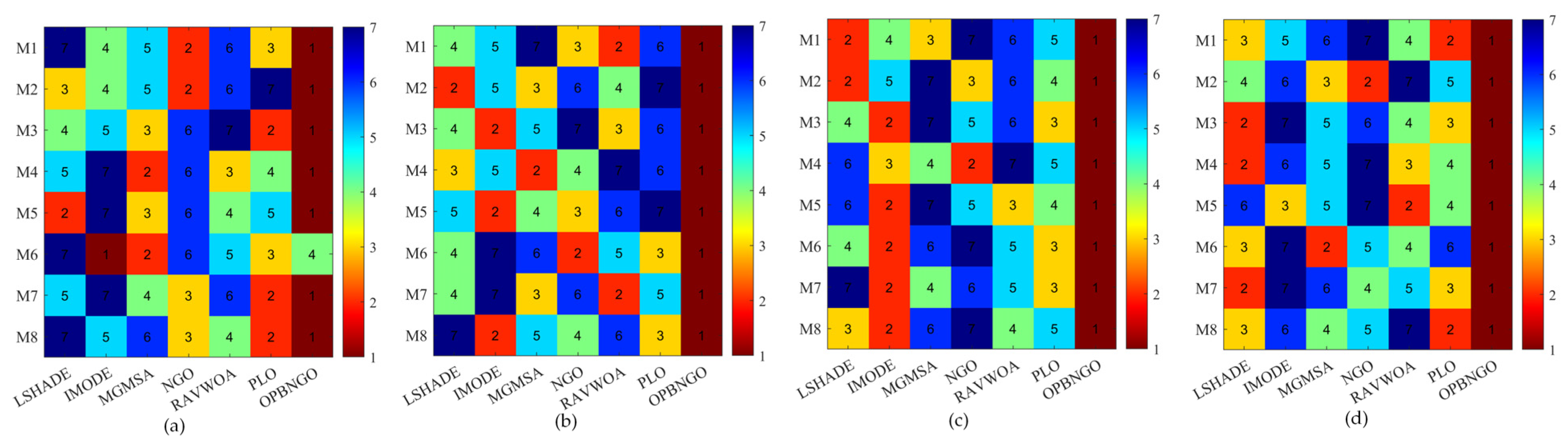
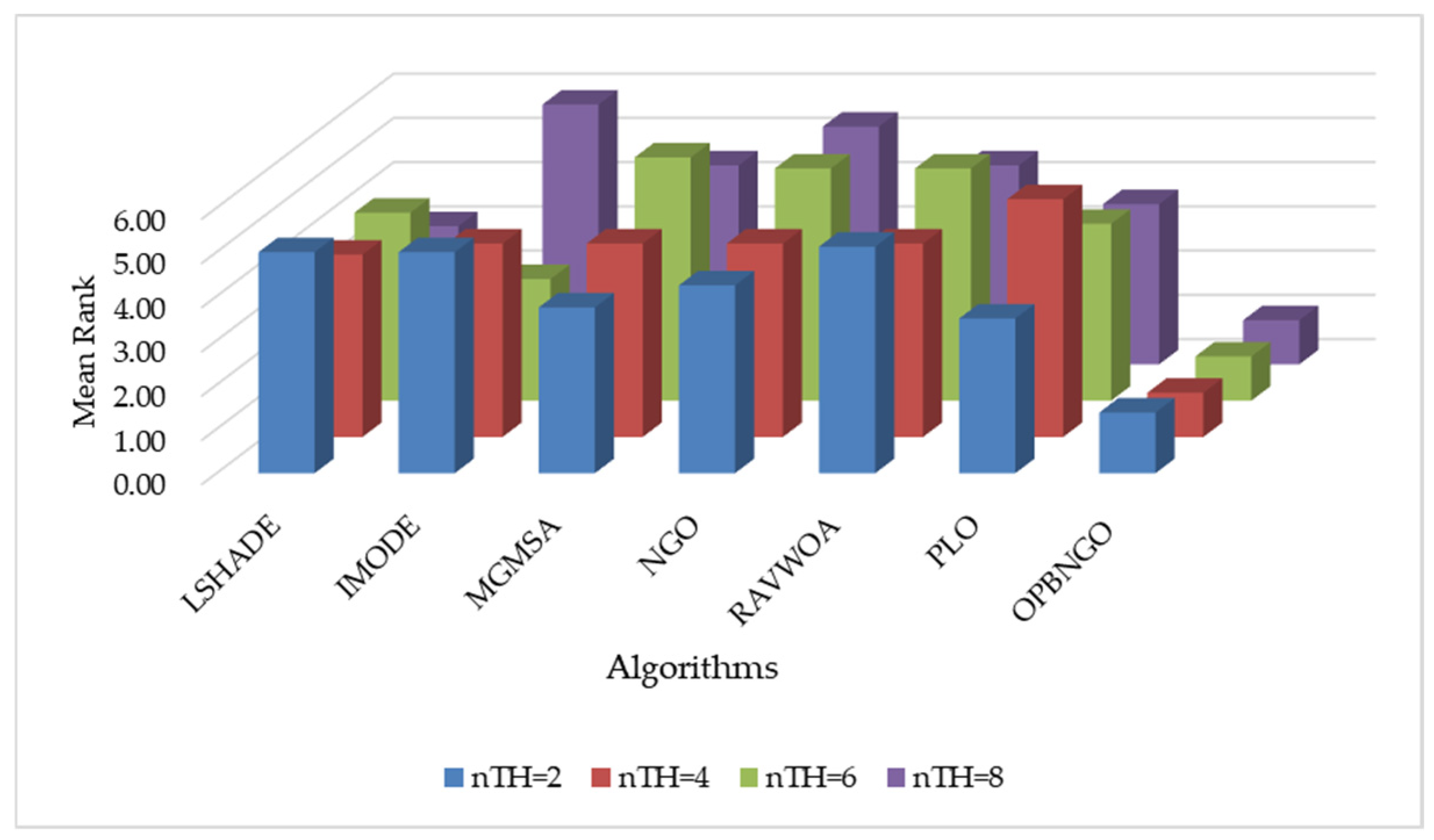
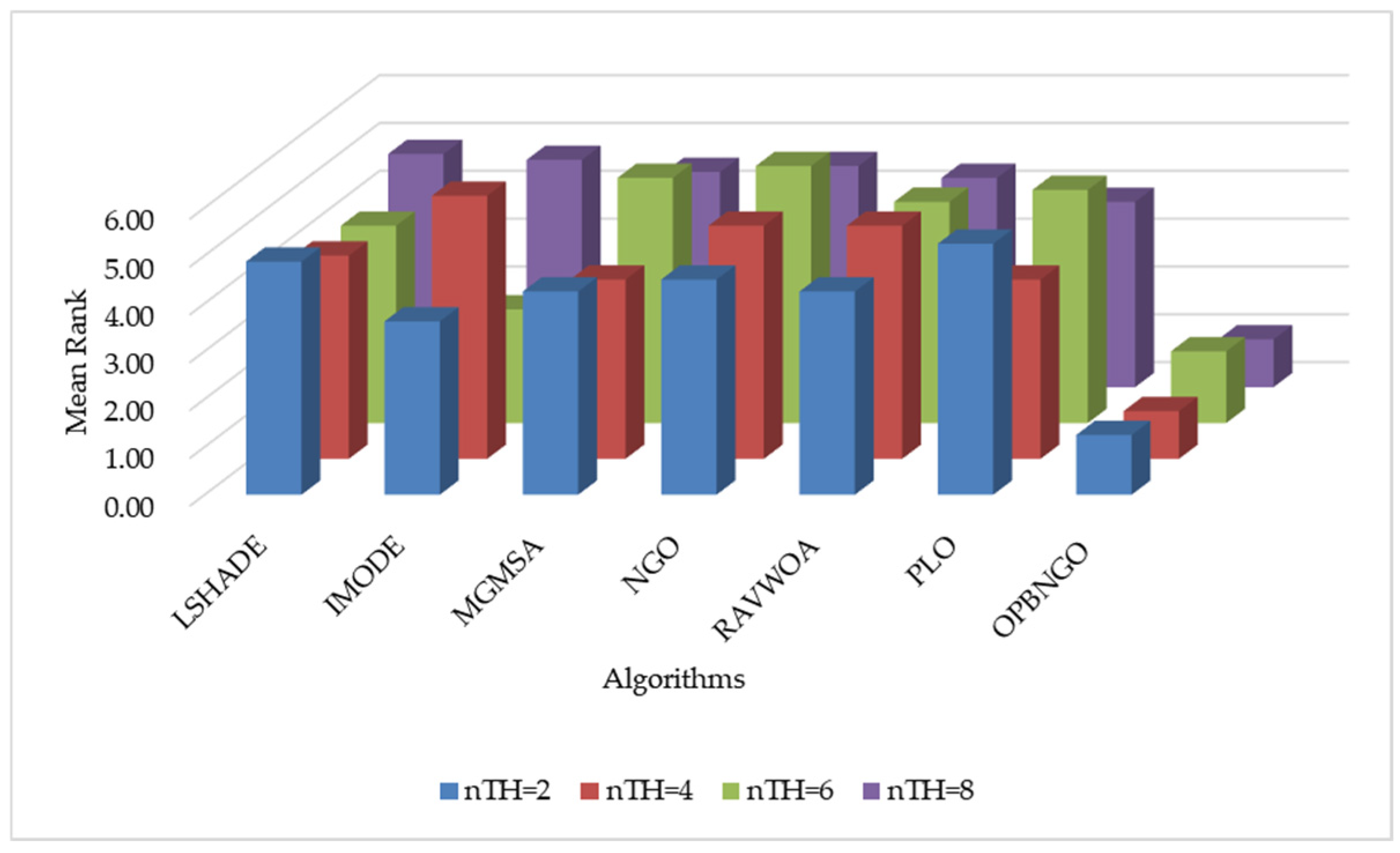
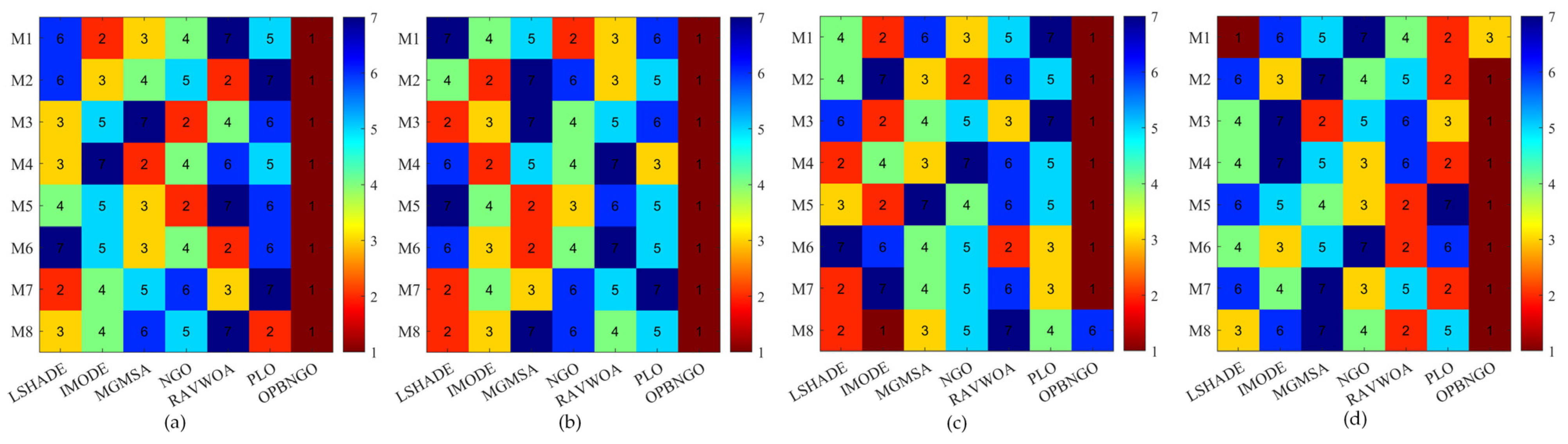
4.2.2. Fitness Value Metric Analysis of Mural Image Segmentation
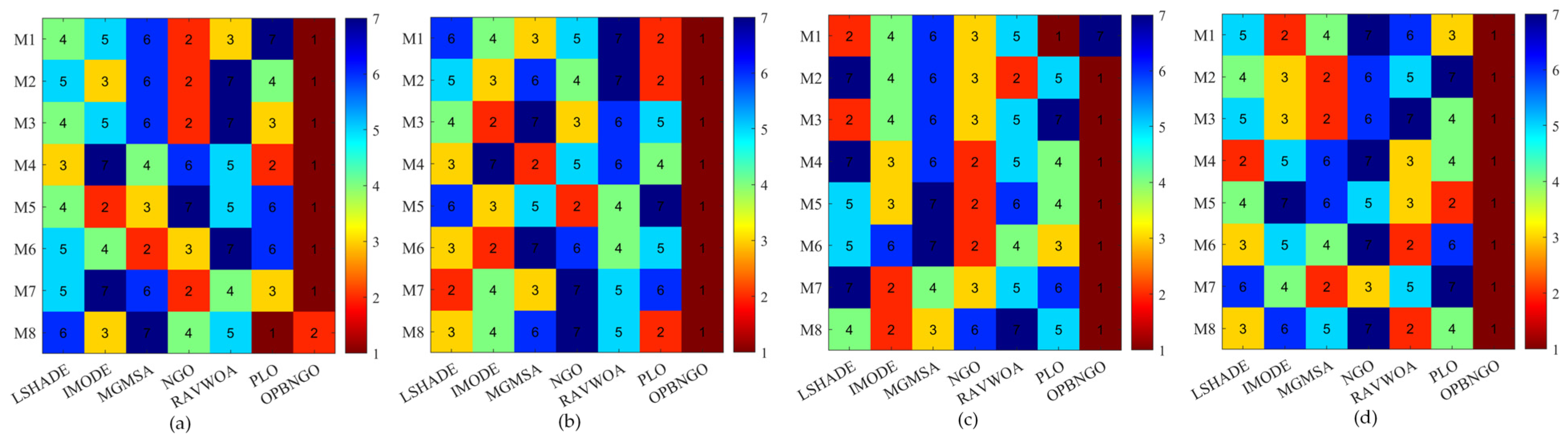
4.2.3. PSNR Metric Analysis of Mural Image Segmentation
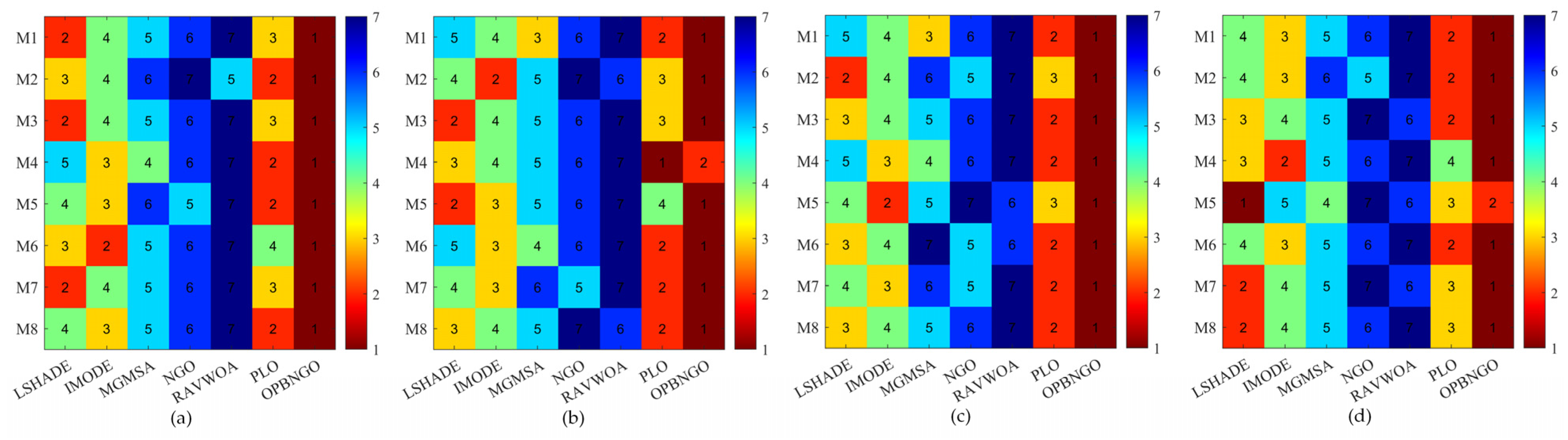
4.2.4. SSIM Metric Analysis of Mural Image Segmentation
4.2.5. FSIM Metric Analysis of Mural Image Segmentation
4.2.6. Convergence Analysis of Mural Image Segmentation
4.2.7. Computational Time Analysis of Mural Image Segmentation
5. Conclusions and Future Works
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H. Intelligent restoration of ancient murals based on discrete differential algorithm. J. Comput. Methods Sci. Eng. 2021, 21, 803–814. [Google Scholar] [CrossRef]
- Krishnan, B.; Ganesan, A.R.; Balasubramani, R.; Nguyen, D.D.; Chang, S.W. Chrysoeriol ameliorates hyperglycemia by regulating the carbohydrate metabolic enzymes in streptozotocin-induced diabetic rats. Food Sci. Hum. Wellness 2020, 9, 346–354. [Google Scholar] [CrossRef]
- Teshita, A.; Khan, W.; Ullah, A.; Iqbal, B.; Ahmad, N. Soil Nematodes in Agroecosystems: Linking Cropping System’s Rhizosphere Ecology to Nematode Structure and Function. J. Soil Sci. Plant Nutr. 2024, 24, 6467–6482. [Google Scholar] [CrossRef]
- Yuexia, C.; Long, C.; Ruochen, W.; Xing, X.; Yujie, S. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar]
- Qiu, H.; Gao, L.; Wang, J.; Pan, J.; Yan, Y.; Zhang, X. A precise and efficient detection of Beta-Cyfluthrin via fluorescent molecularly imprinted polymers with ally fluorescein as functional monomer in agricultural products. Food Chem. 2017, 217, 620–627. [Google Scholar] [CrossRef]
- Mahmood, A.; Hu, Y.; Tanny, J.; Asante, E.A. Effects of shading and insect-proof screens on crop microclimate and production: A review of recent advances. Sci. Hortic. 2018, 241, 241–251. [Google Scholar] [CrossRef]
- Du, Z.; Hu, Y.; Ali Buttar, N.; Mahmood, A. X-ray computed tomography for quality inspection of agricultural products: A review. Food Sci. Nutr. 2019, 7, 3146–3160. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Qiu, Y.; Li, P.; Liu, B.; Yang, L. Highly specific monoclonal antibody and sensitive quantum dot beads-based fluorescence immunochromatographic test strip for tebuconazole assay in agricultural products. J. Agric. Food Chem. 2019, 67, 9096–9103. [Google Scholar] [CrossRef]
- Shen, L.; Xiong, X.; Zhang, D.; Zekrumah, M.; Hu, Y.; Gu, X. Optimization of betacyanins from agricultural by-products using pressurized hot water extraction for antioxidant and in vitro oleic acid-induced steatohepatitis inhibitory activity. J. Food Biochem. 2019, 43, e13044. [Google Scholar] [CrossRef]
- Mao, Y.; Sun, M.; Hong, X.; Chakraborty, S.; Du, D. Semi-quantitative and quantitative detection of ochratoxin A in agricultural by-products using a self-assembling immunochromatographic strip. J. Sci. Food Agric. 2021, 101, 1659–1665. [Google Scholar] [CrossRef]
- Jiao, L.J.; Wang, W.J.; Li, B.J.; Zhao, Q.S. Wutai mountain mural inpainting based on improved block matching algorithm. J. Comput. Aid Des. Comput. Graph 2019, 31, 119–125. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, W. Sponge effect of aerated concrete on phosphorus adsorption-desorption from agricultural drainage water in rainfall. Soil Water Res. 2020, 15, 220–227. [Google Scholar] [CrossRef]
- Osae, R.; Essilfie, G.; Alolga, R.N.; Akaba, S.; Song, X.; Owusu-Ansah, P.; Zhou, C. Application of non-thermal pretreatment techniques on agricultural products prior to drying: A review. J. Sci. Food Agric. 2020, 100, 2585–2599. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Liu, J.; Xu, Z.; Yuan, S.; Li, P.; Wang, J. Development status and trend of agricultural robot technology. Int. J. Agric. Biol. Eng. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Ahmed, S.; Qiu, B.; Ahmad, F.; Kong, C.W.; Xin, H. A state-of-the-art analysis of obstacle avoidance methods from the perspective of an agricultural sprayer UAV’s operation scenario. Agronomy 2021, 11, 1069. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Y.; Wei, W.; Hu, Z.; Li, P. Optimization design of spray cooling fan based on CFD simulation and field experiment for horticultural crops. Agriculture 2021, 11, 566. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, P.; Yosri, N.; Chen, Q.; Elseedi, H.R.; Zou, X.; Yang, H. Detection of heavy metals in food and agricultural products by surface-enhanced Raman spectroscopy. Food Rev. Int. 2023, 39, 1440–1461. [Google Scholar] [CrossRef]
- Awais, M.; Li, W.; Hussain, S.; Cheema, M.J.M.; Li, W.; Song, R.; Liu, C. Comparative evaluation of land surface temperature images from unmanned aerial vehicle and satellite observation for agricultural areas using in situ data. Agriculture 2022, 12, 184. [Google Scholar] [CrossRef]
- Ma, J.; Liu, K.; Dong, X.; Chen, C.; Qiu, B.; Zhang, S. Effects of leaf surface roughness and contact angle on in vivo measurement of droplet retention. Agronomy 2022, 12, 2228. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.; Guo, S.; Tang, Z.; Chen, S. Motor torque distribution strategy for different tillage modes of agricultural electric tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy adaptive energy management strategy for a hybrid agricultural tractor equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Yu, T.; Lin, C.; Zhang, S.; Ding, X.; Wu, J.; Zhang, J. End-to-end partial convolutions neural networks for Dunhuang grottoes wall-painting restoration. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Cui, M.; Guo, Y.; Chen, J. Influence of transfer plot area and location on chemical input reduction in agricultural production: Evidence from China. Agriculture 2023, 13, 1794. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Y.; Li, H. Research progress and analysis on comprehensive utilization of livestock and poultry biogas slurry as agricultural resources. Agriculture 2023, 13, 2216. [Google Scholar] [CrossRef]
- Pan, Q.; Lu, Y.; Hu, H.; Hu, Y. Review and research prospects on sprinkler irrigation frost protection for horticultural crops. Sci. Hortic. 2024, 326, 112775. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Z.; Li, H.; Zhang, X. Maintenance skill training gives agricultural socialized service providers more advantages. Agriculture 2023, 13, 135. [Google Scholar] [CrossRef]
- Wang, B.; Du, X.; Wang, Y.; Mao, H. Multi-machine collaboration realization conditions and precise and efficient production mode of intelligent agricultural machinery. Int. J. Agric. Biol. Eng. 2024, 17, 27–36. [Google Scholar]
- Han, P.H.; Chen, Y.S.; Liu, I.S.; Jang, Y.P.; Tsai, L.; Chang, A.; Hung, Y.P. A compelling virtual tour of the dunhuang cave with an immersive head-mounted display. IEEE Comput. Graph. Appl. 2019, 40, 40–55. [Google Scholar] [CrossRef]
- Abualigah, L.; Almotairi, K.H.; Elaziz, M.A. Multilevel thresholding image segmentation using meta-heuristic optimization algorithms: Comparative analysis, open challenges and new trends. Appl. Intell. 2023, 53, 11654–11704. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Houssein, E.H.; Oliva, D.; Samee, N.A.; Mahmoud, N.F.; Emam, M.M. Liver cancer algorithm: A novel bio-inspired optimizer. Comput. Biol. Med. 2023, 165, 107389. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Wang, L.; Zhang, Z.; Fan, H.; Zhang, J.; Mirjalili, S.; Cao, Q. Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications. Expert Syst. Appl. 2024, 238, 122200. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Abdelhamid, A.A.; Eid, M.M.; Ibrahim, A. Greylag goose optimization: Nature-inspired optimization algorithm. Expert Syst. Appl. 2024, 238, 122147. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Wei, G.; Abualigah, L. Genghis Khan shark optimizer: A novel nature-inspired algorithm for engineering optimization. Adv. Eng. Inform. 2023, 58, 102210. [Google Scholar] [CrossRef]
- Hu, G.; Cheng, M.; Houssein, E.H.; Hussien, A.G.; Abualigah, L. SDO: A novel sled dog-inspired optimizer for solving engineering problems. Adv. Eng. Inform. 2024, 62, 102783. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access 2024, 10, 49445–49473. [Google Scholar] [CrossRef]
- Zhao, Y.; Fu, S.; Zhang, L.; Huang, H. Aitken optimizer: An efficient optimization algorithm based on the Aitken acceleration method. J. Supercomput. 2025, 81, 264. [Google Scholar] [CrossRef]
- Mozhdehi, A.T.; Khodadadi, N.; Aboutalebi, M.; El-kenawy, E.S.M.; Hussien, A.G.; Zhao, W.; Mirjalili, S. Divine Religions Algorithm: A novel social-inspired metaheuristic algorithm for engineering and continuous optimization problems. Clust. Comput. 2025, 28, 253. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Mirjalili, S.; Khodadadi, N.; Ge, Q. Quadratic Interpolation Optimization (QIO): A new optimization algorithm based on generalized quadratic interpolation and its applications to real-world engineering problems. Comput. Methods Appl. Mech. Eng. 2023, 417, 116446. [Google Scholar] [CrossRef]
- Braik, M.; Al-Hiary, H.; Alzoubi, H.; Hammouri, A.; Azmi Al-Betar, M.; Awadallah, M.A. Tornado optimizer with Coriolis force: A novel bio-inspired meta-heuristic algorithm for solving engineering problems. Artif. Intell. Rev. 2025, 58, 123. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Chakrabortty, R.K. Light spectrum optimizer: A novel physics-inspired metaheuristic optimization algorithm. Mathematics 2022, 10, 3466. [Google Scholar] [CrossRef]
- Shehadeh, H.A. Chernobyl disaster optimizer (CDO): A novel meta-heuristic method for global optimization. Neural Comput. Appl. 2023, 35, 10733–10749. [Google Scholar] [CrossRef]
- Houssein, E.H.; Abdalkarim, N.; Hussain, K.; Mohamed, E. Accurate multilevel thresholding image segmentation via oppositional Snake Optimization algorithm: Real cases with liver disease. Comput. Biol. Med. 2024, 169, 107922. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.A.; Chen, H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, K.; Xue, Y.; Tang, W.; Salehnia, T. A multi-level thresholding image segmentation method using hybrid Arithmetic Optimization and Harris Hawks Optimizer algorithms. Expert Syst. Appl. 2024, 241, 122316. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Wu, Z.; Chen, H. Artemisinin optimization based on malaria therapy: Algorithm and applications to medical image segmentation. Displays 2024, 84, 102740. [Google Scholar] [CrossRef]
- Chen, D.; Ge, Y.; Wan, Y.; Deng, Y.; Chen, Y.; Zou, F. Poplar optimization algorithm: A new meta-heuristic optimization technique for numerical optimization and image segmentation. Expert Syst. Appl. 2022, 200, 117118. [Google Scholar] [CrossRef]
- Wang, J.; Bei, J.; Song, H.; Zhang, H.; Zhang, P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023, 137, 110130. [Google Scholar] [CrossRef]
- Das, A.; Namtirtha, A.; Dutta, A. Lévy–Cauchy arithmetic optimization algorithm combined with rough K-means for image segmentation. Appl. Soft Comput. 2023, 140, 110268. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, F.; Wang, D.; Liu, T.; Hu, R. Multi-threshold segmentation of breast cancer images based on improved dandelion optimization algorithm. J. Supercomput. 2024, 80, 3849–3874. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Houssein, E.H.; Hussien, A.G.; Singh, B.; Emam, M.M. An enhanced chameleon swarm algorithm for global optimization and multi-level thresholding medical image segmentation. Neural Comput. Appl. 2024, 36, 8775–8823. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G.; Bouaouda, A.; Samee, N.A.; Khurma, R.A.; Alamro, H.; Al-Betar, M.A. An enhanced exponential distribution optimizer and its application for multi-level medical image thresholding problems. Alex. Eng. J. 2024, 93, 142–188. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Deng, H.; Peng, L.; Zhang, H.; Yang, B.; Chen, Z. Ranking-based biased learning swarm optimizer for large-scale optimization. Inf. Sci. 2019, 493, 120–137. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Q. Three-learning strategy particle swarm algorithm for global optimization problems. Inf. Sci. 2022, 593, 289–313. [Google Scholar] [CrossRef]
- Huynh-Thu, Q.; Ghanbari, M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 2008, 44, 800–801. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Sallam, K.M.; Elsayed, S.M.; Chakrabortty, R.K.; Ryan, M.J. Improved multi-operator differential evolution algorithm for solving unconstrained problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: New York, NY, USA, 2020; pp. 1–8. [Google Scholar]
- Ren, L.; Heidari, A.A.; Cai, Z.; Shao, Q.; Liang, G.; Chen, H.L.; Pan, Z. Gaussian kernel probability-driven slime mould algorithm with new movement mechanism for multi-level image segmentation. Measurement 2022, 192, 110884. [Google Scholar] [CrossRef]
- Ma, G.; Yue, X. An improved whale optimization algorithm based on multilevel threshold image segmentation using the Otsu method. Eng. Appl. Artif. Intell. 2022, 113, 104960. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]










| Authors | Year | Algorithms | Main Strategies | Results |
|---|---|---|---|---|
| Houssein et al. [46] | 2024 | SO-OBL | Opposition-based learning | High search performance |
| Lian et al. [47] | 2024 | PO | Innovative development strategies | High image segmentation performance |
| Qiao et al. [48] | 2024 | AOA-HHO | Hybrid algorithm | Low image distortion rate |
| Yuan et al. [49] | 2024 | AO | Innovative exploration strategies | High structural similarity |
| Chen et al. [50] | 2022 | POA | Innovative exploration strategies | High feature similarity |
| Wang et al. [51] | 2023 | CRWOA | Crossover and similarity removal strategies | Excellent fitness function value |
| Arunita et al. [52] | 2023 | LCAOA | Lévy–Cauchy variation | High feature similarity |
| Wang et al. [53] | 2024 | IDOA | Opposition-based learning | High image segmentation performance |
| Mostafa et al. [54] | 2024 | ICSA | Lévy, Gaussian, and Cauchy perturbation strategies | High feature similarity |
| Hashim et al. [55] | 2024 | mEDO | Phasor operators and an adaptive optimal mutation strategy | Low image distortion rate |
| Name | Time | Parameter Settings |
|---|---|---|
| LSHADE [63] | 2014 | |
| IMODE [64] | 2020 | |
| MGSMA [65] | 2022 | |
| NGO [56] | 2021 | |
| RAVWOA [66] | 2022 | |
| PLO [67] | 2024 |
| Image | nTH = 2 | nTH = 4 | nTH = 6 | nTH = 8 |
|---|---|---|---|---|
| M1 |  | |||
| M2 |  | |||
| M3 |  | |||
| M4 |  | |||
| M5 |  | |||
| M6 |  | |||
| M7 |  | |||
| M8 |  | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Bao, Z.; Dong, H. An Improved Northern Goshawk Optimization Algorithm for Mural Image Segmentation. Biomimetics 2025, 10, 373. https://doi.org/10.3390/biomimetics10060373
Wang J, Bao Z, Dong H. An Improved Northern Goshawk Optimization Algorithm for Mural Image Segmentation. Biomimetics. 2025; 10(6):373. https://doi.org/10.3390/biomimetics10060373
Chicago/Turabian StyleWang, Jianfeng, Zuowen Bao, and Hao Dong. 2025. "An Improved Northern Goshawk Optimization Algorithm for Mural Image Segmentation" Biomimetics 10, no. 6: 373. https://doi.org/10.3390/biomimetics10060373
APA StyleWang, J., Bao, Z., & Dong, H. (2025). An Improved Northern Goshawk Optimization Algorithm for Mural Image Segmentation. Biomimetics, 10(6), 373. https://doi.org/10.3390/biomimetics10060373





