MultiSEss: Automatic Sleep Staging Model Based on SE Attention Mechanism and State Space Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Sleep-EDF Dataset
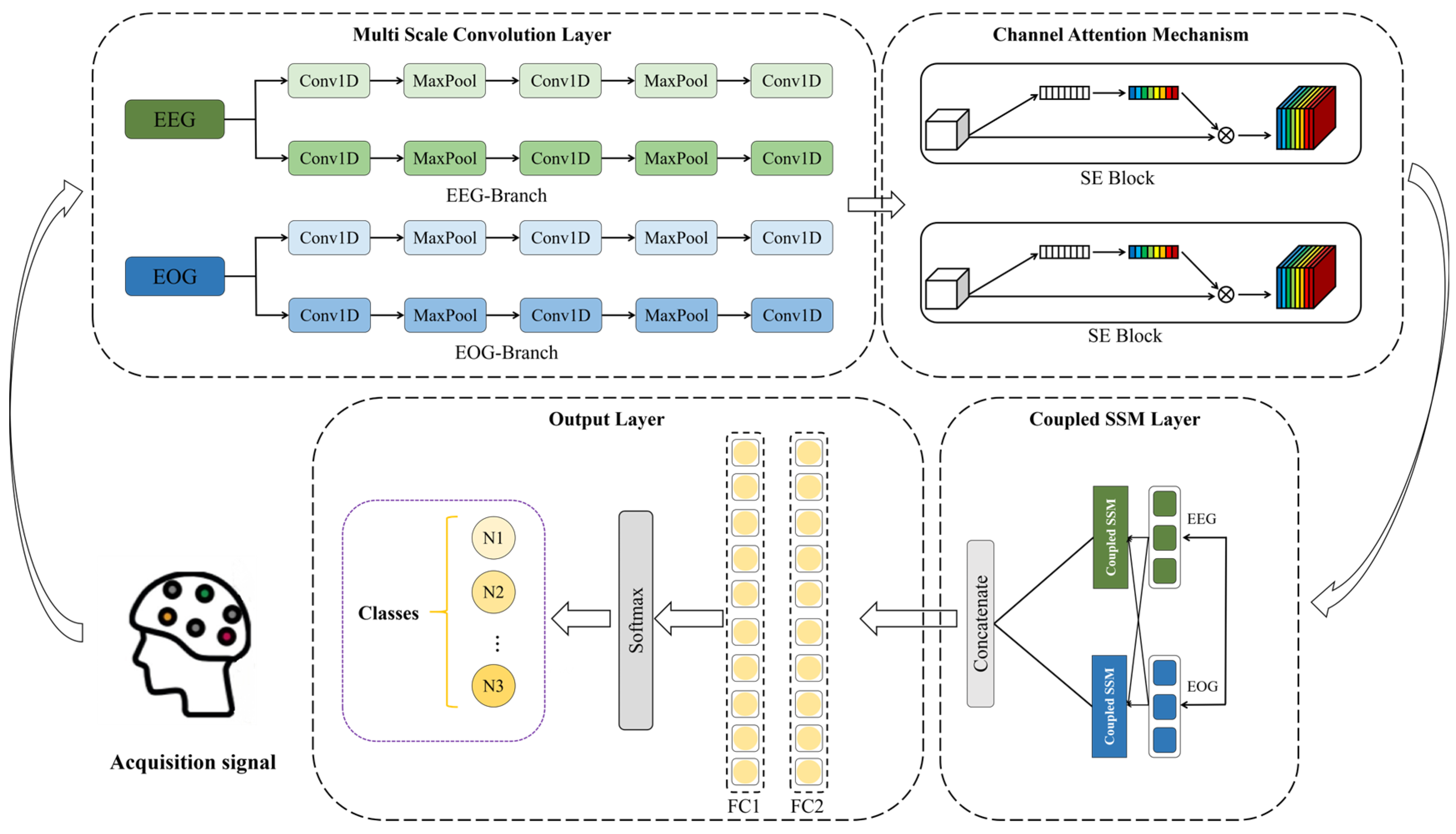
2.2. The Structure of MultiSEss Model
2.2.1. Multiscale Convolution
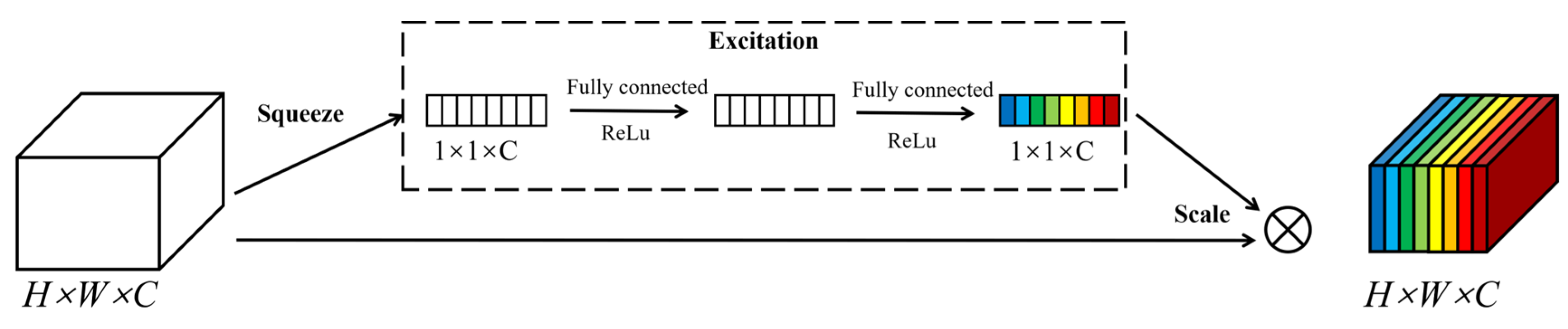
2.2.2. Squeeze-and-Excitation Networks
2.2.3. State Space Model Coupling Module
2.3. Evaluation Indexes
3. Experimental Results and Analysis
3.1. Experimental Setup
3.2. Result of MultiSEss Model
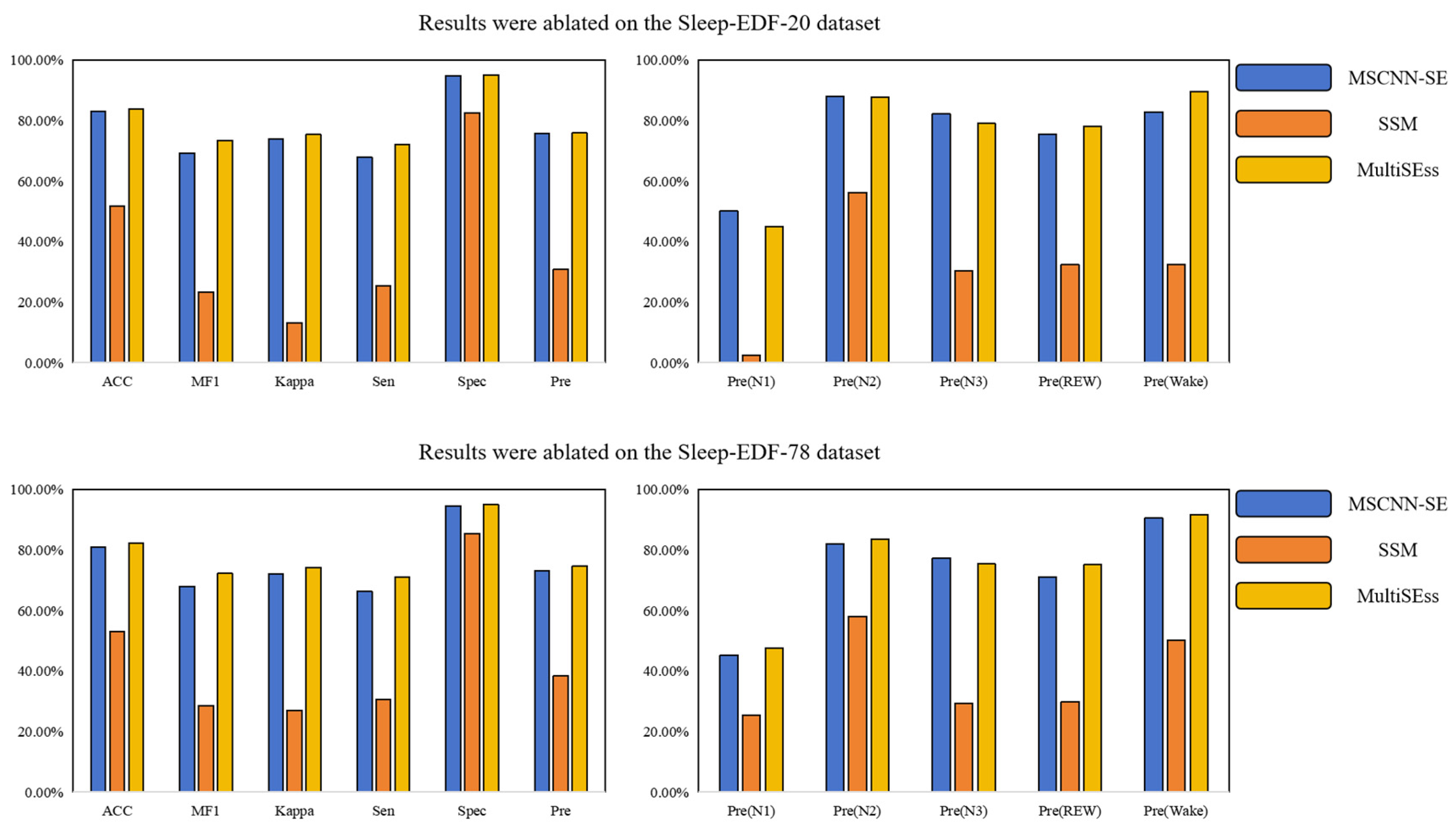
3.3. Ablation Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kasasbeh, E.; Chi, D.S.; Krishnaswamy, G. Inflammatory aspects of sleep apnea and their cardiovascular consequences. South Med. J. 2006, 99, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Khalil, M.; Power, N.; Graham, E.; Deschênes, S.S.; Schmitz, N. The association between sleep and diabetes outcomes—A systematic review. Diabetes Res. Clin. Pract. 2020, 161, 108035. [Google Scholar] [CrossRef]
- Hargens, T.A.; Kaleth, A.S.; Edwards, E.S.; Butner, K.L. Association between sleep disorders, obesity, and exercise: A review. Nat. Sci. Sleep 2013, 5, 27–35. [Google Scholar] [CrossRef]
- Reis, C.; Dias, S.; Rodrigues, A.M.; Sousa, R.D.; Gregório, M.J.; Branco, J.; Canhão, H.; Paiva, T. Sleep duration, lifestyles and chronic diseases: A cross-sectional population-based study. Sleep Sci. 2018, 11, 217–230. [Google Scholar] [CrossRef]
- Wolpert, E.A. A Manual of Standardized Terminology, Techniques and Scoring System for Sleep Stages of Human Subjects. Arch. Gen. Psychiatry 1969, 20, 246–247. [Google Scholar] [CrossRef]
- Iber, C. The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology, and Technical Specification. 2007. Available online: https://cir.nii.ac.jp/crid/1370004237604151044 (accessed on 1 May 2025).
- Rundo, J.V.; Downey, R., III. Polysomnography. Handb. Clin. Neurol. 2019, 160, 381–392. [Google Scholar] [PubMed]
- Phan, H.; Mikkelsen, K. Automatic sleep staging of EEG signals: Recent development, challenges, and future directions. Physiol. Meas. 2022, 43, 04TR01. [Google Scholar] [CrossRef]
- Yue, H.; Chen, Z.; Guo, W.; Sun, L.; Dai, Y.; Wang, Y.; Ma, W.; Fan, X.; Wen, W.; Lei, W. Research and application of deep learning-based sleep staging: Data, modeling, validation, and clinical practice. Sleep Med. Rev. 2024, 74, 101897. [Google Scholar] [CrossRef]
- Loh, H.W.; Ooi, C.P.; Vicnesh, J.; Oh, S.L.; Faust, O.; Gertych, A.; Acharya, U.R. Automated detection of sleep stages using deep learning techniques: A systematic review of the last decade (2010–2020). Appl. Sci. 2020, 10, 8963. [Google Scholar] [CrossRef]
- Alattar, M.; Govind, A.; Mainali, S. Artificial intelligence models for the automation of standard diagnostics in sleep medicine—A systematic review. Bioengineering 2024, 11, 206. [Google Scholar] [CrossRef]
- Soleimani, R.; Barahona, J.; Chen, Y.; Bozkurt, A.; Daniele, M.; Pozdin, V.; Lobaton, E. Advances in Modeling and Interpretability of Deep Neural Sleep Staging: A Systematic Review. Physiologia 2023, 4, 1–42. [Google Scholar] [CrossRef]
- Heng, X.; Wang, M.; Wang, Z.; Zhang, J.; He, L.; Fan, L. Leveraging discriminative features for automatic sleep stage classification based on raw single-channel EEG. Biomed. Signal Process. Control 2024, 88, 105631. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Xu, B.; Song, A. SleepFC: Feature Pyramid and Cross-Scale Context Learning for Sleep Staging. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 2198–2208. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Feng, Y.; Zhao, P.; Zou, X.; Hou, A.; Che, X. Causalattennet: A fast and long-term-temporal network for automatic sleep staging with single-channel eeg. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Duan, L.; Ma, B.; Yin, Y.; Huang, Z.; Qiao, Y. MMS-SleepNet: A knowledge-based multimodal and multiscale network for sleep staging. Biomed. Signal Process. Control 2025, 103, 107370. [Google Scholar] [CrossRef]
- Ying, S.; Wang, L.; Zhang, L.; Xie, J.; Ren, J.; Qin, Y.; Liu, T. HybridDomainSleepNet: A hybrid common-private domain deep learning network for automatic sleep staging. Biomed. Signal Process. Control 2025, 103, 107436. [Google Scholar] [CrossRef]
- Chambon, S.; Galtier, M.N.; Arnal, P.J.; Wainrib, G.; Gramfort, A. A deep learning architecture for temporal sleep stage classification using multivariate and multimodal time series. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 758–769. [Google Scholar] [CrossRef]
- Phan, H.; Chén, O.Y.; Tran, M.C.; Koch, P.; Mertins, A.; De Vos, M. XSleepNet: Multi-view sequential model for automatic sleep staging. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5903–5915. [Google Scholar] [CrossRef]
- Kwon, K.; Kwon, S.; Yeo, W.H. Automatic and accurate sleep stage classification via a convolutional deep neural network and nanomembrane electrodes. Biosensors 2022, 12, 155. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, Y.; Lai, W. MIASS: A multi-interactive attention model for sleep staging via EEG and EOG signals. Comput. Electr. Eng. 2025, 121, 109852. [Google Scholar] [CrossRef]
- Kemp, B.; Zwinderman, A.; Tuk, B.; Kamphuisen, H.; Oberye, J. Analysis of a sleep-dependent neuronal feedback loop: The slow-wave microcontinuity of the EEG. IEEE Trans. Biomed. Eng. 2000, 47, 1185–1194. [Google Scholar] [CrossRef]
- Hu, D.; Gao, W.; Ang, K.K.; Hu, M.; Huang, R.; Chuai, G.; Li, X. CHMMConvScaleNet: A hybrid convolutional neural network and continuous hidden Markov model with multi-scale features for sleep posture detection. Sci. Rep. 2025, 15, 12206. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J. Dynamic Multi-Scale Feature Fusion for Robust Sleep Stage Classification Using Single-Channel EEG. J. Comput. Electron. Inf. Manag. 2025, 16, 14–20. [Google Scholar] [CrossRef]
- JHu, L.; Shen, G. Sun, Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- He, X.; Cao, K.; Zhang, J.; Yan, K.; Wang, Y.; Li, R.; Xie, C.; Hong, D.; Zhou, M. Pan-mamba: Effective pan-sharpening with state space model. Inf. Fusion 2025, 115, 102779. [Google Scholar] [CrossRef]
- Zhang, T.; Yuan, H.; Qi, L.; Zhang, J.; Zhou, Q.; Ji, S.; Yan, S.; Li, X. Point cloud mamba: Point cloud learning via state space model. Proc. AAAI Conf. Artif. Intell. 2025, 39, 10121–10130. [Google Scholar] [CrossRef]
- Perslev, M.; Jensen, M.; Darkner, S.; Jennum, P.J.; Igel, C. U-time: A fully convolutional network for time series segmentation applied to sleep staging. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Sun, Y.; Wang, B.; Jin, J.; Wang, X. Deep convolutional network method for automatic sleep stage classification based on neurophysiological signals. In Proceedings of the 2018 11th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 13–15 October 2018; pp. 1–5. [Google Scholar]
- Pradeepkumar, J.; Anandakumar, M.; Kugathasan, V.; Suntharalingham, D.; Kappel, S.L.; De Silva, A.C.; Edussooriya, C.U.S. Towards interpretable sleep stage classification using cross-modal transformers. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 2893–2904. [Google Scholar] [CrossRef]
- Eldele, E.; Chen, Z.; Liu, C.; Wu, M.; Kwoh, C.-K.; Li, X.; Guan, C. An attention-based deep learning approach for sleep stage classification with single-channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 809–818. [Google Scholar] [CrossRef]
- Yubo, Z.; Yingying, L.; Bing, Z.; Lin, Z.; Lei, L. MMASleepNet: A multimodal attention network based on electrophysiological signals for automatic sleep staging. Front. Neurosci. 2022, 16, 973761. [Google Scholar] [CrossRef]

| Dataset | W | N1 | N2 | N3 | REM | Total |
|---|---|---|---|---|---|---|
| Sleep-EDF-20 | 8285 19.6% | 2804 6.6% | 17,799 42.1% | 5703 13.5% | 7717 18.2% | 42,308 |
| Sleep-EDF-78 | 65,951 14.3% | 21,522 3.2% | 69,132 43.7% | 13,039 18.5% | 25,835 20.3% | 195,479 |
| Model | Overall Results (%) | Per-Class Precisions (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | MF1 | Kappa | Sen | Spec | Pre | Pre(N1) | Pre(N2) | Pre(N3) | Pre(REW) | Pre(Wake) | |
| U-time | 80.52 | 72.07 | 71.87 | 77.86 | 95.03 | 70.56 | 37.66 | 92.99 | 57.24 | 75.89 | 89.02 |
| ResnetLSTM | 81.96 | 73.60 | 73.50 | 75.51 | 95.15 | 72.73 | 37.92 | 90.77 | 68.87 | 76.12 | 89.97 |
| Cross-Modal Transformer | 81.29 | 72.49 | 72.73 | 76.12 | 95.13 | 70.60 | 36.76 | 92.72 | 61.76 | 73.82 | 87.94 |
| AttnSleep | 81.33 | 72.44 | 72.66 | 75.59 | 95.09 | 70.51 | 36.02 | 92.81 | 64.42 | 73.53 | 85.70 |
| MMASleepNet | 79.04 | 71.87 | 70.02 | 78.33 | 94.81 | 70.55 | 33.36 | 94.24 | 57.16 | 77.13 | 90.83 |
| MultiSEss | 83.84 | 73.46 | 75.36 | 72.20 | 95.15 | 75.87 | 45.07 | 87.69 | 79.01 | 78.04 | 89.56 |
| Model | Overall Results(%) | Per-Class Precisions(%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | MF1 | Kappa | Sen | Spec | Pre | Pre(N1) | Pre(N2) | Pre(N3) | Pre(REW) | Pre(Wake) | |
| U-time | 79.74 | 71.84 | 70.97 | 73.50 | 94.79 | 69.78 | 38.97 | 84.42 | 60.04 | 72.94 | 92.53 |
| ResnetLSTM | 79.18 | 71.50 | 70.87 | 76.57 | 94.75 | 69.12 | 40.15 | 88.86 | 52.08 | 70.48 | 94.18 |
| Cross-Modal Transformer | 79.16 | 71.84 | 70.97 | 77.82 | 94.79 | 69.50 | 39.26 | 89.52 | 50.15 | 74.63 | 93.92 |
| AttnSleep | 80.06 | 73.62 | 72.27 | 79.49 | 95.01 | 70.72 | 42.00 | 89.16 | 53.91 | 73.25 | 95.29 |
| MMASleepNet | 76.62 | 69.53 | 67.92 | 78.05 | 94.26 | 67.39 | 38.57 | 88.37 | 41.09 | 73.90 | 95.04 |
| MultiSEss | 82.30 | 72.23 | 74.21 | 71.10 | 95.02 | 74.63 | 47.62 | 83.51 | 75.36 | 75.11 | 91.58 |
| Model | Overall Results (%) | Per-Class Precisions (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | MF1 | Kappa | Sen | Spec | Pre | Pre(N1) | Pre(N2) | Pre(N3) | Pre(REW) | Pre(Wake) | |
| MSCNN-SE | 82.99 | 69.32 | 73.93 | 67.99 | 94.89 | 75.70 | 50.10 | 87.99 | 82.13 | 75.44 | 82.84 |
| SSM | 51.83 | 23.39 | 13.23 | 25.41 | 82.59 | 30.80 | 2.50 | 56.30 | 30.34 | 32.35 | 32.55 |
| MultiSEss | 83.84 | 73.46 | 75.36 | 72.20 | 95.15 | 75.87 | 45.07 | 87.69 | 79.01 | 78.04 | 89.56 |
| Model | Overall Results (%) | Per-Class Precisions (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | MF1 | Kappa | Sen | Spec | Pre | Pre(N1) | Pre(N2) | Pre(N3) | Pre(REW) | Pre(Wake) | |
| MSCNN-SE | 81.01 | 67.98 | 72.17 | 66.38 | 94.60 | 73.20 | 45.23 | 81.96 | 77.30 | 70.99 | 90.52 |
| SSM | 53.15 | 28.54 | 27.02 | 30.72 | 85.45 | 38.51 | 25.35 | 58.11 | 29.21 | 29.79 | 50.12 |
| MultiSEss | 82.30 | 72.23 | 74.21 | 71.10 | 95.02 | 74.63 | 47.62 | 83.51 | 75.36 | 75.11 | 91.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Yang, Y.; Wang, Z.; Li, Y.; Chen, Z.; Ma, Y.; Zhang, S. MultiSEss: Automatic Sleep Staging Model Based on SE Attention Mechanism and State Space Model. Biomimetics 2025, 10, 288. https://doi.org/10.3390/biomimetics10050288
Huang Z, Yang Y, Wang Z, Li Y, Chen Z, Ma Y, Zhang S. MultiSEss: Automatic Sleep Staging Model Based on SE Attention Mechanism and State Space Model. Biomimetics. 2025; 10(5):288. https://doi.org/10.3390/biomimetics10050288
Chicago/Turabian StyleHuang, Zhentao, Yuyao Yang, Zhiyuan Wang, Yuan Li, Zuowen Chen, Yahong Ma, and Shanwen Zhang. 2025. "MultiSEss: Automatic Sleep Staging Model Based on SE Attention Mechanism and State Space Model" Biomimetics 10, no. 5: 288. https://doi.org/10.3390/biomimetics10050288
APA StyleHuang, Z., Yang, Y., Wang, Z., Li, Y., Chen, Z., Ma, Y., & Zhang, S. (2025). MultiSEss: Automatic Sleep Staging Model Based on SE Attention Mechanism and State Space Model. Biomimetics, 10(5), 288. https://doi.org/10.3390/biomimetics10050288






