A Robust Disturbance Rejection Whole-Body Control Framework for Bipedal Robots Using a Momentum-Based Observer
Abstract
1. Introduction
2. Momentum-Based Observer for Disturbance Estimation
2.1. Dynamic Model
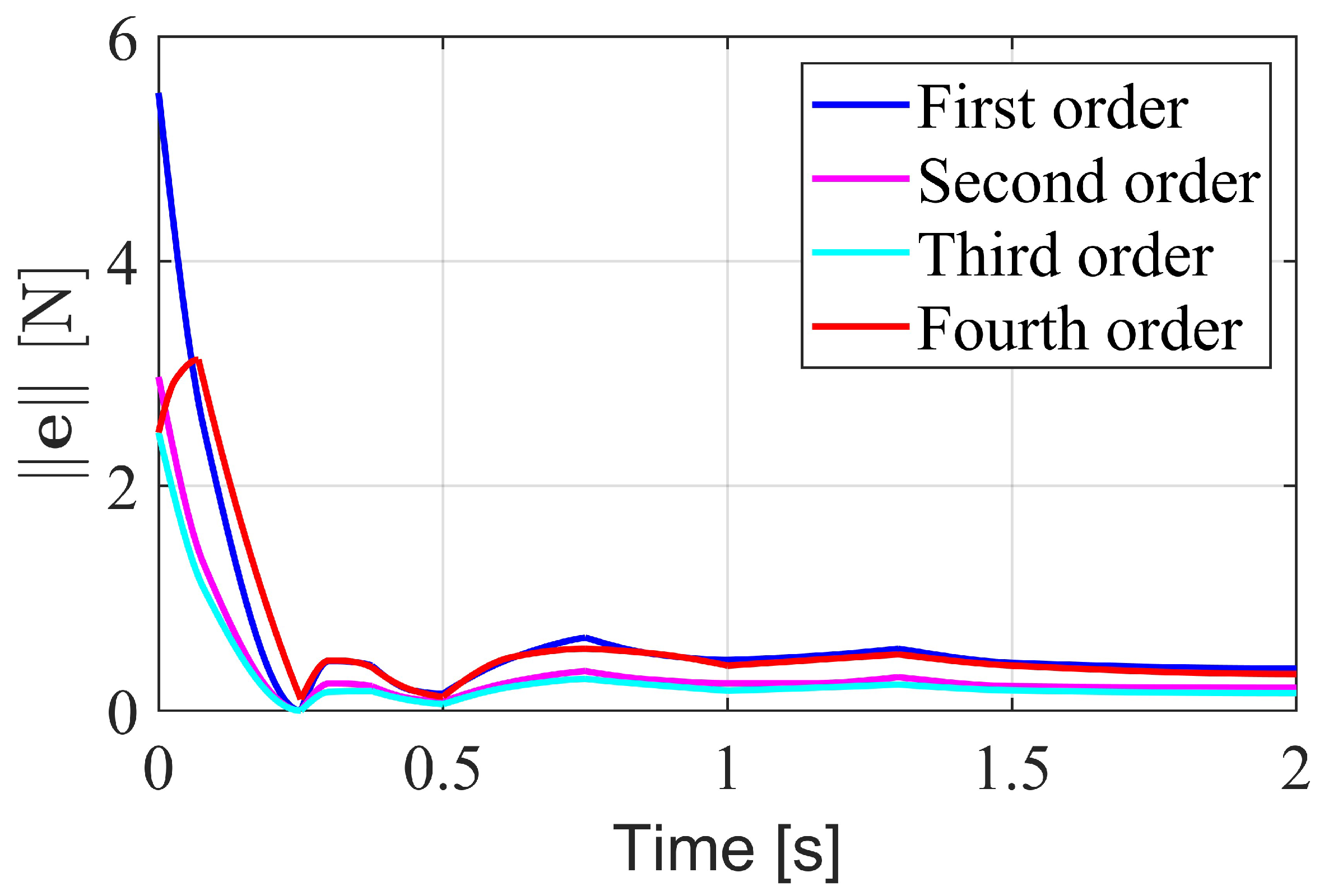
2.2. Momentum-Based Observer Design
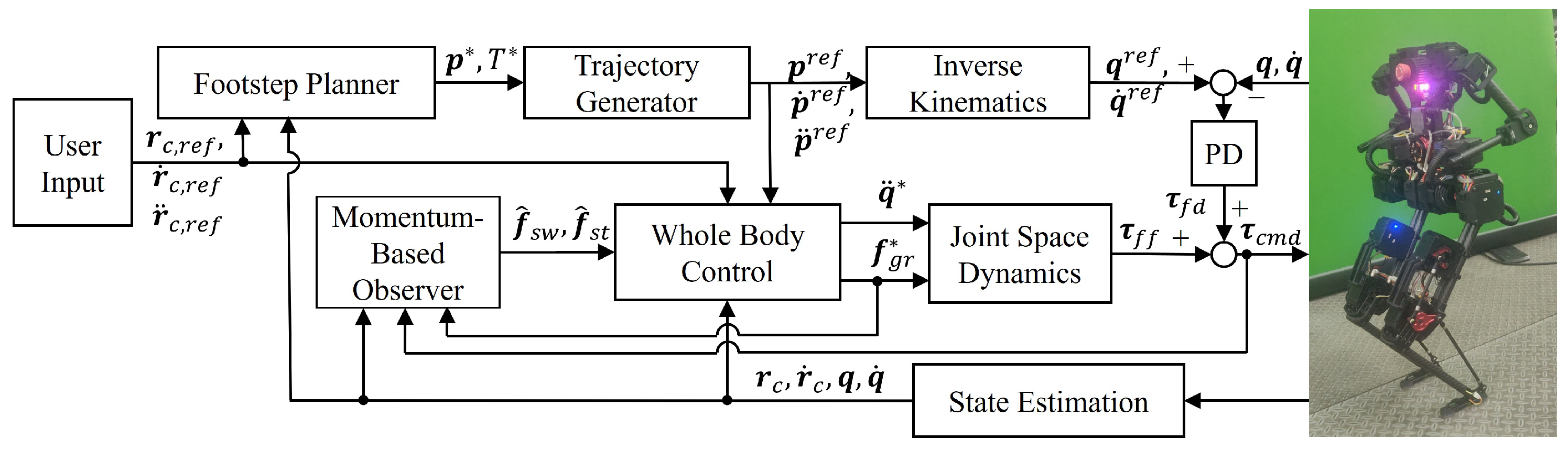
3. Control Framework
3.1. Footstep Planner
3.2. Disturbance Rejection Whole-Body Control
3.2.1. CoM Trajectory Tracking Task
3.2.2. Swing Foot Trajectory Tracking Task
3.2.3. Stance Foot Contact Unmoving Task
3.2.4. Constraints
4. Simulations and Experiments
4.1. Simulations
4.1.1. Stable Walking Under External Disturbance on the Swing Leg
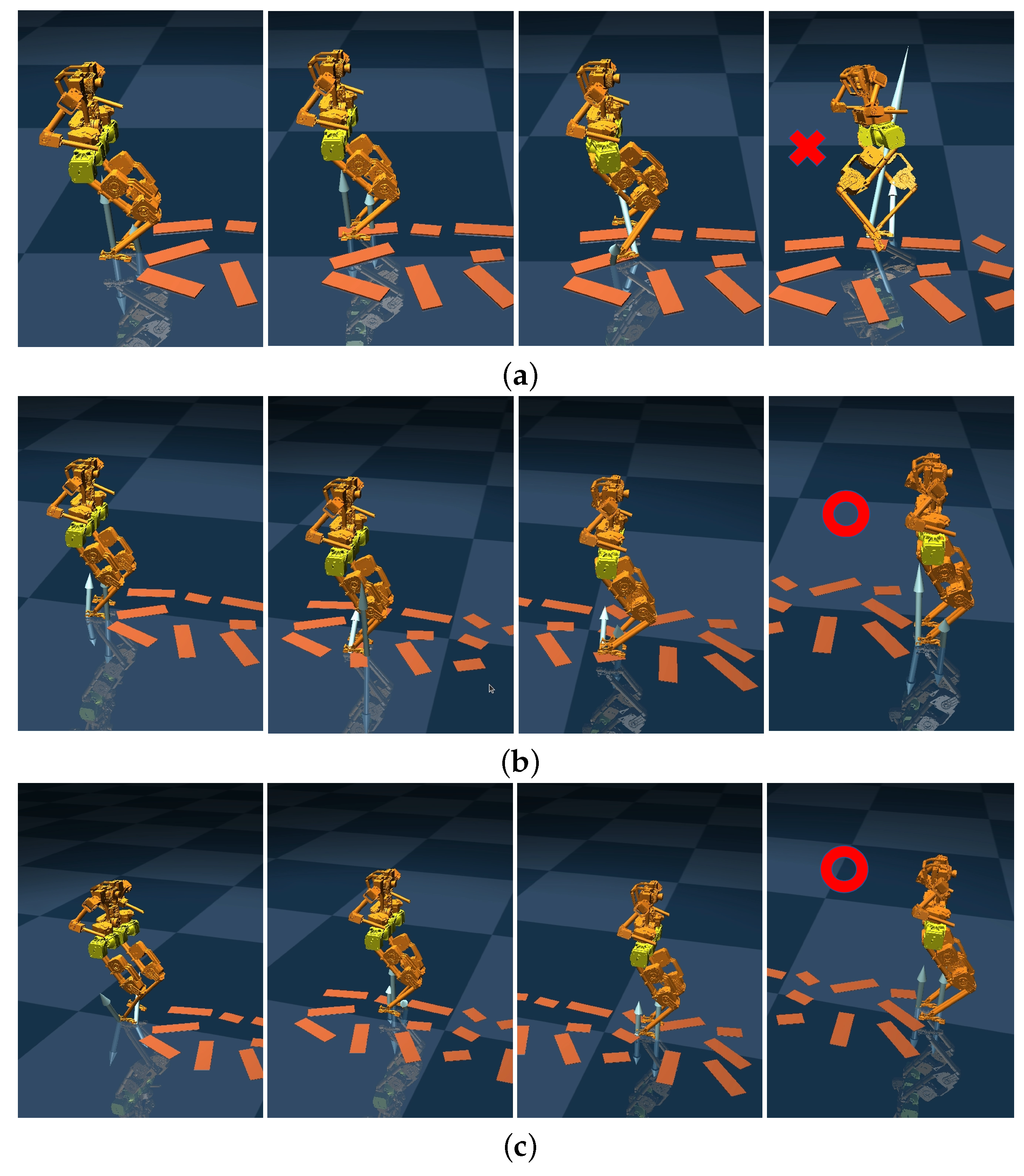
4.1.2. Stable Walking on Uneven Terrain
4.2. Experiment
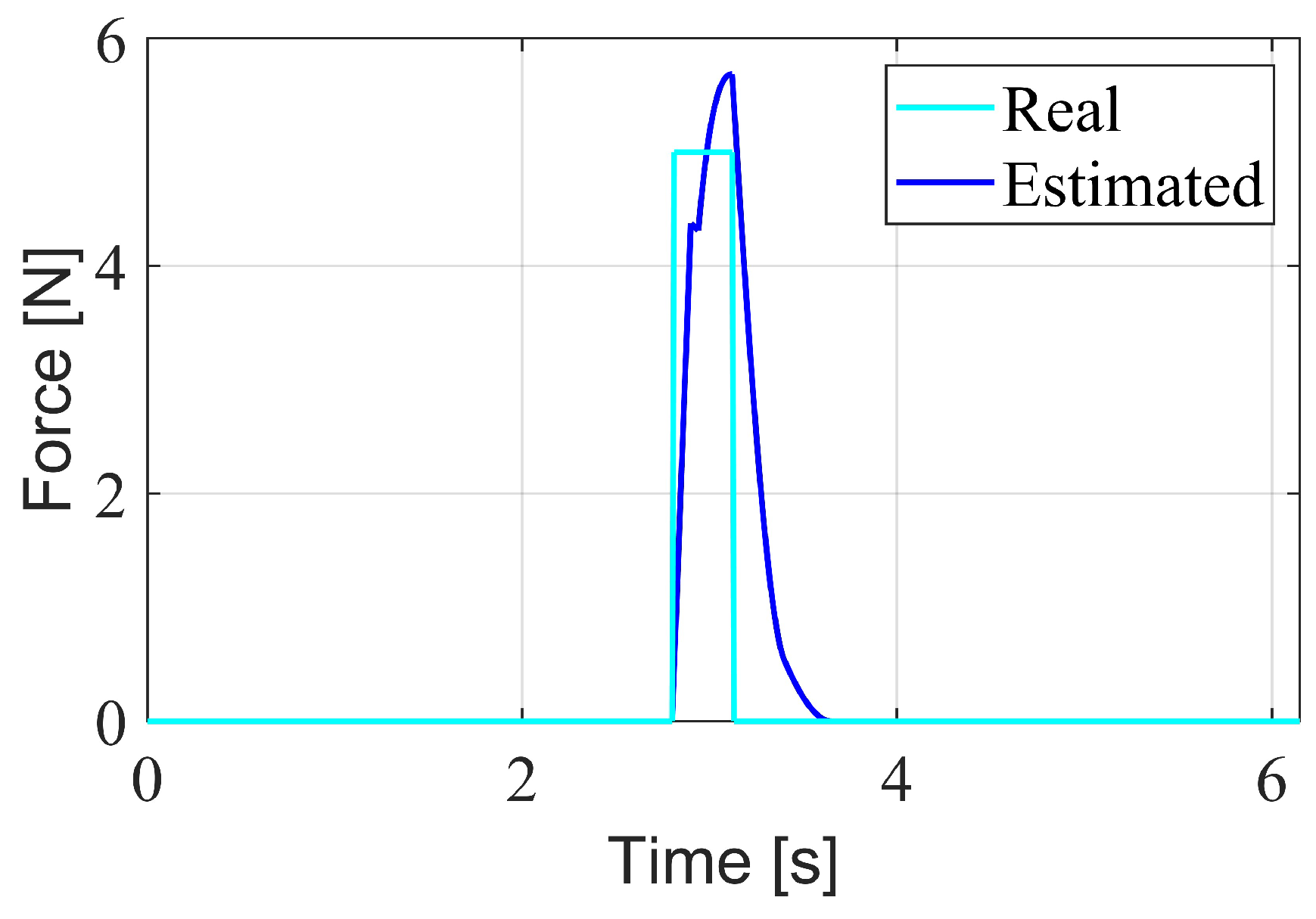
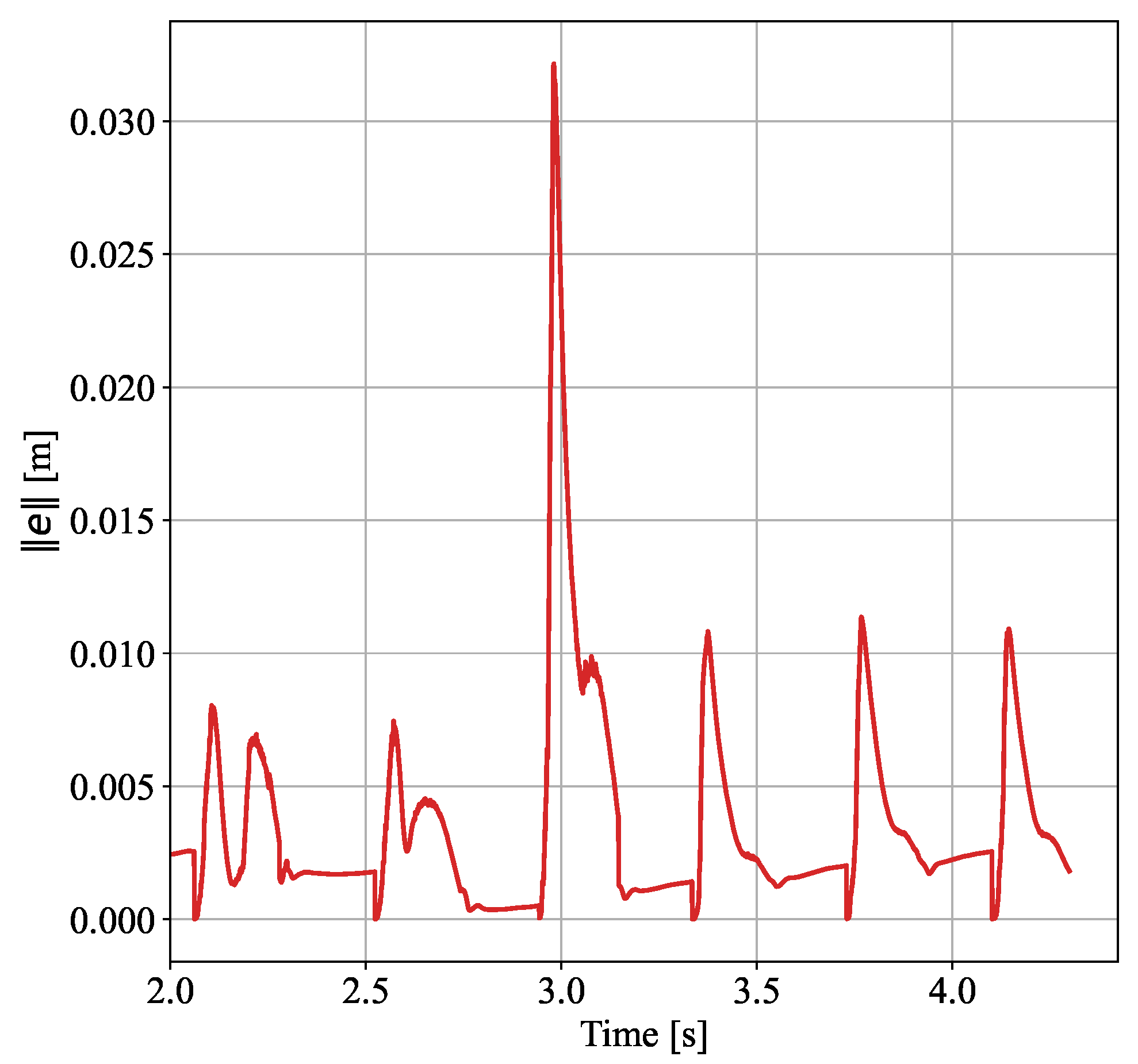
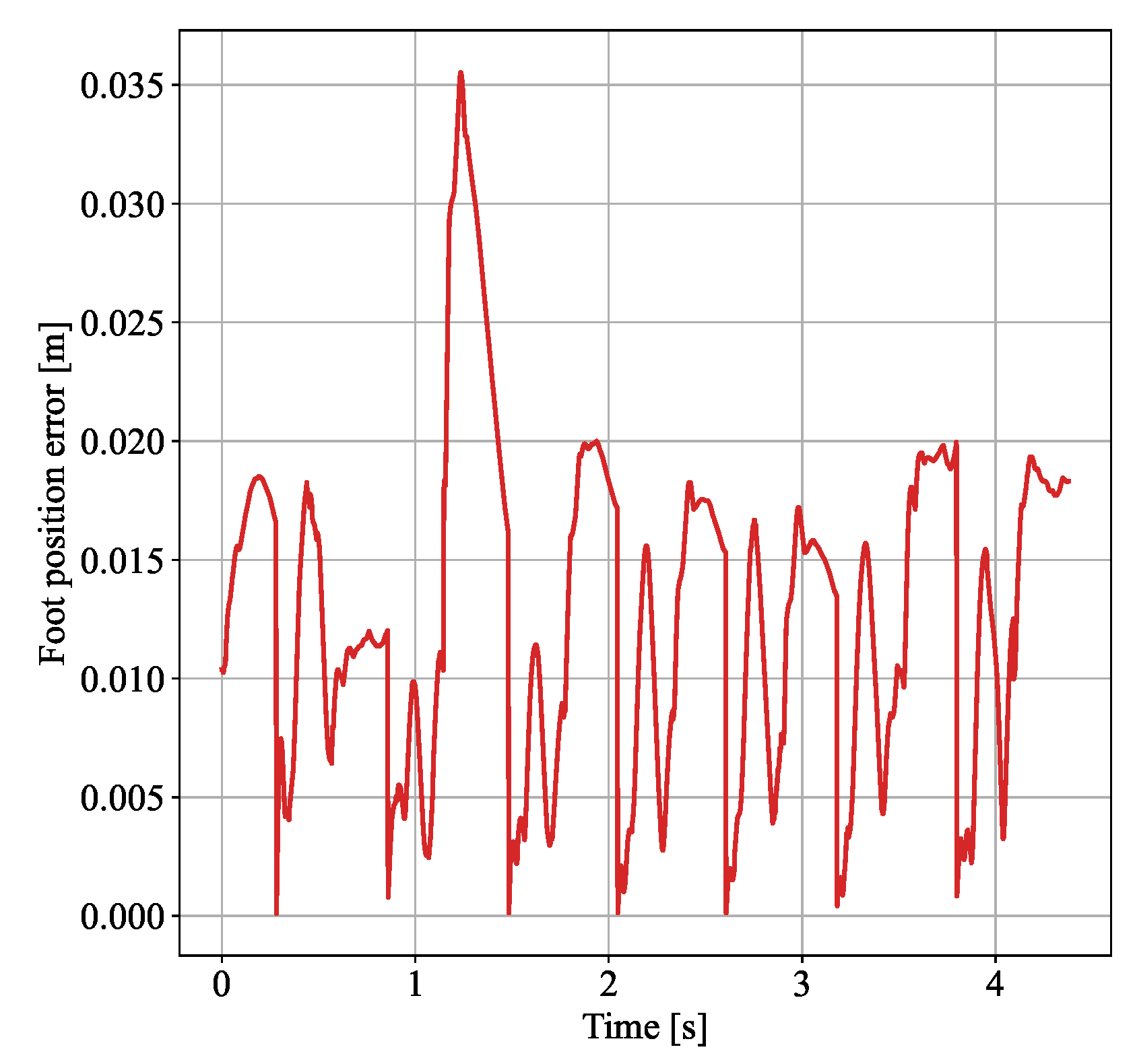
4.2.1. Walking Experiment Under External Swing Leg Disturbance
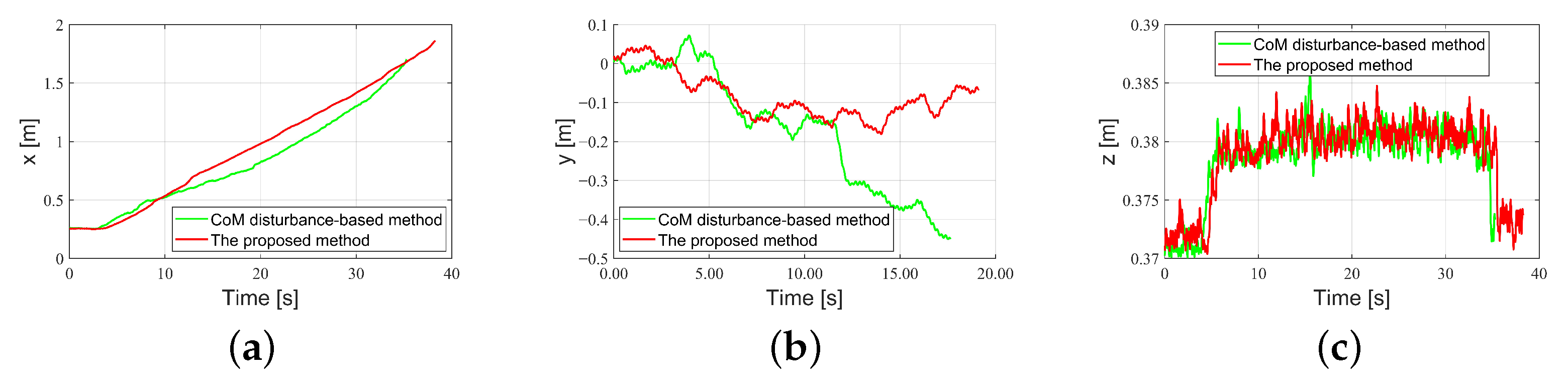
4.2.2. Walking Experiment Under Complex Disturbance
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wensing, P.M.; Posa, M.; Hu, Y.; Escande, A.; Mansard, N.; Prete, A.D. Optimization-Based Control for Dynamic Legged Robots. IEEE Trans. Robot. 2024, 40, 43–63. [Google Scholar] [CrossRef]
- Daneshmand, E.; Khadiv, M.; Grimminger, F.; Righetti, L. Variable Horizon MPC With Swing Foot Dynamics for Bipedal Walking Control. IEEE Robot. Autom. Lett. 2021, 6, 2349–2356. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, J.; Liu, Y.; Hong, D. Implementation of a Robust Dynamic Walking Controller on a Miniature Bipedal Robot with Proprioceptive Actuation. In Proceedings of the 2022 IEEE-RAS 21st International Conference on Humanoid Robots (Humanoids), Ginowan, Japan, 28–30 November 2022; IEEE: New York, NY, USA, 2022; pp. 39–46. [Google Scholar] [CrossRef]
- Koolen, T.; Bertrand, S.; Thomas, G.; De Boer, T.; Wu, T.; Smith, J.; Englsberger, J.; Pratt, J. Design of a Momentum-Based Control Framework and Application to the Humanoid Robot Atlas. Int. J. Humanoid Robot. 2016, 13, 1650007. [Google Scholar] [CrossRef]
- Apgar, T.; Clary, P.; Green, K.; Fern, A.; Hurst, J. Fast Online Trajectory Optimization for the Bipedal Robot Cassie. Robot. Sci. Syst. XIV 2018, 101, 14. [Google Scholar] [CrossRef]
- Mesesan, G.; Englsberger, J.; Garofalo, G.; Ott, C.; Albu-Schaffer, A. Dynamic Walking on Compliant and Uneven Terrain Using DCM and Passivity-based Whole-body Control. In Proceedings of the 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), Toronto, ON, Canada, 15–17 October 2019; IEEE: New York, NY, USA, 2019; pp. 25–32. [Google Scholar] [CrossRef]
- Kajita, S.; Tani, K. Study of Dynamic Biped Locomotion on Rugged Terrain-Derivation and Application of the Linear Inverted Pendulum Mode. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; IEEE: New York, NY, USA, 1991; pp. 1405–1411. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D Linear Inverted Pendulum Mode: A Simple Modeling for a Biped Walking Pattern Generation. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No. 01CH37180), Maui, HI, USA, 29 October–3 November 2001; IEEE: New York, NY, USA, 2001; Volume 1, pp. 239–246. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped Walking Pattern Generation by Using Preview Control of Zero-Moment Point. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422), Taipei, Taiwan, 14–19 September 2003; IEEE: New York, NY, USA, 2003; pp. 1620–1626. [Google Scholar] [CrossRef]
- Wieber, P.B. Trajectory Free Linear Model Predictive Control for Stable Walking in the Presence of Strong Perturbations. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; IEEE: New York, NY, USA, 2006; pp. 137–142. [Google Scholar] [CrossRef]
- Herdt, A.; Diedam, H.; Wieber, P.B.; Dimitrov, D.; Mombaur, K.; Diehl, M. Online Walking Motion Generation with Automatic Footstep Placement. Adv. Robot. 2010, 24, 719–737. [Google Scholar] [CrossRef]
- Brasseur, C.; Sherikov, A.; Collette, C.; Dimitrov, D.; Wieber, P.B. A Robust Linear MPC Approach to Online Generation of 3D Biped Walking Motion. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Republic of Korea, 3–5 November 2015; IEEE: New York, NY, USA, 2015; pp. 595–601. [Google Scholar] [CrossRef]
- Englsberger, J.; Ott, C.; Albu-Schaffer, A. Three-Dimensional Bipedal Walking Control Based on Divergent Component of Motion. IEEE Trans. Robot. 2015, 31, 355–368. [Google Scholar] [CrossRef]
- Khadiv, M.; Herzog, A.; Moosavian, S.A.A.; Righetti, L. Step Timing Adjustment: A Step toward Generating Robust Gaits. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; IEEE: New York, NY, USA, 2016; pp. 35–42. [Google Scholar] [CrossRef]
- Khadiv, M.; Herzog, A.; Moosavian, S.A.A.; Righetti, L. Walking Control Based on Step Timing Adaptation. IEEE Trans. Robot. 2020, 36, 629–643. [Google Scholar] [CrossRef]
- Escande, A.; Mansard, N.; Wieber, P.B. Hierarchical Quadratic Programming: Fast Online Humanoid-Robot Motion Generation. Int. J. Robot. Res. 2014, 33, 1006–1028. [Google Scholar] [CrossRef]
- Herzog, A.; Rotella, N.; Mason, S.; Grimminger, F.; Schaal, S.; Righetti, L. Momentum Control with Hierarchical Inverse Dynamics on a Torque-Controlled Humanoid. Auton. Robot. 2016, 40, 473–491. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Ahn, J.; Campbell, O.; Hwang, H.; Sentis, L. Computationally-Robust and Efficient Prioritized Whole-Body Controller with Contact Constraints. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Yi, S.J.; Zhang, B.T.; Hong, D.; Lee, D.D. Online learning of a full body push recovery controller for omnidirectional walking. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Vadakkepat, P.; Goswami, D.; Meng-Hwee, C. Disturbance rejection by online ZMP compensation. Robotica 2008, 26, 9–17. [Google Scholar]
- Hyon, S.H.; Cheng, G. Disturbance Rejection for Biped Humanoids. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 2668–2675. [Google Scholar] [CrossRef]
- Wang, Y.; Xiong, R.; Zhu, Q.; Chu, J. Compliance control for standing maintenance of humanoid robots under unknown external disturbances. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2297–2304. [Google Scholar] [CrossRef]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture Point: A Step toward Humanoid Push Recovery. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 200–207. [Google Scholar] [CrossRef]
- Dafarra, S.; Romano, F.; Nori, F. Torque-controlled stepping-strategy push recovery: Design and implementation on the iCub humanoid robot. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 152–157. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, G.; Sun, Z.; Chen, T.; Rong, X.; Xie, A.; Li, Y. Proprioceptive-Based Whole-Body Disturbance Rejection Control for Dynamic Motions in Legged Robots. IEEE Robot. Autom. Lett. 2023, 8, 7703–7710. [Google Scholar] [CrossRef]
- Englsberger, J.; Mesesan, G.; Ott, C. Smooth trajectory generation and push-recovery based on Divergent Component of Motion. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 4560–4567. [Google Scholar] [CrossRef]
- Focchi, M.; Orsolino, R.; Camurri, M.; Barasuol, V.; Mastalli, C.; Caldwell, D.G.; Semini, C. Heuristic Planning for Rough Terrain Locomotion in Presence of External Disturbances and Variable Perception Quality. In Advances in Robotics Research: From Lab to Market: ECHORD++: Robotic Science Supporting Innovation; Grau, A., Morel, Y., Puig-Pey, A., Cecchi, F., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 165–209. [Google Scholar] [CrossRef]
- Morlando, V.; Teimoorzadeh, A.; Ruggiero, F. Whole-body control with disturbance rejection through a momentum-based observer for quadruped robots. Mech. Mach. Theory 2021, 164, 104412. [Google Scholar] [CrossRef]
- Wieber, P.B. Holonomy and Nonholonomy in the Dynamics of Articulated Motion. In Fast Motions in Biomechanics and Robotics: Optimization and Feedback Control; Diehl, M., Mombaur, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 411–425. [Google Scholar] [CrossRef]
- Henze, B.; Roa, M.A.; Ott, C. Passivity-based whole-body balancing for torque-controlled humanoid robots in multi-contact scenarios. Int. J. Robot. Res. 2016, 35, 1522–1543. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer Publishing Company, Incorporated: New York, NY, USA, 2010. [Google Scholar]
- Ruggiero, F.; Cacace, J.; Sadeghian, H.; Lippiello, V. Passivity-based control of VToL UAVs with a momentum-based estimator of external wrench and unmodeled dynamics. Robot. Auton. Syst. 2015, 72, 139–151. [Google Scholar] [CrossRef]
- Heng, S.; Zang, X.; Song, C.; Chen, B.; Zhang, Y.; Zhu, Y.; Zhao, J. Balance and Walking Control for Biped Robot Based on Divergent Component of Motion and Contact Force Optimization. Mathematics 2024, 12, 2188. [Google Scholar] [CrossRef]
- Xin, G.; Wolfslag, W.J.; Lin, H.C.; Tiseo, C.; Mistry, M.N. An Optimization-Based Locomotion Controller for Quadruped Robots Leveraging Cartesian Impedance Control. Front. Robot. AI 2020, 7, 48. [Google Scholar] [CrossRef]
- Aghili, F. A unified approach for inverse and direct dynamics of constrained multibody systems based on linear projection operator: Applications to control and simulation. IEEE Trans. Robot. 2005, 21, 834–849. [Google Scholar] [CrossRef]
- Mistry, M.N.; Righetti, L. Operational Space Control of Constrained and Underactuated Systems. In Proceedings of the Robotics: Science and Systems, Los Angeles, CA, USA, 27–30 June 2011. [Google Scholar]
- Feng, S.; Whitman, E.; Xinjilefu, X.; Atkeson, C.G. Optimization based full body control for the atlas robot. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 120–127. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: New York, NY, USA, 2012; pp. 5026–5033. [Google Scholar] [CrossRef]
- Main Page of BRUCE Model. Available online: https://github.com/Westwood-Robotics/BRUCE_simulation_models (accessed on 10 March 2025).
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An operator splitting solver for quadratic programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef]
- Main Page of Posix_ipc. Available online: https://github.com/osvenskan/posix_ipc (accessed on 10 March 2025).
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A LLVM-based Python JIT compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC (LLVM’15), Austin, TX, USA, 15 November 2015; Association for Computing Machinery: New York, NY, USA, 2015. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heng, S.; Zang, X.; Liu, Y.; Song, C.; Chen, B.; Zhang, Y.; Zhu, Y.; Zhao, J. A Robust Disturbance Rejection Whole-Body Control Framework for Bipedal Robots Using a Momentum-Based Observer. Biomimetics 2025, 10, 189. https://doi.org/10.3390/biomimetics10030189
Heng S, Zang X, Liu Y, Song C, Chen B, Zhang Y, Zhu Y, Zhao J. A Robust Disturbance Rejection Whole-Body Control Framework for Bipedal Robots Using a Momentum-Based Observer. Biomimetics. 2025; 10(3):189. https://doi.org/10.3390/biomimetics10030189
Chicago/Turabian StyleHeng, Shuai, Xizhe Zang, Yan Liu, Chao Song, Boyang Chen, Yue Zhang, Yanhe Zhu, and Jie Zhao. 2025. "A Robust Disturbance Rejection Whole-Body Control Framework for Bipedal Robots Using a Momentum-Based Observer" Biomimetics 10, no. 3: 189. https://doi.org/10.3390/biomimetics10030189
APA StyleHeng, S., Zang, X., Liu, Y., Song, C., Chen, B., Zhang, Y., Zhu, Y., & Zhao, J. (2025). A Robust Disturbance Rejection Whole-Body Control Framework for Bipedal Robots Using a Momentum-Based Observer. Biomimetics, 10(3), 189. https://doi.org/10.3390/biomimetics10030189






