FedDyH: A Multi-Policy with GA Optimization Framework for Dynamic Heterogeneous Federated Learning
Abstract
1. Introduction
- We propose a novel federated learning framework called FedDyH, which overcomes the performance degradation issues of existing methods such as FedAvg and FedProx under the static heterogeneity assumption. FedDyH specifically focuses on addressing the dynamic heterogeneity of client data in real-world scenarios.
- We incorporate a regularization mechanism combining orthogonality constraints and knowledge distillation during the training process to ensure the stability and effectiveness of the model in dynamic data environments.
- By introducing a genetic algorithm (GA), we dynamically optimize the weights of the distillation loss and orthogonality constraint loss. Compared to traditional methods that rely on fixed hyperparameters or manual tuning, FedDyH enables the model to adapt to the requirements of different training stages, thereby improving both convergence speed and accuracy.
- We conducted extensive experiments on the MNIST, Fashion-MNIST, and CIFAR-10 datasets to evaluate the performance of the FedDyH framework under varying client selection rates and degrees of heterogeneity. Our experimental results show that FedDyH significantly outperforms other federated learning (FL) baseline methods.
2. Related Work
2.1. Federated Learning with Heterogeneous Data
2.2. Knowledge Distillation
2.3. Genetic Algorithm
2.4. Orthogonality-Related Methods
3. Method
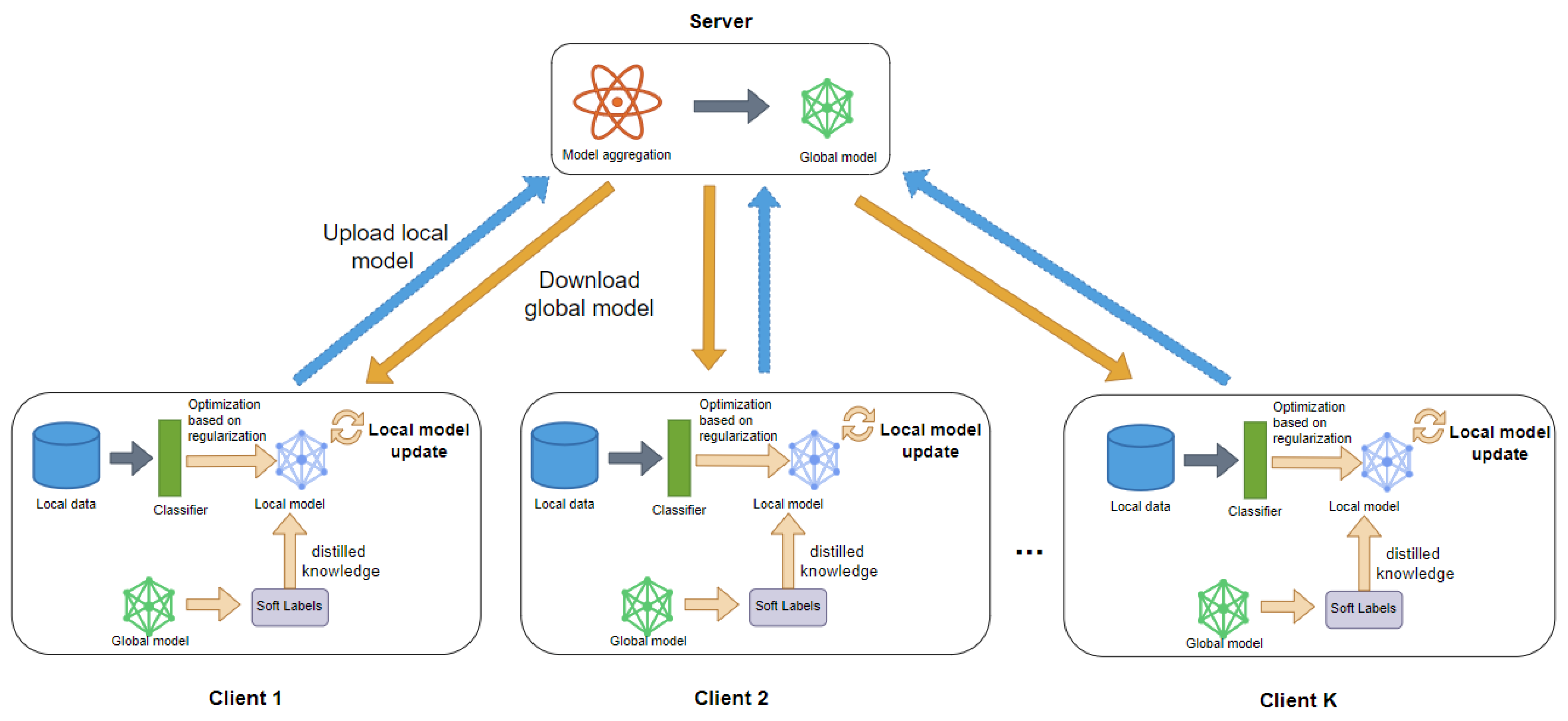
3.1. FedDyH Framework
| Algorithm 1 FedDyH |
|
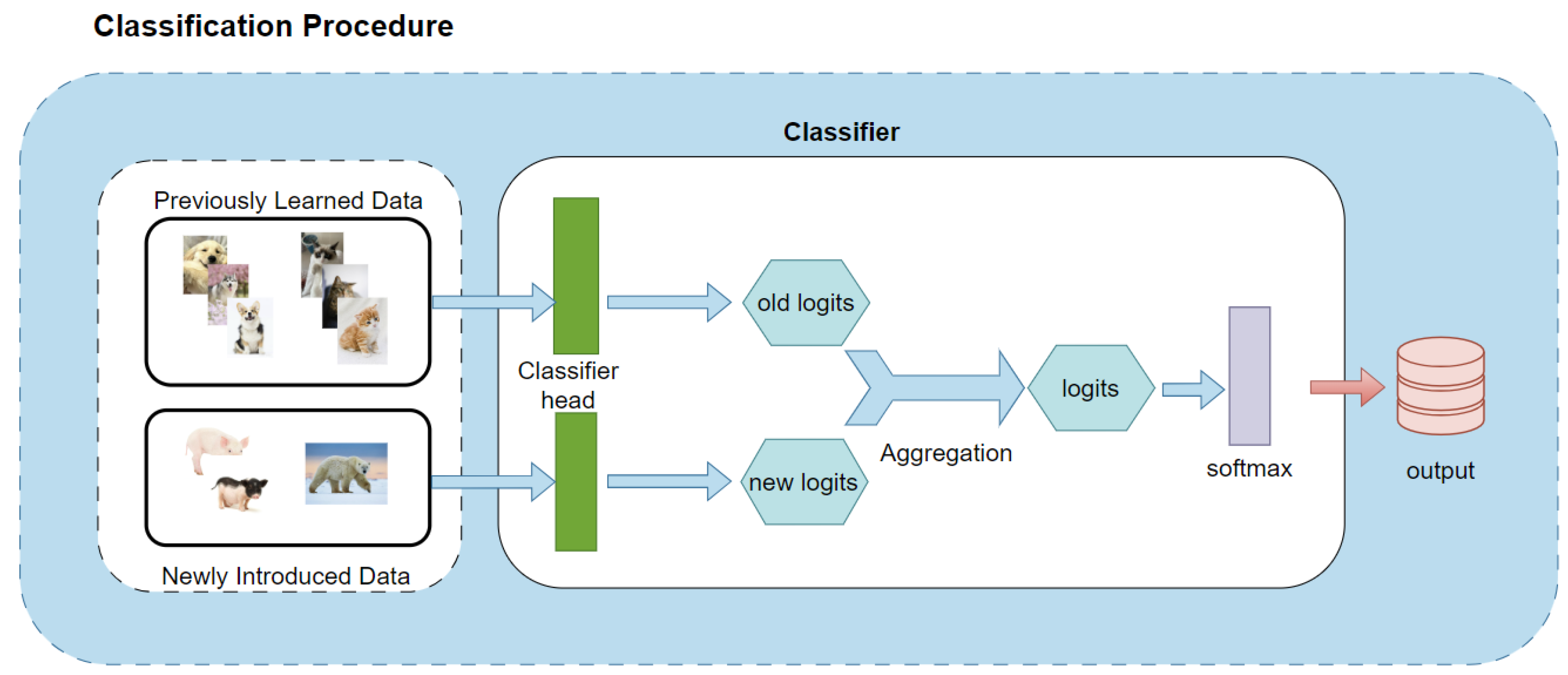
3.2. Classifiers
3.3. Regularization Strategies
3.4. Genetic Algorithm
4. Experiments
4.1. Dataset and Model Setup
4.2. Implementation Details
4.3. Experiment Analysis
4.3.1. Ablation Experiments
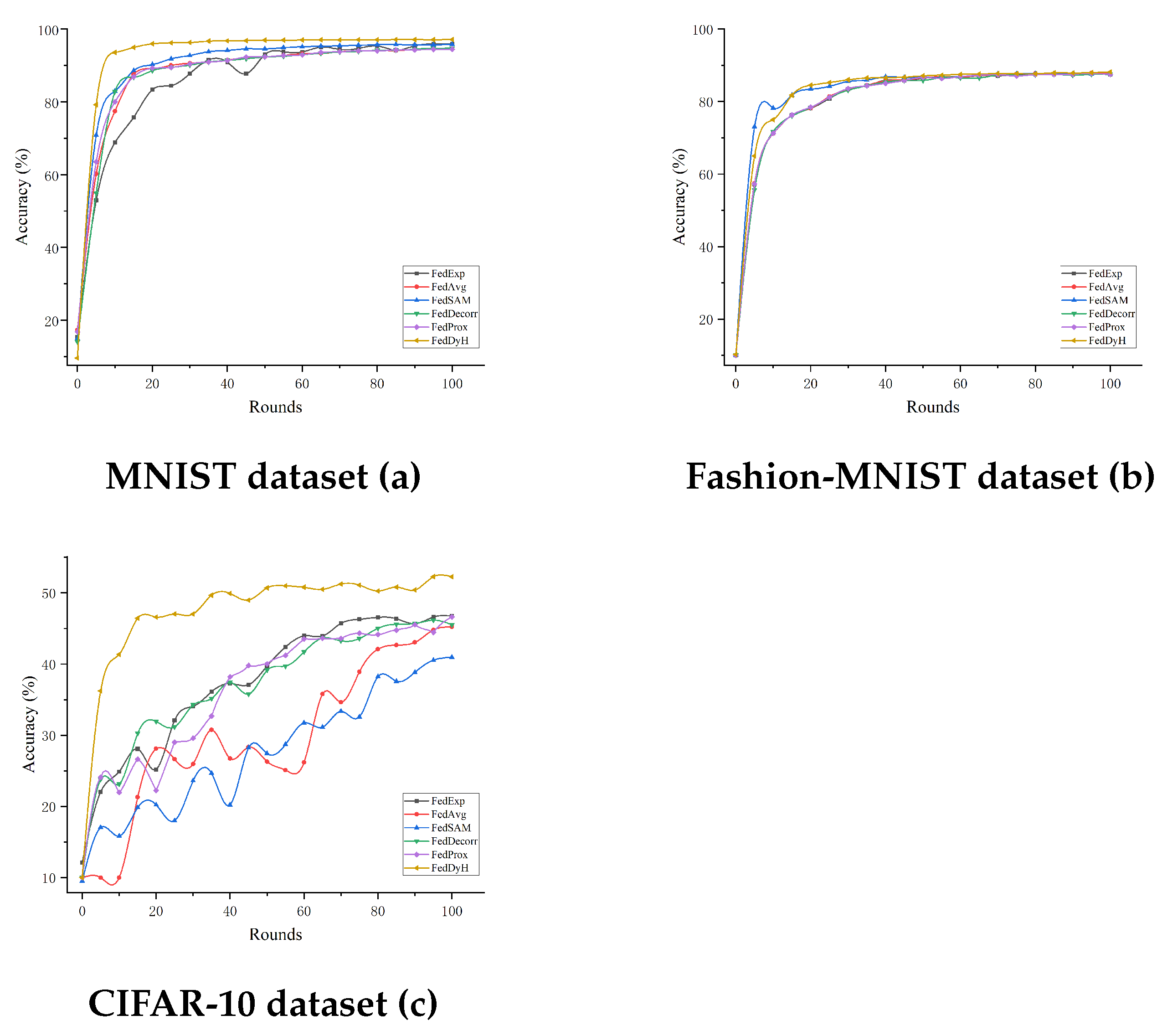
4.3.2. Comparison with Advanced Methods Under Different Heterogeneity Levels
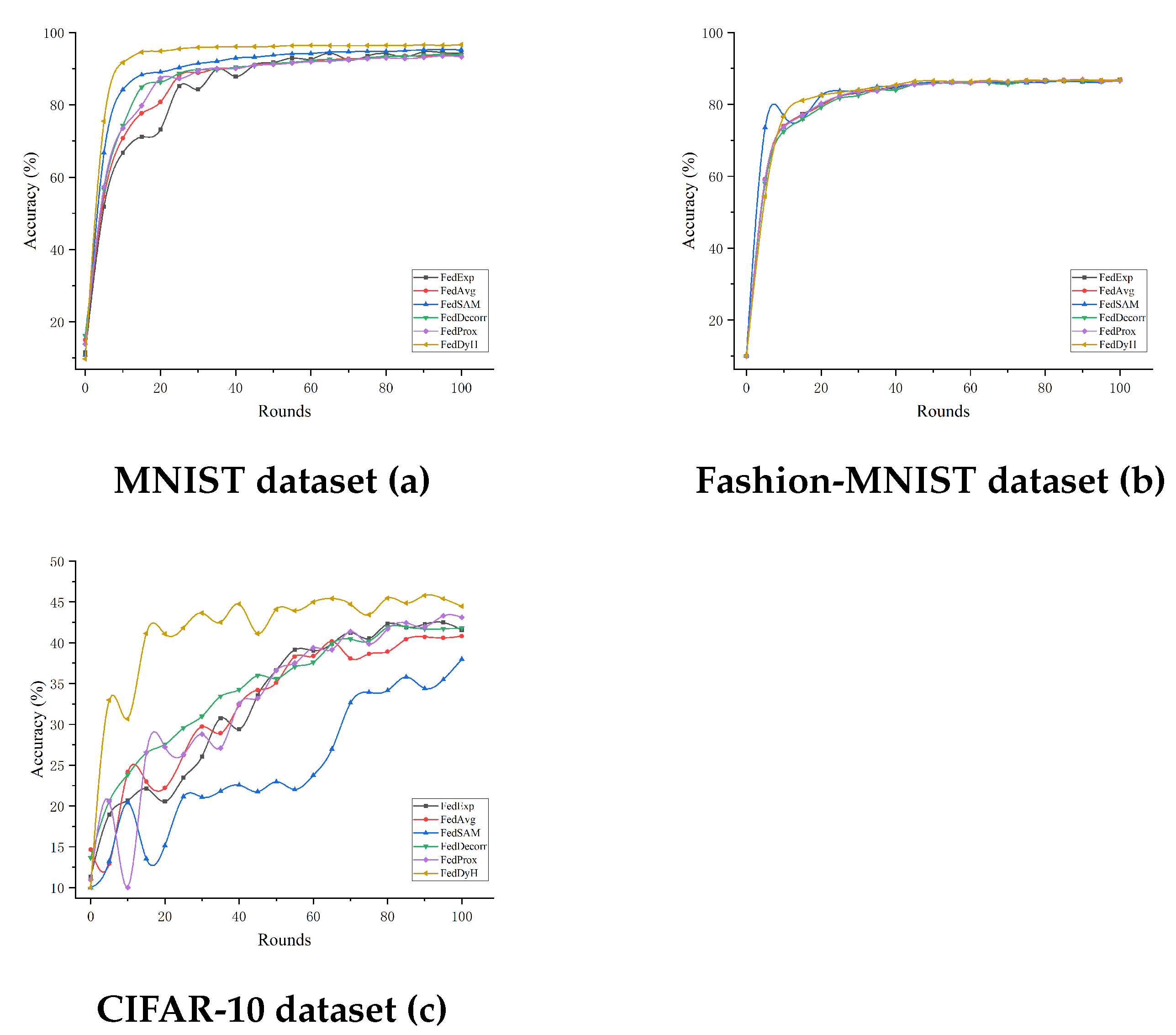
4.3.3. Comparison with Advanced Methods Under Different Client Selection Rates
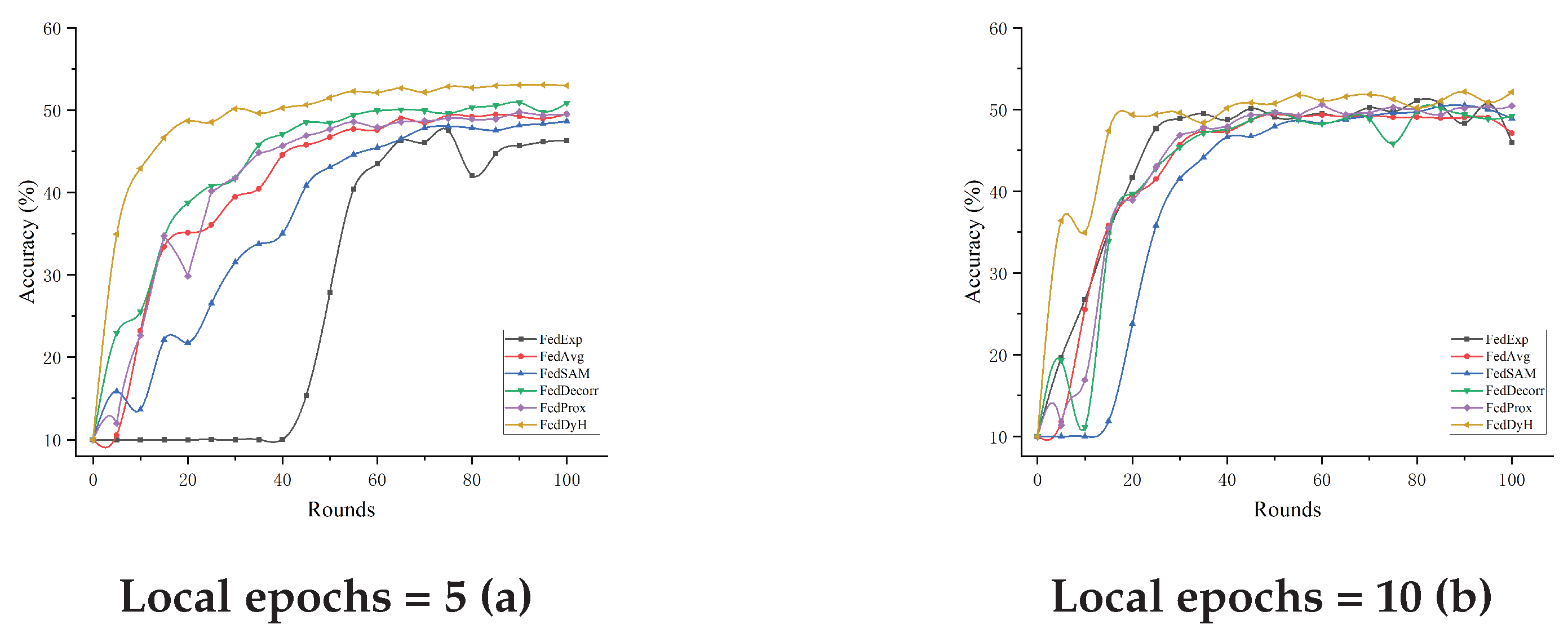
4.3.4. Impact of Local Training Rounds
4.3.5. Hyperparametric Sensitivity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Liang, H.; Xu, Y.; Zhang, C. Reliable and privacy-preserving federated learning with anomalous users. ZTE Commun. 2023, 21, 15. [Google Scholar]
- Jiang, M.; Wang, Z.; Dou, Q. Harmofl: Harmonizing local and global drifts in federated learning on heterogeneous medical images. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 1087–1095. [Google Scholar]
- Yang, W.; Zhang, Y.; Ye, K.; Li, L.; Xu, C.Z. Ffd: A federated learning based method for credit card fraud detection. In Proceedings of the Big Data–bigData 2019: 8th International Congress, Held as Part of the Services Conference Federation, SCF 2019, San Diego, CA, USA, 25–30 June 2019; proceedings 8. Springer: Berlin/Heidelberg, Germany, 2019; pp. 18–32. [Google Scholar]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Poor, H.V. Federated learning for internet of things: A comprehensive survey. IEEE Commun. Surv. Tutor. 2021, 23, 1622–1658. [Google Scholar] [CrossRef]
- Quan, P.K.; Kundroo, M.; Kim, T. Experimental evaluation and analysis of federated learning in edge computing environments. IEEE Access 2023, 11, 33628–33639. [Google Scholar] [CrossRef]
- Huang, W.; Ye, M.; Du, B. Learn from others and be yourself in heterogeneous federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10143–10153. [Google Scholar]
- Jatain, D.; Singh, V.; Dahiya, N. A contemplative perspective on federated machine learning: Taxonomy, threats & vulnerability assessment and challenges. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6681–6698. [Google Scholar]
- Su, T.; Wang, M.; Wang, Z. Federated regularization learning: An accurate and safe method for federated learning. In Proceedings of the 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems (AICAS), Washington, DC, USA, 6–9 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Gong, B.; Xing, T.; Liu, Z.; Xi, W.; Chen, X. Adaptive client clustering for efficient federated learning over non-iid and imbalanced data. IEEE Trans. Big Data 2022, 10, 1051–1065. [Google Scholar] [CrossRef]
- Seo, S.; Kim, J.; Kim, G.; Han, B. Relaxed contrastive learning for federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 12279–12288. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; PMLR: New York, NY, USA, 2017; pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Li, Q.; He, B.; Song, D. Model-contrastive federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 10713–10722. [Google Scholar]
- Mendieta, M.; Yang, T.; Wang, P.; Lee, M.; Ding, Z.; Chen, C. Local learning matters: Rethinking data heterogeneity in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8397–8406. [Google Scholar]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the objective inconsistency problem in heterogeneous federated optimization. Adv. Neural Inf. Process. Syst. 2020, 33, 7611–7623. [Google Scholar]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2351–2363. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Song, C.; Saxena, D.; Cao, J.; Zhao, Y. Feddistill: Global model distillation for local model de-biasing in non-iid federated learning. arXiv 2024, arXiv:2404.09210. [Google Scholar]
- Passalis, N.; Tefas, A. Learning deep representations with probabilistic knowledge transfer. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 268–284. [Google Scholar]
- Sun, S.; Ren, W.; Li, J.; Wang, R.; Cao, X. Logit standardization in knowledge distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 15731–15740. [Google Scholar]
- Kang, D.; Ahn, C.W. Ga approach to optimize training client set in federated learning. IEEE Access 2023, 11, 85489–85500. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhao, K.; Yu, F.; Zeng, B.; Pang, Z.; Wang, L. FedGR: Genetic Algorithm and Relay Strategy Based Federated Learning. In Proceedings of the 2024 27th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Tianjin, China, 8–10 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 2203–2208. [Google Scholar]
- Fu, D.S.; Huang, J.; Hazra, D.; Dwivedi, A.K.; Gupta, S.K.; Shivahare, B.D.; Garg, D. Enhancing sports image data classification in federated learning through genetic algorithm-based optimization of base architecture. PLoS ONE 2024, 19, e0303462. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S. Manta ray foraging optimization based on mechanics game and progressive learning for multiple optimization problems. Appl. Soft Comput. 2023, 145, 110561. [Google Scholar] [CrossRef]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv 2013, arXiv:1312.6120. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Neural photo editing with introspective adversarial networks. arXiv 2016, arXiv:1609.07093. [Google Scholar]
- Wei, Q.; Zhang, W. Class-incremental learning with Balanced Embedding Discrimination Maximization. Neural Netw. 2024, 179, 106487. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 10 October 2024).
- Deng, L. The mnist database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Shi, Y.; Liang, J.; Zhang, W.; Tan, V.Y.; Bai, S. Towards understanding and mitigating dimensional collapse in heterogeneous federated learning. arXiv 2022, arXiv:2210.00226. [Google Scholar]
- Qu, Z.; Li, X.; Duan, R.; Liu, Y.; Tang, B.; Lu, Z. Generalized federated learning via sharpness aware minimization. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; PMLR: New York, NY, USA, 2022; pp. 18250–18280. [Google Scholar]
- Jhunjhunwala, D.; Wang, S.; Joshi, G. Fedexp: Speeding up federated averaging via extrapolation. arXiv 2023, arXiv:2301.09604. [Google Scholar]

| Method | Adaptability to Dynamic Heterogeneous Scenarios | Optimization Strategy | Catastrophic Forgetting Mitigation | Hyperparameter Optimization | Data Heterogeneity Handling | Model Generalization Capability |
|---|---|---|---|---|---|---|
| FedAvg | Weak (assumes static data) | Traditional gradient averaging | None | None | Weak (suitable for IID data) | Moderate (struggles with heterogeneous data) |
| FedProx | Moderate (partially adapts to heterogeneous data) | Traditional gradient optimization + proximal term | None | None | Moderate (constrains local drift) | Moderate (limited by regularization strength) |
| SCAFFOLD | Moderate (partially adapts to heterogeneous data) | Control variate adjustment (reduces local drift) | Weak (not explicitly considered) | None | Moderate (control variate adjustment) | Moderate (depends on data quality) |
| FedSAM | Moderate (enhanced robustness) | SAM optimization (improves smoothness) | None | None | Moderate (adjusts local models) | Strong (improves model robustness) |
| FedDercorr | Moderate (reduces data correlation) | Decorrelation-based optimization | None | None | Strong (decorrelation regularization) | Strong (effective for heterogeneous data) |
| Our | Strong (supports dynamic data changes) | Cosine classifier + orthogonality constraint + knowledge distillation + genetic algorithm | Strong (knowledge distillation reduces forgetting) | Genetic algorithm for adaptive optimization | Strong (orthogonality constraint for regularization) | Strong (dynamic model adjustment) |
| Layer | Kernel Size/Pool Size/Rate | Output Shape | Param # |
|---|---|---|---|
| Conv2D | (5, 5) | (64, 24, 24) | 1664 |
| Conv2D | (5, 5) | (64, 20, 20) | 102,464 |
| Dropout | 0.25 | (64, 20, 20) | 0 |
| Flatten | – | (25,600) | 0 |
| Dense | – | (128) | 3,276,928 |
| Dropout | 0.5 | (128) | 0 |
| CosineClassifier | – | (10) | 1290 |
| Layer | Kernel Size/Pool Size/Rate | Output Shape | Param # |
|---|---|---|---|
| Conv2D | (3, 3) | (128, 28, 28) | 1280 |
| Conv2D | (3, 3) | (128, 28, 28) | 147,584 |
| Conv2D | (3, 3) | (128, 28, 28) | 147,584 |
| MaxPooling | (2, 2) | (128, 14, 14) | 0 |
| Dropout | 0.25 | (128, 14, 14) | 0 |
| Conv2D | (3, 3) | (256, 14, 14) | 295,168 |
| Conv2D | (3, 3) | (256, 14, 14) | 590,080 |
| Conv2D | (3, 3) | (256, 14, 14) | 590,080 |
| MaxPooling | (2, 2) | (256, 7, 7) | 0 |
| Dropout | 0.25 | (256, 7, 7) | 0 |
| Conv2D | (3, 3) | (512, 5, 5) | 1,180,160 |
| Conv2D | (3, 3) | (256, 3, 3) | 1,179,904 |
| Conv2D | (3, 3) | (128, 1, 1) | 295,040 |
| AvgPooling | (1, 1) | (128, 1, 1) | 0 |
| Flatten | – | (128) | 0 |
| CosineClassifier | – | (10) | 1290 |
| Layer | Kernel Size/Pool Size/Rate | Output Shape | Param # |
|---|---|---|---|
| Conv2D (conv1) | (7, 7), stride = 2 | (64, 16, 16) | 9472 |
| BatchNorm2d (bn1) | – | (64, 16, 16) | 128 |
| MaxPool2d | (3, 3), stride = 2 | (64, 8, 8) | 0 |
| ResBlock1 (x2) | [(3, 3),(3, 3)] × 2 | (64, 8, 8) | 148,224 |
| ResBlock2 (x2) | [(3, 3),(3, 3)] × 2 | (128, 4, 4) | 526,336 |
| ResBlock3 (x2) | [(3, 3),(3, 3)] × 2 | (256, 2, 2) | 2,099,200 |
| ResBlock4 (x2) | [(3, 3),(3, 3)] × 2 | (512, 1, 1) | 8,392,960 |
| AvgPool2d | Adaptive(1, 1) | (512, 1, 1) | 0 |
| Flatten | – | (512) | 0 |
| CosineClassifier | – | (10) | 5130 |
| Classifier | Orth | Distill | GA | ACC (%) |
|---|---|---|---|---|
| 47.13 | ||||
| ✓ | 51.48 | |||
| ✓ | ✓ | 51.73 | ||
| ✓ | ✓ | 51.89 | ||
| ✓ | ✓ | ✓ | 53.05 | |
| ✓ | ✓ | ✓ | ✓ | 53.71 |
| Method | MNIST | Fashion-MNIST | CIFAR-10 | |||
|---|---|---|---|---|---|---|
| 0.1 | 0.5 | 0.1 | 0.5 | 0.1 | 0.5 | |
| FedAvg | 93.49 ± 0.15 | 94.14 ± 0.21 | 88.09 ± 0.14 | 88.43 ± 0.18 | 45.42 ± 0.13 | 47.13 ± 0.33 |
| FedProx | 94.56 ± 0.24 | 94.49 ± 0.24 | 87.74 ± 0.12 | 88.56 ± 0.16 | 46.62 ± 0.14 | 49.06 ± 0.17 |
| FedExp | 95.88 ± 0.21 | 96.19 ± 0.14 | 87.92 ± 0.25 | 88.30 ± 0.16 | 47.39 ± 0.34 | 48.34 ± 0.29 |
| FedSAM | 96.11 ± 0.33 | 96.02 ± 0.27 | 88.26 ± 0.28 | 88.14 ± 0.16 | 44.27 ± 0.27 | 44.27 ± 0.27 |
| FedDcorr | 94.64 ± 0.29 | 95.24 ± 0.11 | 87.69 ± 0.12 | 88.15 ± 0.17 | 46.67 ± 0.17 | 47.89 ± 0.12 |
| FedDyH | 97.23 ± 0.14 | 97.42 ± 0.16 | 88.24 ± 0.21 | 89.13 ± 0.18 | 52.46 ± 0.17 | 53.71 ± 0.15 |
| Method | MNIST | Fashion-MNIST | CIFAR-10 | |||
|---|---|---|---|---|---|---|
| 0.2 | 0.5 | 0.2 | 0.5 | 0.2 | 0.5 | |
| FedAvg | 93.26 ± 0.14 | 94.14 ± 0.21 | 86.89 ± 0.23 | 88.43 ± 0.18 | 41.40 ± 0.19 | 47.13 ± 0.33 |
| FedProx | 93.50 ± 0.15 | 94.49 ± 0.24 | 86.97 ± 0.14 | 88.56 ± 0.16 | 44.02 ± 0.17 | 49.06 ± 0.17 |
| FedExp | 94.28 ± 0.25 | 96.19 ± 0.14 | 86.84 ± 0.24 | 88.30 ± 0.16 | 43.12 ± 0.17 | 48.34 ± 0.29 |
| FedSAM | 95.26 ± 0.13 | 96.02 ± 0.27 | 86.72 ± 0.14 | 88.14 ± 0.16 | 37.86 ± 0.14 | 44.27 ± 0.27 |
| FedDcorr | 93.96 ± 0.29 | 95.24 ± 0.11 | 86.84 ± 0.14 | 88.15 ± 0.17 | 42.90 ± 0.16 | 47.89 ± 0.12 |
| FedDyH | 96.59 ± 0.19 | 97.42 ± 0.16 | 87.02 ± 0.23 | 89.13 ± 0.18 | 45.83 ± 0.24 | 53.71 ± 0.15 |
| Method | 1 | 5 | 10 |
|---|---|---|---|
| FedAvg | 47.13 ± 0.33 | 49.53 ± 0.14 | 50.12 ± 0.26 |
| FedProx | 49.06 ± 0.17 | 49.99 ± 0.18 | 50.53 ± 0.15 |
| FedExp | 48.34 ± 0.29 | 47.59 ± 0.21 | 51.35 ± 0.25 |
| FedSAM | 44.27 ± 0.27 | 49.64 ± 0.17 | 50.52 ± 0.21 |
| FedDcorr | 47.89 ± 0.12 | 50.87 ± 0.13 | 50.14 ± 0.18 |
| FedDyH | 53.71 ± 0.15 | 53.19 ± 0.15 | 52.15 ± 0.14 |
| Method | MNIST | Fashion-MNIST | CIFAR-10 |
|---|---|---|---|
| = 0.5 = 0.5 | 97.23% | 87.72% | 50.88% |
| = 0.2 = 0.8 | 97.28% | 87.98% | 52.06% |
| = 0.1 = 0.9 | 97.27% | 88.05% | 52.53% |
| GA Optimisation | 97.32% | 89.13% | 53.71% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Zheng, Y.; Wan, J.; Li, Y.; Zhu, D.; Xu, Z.; Lu, H. FedDyH: A Multi-Policy with GA Optimization Framework for Dynamic Heterogeneous Federated Learning. Biomimetics 2025, 10, 185. https://doi.org/10.3390/biomimetics10030185
Zhao X, Zheng Y, Wan J, Li Y, Zhu D, Xu Z, Lu H. FedDyH: A Multi-Policy with GA Optimization Framework for Dynamic Heterogeneous Federated Learning. Biomimetics. 2025; 10(3):185. https://doi.org/10.3390/biomimetics10030185
Chicago/Turabian StyleZhao, Xuhua, Yongming Zheng, Jiaxiang Wan, Yehong Li, Donglin Zhu, Zhenyu Xu, and Huijuan Lu. 2025. "FedDyH: A Multi-Policy with GA Optimization Framework for Dynamic Heterogeneous Federated Learning" Biomimetics 10, no. 3: 185. https://doi.org/10.3390/biomimetics10030185
APA StyleZhao, X., Zheng, Y., Wan, J., Li, Y., Zhu, D., Xu, Z., & Lu, H. (2025). FedDyH: A Multi-Policy with GA Optimization Framework for Dynamic Heterogeneous Federated Learning. Biomimetics, 10(3), 185. https://doi.org/10.3390/biomimetics10030185








