An Improved Crested Porcupine Optimization Algorithm Incorporating Butterfly Search and Triangular Walk Strategies
Abstract
1. Introduction
2. Advances in Optimization Algorithms
3. Crested Porcupine Optimizer
3.1. Population Initialization
3.2. Cyclic Population Reduction Strategy
3.3. Visual Intimidation
3.4. Auditory Deterrence
3.5. Olfactory Attack
3.6. Contact Attack
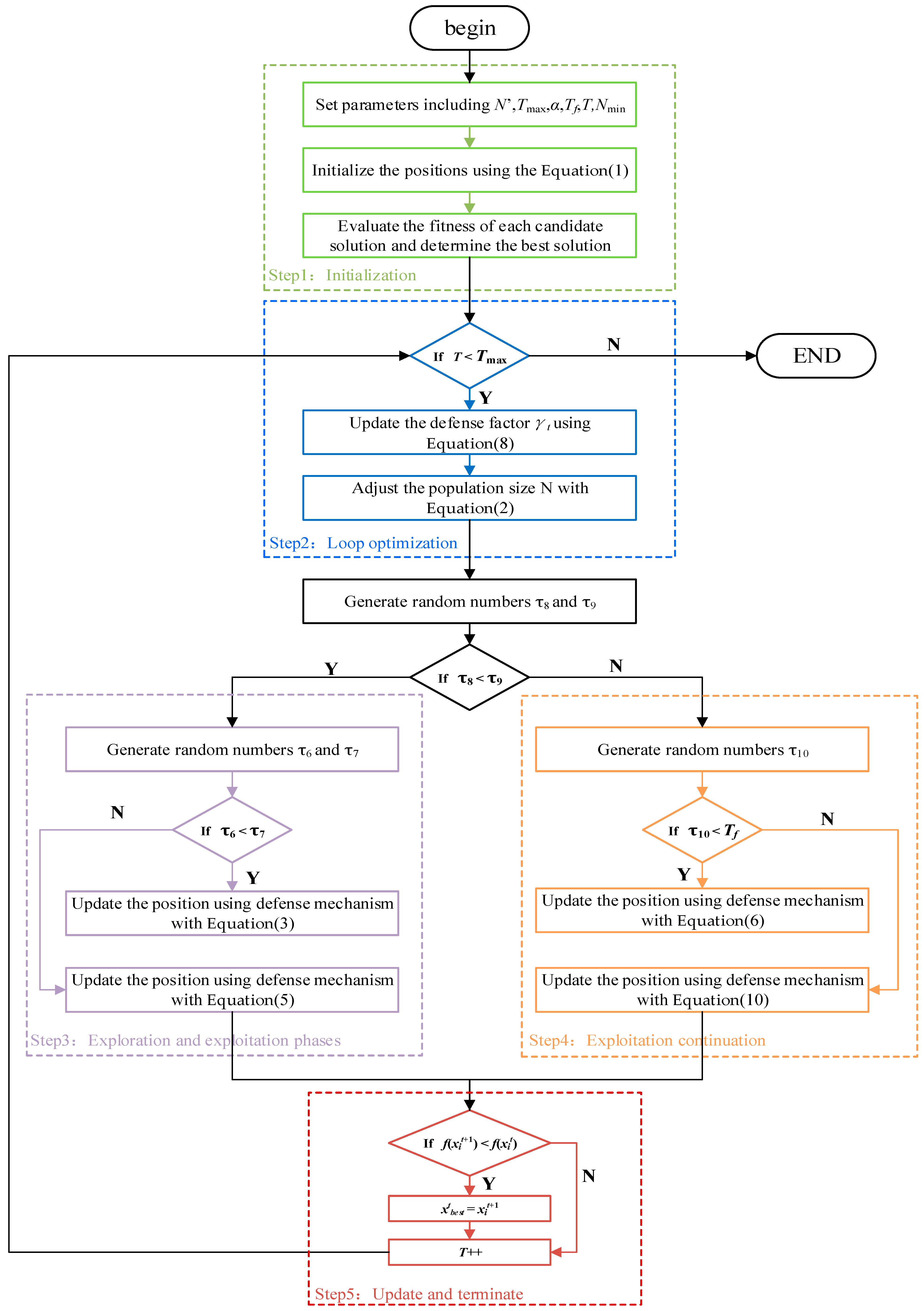
3.7. Execution Procedure of the CPO
4. An Enhanced CPO Algorithm Incorporating Butterfly Search and Triangular Walk Strategies
4.1. Butterfly Search
4.1.1. Mechanism and Fundamental Principles
4.1.2. Advantages of the Butterfly Search
4.2. Triangular Walk Strategies
4.2.1. Mechanism and Fundamental Principles
4.2.2. Advantages and Strengths of the Triangular Walk Strategy
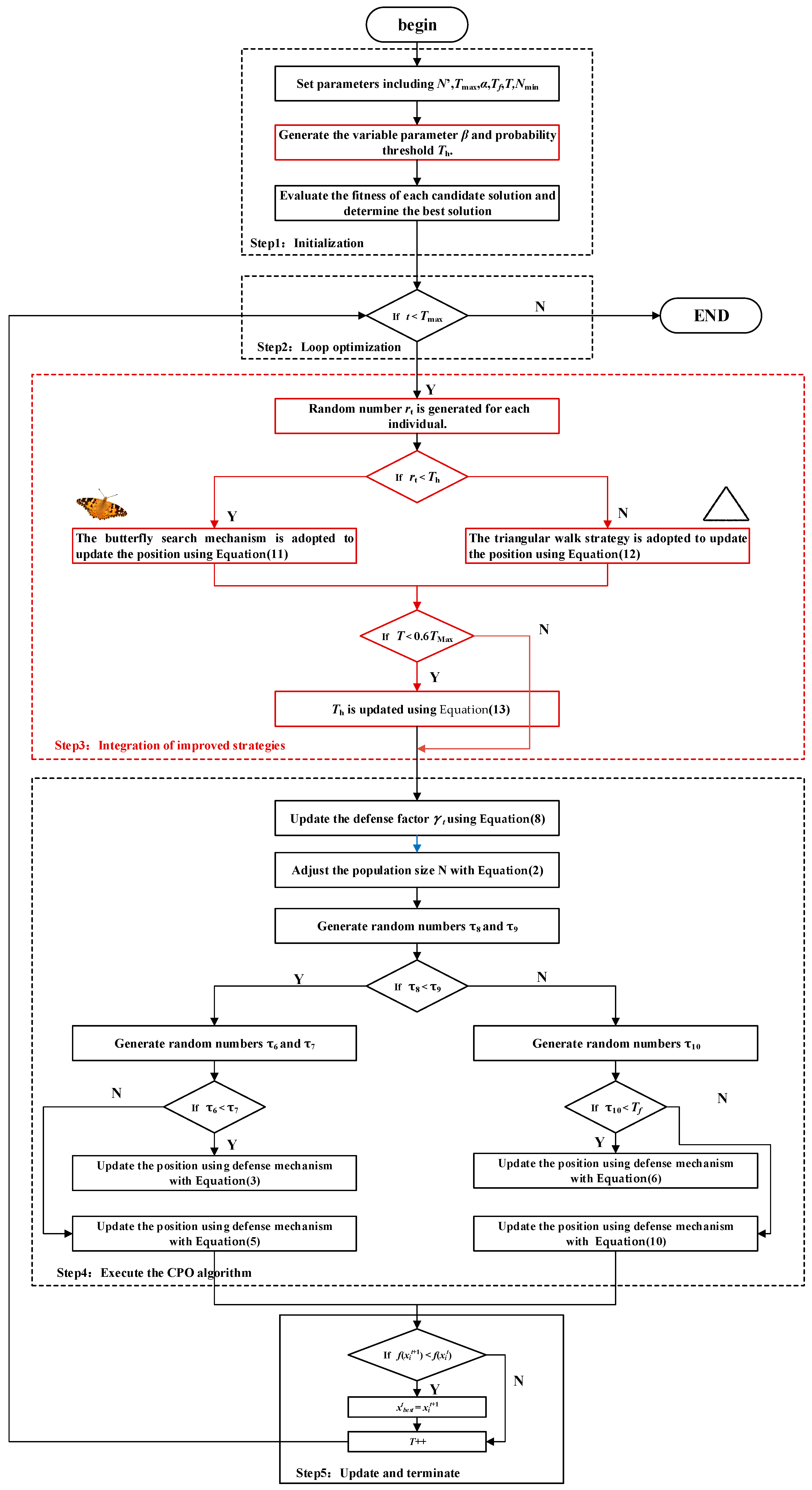
4.3. Implementation Steps of the Improved Algorithm
4.3.1. Enhanced Strategy Through Mechanism Integration
4.3.2. Algorithm Implementation
| Algorithm 1: Butterfly Search and Triangular Walk Porcupine Optimization Algorithm |
| Step1: Initialization Set parameters including N’, Tmax, α, Tf, T, Nmin Generate the variable parameter β and probability threshold Th. Evaluate the fitness of each candidate solution and determine the best solution Step2: Loop optimization If T < Tmax Go to Step3 Else Output the optimal solution and terminate the algorithm Step3: Integration of improved strategies Random number rt is generated for each individual If rt < Th The butterfly search mechanism is adopted to update the position using Equation (11) Else The triangular walk strategy is adopted to update the position using Equation (12) If T < 0.6Tmax Th is updated using Formula (13), Go to Step4 Else Go to Step4 Step4: Execute the CPO algorithm Update the defense factor γt using Equation (8) Adjust the population size N with Equation (2) Generate random numbers τ8 and τ9 If τ8 < τ9 Generate random numbers τ6 and τ7 If τ6 < τ7 Update the position using defense mechanism with Equation (3) Else Update the position using defense mechanism with Equation (5) Go to Step5 Else Generate random numbers τ10 If τ10 < Tf Update the position using defense mechanism with Equation (6) Else Update the position using defense mechanism with Equation (10) Go to Step5 Step5: Update and terminate If , then T++ Go to Step2 Else Go to Step2 |
4.4. Theoretical Analysis of BTCPO
5. Algorithm Performance Testing and Comparative Analysis
5.1. Experimental Design and Test Functions
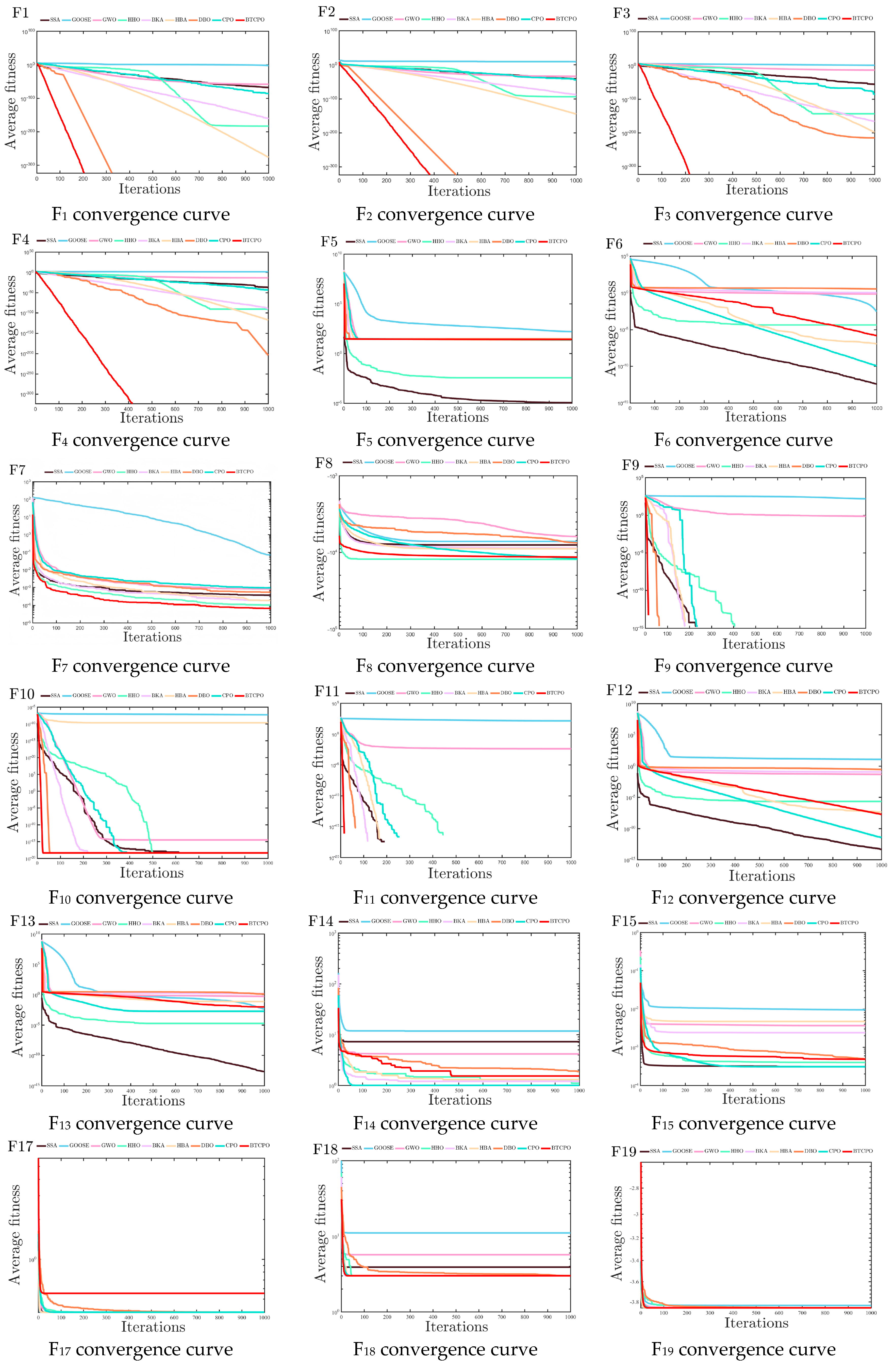
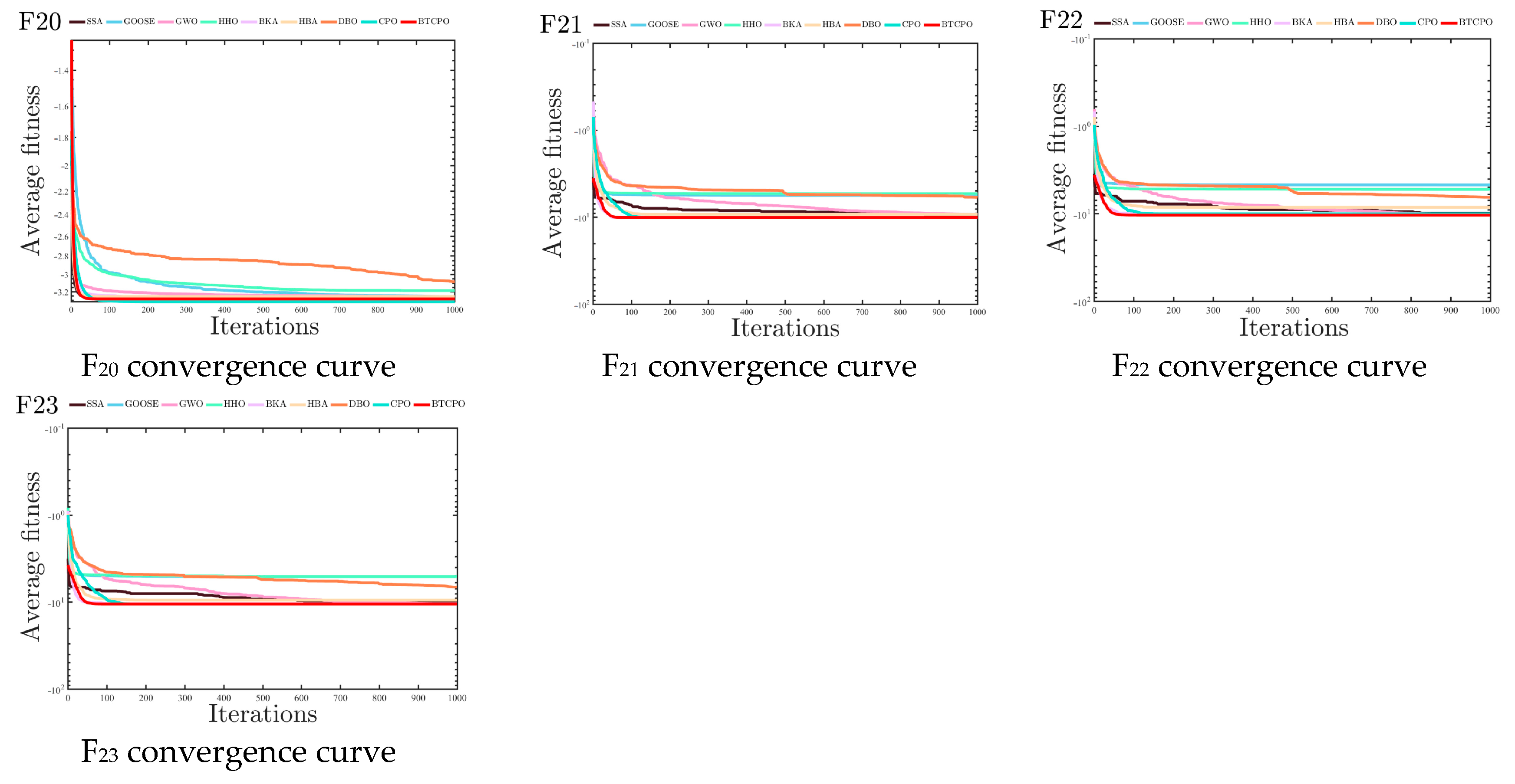
5.2. Comparison of Experimental Results and Algorithm Analysis
5.2.1. Experimental Results of Classical Benchmark Functions
5.2.2. CEC2021 Benchmark Test Function
5.3. Time Complexity Analysis of the Algorithm
5.4. The Application of BTCPO in Engineering
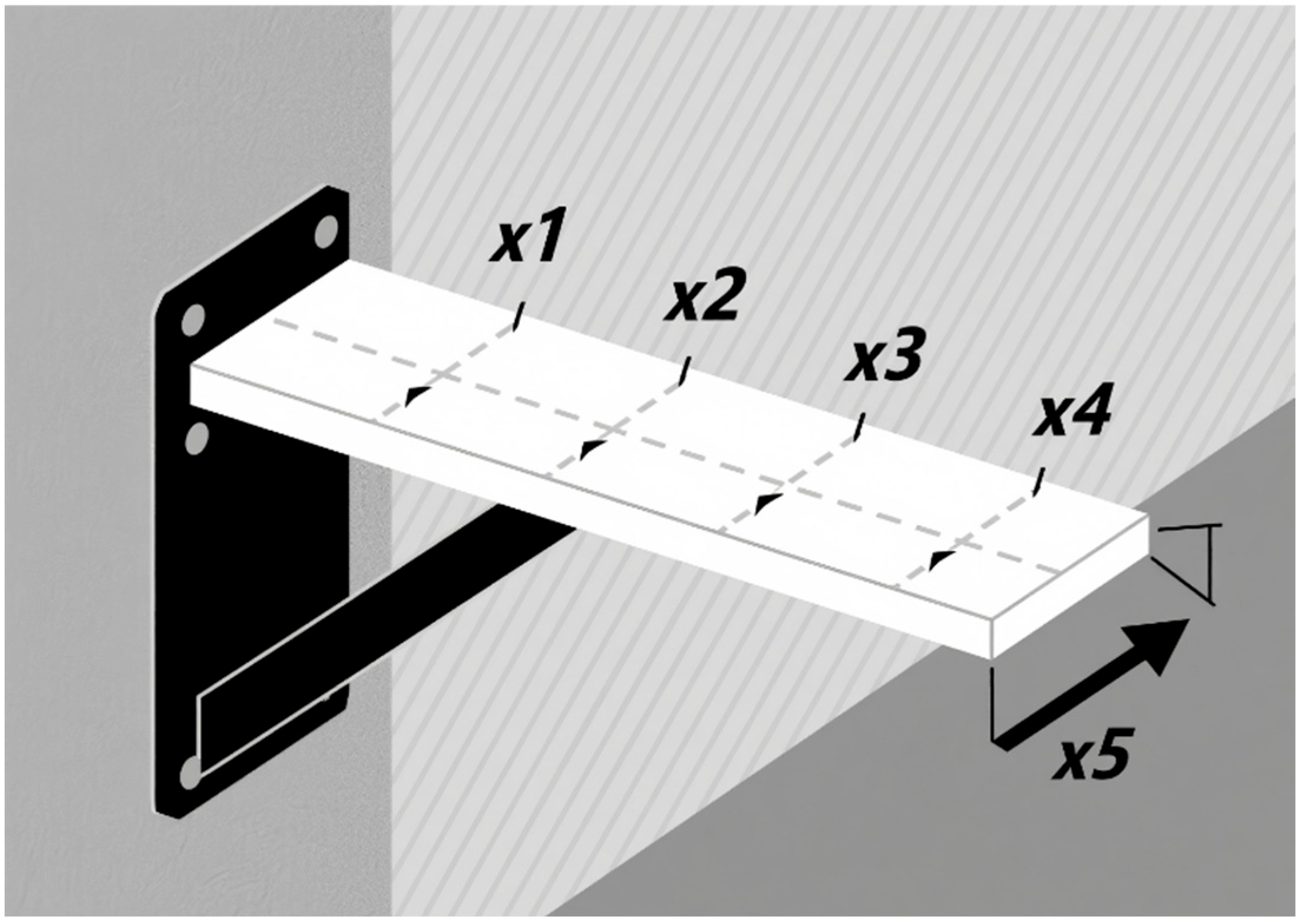
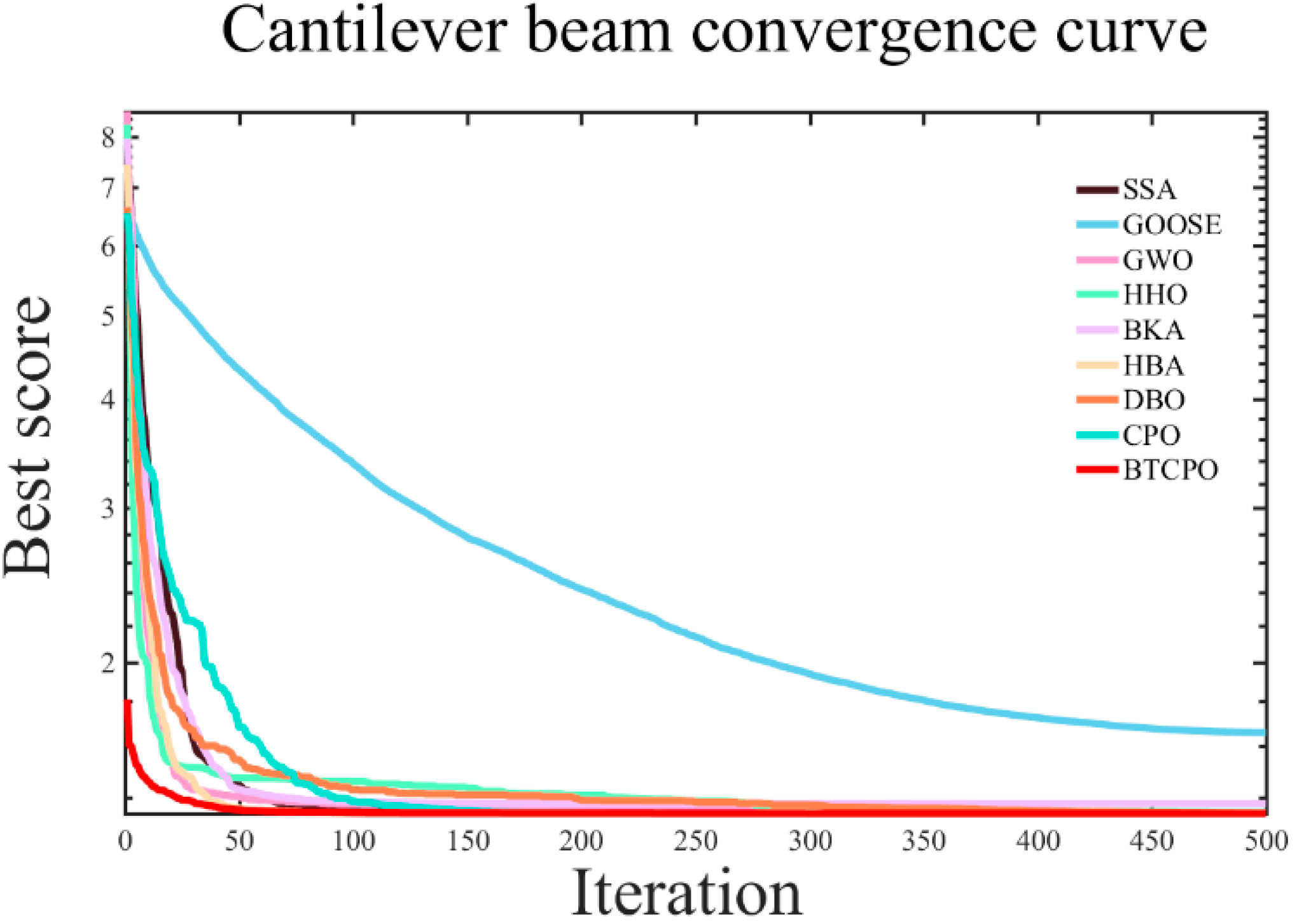
5.4.1. Optimization Problem in Cantilever Beam Design
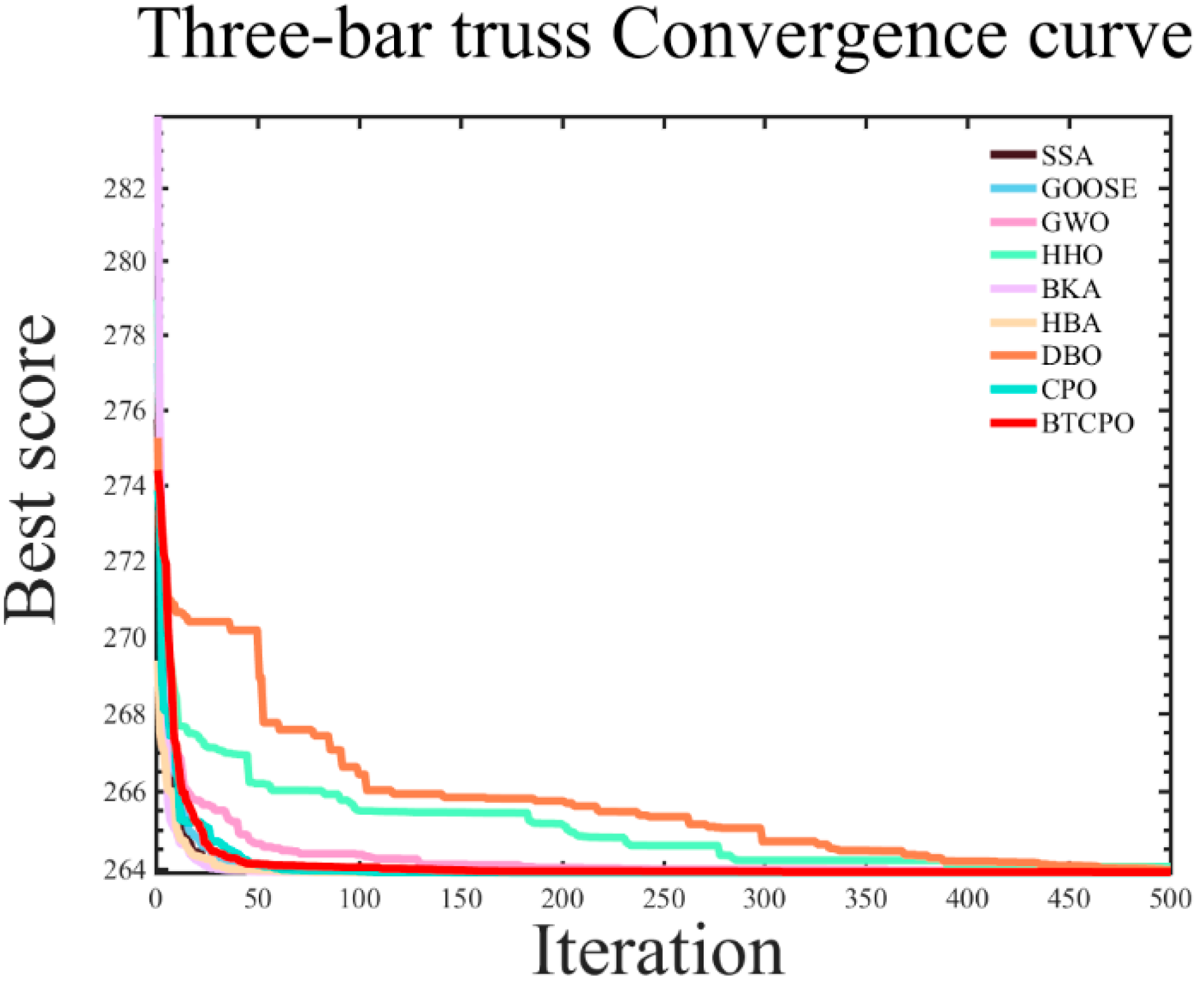
5.4.2. Optimization Problem of the Three-Bar Truss Structure
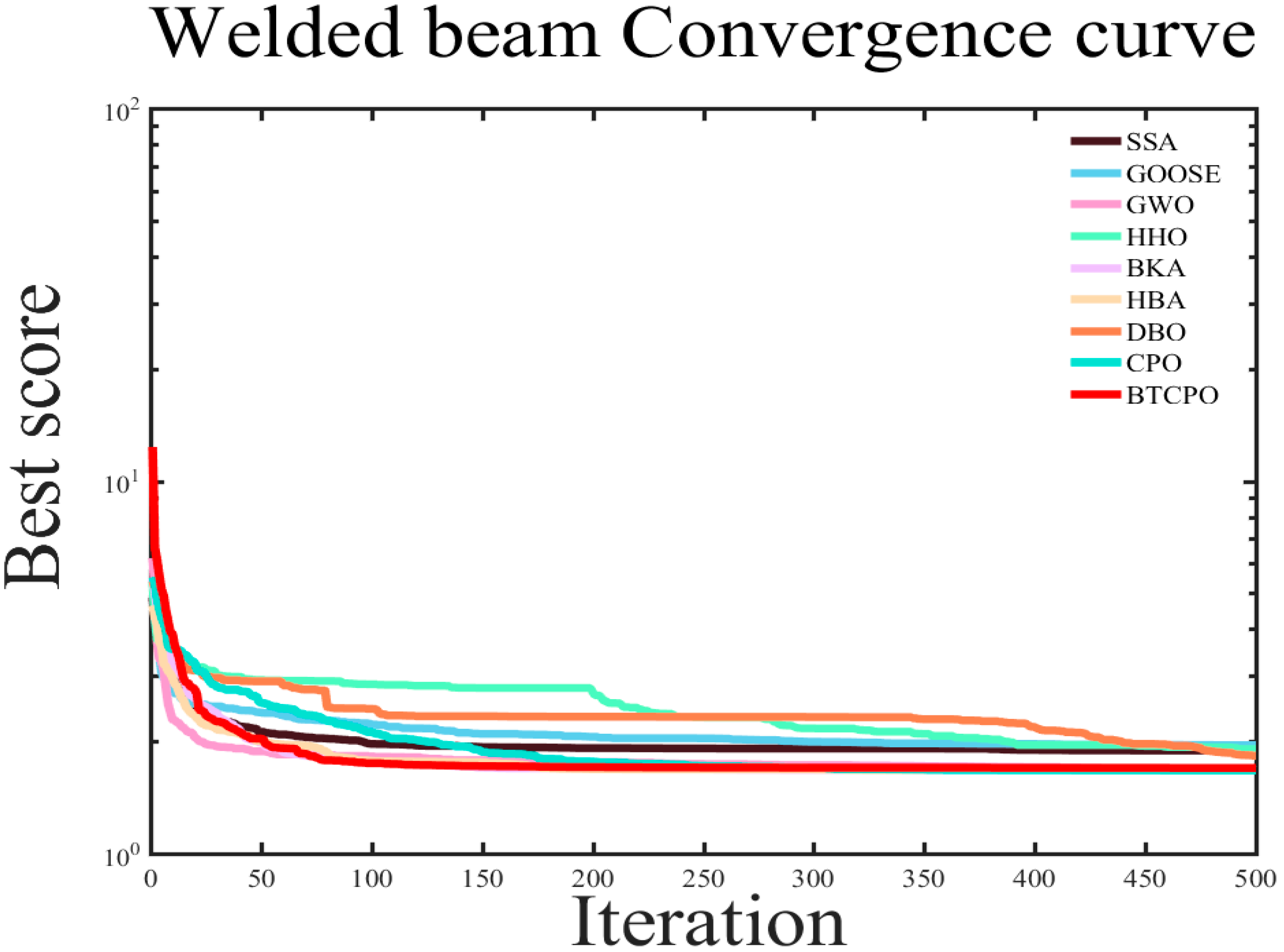
5.4.3. Welded Beam Design Optimization Problem
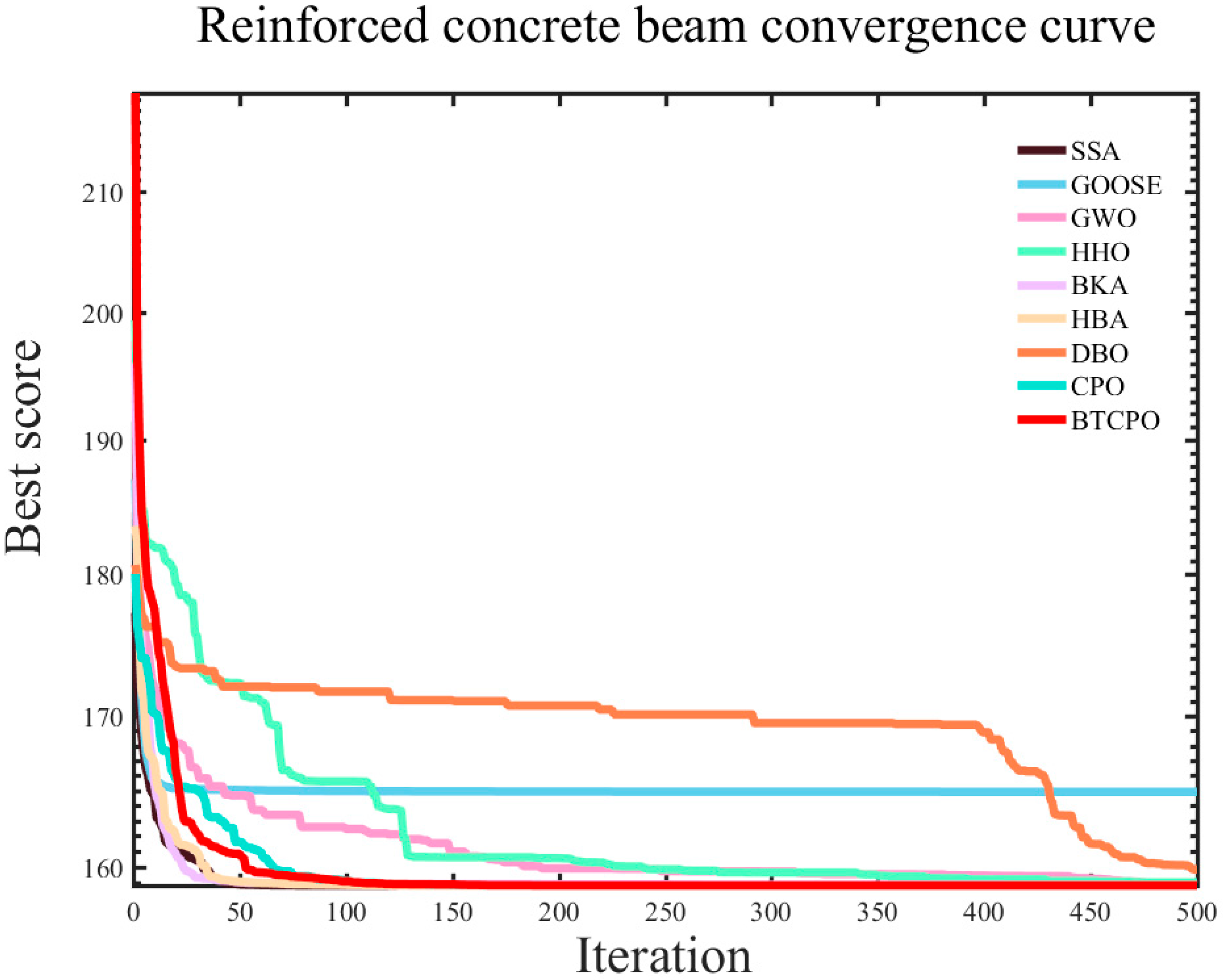
5.4.4. Reinforced Concrete Beam Design
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Selvarajan, S. A comprehensive study on modern optimization techniques for engineering applications. Artif. Intell. Rev. 2024, 57, 194. [Google Scholar] [CrossRef]
- Chen, C.; Cao, L.; Chen, Y.; Yue, Y. A comprehensive survey of convergence analysis of beetle antennae search algorithm and its applications. Artif. Intell. Rev. 2024, 57, 141. [Google Scholar] [CrossRef]
- Zhu, D.; Li, R.; Zheng, Y.; Zhou, C.; Li, T.; Cheng, S. Cumulative major advances in particle swarm optimization from 2018 to the present: Variants, analysis and applications. Arch. Comput. Methods Eng. 2025, 32, 1571–1595. [Google Scholar] [CrossRef]
- Chen, B.; Cao, L.; Chen, C.; Chen, Y.; Yue, Y. A comprehensive survey on the chicken swarm optimization algorithm and its applications: State-of-the-art and research challenges. Artif. Intell. Rev. 2024, 57, 170. [Google Scholar] [CrossRef]
- Dagal, I.; Ibrahim, A.L.W.; Harrison, A.; Mbasso, W.F.; Hourani, A.O.; Zaitsev, I. Hierarchical multi step Gray Wolf optimization algorithm for energy systems optimization. Sci. Rep. 2025, 15, 8973. [Google Scholar] [CrossRef]
- Uddin, M.P.; Majumder, A.; Barma, J.D.; Mirjalili, S. An improved Multi-Objective Harris Hawks optimization algorithm for solving EDM problems. Arab. J. Sci. Eng. 2025, 50, 12403–12448. [Google Scholar] [CrossRef]
- Cao, L.; Yue, Y.; Chen, Y.; Chen, C.; Chen, B. Sailfish Optimization Algorithm Integrated with the Osprey Optimization Algorithm and Cauchy Mutation and Its Engineering Applications. Symmetry 2025, 17, 938. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Adalja, D.; Patel, P.; Mashru, N.; Jangir, P.; Jangid, R.; Gulothungan, G.; Khishe, M. A new multi objective crested porcupines optimization algorithm for solving optimization problems. Sci. Rep. 2025, 15, 14380. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, Z.; Tang, W.; Liang, J.; Xu, P. Using crested Porcupine optimizer algorithm and CNN-LSTM-Attention model combined with deep learning methods to enhance short-term power forecasting in PV generation. Energies 2024, 17, 3435. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, R.; Zhong, X.; Yao, Y.; Shan, W.; Yuan, J.; Xiao, J.; Ma, Y.; Zhang, K.; Wang, Z. Multi-strategy enhanced crested porcupine optimizer: CAPCPO. Mathematics 2024, 12, 3080. [Google Scholar] [CrossRef]
- Wang, S.; Xu, B.; Zheng, Y.; Yue, Y.; Xiong, M. Path Optimization Strategy for Unmanned Aerial Vehicles Based on Improved Black Winged Kite Optimization Algorithm. Biomimetics 2025, 10, 310. [Google Scholar] [CrossRef]
- Gu, Q.; Niu, Y.; Hui, Z.; Wang, Q.; Xiong, N. A hierarchical clustering algorithm for addressing multi-modal multi-objective optimization problems. Expert Syst. Appl. 2025, 264, 125710. [Google Scholar] [CrossRef]
- Zhong, X.; Liang, B. Elite-based butterfly optimization algorithm and its application in speckle projection technique. Appl. Soft Comput. 2025, 169, 112561. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, F.; Zhao, R.; Xing, Y.; He, Z. Synchronous control method for the walking system of the dual forging manipulators based on triangular velocity planning. Mech. Based Des. Struct. Mach. 2025, 53, 1228–1248. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent advances in stochastic gradient descent in deep learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Chen, C.; Chen, Y.; Chen, B. Snake Optimization Algorithm Augmented by Adaptive t-Distribution Mixed Mutation and Its Application in Energy Storage System Capacity Optimization. Biomimetics 2025, 10, 244. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; Towfek, S.K.; Khodadadi, N.; Alhussan, A.A.; Khafaga, D.S.; Eid, M.M.; Ibrahim, A. Waterwheel plant algorithm: A novel metaheuristic optimization method. Processes 2023, 11, 1502. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Makhadmeh, S.N.; Al-Betar, M.A.; Dalbah, L.M.; Al-Redhaei, A.; Kouka, S.; Enshassi, O.S. Multi-objective ant colony optimization. Arch. Comput. Methods Eng. 2025, 32, 995–1037. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Zio, E.; Zhang, C.; Dui, H.; Chen, R. Multi-objective maintenance strategy for complex systems considering the maintenance uncertain impact by adaptive multi-strategy particle swarm optimization. Reliab. Eng. Syst. Saf. 2025, 256, 110671. [Google Scholar] [CrossRef]
- Ye, M.; Zhou, H.; Yang, H.; Hu, B.; Wang, X. Multi-strategy improved dung beetle optimization algorithm and its applications. Biomimetics 2024, 9, 291. [Google Scholar] [CrossRef]
- Khan, M.H.; Ulasyar, A.; Khattak, A.; Zad, H.S.; Alsharef, M.; Alahmadi, A.A.; Ullah, N. Optimal sizing and allocation of distributed generation in the radial power distribution system using honey badger algorithm. Energies 2022, 15, 5891. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H.-F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Hussien, A.G.; Abualigah, L.; Abu Zitar, R.; Hashim, F.A.; Amin, M.; Saber, A.; Almotairi, K.H.; Gandomi, A.H. Recent advances in harris hawks optimization: A comparative study and applications. Electronics 2022, 11, 1919. [Google Scholar] [CrossRef]
- Hou, Y.; Gao, H.; Wang, Z.; Du, C. Improved grey wolf optimization algorithm and application. Sensors 2022, 22, 3810. [Google Scholar] [CrossRef] [PubMed]
- Hamad, R.K.; Rashid, T.A. GOOSE algorithm: A powerful optimization tool for real-world engineering challenges and beyond. Evol. Syst. 2024, 15, 1249–1274. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, M.; Khodadadi, N.; Trojovský, P.; Li, L.; Mansor, Z.; Abualigah, L.; Alharbi, A.H.; El-Kenawy, E.-S.M. Kirchhoff’s law algorithm (KLA): A novel physics-inspired non-parametric metaheuristic algorithm for optimization problems. Artif. Intell. Rev. 2025, 58, 325. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl. Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- Azevedo, B.F.; Rocha, A.M.A.C.; Pereira, A.I. Hybrid approaches to optimization and machine learning methods: A systematic literature review. Mach. Learn. 2024, 113, 4055–4097. [Google Scholar] [CrossRef]
- Zang, J.; Cao, B.; Hong, Y. Research on the fiber-to-the-room network traffic prediction method based on crested porcupine optimizer optimization. Appl. Sci. 2024, 14, 4840. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Shen, B.; Wang, J.; Wang, P.; Zhang, G.; Zhuang, X.; Chen, R.; Luo, W. A Q-Learning Crested Porcupine Optimizer for Adaptive UAV Path Planning. Machines 2025, 13, 566. [Google Scholar] [CrossRef]
- Li, H.; Wei, D.; Wu, Y.; Li, H.; Liu, H.; Hu, X.; Zhang, H.; Zhou, H. Advanced optimization of thermal efficiency in low-low temperature economizers and air heater system employing the crested porcupine optimizer algorithm. Expert Syst. Appl. 2025, 290, 128352. [Google Scholar] [CrossRef]
- Chen, X.; Ma, C.; Dou, Q.; Bai, S.; Sun, K.; Li, Z. Diesel Engine Urea Injection Optimization Based on the Crested Porcupine Optimizer and Genetic Algorithm. Appl. Sci. 2025, 15, 5195. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Wang, J.; Lu, Y.; Han, J.; Guo, B.; Xie, T. Prediction of geometric characteristics of laser cladding layer based on least squares support vector regression and crested porcupine optimization. Micromachines 2024, 15, 919. [Google Scholar] [CrossRef]
- Tang, X.; He, Z.; Jia, C. Multi-strategy cooperative enhancement dung beetle optimizer and its application in obstacle avoidance navigation. Sci. Rep. 2024, 14, 28041. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhang, M.; Yang, M.; Wang, D. NHBBWO: A novel hybrid butterfly-beluga whale optimization algorithm with the dynamic strategy for WSN coverage optimization. Peer-Peer Netw. Appl. 2025, 18, 80. [Google Scholar] [CrossRef]
- Abidi, M.H.; Alkhalefah, H.; Mohammed, M.K.; Gadekallu, T.R. SMGR-BS: Stacking multiple gated recurrent butterfly search model-based innovative AAL for aging and disabled individuals. J. Disabil. Res. 2024, 3, 20240035. [Google Scholar] [CrossRef]
- Slimani, K.; Achard, C.; Tamadazte, B. RoCNet++: Triangle-based descriptor for accurate and robust point cloud registration. Pattern Recognit. 2024, 147, 110108. [Google Scholar] [CrossRef]
- Sharma, P.; Raju, S. Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions. Soft Comput. A Fusion Found. Methodol. Appl. 2024, 28, 3123–3186. [Google Scholar] [CrossRef]
- Toktas, F.; Erkan, U.; Yetgin, Z. Cross-channel color image encryption through 2D hyperchaotic hybrid map of optimization test functions. Expert Syst. Appl. 2024, 249, 123583. [Google Scholar] [CrossRef]
- Marr, K.; Utter, B. Design, modeling, and experimental study of annealed 3D-printed cantilever beam force sensors. Int. J. Adv. Manuf. Technol. 2025, 136, 1025–1034. [Google Scholar] [CrossRef]
- Sait, S.M.; Mehta, P.; Yıldız, A.R.; Yıldız, B.S. Optimal design of structural engineering components using artificial neural network-assisted crayfish algorithm. Mater. Test. 2024, 66, 1439–1448. [Google Scholar] [CrossRef]
- Aydın, Y.; Ahadian, F.; Bekdaş, G.; Nigdeli, S.M. Prediction of optimum design of welded beam design via machine learning. Chall. J. Struct. Mech. 2024, 10, 86–94. [Google Scholar] [CrossRef]
- Azuwa, S.B.; Yahaya, F.B.M. Experimental investigation and finite element analysis of reinforced concrete beams strengthened by fibre reinforced polymer composite materials: A review. Alex. Eng. J. 2024, 99, 137–167. [Google Scholar] [CrossRef]




| Benchmark Function | n | S | Fmin |
|---|---|---|---|
| 50 | [−100, 100]n | 0 | |
| 50 | [−10, 10]n | 0 | |
| 50 | [−100, 100]n | 0 | |
| 50 | [−100, 100]n | 0 | |
| 50 | [−30, 30]n | 0 | |
| 50 | [−100, 100]n | 0 | |
| 50 | [−1.28, 1.28]n | 0 | |
| 50 | [−500, 500]n | −12,569.5 | |
| 50 | [−5.12, 5.12]n | 0 | |
| 50 | [−32, 32]n | 0 | |
| 50 | [−600, 600]n | 0 | |
| 50 | [−50, 50]n | 0 | |
| 50 | [−50, 50]n | 0 | |
| 2 | [−65.536, 65.536]n | 0 | |
| 4 | [−5, 5]n | 0.000307 | |
| 2 | [−5, 5]n | −1.01362 | |
| 2 | [−5, 10] × [0, 15] | 0.398 | |
| 2 | [−2, 2]n | 3 | |
| 4 | [0, 1]n | −3.86 | |
| 6 | [0, 1]n | −3.32 | |
| 4 | [0, 10]n | −10 | |
| 4 | [0, 10]n | −10 | |
| 4 | [0, 10]n | −10 |
| F1 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
|---|---|---|---|---|---|---|---|---|---|
| min | 0.00 | 1.56 × 10−3 | 4.00 × 10−61 | 9.12 × 10−219 | 1.02 × 10−207 | 2.46 × 10−289 | 0.00 | 1.96 × 10−136 | 0.00 |
| std | 6.47 × 10−68 | 8.60 × 10−4 | 9.29 × 10−59 | 0.00 | 6.90 × 10−161 | 0.00 | 0.00 | 4.72 × 10−86 | 0.00 |
| avg | 1.18 × 10−68 | 2.76 × 10−3 | 4.82 × 10−59 | 5.52 × 10−184 | 1.26 × 10−161 | 1.61 × 10−277 | 0.00 | 8.61 × 10−87 | 0.00 |
| median | 7.83 × 10−123 | 2.47 × 10−3 | 1.50 × 10−59 | 3.66 × 10−194 | 4.24 × 10−199 | 1.65 × 10−282 | 0.00 | 4.23 × 10−105 | 0.00 |
| worse | 3.54 × 10−67 | 4.12 × 10−3 | 3.86 × 10−58 | 1.17 × 10−182 | 3.78 × 10−160 | 4.16 × 10−276 | 0.00 | 2.58 × 10−85 | 0.00 |
| time | 7.14 × 10−2 | 4.59 × 10−2 | 9.87 × 10−2 | 4.56 × 10−2 | 5.17 × 10−2 | 0.10 | 7.28 × 10−2 | 6.31 × 10−2 | 0.28 |
| F2 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 0.26 | 1.16 × 10−35 | 2.36 × 10−109 | 1.74 × 10−103 | 1.80 × 10−151 | 0.00 | 1.53 × 10−65 | 0.00 |
| std | 8.62 × 10−42 | 9.84 × 108 | 1.48 × 10−34 | 4.83 × 10−94 | 1.18 × 10−87 | 4.30 × 10−145 | 0.00 | 2.23 × 10−44 | 0.00 |
| avg | 1.77 × 10−42 | 1.80 × 108 | 1.09 × 10−34 | 8.88 × 10−95 | 2.32 × 10−88 | 1.07 × 10−145 | 0.00 | 5.41 × 10−45 | 0.00 |
| median | 6.10 × 10−57 | 16.40 | 6.00 × 10−35 | 8.15 × 10−102 | 4.80 × 10−100 | 3.63 × 10−148 | 0.00 | 8.14 × 10−53 | 0.00 |
| worse | 4.73 × 10−41 | 5.39 × 109 | 7.07 × 10−34 | 2.65 × 10−93 | 6.45 × 10−87 | 2.26 × 10−144 | 0.00 | 1.15 × 10−43 | 0.00 |
| time | 0.99 | 5.98 × 10−2 | 0.12 | 5.73 × 10−2 | 7.09 × 10−2 | 0.11 | 8.03 × 10−2 | 6.82 × 10−2 | 0.27 |
| F3 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 0.28 | 5.58 × 10−21 | 6.07 × 10−187 | 4.90 × 10−206 | 1.08 × 10−216 | 0.00 | 0.00 | 0.00 |
| std | 6.46 × 10−56 | 5.06 | 3.22 × 10−14 | 9.58 × 10−144 | 0.00 | 0.00 | 0.00 | 6.04 × 10−86 | 0.00 |
| avg | 1.18 × 10−56 | 2.79 | 9.41 × 10−15 | 1.75 × 10−144 | 4.37 × 10−167 | 2.66 × 10−199 | 5.91 × 10−216 | 1.11 × 10−86 | 0.00 |
| median | 2.32 × 10−90 | 1.58 | 5.28 × 10−17 | 5.85 × 10−166 | 1.87 × 10−196 | 4.59 × 10−207 | 0.00 | 1.86 × 10−107 | 0.00 |
| worse | 3.54 × 10−55 | 28.20 | 1.50 × 10−13 | 5.25 × 10−143 | 1.31 × 10−165 | 7.97 × 10−198 | 1.77 × 10−214 | 3.31 × 10−85 | 0.00 |
| time | 0.31 | 0.22 | 0.21 | 0.32 | 0.28 | 0.21 | 0.19 | 0.17 | 0.48 |
| F4 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 3.28 × 10−2 | 2.31 × 10−16 | 6.32 × 10−105 | 3.07 × 10−103 | 1.90 × 10−125 | 0.00 | 0.00 | 0.00 |
| std | 2.97 × 10−37 | 14.28 | 3.43 × 10−14 | 1.33 × 10−90 | 3.40 × 10−89 | 7.44 × 10−118 | 0.00 | 1.57 × 10−43 | 0.00 |
| avg | 5.43 × 10−38 | 14.18 | 2.05 × 10−14 | 2.42 × 10−91 | 6.26 × 10−90 | 2.86 × 10−118 | 3.04 × 10−205 | 4.30 × 10−44 | 0.00 |
| median | 4.10 × 10−61 | 16.14 | 7.65 × 10−15 | 2.98 × 10−99 | 5.22 × 10−100 | 1.78 × 10−119 | 0.00 | 2.50 × 10−51 | 0.00 |
| worse | 1.63 × 10−36 | 41.03 | 1.79 × 10−13 | 7.26 × 10−90 | 1.86 × 10−88 | 3.84 × 10−117 | 9.11 × 10−204 | 6.80 × 10−43 | 0.00 |
| time | 7.38 × 10−2 | 4.86 × 10−2 | 9.93 × 10−2 | 6.21 × 10−2 | 5.43 × 10−2 | 9.05 × 10−2 | 6.29 × 10−2 | 6.40 × 10−2 | 0.22 |
| F5 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 1.38 × 10−10 | 22.13 | 25.41 | 1.14 × 10−4 | 24.38 | 20.98 | 27.97 | 22.46 | 24.61 |
| std | 2.77 × 10−5 | 2.57 × 102 | 0.71 | 4.17 × 10−3 | 1.32 | 0.48 | 0.36 | 0.49 | 0.23 |
| avg | 1.12 × 10−5 | 1.56 × 102 | 26.90 | 3.55 × 10−3 | 27.27 | 21.77 | 28.62 | 23.55 | 25.04 |
| median | 3.04 × 10−7 | 29.65 | 27.17 | 1.74 × 10−3 | 27.09 | 21.77 | 28.72 | 23.54 | 25.05 |
| worse | 1.23 × 10−4 | 1.32 × 103 | 29.76 | 1.60 × 10−2 | 29 | 22.69 | 28.94 | 24.59 | 25.52 |
| time | 9.31 × 10−2 | 5.96 × 10−2 | 0.11 | 0.11 | 7.87 × 10−2 | 0.10 | 8.09 × 10−2 | 7.24× 10−2 | 0.24 |
| F6 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 7.54 × 10−17 | 1.46 × 10−3 | 2.61 × 10−5 | 8.74 × 10−8 | 6.30 × 10−5 | 2.04 × 10−9 | 2.56 | 4.50 × 10−12 | 1.23 × 10−7 |
| std | 8.57 × 10−13 | 7.38 × 10−4 | 0.35 | 9.52 × 10−5 | 1.62 | 1.57 × 10−7 | 0.34 | 8.76 × 10−11 | 3.65 × 10−6 |
| avg | 3.61 × 10−13 | 2.78 × 10−3 | 0.69 | 4.14 × 10−5 | 1.02 | 1.04 × 10−7 | 3.32 | 1.09 × 10−10 | 1.48 × 10−6 |
| median | 1.44 × 10−14 | 2.74 × 10−3 | 0.74 | 1.15 × 10−5 | 0.56 | 5.29 × 10−8 | 3.38 | 8.27 × 10−11 | 5.13 × 10−7 |
| worse | 3.53 × 10−12 | 4.87 × 10−3 | 1.48 | 5.06 × 10−4 | 6.42 | 7.88 × 10−7 | 4.00 | 3.12 × 10−10 | 2.03 × 10−5 |
| time | 7.26 × 10−2 | 4.65 × 10−2 | 0.10 | 7.40 × 10−2 | 5.23 × 10−2 | 9.21 × 10−2 | 6.36 × 10−2 | 6.09 × 10−2 | 0.22 |
| F7 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 6.12 × 10−6 | 2.44 × 10−2 | 3.31 × 10−4 | 4.49 × 10−6 | 1.76 × 10−5 | 1.35 × 10−5 | 5.09 × 10−5 | 7.69 × 10−5 | 7.78 × 10−6 |
| std | 2.93 × 10−4 | 3.27 × 10−2 | 3.53 × 10−4 | 1.20 × 10−4 | 2.67 × 10−4 | 1.46 × 10−4 | 4.07 × 10−4 | 6.00 × 10−4 | 4.71 × 10−5 |
| avg | 3.61 × 10−4 | 6.82 × 10−2 | 8.02 × 10−4 | 1.01 × 10−4 | 1.80 × 10−4 | 1.81 × 10−4 | 5.35 × 10−4 | 9.36 × 10−4 | 6.63 × 10−5 |
| median | 2.88 × 10−4 | 6.53 × 10−2 | 7.26 × 10−4 | 6.58 × 10−5 | 7.89 × 10−5 | 1.56 × 10−4 | 3.96 × 10−4 | 7.37 × 10−4 | 6.46 × 10−5 |
| worse | 1.07 × 10−3 | 0.16 | 1.71 × 10−3 | 5.78 × 10−4 | 1.31 × 10−3 | 6.57 × 10−4 | 1.69 × 10−3 | 2.32 × 10−3 | 1.91 × 10−4 |
| time | 0.21 | 0.17 | 0.22 | 0.32 | 0.27 | 0.21 | 0.18 | 0.15 | 0.49 |
| F8 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −9.03 × 103 | −8.72E×103 | −8.03E×103 | −1.26 × 104 | −1.17 × 104 | −1.14 × 104 | −1.22 × 104 | −1.26 × 104 | −1.26 × 104 |
| std | 5.13 × 102 | 7.34 × 102 | 7.06 × 102 | 5.68 × 102 | 1.63 × 103 | 1.36 × 103 | 1.79 × 103 | 2.96 × 102 | 6.82 × 102 |
| avg | −8.05 × 103 | −7.24 × 103 | −6.25 × 103 | −1.24 × 104 | −8.88 × 103 | −9.01 × 103 | −7.54 × 103 | −1.21 × 104 | −1.16 × 104 |
| median | −8.08 × 103 | −7.23 × 103 | −6.07 × 103 | −1.26 × 104 | −8.93E+03 | −9.00 × 103 | −7.11 × 103 | −1.21 × 104 | −1.17 × 104 |
| worse | −7.05 × 103 | −5.40 × 103 | −4.90 × 103 | −9.50 × 103 | −5.13 × 103 | −5.28 × 103 | −5.50 × 103 | −1.14 × 104 | −1.02 × 104 |
| time | 0.16 | 7.31 × 10−2 | 0.14 | 0.14 | 0.10 | 0.13 | 0.11 | 9.79 × 10−2 | 0.32 |
| F9 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 65.90 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 37.02 | 2.17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| avg | 0.00 | 1.50 × 102 | 0.72 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| median | 0.00 | 1.54 × 102 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| worse | 0.00 | 2.26 × 102 | 8.81 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| time | 0.10 | 7.29 × 10−2 | 0.12 | 0.11 | 6.79 × 10−2 | 0.10 | 7.96 × 10−2 | 5.89 × 10−2 | 0.26 |
| F10 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 4.44 × 10−16 | 3.37 × 10−2 | 1.11 × 10−14 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 |
| std | 0.00 | 9.13 | 2.63 × 10−15 | 0.00 | 0.00 | 5.05 | 0.00 | 0.00 | 0.00 |
| avg | 4.44 × 10−16 | 11.92 | 1.56 × 10−14 | 4.44 × 10−16 | 4.44 × 10−16 | 1.33 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 |
| median | 4.44 × 10−16 | 18.92 | 1.47 × 10−14 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 |
| worse | 4.44 × 10−16 | 19.43 | 2.18 × 10−14 | 4.44 × 10−16 | 4.44 × 10−16 | 19.92 | 4.44 × 10−16 | 4.44 × 10−16 | 4.44 × 10−16 |
| time | 9.97 × 10−2 | 7.06 × 10−2 | 0.10 | 0.10 | 6.95 × 10−2 | 0.12 | 0.14 | 8.20 × 10−2 | 0.29 |
| F11 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 9.32 × 10−5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 1.42 × 102 | 7.94 × 10−3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| avg | 0.00 | 1.36 × 102 | 4.00 × 10−3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| median | 0.00 | 1.04 × 102 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| worse | 0.00 | 3.69 × 102 | 2.84 × 10−2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| time | 0.13 | 8.09 × 10−2 | 0.15 | 0.15 | 9.78 × 10−2 | 0.13 | 0.11 | 7.08 × 10−2 | 0.27 |
| F12 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 2.34 × 10−18 | 3.61 | 1.93 × 10−2 | 6.03 × 10−9 | 3.33 × 10−6 | 4.27 × 10−10 | 1.80 × 10−2 | 3.86 × 10−13 | 2.50 × 10−9 |
| std | 1.80 × 10−13 | 5.81 | 2.09 × 10−2 | 2.64 × 10−6 | 0.26 | 9.17 × 10−8 | 0.10 | 4.02 × 10−12 | 1.72 × 10−8 |
| avg | 4.47 × 10−14 | 11.38 | 4.55 × 10−2 | 2.14 × 10−6 | 0.17 | 4.15 × 10−8 | 0.27 | 3.29 × 10−12 | 1.71 × 10−8 |
| median | 5.34 × 10−16 | 9.52 | 3.87 × 10−2 | 8.77 × 10−7 | 2.02 × 10−2 | 5.60 × 10−9 | 0.28 | 2.32 × 10−12 | 1.22 × 10−8 |
| worse | 9.83 × 10−13 | 26.37 | 0.10 | 1.11 × 10−5 | 0.93 | 4.54 × 10−7 | 0.45 | 2.15 × 10−11 | 9.53 × 10−8 |
| time | 0.37 | 0.27 | 0.32 | 0.61 | 0.49 | 0.32 | 0.29 | 0.28 | 0.65 |
| F13 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 1.34 × 10−16 | 5.20 × 10−4 | 0.21 | 1.07 × 10−7 | 0.39 | 8.57 × 10−8 | 1.14 × 10−2 | 9.63 × 10−12 | 8.71 × 10−8 |
| std | 5.16 × 10−13 | 5.27 × 10−3 | 0.18 | 3.09 × 10−5 | 0.47 | 7.66 × 10−2 | 1.19 | 1.00 × 10−2 | 2.63 × 10−2 |
| avg | 2.04 × 10−13 | 4.29 × 10−3 | 0.52 | 1.79 × 10−5 | 1.40 | 7.19 × 10−2 | 1.27 | 1.83 × 10−3 | 9.30 × 10−3 |
| median | 2.50 × 10−14 | 1.00 × 10−3 | 0.47 | 6.62 × 10−6 | 1.48 | 7.07 × 10−2 | 0.65 | 3.66 × 10−11 | 1.13 × 10−5 |
| worse | 2.7 × 10−12 | 1.27 × 10−2 | 0.95 | 1.61 × 10−4 | 2.99 | 0.34 | 2.81 | 5.48 × 10−2 | 0.11 |
| time | 0.37 | 0.27 | 0.32 | 0.61 | 0.50 | 0.32 | 0.29 | 0.29 | 0.66 |
| F14 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 1.00 | 1.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| std | 5.81 | 5.50 | 3.64 | 0.30 | 0.75 | 0.65 | 0.93 | 0.00 | 0.89 |
| avg | 7.23 | 11.72 | 4.14 | 1.10 | 1.20 | 1.30 | 1.86 | 1.00 | 1.53 |
| median | 11.71 | 12.19 | 2.98 | 1.00 | 1.00 | 1.00 | 1.53 | 1.00 | 1.00 |
| worse | 12.67 | 22.90 | 12.67 | 1.99 | 4.95 | 2.98 | 2.98 | 1.00 | 2.98 |
| time | 0.53 | 0.40 | 0.39 | 0.97 | 0.76 | 0.41 | 0.44 | 0.43 | 0.92 |
| F15 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 3.07 × 10−4 | 3.08 × 10−4 | 3.07 × 10−4 | 3.08 × 10−4 | 3.07 × 10−4 | 3.07 × 10−4 | 3.08 × 10−4 | 3.07 × 10−4 | 3.07 × 10−4 |
| std | 1.19 × 10−6 | 9.76 × 10−3 | 7.60 × 10−3 | 2.35 × 10−4 | 6.10 × 10−3 | 8.37 × 10−3 | 2.35 × 10−4 | 5.50 × 10−18 | 2.57 × 10−4 |
| avg | 3.08 × 10−4 | 9.44 × 10−3 | 3.65 × 10−3 | 3.97 × 10−4 | 2.39 × 10−3 | 4.69 × 10−3 | 4.90 × 10−4 | 3.07 × 10−4 | 4.83 × 10−4 |
| median | 3.07 × 10−4 | 1.33 × 10−3 | 3.08 × 10−4 | 3.31 × 10−4 | 3.07 × 10−4 | 3.07 × 10−4 | 4.08 × 10−4 | 3.07 × 10−4 | 3.29 × 10−4 |
| worse | 3.14 × 10−4 | 2.04 × 10−2 | 2.04 × 10−2 | 1.28 × 10−3 | 2.04 × 10−2 | 2.26 × 10−2 | 1.23 × 10−3 | 3.07 × 10−4 | 1.22 × 10−3 |
| time | 8.14 × 10−2 | 4.76 × 10−2 | 3.12 × 10−2 | 6.66 × 10−2 | 5.74 × 10−2 | 7.54 × 10−2 | 7.24 × 10−2 | 6.38 × 10−2 | 0.17 |
| F16 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| std | 5.83 × 10−16 | 0.62 | 1.46 × 10−8 | 1.61 × 10−11 | 6.39 × 10−16 | 6.32 × 10−16 | 8.91 × 10−16 | 6.78 × 10−16 | 6.65 × 10−16 |
| avg | −1.03 | −0.82 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| median | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| worse | −1.03 | 2.10 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| time | 8.26 × 10−2 | 4.53 × 10−2 | 2.64 × 10−2 | 6.87 × 10−2 | 4.79 × 10−2 | 5.74 × 10−2 | 6.77 × 10−2 | 5.46 × 10−2 | 0.16 |
| F17 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 |
| std | 0.00 | 8.12 × 10−11 | 4.32 × 10−5 | 2.17 × 10−6 | 0.00 | 0.00 | 6.27 × 10−6 | 0.00 | 0.85 |
| avg | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.55 |
| median | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 |
| worse | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 5.04 |
| time | 7.22 × 10−2 | 3.76 × 10−2 | 1.73 × 10−2 | 4.84 × 10−2 | 3.18 × 10−2 | 4.98 × 10−2 | 5.98 × 10−2 | 5.15 × 10−2 | 0.14 |
| F18 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 3.00 | 3.00 | 3.00 | 2.99 | 3.00 | 3.00 | 3.00 | 3.00 | 2.99 |
| std | 4.93 | 21.45 | 14,79 | 2.22 × 10−8 | 1.53 × 10−15 | 1.61 × 10−15 | 7.95 × 10−3 | 2.07 × 10−15 | 7.14 × 10−16 |
| avg | 3.90 | 11.10 | 5.70 | 3.00 | 3.00 | 2.99 | 3.00 | 3.00 | 2.99 |
| median | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 2.99 | 3.00 | 3.00 | 2.99 |
| worse | 30.00 | 84.00 | 84.00 | 3.00 | 3.00 | 3.00 | 3.04 | 3.00 | 2.99 |
| time | 7.12 × 10−2 | 3.73 × 10−2 | 1.59 × 10−2 | 4.47 × 10−2 | 2.63 × 10−2 | 4.06 × 10−2 | 5.02 × 10−2 | 4.50 × 10−2 | 0.14 |
| F19 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| std | 2.51 × 10−15 | 0.14 | 2.21 × 10−3 | 9.55 × 10−4 | 2.51 × 10−15 | 2.99 × 10−3 | 1.71 × 10−3 | 2.71 × 10−15 | 2.71 × 10−15 |
| avg | −3.86 | −3.84 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| median | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| worse | −3.86 | −3.09 | −3.85 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| time | 8.81 × 10−2 | 4.55 × 10−2 | 3.19 × 10−2 | 7.41 × 10−2 | 5.28 × 10−2 | 6.42 × 10−2 | 7.41 × 10−2 | 6.31 × 10−2 | 0.16 |
| F20 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −3.32 | −3.32 | −3.32 | −3.32 | −3.32 | −3.32 | −3.32 | −3.32 | −3.32 |
| std | 6.03 × 10−2 | 6.11 × 10−2 | 8.29 × 10−2 | 8.94 × 10−2 | 5.71 × 10−2 | 9.29 × 10−2 | 9.37 × 10−2 | 1.34 × 10−15 | 5.83 × 10−2 |
| avg | −3.26 | −3.26 | −3.26 | −3.19 | −3.28 | −3.26 | −3.08 | −3.32 | −3.29 |
| median | −3.20 | −3.20 | −3.32 | −3.18 | −3.32 | −3.32 | −3.08 | −3.32 | −3.32 |
| worse | −3.20 | −3.20 | −3.02 | −2.99 | −3.20 | −3.02 | −2.84 | −3.32 | −3.14 |
| time | 9.11 × 10−2 | 4.92 × 10−2 | 4.20 × 10−2 | 7.77 × 10−2 | 5.89 × 10−2 | 6.52 × 10−2 | 6.81 × 10−2 | 6.29 × 10−2 | 0.16 |
| F21 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −10.15 | −10.15 | −10.15 | −10.15 | −10.15 | −10.15 | −10.15 | −10.15 | −10.15 |
| std | 1.56 | 3.37 | 1.92 | 1.29 | 2.71 × 10−7 | 2.49 | 1.93 | 6.96 × 10−15 | 6.90 × 10−15 |
| avg | −9.64 | −5.64 | −9.31 | −5.39 | −10.15 | −9.34 | −5.96 | −10.15 | −10.15 |
| median | −10.15 | −5.06 | −10.15 | −5.06 | −10.15 | −10.15 | −5.06 | −10.15 | −10.15 |
| worse | −5.06 | −2.63 | −5.06 | −5.05 | −10.15 | −0.88 | −5.06 | −10.15 | −10.15 |
| time | 8.26 × 10−2 | 4.60 × 10−2 | 3.35 × 10−2 | 7.45 × 10−2 | 5.63 × 10−2 | 5.98 × 10−2 | 6.65 × 10−2 | 6.86 × 10−2 | 0.15 |
| F22 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −10.40 | −10.40 | −10.40 | −10.30 | −10.40 | −10.40 | −10.40 | −10.40 | −10.40 |
| std | 1.62 | 3.07 | 3.18 × 10−4 | 0.95 | 5.00 × 10−5 | 3.29 | 2.39 | 1.35 | 1.04 × 10−15 |
| avg | −9.87 | −4.69 | −10.40 | −5.26 | −10.40 | −8.46 | −6.51 | −10.05 | −10.40 |
| median | −10.40 | −3.25 | −10.40 | −5.09 | −10.40 | −10.40 | −5.09 | −10.40 | −10.40 |
| worse | −5.09 | −1.84 | −10.40 | −5.08 | −10.40 | −1.84 | −5.09 | −5.09 | −10.40 |
| time | 8.83 × 10−2 | 5.05 × 10−2 | 3.84 × 10−2 | 8.57 × 10−2 | 6.44 × 10−2 | 6.46 × 10−2 | 7.17 × 10−2 | 7.42 × 10−2 | 0.16 |
| F23 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | −10.54 | −10.54 | −10.54 | −5.13 | −10.54 | −10.54 | −10.54 | −10.54 | −10.54 |
| std | 1.65 | 3.66 | 2.76 × 10−4 | 4.62 × 10−3 | 0.431 | 2.57 | 2.51 | 1.98 × 10−15 | 2.06 × 10−15 |
| avg | −10.00 | −5.11 | −10.54 | −5.13 | −10.54 | −9.55 | −6.75 | −10.54 | −10.54 |
| median | −10.54 | −2.87 | −10.54 | −5.13 | −10.54 | −10.54 | −5.13 | −10.54 | −10.54 |
| worse | −5.13 | −1.68 | −10.54 | −5.10 | −8.17 | −2.42 | −5.13 | −10.54 | −10.54 |
| time | 9.76 × 10−2 | 5.75 × 10−2 | 4.60 × 10−2 | 0.10 | 7.93 × 10−2 | 7.23 × 10−2 | 7.94 × 10−2 | 8.46 × 10−2 | 0.18 |
| F1 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 1.68 × 10−301 | 6.88 | 4.67 × 10−117 | 7.80 × 10−213 | 2.13 × 10−201 | 0.00 | 0.00 | 1.02 × 10−119 | 0.00 |
| std | 2.10 × 10−52 | 2.75 × 103 | 1.95 × 10−110 | 0.00 | 4.94 × 10−160 | 0.00 | 0.00 | 2.62 × 10−88 | 0.00 |
| avg | 3.86 × 10−53 | 1.91 × 103 | 3.93 × 10−111 | 5.03 × 10−178 | 9.02 × 10−161 | 1.70 × 10−315 | 0.00 | 4.80 × 10−89 | 0.00 |
| median | 1.84 × 10−86 | 5.57 × 102 | 9.11 × 10−114 | 1.84 × 10−192 | 2.97 × 10−194 | 0.00 | 0.00 | 2.29 × 10−100 | 0.00 |
| worse | 1.15 × 10−51 | 9.15 × 103 | 1.07 × 10−109 | 1.42 × 10−176 | 2.70 × 10−159 | 5.09 × 10−314 | 0.00 | 1.43 × 10−87 | 0.00 |
| time | 0.12 | 6.97 × 10−2 | 7.44 × 10−2 | 9.94 × 10−2 | 9.19 × 10−2 | 0.10 | 0.10 | 8.03 × 10−2 | 0.24 |
| F2 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 3.90 × 10−5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| std | 1.66 × 10−13 | 7.53 × 102 | 3.12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| avg | 3.03 × 10−14 | 8.63 × 102 | 1.19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| median | 0.00 | 9.57 × 102 | 9.09 × 10−13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| worse | 9.09 × 10−13 | 2.30 × 103 | 16.23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| time | 0.11 | 7.11 × 10−2 | 7.18 × 10−2 | 0.13 | 9.95 × 10−2 | 9.22 × 10−2 | 9.35 × 10−2 | 8.02 × 10−2 | 0.20 |
| F3 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 2.25 × 102 | 14.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| avg | 0.00 | 2.74 × 102 | 25.91 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| median | 0.00 | 3.32 × 102 | 26.89 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| worse | 0.00 | 6.26 × 102 | 60.32 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| time | 0.11 | 6.77 × 10−2 | 6.93 × 10−2 | 0.13 | 9.79 × 10−2 | 9.06 × 10−2 | 8.90 × 10−2 | 7.96 × 10−2 | 0.21 |
| F4 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 5.00 × 10−2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 8.25 | 0.66 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| avg | 0.00 | 9.03 | 0.52 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| median | 0.00 | 9.87 | 0.28 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| worse | 0.00 | 24.34 | 2.39 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| time | 0.11 | 6.61 × 10−2 | 6.82 × 10−2 | 0.13 | 9.56 × 10−2 | 9.01 × 10−2 | 8.84 × 10−2 | 7.48 × 10−2 | 0.20 |
| F5 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 1.48 × 10−323 | 54.75 | 9.25 × 10−39 | 5.12 × 10−202 | 1.80 × 10−102 | 8.03 × 10−297 | 0.00 | 1.07 × 10−52 | 0.00 |
| std | 7.54 × 10−17 | 2.45 × 103 | 0.48 | 0.00 | 4.83 × 10−25 | 8.28 × 10−45 | 4.90 × 10−29 | 1.08 × 10−27 | 0.00 |
| avg | 2.51 × 10−17 | 3.31 × 103 | 0.198 | 2.95 × 10−171 | 1.18 × 10−25 | 1.51 × 10−45 | 1.35 × 10−29 | 2.19 × 10−28 | 0.00 |
| median | 2.00 × 10−35 | 2.81 × 103 | 3.75 × 10−32 | 1.84 × 10−190 | 9.87 × 10−42 | 1.34 × 10−118 | 0.00 | 3.21 × 10−30 | 0.00 |
| worse | 3.94 × 10−16 | 7.75 × 103 | 2.13 | 8.83 × 10−270 | 2.55 × 10−24 | 4.53 × 10−44 | 2.17 × 10−28 | 5.93 × 10−27 | 0.00 |
| Time | 0.10 | 6.50 × 10−2 | 6.63 × 10−2 | 9.18 × 10−2 | 9.04 × 10−2 | 8.78 × 10−2 | 8.71 × 10−2 | 8.11 × 10−2 | 0.20 |
| F6 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 1.67 × 10−2 | 7.13 × 10−3 | 0.00 | 0.00 | 4.84 × 10−11 | 0.00 | 0.00 | 0.00 |
| std | 5.01 × 10−8 | 2.51 × 102 | 1.12 | 6.46 × 10−5 | 7.46 × 10−7 | 9.48 × 10−5 | 4.24 × 10−22 | 5.64 × 10−22 | 0.00 |
| avg | 1.44 × 10−8 | 2.10 × 102 | 0.56 | 2.00 × 10−5 | 1.55 × 10−7 | 4.81 × 10−5 | 7.75 × 10−23 | 1.03 × 10−22 | 0.00 |
| median | 8.94 × 10−29 | 35.67 | 4.27 × 10−2 | 1.58 × 10−9 | 9.01 × 10−26 | 5.40 × 10−6 | 0.00 | 0.00 | 0.00 |
| worse | 2.72 × 10−7 | 8.15 × 102 | 4.68 | 3.04 × 10−4 | 4.09 × 10−6 | 3.98 × 10−4 | 2.32 × 10−21 | 3.09 × 10−21 | 0.00 |
| Time | 0.10 | 6.39 × 10−2 | 6.58 × 10−2 | 0.12 | 9.03 × 10−2 | 8.59 × 10−2 | 8.66 × 10−2 | 7.52 × 10−2 | 0.20 |
| F7 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 3.28 | 5.38 × 10−4 | 7.19 × 10−214 | 3.03 × 10−128 | 1.79 × 10−9 | 0.00 | 0.00 | 0.00 |
| std | 4.25 × 10−6 | 2.32 × 103 | 0.36 | 2.77 × 10−6 | 2.81 × 10−6 | 8.73 × 10−4 | 0.00 | 8.04 × 10−8 | 0.00 |
| avg | 8.09 × 10−7 | 2.95 × 103 | 0.14 | 5.41 × 10−7 | 5.40 × 10−9 | 1.84 × 10−4 | 4.04 × 10−296 | 1.91 × 10−8 | 0.00 |
| median | 6.97 × 10−18 | 2.60 × 103 | 1.54 × 10−2 | 3.22 × 10−13 | 2.47 × 10−35 | 8.73 × 10−6 | 0.00 | 4.85 × 10−25 | 0.00 |
| worse | 2.33 × 10−5 | 7.48 × 10−3 | 1.41 | 1.52 × 10−5 | 1.54 × 10−7 | 4.80 × 10−3 | 1.21 × 10−294 | 4.18 × 10−7 | 0.00 |
| time | 0.10 | 6.46 × 10−2 | 6.44 × 10−2 | 0.10 | 8.82 × 10−2 | 8.56 × 10−2 | 8.57 × 10−2 | 8.02 × 10−2 | 0.20 |
| F8 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 1.54 × 10−4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 6.53 × 102 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| avg | 0.00 | 8.71 × 102 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| median | 0.00 | 1.07 × 103 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| worse | 0.00 | 2.03 × 103 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| time | 0.16 | 0.10 | 0.10 | 0.21 | 0.17 | 0.13 | 0.13 | 0.11 | 0.27 |
| F9 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 5.33 × 10−3 | 8.88 × 10−15 | 2.60 × 10−213 | 3.57 × 10−209 | 1.40 × 10−315 | 1.39 × 10−315 | 4.26 × 10−136 | 1.39 × 10−315 |
| std | 1.05 × 10−65 | 43.25 | 0.00 | 0.00 | 1.93 × 10−145 | 0.00 | 0.00 | 1.62 × 10−15 | 0.00 |
| avg | 1.95 × 10−66 | 44.25 | 8.88 × 10−15 | 6.17 × 10−186 | 3.52 × 10−146 | 3.31 × 10−315 | 1.53 × 10−315 | 2.96 × 10−16 | 1.57 × 10−315 |
| median | 1.06 × 10−87 | 66.77 | 8.88 × 10−15 | 2.04 × 10−198 | 1.05 × 10−200 | 1.60 × 10−315 | 1.45 × 10−315 | 1.71 × 10−111 | 1.39 × 10−315 |
| worse | 5.78 × 10−65 | 93.91 | 8.88 × 10−15 | 1.60 × 10−184 | 1.06 × 10−144 | 3.15 × 10−314 | 2.74 × 10−315 | 8.88 × 10−15 | 6.45 × 10−315 |
| time | 0.16 | 0.12 | 0.12 | 0.19 | 0.18 | 0.14 | 0.14 | 0.13 | 0.42 |
| F10 | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
| min | 0.00 | 2.62 × 10−2 | 3.70 × 10−3 | 9.41 × 10−205 | 7.46 × 10−203 | 1.75 × 10−4 | 1.11 × 10−315 | 0.00 | 1.11 × 10−315 |
| std | 1.75 × 10−11 | 56.72 | 17.93 | 5.17 × 10−4 | 1.45 × 10−121 | 2.26 × 10−3 | 0.00 | 3.16 × 10−70 | 0.00 |
| avg | 3.59 × 10−12 | 63.46 | 52.16 | 2.52 × 10−4 | 2.65 × 10−122 | 1.37 × 10−3 | 1.12 × 10−315 | 5.78 × 10−71 | 1.11 × 10−315 |
| median | 6.82 × 10−47 | 77.90 | 49.83 | 3.68 × 10−5 | 1.07 × 10−180 | 8.50 × 10−4 | 1.12 × 10−315 | 5.27 × 10−104 | 1.11 × 10−315 |
| worse | 9.61 × 10−11 | 1.59 × 102 | 78.94 | 2.21 × 10−3 | 7.95 × 10−121 | 1.27 × 10−2 | 1.21 × 10−315 | 1.73 × 10−69 | 1.11 × 10−315 |
| Time | 0.15 | 9.72 × 10−2 | 9.86 × 10−2 | 0.19 | 0.15 | 0.12 | 0.12 | 0.11 | 0.39 |
| Algorithm | Convergence Precision | Stability | Time Efficiency | Application Scenarios |
|---|---|---|---|---|
| BTCPO | ★★★★★ | ★★★★★ | ★★★ | High-precision requirements |
| HHO | ★★★★ | ★★★★ | ★★★★ | Precision-efficiency balanced tasks |
| BKA | ★★★ | ★★★★ | ★★★★ | General optimization problems |
| CPO | ★★ | ★★★ | ★★★★★ | Real-time optimization |
| SSA | ★★ | ★★ | ★★★★ | Simple function optimization |
| GWO | ★ | ★ | ★★★★★ | Low-dimensional fast optimization |
| GOOSE | ★ | ★ | ★★★★★ | Time-sensitive applications |
| HBA | ★ | ★★ | ★★★★ | Function-specific optimization |
| DBO | ★ | ★★★ | ★★★★ | Stability-critical scenarios |
| PSO | ★ | ★★ | ★★★★★ | Control System Tuning |
| ABC | ★★ | ★★ | ★★★★ | Data Clustering and Feature Selection |
| CS | ★★★ | ★★ | ★★★★ | Global Optimization |
| Cantilever Beam | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
|---|---|---|---|---|---|---|---|---|---|
| best | 1.33999 | 1.33998 | 1.33997 | 1.34042 | 1.33996 | 1.33996 | 1.34005 | 1.33996 | 1.33638 |
| worst | 1.34149 | 2.29651 | 1.34032 | 1.35014 | 1.69676 | 1.34000 | 1.34105 | 1.34001 | 1.34094 |
| std | 0.00044 | 0.42851 | 0.00009 | 0.00249 | 0.11282 | 0.00001 | 0.00030 | 0.00002 | 0.00031 |
| mean | 1.34038 | 1.66006 | 1.34011 | 1.34457 | 1.37567 | 1.33997 | 1.34049 | 1.33998 | 1.33843 |
| median | 1.34022 | 1.38819 | 1.34009 | 1.34463 | 1.34000 | 1.33996 | 1.34045 | 1.33998 | 1.33947 |
| time | 0.1694 | 0.1107 | 0.1009 | 0.2864 | 0.2093 | 0.1281 | 0.1333 | 0.1241 | 0.2714 |
| Three-Bar Truss | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
|---|---|---|---|---|---|---|---|---|---|
| best | 263.8959 | 263.8959 | 263.8963 | 263.8959 | 263.8958 | 263.8959 | 263.9045 | 263.8958 | 263.8861 |
| worst | 263.9167 | 263.9017 | 263.9668 | 264.8880 | 263.8963 | 263.8966 | 264.1367 | 263.8958 | 263.9487 |
| std | 0.0068 | 0.0017 | 0.0217 | 0.3051 | 0.0002 | 0.0002 | 0.0682 | 0.0000 | 0.0203 |
| mean | 263.9010 | 263.8972 | 263.9107 | 264.0484 | 263.8960 | 263.8961 | 263.9584 | 263.8958 | 263.9089 |
| median | 263.8988 | 263.8967 | 263.9009 | 263.9362 | 263.8959 | 263.8960 | 263.9307 | 263.8958 | 263.8978 |
| time | 0.1525 | 0.0926 | 0.0740 | 0.2214 | 0.1640 | 0.1023 | 0.1076 | 0.1046 | 0.2315 |
| Welded Beam | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
|---|---|---|---|---|---|---|---|---|---|
| best | 1.6705 | 1.7062 | 1.6714 | 1.7319 | 1.6713 | 1.6702 | 1.7029 | 1.6704 | 1.6702 |
| worst | 2.8517 | 2.2185 | 1.6816 | 2.2129 | 1.6741 | 1.6922 | 1.9857 | 1.6739 | 1.7607 |
| std | 0.4235 | 0.1421 | 0.0029 | 0.1490 | 0.0009 | 0.0085 | 0.1120 | 0.0011 | 0.0330 |
| mean | 1.8902 | 1.9541 | 1.6745 | 1.9070 | 1.6725 | 1.6751 | 1.8294 | 1.6711 | 1.6972 |
| median | 1.6716 | 1.9199 | 1.6737 | 1.8500 | 1.6725 | 1.6709 | 1.8125 | 1.6708 | 1.6852 |
| time | 0.1694 | 0.1107 | 0.1009 | 0.2864 | 0.2093 | 0.1281 | 0.1333 | 0.1241 | 0.2714 |
| Test Value | SSA | GOOSE | GWO | HHO | BKA | HBA | DBO | CPO | BTCPO |
|---|---|---|---|---|---|---|---|---|---|
| best | 158.8050 | 158.8055 | 158.8163 | 158.8165 | 158.8050 | 158.8050 | 159.2591 | 158.8050 | 158.8010 |
| worst | 158.8050 | 182.7366 | 158.8817 | 159.2114 | 158.8341 | 158.8050 | 164.1658 | 158.8050 | 158.8069 |
| std | 0.0000 | 8.1121 | 0.0210 | 0.1479 | 0.0109 | 0.0000 | 1.5201 | 0.0000 | 0.0006 |
| mean | 158.8050 | 164.9084 | 158.8438 | 159.0049 | 158.8182 | 158.8050 | 159.8407 | 158.8050 | 158.8052 |
| median | 158.8050 | 162.4429 | 158.8427 | 158.9946 | 158.8186 | 158.8050 | 159.3697 | 158.8050 | 158.8050 |
| time | 0.0768 | 0.0501 | 0.0373 | 0.1013 | 0.0860 | 0.0735 | 0.0789 | 0.0595 | 0.1415 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, Y.; Cao, L.; Chen, C.; Yue, Y. An Improved Crested Porcupine Optimization Algorithm Incorporating Butterfly Search and Triangular Walk Strategies. Biomimetics 2025, 10, 766. https://doi.org/10.3390/biomimetics10110766
Chen B, Chen Y, Cao L, Chen C, Yue Y. An Improved Crested Porcupine Optimization Algorithm Incorporating Butterfly Search and Triangular Walk Strategies. Biomimetics. 2025; 10(11):766. https://doi.org/10.3390/biomimetics10110766
Chicago/Turabian StyleChen, Binhe, Yaodan Chen, Li Cao, Changzu Chen, and Yinggao Yue. 2025. "An Improved Crested Porcupine Optimization Algorithm Incorporating Butterfly Search and Triangular Walk Strategies" Biomimetics 10, no. 11: 766. https://doi.org/10.3390/biomimetics10110766
APA StyleChen, B., Chen, Y., Cao, L., Chen, C., & Yue, Y. (2025). An Improved Crested Porcupine Optimization Algorithm Incorporating Butterfly Search and Triangular Walk Strategies. Biomimetics, 10(11), 766. https://doi.org/10.3390/biomimetics10110766







