Objective Evaluation of the Somatogravic Illusion from Flight Data of an Airplane Accident
Abstract
1. Introduction
Research on the Somatogravic Illusion
2. Materials and Methods
2.1. Vestibular Models
2.2. Recorded Flight Data
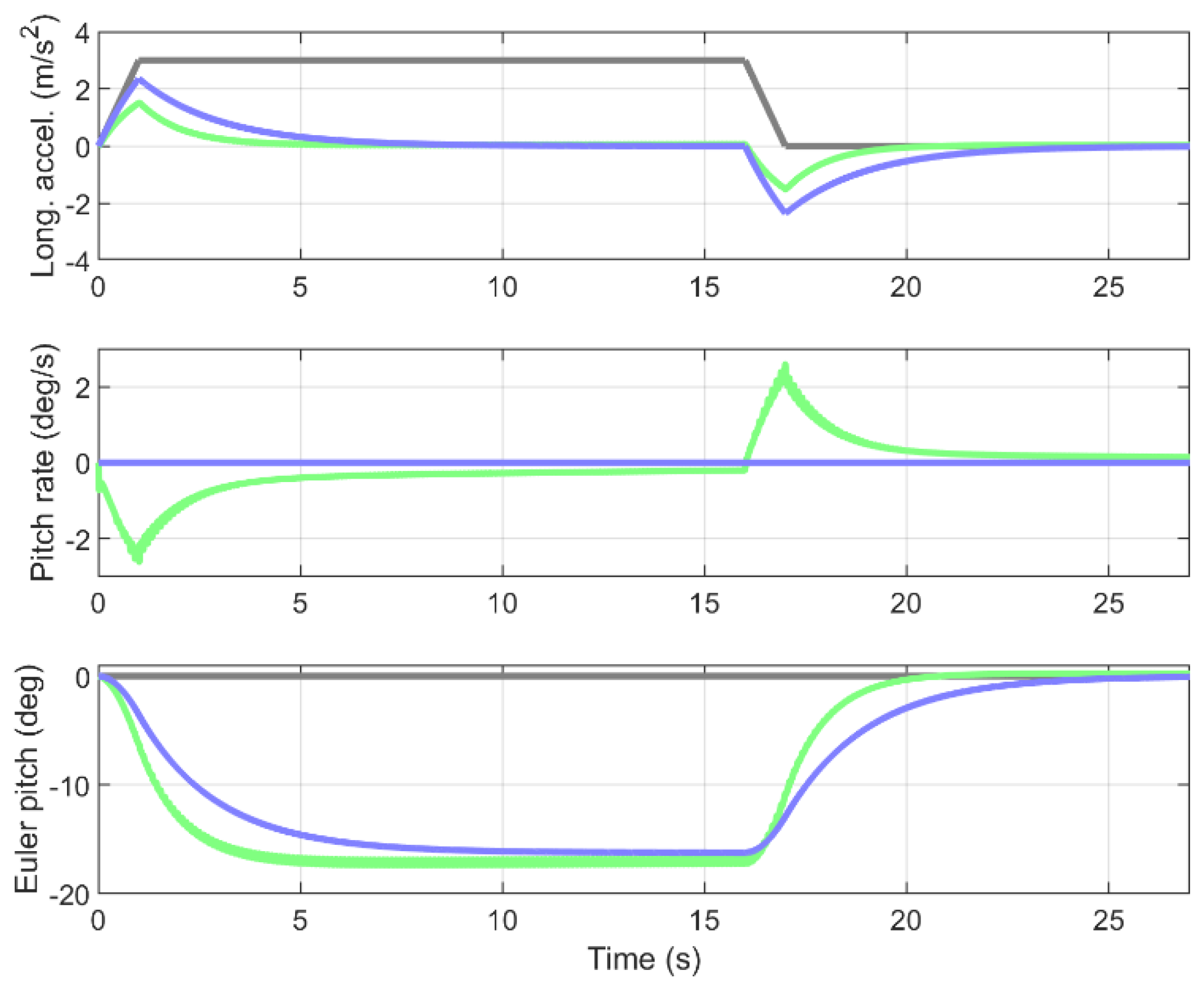
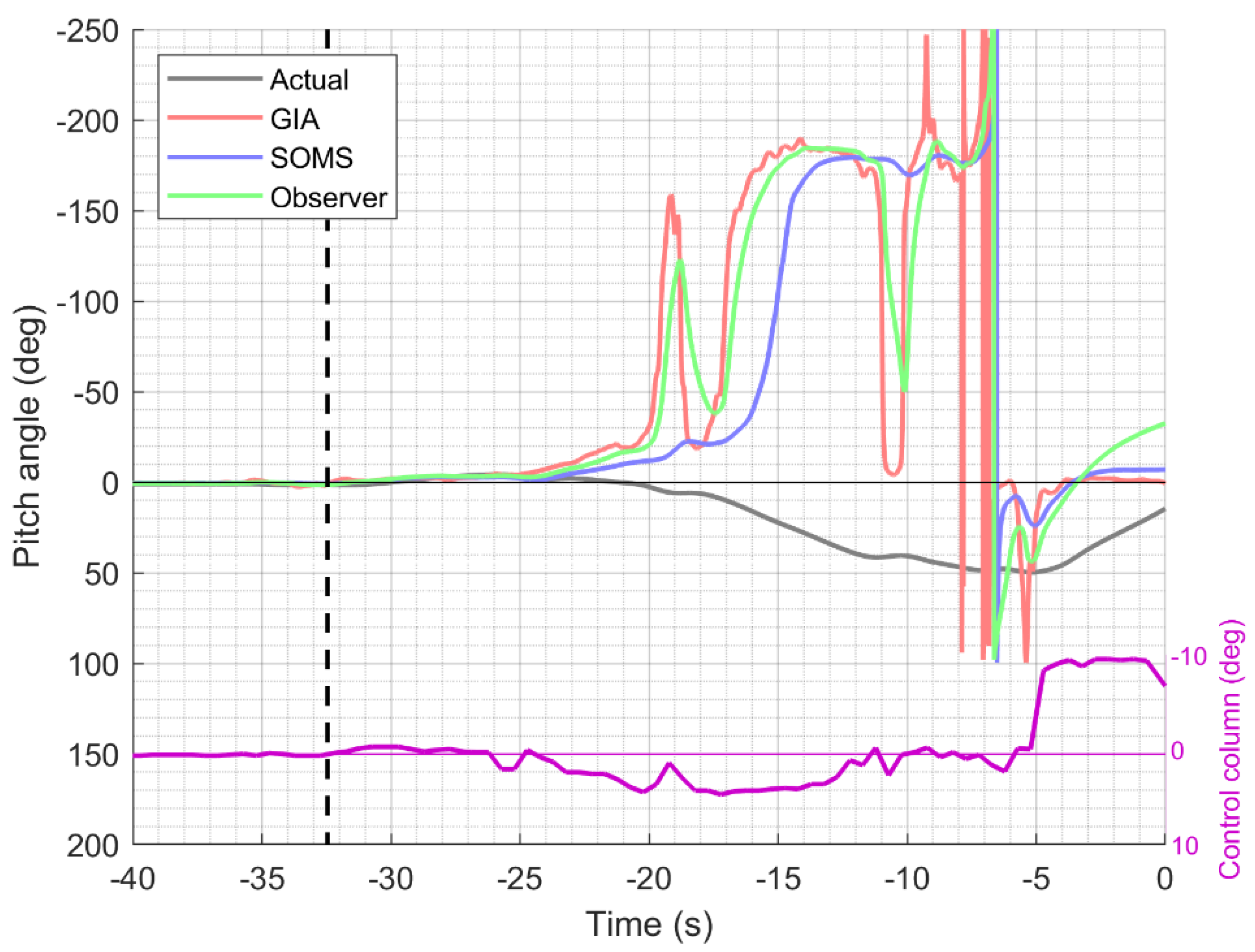
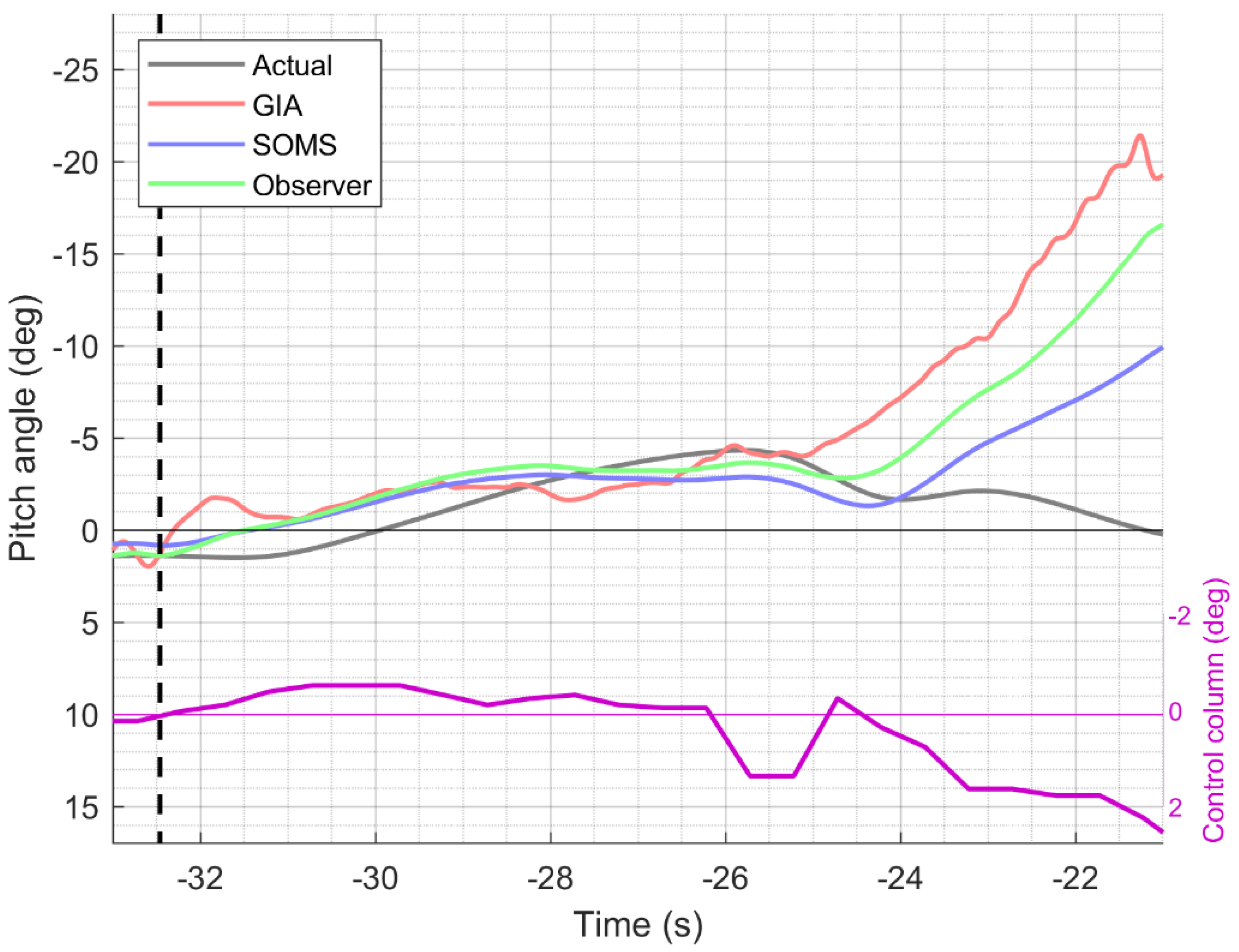
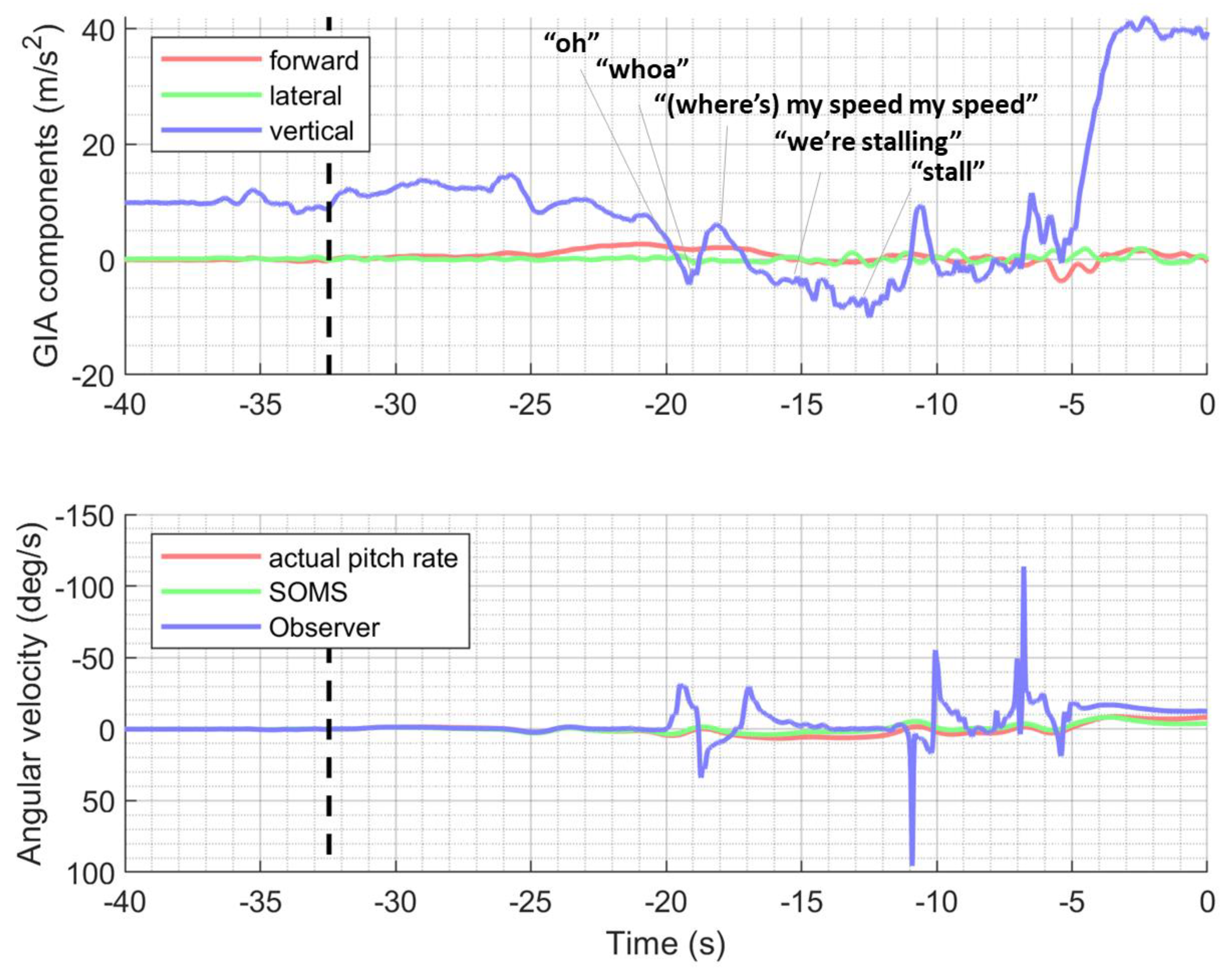
3. Results
3.1. Comparison of Perceived Pitch in Relation to Control Inputs
3.2. Magnitude of the Somatogravic Illusion
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- NTSB. Rapid Descent and Crash into Water, Atlas Air Inc. Flight 3591, Boeing 767-375BCF, N1217A, Trinity Bay, Texas, February 23, 2019; National Transportation Safety Board: Washington, DC, 2020; Contract No.: NTSB AAR-20/02.
- McCarthy, G.W.; Stott, J.R. In flight verification of the inversion illusion. Aviat. Space Environ. Med. 1994, 65, 341–344. [Google Scholar] [PubMed]
- Clark, B.; Graybiel, A. Linear acceleration and deceleration as factors influencing non-visual orientation during flight. J. Aviat. Med. 1949, 20, 92–101. [Google Scholar] [PubMed]
- Buley, L.E.; Spelina, J. Physiological and psychological factors in “the dark night takeoff accident”. Aerosp. Med. 1970, 41, 553–556. [Google Scholar] [PubMed]
- Mumaw, R.J.; Groen, E.L.; Fucke, L.; Anderson, R.; Bos, J.E.; Houben, M.M.J. A New Tool for Analyzing the Potential Influence of Vestibular Illusions; ISASI Forum, January–March 2016, 6–12. Available online: https://www.isasi.org/Documents/library/technical-papers/2015/Vestibular%20Illusion%20Tool.pdf (accessed on 2 August 2022).
- Newman, R.L.; Rupert, A.H. The Magnitude of the Spatial Disorientation Problem in Transport Airplanes. Aerosp. Med. Hum. Perform. 2020, 91, 65–70. [Google Scholar] [CrossRef]
- BEA. Study on Aeroplane State Awareness during Go-Around. Bureau d’Enquêtes et d’Analyses pour la Sécurité de l’Aviation Civile. Paris, France, August 2013. Available online: https://skybrary.aero/bookshelf/study-aeroplane-state-awareness-during-go-around (accessed on 2 August 2022).
- Benson, A.J. Spatial disorientation: Common illusions. In Aviation Medicine, 2nd ed.; Ernsting, J., King, P., Eds.; Butterworths: London, UK, 1988; pp. 297–317. [Google Scholar]
- Bos, J.E.; Bles, W. Theoretical considerations on canal-otolith interaction and an observer model. Biol. Cybern. 2002, 86, 191–207. [Google Scholar] [CrossRef]
- Merfeld, D.M.; Young, L.R.; Oman, C.M.; Shelhamer, M.J. A multidimensional model of the effect of gravity on the spatial orientation of the monkey. J. Vestib. Res. 1993, 3, 141–161. [Google Scholar] [CrossRef]
- Clark, T.K.; Newman, M.C.; Karmali, F.; Oman, C.M.; Merfeld, D.M. Mathematical models for dynamic, multisensory spatial orientation perception. Prog. Brain Res. 2019, 248, 65–90. [Google Scholar]
- Cohen, M.M.; Crosbie, R.J.; Blackburn, L.H. Disorienting effects of aircraft catapult launchings. Aerosp. Med. 1973, 44, 37–39. [Google Scholar]
- Cohen, M.M. Disorienting effects of aircraft catapult launchings. II. Visual and postural contributions. Aviat. Space Environ. Med. 1976, 47, 39–41. [Google Scholar]
- Graybiel, A.; Clark, B. Validity of the oculogravic illusion as a specific indicator of otolith function. Aerosp. Med. 1965, 36, 1173–1181. [Google Scholar]
- Correia Gracio, B.J.; de Winkel, K.N.; Groen, E.L.; Wentink, M.; Bos, J.E. The time constant of the somatogravic illusion. Exp. Brain Res. 2013, 224, 313–321. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Merfeld, D.M.; Park, S.; Gianna-Poulin, C.; Black, F.O.; Wood, S. Vestibular perception and action employ qualitatively different mechanisms. II. VOR and perceptual responses during combined Tilt&Translation. J. Neurophysiol. 2005, 94, 199–205. [Google Scholar] [PubMed]
- Mayne, R. A systems concept of the vestibular organs. In Handbook of Sensory Physiology; Volume VI Vestibular system Part 2: Psychophysics, applied aspects and general interpretations; Kornhuber, H.H., Ed.; Springer: Berlin/Heidelberg, Germany, 1974; pp. 493–580. [Google Scholar]
- St George, R.J.; Day, B.L.; Fitzpatrick, R.C. Adaptation of vestibular signals for self-motion perception. J Physiol. 2011, 589 Pt 4, 843–853. [Google Scholar] [CrossRef]
- Nooij, S.A.; Groen, E.L. Rolling into spatial disorientation: Simulator demonstration of the post-roll (Gillingham) illusion. Aviat. Space Environ. Med. 2011, 82, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Luenberger, D.G. An introduction to observers. IEEE Trans. Autom. Control. 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New Results in Linear Filtering and Prediction Theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Oman, C.M. A heuristic mathematical model for the dynamics of sensory conflict and motion sickness. Acta Otolaryngol. Suppl. 1982, 392, 1–44. [Google Scholar] [CrossRef]
- Cheung, B. Spatial Orientation-Nonvisual Spatial Orientation Mechanisms. In Spatial Disorientation in Aviation. Progress in Astronautics and Aeronautics; Previc, F.H., Ercoline, W.R., Eds.; American Institute of Aeronautics and Astronautics, Inc.: Restoin, VA, USA, 2004; pp. 37–94. [Google Scholar]
- de Winkel, K.N.; Clement, G.; Groen, E.L.; Werkhoven, P.J. The perception of verticality in lunar and Martian gravity conditions. Neurosci. Lett. 2012, 529, 7–11. [Google Scholar] [CrossRef]
- Clark, T.K.; Young, L.R. A Case Study of Human Roll Tilt Perception in Hypogravity. Aerosp. Med. Hum. Perform. 2017, 88, 682–687. [Google Scholar] [CrossRef]
- Soyka, F.; de Winkel, K.; Barnett-Cowan, M.; Groen, E.; Bülthoff, H.H. Integration of Visual and Vestibular Information Used to Discriminate Rotational Self-Motion. i-Perception 2011, 2, 855. [Google Scholar] [CrossRef]
- Clark, T.K.; Newman, M.C.; Oman, C.M.; Merfeld, D.M.; Young, L.R. Human perceptual overestimation of whole body roll tilt in hypergravity. J. Neurophysiol. 2015, 113, 2062–2077. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groen, E.L.; Clark, T.K.; Houben, M.M.J.; Bos, J.E.; Mumaw, R.J. Objective Evaluation of the Somatogravic Illusion from Flight Data of an Airplane Accident. Safety 2022, 8, 85. https://doi.org/10.3390/safety8040085
Groen EL, Clark TK, Houben MMJ, Bos JE, Mumaw RJ. Objective Evaluation of the Somatogravic Illusion from Flight Data of an Airplane Accident. Safety. 2022; 8(4):85. https://doi.org/10.3390/safety8040085
Chicago/Turabian StyleGroen, Eric L., Torin K. Clark, Mark M. J. Houben, Jelte E. Bos, and Randall J. Mumaw. 2022. "Objective Evaluation of the Somatogravic Illusion from Flight Data of an Airplane Accident" Safety 8, no. 4: 85. https://doi.org/10.3390/safety8040085
APA StyleGroen, E. L., Clark, T. K., Houben, M. M. J., Bos, J. E., & Mumaw, R. J. (2022). Objective Evaluation of the Somatogravic Illusion from Flight Data of an Airplane Accident. Safety, 8(4), 85. https://doi.org/10.3390/safety8040085






